buscar Buscar en RED Descartes    

Lunes, 19 Julio 2021 17:16

Primera sesión de la 2ª edición del curso "Edición de libros interactivos"

Escrito por
Valora este artículo
(2 votos)

Primera sesión (16 de julio de 2021)

 

1A. youtube Desarrollo de la primera sesión. Primera sesión en línea.

Descripción   Contenidos temporalizados

Grabación de la primera sesión celebrada el 16 de julio de 2021 dirigida e impartida por el Dr. Rivera vicerrector de la Institución Universitaria Pascual Bravo de Medellín (Colombia) y presidente de RED Descartes Colombia.

 

 

  

 0s: Por error técnico el inicio de la sesión no fue grabado.  

1s: Libros tipo fiipbook.

50s: Primera versión del libro interactivo de RED Descartes.

1m 40s: Segunda versión del libro interactivo de RED Descartes.

2m 5s: Editores de texto plano.

5m 36s: Uso de imágenes en los libros interactivos (ojo con los derechos de autor). Algunos enlaces.

7m 45s: Etiquetas HTML y hojas de estilo (css).

9m 14s: <html>, <head> y <body> y etiquetas de cierre </>. <!DOCTYPE html>.

11m 15s: <head> </head>. Código de la cabecera.

12m 15s: <title></title>. Título en la pestaña del navegador.

12m 41s: <body></body>. Código del cuerpo del libro.

14m 24s: <meta charset="UTF-8">. Codificación de caracteres en UTF-8.

15m 54s: Práctica incial con etiquetas.

16m 45s: <br>. Salto de línea.

17m 55s: <b></b>. Texto en negrita.

19m 10s: Guardar mi primer fichero html y abrirlo en el navegador.

21m 47s: Nos centramos en el cuerpo. Etiqueta <p> </p> de párrafo.

23m 50s: Etiquetas de encabezados a diferente nivel: <h1></h1>, <h2></h2>, <h3></h3>, <h4></h4>.

25m 30s: Texto en cursiva o itálica: <i> </i>.

25m 38s: Edición de nuestro primer libro: Mi_libro.

26m 50s: Cambio de estilo a Mi_libro.

28m 15s: Editar "mi primera página" del libro.

30m 52s: Necesito una nueva página. <div class="page> </div>. Etiqueta comentario <!-- XXXXX -->.

33m 20s: La primera tarea. Edite su libro con dos páginas y practicando con la etiquetas comentadas.

 

1B. youtube Herramientas de edición. Vídeo auxiliar de repaso de los editores de texto plano y primeras etiquetas html.

Descripción   Contenidos temporalizados

Uso de las herramientas de edición para elaborar un libro interactivo. Se parte de una plantilla básica (Mi_libro) que hay que descargar previamente.

Se muestra la edición de Mi_libro con tres editores (Notepad ++, Sublime y Visual Estudio).

Aprendizaje de las primeras etiquetas:

  • Párrafo.
  • División con clase página.
  • Comentario.
  • Sección.
    

10s: La plantilla inicial: Mi_libro.

35s: Descarga del editor html.

1m 30s: Edición de la plantilla del libro interactivo.

4m 0s: Editar la primera página con algunos editores (usted seleccionará el que desee). Uso de la etiqeta párrafo: <p></p>

8m 45s: Incluir más páginas. <div class="page"> </div>. Etiqueta comentario <!-- Comentario -->.

9m 40s: Cambiar el título de una sección del libro (encabezado a segundo nivel) , etiqueta <h2> </h2>
Publicado en RedDescartes
Etiquetado como
¡Escribe el primer comentario!
Leer más ...
Sábado, 17 Julio 2021 17:10

Saludo inicial previo al curso "Edición de libros interactivos"

Escrito por
Valora este artículo
(1 Voto)
 

Saludo inicial

 

0. youtube Vídeo de presentación. Previo al inicio del curso.

Descripción   Contenidos temporalizados
 

En este vídeo damos la bienvenida a los 100 participantes del curso de libros interactivos.

Los enlaces citados en el video son:

    

 10s: Saludos y presentación 

3m 30s: Metodología del curso, objetivos y procedimientos.

6m 30s: Certificaciones del curso.

7m 05s: Elementos mínimos necesarios para comenzar. Herramientas.

9m 35s: Descarga del libro plantilla para realizar las prácticas.

10m: Despedida hasta la primera sesión.

 
Publicado en RedDescartes
Etiquetado como
¡Escribe el primer comentario!
Leer más ...
Sábado, 17 Julio 2021 17:04

Vídeos de la 2ª edición del curso "Edición de libros interactivos" de RED Descartes

Escrito por
Valora este artículo
(10 votos)
 

La segunda edición del curso "Edición de libros interactivos" de la RED Descartes (segundo semestre de 2021) se desarrolló según la siguiente planificación:

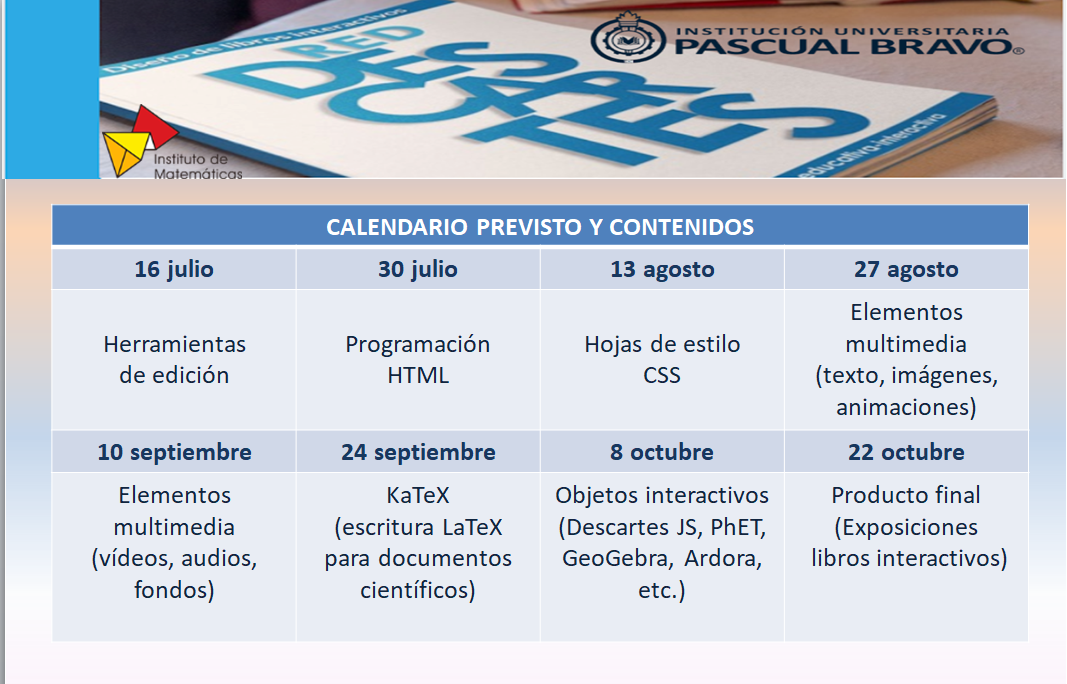
calendario contenidos curso joomla
 
A continuación se enlazan diferentes artículos que incluyen diversos vídeos grabados en las sesiones en línea y que le pueden servir como orientación y guía auxiliar en su autoformación:

 Página inicial curso "Edición de libros interactivos"

 

Publicado en RedDescartes
Etiquetado como
1 comentario
Leer más ...
Sábado, 17 Julio 2021 14:14

Curso "Edición de libros interactivos" de la RED Descartes (2ª edición en línea)

Escrito por
Valora este artículo
(11 votos)
 
Para la formación en la "Edición de libros interactivos" de la RED Descartes, acción que se enmarca en nuestro programa de Educación Abierta, el recurso básico con el que contamos es, como no podía ser otro, el siguiente libro interactivo:
 

Curso Libros interactivos

    Curso de libros interactivos
   Autor: Juan Guillermo Rivera Berrío y Joel Espinosa Longi.
   ISBN 978-958-52963-8-1

Este curso tiene como objetivo abordar la conceptualización y el diseño, desarrollo y experimentación de nuevos libros, basados en la interactividad, que permitan poner de manifiesto que es posible dar una respuesta positiva y asequible a los retos educativos intrínsecos al paradigma educativo emergente (Proyecto iCartesiLibri). 

 
¿Qué necesita para editar su libro interactivo?
 
Lo fundamental es la necesidad de comunicar un contenido y lo colateral conocer el soporte o continente en el que va a volcar ese contenido. Aquí nos centramos en enseñarle el continente y usted, conociendo qué se puede hacer, es quien lo hará. 
Los libros interactivos de RED Descartes se construyen sobre una plantilla que interpretada por una librería javascript y combinada con unas hojas de estilo muestra adecuada, útil y vistosamente lo que se le ha indicado. Esa plantilla está elaborada en HTML y css, pero no necesita ser un experto en estos códigos, basta ser un mero aprendiz o principiante lector de esos lenguajes para conseguir su objetivo. Gran parte de su trabajo se reducirá a escribir en los huecos predefinidos en la plantilla o a copiar y pegar determinadas etiquetas. Así pues, que la técnica no le asuste, ¡será capaz de construir su libro! sin más que poner un poquito de atención y algo de esfuerzo y dedicación. A medida que se adentre verá que lo que le decimos es cierto y a medida que profundice logrará mejorar la vistosidad de su libro.  
 
Prepare las herramientas (puede ver este vídeo)
 
  1. La plantilla o plantillas del libro interactivo. Acceda, mire, observe y descargue la plantilla que vaya a usar.
    En el curso se comienza con una plantilla básica (Mi_libro) que puede ver aquí y también descargarla desde acá.
  2. Necesita un editor de texto plano para poder editar ficheros en código html, puede ser el bloc de notas de Windows o TextEdit de iOS, pero le recomendamos Notepad++ o Sublime text porque estos colorean las etiquetas y faclitan la edición. Por favor, descargue el que vaya a usar.

 Comience su auto-formación

Lea e interactúe con el libro "Curso de libros interactivos", antes enlazado. También puede descargarlo.

¿Alguna ayuda adicional?

  1. Puede escribirnos a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
  2. Puede inscribirse a los cursos de formación en línea cuando se convoquen (ver convocatoria de la segunda edición).
  3. Puede consultar los vídeos grabados en las sesiones de la segunda edición del curso en línea que ha sido promovido por la Institución Universitaria Pascual Bravo (IUPB) de Medellín (Colombia), por RED Descartes de Colombia y RED Descartes España y que está dirigido e impartido por el Dr. Rivera, vicerrector de la IUPB y presidente de la RED Descartes de Colombia.

 

Vídeos de la segunda edición en línea del curso "Edición de libros interactivos"

videoscurso
(Pulse sobre la imagen)


 La editorial "Red Educativa Digital Descartes"
 
La Red Educativa Digital Descartes también desarrolla su labor como editorial de libros interactivos. Nos ofrecemos a los autores de libros de este tipo para publicar su trabajo bajo nuestro sello editorial. Si ése es su deseo, puede contactar con nosotros en la dirección de correo:
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.. 
 
Publicado en RedDescartes
Etiquetado como
¡Escribe el primer comentario!
Leer más ...
Página 10 de 13

Utilizamos cookies para mejorar nuestro sitio web y su experiencia al usarlo. Las cookies utilizadas para el funcionamiento esencial de este sitio ya se han establecido. Para saber más sobre las cookies que utilizamos y cómo eliminarlas , consulte nuestra Política de Privacidad.

  Acepto las Cookies de este sitio.
EU Cookie Directive Module Information