
Publicación electrónica seriada anual. ISSN: 2952-3117.
Editorial: Red Educativa Digital Descartes. Córdoba (España)
En cada número de esta publicación se recogen todos los recursos de RED Descartes, en formato descargable, para que el usuario pueda instalarlos en su sistema informático local y, si lo desea, trabaje sin conexión a Internet. Estos recursos se organizan en subproyectos que agrupan a los que cuentan con una estructura funcional común y unos contenidos ligados a un nivel educativo concreto o aquellos que tienen una finalidad educativa particular.
Todos los recursos interactivos y los contenidos de esta obra colectiva están protegidos por la Ley de Propiedad Intelectual
2ª época. Publicación electrónica. ISSN: 2952-3117. Año 2023 y siguientes.
Año 2026
| Vol. IV, enero de 2026 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Año 2025
| Vol. III, enero de 2025 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vol. II, enero de 2024 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vol. I, enero de 2023 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1ª época: Publicación en DVD. ISSN: 2444-9180 Dep. Legal: CO-2079-2015. Años 2016-2022. | ||
| Vol. VII, enero de 2022 | ||
 |
||
| Vol. VI, enero de 2021 | Vol. V, enero de 2020 | |
 |
 |
|
| Vol. VI - Núm. 1, Núm. 2 y Núm. 3 | Vol. V - Núm. 1, Núm. 2 y Núm. 3 | |
| Vol. IV, enero de 2019 | Vol. III, enero de 2018 | |
 |
 |
|
| Vol. IV - Núm. 1, Núm. 2 y Núm. 3 | Vol. III - Núm. 1 y Núm. 2 | |
| Vol. II, enero de 2017 | Vol. I, enero de 2016 | |
 |
 |
|
| Vol. II - Núm. 1, Núm. 2 y Núm. 3 | Vol. I - Núm. 1, Núm. 2 y Núm. 3 | |
Cuarta sesión del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezCuarta sesión (10 de diciembre de 2021)
|
1A.
|
Tercera sesión del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezTercera sesión (3 de diciembre de 2021)
|
1A.
|
Segunda sesión del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezSegunda sesión (26 de noviembre de 2021)
|
1A.
|
Más...
Primera sesión del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezPrimera sesión (19 de noviembre de 2021)
|
1A.
|
Vídeos de la 2ª edición del curso "Edición de objetos interactivos con DescartesJS"
Escrito por José R. Galo SánchezLa segunda edición del curso "Edición de objetos interactivos con Descartes JS" de la RED Descartes se desarrolló desde el 19 de noviembre de 2021 al 6 de febrero de 2022, según la siguiente planificación:
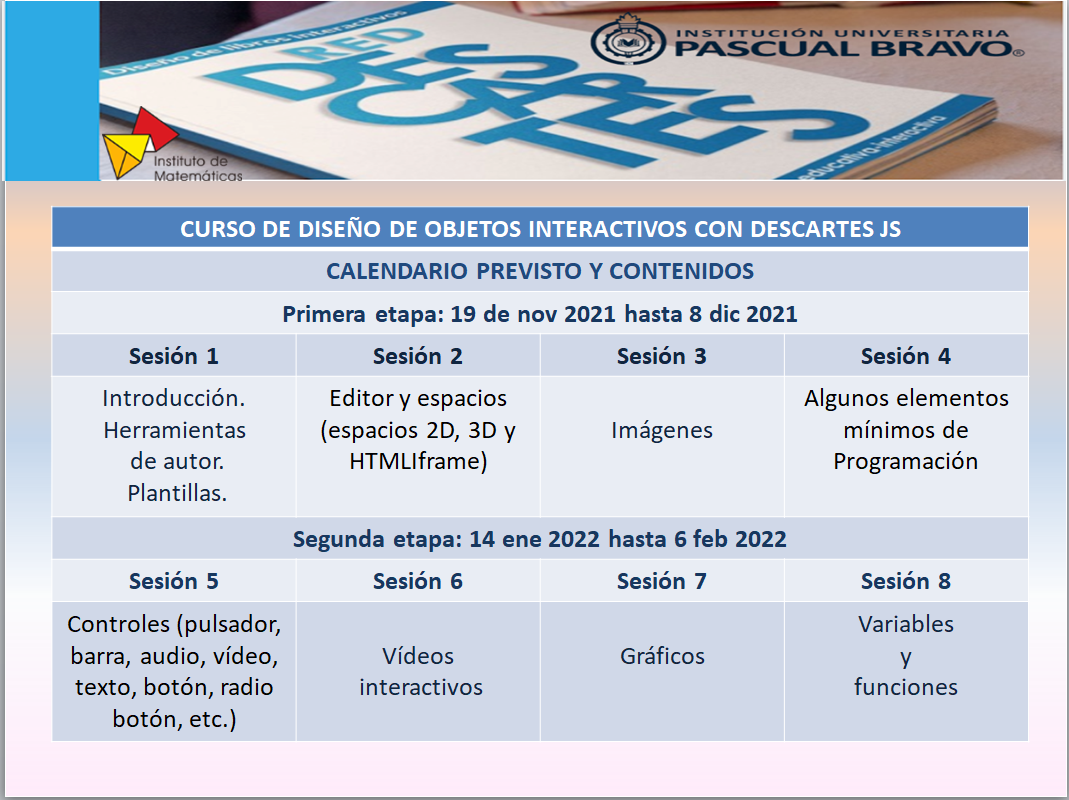
Con una metodología basada en la denominada clase invertida, cada participante recibe con antelación los contenidos a tratar en cada sesión, para que pueda tomar contacto con los mismos, familiarizarse con el editor de escenas, realizar sencillas prácticas y terminar aclarando y consultando dudas durante el desarrollo de la sesión, que será grabada y divulgada poseriormente en el portal de RED Descartes.
- Primera sesión (19 de noviembre de 2021).
- Segunda sesión (26 de noviembre de 2021).
- Tercera sesión (3 de diciembre de 2021).
- Cuarta sesión (10 de diciembre de 2021).
- Quinta sesión (14 de enero de 2022).
- Sexta sesión (21 de enero de 2022).
- Séptima sesión (28 de enero de 2022).
- Octava y última sesión (4 de febrero de 2022).
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)


 CONTACTO
CONTACTO
