|
Acceder a todos los materiales
Ciencias computacionales |
| Descarga | ||
|
|
Tipos de datos y variables
.
|
|
|
|
Algoritmos de ordenamiento
Área: Matemáticas, Informática, Computación |
|
 |
Lógica digital
Área: Matemáticas, Informática, Computación |
|
 |
Lógica digital 2
Área: Matemáticas, Informática, Computación |
|
|
Lógica proposicional
.
|
|
|
|
Diagramas de Carroll y mapas de Karnaugh
* Representar, en un diagrama de Carroll, dos, tres o cuatro atributos. Área: Matemáticas, Informática, Computación |
|
 |
Fundamentos de Programación: Conceptos
Área: Matemáticas, Informática, Computación |
|
 |
Diseño de bases de datos
.
|
|
 |
Mantenimiento Preventivo y predictivo de hardware
Área: Matemáticas, Informática, Computación Nivel: Ingeniería y Tecnología Informática Autor: Carlos Miguel Benitez Grandett |
|
Estática |
| Descarga | ||
|
|
Centroides de áreas planas
|
|
|
|
Momento de inercia de una superficie
|
|
|
|
Momento de una fuerza respecto a un punto
|
|
|
|
Estática de una partícula
|
|
|
|
Fuerzas distribuidas
|
|
|
|
Equilibrio de cuerpo rígido
* Dibujar el diagrama de cuerpo libre de un cuerpo rígido. |
|
|
|
Fuerzas internas
Determinar las fuerzas internas que actúan en un punto cualquiera de un elemento estructural. |
|
Mecánica de materiales |
| Descarga | ||
|
|
Esfuerzo por flexión en vigas
Una viga es un elemento estructural que se somete a cargas que actúan transversalmente al eje longitudinal, originando deformaciones y esfuerzos internos. Es importante, para el diseño de estos elementos, comprender el concepto de flexión, la curva elástica generada y cómo se determinan las deformaciones y esfuerzos internos. Esta unidad puede ayudar a comprender el concepto de flexión en una viga sometida a cargas externas y a calcular los esfuerzos por flexión. |
|
 |
Esfuerzos en secciones inclinadas: círculo de Mohr Miscelánea Se presentan dos escenas para el cálculo de esfuerzos en secciones inclinadas. La primera corresponde a esfuerzos producidos por una fuerza axial, la segunda es el círculo de Mohr, que permite la comparación de esfuerzos normales y cortantes. Área: Mecánica de materiales Nivel: Ingeniería y tecnología Autor: Juan Guillermo Rivera Berrio |
|
Elementos de máquinas |
| Descarga | ||
 |
Motor eléctrico
En este libro se realiza un análisis de los motores eléctricos. Se aborda una descripción de los mismos y de las bases de su funcionamiento. Al incluir actividades interactivas el lector profundiza en su estudio y puede conseguir que su aprendizaje sea significativo. |
|
Hormigón armado o concreto |
| Descarga | ||
 |
Hormigón armado: diseño de vigas
Son muchas las formas estructurales y los materiales utilizados para su construcción. Cada forma y tipo de material se escoge de acuerdo a ciertas condiciones que permitan la funcionalidad y estabilidad de la estructura que se pretende construir. En edificaciones con entrepisos, placas o losas pequeñas, el uso de viguetas en una dirección es normal que se utilice; pero, en el caso de losas grandes, el criterio puede orientarse a otros tipos de sistemas estructurales (losas de hormigón en dos direcciones, combinación de hormigón con estructuras metálicas, etc.). Por otra parte, el tipo de material puede ser una opción que dependa de las preferencias del profesional responsable del diseño o de los intereses económicos o de tipo ambiental; por ejemplo, un edificio es posible que pueda diseñarse utilizando hormigón reforzado o estructuras metálicas, si se pretende un mínimo impacto ambiental (polvo, ruido, etc.), la estructura metálica puede ser la opción. Lo cierto es que las estructuras de hormigón se utilizan en múltiples formas estructurales en cualquier ciudad del mundo. .
Los objetivos de esta unidad son:
|
|
Análisis estructural |
| Descarga | ||
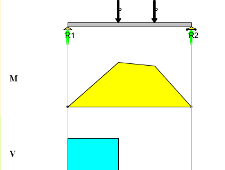 |
Cálculo de flectores y cortantes (vigas isostáticas)
En esta unidad didáctica practicarás con el análisis estructural de vigas estáticas sometidas a cargas concentradas, cargas distribuidas o con cargas combinadas. Es impotante aclarar que no pretendemos reemplazar las aplicaciones de cálculo estructural, para lo cual existe suficiente oferta especializada en el mercado. Nuestro propósito es acercar a los estudiantes de ingeniería a través de varias escenas\par interactivas, que permitan observar el comportamiento de un elemento estructural (viga) al modificar\par algunas de sus condiciones de equlibrio, tales como su longitud, la magnitud y posición de las cargas. Identificar o calcular las fuerzas internas es uno de los objetivos del análisis estructural. En esta unidad, determinaremos estas fuerzas y elaboraremos los diagramas de cortante y momento flector en cada uno de los casos propuestos.
Los objetivos de esta unidad son: |
|
Hidráulica |
| Descarga | ||
|
|
Flujo y contaminación de agua subterránea
|
|
Termodinámica |
| Descarga | ||
 |
Máquinas térmicas
Nivel: Licenciatura, bachillerato Autor: José Luis San Emeterio Peña Diseño del libro: Juan Gmo. Rivera Berrío |
|
Ciencias administrativas y económicas |
| Descarga | ||
 |
Formulación de proyectos. Etapa de diagnóstico
Área: Matemáticas, Administración y Economía |
|
 |
Conociendo la ciencia, la tecnología y la productividad
.
Área: Matemáticas, Administración y Economía |
|
 |
Paletización y empaque
Área: Matemáticas, Administración y Economía |
|
Cálculo de una variable |
| Descarga | ||
|
|
Gráficas de funciones
Área: Ciencias básicas - Cálculo |
|
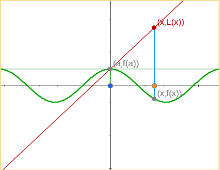 |
Derivada - aproximación lineal
|
|
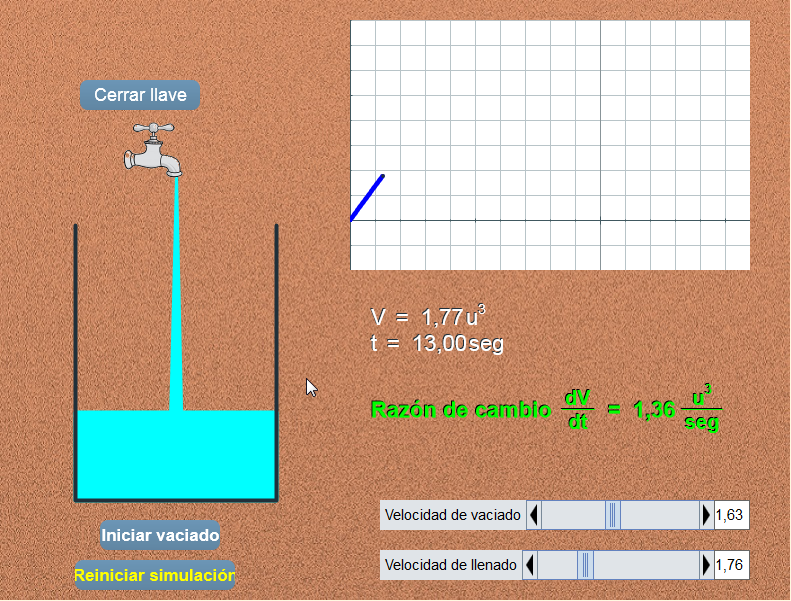 |
La derivada como razón de cambio
.
|
|
 |
Derivadas de funciones elementales
|
|
 |
Regla de la cadena - derivadas
.
|
|
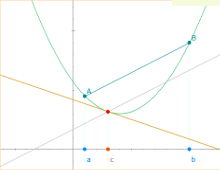 |
Teorema del valor medio
|
|
 |
Cálculo diferencial
|
|
 |
Cálculo diferencial
|
|
|
|
Introducción al cálculo
.
|
|
|
|
Valor promedio de una función
• Conocer el Teorema del Valor Medio integral y comprobarlo en diversos casos prácticos. Área: Ciencias básicas - Cálculo |
|
|
|
Volúmenes de revolución
Una de las aplicaciones de la integral definida es el cálculo del volumen de un sólido de revolución, que se obtiene al rotar una región del plano alrededor de una recta de ese mismo plano. En esta unidad se busca el logro del siguiente objetivo: ''Calcular volúmenes de revolución generados por el giro alrededor del eje OX de la región limitada por una o dos funciones" Área: Ciencias básicas - Cálculo Autor: Juan Guillermo Rivera Berrío |
|
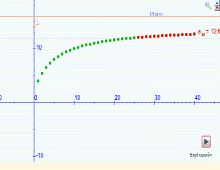 |
Sucesiones
|
|
|
|
Sucesiones numéricas
Área: Ciencias básicas - Cálculo |
|
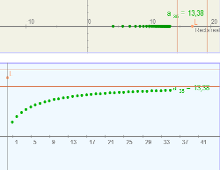 |
Límite de una sucesión
OBJETIVOS 1. Interpretar gráficamente la convergencia de una sucesión Área: Ciencias básicas - Cálculo Nivel: Ingeniería y Tecnología Autor: Elena E. Álvarez Sáiz |
|
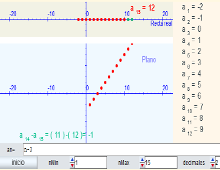 |
Monotonía de una sucesión
|
|
|
|
Sucesiones y series
Área: Ciencias básicas - Cálculo |
|
|
|
Series
- introducir el concepto de convergencia de una serie .
|
|
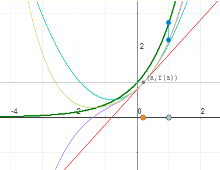 |
Series de potencias. Polinomios de Taylor
|
|
 |
Polinomios de Taylor
|
|
|
|
Polinomios de Taylor
.
|
|
 |
Polinomios de Taylor. Resto de Lagrange
|
|
 |
Series. Suma parcial enésima
Para practicar se pueden considerar o bien dos tipos de series notables (geométricas o armónicas) o bien cualquier otra cuyo término general se pueda escribir con un máximo de dos parámetros.
|
|
 |
Series Alternadas. Suma aproximada
|
|
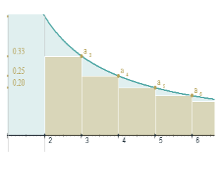 |
Resto enésimo. Criterio de la integral
|
|
|
|
Cálculo integral
a) Formula el Teorema fundamental del Calculo Integral que relaciona a la funcón área con la derivación Área: Ciencias básicas - Cálculo |
|
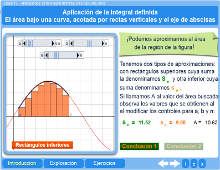 |
Cálculo integral
|
|
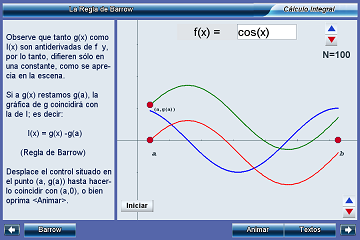 |
La regla de Barrow
|
|
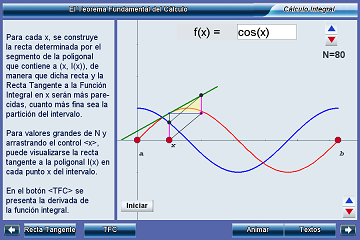 |
El teorema fundamental del cálculo
|
|
Cálculo de varias variables |
| Descarga | ||
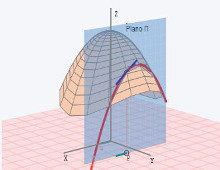 |
Interpretación geométrica de la derivada direccional
Área: Ciencias básicas - Cálculo de varias variables |
|
|
|
Derivada direccional
|
|
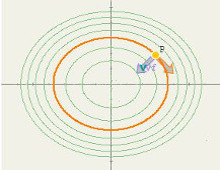 |
Gradiente y cuvas de nivel
La escena ayuda a comprobar la propiedad del gradiente de una función f en un punto P que afirma que es ortogonal a la curva de nivel que pasa por dicho punto. |
|
|
|
Recta y plano tangente
a) La recta tangente a una función en un punto, como la recta que mejor se aproxima a dicha función en el entorno próximo a él, y se determina su ecuación. Se aborda el cálculo de derivadas. |
|
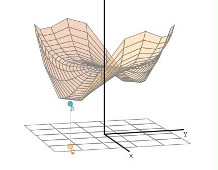 |
Extremos de funciones de dos variables. Método del hessiano.
.
|
|
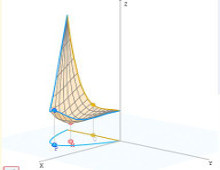 |
Extremos absolutos en una región cerrada y acotada
|
|
 |
Extremos: multiplicadores de Lagrange
|
|
|
|
Extremos de funciones de varias variables
- Introducir el método del hessiano para la clasificación de extremos de funciones de varias variables. |
|
|
|
El Teorema de Green y el planímetro
.
|
|
Métodos numéricos |
| Descarga | ||
 |
Teorema de Bolzano. Método de la bisección
|
|
|
|
Derivación numérica
- mostrar diferentes fórmulas de derivacion numérica (diferencias progresivas, regresivas y centradas) justificando su validez a partir de desarrollos en serie de Taylor. Área: Métodos numéricos |
|
|
|
Integración numérica
- aproximar una integral definida utilizando la regla del trapecio Área: Métodos numéricos |
|
|
|
Métodos del punto fijo
.
|
|
|
|
Resolución numérica de ecuaciones
a) Método de la bisección .
|
|
 |
Simulador de sistemas autónomos y no autónomos
.
|
|
Álgebra lineal |
| Descarga | ||
|
|
Operaciones con matrices
* Calcular la matriz inversa. Área: Ciencias básicas - Álgebra lineal |
|
|
|
Matrices - Sistemas de ecuaciones
* Calcular la matriz inversa.
|
|
|
|
El caleidoscopio y la Teoría de Grupos
|
|
|
|
Valores y vectores propios
* Encontrar el polinimio característico de una matriz. .
|
|
|
|
Mínimos cuadrados.
- Introducir el método de mínimos cuadrados. Área: Ciencias básicas - Álgebra lineal Nivel: Licenciatura, Ingeniería y Tecnología Autor: Elena E. Álvarez Sáiz |
|
Geometría |
||
 |
Gestalt
- Descubrir las leyes de la Gestalt presentes en la representación de un objeto. Área: Ciencias básicas. Geometría Nivel: ESO, Bachillerato, Universidad Autor: Juan Guillermo Rivera Berrío |
|
Estadística |
| Descarga | |||
 |
Elementos de Estadística
Esta unidad didáctica combina diferentes soportes y medios como vídeos, presentaciones HTML5 y escenas interactivas de Descartes para introducir al alumnado en algunos elementos de la Estadística como histogramas, media aritmética, desviación típica, mediana, representaciones de "cajas y bigotes", valores atípicos, mínimos cuadrados, y correlación lineal.
|
|
|
 |
Test Chi-cuadrado
Se introduce el test Chi Cuadrado como herramienta para analizar la relación entre de dos variables estadísticas cualitativas. Teniendo como soporte una escena de Descartes se embeben e integran diferentes soportes y medios como vídeos, presentaciones HTML5, escenas interactivas de Descartes y construcciones de Geogebra, así como la calculadora de la RED Descartes.
|
|
|
|
|
Estadística: Población y muestra
Dirigido a futuros maestros de educación básica
y estudiantes de bachillerato y licenciatura
para ayudarles a comprender la importancia de las muestras
al estudiar las características de una población,
así como el cuidado que debe ponerse al seleccionar
una muestra. |
|
|
|
|
Estadística básica
La estadistica básica es muy útil para resumir información, especialmente en las medidas de
tendencia central y variabilidad. Se utilizan en encuestas, indicadores económicos, predicciones
económicas, tomas de decisión. Permiten presentar la información de una forma clara y facil de
interpretar.
En esta unidad se busca el logro de los siguientes objetivos: |
|
Probabilidad |
| Descarga | |||
 |
Estadística, probabilidad e inferencia para bachillerato
Libro que recoge la experiencia adquirida por los editores en la impartición en el aula de los contenidos de estadística, combinatoria, probabilidad e inferencia del Bachillerato. Puede utilizarse como soporte y medio para el desarrollo de la docencia directa en el aula y también como medio para el aprendizaje autónomo.
|
|
Física General |
| Descarga | ||
 |
Gotas de astrofísica
|
|
 |
La gravedad y las estrellas dobles
|
|
 |
Banco óptico
|
|
 |
La teoría de la relatividad
|
|
|
|
Decaimiento nuclear
En esta unidad didáctica el estudiante comprenderá el comportamiento
del decaimiento radiactivo mediante la determinación de la vida media
de una muestra radiactiva. |
|
|
|
Radiación del cuerpo negro
En esta unidad didáctica el estudiante conocerá las teorías que se
desarrollaron con la intención de darle solución al problema de la radiación del
cuerpo negro. Además conocerá el proceso para encontrar el valor de
la constante de Planck por medio del efecto fotoeléctrico. |
|
|
|
Difracción De Bragg
En esta unidad didáctica el estudiante conocerá las propiedades y
la forma en la que se crean los rayos X,además conocerá los tipos
de estructura que tienen los materiales especialmente la de los
cristales que tienen tamaños similares a la longitud de onda de
los rayos X. Finalmente entenderá la ley de Bragg y conocerá su
utilidad en la cristalografía. |
|
|
|
Campos eléctricos en conductores
A lo largo de esta unidad se desarrollará el concepto de campo eléctrico en un
conductor, haciendo énfasis en la configuración alcanzada por la distribución de
carga eléctrica en la superficie del conductor, para explicar porque dicha
configuarción genera que el campo eléctrico del conductor sea cero. |
|
Química |
| Descarga | ||
 |
Cinética química
|
|
 |
Tabla Periódica
.
|
|
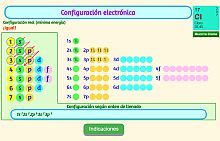 |
Configuración electrónica
.
|
|
 |
Elementos y compuestos
Identificar las propiedades características de los elementos químicos. Área: Ciencias básicas - Química |
|
 |
Los gases y la estructura de la materia
Distinguir los distintos estados de la materia. Área: Ciencias básicas - Química Nivel: Bachillerato, Ingeniería y Tecnología Autor: Pepa Grimá y Javier Soriano |
|
 |
Termoquímica
.Las reacciones endotérmicas absorben calor. Las reacciones exotérmicas liberan calor. La termoquímica funde los conceptos de la termodinámica con el concepto de energía en forma de enlaces químicos. Esto incluye el cálculo de magnitudes tales como la capacidad calorífica, el calor de la combustión, la entalpía, la entropía, la energía libre... Área: Ciencias básicas - Química Nivel: Bachillerato, Ingeniería y Tecnología Autor: Enric Ripoll Mira |
|
 |
Reacciones químicas - 1
Reconocer los cambios químicos y diferenciarlos de los cambios físicos. Nivel: Bachillerato, Ingeniería y Tecnología Autor: Jesú Manuel Muñoz Calle |
|
 |
Reacciones químicas - 2.
Iniciarse en la estequiometría química. .
|
|
 |
Transformaciones químicas
Diferenciar los cambios químicos de los físicos. |
|
 |
Equilibrio químico
Cualquier sistema en equilibrio se encuentra en un estado dinámico en el cual dos o más procesos están ocurriendo a la vez y a la misma velocidad. Los análisis químicos, las reacciones en la naturaleza y los principales procesos industriales de producción de sustancias son en su mayor parte reversibles, es decir, se desarrollan a la vez y en direcciones opuestas. Así son, por ejemplo, la síntesis del amoníaco y del ácido sulfúrico, la solución saturada de carbonato de calcio y el equilibrio del ozono troposférico y estratosférico con el oxígeno diatómico. |
|
 |
Reacciones de oxidación y reducción
Hay una serie de reacciones semejantes a la combustión que no se pueden explicar con la definición anterior. Con el tiempo se demostró que las reacciones de combustión, que se caracterizan por la energía desprendida en forma de calor y de luz, podían llevarse a cabo en presencia de elementos distintos al oxígeno, como la reacción del cloro con el sodio. Además, los metales pueden ser obtenidos a partir de otras sustancias distintas a la de sus óxidos (podemos obtener aluminio o potasio a partir de sus cloruros). También, cuando se pone el hierro en una solución de sulfato de cobre (II), se observa la precipitación de Cu metálico. Por tanto se hizo necesario el uso de una definición diferente a la usada por Lavoisier para englobar todas estas reacciones en un tipo común. Hoy en día clasificamos como reacciones de oxidación y de reducción (redox) a todas las reacciones químicas en las que los átomos cambian su número (o estado) de oxidación.
|
|
 |
La química del carbono
Saber qué estudia la química orgánica o química del carbono. .
|
|
 |
Compuestos del carbono
Los hidrocarburos y su importancia como recursos energéticos. Reacciones de combustión. Área: Ciencias básicas - Química Nivel: Bachillerato, Ingeniería y Tecnología Autor: Luis Ramírez Vicente |
|