A punto de comenzar el nuevo curso académico, desde la Red Educativa Digital Descartes se quiere presentar distintos Proyectos con recursos digitales para su utilización en la Universidad. Estos materiales facilitan la realización de actividades basadas en la exploración, visualización y adquisición y ampliación de conocimientos así como promover el trabajo individual y colaborativo.

Los Proyectos desarrollados por la RED Descartes para el profesorado y para la comunidad educativa universitaria son los siguientes:

•  Misceláneas. Escenas aisladas que puede utilizar el profesorado directamente para ilustrar conceptos o para construir actividades de trabajo en el aula o de forma autónoma por los estudiantes.

• Unidades didácticas Interactivas para la Universidad. Dentro del proyecto Un_100 se han publicado 101 unidades didácticas para nivel universitario desarrollado por docentes de México, España, Colombia y Chile. El desarrollo de las unidades se ha  organizado en los siguientes temas:
  • Álgebra lineal
  • Cálculo de una variable
  • Cálculo de varias variables
  • Combinatoria
  • Economía y finanzas
  • Física general
  • Fractales y caos
  • Geofísica
  • Geometria 1: básica
  • Geometría 2: analitica
  • Geometría 3: avanzada
  • Lógica, conjuntos y categorías
  • Matemáticas de la computación
  • Mecánica celeste
  • Mecánica: estática
  • Métodos numéricos
  • Estadística y probabilidad
  • Termodinámica
  • Variable compleja
• Libros digitales iCartesLibri. Recursos digitales en formato libro con contenidos variados y para distintos niveles.
• Ingeniería y tecnología. Repositorio de recursos digitales agrupados según el siguiente índice temático
  • Ciencias computacionales
  • Física: estática
  • Mecánica de materiales
  • Elementos de máquinas
  • Hormigón o concreto
  • Análisis estructural
  • Hidráulica
  • Topografía
  • Termodinámica
  • Ciencias administrativas y económicas
  • Ciencias básicas
• • • Cálculo de una variable
    • Cálculo de varias variables
    • Métodos numéricos
    • Álgebra lineal
    • Geometría
    • Estadística
    • Probabilidad
    • Física General
    • Química

En el siguiente video se muestra cómo acceder a estos recursos junto con algunos ejemplos de muestra.

En este artículo se presentan dos misceláneas del Proyecto Descartes relacionadas con el cálculo de integrales dobles utilizando cambios de variable. En una de ellas se incluyen diferentes ejemplos que  muestran la interpretación geométrica del jacobiano y en la otra se puede practicar con el cálculo de integrales dobles sobre dominios descritos en coordenadas polares.

Acceso a la miscelánea: Interpretación geométrica del jacobiano.

Cuando en una integral doble o triple se realiza un cambio de variable, además de expresar la función y el dominio de integración en las nuevas coordenadas, se debe introducir en el integrando un factor que se corresponde con el valor absoluto del jacobiano de la transformación. Este término juega un papel equivalente al que tendría la derivada x'(t) cuando en una integral simple de una función de una variable x se realiza un cambio de la forma x=x(t) y se sustituye dx por x'(t)dt.

La miscelánea Interpretación geométrica del jacobiano incluye distintos ejemplos que justifican el papel del jacobiano como factor de escala entre las áreas o volúmenes de un dominio y su transformado cuando se realiza un cambio de variable.

En el siguiente video se explica el funcionamiento de esta miscelánea.

Acceso a la miscelánea: Integral doble sobre dominios en polares.

El cambio a coordenadas polares resulta especialmente útil en el cálculo de integrales dobles cuando la región cuenta con alguna simetría radial y/o la función de integración tiene una expresión más simple en estas coordenadas.

Plantear integrales utilizando estas coordenadas exige describir adecuadamente el dominio en las nuevas variables e introducir el jacobiano de la transformación. En la miscelánea Integral doble en dominios en polares se puede practicar con distintas regiones delimitadas por curvas en polares así como con el cálculo de las integrales iteradas que resultan.

En el siguiente video se ilustra las opciones y el funcionamiento de la miscelánea.

En este artículo se presentan dos misceláneas del Proyecto Descartes que abordan el tema de la integración de funciones de dos variables. En una de ellas se introduce la definición de integral doble y en la otra se practica con su cálculo cuando el dominio de integración es un dominio plano regular.

En el siguiente video se explica la utilización de la primera de las escenas que tiene por objetivo comprender el concepto de integral doble de una función de dos variables sobre un rectángulo. Además, la miscelánea permite experimentar con la aproximación que proporciona la suma de Riemann dada una partición y visualizar la interpretación geométrica de la integral doble cuando se considera una función positiva.

Acceso a la miscelánea: Sumas de Riemann sobre rectángulos

Con la segunda miscelánea se puede practicar el cálculo de integrales dobles de funciones de dos variables sobre dominios regulares, es decir, sobre dominios planos que pueden describirse mediante franjas horizontales y/o franjas verticales.

El video muestra las posibilidades de la escena para definir un dominio regular y para plantear, a partir de la descripción establecida, las integrales iteradas que permiten calcular la integral doble. Para el cálculo de estas integrales se precisa tener conexión a internet.

Acceso a la miscelánea: Integral doble sobre dominios regulares

Del 15 al 19 de julio se ha celebrado en la Universidad de Valencia el International Congress on Industrial Mathematics (ICIAM) en el que se han expuesto las últimas novedades de la aplicación de las matemáticas en las ciencias, la ingeniería y la industria. El ICIAM tiene lugar cada cuatro años y se inició en París en 1987. En esta novena edición han participado más de 4000 investigadores de todo el mundo y se han abordado los avances más importantes relacionados con las matemáticas y sus aplicaciones.

Dentro del Programa del Congreso se desarrolló el minisimposio Mathematics Education in Engineering and Applied Sciences  donde Elena Álvarez, miembro de la RED Educativa Digital Descartes, presentó la charla titulada Digital resources in mathematics teaching at university. Experiences and challenges.

El objetivo de esta charla era mostrar distintas experiencias aplicadas en la docencia de las asignaturas de Cálculo de primer curso de varios Grados de Ingeniería en la Universidad de Cantabria que tienen en común la incorporación de recursos digitales en el aula. Estos recursos digitales se han utilizado como apoyo en las exposiciones teóricas, como simulaciones en las sesiones prácticas y como herramienta para el diagnóstico y corrección de errores habituales detectados en los estudiantes durante el proceso de aprendizaje.

Para la creación de los recursos se ha utilizado DescartesJS que constituye una herramienta de autor muy potente para elaborar unidades didácticas interactivas al permitir incluir varios espacios, elementos gráficos, controles numéricos, elementos textuales, de audio y video, así como la posibilidad de intercambiar datos con otras herramientas.

Como ejemplos de aplicación de los recursos digitales en la docencia se expusieron distintas estrategias que utilizan materiales que están disponibles en abierto en la RED Educativa Digital Descartes y en la página del grupo GIEMATIC UC constituido por profesoras de la Universidad de Cantabria que trabajan de forma conjunta elaborando materiales que comparten públicamente.

Estrategia 1. Incorporación de actividades interactivas en el proceso de enseñanza.

Con estas actividades se pretende:

• motivar o introducir el contenido a explicar en una clase,
• resumir la información relevante después de una exposición,
• reactivar conocimientos que se han considerado prerrequisitos para abordar un tema,
• proporcionar aplicaciones y ejemplos que afiancen los conceptos y métodos explicados.

Para mostrar sus posibilidades, se presentaron ejemplos de actividades con características distintas. En primer lugar, una unidad creada dentro del Proyecto Un_100 donde el material está estructurado en cuatro apartados: motivación, inicio, desarrollo y cierre a modo de conclusión. Esta unidad incluye tanto la parte teórica como ejercicios aleatorios que facilitan la práctica con los contenidos abordados. El segundo ejemplo consistía es una miscelánea o escena interactiva aislada, complementada con un video explicativo, donde se facilita la interpretación geométrica de un concepto (en concreto el de la derivada direccional de funciones de varias variables). Con el tercer ejemplo se pretendía mostrar una unidad que, además de permitir interpretar visualmente la convergencia de una serie de Fourier, incluyera la posibilidad de obtener cálculos simbólicos a partir de una función que se puede introducir como dato. En esta escena se establece una comunicación entre DescartesJS y Geogebra gracias a la incorporación de espacios HTMLFrame en DescartesJS y programación Javascript

Se aportan a continuación los enlaces a estas tres actividades.

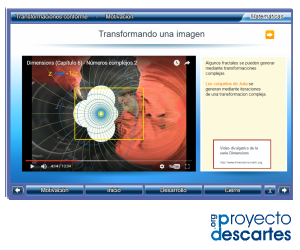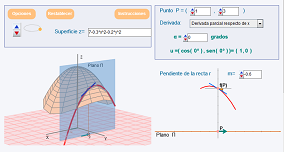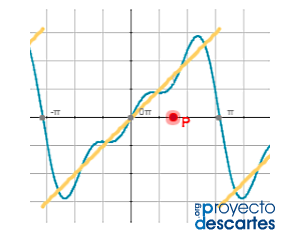Unidad Proyecto_Un100	Interpretación geométrica de la derivada direccional	Series de Fourier

Estrategia 2. Programa de recuperación de verano desarrollado para ayudar a preparar asignaturas pendientes en la convocatoria extraordinaria.

Este programa de recuperación se viene desarrollando en distintas asignaturas de Cálculo de los Grados de Ingeniería de la Universidad de Cantabria desde hace cinco años dado el éxito de resultados y la participación de los estudiantes. El programa establece la realización de distintos test en los meses de julio y agosto trabajando con actividades que persiguen una evaluación formativa. Para ello se recurre a la realización de actividades matemáticas auto-evaluables utilizando mecanismos de tutorización automática centrados en el proceso y no únicamente en el resultado final.

Para el diseño y la creación de estos test se ha considerado importante generar conflictos cognitivos en los estudiantes, reconociendo contradicciones, y fomentando la autorregulación por medio de actividades de autoevaluación poniendo el foco especialmente en la gestión de errores. Con estos recursos se pretende que los estudiantes reflexionen sobre razonamientos habituales erróneos y forzarles a analizar cada paso en la resolución de ejercicios.

En cada test se plantean cuestiones con tres niveles de dificultad: un primer nivel para reproducir procedimientos rutinarios, un segundo para establecer conexiones y resolver problemas estándar y un tercer nivel para generalizar y resolver problemas más complejos y originales. 

Ejemplo de uno de los test de recuperación utilizado en este Programa

Estrategia 3. Píldoras de contenidos desarrolladas por los estudiantes y por el profesorado.

En este caso se ha utilizado como estrategia la creación de cápsulas de información para transmitir en un tiempo reducido una idea o un concepto matemático de forma clara y comprensible. Además, se ha experimentado con la incorporación de los dispositivos móviles en la docencia mediante el diseño de actividades que requerían el uso de aplicaciones móviles educativas para la visualización y el cálculo matemático. Los micro-contenidos han sido diseñados y construidos tanto por el estudiante como por el profesor. En el primer caso el alumnado se ha convertido en agente activo de su aprendizaje y ha actuado como generador de contenido, principalmente en formato video. En el segundo, el profesorado ha creado actividades más integradoras que engloban varios recursos interconectados.

Enlace: Página con los micro-contenidos generados por los estudiantes.

En el próximo curso, se aprovechará el conocimiento generado para que el alumnado pueda analizarlo y evaluarlo críticamente. Se quiere utilizar así la experiencia de aprendizaje de los estudiantes de un año para mejorar el aprendizaje en los años siguientes. Con este objetivo, se está trabajando en generar actividades que incluyan videos interactivos, esto es, videos que incorporen paradas en distintos momentos de la reproducción para pedir al estudiante contestar preguntas, realizar actividades, etc.

Ejemplo de video interactivo

Como conclusiones principales, se destacó la oportunidad que supone trabajar de forma colaborativa entre profesores, tal y como favorece la RED Descartes o el grupo Giematic UC, y las posibilidades que permiten la utilización de recursos como los presentados en la enseñanza y el aprendizaje de las matemáticas.

Guion de la presentación de la charla

Como se informó desde este blog, durante la celebración del VIII Congreso Iberoamericano de Educación Matemática (CIBEM) en julio del 2017 en Madrid, la Red Educativa Descartes participó con el taller “El Proyecto Descartes en el aula” y la comunicación “Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automática”. El objetivo del taller dirigido por Rita Jiménez Igea fue dar a conocer el portal de la Red Educativa Digital Descartes a los profesores y profesoras de Matemáticas, mostrando los recursos educativos generados en el Proyecto Descartes para todas las etapas del sistema educativo.

En la comunicación presentada por Elena Álvarez Sáiz y Mª Reyes Ruiz Cobo, se expuso una experiencia de aula desarrollada durante el curso 2016-2017 en dos asignaturas que se imparten en el primer curso de los Grados de Ingeniería de la E.T.S.I. Industriales y Telecomunicación de la Universidad de Cantabria. Su diseño y desarrollo ha formado parte de un Proyecto apoyado por esta universidad dentro de la III Convocatoria de Innovación Docente.

Teniendo en cuenta la problemática específica de las asignaturas de Matemáticas en los primeros cursos de Grado respecto a la heterogeneidad del alumnado y las dificultades de su adaptación a la universidad, el Proyecto se planteó como primer objetivo la creación de actividades de autoevaluación que favoreciesen la evaluación continua formativa y tutorizada. Para su diseño se adoptó como estrategia didáctica la gestión de errores de forma que, mediante la intervención docente, se pudiera llegar a un fortalecimiento de los contenidos de más difícil comprensión.

En el desarrollo de estas actividades se ha utilizado la herramienta DescartesJS y su posibilidad de comunicación con páginas html. Gracias a las potentes funcionalidades de esta herramienta se han podido construir actividades de evaluación multimedia que incorporan, entre otros elementos, videos interactivos, animaciones, representaciones gráficas, controles numéricos y gráficos así como evaluación de resultados por un sistema de álgebra computacional (CAS). Las características más destacables de estas actividades son:

1. Se adaptan a cada alumno.
2. Contemplan distintos niveles de aprendizaje.
3. Incluyen asistencia personalizada y retroalimentación inmediata a la actuación del estudiante utilizando para ello botones de acción, menús de navegación y diálogos multimedia que hacen sentir al estudiante que está ayudado en todo momento.
4. Sitúan al estudiante en el centro del proceso de aprendizaje.
5. Se integran en un entorno de aprendizaje virtual estando disponibles en abierto.

El material generado se puso a disposición de los estudiantes al finalizar los temas seleccionados en cada asignatura como actividad voluntaria a realizar dentro de la evaluación continua. La participación del alumnado en esta experiencia ha sido alta y su satisfacción ha sido muy positiva valorando la utilidad del material en el aprendizaje de los contenidos abordados.

El guión de la presentación que se realizó en el VIII CIBEM muestra los aspectos destacados de esta experiencia.

Puede obtenerse más información accediendo al texto de la comunicación presentada en el VIII CIBEM: Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automática .