Ejercicios interactivos con tutorización automática. Una experiencia de aula
Como se informó desde este blog, durante la celebración del VIII Congreso Iberoamericano de Educación Matemática (CIBEM) en julio del 2017 en Madrid, la Red Educativa Descartes participó con el taller “El Proyecto Descartes en el aula” y la comunicación “Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automática”. El objetivo del taller dirigido por Rita Jiménez Igea fue dar a conocer el portal de la Red Educativa Digital Descartes a los profesores y profesoras de Matemáticas, mostrando los recursos educativos generados en el Proyecto Descartes para todas las etapas del sistema educativo.
En la comunicación presentada por Elena Álvarez Sáiz y Mª Reyes Ruiz Cobo, se expuso una experiencia de aula desarrollada durante el curso 2016-2017 en dos asignaturas que se imparten en el primer curso de los Grados de Ingeniería de la E.T.S.I. Industriales y Telecomunicación de la Universidad de Cantabria. Su diseño y desarrollo ha formado parte de un Proyecto apoyado por esta universidad dentro de la III Convocatoria de Innovación Docente.
Teniendo en cuenta la problemática específica de las asignaturas de Matemáticas en los primeros cursos de Grado respecto a la heterogeneidad del alumnado y las dificultades de su adaptación a la universidad, el Proyecto se planteó como primer objetivo la creación de actividades de autoevaluación que favoreciesen la evaluación continua formativa y tutorizada. Para su diseño se adoptó como estrategia didáctica la gestión de errores de forma que, mediante la intervención docente, se pudiera llegar a un fortalecimiento de los contenidos de más difícil comprensión.

En el desarrollo de estas actividades se ha utilizado la herramienta DescartesJS y su posibilidad de comunicación con páginas html. Gracias a las potentes funcionalidades de esta herramienta se han podido construir actividades de evaluación multimedia que incorporan, entre otros elementos, videos interactivos, animaciones, representaciones gráficas, controles numéricos y gráficos así como evaluación de resultados por un sistema de álgebra computacional (CAS). Las características más destacables de estas actividades son:
- Se adaptan a cada alumno.
- Contemplan distintos niveles de aprendizaje.
- Incluyen asistencia personalizada y retroalimentación inmediata a la actuación del estudiante utilizando para ello botones de acción, menús de navegación y diálogos multimedia que hacen sentir al estudiante que está ayudado en todo momento.
- Sitúan al estudiante en el centro del proceso de aprendizaje.
- Se integran en un entorno de aprendizaje virtual estando disponibles en abierto.
El material generado se puso a disposición de los estudiantes al finalizar los temas seleccionados en cada asignatura como actividad voluntaria a realizar dentro de la evaluación continua. La participación del alumnado en esta experiencia ha sido alta y su satisfacción ha sido muy positiva valorando la utilidad del material en el aprendizaje de los contenidos abordados.
El guión de la presentación que se realizó en el VIII CIBEM muestra los aspectos destacados de esta experiencia.
Puede obtenerse más información accediendo al texto de la comunicación presentada en el VIII CIBEM: Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automática .
Incorporando construcciones Geogebra en escenas Descartes. Ejemplo 1: Ejecutando comandos Geogebra.
La posibilidad de comunicar escenas Descartes con páginas html facilita incorporar resultados obtenidos de la ejecución de comandos Geogebra e incluso construcciones completas que pueden ser manipuladas desde la propia escena.
En este artículo se presenta una primera escena de ejemplo que utiliza los resultados de tres comandos Geogebra: Derivada, Integral y Circunferencia. Estos tres comandos tienen en común que su ejecución devuelve un único valor que puede enviarse a la escena Descartes como una cadena de caracteres. En próximos artículos se verá cómo incorporar los resultados de comandos que devuelven una lista de datos o una lista de listas.
Para poder comprender el código con el que se establece la comunicación desde Descartes, se recuerda la sintáxis de los comandos Geogebra que se utilizan en este ejemplo:
- Derivada[función,orden].
Por ejemplo: Derivada[cos(x),2] calcula la segunda derivada de la función cos(x)
- Integral[función,extremo_Inf,extremo_Sup].
Por ejemplo: Integral[cos(x),1,2] calcula la integral definida de la función cos(x) en el intervalo [1,2]
- Circunferencia[Punto1,Punto2,Punto3].
Por ejemplo: Circunferencia[(0,0),(1,1),(2,2)] calcula la ecuación de la circunferencia que pasa por los puntos A=(0,0), B=(1,1) y C=(2,2).
La escena Descartes que se presenta en este artículo incluye cuatro espacios.
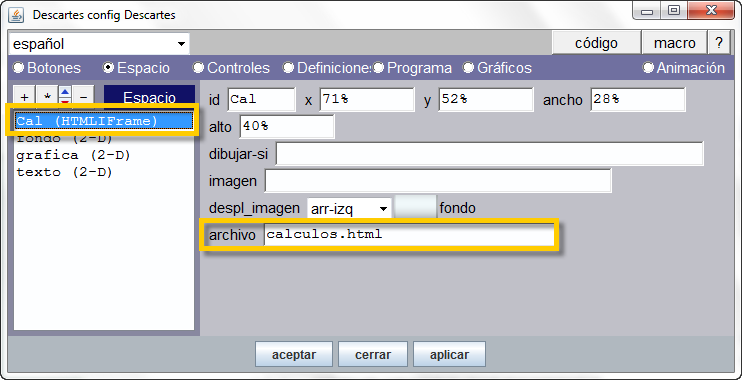
Uno de ellos es un espacio HTMLFrame que tiene como identificador el nombre Cal y será el que permitirá la comunicación con la página calculos.html que está vinculada a este espacio a través del parámetro 'archivo'.
La página calculos.html incluye el código javascript necesario para poder enviar y recibir datos de la construcción Geogebra que está embebida en ella. Esta página no necesita ser modificada y debe incorporarse en el mismo directorio que la página que contenga la escena Descartes (de no ser así se tendrá que modificar la ruta de acceso a ella en el parámetro 'archivo' del espacio HTMLFrame).
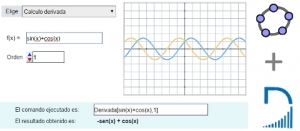
El funcionamiento de la escena Descartes que se presenta como ejemplo es sencilla. Elegida una de las tres opciones del menú, se inicia la comunicación con Geogebra. Si la opción elegida del menú es 'Calculo de la Derivada' se ejecuta la función Calculo1(), si se elige la opción 'Circunferencia por tres puntos' la función a ejecutar será Calculo2() y en el caso de que la opción sea 'Cálculo de la integral de un intervalo' la función asociada es Calculo3().
Las tres funciones tienen un código similar, en primer lugar construyen una cadena de caracteres con la sintásis del código Geogebra a ejecutar y después inician la comunicación enviando a la página incluida en el espacio Cal el evento 'evalua' pasándole como parámetro esta cadena de caracteres. Por ejemplo, el código incluido en la función Calculo1() es el siguiente:
n1='Derivada['+f+','+orden+']'
Cal.set('evalua',n1)
A la hora de generar la cadena de caracteres n1 se ha utilizado los valores de f y orden que están vinculados a los dos controles que se muestran en la escena para modificar, respectivametne, la expresión de la función y el orden de la derivada.
La página calculos.html, que está asociada al espacio Cal, recibe entonces el mensaje y ejecuta el código asociado al evento 'evalua' tras lo cual devuelve a la escena Descartes el resultado en una cadena de caracteres que siempre tiene por nombre vCalculado.
Todo este proceso es totalmente transparente al autor de la escena que puede utilizar el valor de la variable vCalculado de la misma forma que cualquier otra variable creada en la propia escena. Así, si por ejemplo se quiere representar la función derivada obtenida tras ejecutar Calculo1(), bastaría con:
- Evaluar la cadena de caracteres que se ha devuelto con el valor de la derivada: f1=_Eval_(vCalculado)
- Definir una función fun1(x)=f1 para poder crear un objeto gráfico de tipo ecuación cuya expresión sea: y=fun1(x)
Se puede practicar con la escena descargándola del siguiente enlace: Ejemplo1_CAS-JS.zip
Descartes en las Jornadas de Matemáticas de Profesores de Cantabria
El último fin de semana de Febrero se celebró en la Facultad de Ciencias de la Universidad de Cantabria, las VII Jornadas de Enseñanza de las Matemáticas en Cantabria (JEMC) organizadas cada dos cursos por la Sociedad Matemática de Profesores de Cantabria (SMPC). Las JEMC contaron con la asistencia de más de 150 profesores de Matemáticas de todos los niveles educativos: Infantil, Primaria, Secundaria y Universitaria.
Se puede acceder al resumen de las Jornadas en este enlace.
Desde la RED Descartes, Elena Álvarez, presentó el taller titulado "Descartes y Geogebra: una relación de conveniencia" en el que mostró ejemplos de los últimos proyectos promovidos por la Red Descartes para los diferentes niveles educativos y presentó las últimas novedades que proporciona la herramienta Descartes.
Entre estas novedades se enseñó la posibilidad de incluir audios y vídeos interactivos y la capacidad de establecer una comunicación de Descartes con Geogebra. Se exploró algunas de las posibilidades didácticas de esta comunicación a través de varios ejemplos mostrando que el nivel de diálogo que se puede conseguir entre Descartes y Geogebra facilita la construcción de objetos educativos con un alto nivel de interactividad, siendo el procedimiento totalmente transparente para el estudiante que lo utilice.
En próximos artículos se describrirá en detalle algunos de los ejemplos que se expusieron en este taller.
Crear actividad SCORM con Reload a partir de una actividad Descartes
En el siguiente vídeo se muestra cómo incorporar una actividad evaluable realizada con Descartes dentro de Moodle como un paquete SCORM. De esta manera se puede almacenar, en el cuaderno de calificaciones, la puntuación obtenida por el alumno cuando realice la tarea.
Un SCORM (Sharable Content Object Reference Model), es un conjunto de especificaciones técnicas en el ámbito de aprendizaje a través de Internet (e-Learning) que definen la estructura de los contenidos, su comportamiento y el comportamiento de los LMS a la hora de alojar y ejecutar dichos contenidos.
Para realizar el paquete SCORM se ha utilizado, por un lado, la posibilidad de comunicación de las escenas Descartes con páginas html (http://descartesjs.org/documentacion/?p=2729) y, por otro, el editor gratuito de SCORM Reload (http://www.reload.ac.uk/editor.html).
En el video se describen tres etapas con los pasos a realizar:
- Etapa 1. Crear la actividad y preparar los ficheros para generar el SCORM.
- Etapa 2. Construir el SCORM que incluya la actividad.
- Etapa 3. Incorporar la actividad SCORM dentro de Moodle.
Se pueden descargar los ficheros a los que se hace referencia en el vídeo haciendo clic en los siguientes enlaces:
Descartes en la Universidad. Miscelánea: Desarrollo en serie de Fourier
Acceso a la miscelánea: Desarrollo en Serie de Fourier
Con esta escena se puede calcular el desarrollo en Serie de Fourier de una función periódica y representar la suma de sus primeros términos. Su objetivo es mostrar que una función periódica puede descomponerse como suma de funciones trigonométricas, senos y cosenos, cuyas frecuencias son múltiplos enteros de la frecuencia fundamental.
A modo de ejemplo se incluye el desarrollo de varias funciones y se representa, en una misma gráfica, la función y la suma de los primeros términos de su desarrollo. Esta representación permite visualizar la aproximación que proporcionan las Series de Fourier.
La miscelánea facilita también introducir una función cualquiera y obtener su desarrollo utilizando cálculo simbólico para mostrar la expresión de los coeficientes de la serie. Cuando la función no es periódica y está definida en un intervalo de la forma [0, p], se puede obtener el desarrollo en Serie de Fourier de su extensión par o impar.
En el siguiente video se muestra cómo utilizar esta miscelánea.
Acceso a la miscelánea: Desarrollo en Serie de Fourier
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



 CONTACTO
CONTACTO
