En nuestro artículo "Euclides y el Teorema de Pitágoras", publicado en este blog de la RED Descartes, acudimos a "Los Elementos” de Euclides como fuente primigenia de la demostración académica del Teorema de Pitágoras con el objetivo de mostrar e introducir al lector interesado en la demostración matemática de una propiedad basándose en un sistema axiomático y deductivo y, a la vez, difundir la menos conocida generalización de esta propiedad. En concreto, acudimos a la primera versión en español de estos libros debida a Rodrigo Çamorano y seguimos en la guía lógica-deductiva aportada por David E. Joyce en su versión interactiva con applets de Java (actualmente estos applets presenta problemas de compatibilidad en algunos sistemas y cuando eso ocurre se suplen con imágenes).
En 1847, Oliver Byrne publicó su libro "The First six books of the Elements of Euclid whith coloured diagrams and symbols" en el que, como él indica, el uso de diagramas coloreados y símbolos en lugar de letras facilita el aprendizaje a los estudiantes. El libro de Byrne puede considerarse una revolucionaria propuesta innovadora en la enseñanza de las Matemáticas ya que sustituye el usual sistema literal e introduce atractivos elementos gráficos coloreados que le sirven de soporte y medio para abordar las demostraciones matemáticas de manera visual y por ende evitando la, muchas veces, farragosa expresión escrita que requiere una interpretación de lo leído, es decir, pone en práctica el conocido dicho: "más vale una imagen que mil palabras". De hecho, basta ver por primera vez una página de este precioso libro de Byrne para sentirse atraído con su diseño y verse sorprendido por el potencial comunicador y didáctico que encierra. El libro de Byrne podemos consultarlo en español en la versión elaborada por Nicholas Rougeux, y nosotros, con modestia introduciremos algo más de interactividad.
Fig. 1. Demostración del teorema de Pitágoras según Byrne
Pulse sobre la imagen para verlo en el libro de Byrne.
Si en el artículo antes citado buscábamos introducir al lector en el academicismo euclidiano, en éste buscamos mostrar cómo Euclides puede adentrarse en el aula de una manera didáctica, aproximándonos al aprendiz, pero respetando al gran maestro y referente. Para ello, hemos desarrollado dos escenas interactivas que abordan las demostraciones gráficas del Teorema de Pitágoras y de la generalización del mismo. Le invitamos a acceder a ellas y a interactuar con las mismas.
Byrne y su demostración gráfica del teorema de Pitágoras
Con esta primera escena se busca conseguir los siguientes objetivos:
- Conocer una versión de "Los elementos" de Euclides con una perspectiva .
- Percibir la plasticidad de la mente humana y cómo un mismo concepto tiene diversas formas de reflejarse.
- Tomar contacto con la didáctica matemática en el sistema axiomático euclidiano.
- Ver cómo Byrne realiza la demostración euclidiana del teorema de Pitágoras con una metodología deductiva basada en gráficos de colores.
- Comprender cómo se aborda un razonamiento deductivo apoyándose en axiomas y proposiciones.
- Sentar las bases para asimilar que la metodología empleada condiciona el aprendizaje.
Fig. 2. Acceso a la miscelánea "Byrne y su demostración gráfica del teorema de Pitágoras".
Pulse sobre la imagen para acceder.
La versión clásica euclidiana de este resultado puede consultarla en nuestra miscelánea "Demostración euclidiana del Teorema de Pitágoras".
Byrne y su demostración gráfica de la generalización del teorema de Pitágoras
Siguiendo la línea de trabajo abordada en la miscelánea anterior, a continuación, divulgamos el resultado menos conocido que es "La generalización del Teorema de Pitágoras" y aquí, de nuevo, lo haremos según la versión coloreada de Byrne, expuesta en la p. 259 de su libro "The First six books of the Elements of Euclid whith coloured diagrams and symbols".
Los objetivos a lograr son los mismos que en la miscelánea anterior, pero centrados en esta generalización.
Fig. 6. Acceso a la miscelánea "Byrne y su demostración gráfica de la generalización euclidiana del teorema de Pitágoras".
Pulse sobre la imagen para acceder.
La versión clásica euclidiana de esta generalización puede consultarla en nuestra miscelánea "Generalización euclidiana del Teorema de Pitágoras".
Reflexión
Comparando las versiones clásicas con las que aquí presentamos podrá experimentar la dureza que pueden encerrar algunos argumentos literarios matemáticos y el lenguaje matemático en sí —una posible causa de la desmotivación de nuestro alumnado— y cómo esta aspereza puede ser salvada con métodos didácticos innovadores. El academicismo euclidiano y, en general, de nos, los matemáticos, siendo en nuestra profesión necesario, esencial, imprescindible y loable, pensamos ha de saber reconducirse cuando lo que se desea es enseñar y divulgar el conocimiento. Byrne así lo entendió y nos marcó un esplendoroso camino del que aprender y tratar de adaptar, más en estos tiempos en los que las herramientas tecnológicas son una ayuda innegable e imprescindible que no se pueden obviar en nuestra labor docente.
Euclides y el Teorema de Pitágoras
Escrito por Ángel Cabezudo BuenoEl Teorema de Pitágoras es, posiblemente, el resultado matemático más "conocido" tanto por legos como expertos, al menos como sabedores de su existencia, aunque incluso no se sea capaz de dar un enunciado correcto y ni siquiera se sepa el porqué de su importancia ni su aplicación. Un resultado con más de dos mil años de antiguedad y que fue recogido y divulgado por Euclides en "Los Elementos”. Es una propiedad que está indisolublemente ligada a la perpendicularidad que condiciona nuestras vidas y nuestro entorno, dado que estamos sujetos a la fuerza gravitatoria y, de ahí, su máxima importancia en cualquier construcción o diseño ergonómico que permita satisfacer nuestras necesidades de movilidad y acomodación. ¿Quién no ha visto la representación geométrica de este Teorema?:
.png)
Fig. 1. Representación geométrica del Teorema de Pitágoras
o ¿quién no ha visto en algún momento su más críptica representación algebraica?:
a2 + b2 = c2
Fig. 2. Representación algebraica del Teorema de Pitágoras
Pero menos divulgado, aunque Euclides también lo incluye en el libro VI de los Elementos, es la "Generalización del Teorema de Pitágoras" donde se extiende el resultado a cualquier terna de figuras semejantes que se dibujen sobre los catetos y la hipotenusa de un triángulo rectángulo. Euclides en su demostración hace una representación gráfica con rectángulos, pero la demostración se realiza de manera general.
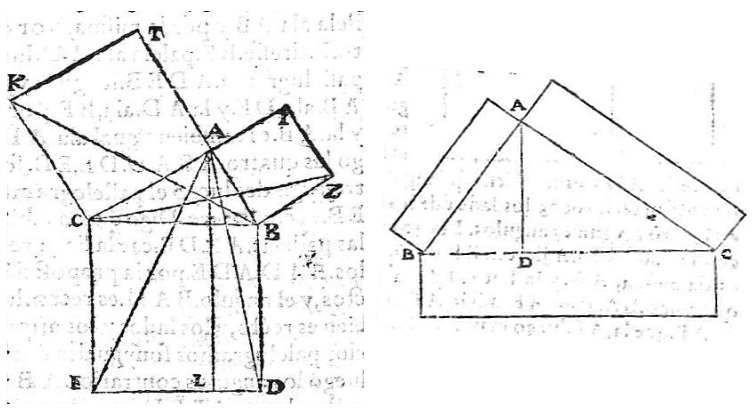
Fig. 3. Ilustraciones originales de los Elementos.
Izq. Teorema de Pitágoras. Dcha. Generalización del teorema de Pitágoras
El artista renacentista Alberto Durero mostró un profundo interés por la geometría, un conocimiento que se revitalizó en Europa gracias a la primera edición impresa de los Elementos de Euclides. Esta edición, publicada en 1482, se basó en la traducción y comentarios del matemático Campano de Novara. A su vez, el trabajo de Campano se fundamentó en versiones árabes, una de las cuales fue la influyente traducción que realizó en el siglo XII Adelard of Bath. Aunque Adelard de Bath tradujo la obra de un texto en árabe andalusí, la afirmación de que lo obtuvo por espionaje de la biblioteca de Madīnat al-Zahrā (Medina Azahara) en Córdoba es una leyenda sin fundamento histórico.
Durero, formador de artesanos a los que dedicó sus libros, conocidos colectivamente como los libros "De la Medida", fundamental para la construcción de formas y la perspectiva, también refleja la generalización del Teorema de Pitágoras y dibuja los casos particulares de triángulos y cuadrados en dicha construcción sobre un triángulo rectángulo.
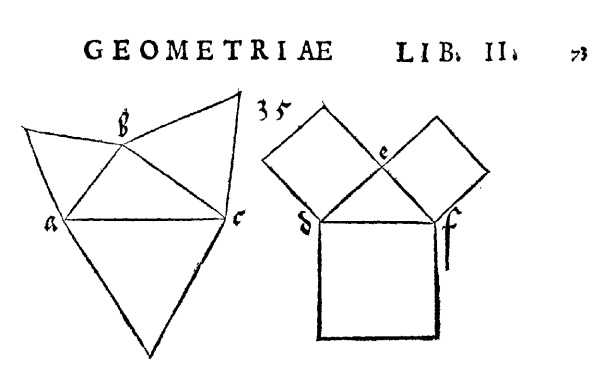
Fig. 4. Ilustraciones de Albert Durero en el libro II de la Medida.
Izq. Generalización del Teorema de Pitágoras con triángulos. Dcha. teorema de Pitágoras con cuadrados.
Y en la siguiente imagen podemos observar otras muestras de este resultado:
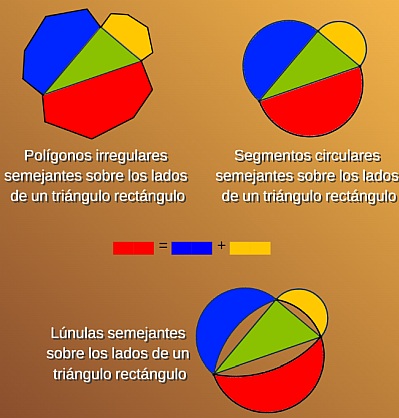
Fig. 5. Otros ejemplos de la generalización del Teorema de Pitágoras.
Para quienes estén interesados en profundizar sobre este tema hemos desarrollado dos misceláneas que se adentran en estos contenidos y los detallan. Les invitamos a acceder e interactuar con ellas.
Demostración euclidiana del teorema de Pitágoras
En las indicaciones de la miscelánea con este título, puede leer la motivación, los objetivos y las instrucciones e interactuando con ella podrá acceder a su contenido.
Fig. 6. Acceso a la miscelánea "Demostración euclidiana del teorema de Pitágoras".
Pulse sobre la imagen para acceder.
Generalización euclidiana del teorema de Pitágoras
De manera análoga también en las indicaciones de la miscelánea con este título, puede leer la motivación, los objetivos y las instrucciones e interactuando con ella podrá acceder a su contenido.
Fig. 6. Acceso a la miscelánea "generalización euclidiana del teorema de Pitágoras".
Pulse sobre la imagen para acceder.
Universidad, curso 2025-2026. Recursos de enseñanza-aprendizaje del Proyecto Descartes
Escrito por Elena Álvarez SáizUn nuevo curso, nuevas oportunidades
Comienza un nuevo curso universitario y, con él, el desafío de hacer que nuestras clases sean más dinámicas, claras y motivadoras. ¿Y si este año contaras con recursos interactivos y gratuitos que pudieran ayudarte a enriquecer tu manera de enseñar?
La RED Descartes pone a disposición del profesorado universitario una colección de materiales digitales agrupados en distintos Proyectos con los que se puede experimentar, visualizar y comprender conceptos complejos de una manera más intuitiva. Se trata de simuladores, applets y actividades interactivas diseñados para favorecer tanto la docencia como el aprendizaje autónomo de los estudiantes. Todos estos recursos cuentan con licencia Creative Commons, lo que permite adaptarlos y utilizarlos, facilitando su integración en diferentes contextos educativos.
Mapa de recursos universitarios
El siguiente Mapa de recursos para la universidad resume diversas propuestas del Proyecto Descartes que pueden aplicarse en el ámbito universitario como por ejemplo: iCartesiLibri (libros digitales interactivos), Misceláneas (escenas y simuladores), Aplicación de Juegos Didácticos de Aula (AJDA), Proyecto Prometeo y el Proyecto Ingeniería y Tecnología. Cada categoría incluye ejemplos con una breve descripción y enlaces tanto al recurso como a la página de presentación del proyecto, ofreciendo así una visión general de los contenidos disponibles en cada uno de ellos.
Libros y unidades interactivas para Cálculo, Álgebra, Física, etc.
AccederColección de 100+ unidades interactivas (Matemáticas, Física, Estadística, etc.).
AccederRecursos curriculares de ingeniería y tecnología para Universidad.
AccederJuegos didácticos y retos para gamificar prácticas y refuerzos en el campus virtual.
AccederUnidades con una o varias escenas interactivas diseñadas para abordar temas principalmente de matemáticas y física.
AccederNovedades del Proyecto Descartes para la Universidad
La RED Descartes incorpora continuamente nuevos recursos, ampliando y actualizando su catálogo. A continuación, se presentan las novedades del Proyecto Descartes publicadas entre diciembre de 2024 y agosto de 2025, organizadas por categorías (iCartesiLibri, Miscelánea y AJDA). Cada tarjeta ofrece un resumen del recurso, incluye la fecha de su publicación como referencia y proporciona acceso directo al material. Se puede navegar por las pestañas para explorar los contenidos y seleccionar fácilmente aquellos que se desee integrar en las clases o actividades del nuevo curso.
Herramientas basadas en la inteligencia artificial
En los últimos meses, desde la Red Descartes se ha trabajado intensamente en difundir y dar a conocer de manera puntual las novedades en inteligencia artificial (IA), acercando al profesorado universitario herramientas innovadores que pueden generar contenido para integrarse fácilmente en la docencia y la investigación. En este momento, se han incorporado 100 herramientas de inteligencia artificial al repositorio de la RED con funcionalidades muy diversas. Desde la página que contiene este listado de herramientas, se puede acceder a ellas agrupadas por su funcionalidad: herramientas de chat e iteracción con IA, generadores de imágenes visuales y contenido visual, generadores de contenido educativo y didáctico, herramientas para generación de juegos, etc.
Por ejemplo, el generador de cuestionarios permite crear test de selección múltiple a partir de un tema, con 3, 5, 7 o 10 preguntas, cada una acompañada de una imagen. También encontramos propuestas como el generador de iceberg, donde se elige el tema y el número de niveles, o el generador de presentaciones, por mencionar algunas.
Estas propuestas evidencian cómo la IA puede integrarse en la universidad para diversificar metodologías, fomentar la autonomía del alumnado y potenciar la calidad de los recursos digitales.
Experiencias de la Revista Digital Descartes
Como inspiración para planificar clases en el ámbito universitario, se presenta a continuación una selección de experiencias publicadas en la Revista Digital Red Descartes. Esta revista tiene como objetivo principal difundir todo lo relacionado con el Proyecto Descartes y es una iniciativa educativa de alcance global orientada a la mejora de la enseñanza mediante el uso de las tecnologías de la información y la comunicación (TIC) y de las tecnologías del aprendizaje y el conocimiento (TAC). La revista incluye además propuestas que representan avances significativos en la innovación educativa con herramientas y recursos afines.
A modo de ejemplo, se recogen algunas aplicaciones recientes de DescartesJS en el aula, tales como inteligencia artificial y gamificación, chatbots disciplinares, libros inmersivos, escape rooms educativos y simulaciones, publicadas en los números más recientes de la revista (n.º 8, 2024, y n.º 9, 2025). Cada experiencia incluye una breve contextualización y un enlace directo al artículo original, para facilitar que pueda ser replicada o adaptada a una asignatura, seminario o a un proyecto de innovación.
Cómo usar IA (imágenes, audio, vídeo) para mejorar narrativa, portadas y retos de juegos AJDA.
En tu asignatura: diseña una misión gamificada y evalúa con rúbrica.
Guía para integrar chatbots en escenas DescartesJS.
En tu asignatura: crea un bot tutor para prácticas o dudas frecuentes.
Metodología para evolucionar materiales de iCartesiLibri hacia experiencias inmersivas.
En tu asignatura: convierte una unidad con storytelling, checkpoints interactivos y mini-quiz integrados.
Itinerarios y variedad de actividades para personalizar el progreso del estudiante.
En tu asignatura: ofrece dos rutas (básica/avanzada) con informes de progreso por actividad.
Diseño y resultados de un escape room con objetivos curriculares y trabajo cooperativo.
En tu asignatura: usa un escape como evaluación formativa de cierre de tema.
Propuesta para prototipar simuladores rápidos y discutir límites/ventajas frente a IA pura.
En tu asignatura: mini-proyecto de simulación.
Explora, adapta y comparte
El Proyecto Descartes no se limita a ofrecer materiales docentes: promueve una forma diferente de enseñar y aprender en la universidad. Su enfoque se apoya en recursos visuales, interactivos y abiertos, que facilitan la comprensión profunda de los contenidos, favorecen la evaluación formativa y promueven la reutilización gracias a licencias libres. Integrar estos recursos en la práctica docente abre la puerta a experiencias de aula más dinámicas y motivadoras. Así, la docencia no solo se enriquece, sino que también se convierte en una oportunidad para compartir resultados en la Revista Digital Red Descartes, visibilizando buenas prácticas y fortaleciendo una comunidad de profesorado que innova de manera colaborativa.
Este curso, únete a la comunidad Descartes: utiliza un recurso, llévalo al aula y comparte tu experiencia.
Bachillerato, curso 2025-2026. Recursos de enseñanza-aprendizaje del Proyecto Descartes
Escrito por Ángel Cabezudo BuenoEste artículo es parte de una serie de publicaciones de la Red Educativa Digital Descartes, diseñada para el inicio del año escolar en España. Aunque está dirigido a profesores de Bachillerato también será útil para docentes de otros países que trabajen en el nivel educativo correspondiente con estudiantes de entre 15 y 18 años.
Red Educativa Digital Descartes (RED Descartes), asociación no gubernamental sin ánimo de lucro constituida el 1 de junio de 2013 que tiene como fin promover la renovación y cambio metodológico en los procesos de aprendizaje y enseñanza de las Matemáticas, y también en otras áreas de conocimiento, utilizando los recursos digitales interactivos generados en el Proyecto Descartes. En particular, para la consecución de este fin, se promueve el desarrollo y difusión de la herramienta de autor denominada "Descartes".
Actualmente, el proyecto cuenta con una gran colección de materiales didácticos interactivos y se organiza en subproyectos con soporte HTML5 adaptados y desarrollados con DescartesJS que pueden utilizarse en cualquier ordenador o dispositivo móvil independientemente del sistema operativo que porten. Nuestra tarea como asociación se centra en esta sección y aquí podrá el docente dirigirse para revisar su contenido y seleccionar para cada momento de su programación los materiales más adecuados para su uso en el aula, bien directamente o previa adaptación, o en su caso la adecuada recomendación de uso a sus alumnos. Estos materiales pueden ser utilizados en línea o en local pues todos ellos pueden ser descargados e instalados en el equipo informático de que se disponga y ¡totalmente gratis!
Cada subproyecto fue diseñado con un determinado propósito, tiene su cabida en un determinado área del conocimiento y adecuado a un determinado nivel educativo.
A continuación hacemos una reseña de aquellos subproyectos que contiene materiales didácticos para el nivel de Bachillerato indicando las novedades de los recursos que se han incorporado a nuestro repositorio desde la publicación del artículo similar al comienzo del curso escolar y académico anterior, 2024-25, hasta este momento.
| Subproyecto: Unidades Didácticas | |||
|
Las unidades didácticas son bloques de programación docente, base del desarrollo del proceso de enseñanza y aprendizaje y que integran una metodología y una planificación temporal para la consecución de los objetivos contemplados. Las unidades didácticas son un nivel docente de concreción del currículo que refleja el qué, cómo y cuándo enseñar y evaluar. |
La estructura de una unidad didáctica incluye una introducción, los objetivos y un índice de contenidos. Los siguientes enlaces conducen al índice por niveles Matemáticas Primer Curso Segundo Curso Novedad: La integral definida y la función área Física y Química Primer Curso Segundo Curso |
||
| Subproyecto: Miscelánea | |||
|
Recoge escenas aisladas que tratan aspectos muy variados del currículo de Matemáticas y que pueden servir para que el profesorado las utilice directamente para ilustrar conceptos y técnicas básicas, o para que construyan con ellas actividades y propuestas de trabajo en el aula. |
El profesorado podrá disponer de escenas para crear sus propias lecciones, creando actividades para que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo.
Matemáticas
Primer Curso https://proyectodescartes.org/miscelanea/nivel_bach_primero.htm Segundo Curso https://proyectodescartes.org/miscelanea/nivel_bach_segundo.htm Novedades: |
||
| Subproyecto: iCartesiLibri (Libros intractivos) | |||
|
Nuestro diseño hace que estos libros sean accesibles y plenamente operativos en cualquier ordenador personal o en cualquier dispositivo móvil tipo tableta y smartphone, independientemente del sistema operativo que porte. El interes de estos libros digitales radica en que incorporan recursos multimedia con los que el usuario puede interactuar cuando le interese complementar la lectura del texto con un vídeo, una grabación en audio o un material interactivo, básicamnete escenas realizadas con DescartesJS. Los hipervínculos también le pueden conducir a la consulta de recursos como defininiciones, imágenes y artículos publicados en la web y que se relaciona con algun contenido del libro lo que supone un refuerzo y apoyo para una mejor comprensión. |
La temática del subproyecto iCartesiLibris es muy variada y está en constante ampliación dado que cualquier profesor puede redactar y publicar su propio libro digital interactivo disponiendo para ello del libro titulado “Diseño de libros intractivos” ISBN 978-84-18834-27-1 que puede ser descargado en formato ZIP y consultado accediendo al apartado de Formación del Índice Materiales del subproyecto.
Los temas que el profesor interesado puede consultar en iCartesiLibri son, como hemos dicho anteriormente, muy variados y con ello está abierto a otros nuevos.
Novedad: Estilos artísticos Novedad: Ecosistemas Novedad: Solo Arte Novedades: Novedad: Física básica I Novedades: |
||
| Proyecto Prometeo - Bachillerato UNAM | |||
|
El proyecto Prometeo está promovido por el Departamento de Educación del Instituto de Matemáticas de la UNAM (Universidad Nacional Autónoma de México) e incluye las unidades didácticas interactivas creadas por el Equipo Descartes. Las unidades consisten en una o varias escenas interactivas diseñadas para abordar temas principalmente de matemáticas y física, aunque también hay de otras materias. Los contenidos se desarrollan y cubren diferentes niveles educativos. Los diferentes materiales del proyecto Prometeo se organizan según el nivel educativo al que va dirigido y también su temática. En la web de RED Descartes hemos incluido los siguientes. Dado que no existe una equivalencia unívoca entre los niveles de los sistemas educativos Mexicano y Español el profesor en busca de recursos según convenencia debería consultar |
La secuencia didáctica utilizada se encuentra conformada por: 1. Introducción; 2. Desarrollo; 3. Ejercicios; y 4. Evaluación. En la evaluación se presentan 5 preguntas de opción múltiple. |
||
| Proyecto Newton - Problemas | |||
|
Esta página recoge enunciados de problemas que tratan aspectos muy diversos de Física y Química y que pueden servir para que el profesorado los utilice directamente para ilustrar los conceptos o para construir con ellos actividades y propuestas de trabajo en el aula. El profesorado podrá disponer de materiales para que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo. . |
Es más, el profesorado podrá adaptar estos problemas a sus necesidades (si así lo desea) usando la herramienta de autor Descartes. Esta web recoge escenas aisladas que tratan aspectos muy variados del currículo de Física y Química en forma de resolución de un problema. Esta página pretende ser una zona de la Red Descartes donde el alumno pueda desmenuzar con la ayuda de las TIC los problemas que con mayor carga conceptual se incorporan en el currículo de Física y Química Los recursos de este subproyectos se centan en los niveles de 4º curso Secundaria Obligatoria y 1º y 2º cursos de Bachillerato, del plan educativo español. La estructura didáctica sigue el esquema siguiente
|
||
| Proyecto Un_100 | |||
|
El proyecto Un_100 recoge 101 unidades didácticas o recursos educativos de las áreas de Matemáticas y Física y son para el nivel de Licenciatura, algunos también pueden ser usados en el bachillerato. En su elaboración han participado académicos de México, España, Colombia y Chile. Casi todos pueden ser visualizados en tabletas y smartphones, además de en ordenadores con cualquier sistema operativo, y para ello basta contar con un navegador de internet actualizado a los estándares de HTML5.
|
Todas las unidades tienen un mismo esquema o plantilla común, con un diseño gráfico genérico, y sobre él cada desarrollador ha incorporado los contenidos y ha elaborado su secuencia didáctica personal. Se distinguen cuatro fases o momentos: Motivación, Inicio, Desarrollo y Cierre, y se complementa con un acceso a la documentación de la unidad en la que además se incluyen los créditos. El siguiente índice es una clasificación por áreas de contenidos y aunque algunos estén indicados para un nivel de Licenciatura podrían ser incluidos en parte o en su totalidad en un nivel de Bachillerato según el plan educativo español.
|
||
| Proyecto Ingeniería y Tecnología | |||
|
El proyecto Ingeniería y Tecnología tiene como objetivo ofrecer contenidos digitales que se encuadran en diferentes áreas de conocimiento y que en la mayoría de los currículos de programas de ingeniería o formación tecnológica se agrupan en cuatro apartados principales: ciencias básicas, ciencias de ingeniería, ciencias sociales y humanas, y aspectos o contenidos específicos de la profesión. |
El apartado de Ciencias básicas incluye una relación de materias que pueden ser de utilidad como complemento al planificar estrategias educativas en el desarrollo del temario de Bachillerato del plan de estudios español en las siguientes áreas: Podrá observarse cierta variedad organizativa, funcional o estética dependiendo del subproyecto de RED Descartes del que procede el objeto educativo enlazado, pero comparten una misma finalidad didáctica y una común estrategia educativa.
|
||
| Proyecto Plantillas con DescartesJS | |||
|
Con este proyecto es posible generar atractivos juegos, puzles, actividades y test de memoria, de arrastre y asociación, sin más que realizar simples y usuales tareas de edición de imágenes y de ficheros de texto “plano” (es decir sin incluir formato codificado). Para ello se usan escenas, previamente desarrolladas, como cajas negras que recibiendo como entrada un conjunto de datos preparados por el profesor o profesora aportan una actividad interactiva que pueden utilizarse e incorporarse en el proceso de enseñanza-aprendizaje. |
Los materiales que pueden elaborarse tienen encuadre en cualquier nivel educativo y materia, ya que es el contenido en sí el que marca su ubicación. Por ejemplo, un test de asociación puede establecerse entre poliedros regulares y sus denominaciones o bien entre imágenes de animales y sus nombres en castellano o en otro idioma; o en un test de memoria es posible identificar figuras geométricas con igual o análoga forma o bien animales de la misma especie, o palabras sinónimas. En definitiva la creatividad docente es la que mueve la herramienta en la consecución de los logros educativos. Las actividades que el docente tiene que realizar utilizando plantillas para el desarrollo de estos materiales se encuadran en tres tipos de acciones:
Sencillas tareas que permitirán la construcción rápida y fácil de recursos didácticos sin necesidad de estudiar ni conocer la herramienta de edición de Descartes. Todo irá acompañado de su correspondiente guía o tutorial para, a partir de la plantilla, abordar y lograr el recurso deseado. En el índice del subproyecto Plantillas se encuentra el apartado de Tutoriales donde el docente interesado encontrará un Manual completo de plantillas El apartado de Aplicaciones incluye una serie de unidades organizadas en áreas de conocimiento y niveles educativos desarrolladas por el profesorado y en algunos casos por algunos de sus alumos a partir de las plantillas existentes. Para el nivel bachillerato y el área de matemáticas tenemos los siguientes rescursos Matemáticas |
||
| Revista Digital | |
|
Desde RED Descartes ofrecemos nuestra Revista Digital, Panhispánica – Educativa - Interactiva, una plataforma cuyo primer número apareció en 2021 con periodicidad semestral y que tiene como principal objetivo difundir cualquier contenido relacionado con el Proyecto Descartes. |
Esperamos que la Revista Digital interese al profesor de Bachillerato y que pudiera compartir con sus alumnos, en algun caso, si lo considera adecuado . El formato que toma la revista es la de libro digital interactivo. Los artículos tienen una temática muy diversa, aunque siempre relacionada con los objetivos del Proyecto Descartes y su herramienta homónima Descartes, sin excluir a ningún otro recurso, como soporte en el proceso de enseñanza-aprendizaje en cualquiera de sus ámbitos científico, tecnológico, pedagógico, social, lingüístico-literario… |
Como aprender a programar las escenas interactivas de DescartesJS
Para crear tus propios contenidos educativos, puedes modificar los recursos existentes. Los recursos del tipo Misceláneas son muy adaptables y con solo unos pocos cambios, pueden convertirse en herramientas personalizadas que satisfagan las necesidades específicas de tu clase.
El Editor Descartes es la herramienta que necesitas para realizar estas modificaciones. Es un editor intuitivo y fácil de usar, diseñado para que puedas adaptar los contenidos sin complicaciones.
Una vez que comprendas cómo están estructurados estos recursos, podrás crear los tuyos propios con facilidad. Para ayudarte en este proceso, el subproyecto iCartesiLibri ofrece varios libros interactivos, como "Formación en DescartesJS", que explican detalladamente las funcionalidades del editor. También hay una documentación completa disponible en línea.
Esperamos y deseamos que este artículo le haya sido de ayuda y pueda encontrar en Red Educativa Digital Descartes todo que necesite.
Más...
Planifica el curso escolar 2025-2026 con los recursos del Proyecto AJDA
Escrito por Jesús Manuel Muñoz CalleInicia un nuevo curso y, con él, llegan nuevos retos y oportunidades para motivar a nuestro alumnado, diversificar metodologías y mejorar el proceso de enseñanza-aprendizaje. El Proyecto AJDA (Aplicación de Juegos Didácticos en el Aula), integrado en la Red Educativa Digital Descartes, ofrece recursos digitales gratuitos, interactivos y listos para usar, que permiten gamificar el aula con facilidad.
¿Qué es el Proyecto AJDA?
El Proyecto AJDA nació con la idea de incorporar juegos didácticos digitales en el proceso de enseñanza, como una forma de hacer del aprendizaje una experiencia más dinámica, activa y motivadora. Desde 2008 ha evolucionado hasta ofrecer hoy:
- Más de 500 juegos didácticos gratuitos y listos para usar.
- Un portal web donde se organizan los juegos por etapas, áreas y temáticas.
- Un blog con novedades, guías y experiencias docentes.
- Canal de YouTube con tutoriales prácticos y ejemplos de aula.
- Libros interactivos que recopilan y explican cómo utilizar los juegos.
El profesorado encuentra en AJDA un repositorio dinámico, versátil y en constante crecimiento, que le permite diseñar secuencias de aprendizaje activas, motivadoras e inclusivas.
Planifica el curso escolar 2025-2026 con AJDA
Organizar tu curso con AJDA significa disponer de una biblioteca ordenada y estructurada de juegos que se pueden usar en diferentes momentos:
- Inicio de tema: para introducir conceptos de forma motivadora.
- Desarrollo: como dinámica de trabajo en grupos cooperativos.
- Refuerzo y ampliación: actividades adaptadas a distintos niveles.
- Evaluación: juegos tipo concurso para comprobar aprendizajes.
Además, puedes trabajar con los juegos en línea o en modo offline, descargando el DVD del proyecto o los paquetes ZIP, lo que facilita su uso en todo tipo de contextos, incluso en aulas sin conexión.
Ejemplos concretos de juegos del Proyecto AJDA
A continuación, comparto dos portales del Proyecto con todos los recursos necesarios para poder realizar una actividad gamificadas (juegos, instrucciones, vídeos, material complementario, etc.:
Portal Alquimistas
Portal del Gran Torneo de Magia y Hechicería
Estos son solo dos ejemplos, pero el catálogo incluye cientos de opciones, muchas de ellas inspiradas en programas de televisión (¿Quién quiere ser millonario?, Boom, Pasapalabra, Saber y Ganar, Password, La ruleta de la fortuna…), juegos de tablero, juegos deportivos digitales, digitales y dinámicas colaborativas.
Beneficios de utilizar AJDA
- Motivación: los juegos despiertan interés y predisposición positiva hacia el aprendizaje.
- Aprendizaje activo: cada juego supone un reto cognitivo que fomenta la participación.
- Personalización: el profesorado puede adaptar preguntas, niveles de dificultad y temáticas.
- Accesibilidad: materiales gratuitos, online y offline, multiplataforma.
- Trabajo cooperativo: muchos juegos se diseñan para equipos, lo que favorece la interacción social y la construcción conjunta del conocimiento.
- Inclusión: recursos útiles para alumnado con diferentes ritmos y estilos de aprendizaje.
Formación y apoyo docente
Además de los juegos, AJDA ofrece un completo ecosistema de recursos de apoyo:
- Lista completa de juegos.
- Relación de vídeos.
- Repositorio de ficheros de preguntas.
- Curso de formación sobre la aplicación de juegos.
- Curso de formación sobre la creación de juegos.
- Recursos off-line.
- Libros interactivos.
Libro Interactivo. "Juegos didácticos. Proyecto AJDA"
Resumen e invitación final
El curso 2025-2026 es una magnífica oportunidad para integrar en tu aula la gamificación educativa de la mano del Proyecto AJDA. Dispones de cientos de juegos, listos para usar, que motivarán al alumnado, facilitarán la personalización de la enseñanza y enriquecerán tus clases.
Te invito a explorar los recursos de este proyecto y a aplicar de forma libre y gratuita AJDA con tus alumnos.
Planifica con motivación, juego y aprendizaje.
Educación Secundaria, curso 2025-2026. Recursos de enseñanza-aprendizaje del Proyecto Descartes
Escrito por Montserrat Gelis BoschEl inicio del curso 2025-2026 en Educación Secundaria abre nuevas oportunidades para potenciar el aprendizaje a través de recursos digitales que favorezcan la autonomía, la motivación y el pensamiento crítico del alumnado. En este contexto, el Proyecto Descartes, impulsado por la Red Educativa Digital Descartes, se consolida como una referencia en el ámbito de la innovación educativa, ofreciendo materiales interactivos de acceso libre que combinan rigor académico con un diseño atractivo y dinámico.
La Red Descartes es una comunidad de docentes que, desde hace más de dos décadas, desarrolla y comparte propuestas didácticas en formato digital, basadas en la interactividad y en el uso de tecnologías abiertas. Estos materiales abarcan todas las etapas educativas, pero en especial resultan valiosos para Secundaria, ya que permiten reforzar conceptos clave en matemáticas, ciencias, lengua y otras áreas mediante actividades prácticas, simulaciones y juegos didácticos que sitúan al estudiante en el centro del proceso de aprendizaje.
En este artículo se presentan algunos de los proyectos de la Red Descartes más adecuados para Educación Secundaria, mostrando cómo pueden integrarse en el aula para enriquecer las experiencias de enseñanza-aprendizaje durante el curso 2025-2026.
Proyectos destacados
ED@D
Unidades completas en Matemáticas, Física y Química, con teoría, ejemplos interactivos y ejercicios autocorregibles. Están disponibles en castellano, catalán, gallego y portugués.
Unidades Didácticas
Unidades didácticas de Matemáticas y de Física y Química. Son independientes unas de otras y ello permite que cualquiera pueda seleccionarlas, reorganizarlas y adaptarlas a sus necesidades y generar secuencias didácticas y planes educativos personalizados.
Miscelánea
Escenas breves y visuales para explicar conceptos de manera rápida y atractiva, complementando la enseñanza diaria.
Canals
Aunque la mayoría de objetos interactivos elaborados a partir de los materiales de M.A. Canals son para primaria, encontramos algunas actividades para 1º de la ESO.
Telesecundaria
Unidades didácticas de Matemáticas, Física y Química adaptables a Secundaria, con gran variedad de recursos interactivos.
Plantillas
Usando diferentes plantillas, se pueden generar atractivos puzles, test de memoria, de arrastre, asociación, interesantes vídeos interactivos, etc. sin más que realizar simples y usuales tareas de edición de imágenes y de ficheros de texto.
ASIPISA
Materiales educativos, digitales e interactivos, basados en las unidades liberadas del Programa Internacional PISA.
iCartesiLibri
Desarrollo de libros dinámicos, interactivos, multimedia, centrados en el aprendizaje y potenciadores de la educación de personas que aprenden a aprender, que adquieren autonomía y se forman competencialmente.
Competencias
Objetos de aprendizaje interactivos cuyos contenidos se basan en unidades liberadas PISA y Pruebas de Evaluación Diagnóstico de diferentes Comunidades Autónomas.
ADJA
Una amplia colección de juegos y materiales relacionados con ellos, con el objetivo de que sirvan como recursos didácticos de aplicación en el aula.
EECL
Se presentan en esta web las preguntas de las pruebas propuestas en el primer Estudio Europeo de Competencia Lingüística, realizado en 2011, adaptadas como recursos interactivos TIC.
GEOgráfica
Colección de recursos educativos interactivos que ayudan al aprendizaje de la Geografía mundial con diferentes niveles de detalle --desde el contexto global al local--, y con diferentes ámbitos disciplinarios, es decir, la Geografía general, física y humana, y la Geografía regional.
Para ilustrar mejor todo lo anterior, compartimos un breve vídeo en el que se muestran algunos de los materiales interactivos más representativos de la Red Descartes. Se trata de una pequeña muestra que refleja la riqueza y variedad de recursos disponibles para la enseñanza en Secundaria.
Los ejemplos presentados en el vídeo son solo una pequeña muestra del enorme potencial que ofrece la Red Educativa Digital Descartes. Cada recurso está diseñado con un objetivo claro: facilitar la comprensión de los contenidos, favorecer el aprendizaje activo y motivar al alumnado mediante la interacción y la experimentación.
Novedades recientes
Desde sus inicios, la Red Educativa Digital Descartes no solo continúa expandiendo sus propuestas interactivas, sino que también ha intensificado su innovación al integrar recursos vinculados a la inteligencia artificial, la gamificación y nuevas formas de autoría digital. Estas incorporaciones refuerzan su compromiso con una educación secundaria más actual, dinámica y personalizada.De cara al curso 2025-2026, la incorporación de materiales innovadores —que integran gamificación, inteligencia artificial y propuestas didácticas interactivas— reafirma el valor del Proyecto Descartes como aliado del profesorado en la enseñanza de la Educación Secundaria. A continuación, se destacan los materiales más relevantes que se han incorporado desde octubre de 2024:
Subproyecto iCartesiLibri
Subproyecto Miscelánea
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)





















 CONTACTO
CONTACTO
