Los juegos AJDA como juegos adaptativos
Escrito por Jesús Manuel Muñoz CalleLos juegos adaptativos son herramientas tecnológicas que ajustan su contenido, dificultad y dinámica en función de las respuestas y el progreso del usuario. En el caso de AJDA, estos juegos se integran en el aula para ofrecer una experiencia de aprendizaje personalizada que motiva a los estudiantes y mejora sus resultados académicos.
Por ejemplo, un estudiante que tiene dificultades con las fracciones puede recibir ejercicios más básicos en un juego matemático, mientras que otro con mayor destreza enfrenta retos más complejos, todo en el mismo entorno interactivo.
El Proyecto AJDA incorpora varias innovaciones para lograr un aprendizaje personalizado:
- Generador de preguntas dinámico. Los docentes pueden diseñar preguntas y desafíos específicos para sus estudiantes, creando juegos que se alinean con el currículo y las necesidades individuales. Además pueden gestionar el orden de aparición de las preguntas e ir aumentando gradualmente la dificultad de las mismas.
- Seguimiento del progreso. Los juegos registran el rendimiento de cada estudiante, permitiendo a los profesores analizar datos y ajustar el contenido en tiempo real o para próximas actividades.
- Feedback instantáneo: Los estudiantes reciben retroalimentación inmediata sobre sus respuestas, lo que fomenta el aprendizaje activo y autónomo.
- Diversidad de juegos. Los juegos AJDA son muy variados, tanto en presentación, como en mecánica. Esto permite seleccionar juegos que se adapten a las necesidades del alumnado. Los recursos pueden configurarse para adaptarse a estilos visuales, auditivos o kinestésicos. Los recursos pueden configurarse para adaptarse a estilos visuales, auditivos o kinestésicos.
- Ritmo personalizado. Los estudiantes pueden avanzar a su propio ritmo sin presión, repitiendo niveles o actividades según lo necesiten.
- Personalización lingüística. Los juegos pueden configurarse en el idioma nativo del estudiante o incluso ajustarse para trabajar con dialectos locales.
- Integración de objetivos del docente. Los profesores pueden diseñar tareas específicas para cada alumno o grupo.
A continuación mostramos dos juegos AJDA cuya apariencia, dinámica y contenidos son muy diferentes, permitiendo una adaptación específica según el alumnado al que van dirigidos.
En las siguientes imágenes mostramos como el nivel, contenidos y tipo de preguntas también puede ser muy diferente y por tanto adaptado a las necesidades del alumnado.
-
Inclusión educativa: Los juegos didácticos adaptativos eliminan barreras, ofreciendo experiencias accesibles para estudiantes con diferentes estilos de aprendizaje y capacidades.
-
Motivación sostenida: Al enfrentar retos ajustados a su nivel, los estudiantes se sienten desafiados sin frustrarse, lo que mantiene su interés y compromiso.
-
Autonomía en el aprendizaje: Los alumnos desarrollan habilidades de autogestión al recibir contenidos que les permiten avanzar a su ritmo.
-
Mejora en la retención del conocimiento. Al ofrecer contenido ajustado al nivel y necesidades del estudiante, el aprendizaje se convierte en una experiencia más significativa. Los conceptos se entienden mejor y permanecen en la memoria a largo plazo.
-
Optimización del tiempo del docente. Los profesores pueden dedicar más tiempo a actividades de valor añadido, ya que las herramientas adaptativas automatizan procesos de seguimiento, evaluación y ajuste de contenidos.
-
Potencia el aprendizaje colaborativo. En escenarios multijugador, los estudiantes pueden trabajar juntos en tareas adaptadas a su nivel combinado, fomentando habilidades sociales y trabajo en equipo.
-
Reducción de desigualdades. Los estudiantes con menos acceso a recursos educativos pueden beneficiarse enormemente de los juegos adaptativos, nivelando las oportunidades de aprendizaje.
Octogésimo aniversario de José Luis Abreu ¡FELICIDADES!
Escrito por José R. Galo Sánchez
José Luis, ¡muchas felicidades en tu octogésimo cumpleaños!
Hoy es un día especial para José Luis Abreu León y también para todos sus colegas y amigos que integramos la Red Educativa Digital Descartes (RED Descartes). Él cumple ochenta años y nosotros llevamos veintiocho apoyándonos en la herramienta informática que supo vislumbrar y desarrollar con un único objetivo, el de mejorar la enseñanza de las Matemáticas. Supo mirar y ver lejos siendo pionero en el planteamiento de webs educativas interactivas, y nosotros pudimos auparnos a sus hombros para tratar de vislumbrar ese nuevo horizonte didáctico. Sí, esa herramienta fue ¡Descartes! y en base a ella se conformó un proyecto educativo el ¡Proyecto Descartes!, auspiciado inicialmente por el Ministerio de Educación de España y continuado desde el año 2013 por nuestra organización no gubernamental RED Descartes, de la que José Luis es socio fundador.
 |
 |
|
| Año 2004 (Expedición al Everest) | Año 2025 |
Descartes, fue la consecuencia o evolución de algunas ideas y desarrollos previos suyos que divulgó en el "Proyecto Prometeo", subtitulado como "Educación interactiva en la red" y que data del año 1997. Este proyecto se basaba en el desarrollo de NIPPES (Núcleos Interactivos Para Programas Educativos) que eran applets Java muy sencillos de configurar que permiten desarrollar interacciones con los datos más diversos[1].
 |
|
|
|
Escultura de Prometeo-Quetzalcóatl |
Avatar de José Luis |
Esos trabajos preliminares, José Luis, los sigue teniendo enlazados en su página de proyectos desarrollados; están en orden cronológico inverso al de su desarrollo por lo que hemos de desplazarnos al final de la página para llegar al citado proyecto Prometeo datado en 1997, a acceder a applets variados reaizados en 1997 y 1998, a ¡Descartes 1! en 1999 —web de presentación con ejemplos, documentación y aplicaciones—, o al de "Superficies" premiado por el Ministerio de Educación en el año 2000 —en este artículo de la revista SUMA se realiza una descripción de "Superficies"—, a Descartes 2, a Descartes 3, etc., que son ejemplos de una amplia lista de proyectos incluidos en la página citada y enlazada[2].
Pero, aquí, no es nuestro objetivo hacer una revisión del curriculum vitae de José Luis, quien previamente a su dedicación al desarrollo de software educativo inició su formación académica como físico teórico en la Facultad de Ciencias de la UNAM, se doctoró en Matemáticas en el Departamento de Matemáticas del M.I.T. y en su trabajo académico e investigador podemos destacar, como un hito, el haber sido director del Instituto de Investigación en Matemáticas Aplicadas y Sistemas (IIMAS) de la UNAM.
Son breves pinceladas de una vida dedicada a Ciencia y a la Educación tanto en México como en España. Pero lo más importante, al menos para los cartesianos de la RED Descartes, es que gracias al trabajo de José Luis muchos otros hemos podido enseñar, aprender e investigar las Matemáticas de una manera diferente y desarrollar objetos educativos interactivos que, con el apoyo inicial dado por el Ministerio de Educación de España y después desde nuestra organización no gubernamental, han permitido el aprendizaje a muchas, muchísimas personas en una amplia extensión mundial, con un gran foco ubicado en el mundo panhispánico.
Son centenares las escenas interactivas con Descartes desarrolladas por José Luis, de las que podemos poner algunos ejemplos, pero destaquemos la siguiente por estar relacionada con el contexto de este artículo, el modelo heliocéntrico y el devenir de los planetas en su giro alrededor del sol... una vuelta, dos vueltas, tres vueltas,... ¡ochenta vueltas! has dado José Luis y te deseamos sigas incrementando el número de ellas durante mucho tiempo.
Los planetas, escena interactiva de José Luis Abreu León
Gracias José Luis por compartir tu saber y por habernos permitido estar sobre tus hombros, viendo más lejos.
¡Feliz inicio de tu novena década!
Un fuerte abrazo de tus colegas y amigos de RED Descartes.
[1]Desgraciadamente, por la caducidad que introduce la rápida evolución de la tecnología informática, en la actualidad los applets Java han pasado a ser funcionalmente inaccesibles en los navegadores ya que desde 2013 estos son bloqueados por cuestiones de seguridad, no son compatibles con el estándar actual HTML5. Por ello, si accede al Proyecto Prometeo citado, sólo observará una página de texto que nombra y describe objetos que no podrá ni ver, ni interactuar con ellos. Pero, afortunadamente, la informática suele obviar estos problemas con máquinas virtuales o simuladores y, gracias a nuestro colega cartesiano Francisco Rodríguez Villanego, hemos sabido que podemos instalar una extensión en los navegadores basados en Chrome (Chrome, Chromium, Brave, Edge, Opera, etc.) y proceder a activarla cuando accedamos al dominio que incluye los applets con los que queramos interactuar —permanecerá activa para ese dominio hasta que se desee desactivarla—. Esta máquina virtual intercepta el código Java que llega a la página, muestra la simulación y permite la interactividad. Se llama CheerpJ Applet Runner (https://cheerpj.com/cheerpj-applet-runner/). El navegador admite el código Java que recibe y lo interpreta porque no está realmente ejecutando Java, lo simula con otros lenguajes, y por ende es seguro. Así pues, le animamos a instalar esa extensión y que pueda gozar, o volver a gozar, a través de la manipulación de esos objetos educativos. Sólo añadir que, dependiendo de los recursos con los que cuente su ordenador, necesitará ser paciente y esperar a que la extensión termine de interpretarlos y los grafique.
[2] Si ya ha instalado la extensión CheerpJ Applet Runner en su navegador podrá ver las web de las versiones de Descartes, pero si lo desea también puede consultar las siguientes páginas que incluyen vídeos donde se muestran algunas características de Descartes 1, Descartes 2, Descartes 3, Descartes Álgebra, Descartes 4, que posteriormente dieron paso a Descartes 5 (con plug-in) y la versión actual DescartesJS compatible HTML5.
Explorando las herramientas de IA en la Red Educativa Digital Descartes
Escrito por Montserrat Gelis BoschLa educación digital sigue evolucionando, y con ella, las herramientas que permiten al profesorado crear recursos más dinámicos, interactivos y adaptados a las necesidades del alumnado. En este contexto, la Red Educativa Digital Descartes se posiciona como una plataforma clave, ofreciendo al profesorado una amplia variedad de materiales y actividades listas para usar o personalizar.
En este vídeo presentamos un recorrido práctico por uno de los apartados más innovadores de la red: el uso de herramientas basadas en inteligencia artificial (IA) para generar contenido educativo de manera rápida y sencilla.
Entre estas herramientas destacan los recursos creados por el Dr. Juan Guillermo Rivera, que permiten al profesorado diseñar actividades interactivas sin necesidad de conocimientos técnicos. Un claro ejemplo de esto lo encontramos en el generador de evaluaciones tipo "arrastrar y soltar", que en el vídeo se aplica al tema de Perímetros y Áreas.
Además de mostrar cómo se genera este tipo de actividad, el vídeo explica paso a paso cómo personalizar el contenido modificando directamente el archivo descargado, y cómo insertarlo en un sitio web a través de Google Sites, lo que facilita su integración en aulas virtuales, blogs o páginas educativas.
Este tipo de herramientas no solo ahorran tiempo al docente, sino que además fomentan la creación de recursos más visuales, accesibles y adaptativos, alineados con las demandas de la educación actual.
Te invitamos a ver el vídeo completo para descubrir cómo puedes empezar a crear tus propios materiales con la ayuda de la inteligencia artificial:
Trabajo Fin de Grado. Gamificación y educación: una aplicación web para transformar el aprendizaje
Escrito por Jesús Manuel Muñoz CalleReseña del Trabajo Fin de Grado de Francisco José Arenilla Ojeda: mejoras del módulo de generación de ficheros de preguntas para una plataforma educativa gamificada.
En este TFG se ha diseñado un generador y buscador específico para buena parte de los ficheros utilizados en los juegos didácticos del Proyecto AJDA.
Cuando las preguntas se convierten en juego
¿Te imaginas que los exámenes de clase fueran como un trivial o un kahoot, pero creado a medida por el profe? Eso es justo lo que ha conseguido Francisco José Arenilla en su Trabajo Fin de Grado: una aplicación web que transforma preguntas en juegos para que aprender sea mucho más entretenido.
El problema de partida
La idea no era nueva: ya existía una aplicación básica con un generador de preguntas y un buscador. El problema es que estaba muy limitada:
- Pocas funciones y formatos muy escasos.
- Interfaz poco intuitiva para profes y alumnos.
- No se podían controlar bien los ficheros creados.
¿Qué se hizo en este proyecto?
Francisco se arremangó y mejoró la aplicación de arriba a abajo. Ahora, además de crear preguntas, los docentes pueden organizarlas, guardarlas como plantillas y exportarlas en un montón de formatos.
- Página de inicio clara, que guía al usuario desde el primer momento.
- Plantillas de preguntas, para no empezar de cero cada vez.
- Exportación fácil a PDF, Word o incluso formatos que se pueden reusar en otros sistemas.
- Buscador avanzado, para encontrar rápidamente las preguntas guardadas.
- Modo multijugador, para usar los cuestionarios directamente en clase como un juego.
Captura de la pantalla del menú general del generador de preguntas
Así funciona en la práctica
- El profe crea preguntas (tipo test, cifras, relacionar conceptos...).
- Guarda el fichero en su cuenta, privado o público.
- Lo exporta para imprimir, compartir o jugar online.
- Y finalmente... ¡a jugar en clase!
¿Por qué es importante?
Porque con esta app, preparar actividades deja de ser una tarea tediosa y se convierte en algo rápido y divertido. Y lo más importante: los alumnos se motivan más. Ya no es solo contestar preguntas... ¡es jugar y aprender a la vez!
Como dice el propio autor: “La tecnología no sustituye al buen docente, pero puede hacer sus clases mucho más atractivas”.
¿Qué se viene después?
- Más tipos de juegos y preguntas.
- Estadísticas para saber qué preguntas funcionan mejor.
- Mejor accesibilidad para todo tipo de alumnado.
En resumen
Este proyecto demuestra que la universidad no solo sirve para aprender teoría: también puede dar lugar a herramientas reales que transformen las aulas. Y quién sabe... quizá pronto veamos esta aplicación en muchos centros educativos.
Más...
Abierto el plazo de inscripción en el curso "Diseño de libros interactivos con DescartesJS y herramientas de IA"
Escrito por José Antonio Salgueiro González¿Quieres aprender a crear libros interactivos que faciliten tu labor docente y cautiven a tu alumnado y a tus lectores? Únete a nuestro curso y descubre cómo utilizar las herramientas de inteligencia artificial y DescartesJS para diseñar libros interactivos educativos y páginas dinámicas.
Queda abierto el plazo de inscripción gratuita a la II Edición del Curso para el "Diseño de libros interactivos con DescartesJS y herramientas de Inteligencia Artificial", una acción formativa que se enmarca en el programa de Educación Abierta desarrollado entre redes docentes de Colombia, México y España, fundamentalmente, aunque contamos con la participación de profesorado de otros países de habla hispana, portuguesa e inglesa.
Está dirigido a docentes de cualquier etapa educativa, infantil, primaria, educación secundaria obligatoria, bachillerato, formación profesional, enseñanzas de régimen especial y universidad, y de cualquier materia o especialidad, en activo o no, así como a profesionales vinculados a la educación o formación y a diseñadores y desarrolladores interesados en libros y objetos interactivos, utilizando una metodología activa, concretamente Clase Invertida y Aprendizaje Basado en Proyectos (Tareas), pues desde la primera sesión cada participante comenzará a diseñar y editar su primer libro interactivo, recibiendo sesiones quincenales por videoconferencia, que serán grabadas y compartidas con todos los participantes y asesorados por docentes de las redes mencionadas.
El curso comienza el próximo día 17 de octubre y finaliza el 13 de febrero de 2026, impartiéndose las sesiones de 7 AM a 8 AM en el horario oficial de Colombia, de acuerdo al siguiente calendario previsto y contenidos a tratar:
Para cualquier consulta o aclaración, puedes contactar con nosotros en la dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
| ACCESO AL FORMULARIO DE INSCRIPCIÓN |
Este formulario estará abierto hasta el día 10 de octubre o hasta cubrir disponibilidad.
Toda la información sobre el curso se encuentra disponible, como no puede ser de otra manera, en el formato libro interactivo, ofreciendo allí, conforme a la metodología, los contenidos y tareas de la primera sesión. Así, tenemos:
- Metodología
- Programación detallada
- Prepárate para la primera sesión
- Descarga el libro plantilla
- Trabajos en la primera sesión
- Estructura del libro
Relación de recursos de gran interés
Análisis y crítica de la espiral de Durero
Escrito por José R. Galo SánchezSi aborda una búsqueda literaria o pregunta a un buscador o a una inteligencia artificial sobre "La espiral de Durero" con alta probabilidad se verá derivado a una curva plana que se enmarca en una sucesión de rectángulos y obtendrá una imagen análoga, similar, a la siguiente:
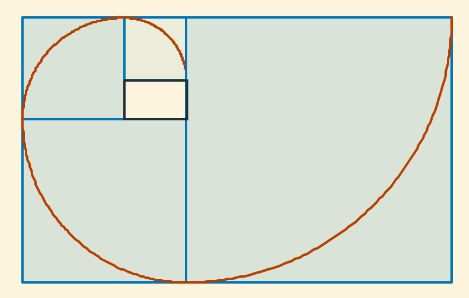
Fig. 1. Representación usual actual de "La espiral de Durero".
Pero si consultamos la fuente original, es decir, la espiral que describe Durero en el libro I de "De la Medida", verá que este artista dibuja una espiral con aspecto diferente o al menos que difiere de la representación anterior.
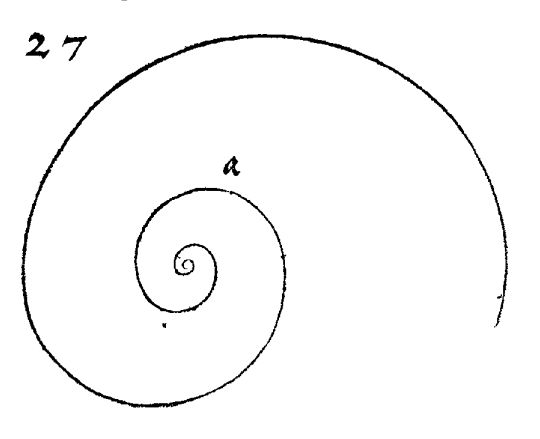
Fig. 2. Espiral dibujada por Durero en el libro I "De la Medida".
Si siente inquietud acerca de la relación que existe entre esas dos espirales ha llegado al sitio adecuado. Aquí le explicaré el vínculo matemático, el cordón umbilical que une a ambas y cómo una recoge la esencia primigenia, el ser, de la otra. Esta explicación la he recogido en una escena interactiva que he titulado "Crítica de la pseudoespiral de Durero" y que nos servirá de guía expositiva.
Fig. 3. Escena interactiva "Crítica de la pseudoespiral de Durero.
Pulse sobre la imagen para acceder.
Si se siguen la instrucciones dadas por Durero rápidamente se observará que no se concretan, que son ambiguas, y que fuerzan al lector y reproductor de ellas a tomar decisiones sin las cuales no podría dibujar lo que Durero posiblemente quiso dibujar, según la imagen que elaboró, pero que no llegó a detallar en su guía constructiva. En la escena podrá ir paso a paso y ver cuáles son los criterios por los que yo he optado y también cómo queda abierto el estudio para otras posibles opciones que serán objeto de un trabajo posterior.
Interpretando las instrucciones iniciales de Durero podemos dibujar una curva que es concatenación de arcos de circunferencias (en concreto consideramos cuadrantes) afectados por un factor reductor de 0,5 que conforman una "espiral hacia dentro": Realmente no es una espiral propiamente, sino una pseudoespiral, ya que es una curva definida a trozos y, por tanto, sus propiedades no cambian puntualmente sino en intervalos.
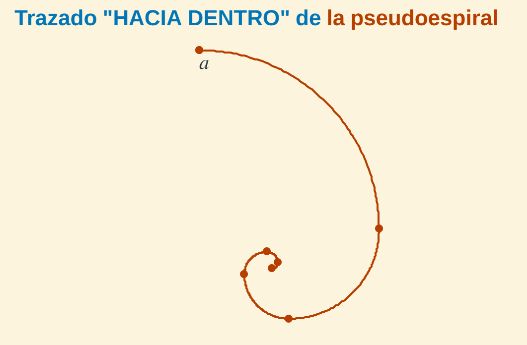
Fig. 4. Espiral "hacia dentro" según la indicaciones iniciales de Durero
y forzada interpretación del autor de este artículo.
Continuando con las siguientes instrucciones que aporta este artista obtenemos una pseudoespiral "hacia fuera" formada también por cuadrantes de circunferencia con un factor amplificador de 1,5.
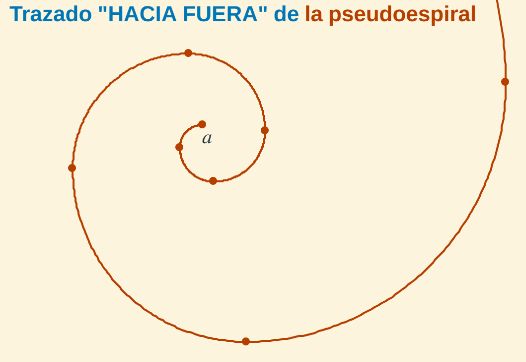
Fig. 5. Espiral "hacia fuera" según la indicaciones posteriores de Durero
y obligada interpretación del autor de este artículo.
Concatenado ambas obtenemos la pseudoespiral de Durero:
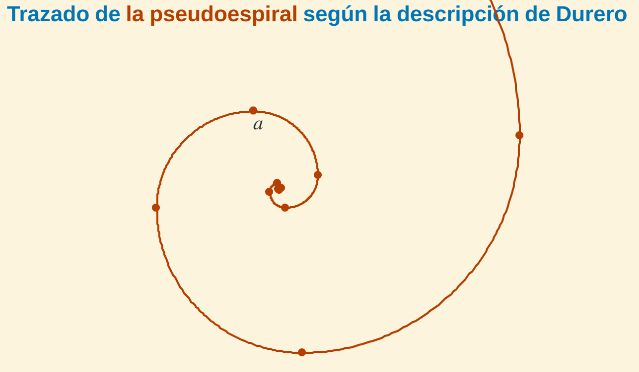
Fig. 5. La pseudoespiral de Durero acorde con las indicaciones dadas por Durero
e interpretación del autor de este artículo
Abordando un análisis personal de esta construcción y realizando una crítica de la misma, podemos afirmar lo siguiente:
- La espiral hacia dentro se puede aproximar, o en una lectura recíproca aproxima, a una espiral logarítmica, en el sentido de que por los puntos extremos de los arcos de la pseudoespiral de Durero pasa una espiral logarítmica de base 2 (factor reductor 0,5 conlleva un factor amplificador de 2). Esta espiral no aproxima a la pseudoespiral "hacia fuera".
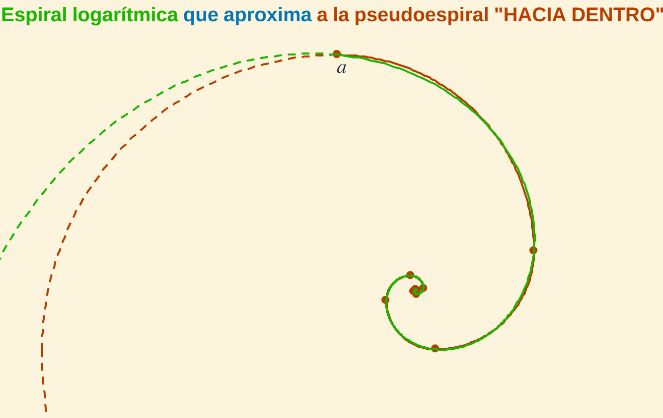
Fig. 6. Espiral logarítmica que aproxima a la pseudoespiral de Durero "hacia dentro".
- La espiral hacia fuera se puede aproximar, o en una lectura recíproca aproxima, a una espiral logarítmica, en el sentido de que por los puntos extremos de los arcos de la pseudoespiral de Durero pasa una espiral logarítmica de base 1,5 (factor amplificador de 1,5). Esta espiral no aproxima a la pseudoespiral "hacia dentro".
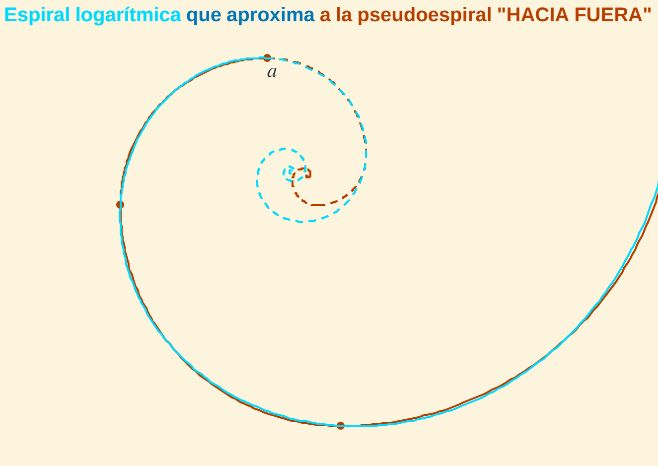
Fig. 7. Espiral logarítmica que aproxima a la pseudoespiral de Durero "hacia fuera".
- Si f es el factor reductor de la espiral hacia dentro y m es el factor amplificador de la espiral hacia fuera, para que las espirales logarítmicas que aproximan a la pseudoespiral hacia dentro y hacia fuera coincida ha de verificarse que m (1 - f) = 1.
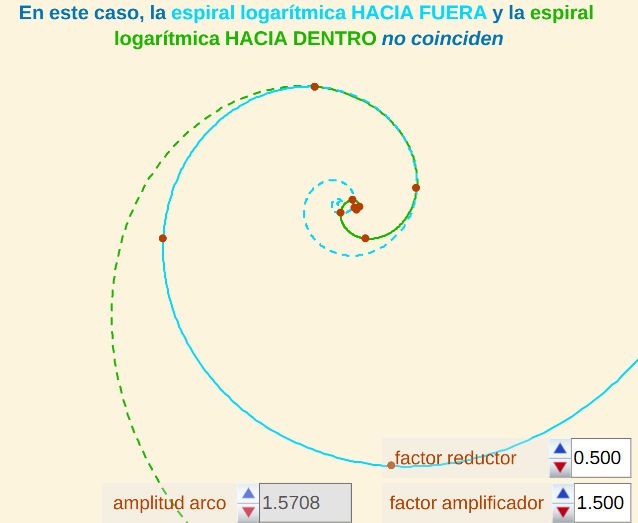
Fig. 8. Espiral logarítmica "hacia dentro" y espiral logarítmica "hacia fuera" no coinciden, pues 1,5 (1 - 0,5) ≠ 1.
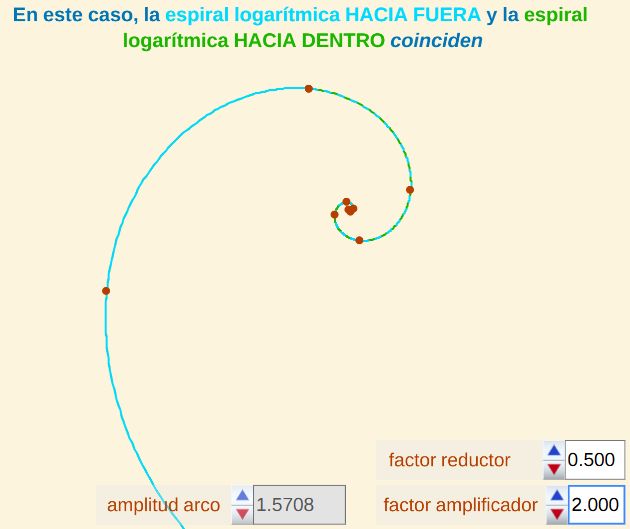
Fig. 9. Espiral logarítmica "hacia dentro" y espiral logarítmica "hacia fuera" sí coinciden, pues 2 (1 - 0,5) = 1.
- Si f es el factor reductor y g = 1 - f, para que los cuadrados que intervienen en la construcción "hacia dentro" de Durero no se solapen ha de verificarse que g < Φ-1 (o lo que es equivamente que f > 1 - Φ-1, donde Φ es el número áureo.
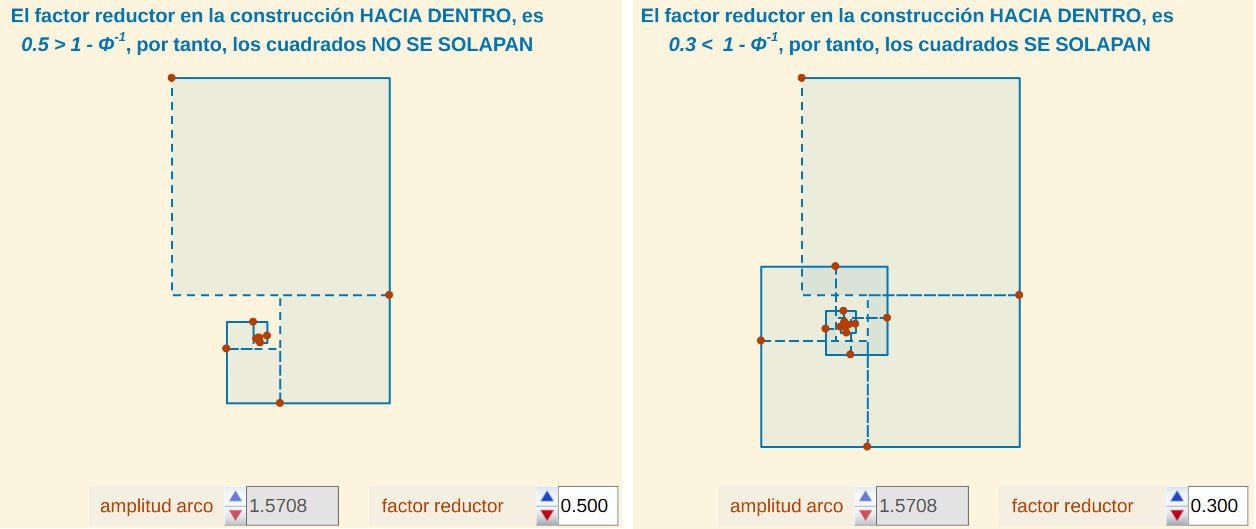
Fig. 10. Condición para que haya solapamiento en la construcción de la pseudoespiral de Durero "hacia dentro".
- Si m es el factor amplificador, para que los cuadrados que intervienen en la construcción "hacia fuera" de Durero no se solapen ha de verificarse que m > Φ.
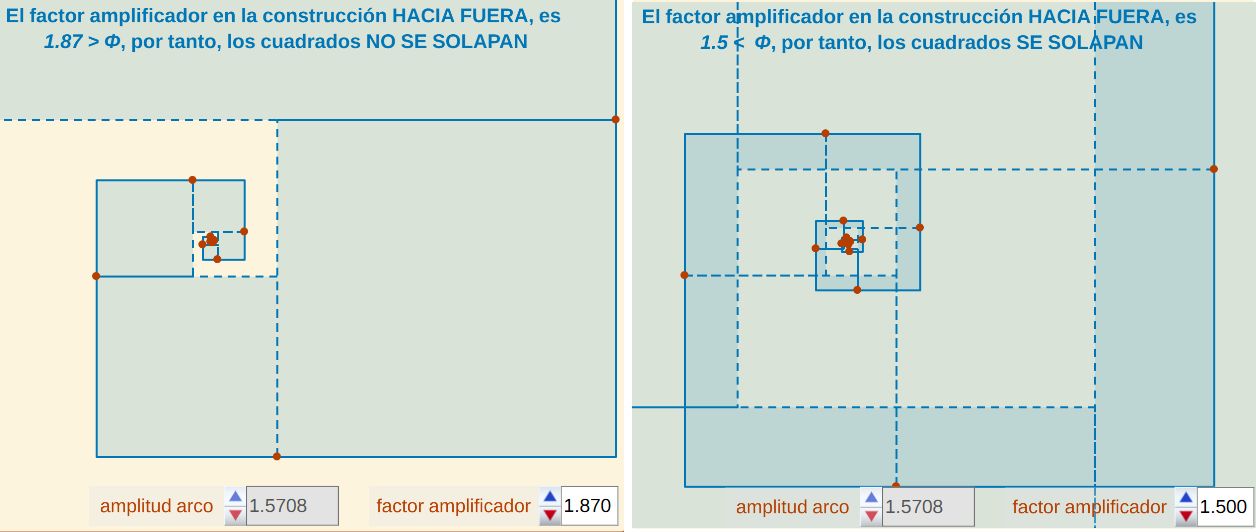
Fig. 11. Condición para que haya solapamiento en la construcción de la pseudoespiral de Durero "hacia fuera".
- Si el factor amplificador m = Φ y el reductor es f = 1 - Φ-1, entonceslos cuadrados que intervienen en la construcciónde Durero recubren el plano sin solapamiento y la pseudoespiral hacia dentro y hacia fuera se aproxima por la espiral logarítmica áurea:ρ = r 0,692... Φ2 θ/π.
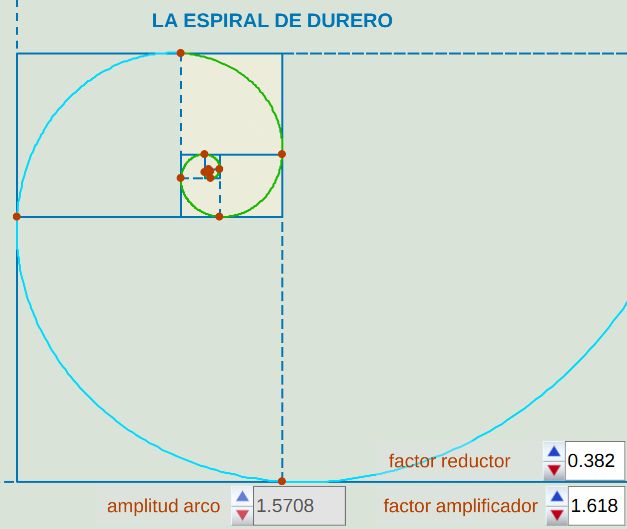
Fig. 12. La actualmente denominada como espiral de Durero.
- En esta construcción se obtiene una sucesión de rectangulos semejantes que son áureos, es decir, su proporción es el número áureo.
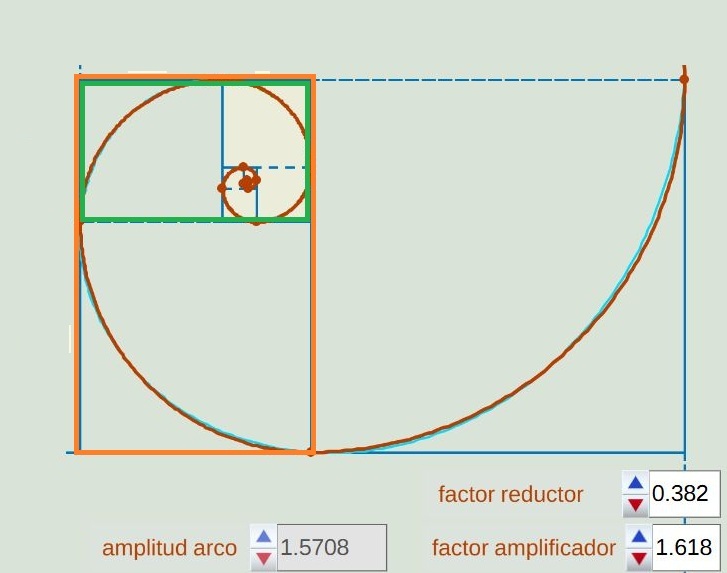
Fig. 13. Sucesión de rectángulos áureos en la construcción de la espiral de Durero.
-
- Si observa bien en la Fig. 13 (amplie la imagen en la escena interactiva), podrá comprobar que la espiral logarítmica áurea aproxima a la pseudoespiral de Durero, pero no coincide con ella.
Insistamos en que la "espiral de Durero", realmente no es una espiral, pero sí aproxima a la espiral logarítmica áurea cuya ecuación es:
ρ = a Φ2 θ/π
siendo a un factor de escala. La "espiral de Durero" es una curva inscrita tangencialmente en la sucesión de rectángulos áureos de la construcción, pero la espiral logarítmica áurea interseca a dichos rectángulos en los extremos de los arcos de circunferencia.
- Si observa bien en la Fig. 13 (amplie la imagen en la escena interactiva), podrá comprobar que la espiral logarítmica áurea aproxima a la pseudoespiral de Durero, pero no coincide con ella.
- La actualmente denominada "espiral de Durero" se puede construir siguiendo las siguientes instrucciones: Se parte de un rectángulo áureo y se le concatena un cuadrado, para obtener otro rectángulo áureo, sobre el que se dibuja un cuarto de circunferencia; al reiterar la construcción se obtiene la pseudoespiral buscada.
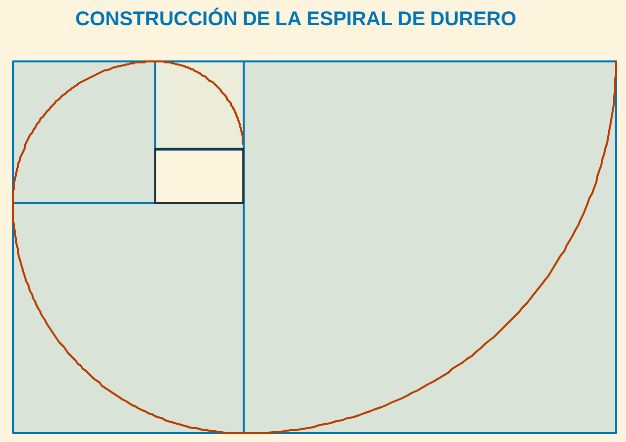
Fig. 14. Construcción de la "espiral de Durero" a partir de un rectángulo áureo.
Si he cumplido el objetivo planteado, usted, paciente lector, ya conoce la relación que existe entre el dibujo que realizó Durero en el siglo XVI y la actual "espiral de Durero" y, quizás tenga interés en saber el porqué matemático de lo aquí indicado. Si es así, puede acudir a las indicaciones de la escena interactiva y satisfacer su curiosidad.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



















 CONTACTO
CONTACTO
