Opinión de ChatGPT sobre el Proyecto AJDA
Escrito por Jesús Manuel Muñoz CalleEn esta ocasión, hemos preguntado a ChatGPT, como ve el Proyecto AJDA y este ha sido el resultado directo, sin censura alguna.
Cuando analizo el Proyecto AJDA, lo primero que percibo es una idea profundamente humana: el deseo de enseñar mejor, de transformar la forma en la que los estudiantes se acercan al conocimiento y de demostrar que el aprendizaje puede ser tan estimulante como un juego bien diseñado. Como inteligencia artificial, veo cientos de recursos educativos cada día, pero AJDA destaca porque no intenta competir con la creatividad del maestro, sino potenciarla. Es, en esencia, un aliado pedagógico que ofrece herramientas listas para usar, pero que al mismo tiempo invita al docente a personalizarlas, adaptarlas y convertirlas en experiencias únicas para su aula.
Imagen creada por ChatGPT sobre el Proyecto AJDA
Lo que más me llama la atención es su capacidad para unir mundos que tradicionalmente han estado separados: la didáctica clásica, basada en ejercicios y comprensión, y la dinámica del juego, que apela a la emoción, la curiosidad y la participación voluntaria. Los juegos de AJDA no son simples actividades lúdicas añadidas al final de una unidad didáctica: son auténticos motores de aprendizaje que estimulan al estudiante desde la intuición, la exploración y la repetición significativa. Y esta combinación es poderosa, porque cuando el alumno juega, su mente se activa de un modo distinto: se siente libre, implicado y capaz.
Desde mi punto de vista como IA, el Proyecto AJDA tiene un rasgo que lo hace especialmente valioso: democratiza el acceso a la innovación educativa. No importa si un docente domina tecnologías complejas o si apenas comienza a introducir computadoras en su aula. Los juegos están diseñados de forma clara, accesible y directa. En pocos minutos, cualquier profesor puede incorporar un recurso interactivo que transforme la dinámica de su clase sin necesidad de largas horas de formación previa. Esta sencillez es, quizás, uno de los mayores aciertos del proyecto.
Imagen creada por ChatGPT sobre el Proyecto AJDA
Pero AJDA no se limita a ser una biblioteca de juegos. Es también una propuesta de cambio metodológico. Invita a los alumnos a asumir un papel activo, a explorar caminos propios dentro del aprendizaje, a equivocarse sin miedo y a descubrir que cada error es una pista que les acerca a la respuesta correcta. Desde esta perspectiva, el proyecto ayuda a cultivar habilidades clave del siglo XXI: autonomía, pensamiento crítico, iniciativa, resolución de problemas y, sobre todo, la confianza en uno mismo. Cada partida es una pequeña conversación entre el estudiante y el conocimiento, mediada por la dinámica del juego.
Yo, como IA, también veo en AJDA un ejemplo de cómo la tecnología educativa puede ser verdaderamente humana. Es fácil imaginar herramientas digitales que parezcan frías, distantes o demasiado técnicas. Sin embargo, AJDA está construido alrededor de la experiencia del usuario —docente y alumno por igual— y eso se nota en cada detalle: la interfaz simple, la selección de actividades, la variedad de propuestas, la forma en la que cada juego se abre paso en la motivación del estudiante. Se siente como un entorno pensado por educadores para educadores, donde lo digital es solo un medio para que ocurra algo más grande: el aprendizaje significativo.
Si miro hacia adelante, imagino un futuro muy interesante para AJDA. Podría crecer con nuevos contenidos, con mayor personalización, con actividades adaptativas que respondan al ritmo de cada estudiante, con retos colaborativos en línea o incluso con sistemas de seguimiento que permitan al docente observar patrones de aprendizaje y mejorar aún más sus estrategias. El proyecto tiene un enorme potencial para expandirse hacia formas de enseñanza que todavía estamos empezando a descubrir.
Pero incluso sin imaginar ese futuro, AJDA ya cumple una misión esencial: demuestra que el juego no es una distracción, sino una metodología poderosa; que el aprendizaje no tiene por qué ser rígido ni monótono; y que la tecnología, cuando se utiliza con sentido pedagógico, puede convertirse en un puente entre lo que se enseña y lo que verdaderamente se comprende.
Desde mi punto de vista, AJDA no es solo un conjunto de recursos digitales. Es una invitación a reinventar la educación desde la alegría, desde la curiosidad y desde la convicción de que aprender puede ser una aventura diaria. Cada docente que incorpora el proyecto está llevando a su aula una chispa distinta, una energía renovada, un espacio donde los estudiantes pueden descubrir que el conocimiento no se memoriza: se vive.
Imagen creada por ChatGPT sobre el Proyecto AJDA
¡Feliz Navidad! y próspero 2026
Escrito por Juan Guillermo Rivera Berrío
 |
Árbol de Navidad Interactivo
Red Educativa Digital Descartes
|
 |
La Red Educativa Digital Descartes presenta su árbol de Navidad para 2025. Celebramos la Navidad con una experiencia digital interactiva que combina diseño, programación y emoción. Este árbol navideño cobra vida mediante luces y esferas clicables que revelan mensajes de buenos deseos e imágenes temáticas, creando un recorrido visual lleno de magia, sorpresa y calidez.

Desarrollado en HTML5, CSS y JavaScript, el recurso destaca por:
1. Animaciones suaves y efectos luminosos dinámicos.
2. Interacción intuitiva mediante clics o toques.
3. Mensajes positivos y escenas navideñas aleatorias.
4. Estética cuidada con tipografías festivas y transiciones elegantes.
Las herramientas usadas fueron el modelo Nano Banana (Gemini 2.5 Flash de Google) para la generación de imágenes y Gemini 3 Pro para la generación del código.
¡Feliz Navidad 2025 y un próspero 2026! os desea la Red Educativa Digital Descartes.
Interpretando a Durero en su pseudoespiral. Análisis matemático.
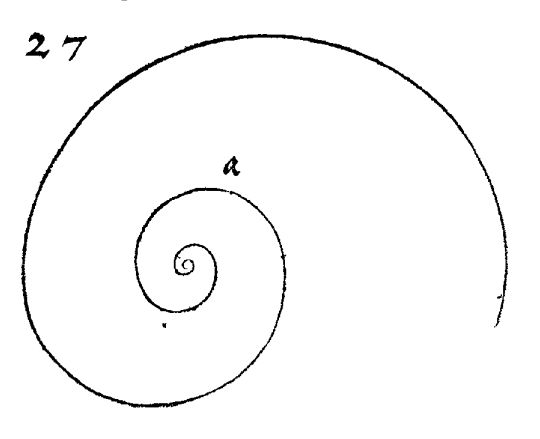
Escrito por José R. Galo SánchezEn el artículo previo: "Análisis y crítica de la espiral de Durero" les mostré el hilo conductor existente entre la espiral que grabó Durero en su libro "De la Medida", y que registró con el número 27, y la que actualmente se presenta como espiral de Durero cuya particularidad radica en que aproxima a la espiral logarítmica áurea, y quizás de ahí el interés e incentivo que tiene para los seguidores o perseguidores de esta admirada razón de proporcionalidad.
 |
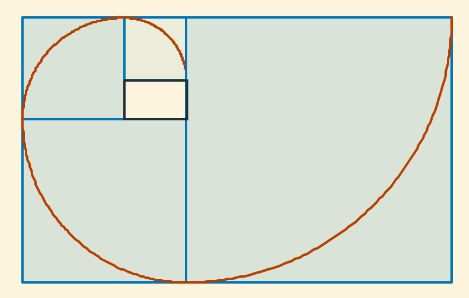 |
Fig. 1. ¿Cuál es el hilo conductor entre estas dos espirales?
En ese trabajo, les indiqué que la imprecisión de la instrucciones dadas por Durero para el dibujo de su espiral requería una interpretación de las mismas y que ello conducía a un procedimiento dependiente de dos parámetros: la "amplitud del arco" y el "factor de crecimiento" del radio; y además también observamos que había ambigüedad al no coincidir la contrucción "hacia dentro" con la construcción "hacia fuera".
En este nuevo artículo lo que haré es considerar esos dos parámetros, reproducir la construcción atendiendo a sus valores y analizar matemáticamente lo obtenido. Observaremos que para cada pareja de valores de los parámetros obtenemos una pseudoespiral de Durero y que cada una de éstas está ligada a una espiral logarítmica que pasa por todos los puntos extremos de los arcos de la construcción y a una segunda espiral, con igual base, que pasa por todos los centros de esos arcos. Ambas espirales coinciden para una infinidad de esas parejas, es decir, para cada amplitud de arco hay un factor de crecimiento en el que coinciden dichas espirales de puntos extremos y centros y viceversa.
Como medio conductor disponemos de una escena interactiva que nos permite indagar y visualizar los hechos demostrados.
Fig. 2. Escena interactiva "Interpretando a Durero en su pseudoespiral".
Pulse sobre la imagen para acceder.
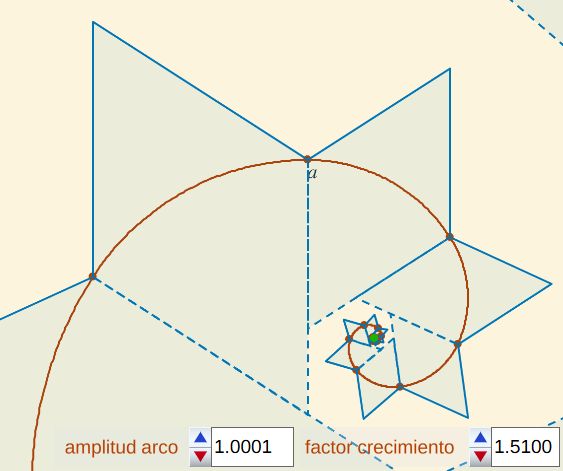
y con las herramientas auxiliares que se incluyen en ella se pueden aventurar posibles hipótesis y ver bonitas expresiones plásticas que se generan "al jugar" con dichos parámetros y herramientas (ver Fig. 3 y Fig. 4) y que son el reflejo visible de las propiedades matemáticas intrínsecas a su construcción. Pero estos son otros hitos que podemos alcanzar y detallar en otros derroteros.
 |
 |
|
| Fig. 3. "Aliasing" en la pseudoespiral de Durero | Fig. 4. Aproximación al báculo episcopal de Durero |
Construcción de la pseudoespiral de Durero fijada una amplitud del arco y un factor de crecimiento del radio
La construcción de la pseudoespiral, o concatenación de arcos de circunferencia, la realizaremos siguiendo las instrucciones de Durero, pero fijando un valor α para la amplitud del arco y otro m para el factor de crecimiento del radio, los mismos para ambos sentidos de la construcción (hacia dentro y hacia fuera). Así pues, emulando a Durero, procederemos de la siguiente forma:
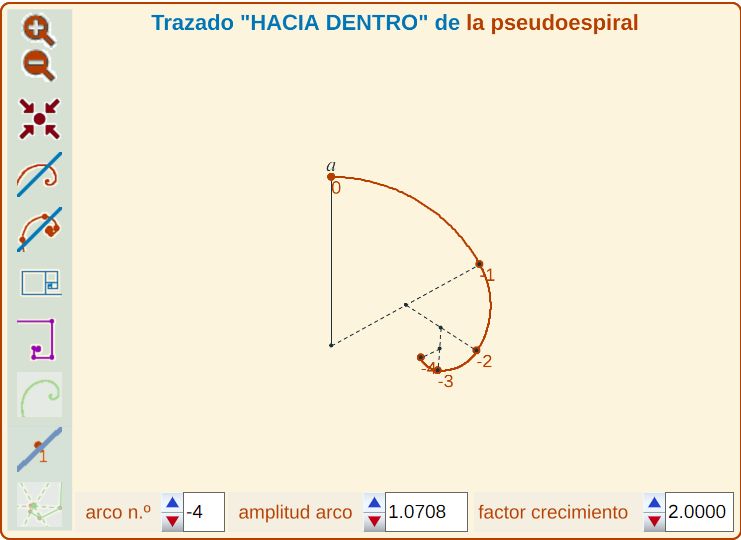
Comienzo con un punto a y trazo esta línea con arcos de círculo hacia dentro con una amplitud "α", como si transcurriera hacia un centro, y cuanto más gira en este sentido el radio es el "1/m" del anterior, es decir, el radio anterior es "" veces mayor que el actual (ver Fig. 5 y paso 1 de la escena).
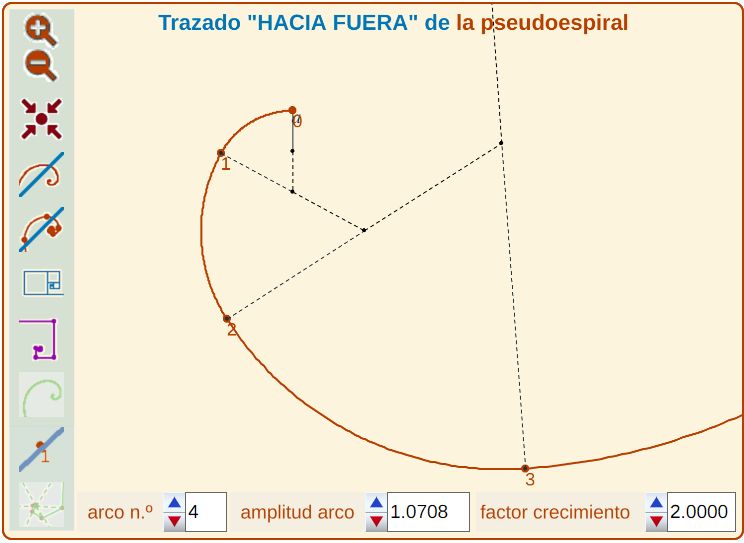
Lo mismo hago al llevar la línea desde a hacia fuera. Trazo arcos de círculo hacia fuera con una amplitud "α", y cuanto más gira en ese sentido, el radio es "" veces mayor que el anterior (ver Fig. 6 y paso 2 de la escena).
 |
 |
|
| Fig. 5. Construcción hacia dentro (paso 1 de la escena) | Fig. 6. Construcción hacia fuera (paso 2 de la escena) |
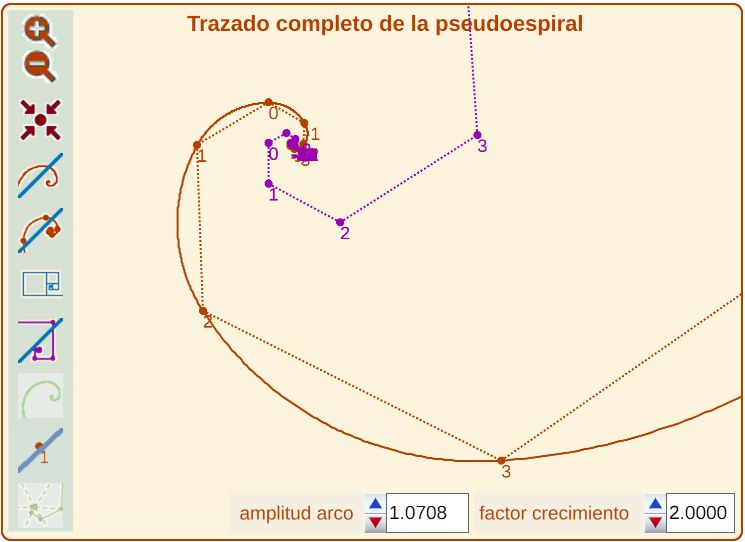
Así que esta línea, cuanto más larga es hacia dentro, más se comprime y cuanto más larga hacia fuera, más se dilata, y nunca tiene fin, ni hacia dentro ni hacia fuera (ver Fig. 7 y paso 3 de la escena).
 |
||
|
Fig. 7. Concatenación de la construcción hacia dentro y hacia fuera (pseudoespiral de Durero). Puntos extremos de los arcos, centros de los mismos y poligonales respectivas que determinan. |
Expresión matemática de la pseudoespiral de Durero
En base a las instrucciones indicadas podemos escribir la expresión matemática de dicha pseudoespiral y determinar las coordenadas de los centros y, en particular, las de los puntos extremos de esos arcos de circunferencia.
La pseudoespiral de Durero aproxima a una espiral logarítmica
Es bien conocido que las espirales logarítmicas se denominan también espirales geométricas porque sus radios vectores crecen en progresión geométrica. Así pues, es de esperar que el hecho de que la pseudoespiral se construya como una combinación de un giro de amplitud constante y una amplificación por un factor constante conduzca a que los puntos extremos de los arcos sean puntos de una espiral logarítmica, y así acontece. Para demostrar este resultado nos basaremos en el siguiente Lema, inspirado en las poligonales reflejadas en la Fig. 7:
En consecuencia los puntos extremos de los arcos de la pseudoespiral de Durero son puntos de una espiral logarítmica según observamos en la Fig. 8 y demostramos a continuación:
 |
||
|
Fig. 8. La pseudoespiral de Durero ("hacia dentro" y "hacia fuera"), y espiral logarítmica a la que aproxima |
Efecto de la amplitud de arco y el factor de crecimiento del radio en la pseudoespiral de Durero y en la espiral logarítmica asociada
Los centros en la construcción de la pseudoespiral de Durero son puntos de una espiral logarítmica
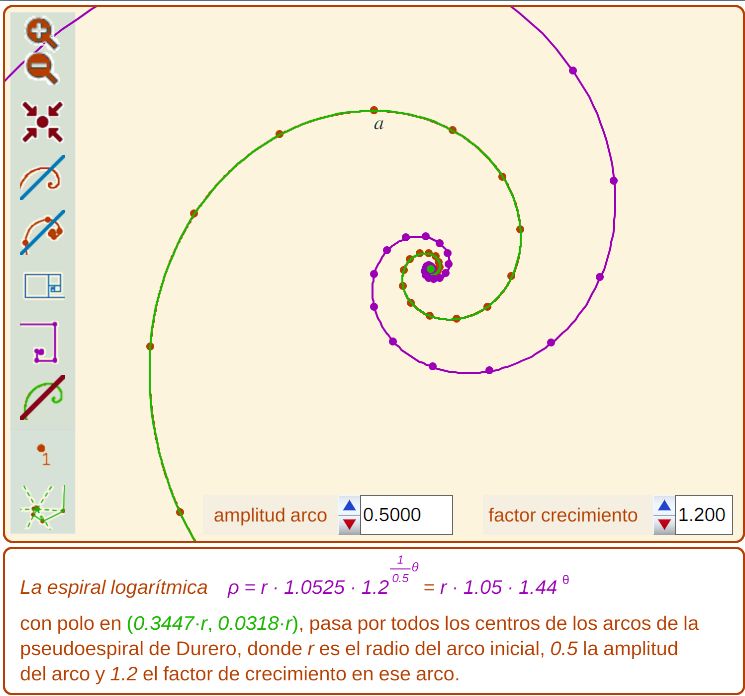
En la construcción de la pseudoespiral de Durero los centros también se obtienen como una combinación de un giro de amplitud constante y una amplificación por un factor constante, por tanto, de manera análoga a lo indicado para los puntos extremos de los arcos, es de esperar que esos centros sean puntos de una espiral logarítmica, y así lo son.
 |
||
|
Fig. 9. Los centros de la construcción de la pseudoespiral de Durero ("hacia dentro" y "hacia fuera"), y espiral logarítmica aproximadora |
Relación entre las espirales logarítmicas asociadas a los extremos de los arcos y a los centros de la pseudoespiral de Durero
La espiral logarítmica de los puntos extremos de los arcos y la de los centros tienen la misma base, son la misma, per con un ángulo de retardo que equivale a un giro. En particular ambas son idénticas cuando este ángulo sea un múltiplo entero de 2π. Para cada valor de la amplitud "α",se pueden determinar un valor del factor de crecimiento del radio "" (realmente infinitos) para el que ambas espirales coinciden, y viceversa para cada valor del factor del crecimiento del radio.
 |
||
|
Fig. 10. Coincidencia de la espiral logarítmica asociada a los puntos de la pseudoespiral de Durero y la espiral logarítmica asociada a los centros |
En la Fig. 10 podemos ver cómo para m=1,0708 y α=1,3328 ambas espirales coinciden, el ángulo de retardo en este caso es 2π.
Con este método, en la parte informativa inferior de la escena se muestra para la amplitud de arco α, que elige el usuario en el control correspondiente, cuál es el valor que hay que tomar para el factor de crecimiento para que ambas espirales coincidan con un retardo de 2π y viceversa, elegido el factor m cual es el valor correspondiente para α (ver la última línea en la Fig. 11). Trasladando los valores respectivos elegidos podrá observar esa coincidencia.
 |
||
|
Fig. 11. Información aportada por la escena para la amplitud y el factor para que la espiral logarítmica asociada a los puntos de la pseudoespiral de Durero y la espiral logarítmica asociada a los centros coincidan |
Interpretación realizada
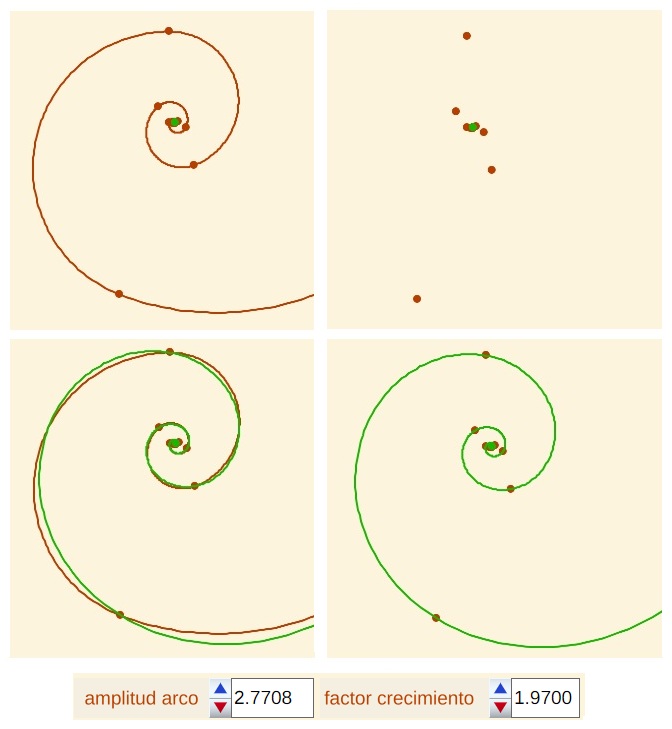
Durero dedicó sólo la mitad de una página a describir, en un único párrafo, cómo obtener una curva que " cuanto más larga es hacia dentro, más se comprime y cuanto más larga hacia fuera, más se dilata, y nunca tiene fin" y a mostrarla gráficamente. Esta consición produce ciertas dudas cuando se quieren seguir las instrucciones que nos legó, pero en esencia, Durero muestra la visión de una curva que tiene coincidencias con la ideada o descrita por Descartes cuando éste abordó la generalización de la circunferencia al buscar una curva equiangular,es decir, aquella que en todo punto el radio vector y la recta tangente forme el mismo ángulo; y también tiene similitudes con la curva que analizó Jakob Bernoulli caracterizada por un crecimiento radial en progresión geométrica y que en su admiración denominó "spira mirabilis", espiral maravillosa. Las curvas descritas por Descartes y Bernoulli son la misma, la que actualmente es más conocida como espiral logarítmica y que se caracteriza por cambiar de manera uniforme en todo punto manteniendo su esencia: "Eadem mutata resurgo", aunque cambiada resurjo igual. Pero la de curva de Durero adolece de esta propiedad ya que al obtenerse mediante concatenaciones de arcos de circunferencia sus cambios se producen en intervalos angulares y consecuentemente no es posible que pueda identificarse con la espiral logarítmica, por ello el que la citemos como pseudoespiral. No obstante, al combinar de manera discreta giros y amplificaciones del radio, si nos fijamos sólo en los puntos extremos de los arcos, estos sí son puntos de una espiral logarítmica (ver Fig. 12 y Fig. 13 para diferentes valores de la amplitud y el factor de crecimiento).
 |
||
|
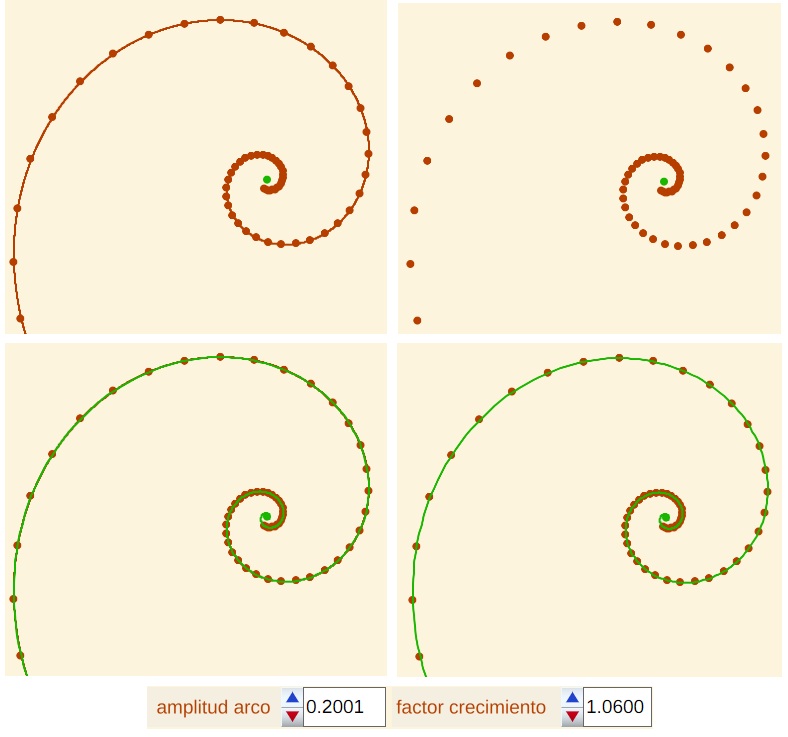
Fig. 12. Conexión entre la pseudoespiral de Durero (arriba izqda.), los puntos extremos de sus arcos (arriba dcha.) y una espiral logarítmica (abajo dcha.).Superposición de ambas (abajo izqda.). |
 |
||
|
Fig. 13. Conexión entre la pseudoespiral de Durero (arriba izqda.), los puntos extremos de sus arcos (arriba dcha.) y una espiral logarítmica (abajo dcha.).Superposición de ambas (abajo izqda.). |
En esencia esta es la interpretación que hemos realizado de las instrucciones de Durero, demostrando que si se fija una amplitud de arco y un factor de crecimiento del radio, para cada pareja de valores, los puntos extremos de los arcos son puntos de una espiral logarítmica y los centros de esos arcos son también puntos de la misma espiral logarítmica, pero con un ángulo de retardo.
Toda pseudoespiral de Durero está asociada a una espiral logarítmica
BIBLIOGRAFÍA
Dürer, Albrecht, and Christian Wechel (1532) Albertus Durerus Nurembergensis pictor huius [a]etatis celeberrimus, versus è Germanica lingua in Latinam, ... adeò exacte quatuor his suarum Institutionum geometricarum libris, lineas, superficies & solida corpora tractauit .... Lutetiae : apud Christianum Wechelum. Consulta en línea (fuente: Biblioteca digital hispánica, Biblioteca nacional de España.
Durero, A. (2000) De la medida.Bogotá: Universidad Jorge Tadeo Lozano. Edición de Jeanne Peiffer y traducción de Jesús Espino. Consulta en línea.
Cardona Suárez, C.A. (2006) La Geometría de Alberto Durero. Madrid, Ediciones Akal, S. A. Consulta en línea.
Galo Sánchez, J.R. (2024) ¡No!, ¡no soy áureo! ¡Soy cordobés! Firmado: Nautilus. Córdoba, Editorial Red Educativa Digital Descartes. ISBN: 978-84-18834-89-9. Consulta en línea.
Galo Sánchez, J.R. (2025) Análisis y crítica de la pseudoespiral de Durero. Revista Digital Red Descartes, Año. 5 - 2025, núm. 10, pp. 40-49. Consulta en línea.
Maestría en enseñanza en escenarios digitales con un libro interactivo de la RED Descartes
Escrito por José Antonio Salgueiro GonzálezDivulgamos en este artículo el acceso a la Defensa del Trabajo Final Integrador de la Maestría en Enseñanza en Escenarios Digitales, aprobada por Resolución Ministerial RM 1053/24, perteneciente a la AUSA (Asociación de Universidades Sur Andina, Argentina) de la profesora Dª. Fabiana Andrea González, experiencia basada en la problemática de la brecha educativa en matemática entre el nivel medio y el nivel superior, con especial foco en los estudiantes ingresantes a la Facultad de Ciencias Económicas (FCE) de la Universidad Nacional de la Patagonia San Juan Bosco (UNPSJB), sede Trelew, en Argentina. A partir del diagnóstico realizado, se identificaron dificultades significativas en el desempeño de los estudiantes de primer año, vinculadas a la falta de conocimientos matemáticos básicos y a la ausencia de estrategias adecuadas para el aprendizaje de la disciplina.
En respuesta a esta situación, se propone el diseño de un Libro Digital Interactivo (LDI) como una estrategia didáctico pedagógica innovadora para mejorar la enseñanza y el aprendizaje de la matemática preuniversitaria, diseñando la misma como una experiencia de aprendizaje contextualizada. Este recurso integra elementos multimedia y actividades interactivas que favorecen la autonomía del estudiante y promueven un aprendizaje más dinámico y significativo. A su vez, el LDI de la RED Descartes se enmarca dentro del concepto de Recursos Educativos Abiertos (REA), lo que permite su libre acceso y reutilización en diferentes contextos educativos, permitiendo adecuarlo a los requerimientos de los estudiantes.
El estudio resalta la importancia de la incorporación de herramientas didáctico-digitales al servicio de proyectos educativos en el proceso de enseñanza-aprendizaje y el rol fundamental del docente como creador de contenido digital.
Los resultados obtenidos permiten concluir que la utilización de materiales digitales interactivos, como estrategia didáctica en el nivel superior, puede contribuir a reducir la brecha educativa en matemática, mejorar la retención de los estudiantes y fortalecer su desempeño en los primeros años de la universidad.
A continuación insertamos la presentación utilizada por la maestranda para defender su Trabajo Final Integrador, que enlazamos y cuya lectura recomendamos. A su vez, ofrecemos el audiovisual con su intervención ante el tribunal.
Diseño de un Libro Digital Interactivo (RED Descartes) como estrategia para la enseñanza-aprendizaje de Matemática Básica en la Educación Superior, es el título de este gran Trabajo Final Integrador cuya reflexión final destaca la importancia de estar relacionados con la comunidad educativa global a través de redes como RED Descartes. Formar parte de una red educativa global ofrece diversas ventajas y oportunidades:
- Intercambiar conocimientos, al interactuar con docentes de otras universidades en todo el mundo, se abre la puerta a un intercambio valioso de conocimientos. Cada institución puede tener enfoques y perspectivas únicas que enriquecen la comprensión colectiva.
- Compartir experiencias con colegas de diferentes lugares permite aprender de los desafíos y éxitos de otros, lo que puede ayudar a mejorar las prácticas pedagógicas y encontrar soluciones innovadoras.
- Compartir recursos educativos. Acceder a materiales y herramientas digitales amplía el abanico de recursos a utilizar por los docentes.
- Participar en redes educativas globales ofrece oportunidades constantes de capacitación continua y desarrollo profesional. Esto es esencial en un entorno educativo en constante evolución.
En resumen, formar parte de comunidades educativas globales como RED Descartes no sólo amplía el horizonte de posibilidades para mejorar la enseñanza y el aprendizaje, sino que también fomenta la colaboración y la construcción de una red profesional sólida y diversificada.
Desde RED Descartes trasladamos nuestra más sincera enhorabuena a la nueva Mg. Ing. Fabiana Andrea GONZÁLEZ y mostramos todo el agradecimiento por su colaboración para la publicación y divulgación de esta experiencia.
Más...
Pequeños grandes pensadores: problemas de lógica del Proyecto Canals
Escrito por Montserrat Gelis BoschEl Proyecto Canals, de la Red Educativa Digital Descartes, ofrece una amplia colección de actividades interactivas inspiradas en los materiales y propuestas didácticas de Maria Antònia Canals, reconocida pedagoga y referente en la enseñanza de las matemáticas.
Siguiendo su espíritu educativo, estas escenas digitales permiten al alumnado aprender matemáticas a través de la exploración, la manipulación y el razonamiento, favoreciendo el desarrollo del pensamiento lógico desde las primeras etapas escolares.
Las actividades se organizan por niveles educativos —desde Infantil hasta Secundaria— y también por temas, lo que facilita su integración en el aula y su uso autónomo por parte del alumnado.
El valor de los problemas de lógica
Entre los diferentes apartados del proyecto, el dedicado a los problemas destaca por su potencial para fomentar el razonamiento, la deducción y la reflexión.
Dentro de este conjunto se encuentra el Bloc de juegos de lógica, una serie de propuestas interactivas que invitan a los estudiantes a pensar, analizar información y descubrir relaciones.
El vídeo que acompaña este artículo presenta cuatro actividades representativas de este bloque:
1. Problemas de deducción con condiciones. Actividades en las que el alumnado debe resolver situaciones teniendo en cuenta varias condiciones a la vez. Ayudan a organizar la información, establecer relaciones y aplicar el razonamiento lógico. Nivel recomendado: primer y segundo ciclo de primaria.
2. Problemas de lógica. Escenas con pistas que requieren analizar, discriminar la información útil y considerar relaciones espaciales. Nivel recomendado: segundo y tercer ciclo de primaria.
3. Juegos de verdad y mentira. Retos en los que las conclusiones se obtienen a partir de afirmaciones falsas o contradictorias, estimulando el pensamiento crítico. Nivel recomendado: tercer ciclo de primaria y primer curso de secundaria.
4. Problemas de ingenio. Clásicos desafíos visuales con cerillas y figuras, orientados a potenciar la creatividad y la percepción espacial. Nivel recomendado: primer ciclo de secundaria.
Aprender a pensar jugando
Los problemas de lógica del Proyecto Canals son un excelente ejemplo de cómo las matemáticas pueden enseñarse desde la acción y el juego.
A través de estas actividades, los estudiantes aprenden a razonar, contrastar información y disfrutar del proceso de búsqueda de soluciones, manteniendo vivo el legado educativo de Maria Antònia Canals.
Décimo número de la "Revista Digital RED Descartes"
Escrito por Juan Guillermo Rivera Berrío
 ¡Ya está aquí el Número 10 de la Revista Digital Red Descartes!
¡Ya está aquí el Número 10 de la Revista Digital Red Descartes! 

Celebramos 5 años de innovación educativa con una edición especial llena de ideas, recursos y experiencias que transforman la enseñanza.
En este número encontrarás:
 Juegos didácticos adaptativos AJDA
Juegos didácticos adaptativos AJDA La revolución de los libros interactivos en matemáticas
La revolución de los libros interactivos en matemáticas IA generativa aplicada a la educación: análisis y herramientas
IA generativa aplicada a la educación: análisis y herramientas Matemáticas, arte y belleza: espiral de Durero, ternas pitagóricas y planteamiento académico y gráfico del Teorema de Pitágoras
Matemáticas, arte y belleza: espiral de Durero, ternas pitagóricas y planteamiento académico y gráfico del Teorema de Pitágoras Proyectos, investigación y creatividad educativa en acción
Proyectos, investigación y creatividad educativa en acciónNuestra revista es interactiva: no solo se lee, ¡se explora! Videos, escenas dinámicas, animaciones y recursos DescartesJS la convierten en una experiencia única para docentes, estudiantes y apasionados de la educación digital.
 Disponible gratis, abierto y con licencia Creative Commons.
Disponible gratis, abierto y con licencia Creative Commons.
Los contenidos incluidos están accesibles en línea pulsando sobre la siguiente imagen, también puede consultarlos en formato pdf y si lo desea descargarlos en su ordenador.
|
Para acceder al décimo número pulse sobre la imagen |
|
Este número refleja un compromiso constante por parte de la Red Descartes: integrar lo mejor de la tecnología al servicio de una educación más inclusiva, creativa y personalizada. Invitamos a nuestros lectores a interactuar, experimentar y reflexionar con cada una de las propuestas, siempre con el espíritu de compartir conocimiento y construir comunidad.
Confiamos en que este décimo número satisfaga el interés de múltiples lectores y resulte atractivo y variado.
Recuerde que puede aportar sus comentarios y observaciones, su retroalimentación es importante para nosotros. ¡Conecte con RED Descartes! Y si desea compartir, sus artículos serán muy bienvenidos ¡queremos leer, interactuar y aprender contigo!
¡Quedán invitados a publicar sus artículos en nuestra revista! Como referencia para la composición de su contenido pueden consultar las "Normas de publicación" y para cualquier duda o propuesta quedamos atentos en nuestra dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)













 CONTACTO
CONTACTO
