Trigonometría interactiva en Telesecundaria.
Escrito por Montserrat Gelis BoschEn esta ocasión, presentamos la unidad de Trigonometría, perteneciente al subproyecto Telesecundaria de la Red Educativa Digital Descartes. Este subproyecto integra y difunde objetos de aprendizaje interactivos desarrollados en México, específicamente para la modalidad educativa de Telesecundaria. Los recursos están organizados en tres áreas de conocimiento: Matemáticas, Física y Química, clasificados según el sistema educativo de México.
Acceso y estructura de los materiales
Para acceder a los recursos, simplemente seleccionamos el apartado de Materiales y navegamos hasta Matemáticas 3º. Aquí encontramos un índice con enlaces directos a cada objeto interactivo, lo que facilita un acceso rápido y evita recorrer toda la página en busca del contenido deseado. Cada recurso está identificado con un código que indica el curso, el área de conocimiento, el bloque, el tema y el subtema, además de contar con una imagen identificativa y un enlace para acceder al recurso o descargarlo.
Explorando la unidad de Trigonometría
La unidad de Trigonometría está dividida en cuatro apartados fundamentales:
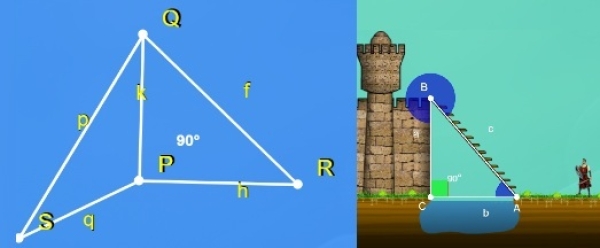
- Explora: el estudiante aprende los conceptos básicos del triángulo rectángulo, como los catetos, la hipotenusa y las razones trigonométricas.
- Reconoce: se presentan diferentes polígonos para identificar lados y ángulos específicos de los triángulos rectángulos.
- Tablas y Círculo: en este apartado, el alumno interactúa con una circunferencia moviendo un punto, mientras se completa una tabla con los valores de las razones trigonométricas.
- Problemas: se proponen dos situaciones prácticas:
- Medición de la amplitud de un río, utilizando un triángulo rectángulo ajustable sobre el escenario interactivo.
- Cálculo de la altura de una torre y la amplitud del foso que la rodea, aplicando el mismo principio de manipulación del triángulo.
Un aprendizaje interactivo y significativo
La propuesta didáctica de esta unidad permite al estudiante explorar, reconocer y aplicar los conceptos de trigonometría de forma dinámica y práctica, favoreciendo un aprendizaje significativo y alineado al currículo educativo.
Te invitamos a explorar esta unidad de Trigonometría en el subproyecto Telesecundaria de la Red Descartes, un recurso que, sin duda, enriquecerá la enseñanza y el aprendizaje de esta área de las matemáticas.
Para acceder a esta y otras unidades, visita el sitio oficial de la Red Descartes y descubre el aprendizaje interactivo que ofrece cada uno de sus recursos.
Conversor de ficheros del Proyecto AJDA
Escrito por Jesús Manuel Muñoz CalleUno de los aspectos más destacados de los juegos didácticos del Proyecto AJDA es su capacidad para personalizar contenidos mediante la creación de ficheros de preguntas adaptados a las necesidades del usuario. Estos ficheros pueden ser archivados, clasificados y reutilizados, lo que fomenta una experiencia de aprendizaje propia más dinámica y versátil.
Con el propósito de ampliar las posibilidades de uso, mejorar la compatibilidad y fomentar la reutilización de estos contenidos, se ha desarrollado un conversor de ficheros para el Proyecto AJDA. Este conversor, creado con el apoyo de diversas inteligencias artificiales generativas, representa un avance en la gestión de contenidos personalizados. Pulsando sobre la siguiente imagen se accede a la página principal del conversor.
En esta página, al seleccionar el formulario correspondiente al tipo de fichero deseado, se mostrarán sus características junto con una imagen representativa de un juego AJDA de ese tipo y una captura de pantalla del conversor. Al hacer clic en el botón Abrir conversor, se abrirá una nueva ventana con el conversor específico para el tipo seleccionado.
Los conversores de los diferentes tipos comparten un diseño uniforme. En la parte superior se encuentran el logotipo de AJDA, el título y una breve descripción del conversor. Justo debajo, una línea indica el formato y muestra un fondo de color verde, naranja o rojo, dependiendo de la idoneidad del archivo seleccionado.
A continuación, se encuentra el área destinada para seleccionar o arrastrar los archivos de entrada. Debajo de esta, hay una sección dedicada a visualizar posibles errores detectados durante el proceso.
En la parte inferior, se presentan dos campos de texto numerados: el de la izquierda muestra el contenido de entrada, que puede ser modificado manualmente, y el de la derecha contiene el contenido de salida generado por el conversor.
Por último, en el pie de la página, se encuentra una barra de herramientas con botones para realizar acciones clave como conversión, descarga, exportación y limpieza de los datos.
Los ficheros de entrada admiten dos formatos: el formato TXT, propio de los juegos didácticos AJDA, y el formato GIFT (General Import Format Technology), un estándar ampliamente utilizado para crear preguntas de evaluación en plataformas educativas como Moodle.
Realizamos una realización de los formatos utilizados en el conversor:
- TXT. Formato nativo de los juegos didácticos del Gran Torneo.
- GIFT. Ampliamente utilizado en plataformas de e-learning como Moodle, Chamilo, Open edX o Canvas LMS.
- PDF. Ideal para conservar su diseño y estructura.
- DOC. Compatible con procesadores de texto.
- CSV. Pensado para su uso en hojas de cálculo.
- HTML. Formato estándar para contenido web.
- XML. Lenguaje muy extendido basado en etiquetas.
El siguiente vídeo ofrece una explicación sencilla sobre cómo utilizar el conversor.
Boletín 9 - Novedades IA Generativas
Escrito por Juan Guillermo Rivera Berrío
 ¡Ya está disponible el Boletín de abril 2025 de la Red Educativa Digital Descartes!
¡Ya está disponible el Boletín de abril 2025 de la Red Educativa Digital Descartes! 
Sumérgete en las últimas novedades en inteligencia artificial generativa, con análisis de OpenAI o3, Gemini 2.5 Pro, Llama 4 y los lanzamientos más impactantes en generación de imágenes y videos.
Esta edición especial, impregnada del espíritu de Pascua, también reflexiona sobre cómo la IA puede transformar el arte, la espiritualidad y la memoria colectiva.
Además, descubre nuevas herramientas educativas, investigaciones de vanguardia, y la evolución de plataformas como Gamma, NotebookLM, Hugging Face, DeepSite y más.
Una edición imperdible para quienes quieren estar al día en tecnología, innovación y cultura digital. 
Descubre el Proyecto PI de la RED Descartes
Escrito por Montserrat Gelis BoschEl Proyecto PI, desarrollado por la RED Descartes, ofrece una completa colección de recursos educativos digitales e interactivos para la Educación Primaria, centrados en dos áreas clave: Lengua Castellana y Matemáticas.
Estos materiales están especialmente diseñados para fomentar el aprendizaje autónomo y activo del alumnado, tanto en el aula como en casa. Se pueden utilizar con pizarras digitales, ordenadores o tabletas, y todos ellos se encuentran disponibles de forma gratuita.
Estructura de las unidades:
Cada unidad del Proyecto PI sigue una estructura común, que facilita el trabajo progresivo de los contenidos:
- Introducción: se presentan los conceptos básicos a través de explicaciones claras y ejemplos visuales.
- Exploración: se proponen actividades guiadas para afianzar el aprendizaje paso a paso.
- Ejercicios: serie de actividades interactivas para practicar y comprobar los resultados.
- Evaluación: ejercicios finales con autocorrección que permiten valorar lo aprendido.
Esta estructura coherente favorece la comprensión, el refuerzo y la evaluación de los contenidos trabajados.
En el vídeo que acompaña este artículo, se realiza un breve recorrido por la página web del proyecto y se exploran dos ejemplos concretos, uno por cada área:
- En el área de Matemáticas, se accede al tema Medidas y se muestra la unidad Razones, donde se aprende a calcular razones y resolver problemas aplicando este concepto.
- En el área de Lengua Castellana, dentro del tema Vocabulario, se presenta la unidad Artículos, demostrativos y posesivos, que trabaja el uso correcto de estas palabras a través de explicaciones, ejemplos y ejercicios interactivos.
El Proyecto PI es una herramienta valiosa para docentes, familias y alumnado. Te invitamos a explorar sus múltiples unidades y a integrar estos recursos en tu práctica educativa diaria.
¡Aprender puede ser interactivo, dinámico y muy motivador!
Puedes ver el vídeo a continuación para conocer mejor este proyecto.
Más...
Ejemplos de ayuda de IA en la mejora de juegos didácticos AJDA
Escrito por Jesús Manuel Muñoz CalleLas inteligencias artificiales generativas son una herramienta poderosa en muchos ámbitos y, como no podía ser de otra manera, también pueden aportar valor a los juegos didácticos AJDA. En este artículo, exploraremos algunos ejemplos concretos de su aplicación.
Comenzaremos por la carátula del juego. Con el apoyo de inteligencias artificiales generativas, es posible crear diseños atractivos e interesantes, incluyendo el título del juego. A continuación, presentamos un ejemplo para juego El lienzo del destino.
Otra posible aportación es la creación de una portada ilustrativa que represente la esencia del juego.
Además, es posible incorporar imágenes, elementos, fondos y decorados al juego, todos ellos generados mediante inteligencia artificial.
La integración de música de fondo o efectos sonoros es otra opción interesante para mejorar la experiencia del juego.
Además de las mencionadas, se pueden incorporar muchas otras, como por ejemplo:
Asistencia en la redacción de las instrucciones o reglas del juego.
- Apoyo en la creación de una narrativa envolvente.
- Generación de elementos visuales para el juego, como avatares, símbolos, escudos, cartas, banderas o escenarios.
- Creación de personajes animados que formen parte de la historia.
- Asistencia en la creación de preguntas y respuestas para desafíos educativos.
- Desarrollo de misiones o tareas que se ajustan al estilo de aprendizaje del jugador.
- Generación de voces para personajes.
Participantes de tres continentes y trece países
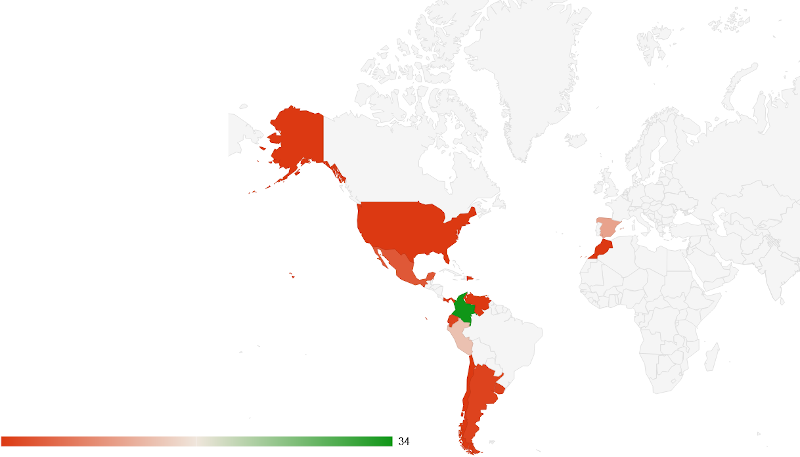
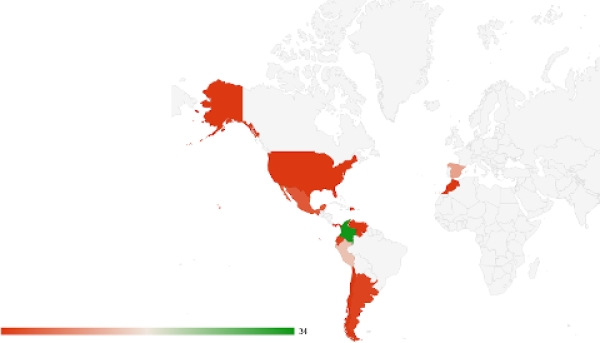
Escrito por José Antonio Salgueiro GonzálezComienza la I Edición del Curso para el Diseño de Objetos interactivos con DescartesJS e IA, que forma parte del programa de Educación Abierta de RED Descartes y cuenta con participantes distribuidos en tres continentes y doce países, todos profesionales de la educación que comprenden diversas etapas educativas y una amplia gama de especialidades. Como viene siendo habitual, compartimos el diagrama de sectores con el porcentaje de personas inscritas según el país de origen:
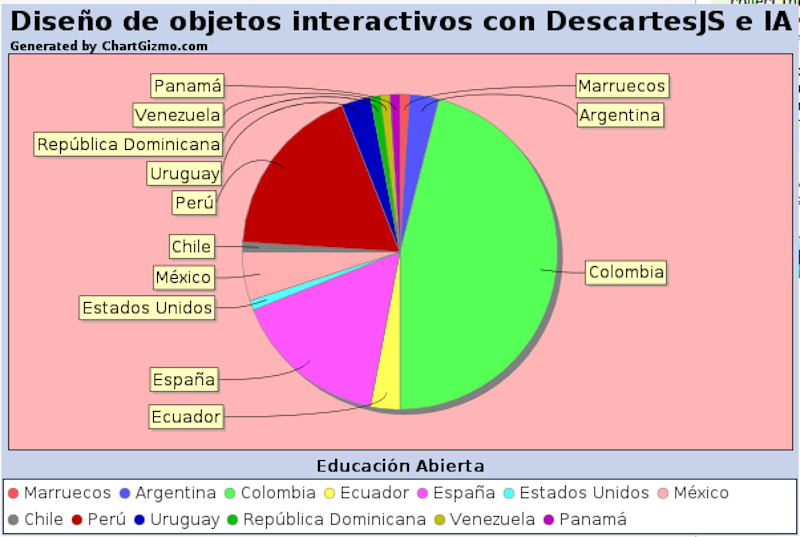
Nuestra gran experiencia y trayectoria en el desarrollo de acciones formativas nos ha encaminado a convocar un curso bastante demandado en el que se aúnan las herramientas de inteligencia artificial para la enseñanza y la potente herramienta de autor DescartesJS, de software libre, promovida y soportada por nuestra asociación en colaboración con instituciones y organizaciones de Colombia y México, fundamentalmente.
Pues bien, una vez han sido atendidas todas las inscripciones de forma personalizada y cada participante ha recibido las debidas instrucciones iniciales y los recursos y materiales para la primera sesión, corresponde, en el marco del programa de Educación Abierta de nuestra red, compartir la información con nuestros seguidores, usuarios y personas interesadas en aprender de forma independiente. Así que, en primer lugar, proporcionamos la
para continuar con el resto de recursos:
- Descarga el software libre DescartesJS para tu sistema operativo
- Tutorial sobre DescartesJS - Nivel I
- Herramientas de Inteligencia Artificial para la enseñanza
- Lista en Youtube con vídeos de apoyo
- Descripción detallada de cada sesión
Los vídeos con la grabación de cada sesión del curso, que se imparte por videoconferencia según el calendario establecido, se irán publicando progresivamente en la página denominada
Diseño de objetos interactivos con DescartesJS e IA
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)





 Lee el boletín completo aquí: [
Lee el boletín completo aquí: [





 CONTACTO
CONTACTO
