Este mes vamos a ver la unudad de sistemas de ecuaciones de 2ºESO del Proyecto EDAD:

Hemos visto los siguiente puntos:

1.Ecuaciones lineales
   Definición. Solución

2.Sistemas de ecuaciones lineales    
   Definición. Solución
   Número de soluciones

3.Métodos de resolución
   Reducción
   Sustitución
   Igualación

4.Aplicaciones prácticas
   Resolución de problemas

Materiales publicados en DVD. ISSN: 2444-9180 Dep. Legal: CO-2079-2015

Vol. I, enero de 2016
Vol. I - Núm. 1 (3,7 GB)		Vol. I - Núm. 2 (4,7 GB)		Vol. I - Núm. 3 (4,3 GB)
Incluye los materiales de los subproyectos @prende.mx, Pizarra interactiva, Proyecto Canals, Unidades didácticas, Comperetencias,ASIPISA, Misceláneas, iCartesiLibri, Ingeniería y Tecnología, Un_100, Problemas, Estudio Europeo de Comunicación Lingüística y GEOgráfica.		Incluye los materiales del Proyecto ED@D Matemáticas (1º, 2º y 3º de Secundaria) y Aplicaciones de juegos didácticos en el aula.		Incluye los materiales del Proyecto ED@D Matemáticas (4º de Secundaria) y Proyecto ED@D Ciencias Naturales y Física y Química de Secundaria.
Carátulas		Carátulas		Carátulas
Portada Contraportada Galleta		Portada Contraportada Galleta		Portada Contraportada Galleta

Materiales publicados en DVD. ISSN: 2444-9180 Dep. Legal: CO-2079-2015

Vol. II, enero de 2017
Vol. II - Núm. 1 (3,9 GB)		Vol. II - Núm. 2 (4,1 GB)		Vol. II - Núm. 3 (3,2 GB)
Incluye los materiales de los subproyectos Misceláneas, iCartesiLibri, ED@D Matemáticas LOMCE (1º, 2º y 3º de Secundaria), Telesecundaria  y GEOgráfica.		Incluye los materiales del Proyecto Unidades didácticas, Competencias y ED@D Matemáticas LOMCE (4º de Secundaria).		Incluye los materiales de Aplicaciones de juegos didácticos en el aula y Plantillas.
Carátulas		Carátulas		Carátulas
Portada Contraportada Galleta		Portada Contraportada Galleta		Portada Contraportada Galleta

El proyecto Miscelánea de la RED Descartes contiene un conjunto de actividades que tratan aspectos muy variados del currículum de Matemáticas y que se pueden utilizar como apoyo y refuerzo de los temas que se estén trabajando en clase.

Es un conjunto de materiales digitales interactivos, clasificados por temas o por niveles, que han sido diseñados con el objetivo de que el alumnado investigue, deduzca y llegue a conclusiones por sí mismo.

En este video se muestra una pequeña selección de actividades de álgebra y su inserción en un curso Moodle para su aplicación en el aula.

Este mes vamos a ver la unidad de "Expresiones algebraicas" de 1ºESO que va a ser la primera toma de contacto de nuestros alumnos con el álgebra y las ecuaciones:

En este vídeo hemos visto los siguientes puntos:

1.Lenguaje algebraico
   Expresiones algebraicas
   Traducción de enunciados
   Valor numérico

2.Monomios
   Características
   Suma y resta
   Producto

3.Ecuaciones
   Solución de una ecuación
   Ecuaciones equivalentes
   Resolución de ecuaciones
   Resolución de problemas

Lugares geométricos: Trisectriz de Maclaurin.

Continuamos con el estudio de los lugares geométricos y en esta entrada vamos a desarrollar una aproximación al conocimiento del l.g. conocido como "Trisectriz de Maclaurin". Este l.g. resuelve, en el siglo XVIII, el problema clásico de la trisección de un ángulo pero no como pretendían los antiguos sabios griegos; aunque sí de una forma muy elegante y funcional.

Para profundizar en el estudio del lugar geométrico y en el de uso del editor DescartesJS, hemos elaborado, de forma muy esquemática, las pequeñas utilidades que se muestran a lo largo del capítulo. Son escenas basadas en la obra del profesor Pedro González Enríquez, trabajo que está en proceso de adaptación a las nuevas versiones del editor DescartesJS.

La primera de las escenas genera la Trisectriz de Maclaurin de la siguiente manera:

• Establecido un sistema de referencia y considerada una distancia cualquiera, por ejemplo a = 1 se crean los siguientes elementos:
  • Con centro en el punto (4·a,0) y radio 4·a se traza una circunferencia.
  • Dibujar la recta vertical x = -2·a
  • Se considera un punto cualquiera, A, de la circunferencia. Este punto es importante pues hará posible la creación del lugar geométrico.
  • Trazar la cuerda que pasa por el origen de coordenadas y por el punto A. Esta cuerda cortará a la recta  x = -2·a  en un punto que hemos llamado B que variará según A se desplaza por la circunferencia.
  • Se considera el punto medio del segmento AB al que llamaremos C y que, solidario con la cuerda se desplaza por el plano. Este es el punto fundamental ya que es el que genera, en su desplazamiento, el l.g. en estudio.
• Cuando el punto A recorre la circunferencia, el punto C define la Trisectriz de Maclaurin
• Para observar la generación del l.g. basta con pulsar el botón "anima/para" de la escena.
• Conviene ver la generación del l.g. con la curva oculta.
• El botón "curva" oculta/muestra la gráfica de la curva:
  x·(x² + y²) = a·(3·x²-y²)   - ecuación cartesiana del l.g.

lugar geométrico

Para los lectores menos familiarizados con el proceso de creación de escenas DescartesJS indicamos que:

• Si se observan trazos o gráficas, generalmente de color rojo, no justificados, o se desea volver a ver la generación del l.g. es suficiente con pulsar el botón limpia, que quitará de la escena los trazos indeseados.
• El botón zum ajusta el tamaño de la parte visible. Este botón al ser activado limpia, de forma predeterminada, la escena.
• El pulsador a controla el tamaño del lazo de la trisectriz y el botón inicio reinicia la escena.

Como en anteriores ocasiones indicamos que la utilidad es fácilmente adaptable y admite las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.

La escena que exponemos a continuación muestra como el lazo de la trisectriz es en realidad un trisector de ángulos. Esto se evidencia de la siguiente forma:

• En esta ocasión el punto A, que pertenece al l.g., es un control gráfico que puede desplazarse por la parte superior de la curva. Conviene que este desplazamiento se haga lentamente para así observar la formación del ángulo principal BCA y su trisección COA (o COA').
• El vértice del ángulo principal es el punto C (2·a,0)
• El punto B (3·a,0) define con el C el lado CB de dicho ángulo principal. El otro lado del ángulo es el segmento CA o en su caso, A en el 2º cuadrante, CA'. La trisección del ángulo BCA es el ángulo COA (COA'). Observar la definición gráfica de los ángulos al desplazar el control A.
• Cuando el ángulo principal se aproxima a 180º la secante OA, o bien OA', tiende a ser la tangente del l.g. en 0⁺ que en este punto tiene de ecuación   y = 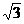x  por lo tanto la trisección de 180º es el ángulo que dicha tangente forma con la parte positiva del eje horizontal, esto es 60º.

Lazo trisectriz de Maclaurin.

En los siguientes trabajos presentamos una recreación de las escenas anteriores realizadas con el programa GeoGebra con los propósitos de ahondar en el conocimiento de ambas plataformas: GeoGebra y DescartesJS de forma paralela para lograr los objetivos señalados en entradas anteriores.

La siguiente utilidad genera la trisectriz al desplazar el punto A por la circunferencia.

creación del l.g.

En la siguiente escena se usa el lazo de la curva de Maclaurin como trisector de ángulos.

Lazo trisector de Maclaurin

Proponemos al lector el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.

En la sección de vídeo, hemos elegido uno que trata sobre lugares en el mundo conocidos, fundamentalmente, por sus características geométricas. El objetivo  es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Los Lugares Geométricos".

Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.

En próximas entradas continuaremos el estudio de los lugares geométricos y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.

Bibliografia:

• Parte de la Unidad creada por el profesor Pedro González Enríquez que se encuentra en fase de adaptación a DescartesJS.
• Caracol de Pascal
• Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
• Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
• La abundante información encontrada en la Wikipedia

Ildefonso Fernández Trujillo. 2017

El Grupo Empresarial IC S.L., prestigiosa Institución Comercial especializada en la ejecución integral de grandes proyectos de interior que abarcan la construcción, las instalaciones, el mobiliario y el mantenimiento, muestra, además, su interés por el mundo de la Educación y la difusión del conocimiento, como base de cualquier actividad humana, y por ello ha patrocinado cincuenta recursos educativos interactivos generados con Descartes JS, que son funcionales en cualquier tipo de dispositivo (ordenador, tableta o smartphone), englobados en tres apartados o bloques:

• Tres libros interactivos de 2º de ESO correspondientes al currículo de Matemáticas respectivamente en castellano, catalán y gallego. Cada libro se compone de trece unidades didácticas, es decir, treinta y nueve recursos.
• Seis objetos para el aprendizaje competencial de 3º de Primaria desarrollados en base a materiales de las pruebas de diagnóstico. Realmente se contabilizan doce recursos ya que se incluye una versión original estática y otra versión dinámica, que es lo usual en nuestros proyectos.
• Cinco misceláneas de álgebra y funciones de 2º de ESO.

Grupo IC trabaja en exclusiva para grandes marcas de los sectores retail, hoteles, lujo, sanitario, oficinas y restauración, siendo cuatro las empresas que conforman el grupo:

• IC Construction.- Es la constructora del grupo especializada en construcción integral de interiores.
• Efficentre.- Es la instaladora del grupo especializada en soluciones de eficiencia energética.
• Ekipashop.- Empresa del grupo dedicada a la fabricación y montaje de mobiliario a medida realizado con maderas ecológicas certificadas PEFC o FSC®.
• Servishop.- Dedicada a la gestión integral del mantenimiento con un call center técnico 24h/365d.

Aunque Grupo IC construye grandes proyectos de interior para importantes y conocidas empresas en cualquier lugar del mundo, es posible que sea Primark Gran Vía Madrid el más conocido, pues con sus 12.300 metros cuadrados de superficie de ventas es la mayor tienda que esta firma posee en España.

Guardar

Guardar

Guardar

Guardar

Un_100 es un proyecto de la RED que recoge unidades didácticas de matemáticas y física para el bachillerato y la universidad.

Los materiales están clasificados por temas y todas las unidades se han desarrollado utilizando el mismo esquema o plantilla común, se organiza la información en cuatro fases: motivación, inicio, desarrollo y cierre.

En este vídeo vamos a ver con detalle la unidad cálculo integral que consta de una serie de actividades de introducción al cálculo para bachillerato y los primeros cursos universitarios. Esta unidad contiene muchos ejemplos de muestra y diferentes tipos de ejercicios autocorregibles lo cual permite al alumnado practicar según sus necesidades favoreciendo así su aprendizaje.