La ficción de Radio Descartes en el programa Boulevard de Radio Euskadi
Escrito por José Antonio Salgueiro GonzálezProyecto Descartes estuvo invitado al programa Boulevard de Radio Euskadi en su emisión del día 25 de agosto, para tratar el tema de la radio ficción en la divulgación de personajes matemáticos.
Boulevard es un programa que reúne, desde las 6:00, información y análisis de la información de Euskadi y el mundo, mientras que a partir de las 10:00 el espacio se dedica a la actualidad más cercana y a los temas que nos interesan.
En la imagen superior hay un enlace a la página del programa en su totalidad, mientras que compartimos el audio con la entrevista dedicada a la asociación Red Educativa Digital Descartes o Proyecto Descartes, agradeciendo a Radio Euskadi y al programa Boulevard su difusión y la posibilidad de acceder a su contenido.
Recordamos que "El personaje misterioso" es un programa de Radio Descartes conducido por Eva Perdiguero y Ángel Cabezudo con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Concretamente, tras la entrevista del invitado, que no se desvela, el escuchante debería conocer su nombre o bien tomar los datos que se aportan en la dramatización y tomarse un tiempo para averiguarlo consultando en la múltiple documentación que hoy día se encuentra disponible, principalmente en Internet o en libros divulgativos de Historia de las Matemáticas o de Matemáticos célebres, pasando a responder en un comentario del blog de nuestro portal. A la semana siguiente, se publica un puzle creado con Descartes JS que incluye imágenes alusivas, alegóricas o de efemérides que descubren al personaje.
Hasta la fecha se han realizado un total de doce entrevistas ficticas a personajes matemáticos, que enlazamos junto a su intérprete:
- Personaje misterioso - 1, interpretado por Ángel Cabezudo Bueno
- Personaje misterioso - 2, interpretado por Eva Perdiguero Garzo
- Personaje misterioso - 3, interpretado por José Antonio Salgueiro González
- Personaje misterioso - 4, interpretado por Ricardo Alonso Liarte
- Personaje misterioso - 5, interpretado por Antonio Pérez Sanz
- Personaje misterioso - 6, interpretado por Marta Macho Stadler
- Personaje misterioso - 7, interpretado por Elena Vázquez Abal
- Personaje misterioso - 8, interpretado por José María Sorando Muzás
- Personaje misterioso - 9, interpretado por Montse Gelis Bosch
- Personaje misterioso - 10, interpretado por Xosé Eixo Blanco
- Personaje misterioso - 11, interpretado por Elena Ramírez Ezquerro
- Personaje misterioso - 12, interpretado por Bernat Ancochea Millet
Hay que recordar también que "El personaje misterioso" resultó finalista en la categoría de Mejor Iniciativa Educativa a los V Premios Asociación Podcast, entregados en Barcelona en 2014.
Por último, y como anunciamos al final de la entrevista del programa Boulevard de Radio Euskadi, añadir que esta iniciativa se ha extrapolado al entorno educativo de Secundaria, de manera que son ya alumnos y alumnas de 3º ESO los encargados de realizar entrevistas a personajes matemáticos, como iremos difundiendo en próximos artículos donde las divulgaremos.
Resolvemos problemas con Descartes y Photomath y comunicamos y compartimos usando medios tecnológicos
Escrito por José Antonio Salgueiro GonzálezEn mi último artículo hacía referencia a la reciente publicación de la Orden por la que se desarrolla el currículo correspondiente a la Educación Secundaria Obligatoria en la Comunidad Autónoma de Andalucía, convencido de que tendrá gran similitud con las publicadas por los organismos competentes en otras comunidades autónomas. Extraído literalmente, podemos encontrar que la habilidad de formular, plantear, interpretar y resolver problemas es una de las capacidades esenciales de la actividad matemática, estando involucradas muchas otras competencias además de la matemática (CMCT), entre otras, la comunicación lingüística (CCL), al leer de forma comprensiva los enunciados y comunicar los resultados obtenidos; el sentido de iniciativa y emprendimiento (SIEP), al establecer un plan de trabajo en revisión y modificación continua en la medida que se va resolviendo el problema; la competencia digital (CD), al tratar de forma adecuada la información y, en su caso, servir de apoyo a la resolución del problema y comprobación de la solución; o la competencia social y cívica (CSC), al implicar una actitud abierta ante diferentes soluciones.
En otro de los párrafos de la orden se nos dice que el uso de los recursos TIC en la enseñanza y el aprendizaje de las matemáticas, las calculadoras y el software específico deben convertirse en herramientas habituales para la construcción del pensamiento matemático, introduciendo elementos novedosos como las aplicaciones multimedia tales como libros interactivos con simuladores, cuestionarios de corrección y autoevaluación automatizados, etc. que, en cualquier caso, deben enriquecer el proceso de evaluación del alumnado. Además, el uso de blogs, wikis, gestores de contenido CMS, plataformas de e-learning, repositorios multimedia, aplicaciones en línea y entornos colaborativos favorecen el aprendizaje constructivo y cooperativo.
Finalmente, también hay una frase en la que se menciona la utilización de medios tecnológicos en el proceso de aprendizaje para la realización de cálculos de tipo numérico, algebraico o estadístico, así como para comunicar y compartir, en entornos apropiados, la información y las ideas matemáticas.
Pero como docentes, ¿de qué forma podemos afrontar esta demanda y qué tipo de actividades planificar para conseguirlo?
El Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija ha realizado con un grupo de 4º ESO durante el curso 2015/2016 la iniciativa denominada "Aprendemos a resolver problemas con Descartes", basada en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes" y llevaba a cabo anteriormente con el alumnado de 1º de Bachillerato de Ciencias e Ingeniería.
En el primer artículo enlazado en el párrafo anterior encontrarás todos los detalles de la experiencia, desglosada en tres fases en las que puedes comprobar que es una sencilla actividad que se adapta a lo establecido en la orden, así que te animamos a ponerla en práctica con tus alumnos y alumnas y, por supuesto, a compartir tus iniciativas.
Con Descartes, ¡no todo son TIC!
Escrito por José Antonio Salgueiro GonzálezRecientemente se ha publicado la Orden por la que se desarrolla el currículo correspondiente a la Educación Secundaria Obligatoria en la Comunidad Autónoma de Andalucía, se regulan determinados aspectos de la atención a la diversidad y se establece la ordenación de la evaluación del proceso de aprendizaje del alumnado. Como docente andaluz, hago referencia a la misma, aunque estoy convencido de que tendrá gran similitud con las publicadas por los organismos competentes en otras comunidades autónomas.
Pues bien, en la sección dedicada a las estrategias metodológicas, se recoge que para el bloque de Geometría es conveniente la experimentación a través de la manipulación y aprovechar las posibilidades que ofrecen los recursos digitales interactivos para construir, investigar y deducir propiedades. En base a ello, quiero compartir con todos esta sencilla actividad consistente en la construcción, manipulación y experimentación con los sólidos platónicos, que desarrollé con mi alumnado del 2º curso del desaparecido Programa de Cualificación Profesional Inicial, hoy Formación Profesional Básica, con quien tuve la fortuna de trabajar y aprender todo lo que son capaces de conseguir y ofrecer.
Organizados en equipos, prácticamente en una sesión tienen los cinco sólidos construidos en papel, pudiendo manipular, observar, tocar y contar sus elementos. Así que, en la siguiente sesión se puede pasar a la investigación, creando una tabla con los nombres de cada poliedro regular y contar y anotar el número de caras de cada uno, el número de aristas y el de vértices para que intenten redescubrir la fórmula de Euler.
Los recursos proceden del Proyecto Descartes y comparto la relación de los recomendados junto a sus enlaces para descarga o visualización:
- Poliedros regulares
- Desarrollo de los sólidos platónicos
- Test interactivo de 15 preguntas sobre poliedros regulares
- Tabla interactiva para experimentar con la fórmula de Euler
- Ejercicios interactivos sobre poliedros regulares y relación de Euler, eligiendo la opción del menú contextual
Puede concluirse la experiencia proponiendo una actividad de ampliación, según la edad y capacidad del alumnado, consistente en dibujar en dos dimensiones los cinco sólidos platónicos conocidos sus vértices y teniendo en cuenta las aristas que no se ven, cuyos recursos también puedes encontrar en los siguientes enlaces de Proyecto Descartes:
- Plantilla con los vértices del tetraedro
- Plantilla con los vértices del cubo
- Plantilla con los vértices del octaedro
- Plantilla con los vértices del dodecaedro
- Plantilla con los vértices del icosaedro
La mayoría de estos recursos están seleccionados de la unidad interactiva del Proyecto ED@D" denominada "Cuerpos geométricos", que también se encuentra disponible en catalán y gallego: "Cossos geomètrics" y "Corpos xeométricos, aunque también algunos tienen su origen en la unidad didáctica dedicada a "Los poliedros regulares y la esfera".
Si compartimos nuestras experiencias de aula, que no tienen por qué ser grandiosas, aprendemos todos de todos y facilitamos nuestra tarea.
No olvides que estamos en la era de las cuatro ces: compartir, comunicar, colaborar y confiar. Además, RED Descartes pone sus servidores a tu disposición para divulgar las experiencias que desarrolles con los recursos de Proyecto Descartes. ¿Te animas?
Contacta con nosotros en Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Esta semana presentamos una serie de actividades que forman parte del grupo de objetos PISA con ordenador, incluido en el Proyecto Competencias de la RED Descartes. Estos recursos están estructurados como objetos de aprendizaje y se han creado a partir del conjunto de preguntas liberadas en la edición PISA 2015, en la cual se introdujo la evaluación por medios informáticos.
Para cada tipo de pregunta se dispone de la versión original y la versión adaptada por la RED Descartes. En la versión adaptada, una vez finalizado el último ejercicio, se presentan diferentes opciones de corrección: corrección en pantalla, descarga en un fichero, envío por correo o impresión.
En el siguiente vídeo se presentan los objetos que forman parte de este proyecto y se muestran las actividades propuestas en el recurso síndrome de despoblamiento de colmenas.
EDAD 4ºESO Opción B Funciones y gráficas
Escrito por Alfonso Saura EspínEn este video vamos a revisar la unidad correspondiente a "Funciones y gráficas" de 4ª ESO Opción B:
En este vídeo se han tratado los siguientes apartados:
1.Funciones reales
Funciones, concepto
Gráfica de una función
Dominio y recorrido
Funciones definidas a trozos
2.Propiedades de las funciones
Continuidad y discontinuidades
Funciones periódicas
Simetrías
3.Tasa de variación y crecimiento
Tasa de variación media
Crecimiento y decrecimiento
Máximos y mínimos
Puntos de inflexión
Ya puedes "pinear" y seguir los tableros de RED Descartes en Pinterest
Escrito por José Antonio Salgueiro GonzálezYa puedes "pinear" los recursos digitales interactivos y seguir los tableros de RED Descartes en Pinterest, pudiendo acceder desde el enlace que te proporcionamos o, mejor aún, desde el menú de redes sociales que encontrarás en la zona superior derecha de nuestro portal.

Si no eres usuario habitual de esta red social, te indicamos que debes estar registrado y con la sesión abierta en Pinterest para poder visitar los diferentes tableros que hemos creado, así como para recorrer la variedad de recursos que los componen, cuya descripción te informará sobre el proyecto de RED Descartes al que pertenecen y sobre su contenido u objetivos.
Si desconoces Pinterest, puedes tomar contacto rápidamente con el vídeo del canal TEC titulado "¿Qué es y cómo se usa Pinterest?
Proporcionalidad. Las espirales XII
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales XII
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.
Como muestra enlazamos la unidad sobre Crecimiento Exponencial, del subproyecto TELESECUNDARIA,
la GEOevaluación de los estados y ciudades de México.
y el ejemplo de: Asocia parejas de imágenes y textos (2).
Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D en particular los materiales de 2º y 4º LOMCE y las adaptaciones de los trabajos de Javier de la Escosura Caballero: "Geometría dinámica del trángulo" que enlazamos a continuación
y el de Cuadrilateralia, donde se fomenta el estudio y conocimiento de las características matemáticas de los objetos mediante la manipulación virtual de los mismos y que enlazamos con la imagen siguiente.
Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el primero de los métodos para trisecar un ángulo con la Concoide de Nicomedes. El ángulo a trisecar es el formado por el eje polar y la recta que une el polo con el punto que se desplaza por la directriz.
El análisis de la escena y su modificación, fundamentalmente en la situación del tercio del ángulo mencionado anteriormente, nos lleva a descubrir interesantes características de la Concoide. También son interesantes las modificaciones funcionales que mejoren las prestaciones de la utilidad.
Mencionar, por último, que la escena es copia de la que en su día publicó el profesor Pedro González Enríquez en su trabajo sobre las trisectrices.
Entradas anteriores mostraban, paso a paso y exhaustivamente, escenas interactivas con la creación de lugares geométricos (l.g.) por uno y dos puntos y algunas de las utilidades de los l.g. generados por un punto, en la actual comenzamos a mostrar algunos de los usos de la Concoide.
En esta ocasión, en la sección de vídeo, hemos elegido, debido a su calidad e interés, el mismo que en la entrada anterior, que muestra con una belleza y claridad incuestionables la relación de la espiral con el origen del conocimiento tanto física como metafísicamente y son de especial relevancia la calidad de las fotografías y composiciones expuestas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Lituus" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Lituus
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Lituus incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y la trisección del ángulo, hemos incluido los trabajos realizados con el programa GeoGebra donde se muestran dos metodos para trisecar un ángulo con la Concoide de Nicomedes.
Método 1.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Escenas con DescartesJS: Técnicas y trucos (M06)
Escrito por Ángel Cabezudo BuenoEscenas con voz y sonido. Secuenciación temporal.

Introducción
El programa Descartes nos permite elaborar escenas incluyendo voces y sonidos. Podemos hacer que aparezcan en determinadas circunstancias según la actuación del alumno y pueden servir como explicación, como mensajes de ayuda o como felicitación cuando se ha resuelto bien una actividad.
También podemos hacer que sea el alumno quien ponga en marcha esos sonidos mediante controles, pero no trataremos con detalle en este artículo este tipo de controles de audio sino los eventos que darán origen a la reproducción de audio cuando se cumple cierta condición en el programa.
Hay que tener en cuenta que muchos ordenadores tienen deshabilitado el audio, por ello es conveniente que la actividad que se pide al alumno en la escena no dependa exclusivamente de los mensajes de voz que en ella se den.
Un programa interesante de uso libre que permite grabar voz y editar sonido para incorporar en las escenas de Descartes es Audacity. Puede exportarse el audio producido en diferentes formatos. Lo usual es el formato mp3 aunque en principio se puede utilizar cualquier formato compatible con HTML y el navegador Web utilizado.
Conviene tener en cuenta que el actual Editor de Escenas de Descartes no reproduce sonidos, aunque se puedan programar. Para comprobar que el sonido programado con Descartes funciona correctamente debemos guardar la escena en un archivo HTML y abrirla en un navegador Web – consultar este enlace sobre compatibilidad-.
Como se programan los sonidos en la escena
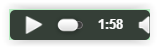
Podemos hacer que un sonido se escuche a través de un control de tipo audio.
 |
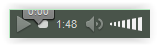 |
| Aspecto con Google Chrome | Aspecto con Mozilla Firefox |
Figuras 1a-b
Por ser de sobra conocido por todos no es necesario describir el funcionamiento de reproducción, pausa y parada proporcionado por este elemento multimedia.
La siguiente imagen muestra el panel Controles y los parámetros que se han establecido para el control de audio que se ha añadido en una escena. El control ha quedado identificado en este ejemplo por el nombre “sonido”.
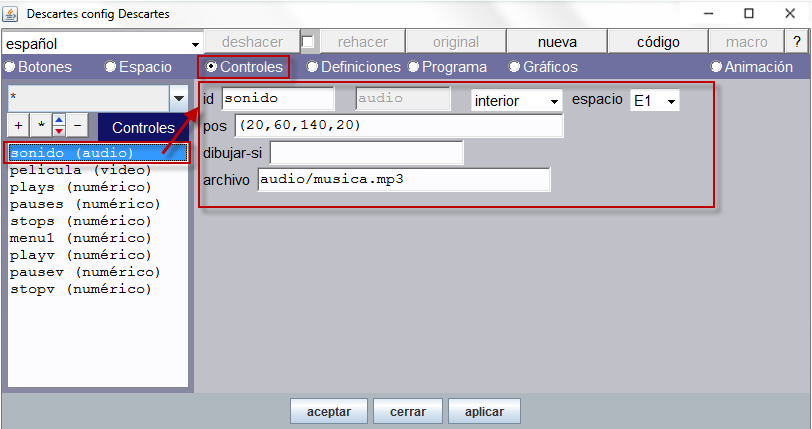
Figura 2
Los parámetros de este control son los referidos a la posición, el espacio, la condición dibujar-si y la trayectoria donde se encuentra el archivo de sonido p.e. "audio/musica.mp3" -ver documentación http://reddescartes.org/documentacion/audio-video/ -
Por lo general suele interesar que el sonido se escuche en situaciones especiales y por tanto se programa como auxiliar evento. En el artículo anterior, Escenas con DescartesJS: Técnicas y trucos (M05) - Adaptación de escenas. Librería de proyecto. Espacios HTMLIframe, se producía un sonido característico cuando un puzle quedaba armado correctamente. Este sonido se había programado como evento.
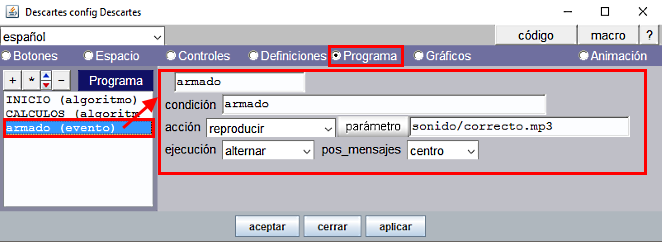
Figura 3
Verificar dicho sonido, desde este enlace, después de armar el puzle.
En la condición ponemos una expresión lógica que cuando es verdadera se reproduce el sonido. La acción que hay que seleccionar es "reproducir". El parámetro que se declara es la trayectoria donde se encuentra el archivo de audio, "sonido/correcto.mp3". En el apartado ejecución elegimos de entre las opciones "una-sola-vez", "alternar" o "siempre" que determina el modo de ejecución de la acción del evento, esto es:
- Una-sola-vez, sólo se ejecuta la primera vez que se cumple la condición.
- Alternar, se ejecuta la primera vez que la condición se cumple, pero si la condición deja de ser válida y vuelve a serlo luego, entonces vuelve a ejecutarse la acción.
- Siempre, se ejecuta siempre que se cumpla la condición.
El valor por defecto es "alternar".
Ejercicio práctico
Como práctica de la inclusión de sonidos te proponemos que selecciones una de tus escenas o bajes una de las cuatro escenas que ya han sido publicadas en esta sección del blog e incluyas en ella voz y sonido.
Los temas que hemos tratado son:
- Escenas con DescartesJS: Técnicas y trucos (B01) – Situar puntos en el plano cartesiano
- Escenas con DescartesJS: Técnicas y trucos (B02) – Identificar nombres en una imagen
- Escenas con DescartesJS: Técnicas y trucos (B03) – Distribución de nombres en un mapa
- Escenas con DescartesJS: Técnicas y trucos (M04) – Puzle de arrastre con efecto imán
Puedes grabar tu voz o buscar voz y sonido ya publicado, grabarlo y editarlo. También te aportamos los sonidos “correcto.mp3” y “Error.mp3” que se utilizan en las unidades “La suma 1” y “La resta 1” y que puedes descargar desde el enlace al final de este artículo.
- Primeramente, coloca la carpeta "audio", que contiene los sonidos, junto al archivo de la página HTML en la que está la escena donde vas a incluirlos.
- Vamos a poner un sonido para indicar que se ha resuelto bien la actividad de la escena.
- Abre el Editor de escenas y con él la página con la escena que vas a modificar.
- En el Panel programa haz clic sobre el signo + para añadir un auxiliar evento. En condición observa y pon lo mismo que hay en el mensaje de felicitación en el apartado dibujar-si.
- Puesto que con el Editor de escenas no se reproducen los sonidos, guarda los cambios y comprueba su funcionamiento abriendo la página con el navegador Web.
Sonido secuenciado
Cuando se incluyen varios sonidos que se deben de reproducir de forma sucesiva, si no queremos que se solapen uno con otro, tenemos que producir una secuenciación de los mismos y separarlos en el tiempo mediante una animación, asignando a cada uno de ellos el momento en el que debe comenzar a reproducirse.
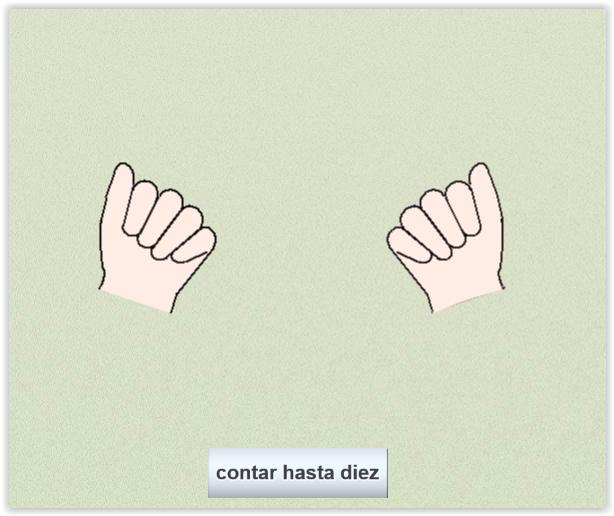
Vamos a utilizar un ejemplo muy sencillo de secuenciación programado para esta ocasión. El diseño está inspirado en la escena Sumando con los dedos de la unidad didáctica de Eduardo Barbero Corral titulada “La suma 1” para 2º curso de Primaria, que como se podrá observar atiende aspectos didácticos más amplios. Se utilizan los mismos sonidos de voz para contar (1a.mp3, 2a.mp3, 3a.mp3, …, 10a.mp3) y las imágenes de las manos han sido coloreadas. También puede consultarse, del mismo autor, la escena similar Restando con los dedos de la unidad didáctica “La resta 1”.
En la escena del ejemplo una animación ha hecho posible la secuenciación temporal de los distintos sonidos y también de la representación gráfica de los números 1 al 10.
Figura 4 (Abre la escena)
En el Editor de Descartes disponemos de un panel para configurar la animación. Una animación en Descartes es un algoritmo especial que refresca la escena cada vez que realiza un ciclo. Como todo algoritmo tiene la estructura inicio – hacer – mientras que se corresponde con la estructura de bucle “do… while” de los lenguajes C y Java y “repeat… while” de Pascal.
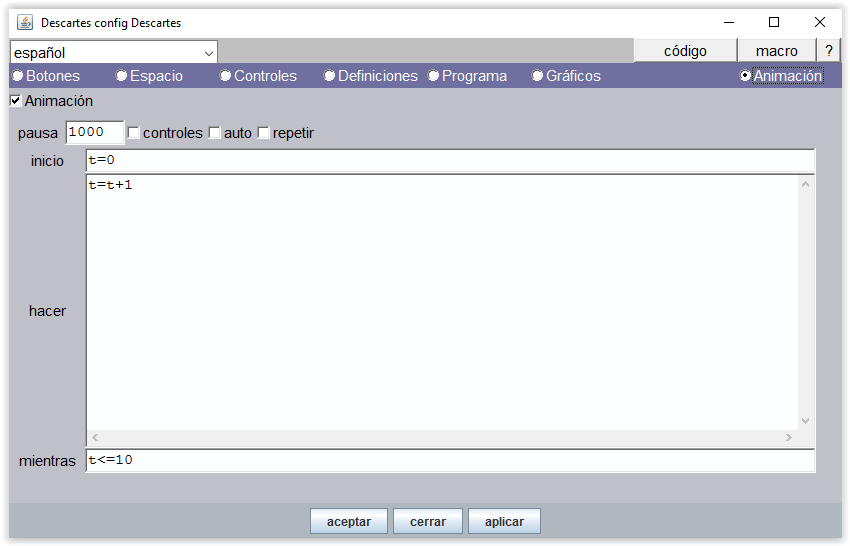
Figura 5
Interesa ver la documentación referida a Animaciones
Animación
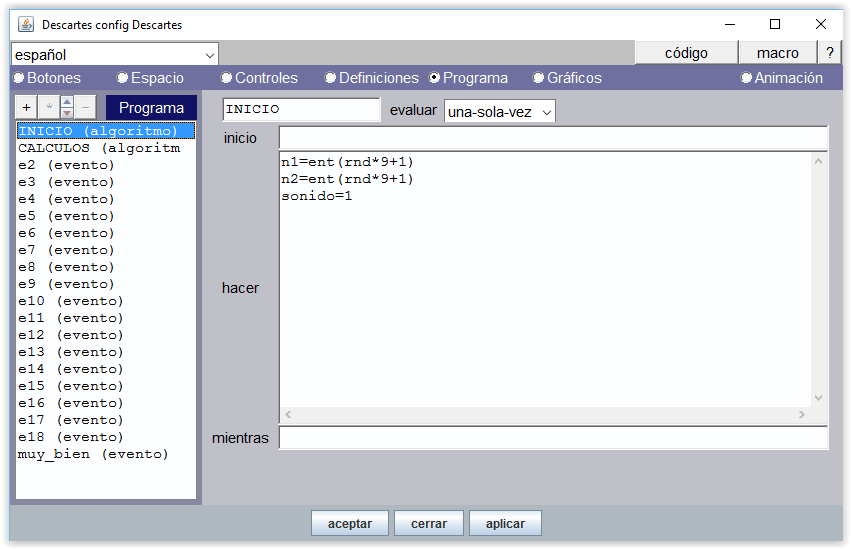
La animación funciona como los algoritmos de Descartes, pero tiene sus propias singularidades. Se pone en marcha cuando se activa la acción de animar, ejecuta al principio las operaciones reflejadas en la casilla inicio, separadas por “;”, transforma sus valores según lo que se le indica en hacer y se detiene cuando deja de cumplirse la condición que se pone en mientras. Pero eso lo realiza no de forma instantánea, sino ralentizada por lo indicado en pausa. La pausa indica los milisegundos que espera el programa entre dos pasos sucesivos de la animación que por defecto vale 60.
La figura anterior es el panel animación de la escena de “contar hasta 10”.
Hay que seleccionar la casilla Animación para que esta esté activada y se puedan editar sus parámetros. Si esta casilla no se selecciona no se puede editar los campos del panel ni se puede activar la animación en el programa, aunque esté editada.
El bucle se inicia poniendo el contador a cero, t=0 y en cada ciclo o paso se incrementa en una unidad t=t+1. Cuando el contador supera el valor 10 la animación finaliza.
Es importante entender que una animación se puede poner en marcha de dos formas:
- De forma automática al iniciarse la escena. Para ello tiene que haberse seleccionado la casilla “auto”.
- Cuando se ejecuta la acción animar. Esta acción es una posible opción que tienen los controles numéricos en el panel Controles y también los eventos en el panel Programa.
En la siguiente imagen se muestra cómo se consigue poner en marcha la animación de la escena “contar hasta 10”
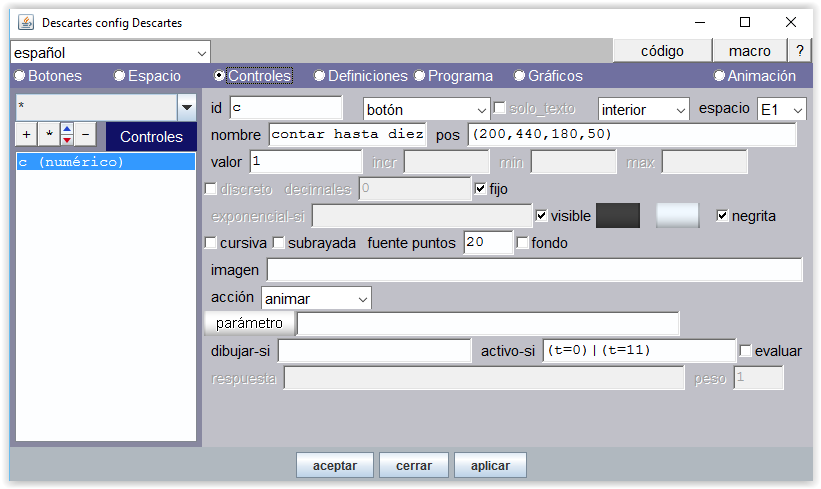
Figura 6
Se ha añadido a la escena un control numérico de tipo botón identificado por la variable c, rotulada con el nombre “contar hasta diez” y lleva la acción “animar” cuando se pulsa, en cuyo caso toma el valor 1 (este valor puede utilizarse para averiguar, p.e, si el control de botón ha sido pulsado).
En la ventana de activo-si se ha escrito la condición "(t=0)|(t=11)"; esto supone que el botón se puede pulsar y activar la animación cuanto t=0 ó t=11. En consecuencia, el botón queda desactivado a lo largo de la animación. Por defecto activo-si está en blanco.
Sonidos y gráficos secuenciados
Sonidos
La animación lo que produce es que una variable t se incrementa cada cierto tiempo, indicado por el parámetro pausa. En nuestra escena del ejemplo, t es un contador que se incrementa cada 1000 ms (1 segundo). Este tiempo es suficiente para que se reproduzca de forma secuenciada (para cada valor de t) cada uno de los 10 archivos de voz independientes: “uno”, “dos”,…, “diez”. Cada sonido se reproduce para un valor determinado del contador. Un evento, en este contexto, consiste en reproducir un archivo de voz cuando el contador t toma cierto valor.
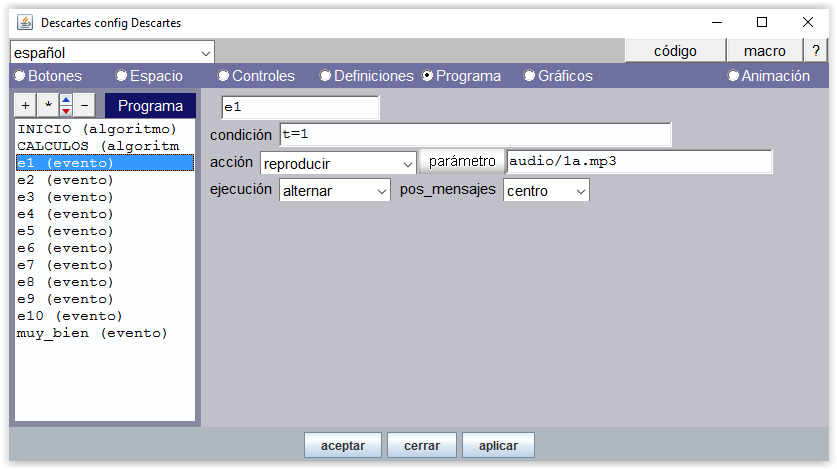
Figura 7
Un sonido de felicitación, "muy_bien.mp3" se reproduce cuando se termina de contar (condición t=11)
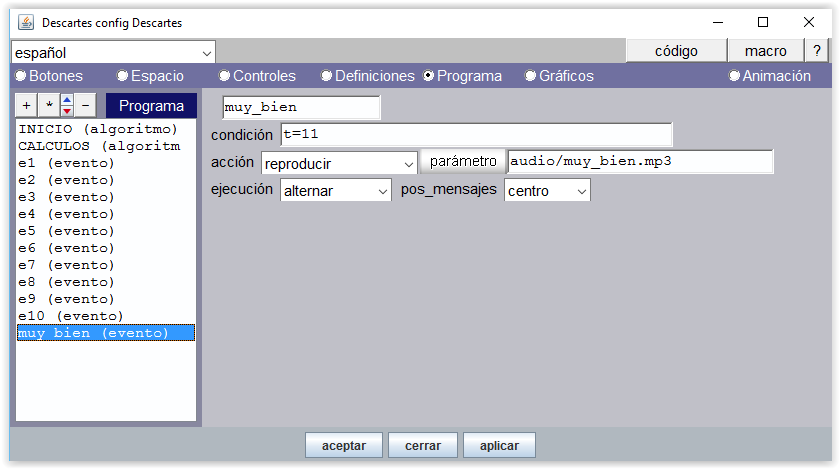
Figura 8
Gráficos
La misma animación que reproduce sonidos como eventos puede llevar aparejada la representación simultánea de gráficos de imágenes, textos, etc., que se vinculan con el valor del contador t.
En la escena de “contar hasta 10”, para cada valor de t, se representa la composición de las dos manos (derecha e izquierda) mostrando el número de dedos que señalan cada cantidad contada.
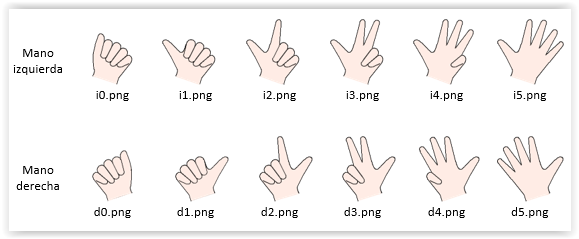
Figura 9
Así, para contar del 1 al 5, la mano izquierda tiene que estar cerrada, representada por "i0.png".
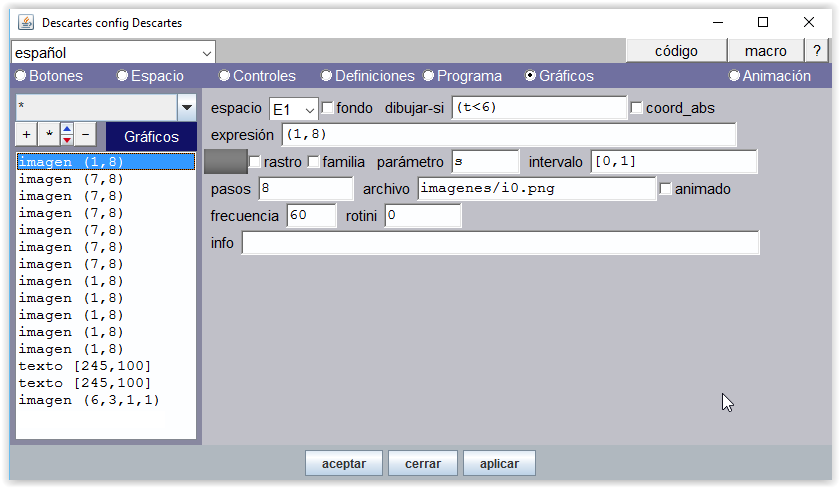
Figura 10
Antes de empezar a contar, t=0, la mano derecha está cerrada y queda representada por "d0.png".
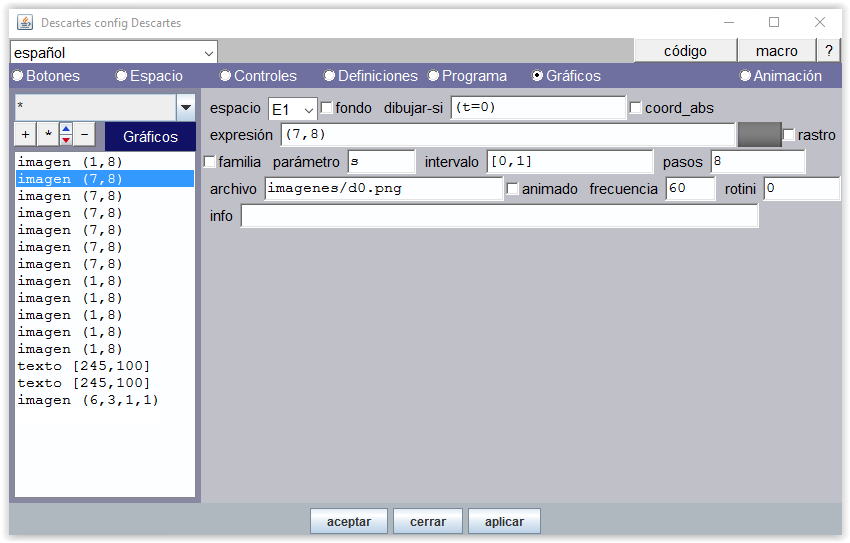
Figura 11
De t=1 a t=5 la mano derecha va mostrando sucesivamente el mismo número de dedos: d1.png,... , d5.png.
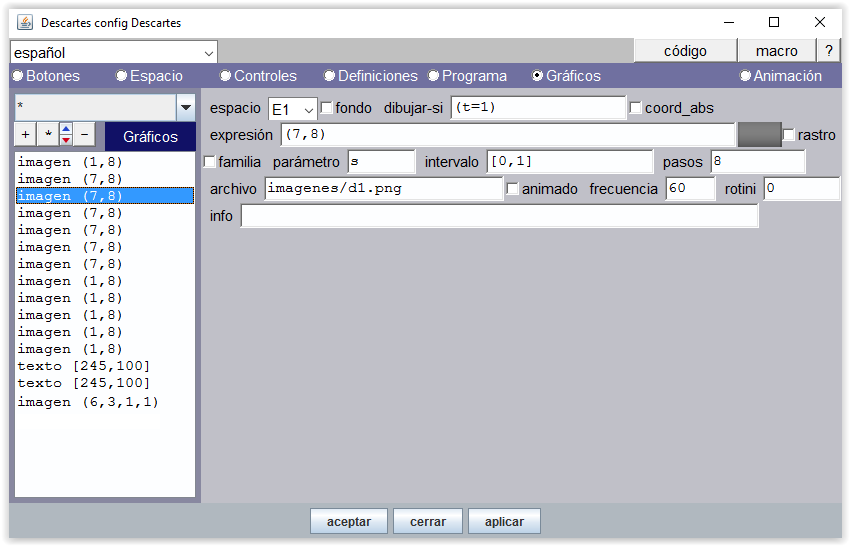
Figura 12
A partir de 5, la mano derecha tiene que mostrar los 5 dedos.
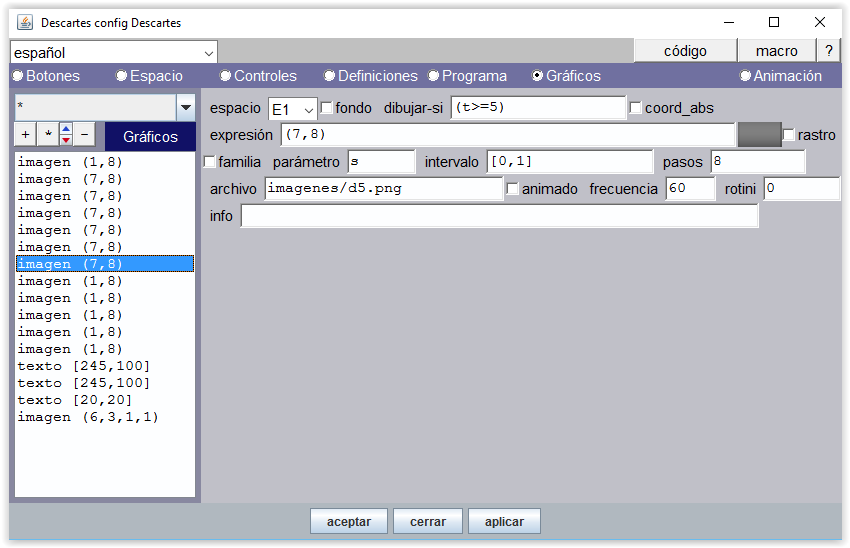
Figura 13
De t=6 a t=10, la mano izquierda va mostrando sucesivamente i1.png,... , i5.png.
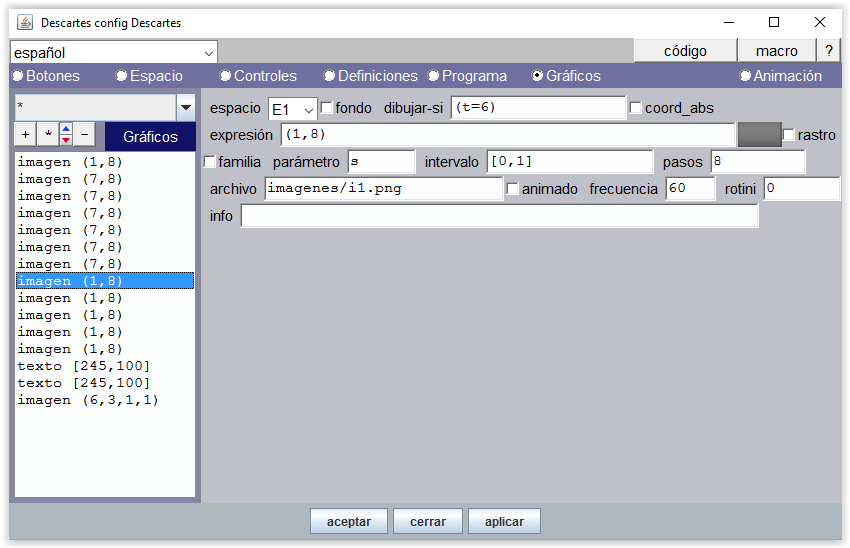
Figura 14
A partir de 10 la mano izquierda mostrará 5 dedos.
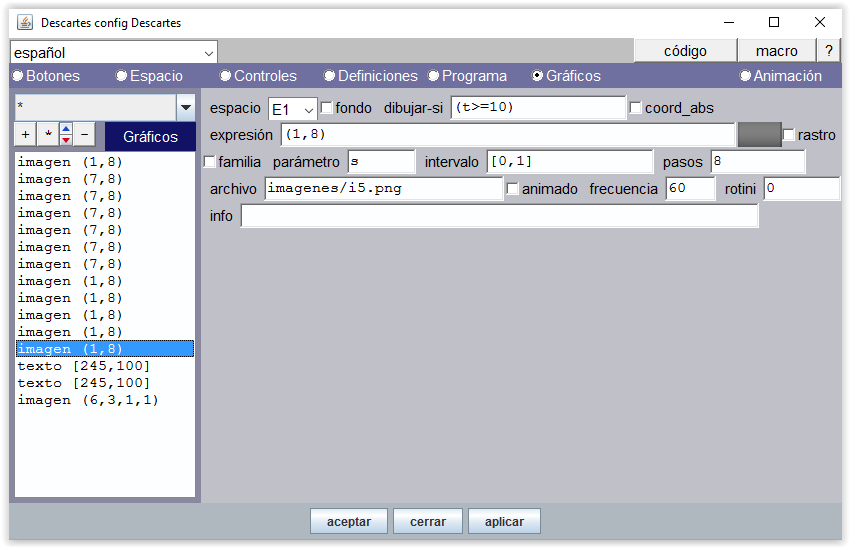
Figura 15
Un gráfico tipo texto reproduce el valor de la variable t en cada momento.
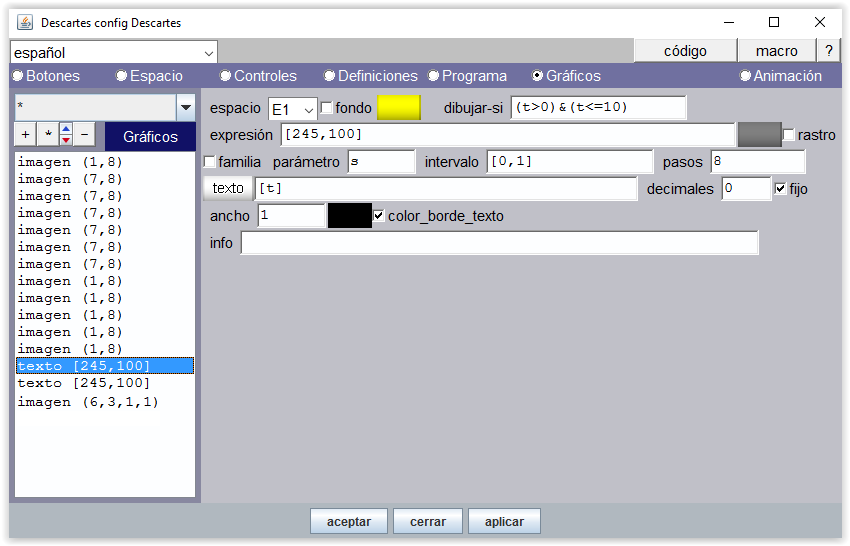
Figura 16
Cuando se termina de contar, t=11, por lo que hay que reproducir el valor de t-1 para mantener el valor 10 del texto.
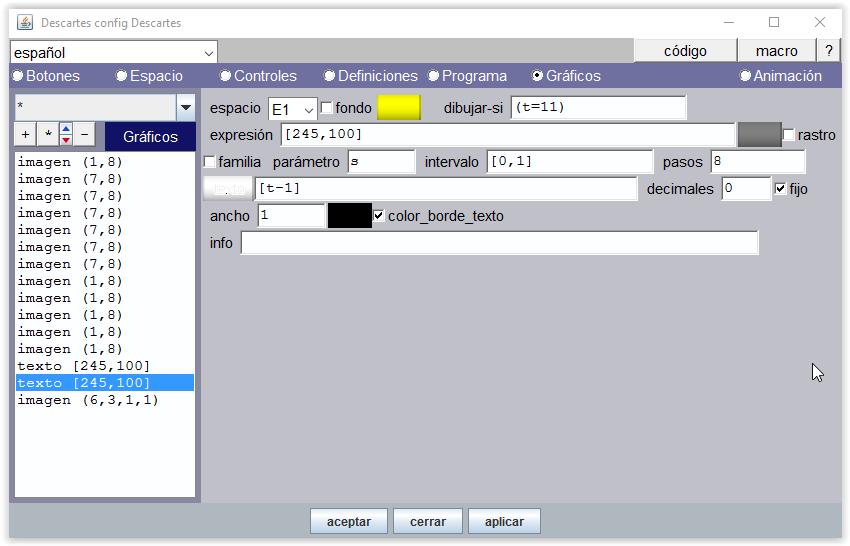
Figura 17
Una imagen acompaña al sonido de felicitación cuando se termina de contar (condición t=11).

Figura 18
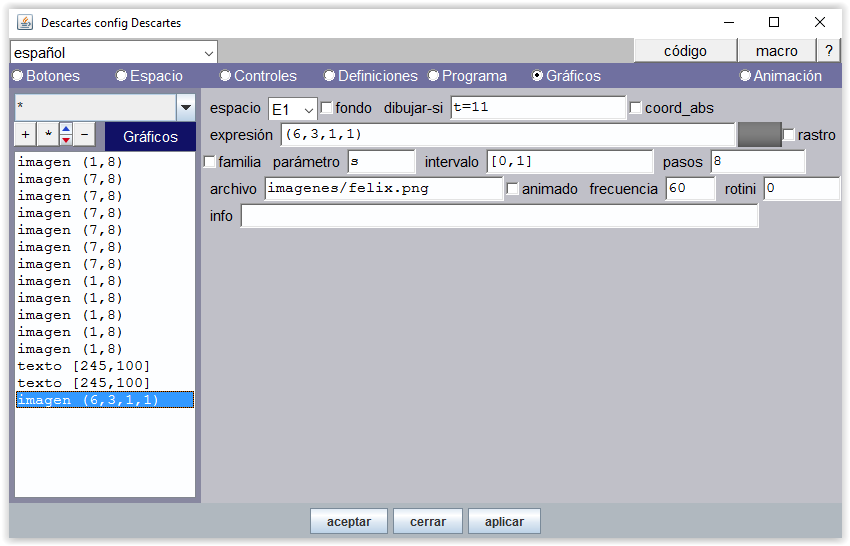
Figura 19
Proyecto
|
Escena_M06: Escenas con voz y sonido. Secuenciación temporal Como viene siendo habitual en esta serie de artículos vamos a proponer un proyecto relacionado con la secuenciación y el uso de la animación de Descartes para aquellos lectores que estén interesados en practicar y progresar un poco más en la programación con DescartesJS. Se trata de conseguir una escena lo más parecida a la siguiente. Figura 20 (Abre la escena) Como podrá observase está inspirada en la escena Sumando con los dedos de la unidad didáctica “La suma 1”. Pero se ha simplificado para quedarnos solo con los elementos de la programación relacionados con la secuenciación temporal de eventos producida por una animación, motivo de este artículo. He pretendido conseguir los mismos efectos de la escena original pero sin poner empeño alguno en que coincidieran sus respectivos códigos de programación. Se trata de practicar la suma de dos cantidades n1 y n2 que toman valores espectivos de 1 a 9. Para ello la escena tiene que contar con los dedos desde la composición con ambas manos para representar n1 hasta n1+n2: “Contar desde n1 otros n2 más”. Los sumandos n1 y n2 se generan aleatoriamente cada vez que se pulsa el control numérico de botón que lleva la acción de inicio (rotulado con el nombre “otra cuenta”). La expresión de DescartesJS que genera un número natural entre 1 y 9 es ent(rnd*9+1)
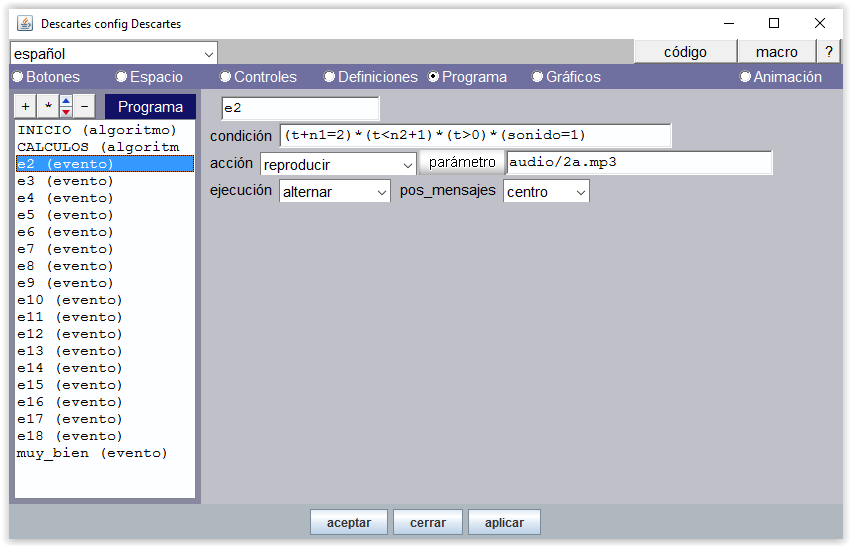
Figura 21-a Es decir, calcula la parte entera de rnd*9+1, siendo rnd una variable reservada en DescartesJS que cuando se invoca obtiene un valor real alatorio en el intervalo [0, 1). El control numérico de botón etiquetado con el nombre “contar” ejecuta la acción animar cuando se pulsa. La animación realiza un contador t=t+1 mientras t<n2+1. Los sonidos de voz se corresponden con los valores n1+1, n1+2, …, n1+n2 y en la práctica se utilizan desde 2a.mp3 (cuando n1=1) hasta 18a.mp3 (cuando n1=n2=9).
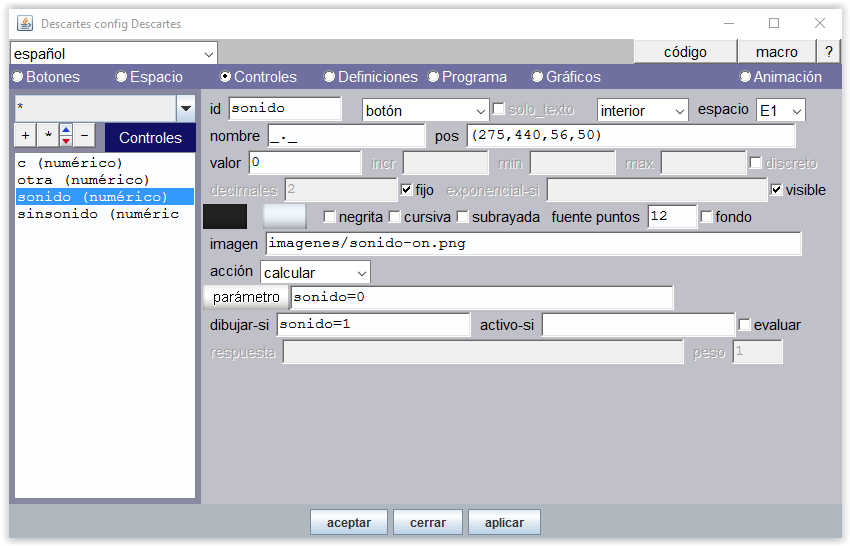
Figura 21-b Incluimos la posibilidad de contar sin reproducir la voz. Para ello se utiliza un control numérico de botón id="sonido", sin etiquetado de nombre “_._”, que lleva asociada la imagen de un altavoz "sonido-on.png". En la casilla pos de posición que ocupa el control se pone las dimensiones de la imagen 56x50 píxeles. Se muestra con la condición (dibujar-si) "sonido=1". Al pulsarlo toma el valor 0, acción calcular "sonido=0".
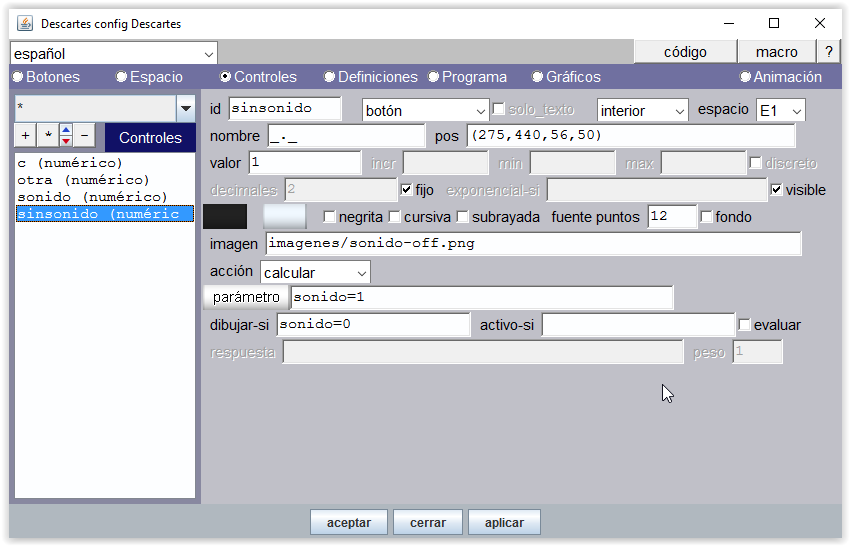
Figura 21-c Al pulsar el control id="sonido" se muestra en su lugar el control id="sinsonido", que lleva la imagen de un altavoz tachado "sonido-off.png". Este control al ser pulsado calcula "sonido=1", con lo que se activa la voz y se dibuja el control id="sonido".
Figura 22 El siguiente tríptico indica tres detalles que se deben de conseguir al programar la escena:
Figura 23-a
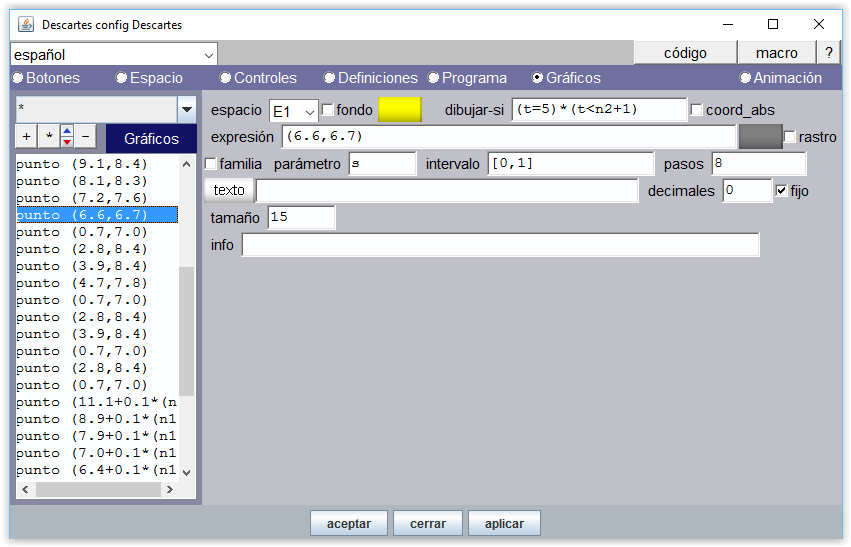
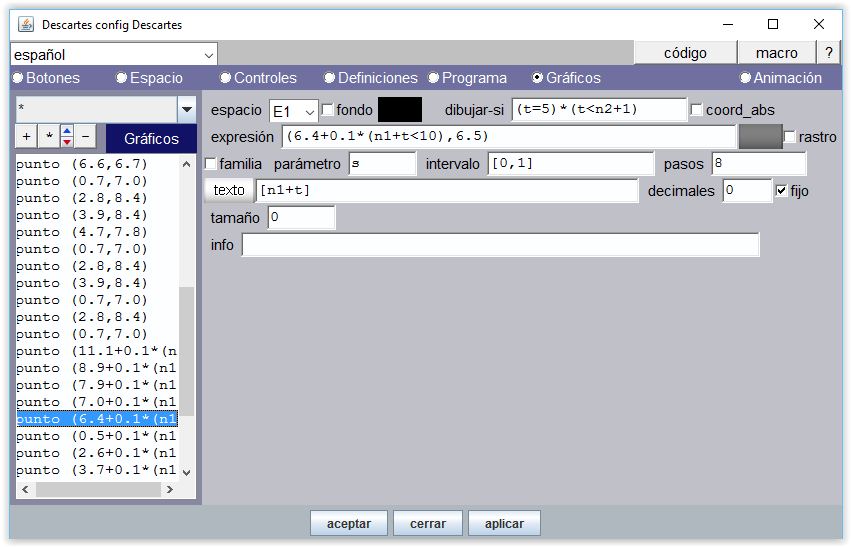
Para asignar posiciones de los controles y los elementos gráficos (imágenes, puntos, textos,…) en la escena hay que configurar en primer lugar el tamaño que tendrá la escena, asignar un valor de escala y determinar dónde tiene que aparecer el origen de coordenadas cartesianas. Cada punto amarillo, cuya posición es la de su centro, debe ir por encima de la punta del dedo correspondiente y el punto asociado de tamaño 0 cuya misión es la de poner texto [n1+t] sobre aquel, se posiciona teniendo en cuenta que este texto se muestra a cierta distancia del centro del punto correspondiente.
Figura 23-b
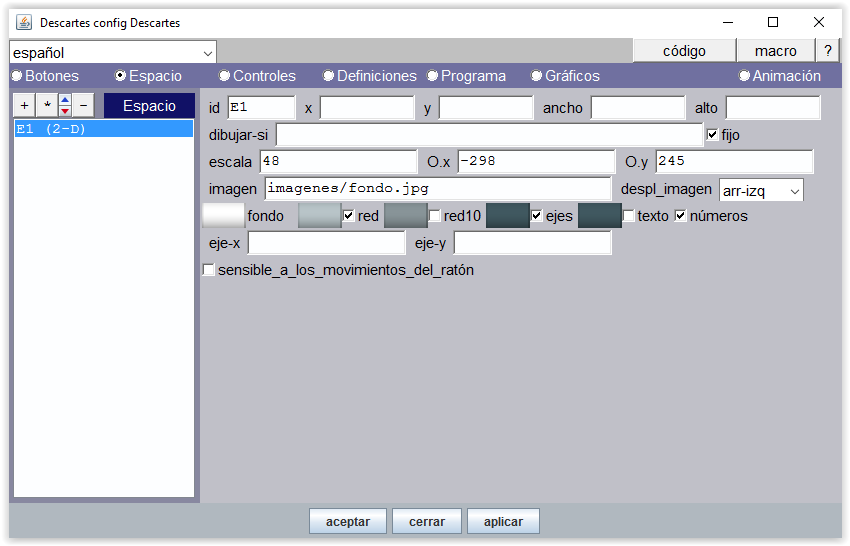
Figura 23-c En la solución que damos a este proyecto, se puede comprobar que la escena tiene dimensión 600x500 píxeles. La imagen siguiente muestra el panel Espacio del Editor de Descartes de dicha escena.
Figura 24 Las marcas red, ejes y números muestran un espacio con cuadrícula y ejes cartesianos numerados. Una vez situados los controles y gráficos se pueden desactivar. Este es el aspecto que presenta el espacio después de programado.
Figura 25 El espacio debe quedar fijo. El origen de coordenadas se ha desplazado hacia abajo 245 px y hacia la izquierda -298 px La unidad cartesiana (escala) es de 48 px. Recuérdese que las posiciones de los controles y los gráficos tipo texto se hace en píxeles tomando como origen [0, 0] el vértice superior izquierdo de la escena mientras que los gráficos tipo punto y tipo imagen se posicionan en coordenadas cartesianas con origen en (O.x, O.y). Como el tamaño de las imágenes de las manos es de 199x199 px y el posicionamiento de las mismas en el espacio es el del vértice superior izquierdo de la imagen podemos verificar en la figura anterior que la mano izquierda está posicionada en (1, 8) y la derecha en (7,8). |
Animamos a que con esta descripción y las herramientas de DescartesJS facilitadas en la serie de artículos publicados hasta este momento, el lector interesado sea capaz de programar la escena de este proyecto.
Facilitamos en los enlaces siguientes las descargas de las carpetas de contenidos de los materiales para que se pueda hacer uso de los archivos de sonido e imágenes y servir de ayuda al comprobar la estructura de carpetas y revisar o estudiar el código de las escenas con el Editor de Descartes.
|
Autoría:
Eduardo Barbero Corral
- Propuesta del proyecto.
- Técnicas de programación contenidas en las unidades didácticas inspiradoras “La suma 1” y “La resta 1” para 2º de Primaria
Ángel Cabezudo Bueno
- Interpretación, ilustraciones y redacción.
- Programación y edición de las escenas contenidas en la carpeta del proyecto “escena_M06”
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Aprendemos a resolver problemas con Descartes y Wiris
Escrito por José Antonio Salgueiro GonzálezAprendemos a resolver problemas con Descartes es una iniciativa del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, realizada con alumnos y alumnas de 4º ESO durante el curso escolar 2015/2016, basada en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes" y llevaba a cabo anteriormente con el alumnado de 1º de Bachillerato de Ciencias e Ingeniería, con objeto de fomentar en nuestros alumnos y alumnas el aprendizaje de las técnicas necesarias del lenguaje cinematográfico y audiovisual, a la vez que proporcionarles una formación básica que les permita, de forma autónoma, generar y producir sus propios contenidos audiovisuales.
Con el lema “Resolvemos problemas con Descartes“, abrimos un foro de suscripción forzosa en el aula virtual de Matemáticas-4º para coordinar la experiencia, dar las indicaciones, organizar los equipos, elegir los problemas, prestar asesoramiento y fomentar el trabajo en colaboración, aunque también se generaba debate en el día a día del aula física.
Decir que, durante todo el curso, los alumnos y alumnas asistieron a clase con sus portátiles de la Escuela TIC 2.0 que les entregaron cuando se encontraban en 5º de Primaria, usando junto a la PDI el libro digital interactivo del Proyecto ED@D y los cuadernos de trabajo Descartes que incorpora cada unidad interactiva, estando en contacto permanente con el profesor desde el aula virtual y desde la red social Twitter.
| 1ª FASE: PROPUESTA DE PROBLEMAS Y DIFUSIÓN EN TWITTER |
Cada equipo tuvo que seleccionar dos problemas de la unidad interactiva "Ecuaciones y sistemas", concretamente uno de primer grado y otro de segundo, que se encuentran en el menú ejercicios y que se denominan "Sistemas de ecuaciones lineales" y "Sistemas de segundo grado", respectivamente, y comunicarlo en el foro del aula virtual para conocimiento del profesor y del resto de equipos. Posteriormente, y una vez acordado con el profesor los dos problemas seleccionados para su resolución en lo que sería su "ópera prima", al menos en Matemáticas, tuvieron que diseñar una imagen alusiva al contenido de los problemas, incorporar sus enunciados y darle difusión por la red social Twitter con el hashtag del curso #MATES4ABAJO.
| 2ª FASE : DOCUMENTACIÓN Y GUIÓN DE LA OBRA |
Comienza la fase de investigación y documentación, así que damos las indicaciones desde el aula virtual, aportamos sugerencias, consejos y recomendamos espacios y recursos. Por ejemplo:
- Guía rápida para grabar en vídeo. ¡Muy bueno!
- Necesitáis un guión de lo que váis a grabar y a decir, pudiendo alternar planos virtuales de lo que se visualiza en el ordenador, tableta o smartphone con planos reales de la ejecución técnica de los ejercicios, que podéis realizar en una pizarra, en un cuaderno o folio, con un software que lo permita, grabando en interior o en exterior y, por supuesto, todo lo que se os ocurra. Aquí es donde entra en juego vuestra creatividad e imaginación.
- Recordad que publicaremos en internet el producto final, así que procurad la mejor calidad de imagen y audio posibles.
- El lenguaje matemático será primordial para las explicaciones y la comunicación audiovisual, por eso me enviaréis el borrador del guión, a través de la tarea del aula virtual, para que yo pueda revisarlo.
- No podéis usar ni imágenes ni música con derechos de autor. Para estos casos, os recomiendo:
- Banco de imágenes y sonidos del INTEF.
- Imágenes con licencia Creative Commons, del mismo banco anterior o de Pixabay.
- Jamendo, descarga de música libre y gratis.
- En cualquier caso, es recomendable dedicar una página de créditos para citar en el vídeo la autoría y el lugar de procedencia de las imágenes y audios usados.
- Debería aparecer, al menos, el logotipo del IES Bajo Guadalquivir, nuestro instituto.
- Cuando tengáis todo preparado y ensayado, os aconsejo hacer algunas pruebas de grabación cortas para comprobar si obtenéis el resultado deseado y las calidades demandadas
Si tenéis alguna idea y no sabéis cómo llevarla a efecto, podéis consultar en este foro o por el servicio de mensajería de la Moodle.
¡Es el momento de la CREATIVIDAD E IMAGINACIÓN!
| 3ª FASE : EVALUACIÓN |
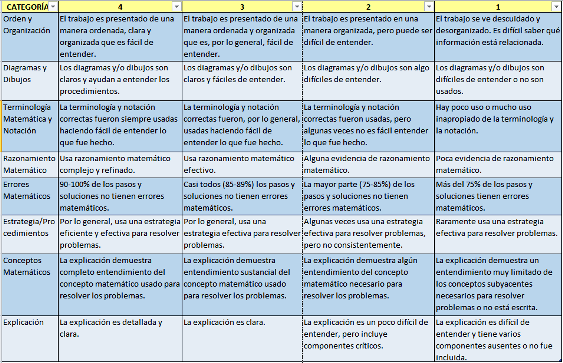
Para la evaluación relativa a los aspectos curriculares del producto final presentado por cada equipo, se ha utilizado la rúbrica que compartimos en este artículo, elaborada desde Rubistar, y que ya empleamos en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes". Con un clic sobre la imagen puede ampliarse para una correcta visualización.
Si visualizas y oyes el vídeo con detenimiento, sin duda, encontrarás leves errores de expresión escrita o verbal, tanto en el lenguaje ordinario como en el lenguaje matemático, lo que nos induce a dar una continuidad a la iniciativa y extrapolarla a otros cursos para ir consiguiendo nuestro objetivo paulatinamente. Además, la localización y análisis de errores es una de las mejores estrategias de aprendizaje. No obstante, quiero desde aquí felicitar a todos mis alumnos y alumnas de 4º A por sorprenderme con su creatividad e imaginación, por ser competentes para generar contenido multimedia con sus dispositivos móviles, sin que su profesor sepa ayudarles en este ámbito, por afrontar todos los retos que se han encontrado por el camino hasta conseguir el producto final y por permitirme descubrir y fomentar algunas de sus capacidades ocultas.
Muchas gracias también a sus familias por apoyar la iniciativa autorizando las grabaciones y su difusión por las redes sociales, lo que obviamente repercute en una mejora de la formación de sus hijos e hijas como ciudadanos y ciudadanas del s. XXI y en su preparación para la siguiente etapa educativa.
El subproyecto Miscelánea de la Red está formado por escenas aisladas que se pueden utilizar como complemento a los contenidos que se estén trabajando en el aula, ya sea para reforzar, consolidar o ampliar conocimiento.
En el siguiente vídeo se muestra con detalle una unidad perteneciente a dicho subproyecto y como insertar este objeto en un curso Moodle para su aplicación en el aula.
La unidad PISA. Sistemas de ecuaciones que hoy se presenta ha sido creada en base a las indicaciones para la elaboración de las pruebas PISA de 2000 - 2003 en el área de las ciencias aplicadas. Se plantean temas relacionados con la observación científica de situaciones reales (en este caso mezclas y aleaciones) para su traducción a lenguaje algebraico. En todos los ejercicios se introducen mecanismos para evaluar la respuesta y que sirvan también de guía al alumno, incluso aunque la respuesta sea correcta.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)














 CONTACTO
CONTACTO
