EDAD 4ºESO Académicas - Potencias y radicales
Escrito por Alfonso Saura EspínEste mes vamos a ver la unidad de 4ºESO Académicas correspondiente a "Potencias y radicales":
En el vídeo hemos tratado los puntos siguientes:
1.Radicales
Definición. Exponente fraccionario
Radicales equivalentes
Introducir y extraer factores
Cálculo de raíces
Reducir a índice común
Radicales semejantes
2.Propiedades
Raíz de un producto
Raíz de un cociente
Raíz de una potencia
Raíz de una raíz
3.Simplificación
Racionalización
Simplificar un radical
4.Operaciones
Suma y resta
Multiplicación de radicales
División de radicales
Actividades de geometría. Formación competencial
Escrito por Montserrat Gelis BoschEntre los proyectos de la RED Descartes se encuentra un grupo de actividades creadas a partir de unidades liberadas de PISA y de Pruebas de Evaluación Diagnóstico utilizadas en diferentes Comunidades autónomas. Se trata del Proyecto Competencias.
Las unidades digitales pertenecientes a este proyecto se basan en situaciones y contextos cotidianos. Las actividades que se proponen son interactivas y autoevaluables y permiten que un mismo alumno puede realizar muchas veces la misma actividad, que presentará pequeñas variaciones. Esta característica convierte a las unidades de este proyecto en un recurso importante para la formación en competencias del estudiante.
En el siguiente vídeo se han seleccionado una serie de objetos en los cuales se deben utilizar propiedades geométricas y equivalencias entre medidas para resolver situaciones reales. Una vez seleccionadas las actividades, se muestran los pasos a seguir para insertar estas actividades en nuestra aula virtual Moodle.
Sobre la forma y el crecimiento cordobés del Nautilus pompilius
Escrito por José R. Galo SánchezHay una tendencia a tratar de asociar o encontrar en todo aquello que es bello la proporción áurea o divina, o a construir objetos a partir de esta razón porque se presuponen serán apreciados como bellos por el simple hecho de seguir dicha pauta. Esto, como no, también ha acontecido con la modelación matemática de la concha del Nautilus pompilius sobre la que suele afirmarse que su forma y crecimiento es áureo. Sin embargo, en este artículo se muestra y se analiza en detalle cómo dicha concha lo que realmente sigue es un patrón ubicado en la denominada proporción cordobesa o humana. Con apoyo en un recurso interactivo desarrollado con la herramienta Descartes se motiva el análisis y comportamiento y se procede a partir de la yocto-yotta realidad observada a construir el modelo matemático, el cual se detalla ampliamente.
Pulsando sobre la siguiente imagen se accede a dicho recurso interactivo que se aborda o plantea en seis fases:
- Ajuste de la concha por una espiral logarítmica.
- Ajuste del sifúnculo por una espiral logarítmica.
- Ajuste global por una familia de espirales cordobesas.
- Mejora del modelo discreto.
- Aproximación de los septos.
- Modelo matemático del Nautilus pompilius.
|
|
En cada fase se dispone de un botón de información que, al pulsarlo, da acceso a un detalle de las propiedades que pueden inducirse a partir de la interacción con la escena. |
 |
| Y en el botón de indicaciones se aborda una introducción, los objetivos, las instrucciones de uso en cada fase y finalmente se enlaza un artículo donde se detalla el análisis matemático realizado. Este artículo está embebido a continuación o bien puede abrirse y/o descargarse desde este enlace. |
En las conclusiones del artículo anterior afirmamos:
A través del detallado y progresivo análisis realizado hemos ido construyendo la base teórica o modelo matemático que soporta a la bella morfología del Nautilus Pompilius y hemos tratado del encontrar el modelo de crecimiento que conduce a poder explicar y a comprender por qué adquiere esa forma. Desde su inicio la espiral logarítmica cordobesa tomó presencia y a medida que la mirada se deslizaba hacia algún nuevo detalle esta espiral ha vuelto a imponer su presencia marcándonos y alumbrándonos el camino del descubrimiento y de la adquisición del conocimiento. La belleza del Nautilus pompilius se sustenta en la proporción cordobesa o humana y todo punto de su concha o del interior ha quedado determinado por la intersección de dos espirales cordobesas. El germen o base inicial matemática que explica el por qué acontece todo lo observado, se ha ubicado en el crecimiento gnomónico de un triángulo cordobés, las propiedades de éste se trasladan al desarrollo y comportamiento global detectado y modelado.
Deseamos que nuestro trabajo de investigación satisfaga tu curiosidad y te animamos a interactuar con nosotros bien realizando algún comentario en este blog (los comentarios no se publicarán directamente sino que pasan por una moderación previa a su publicación) o bien escribe al correo de nuestra RED Descartes: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
Esta semana presentamos un libro digital interactivo sobre los números complejos que forma parte del proyecto iCartesiLibri de la RED.
En cada página de este libro encontramos múltiples ejemplos y representaciones gráficas modificables para introducir los contenidos a estudiar: los números complejos y sus distintas formas de representación, las operaciones y algunas aplicaciones. Se dispone también de una serie de ejercicios autocorregibles sobre los conceptos estudiados que permiten al estudiante practicar y consolidar lo aprendido.
Siguiendo el diseño de las unidades del proyecto iCartesiLibri, en el desarrollo de estas actividades se ha tenido en cuenta la interactividad, para facilitar el autoaprendizaje a través de la intervención directa del estudiante.
Este mes vamos a ver un vídeo sobre Polinomios:
En este video hemos tratado los siguientes puntos
1.Polinomios
Grado. Expresión en coeficientes
Valor numérico de un polinomio.
2.Operaciones con polinomios
Suma diferencia, producto
División.
3.Identidades notables
(a+b)2
(a-b)2
(a+b)·(a-b)
Potencia de un binomio
4.División por x-a
Regla de Ruffini
Teorema del resto
5.Descomposición factorial
Factor común xn
Raíces de un polinomio
Fracciones algebraicas
Misceláneas: Proporcionalidad. Las Espirales XIV.
Escrito por Ildefonso Fernández Trujillo
Proporcionalidad. Las Espirales XIV
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación e iCartesiLibri.
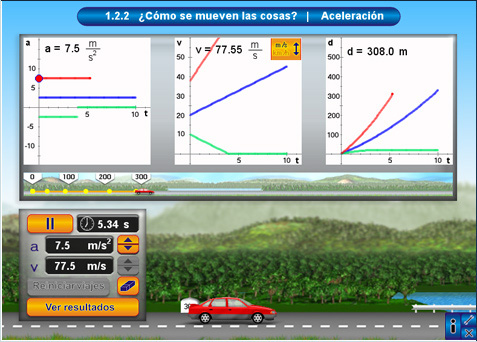
Como muestra enlazamos la unidad sobre Como se mueven las cosas. Aceleración, del subproyecto TELESECUNDARIA,
la GEOevaluación de SurAmérica,
y el libro interactivo Paletización y Empaque.
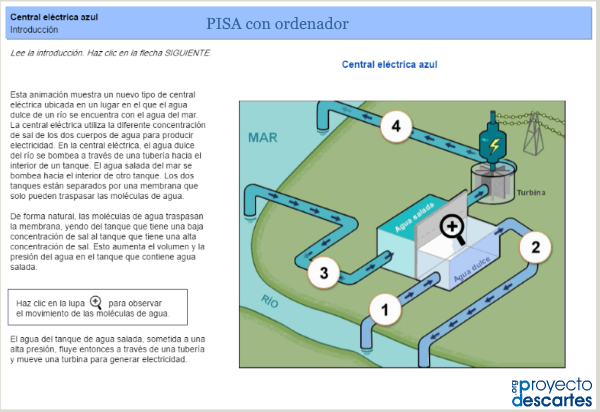
Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D cuyos materiales pueden enlazarse desde este espacio web mediante los botones MATEMÁTICAS y FÍSICA Y QUÍMICA y los contenidos del subproyecto Competencias en general y en particular los referidos como PISA con ordenador. De entre ellos enlazamos, con la siguiente imagen, el extraordinario trabajo sobre la generación de energia Central eléctrica azul
Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el instrumento ideado por la escuela platónica para duplicar un cubo, esto es, dado un cubo de arista a y volumen V halla de forma mecánica y basandose en los razonamientos de Hipócrates, el segmento de longitud a'= a·21/3 que será la arista del cubo de volumen V' = 2·V.
La escena permite, con cierta facilidad, determinar el segmento OD pero si el usuario no está familiarizado con el uso del instrumento puede pulsar el botón de información, ![]() , que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la construcción de Platón, o atribuida a la escuela platónica, del hecho de la duplicidad.
, que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la construcción de Platón, o atribuida a la escuela platónica, del hecho de la duplicidad.
La utilidad es facilmente adaptable y admite las modificaciones y/o ampliaciones que el usuario considere convenientes para su uso personal.
En el siguiente trabajo presentamos el instrumento conocido como Mesolabio de Eratóstenes y la manera de encontrar, con su uso virtual, el segmento que sirva de arista al cubo que doble en volumen a uno inicial dado.
Repetimos lo dicho anteriormente: la escena permite, con cierta facilidad, determinar la arista del cubo con volumen doble a uno dado, pero si el usuario no está familiarizado con el uso del instrumento puede pulsar el botón de información, ![]() , que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la semejanza de triángulos, del hecho de la duplicidad.
, que muestra un breve texto con las indicaciones adecuadas y una demostración, que usa la semejanza de triángulos, del hecho de la duplicidad.
En esta ocasión, en la sección de vídeo, hemos elegido la tercera parte de los que se han mostrado en las últimas entradas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales".
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral Compleja" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Se ha creado la siguiente escena: Espiral compleja. El crecimiento de esta espiral, tal y como se ha construido, es extremadamente rápido debido al factor rn el lector puede modificar facilmente el comportamiento de la escena añadiendo más controles y/o modificando el rango de valores de los actuales.
La demostración de las fórmulas (teoremas) de Moivre y Euler están disponibles en la wikipedia. - Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral Compleja incluida.
Con el siguiente trabajo realizado con GeoGebra, tendremos la oportunidad de manejar, virtualmente, un mesolabio para hallar la arista de un cubo que tenga doble volumen que uno dado. Esto es, partiremos de esta situación
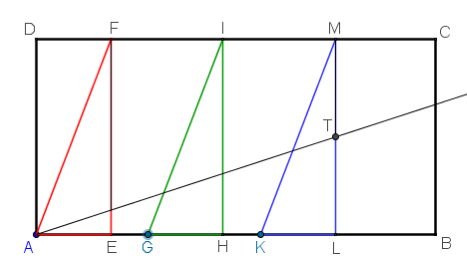
y trataremos de llegar a esta otra
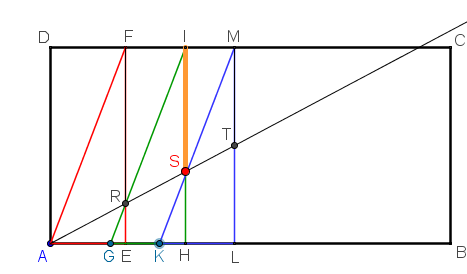
solución
al manipular los controles gráficos G y K y conseguir el objetivo, se muestran las dos medias proporcionales, FR e IS, propuestas por Hipócrates, entre dos segmentos, MT y DA, de longitudes a y 2·a respectivamente, donde a es la longitud de la arista del cubo inicial. La recta determina el segmento que se usará de arista del cubo de volumen doble al primero.
Con ayuda de los cursores y seleccionando alternativamente con el ratón los puntos G y K el ajuste puede ser bastante exacto tal y como muestra la imagen solución.
Se ha creado el recurso en la web de GeoGebra: 'Las espirales complejas.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografia:
- Documentación de Yuli Andrea Rodríguez Rodríguez y Benjamin R. Sarmiento Lugo
- El problema de la Duplicación del cubo de Juana Contreras S. y Claudio del Pino O. Instituto de Matemática y Física. Universidad de Talca.
- Una aproximación a la curva de transición Clotoide vista desde Mathematica de:
Luís Blanch, Emilio Checa, Josefa Marín
Universitat Politecnica de Valencia
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo. - Problema de la duplicación del cubo de Juan Pablo Mora.
- Consideraciones sobre los complejos y las espirales de:
Miguel Ángel Morales Medina - Otros documentos buscados en Internet.
Ildefonso Fernández Trujillo
Proporcionalidad. Las espirales XIII
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales XIII
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.
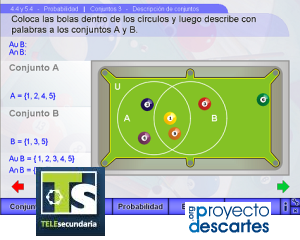
Como muestra enlazamos la unidad sobre Probabilidad, del subproyecto TELESECUNDARIA,
la GEOevaluación de Francia.
y los cinco ejemplos de plantillas transparentes, de los que enlazamos el primero.
Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D en particular los materiales de 2º y 4º LOMCE y LOE y la experiencia: Aprendemos a resolver problemas con Descartes y Wiris
Aprendemos a resolver problemas con Descartes es una iniciativa del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, realizada con alumnos y alumnas de 4º ESO durante el curso escolar 2015/2016, basada en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes"
Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el primero de los métodos para duplicar un cubo, esto es, dado un cubo de arista a y volumen V halla, mediante la Duplicatriz de Hipócrates, un segmento de longitud a'= a·21/3 que será la arista del cubo de volumen V' = 2·V.
La escena, en primer lugar, construye dinámicamente la curva duplicatriz pulsando en el botón ![]() , en el momento en que la recta MA corta a la recta PO (M = C y A = B) se activa el botón de información que al pulsarlo deja ver un breve texto con la definición del l.g. y una demostración, que usa la construcción de Platón, del hecho de la duplicidad. En cualquier instante puede detenerse la animación mediante el botón
, en el momento en que la recta MA corta a la recta PO (M = C y A = B) se activa el botón de información que al pulsarlo deja ver un breve texto con la definición del l.g. y una demostración, que usa la construcción de Platón, del hecho de la duplicidad. En cualquier instante puede detenerse la animación mediante el botón ![]() .
.
La escena es facilmente adaptable y admite las modificaciones y/o ampliaciones que el usuario considere convenientes para su uso personal.
En el siguiente trabajo se muestra la forma en que se genera el l.g. conocido como Cisoide de Diocles y la manera de encontrar con dicha curva el segmento que sirva de arista al cubo que doble en volumen a uno inicial dado.
En esta ocasión, en la sección de vídeo, hemos elegido la primera parte del que se ha mostrado en las últimas entradas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.
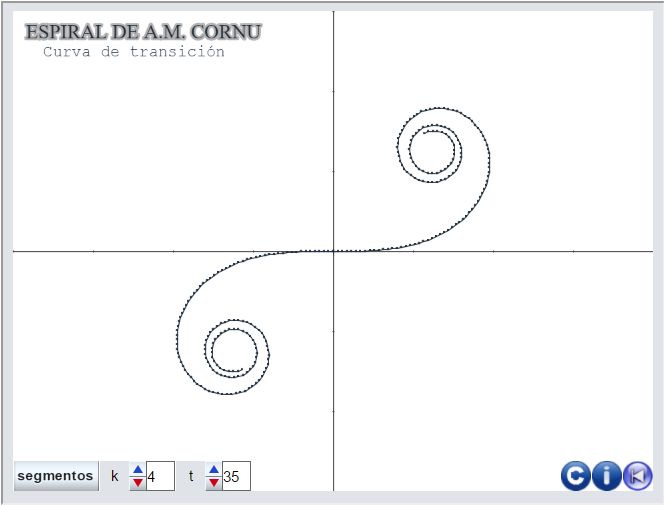
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Cornu" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Cornu (pulsad sobre la imagen para acceder a ella). Debemos advertir que, tal y como hemos procedido, esta realiza cálculos intensivos con números extremadamente grandes y pequeños, lo que hace que la ejecución de la misma sea muy lenta. Esta manera de proceder tiene la intención de hacer visible la sensibilidad de las aproximaciones polinómicas y sus efectos secundarios según muestra el trabajo posterior realizado con GeoGebra y que puede reproducirse con la escena actual con unas pocas modificaciones.
- Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Cornu incluida.
En el siguiente trabajo realizado con GeoGebra, al activar la animación puede observarse como se genera el lugar geométrico conocido como curva Duplicatriz. En primer lugar se obtienen las dos medias proporcionales, propuestas por Hipócrates, entre dos segmentos de longitudes a y 2·a, donde a es la longitud de la arista del cubo inicial. A continuación la curva determina el segmento que se usará de arista del cubo de volumen doble al primero. Para la demostración se usa la composición de triángulos rectángulos semejantes atribuida a la escuela platónica.
De los recursos de la web de GeoGebra hemos tomado como origen para el análisis de las características de la aproximación polinómica de las integrales de Fresnel el "material-956849" y entre otras hemos encontrado ocurrencias como las que se exponen a continuación, que se ponen en evidencia pulsando el botón 'GO'.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- Documentación de Yuli Andrea Rodríguez Rodríguez y Benjamin R. Sarmiento Lugo
- El problema de la Duplicación del cubo de Juana Contreras S. y Claudio del Pino O. Instituto de Matemática y Física. Universidad de Talca.
- Una aproximación a la curva de transición Clotoide vista desde Mathematica de:
Luís Blanch, Emilio Checa, Josefa Marín
Universitat Politecnica de Valencia
Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo. - Problema de la duplicación del cubo de Juan Pablo Mora.
- Y otros documentos buscados en Internet.
Ildefonso Fernández Trujillo
La vuelta al cole con Descartes para el curso 2016/2017
Escrito por José Antonio Salgueiro GonzálezModificar una plantilla y subir los archivos en nuestro moodle
Escrito por Montserrat Gelis Bosch¿Conoces el Proyecto Plantillas?
Se trata de una propuesta de la RED Descartes que contiene múltiples y diversos recursos. La particularidad de este proyecto reside en la facilidad con que se pueden modificar los materiales para adaptarlos a las necesidades del profesorado, generando actividades mediante simples cambios de imágenes o textos, sin necesidad de conocer lenguaje de programación.
En la página del proyecto encontramos toda la información sobre estos recursos e indicaciones para modificarlos, un manual en formato pdf y una serie de vídeos en los cuales se explican los pasos a seguir para modificar cada uno de los tipos de actividades que podemos encontrar.
A modo de ejemplo, en este vídeo vamos a modificar el conocido juego del ahorcado. En la plantilla original se proponen distintas capitales de América, nosotros substituiremos las capitales por conceptos que hagan referencia a triángulos. Una vez modificado el recurso, vamos a ver cómo subir estos materiales en nuestra aula virtual moodle para su aplicación en el aula.
Hoy vamos a reportar la unidad de 2ºESO Fracciones que es válida tanto para la LOMCE como para la LOE:
Hemos tratado los siguientes epígrafes:
1. Fracciones
Fracciones Equivalentes
Simplificación de Fracciones
2.Fracciones con igual denominador
Reducción a común denominador
Comparación de fracciones
3.Operaciones con fracciones
Suma y resta
Producto
Cociente
Potencia
Raíz cuadrada
Operaciones combinadas
4.Aplicaciones
Problemas de aplicación
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)












 CONTACTO
CONTACTO
