Matemáticas para todo el mundo. Día Internacional de las Matemáticas
Escrito por José Antonio Salgueiro GonzálezEn noviembre de 2019, la UNESCO proclamó el 14 de marzo de cada año como Día Internacional de las Matemáticas, con el fin de destacar el papel fundamental que desempeñan las ciencias matemáticas para hacer frente a los desafíos de nuestro tiempo en ámbitos como la inteligencia artificial, la salud, el cambio climático, la energía y el desarrollo sostenible y la mejora de la calidad de vida de la sociedad en general.
Para las personas que accedan por primera vez a esta información, debemos recordar que hemos venido celebrando desde hace años el conocido como "Día de π", una efemérides motivada por la forma de expresar la fecha diaria en el mundo anglosajón, es decir, 3/14, coincidiendo con las primeras cifras de este irracional número, considerado como una de las constantes matemáticas más importantes y conocidas.
La organización corresponde al Comité Español de Matemáticas (CEMat) a través de su Comisión de Educación y se ha habilitado una página oficial para la efemérides en España.

Como el fin de RED Descartes es promover la renovación y cambio metodológico en los procesos de aprendizaje y enseñanza de las Matemáticas, y también en otras áreas de conocimiento, utilizando los recursos digitales interactivos generados con la herramienta de autor Descartes JS, aportamos una humilde propuesta de recursos interactivos con los que, cualquier docente que no haya podido planificar este evento previamente para su aula, o cualquier alumno o alumna autodidacta, cualquier familia, cualquier persona de la aldea global puede participar desde un equipo tecnológico instalado en el aula o desde sus propios dispositivos móviles, tanto de forma colaborativa como individual.
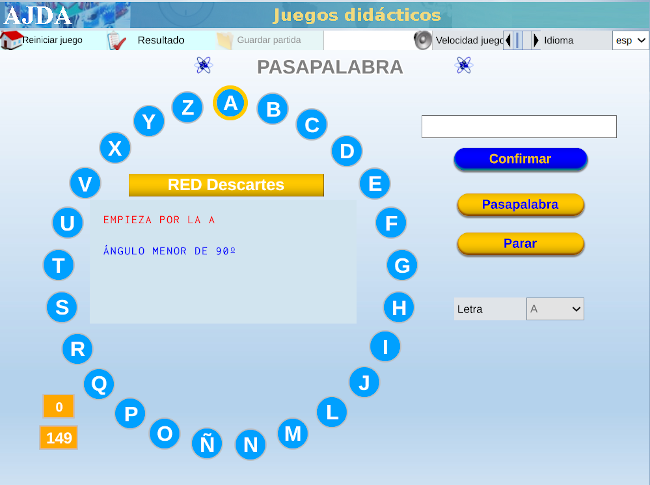
| MATEMÁTICAS PARA TODO EL MUNDO CON ... PASAPALABRA |
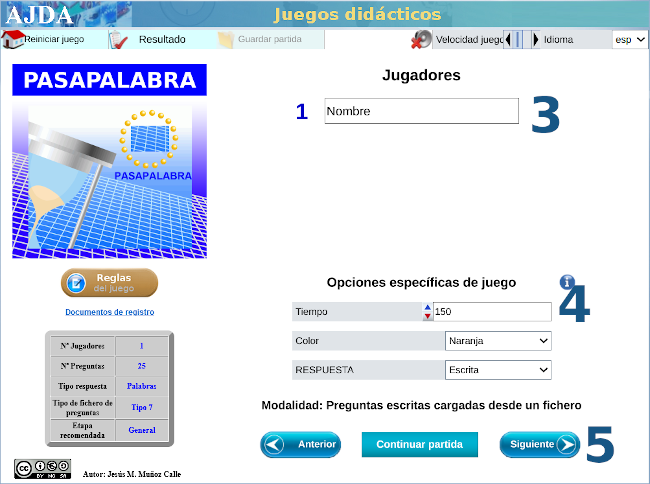
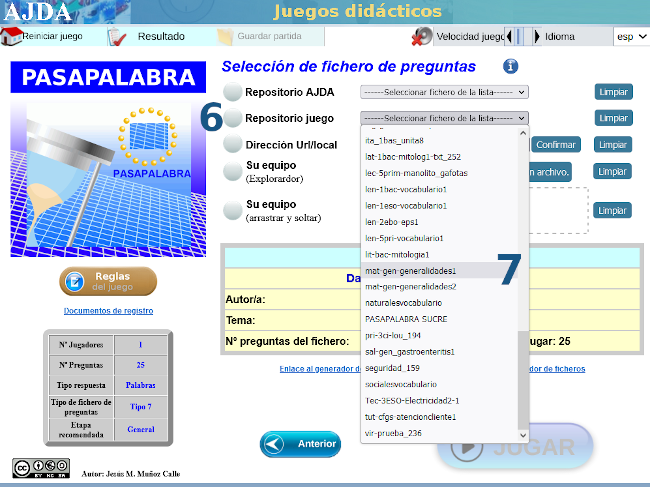
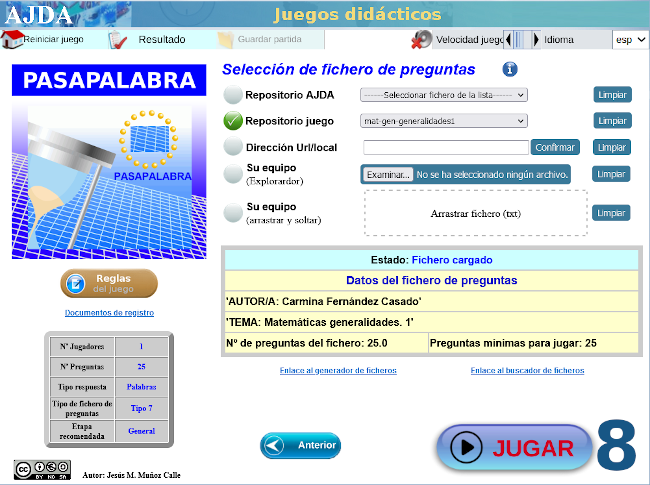
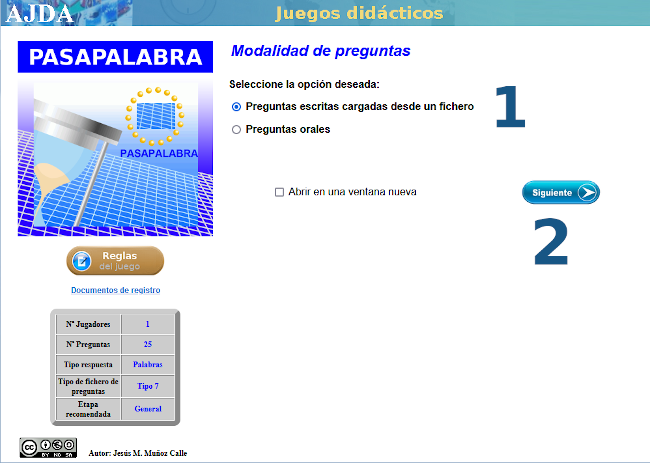
Con varias capturas de pantalla como tutorial, mostramos las sencillas instrucciones para acceder al juego didáctico, desde este enlace o sobre la imagen inferior. Te advertimos que hay una pregunta sorpresa y, además, te recomendamos ajustar el tiempo en función de la edad.
Nuestro más sincero agradecimiento a su autora, Carmina Fernández Casado.
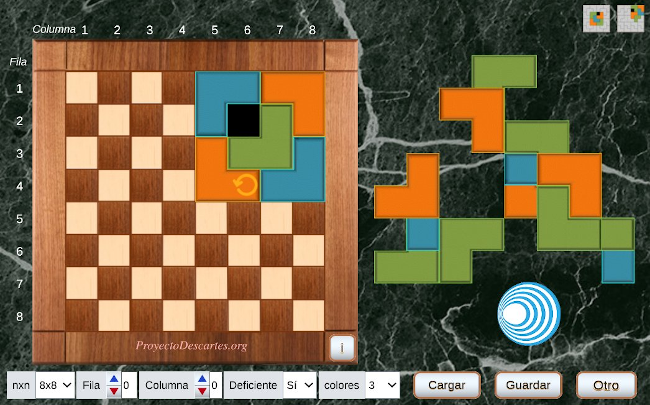
| MATEMÁTICAS PARA TODO EL MUNDO CON ... EMBALDOSADOS |
Este reto supone un desafío superior, aunque siempre es bueno desarrollar la visualización geométrica jugando con embaldosados. Te recomendamos comenzar por el tablero 4x4 para ir ampliando sus dimensiones en función del éxito obtenido.
Si quisieras sacar el máximo partido al problema planteado, tendrías que acceder a la información del artículo enlazado. En caso contrario, comienza ya a "jugar" accediendo desde la imagen inferior.
| MATEMÁTICAS PARA TODO EL MUNDO CON ... OTROS RECURSOS |
Si no tienes suficiente con nuestra propuesta o buscas algo diferente, te recomendamos visitar los artículos de las ediciones anteriores:
¡FELIZ DÍA INTERNACIONAL DE LAS MATEMÁTICAS!
En marcha la Open Education Week 2023
Escrito por José Antonio Salgueiro GonzálezLa Semana de la Educación Abierta (Open Education Week) es una oportunidad para compartir activamente y aprender sobre los últimos logros en Educación Abierta en todo el mundo. OE Week brinda a los profesionales, educadores y estudiantes la oportunidad de obtener una mayor comprensión de las prácticas educativas abiertas y de inspirarse en el maravilloso trabajo que está desarrollando la comunidad en todo el mundo. Unos objetivos que encajan perfectamente con el lema de Red Descartes: "trabajando altruistamente por la comunidad educativa de la aldea global". Por ello, en esta nueva edición, que se desarrolla durante los días comprendidos entre el 6 y el 10 de marzo de 2023, desde Proyecto Descartes hemos decidido colaborar, compartir y aportar algunos de nuestros proyectos en la línea de la OE Week, centrándonos en los más recientes y abarcando las diferentes líneas de la Educación Abierta.
Pero antes, para nuestros seguidores, docentes, comunidad educativa y ciudadanía, en general, conviene recordar el origen oficial y concepto de Recurso Educativo Abierto, que aparece en París en junio de 2012, durante el Congreso Mundial sobre los Recursos Educativos Abiertos (REA), posteriormente actualizado en el conocido como Plan de Acción de Liubliana sobre los REA, celebrado en 2017 en la capital eslovena y, finalmente, ampliado con la Recomendación sobre los Recursos Educativos Abiertos de la UNESCO: materiales de aprendizaje, enseñanza e investigación, en cualquier formato y soporte, de dominio público o protegidos por derechos de autor y que han sido publicados con una licencia abierta que permite el acceso a ellos, así como su reutilización, reconversión, adaptación y redistribución sin costo alguno por parte de terceros. Una definición cuyos requisitos cumplen escrupulosamente los recursos interactivos generados con la herramienta de autor Descartes JS y compartidos con la aldea global en el portal de la ong RED Descartes.

Seguidamente, recopilamos en varias tablas los REA y cursos abiertos presentados en esta edición, identificados con una imagen que enlaza a la librería de la Open Education Week, con quien venimos colaborando desde varios años atrás, aprovechando para agradecer su acogida.
| RECURSOS EDUCATIVOS ABIERTOS EN ESPAÑOL |
||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| RECURSOS EDUCATIVOS ABIERTOS EN OTROS IDIOMAS |
||
 |
 |
 |
 |
 |
 |
| REVISTA DIGITAL DE LA RED DESCARTES |
||
 |
 |
|
| FORMACIÓN ABIERTA | |
 |
 |
¿Por qué es importante la Educación Abierta?
"La gente quiere aprender. Al proporcionar acceso gratuito y abierto a la educación y al conocimiento, la educación abierta ayuda a crear un mundo para apoyar el aprendizaje. Los estudiantes pueden obtener información adicional, puntos de vista y materiales para ayudarlos a tener éxito. Los trabajadores pueden aprender cosas que los ayudarán en el trabajo. La facultad puede recurrir a recursos de todo el mundo. Los investigadores pueden compartir datos y desarrollar nuevas redes. Los maestros pueden encontrar nuevas formas de ayudar a los estudiantes a aprender. Las personas pueden conectarse con otras personas que de otra manera no se encontrarían para compartir ideas e información. Los materiales se pueden traducir, mezclar, dividir y compartir abiertamente de nuevo, lo que aumenta el acceso e invita a nuevos enfoques. Cualquiera puede acceder a materiales educativos, artículos académicos y comunidades de aprendizaje de apoyo en cualquier momento que lo deseen. La educación está disponible, accesible, modificable y gratuita".
(El párrafo anterior ha sido extraído literalmente de la web de la Open Education Week)
| HERRAMIENTA DE AUTOR DE SOFTWARE LIBRE DESCARTES JS |
 |
Otro elemento introducido en el juego 10x10 en particular, y en otros muchos en general, es un espacio desplegable lateral en su zona izquierda. Se trata de un espacio de mayor tamaño que el menú superior desplegable y cuya función suele ser de marcador de resultados, escaleta, tabla de clasificación, etc.
Este espacio está disponible en todo momento del juego, salvo en las pantallas iniciales de configuración del mismo. Dado que es de mayor tamaño, dispone de dos controles de despliegue situados en el borde izquierdo y hacia la zona superior de la pantalla. Uno de ellos contiene una flecha negra y otro roja. La diferencia entre ambos es que la flecha roja provoca un despliegue instantáneo, mientas que la negra lo hace gradual. Dichos controles sirven tanto para abrir como para cerrar el espacio.
En el juego 10x10, este espacio lateral izquierdo presenta la escaleta del juego. En el juego Liguilla 6J, en este espacio se recogen los resultados de todos los partidos disputados en la "liguilla".
Finalmente, comentar que en el espacio que estamos tratando se podrían incluir, dependiendo de la naturaleza del juego, otra serie de contenidos, elementos u accesorios que mejoren el recurso didáctico.
Continuando con las nuevas aportaciones incluidas en el nuevo juego 10x10, nos centramos en la unificación de versiones o modalidades en un mismo juego.
En general los juegos pueden presentan diferentes modalidades o versiones de los mismos dependiendo de la forma de introducción de las preguntas para el juego: a través de ficheros, de forma oral, sin preguntas, a través de formularios incluidos en el mismo juego, generadas por el propio juego... Anteriormente, cada una de estas modalidades o versiones se presentaba en una escena de Descartes diferente. Esto implicaba que si un juego se estaba utilizando en una modalidad y se quería pasar a otra, había que grabar la partida que se estaba usando, abrir otra escena del juego de la nueva modalidad que se quiere utilizar y cargar la partida que se había guardado anteriormente.
Con la nueva mejora que presentamos, ahora todas las versiones o modalidades de un mismo juego se integran en una única escena, permitiéndose pasar de una modalidad a otra al principio o durante una partida del juego. La opción de para seleccionar la modalidad o versión se encuentra en la pantalla inicial de configuración de los parámetros del juego, en la opción específica Formato de las preguntas.
Más...
Presentación del libro interactivo "Mucho teatro"
Escrito por José Antonio Salgueiro GonzálezMucho Teatro ha sido el nombre de un proyecto educativo que durante unos años fue llevado a efecto en el I.E.S. Blas Infante de Córdoba (España). El libro ofrece a aquellos que todavía estén inmersos en el maravilloso mundo del teatro en las aulas, las obras que el autor escribió para tantos grupos de alumnos y de profesores. Pues bien, Paco Torres, su autor, ha tenido la gentileza de acceder a nuestra propuesta de presentación de este libro interactivo, de y para instituto, mediante el siguiente vídeo que compartimos en este artículo.
Con objeto de facilitar la accesibilidad, o para aquellas personas que necesiten visualizarlo en silencio, hemos incorporado subtítulos en lengua castellana, así que te recordamos que, posiblemente, tengas que activarlos desde la barra del reproductor de Youtube.
- Acceso directo al recurso para su visualización en línea.
- Acceso a la versión PDF con enlaces a los interactivos de su interior.
- Descargar el recurso en archivo comprimido para su visualización en local, aunque necesitarás conexión solamente para los multimedias embebidos.
- Doña Juana Tenorio
- Luces de pandemia
- La casa de Bernardo Amanecer
- Historia de un ascensor
Resumen estadístico anual de 2022 ¡Regresando a la normalidad y creciendo!
Escrito por José R. Galo SánchezEn este año 2022, en RED Descartes y en nuestro entorno educativo, hemos ido regresando a la normalidad prepandemia. Después de los récords estadísticos que alcanzamos en nuestro servidor proyectodescartes.org y que fueron provocados por la imperiosa necesidad de disponer de recursos educativos que cubrieran la enseñanza a distancia, a la que nos forzó la COVID 19, ¡afortunadamente! las aulas han vuelto a su normalidad y nosotros también. Estadísticamente hemos subido en las descargas (un 14 %) y hemos decrecido tanto en el número de páginas servidas (-20 %) como en las visitas recibidas respecto a la anormalidad de los años 2020 y 2021, pero hemos seguido creciendo en todos los parámetros respecto a la normalidad de 2019.
Son meros datos informativos que nos ilustran, aunque no pueden reflejar la satisfacción de nuestra organización no gubernamental por ayudar a quienes se acercan a nuestro servidor con ganas de aprender, esta satisfacción obviamente es independiente de los meros datos recopilados.
Y, año a año, hemos sumado ¡veinticinco años! desarrollando el proyecto Descartes, nos congratulamos con ello y compartimos nuestra complacencia con todos vosotros... ¡seguiremos creciendo y madurando con vuestra compañía!
¡Qué el año 2023 os colme de ansia por aprender y amplíe vuestro conocimiento, sin dejaros saciados!
¡Desde RED Descartes esperamos y deseamos seguir aportando a la comunidad educativa de la aldea global!
En el año 2022 hemos alcanzado la cifra global de ¡treinta y cinco millones de páginas servidas! frente a los cuarenta y dos millones del año 2021 (un 20% menos), si embargo el récord anual lo hemos alcanzado en el número de TB descargados por todos vosotros, han sido un total de 12,9 TB, un 14 % superior a las descargas de 2021 (11,3 TB), lo cual muestra, o quizás pueda interpretarse, que hay un cambio de estrategia en parte de nuestros usuarios los cuales han optado por instalar en local nuestros recursos y evitar estar conectado a internet en su trabajo diario. Eso puede ser consecuencia del paso a la enseñanza tradicional, en el aula o salón de clase, frente a la telemática a la que nos forzó la pandemia. Es posible que los centros docentes hayan continuado su enseñanza con nuestros recursos in situ, descargados en los dispositivos del aula, y de esa manera hayan disminuido la conexión directa a nuestro servidor.
En la siguiente tabla resumen reflejamos un detalle por meses de lo acaecido en nuestro dominio proyectodescartes.org. En la primera columna se cuenta con un enlace que da acceso a un desglose detallado por días y horas para cada uno de esos meses.
El las siguientes imagenes, en diagramas de barras, reflejamos el desglose mensual de páginas servidas, GB descargados y clientes que han accedido.
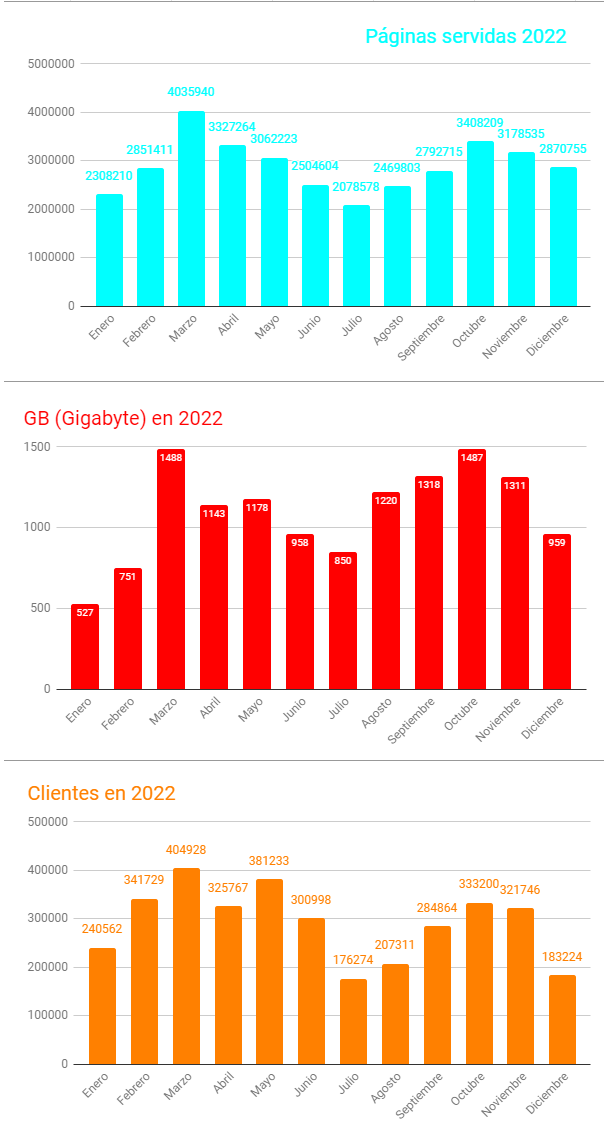
Y en las siguientes, podemos observar la diferencia porcentual entre lo contabilizado en 2022 y en el 2021. En ellas podemos ver cómo en todos los meses, salvo en diciembre, se manifiesta un decremento en el número de páginas servidas, siendo más significativo en los seis primeros y más irrelevante en el segundo, con cambio de tendencia final. En los seis primeros meses de 2021 estábamos aún con aulas virtuales o al menos semipresenciales y en el segundo semestre ya nos adentramos en la normalidad, así pues la causa parece obvia al estar reflejándose en ese primer semestre dos situaciones educativas diferentes y, por tanto, con necesidades también diferentes; mientras que en el segundo se corresponden a situaciones presenciales similares.
Respecto a las descargas, éstas aumentan significativamente en el segundo semestre. La posible causa ya la hemos adelantado anteriormente.
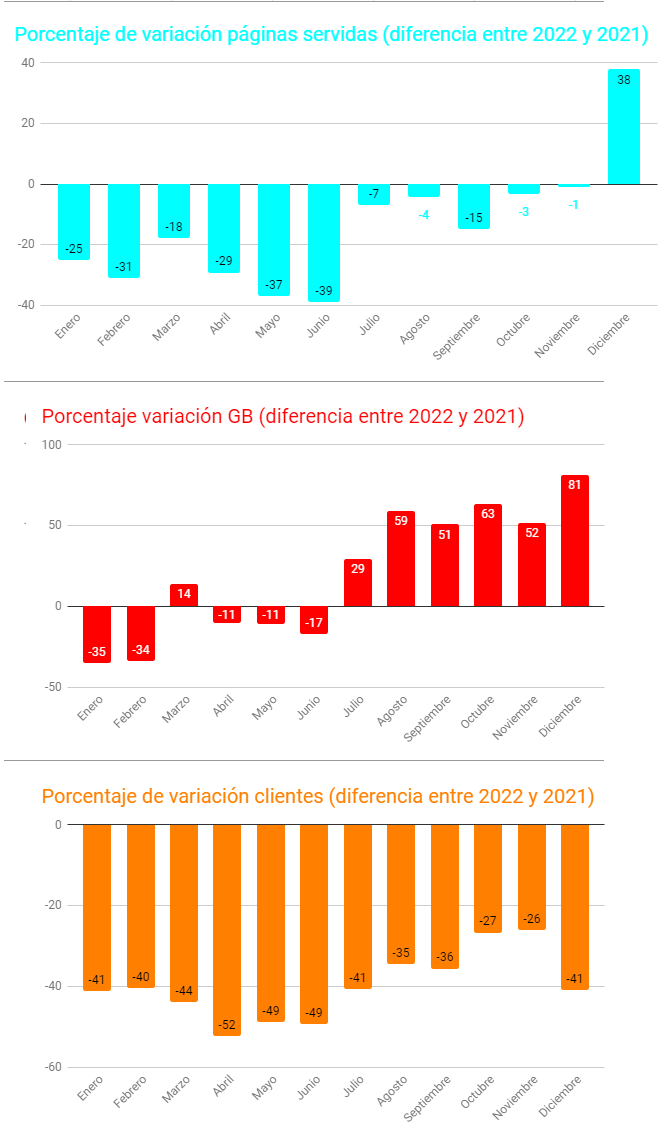
Si realizamos esa comparativa, también en términos porcentuales, con respecto a la situación prepandémica de 2019, comprobamos el incremento acaecido en situaciones escolares análogas:
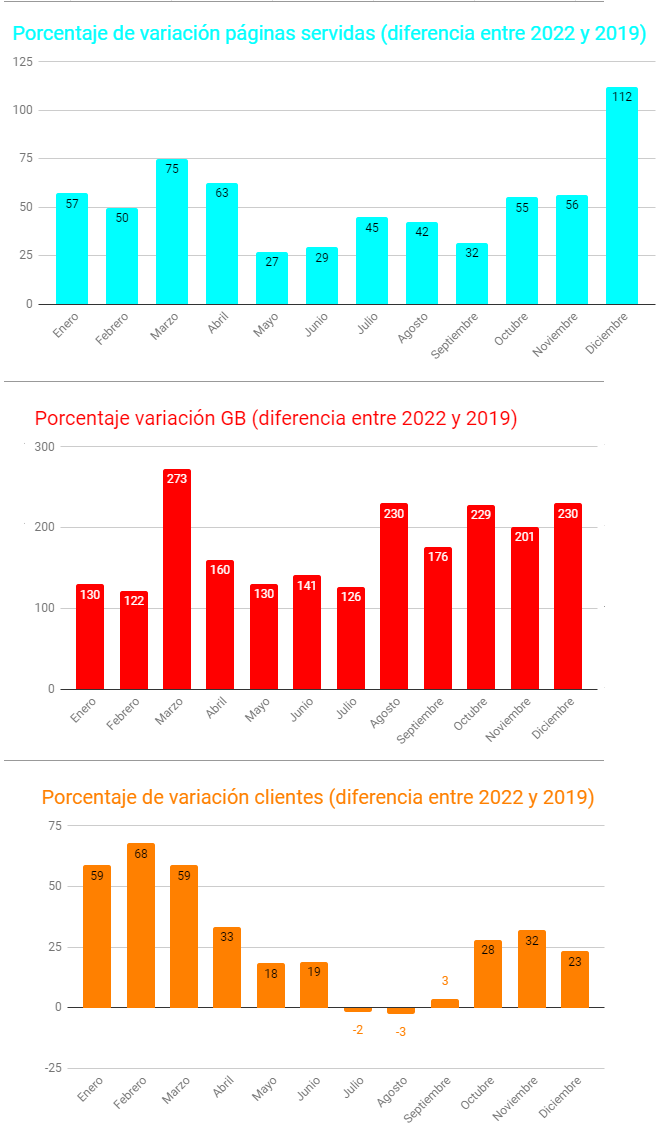
Continuaremos con igual ahinco tratando de satisfacer vuestras necesidades y confiando en que sigáis accediendo a nuestro/vuestro servidor. Nos tenéis atentos a cualquier comentario, observación y/o petición que estiméis oportuna realizar. Recibiremos con alegría vuestras aportaciones bien en nuestro correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo. o bien a través de los comentarios que podéis realizar en este servidor de contenidos.
¡Feliz 2023!
¡Continuemos, juntos, aprendiendo con Descartes! ¡Son 25 años contigo!
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
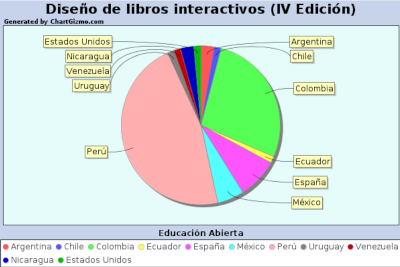
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



















 CONTACTO
CONTACTO
