En este nuevo artículo sobre la ontogenia matemática del Nautilus, después de haber modelizado los septos en el segundo y tercer verticilio bajo el invariante de tangencialidad, nos adentramos en la modelización de los septos en el primer verticilo. Esta primera fase de crecimiento vimos que se muestra diversa y con apariencia poco regular, cambiante (menor número de cámaras septales,  ocho frente a las dieciséis de la etapa juvenil y adulta, con secciones y amplitudes que cambian como necesidad biológica para alcanzar la flotabilidad) y, ahora, ha llegado el momento de mostrar el modelo matemático que da explicación a esta etapa e introduce la regularidad esperada que parecía no acaecer, pero que queda al descubierto bajo la perspectiva matemática. De nuevo, el hecho de que intervengan dos espirales con diferente polo, en este caso  la espiral de la pared ventral y la espiral de los polos de los septos, conduce a proporciones variables entre los radios vectores y consecuentemente a que se formen septos con factores de escala variables. Ello nos conduce y permite determinar las ecuaciones de los septos, los puntos de tangencia con la pared ventral y los de intersección con la pared dorsal (para ello necesitaremos introducir un grosor en el modelo matemático de esa pared, que es lo que físicamente acontece).

Completaremos el contenido de este documento agrupando y relacionando entre sí diferentes puntos que se han ido detectando en este análisis. Unos que denominamos notables, porque matemáticamente son los que establecen el modelo matemático y dan explicación causal al mismo, y que son polos de diferentes espirales. Y otros que catalogaremos como destacables, posible fuente de inspiración matemática futura, y que son centros desde los que algunos objetos se observan con perspectiva angular constante.

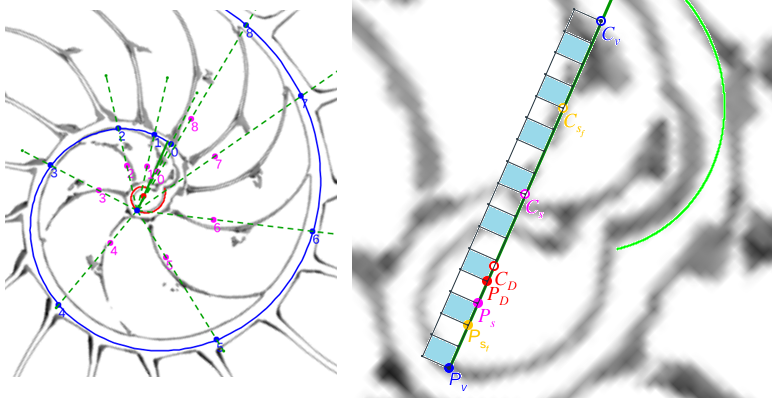
Propociones entre los radios vectores de la espiral ventral y los de la espiral de los polos de los septos	Puntos notables y destacables

Así pues, doy continuidad a los artículos anteriores (I, II, III, IV y V), con un contenido adicional que espero sea de su interés —¡para mí es siempre una satisfacción! ir pudiendo relatarles progresivamente lo que, poco a poco, me cuenta la concha de este animalito—, y he de adelantarles que serán necesarios algunos artículos adicionales porque aún nos quedan secretos que dilucidar en esta ontogenia, en particular lo que acontece en la transición de la fase embrionaria (primera y segunda cámara septal) donde el sifúnculo cambia abruptamente de posición, y en la fase de transición entre el primer y segundo verticilo (cámaras octava, novena y décima) donde al finalizar la primera vuelta se produce el encuentro del fragmacono con la concha embrionaria. Y también habrá que abordar la síntesis o resumen final, es decir, plasmar y reproducir ese modelo ontogénico de la concha del Nautilus.​

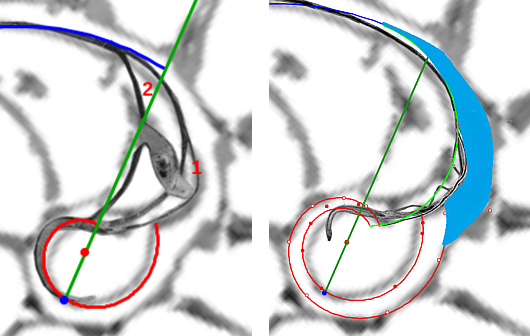
El sifúnculo en la segunda cámara septal	Transición entre el pimer y segundo verticilo

Como observamos, una mirada atenta y un continuo deseo de comprensión nos hace ir visualizando cada vez más detalles que inicialmente pueden parecer nimios, pero que finalmente se han ido mostrando como retos cuya resolución es de interés. Todo ello, a costa de que a ustedes a lo mejor les ocurra como a mi sobrina nieta (Aurora, cerca de los cuatro años) que ayer, al verme una vez más delante de la pantalla de mi ordenador, indagando la imagen de la sección del Nautilus con diversos objetos matemáticos superpuestos, la cual ya ha observado en multitud de ocasiones y quizás hayan sido demasiadas para ella, dijera: "¡Tita!, ¡el tito todavía no ha hecho sus deberes!". Por tanto, espero poder ir finalizando mis deberes, que realmente no son más que satisfacciones aunque requieran esfuerzo y dedicación, y que en el trancurso hacia su final les pueda tener como lectores y juntos podamos desarrollar nuestra vocación como  μαθηματικός (mathēmatikós) o amantes del conocimiento. 

En el siguiente pdf (o desde este enlace) tienen desarrollados los contenidos de este artículo

Ontogenia matemática del Nautilus VI

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional