En el primer verticilo del Nautilus encontramos algunos sitios que podemos catalogar como singulares, pues se muestran como específicos respecto a su entorno o que aparentemente se salen de la uniformidad cordobesa que hemos ido detectando y desgranando en los artículos publicados anteriormente sobre la "Ontogenia matemática del Nautilus". Pero, hasta en estas situaciones, la proporción cordobesa y la espiral cordobesa aparece sin más que rascar matemáticamente en la concha del Nautilus, por supuesto con gran mimo.

Esos sitios singulares son:

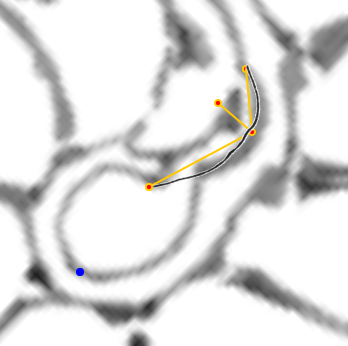
• La concha embrionaria.
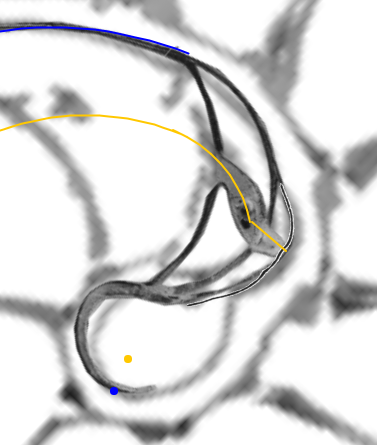
• El sifúnculo en la segunda cámara septal y su relación con la ampliación del fragmacono en el primer septo.
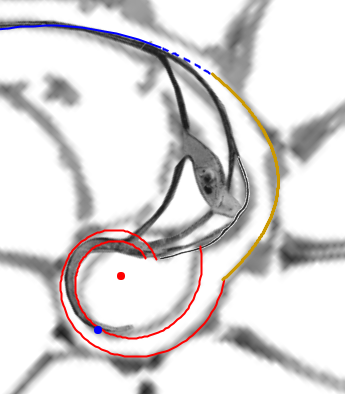
• La confluencia de la pared dorsal con la concha embrionaria en la fase de transición entre el primer y segundo verticilo (cámaras octava, novena y décima).

La concha embrionaria	El sifúnculo en la segunda cámara septal y la ampliación del fragmacono	La pared dorsal en la transición entre el primer y segundo verticilo

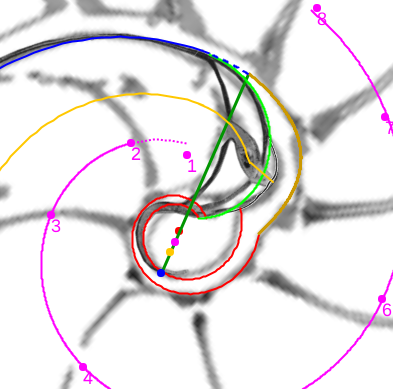
En este artículo analizamos estas singularidades y encuadramos su modelado en el contexto cordobés del Nautilus. Para ello, acudimos y aplicamos la invariante enunciada desde el inicio y que reiteradamente hemos ido aplicando en toda la modelación: "Todo punto interior a la concha o sobre ella se obtiene como la intersección de dos espirales cordobesas, una longitudinal similar a la ventral y otra transversal similar a la septal". La siguiente escena interactiva ha servido de base para el análisis de estos sitios singulares. 

Modelando los sitios singulares del Nautilus en el primer verticilo 
Pulsad sobre la imagen para acceder a la escena

En el siguiente pdf (o desde este enlace) tienen desarrollados los contenidos de este artículo

Ontogenia matemática del Nautilus VII

Aquí, hemos dado continuidad a los artículos anteriores (I, II, III, IV, V y VI) y por fin, creo, he cumplido mis deberes, si bien no seré yo quien excluya la posibilidad de que puedan surgir nuevas cuestiones, pues eso es lo que ha ido aconteciendo a lo largo de estos meses en los que les he ido relatando mi investigación a través de este blog de RED Descartes. Pero, independientemente de que afloren nuevas cuestiones o no, sí les indico que éste no será este el último artículo de esta serie, tengo que tratar de completarla adecuadamente y, por tanto, estimo necesario recopilar todo lo expuesto en una escena interactiva de Descartes o en una animación o en un gif animado o en un recurso similar o... y así mostrar la ontogenia matemática del Nautilus en un hilo temporal que recoja su crecimiento, si bien real y paradójicamente éste ha de ser atemporal porque en la literatura existente los datos relativos a los tiempos en el crecimiento de la concha son muy genéricos o yo no he logrado localizarlos. En la siguiente animación reflejamos el modelo uniforme del Nautilus y próximamente podremos aportar el modelo ontogénico (de nuevo les pido un poquito más de paciencia, no nos demos un atracón que pueda conducir a una indigestión).

Modelo uniforme del Nautilus 

Y también tendremos que desarrollar alguna cosita en 3D ¿no les parece?... Hasta pronto...

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional