Asamblea general en el IES José Manuel Blecua de Zaragoza
Escrito por José Antonio Salgueiro González¡Por fin!, una vez superados estos dos años de restricciones motivadas por la pandemia, hemos podido celebrar nuestra asamblea general de forma presencial, simultaneada con modalidad virtual para aquellos socios y socias que no han podido asistir físicamente. El acto, con periodicidad anual, tuvo lugar en esta ocasión en el IES José Manuel Blecua de Zaragoza, el lunes día 4 de julio, lugar al que nos desplazamos desde distintos puntos geográficos de la península: Santomera, Logroño, Barcelona, Burgos, Santiago de Compostela, Córdoba, Santander, Madrid y Lebrija. Particularmente, para quien suscribe este artículo, ha sido un placer conocer personalmente a nuestra compañera Begoña Campos, y espero en sucesivas asambleas poder desvirtualizar a otros miembros de RED Descartes.
Durante una fructífera jornada hemos tratado, a grosso modo, asuntos de relevancia como las mejoras técnicas en la herramienta de autor y de software libre DescartesJS, así como en el núcleo del libro interactivo, gracias al soporte proporcionado por el Instituto de Matemáticas de la Universidad Nacional Autónoma de México. A su vez, otra de las claves del éxito, nos llega desde el programa de Educación Abierta entre ColDescartes y la Institución Universitaria Pascual Bravo de Colombia, lo que nos ha llevado a constituir la Editorial RED Descartes, con una biblioteca que no cesa en su producción de volúmenes para ofrecer recursos educativos abiertos y realizar nuestra humilde aportación a los Objetivos de Desarrollo Sostenible de la UNESCO, especialmente el denominado ODS4, Educación de Calidad: la educación es la base para mejorar nuestra vida y el desarrollo sostenible. Además, en gran parte gracias a este programa, hemos analizado la extensión de la red cartesiana a profesionales de la enseñanza en otros países de lengua hispana, de lengua portuguesa e incluso de lengua inglesa. También se ha reflexionado sobre los avances en nuevos recursos educativos abiertos, como la Revista Digital de la RED Descartes, el Proyecto PI, las novedades en el subproyecto AJDA, de Aplicación de Juegos Didácticos en el Aula, de las que iremos dando información periódica, así como otros recursos en los subproyectos Misceláneas y Prometeo. Por otra parte, se ha valorado el gran esfuerzo desempeñado en la difusión desde nuestro portal, en eventos educativos, en la conmemoración de ciertas efemérides y en los perfiles de nuestras redes sociales. En este sentido, hemos presentado nuestro nuevo perfil en PubHTML5, un software que convierte archivos PDF y otros materiales impresos en ediciones digitales geniales personalizadas en línea y fuera de línea.
En otro orden de cosas, y como resulta preceptivo en estas asambleas, hemos tratado asuntos de gestión y organización, memoria y propuesta de actividades, cierre económico y propuesta de presupuestos, así como el lanzamiento de iniciativas para celebrar en 2023 el 25 aniversario del Proyecto Descartes.
Queremos mostrar desde aquí nuestro más sincero agradecimiento a Dª. Izarbe García Gareta, directora del IES José Manuel Blecua, por su cálida acogida y exquisito trato dispensado, así como por facilitar el desarrollo de la asamblea general de RED Descartes en la capital de la comunidad aragonesa y, como no puede ser de otra manera por nuestra profesión, en un entorno educativo y académico.
Aprovechando la estancia en Zaragoza, y con nuestra compañera María José García Cebrián como anfitriona, pudimos visitar la Catedral-basílica de Nuestra Señora del Pilar, la Seo o Catedral del Salvador, pues en la capital maña coexisten dos catedrales, admirando el arte mudéjar que la envuelve exteriormente hasta llegar al Arco y Casa del Deán. También posamos ante el Puente de Piedra, en la exposición de tapices del Patio de la Infanta, recorrimos las distintas torres mudéjares y realizamos una visita guiada al impresionante Palacio de la Aljafería, sede actual de las Cortes de Aragón. Y, por supuesto, pudimos degustar la gastronomía de la tierra y catar caldos con denominación de origen en la Comunidad Autónoma de Aragón. Finalmente, en la mañana de la última jornada, concertamos una visita al Museo de Matemáticas del Planetario de Aragón, donde pudimos "tocar las matemáticas" y disfrutar con la realización de las interesantes y didácticas actividades propuestas.
La figura de la escena (que puedes admirar en el embaldosado del suelo frente a la entrada principal de la catedral de La Seo de Zaragoza) está compuesta de áreas de color blanco (cuadrados y triángulos), rojo (pentágonos) y negro. Calcula el área de cada una de ellas. Toda la figura es un cuadrado de 12 m de lado.
Este último párrafo está literalmente extraído de una actividad interactiva que aparece en la unidad titulada "Figuras planas. Propiedades métricas", del Proyecto ED@D para la materia de Matemáticas Orientadas a las Enseñanzas Académicas en 3º ESO, y que embebemos a continuación:
Durante muchos años había propuesto esta actividad, que recomiendo, a mi alumnado para afrontar el reto en equipos de aula, y siempre había tenido la inquietud y curiosidad de ver in situ este embaldosado tan singular y tan familiar, así que apovechamos la ocasión para inmortalizarnos sobre él:

Concluimos este pequeño resumen sobre la asamblea general 2022 con una selección de fotografías gracias a Josep María Navarro, nuestro reportero gráfico, habiendo elegido para ello un presentador de diapositivas en HTML5, que podemos visualizar en dispositivos móviles sin más que utilizar el dedo adelante o atrás para la transición de las mismas. Ahora bien, en un ordenador personal lo conseguiremos con las teclas o flechas de movimiento del cursor, pudiendo pulsar la tecla F (full) para el modo de pantalla completa.
El uso de este tipo de presentadores permite evitar la dependencia con presentadores comerciales como el PowerPoint de Microsofot o el KeyNote de Apple que, además, restringen la incorporación de algunos objetos diseñados en JavaScript, como las escenas interactivas de DescartesJS, GeoGebra, entre otros. Otra ventaja de usar HTML5 es poder compartir nuestras presentaciones vía web.
Si tienes interés en usar alguno de estos presentadores, te recomendamos el libro digital interactivo homónimo "Presentadores de diapositivas HTML5", donde encontrarás toda la información necesaria.
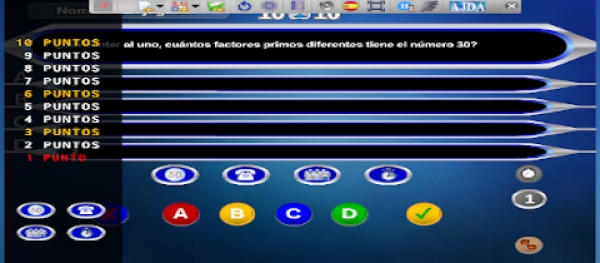
El primer juego didáctico que se realizó dentro del Proyecto AJDA fue una versión del programa de TV ¿Quién quiere ser millonario?, allá por el año 2007, llamada 10x10, ya que había que conseguir 10 puntos contestado a 10 preguntas, siguiendo la dinámica del popular concurso.
Este juego ha sido elegido como punta de lanza para realizar una ambiciosa potenciación de los juegos del Proyecto AJDA, mejorando su programación, funcionalidades y estilos. Por ello, el presente artículo va a ser el primero de una serie en la que se van a ir tratando y detallando los elementos y cambios introducidos. En esta primera publicación de la secuencia vamos a presentar de forma general las mejoras introducidas y en los siguientes las iremos desgranando. La relación de novedades es la siguiente:
- Nuevo menú superior desplegable.
- Nueva interfaz de introducción de parámetros de configuración de la partida.
- Rediseño de la pantalla para la introducción de ficheros de contenidos para juegos.
- Unificación en un sólo juego de todas las modalidades del mismo (modalidad con preguntas en ficheros, preguntas orales, sin preguntas...).
- Mejora integral de la presentación y estilos.
- Utilización de un diseño "Responsive".
- Perfeccionamiento del sistema de carga de los ficheros de preguntas.
- Potenciación de la interfaz traductora.
- Mejora en el código de programación y adaptación a la última versión de DescartesJS.
- Implementación de nuevas funcionalidades: guardado de configuración y partida, continuación de partidas, control de velocidad de animación, nuevos elementos de navegación y visualización, etc.
- Introducción de otros elementos y detalles.
Finalmente dejamos el enlace del nuevo juego 10x10 y emplazamos a seguir la serie de artículos que comenzamos.
Ontogenia matemática del Nautilus (VII)
Escrito por José R. Galo SánchezEn el primer verticilo del Nautilus encontramos algunos sitios que podemos catalogar como singulares, pues se muestran como específicos respecto a su entorno o que aparentemente se salen de la uniformidad cordobesa que hemos ido detectando y desgranando en los artículos publicados anteriormente sobre la "Ontogenia matemática del Nautilus". Pero, hasta en estas situaciones, la proporción cordobesa y la espiral cordobesa aparece sin más que rascar matemáticamente en la concha del Nautilus, por supuesto con gran mimo.
Esos sitios singulares son:
- La concha embrionaria.
- El sifúnculo en la segunda cámara septal y su relación con la ampliación del fragmacono en el primer septo.
- La confluencia de la pared dorsal con la concha embrionaria en la fase de transición entre el primer y segundo verticilo (cámaras octava, novena y décima).
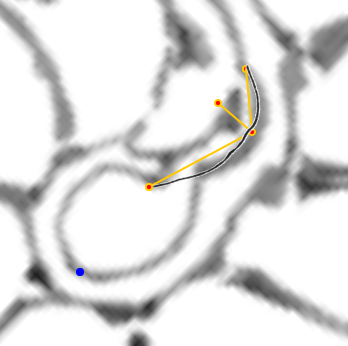 |
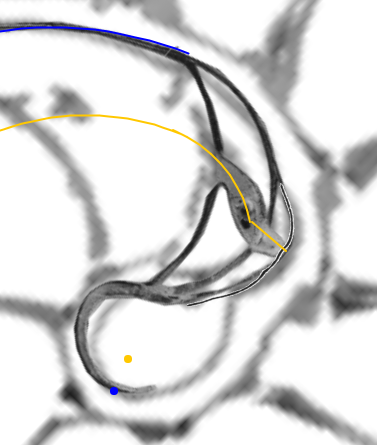 |
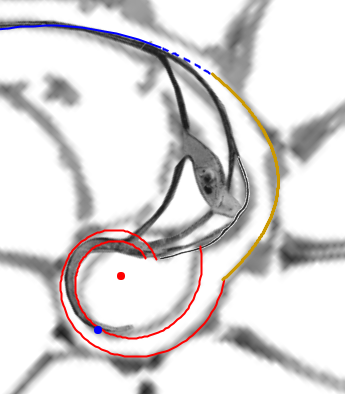 |
| La concha embrionaria | El sifúnculo en la segunda cámara septal y la ampliación del fragmacono |
La pared dorsal en la transición entre el primer y segundo verticilo |
En este artículo analizamos estas singularidades y encuadramos su modelado en el contexto cordobés del Nautilus. Para ello, acudimos y aplicamos la invariante enunciada desde el inicio y que reiteradamente hemos ido aplicando en toda la modelación: "Todo punto interior a la concha o sobre ella se obtiene como la intersección de dos espirales cordobesas, una longitudinal similar a la ventral y otra transversal similar a la septal". La siguiente escena interactiva ha servido de base para el análisis de estos sitios singulares.
Modelando los sitios singulares del Nautilus en el primer verticilo
Pulsad sobre la imagen para acceder a la escena
En el siguiente pdf (o desde este enlace) tienen desarrollados los contenidos de este artículo
Ontogenia matemática del Nautilus VII
Aquí, hemos dado continuidad a los artículos anteriores (I, II, III, IV, V y VI) y por fin, creo, he cumplido mis deberes, si bien no seré yo quien excluya la posibilidad de que puedan surgir nuevas cuestiones, pues eso es lo que ha ido aconteciendo a lo largo de estos meses en los que les he ido relatando mi investigación a través de este blog de RED Descartes. Pero, independientemente de que afloren nuevas cuestiones o no, sí les indico que éste no será este el último artículo de esta serie, tengo que tratar de completarla adecuadamente y, por tanto, estimo necesario recopilar todo lo expuesto en una escena interactiva de Descartes o en una animación o en un gif animado o en un recurso similar o... y así mostrar la ontogenia matemática del Nautilus en un hilo temporal que recoja su crecimiento, si bien real y paradójicamente éste ha de ser atemporal porque en la literatura existente los datos relativos a los tiempos en el crecimiento de la concha son muy genéricos o yo no he logrado localizarlos. En la siguiente animación reflejamos el modelo uniforme del Nautilus y próximamente podremos aportar el modelo ontogénico (de nuevo les pido un poquito más de paciencia, no nos demos un atracón que pueda conducir a una indigestión).

Modelo uniforme del Nautilus
Y también tendremos que desarrollar alguna cosita en 3D ¿no les parece?... Hasta pronto...

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Proyecto de investigación en AJDA (IV)
Escrito por Jesús Manuel Muñoz CalleEn este artículo cometamos las principales actuaciones que se están desarrollando dentro del Proyecto de Investigación que llevan conjuntamente el departamento de Ingeniería Telemática de la ETSI de la Universidad de Sevilla y el Proyecto AJDA durante el curso 2021-2022.
Los Trabajos Fin de Grado en que están actualmente en desarrollo son los siguientes:
- Módulo de administración general.
- Módulo de comunicación síncrona con juegos.
- Módulo de generación y administración de ficheros de preguntas.
- Módulo de LTI.
- Módulo de realización de estadísticas.
- Investigación sobre el estado del arte sobre gamificación on-line y propuesta de validación.
- Realización de documentación para el desarrollo de Proyectos.
- Generación de un cuerpo común de bibliografía.
- Actualización de la guía para desarrolladores.
- Mejora de la plataforma de gestión común para desarrolladores.
- Puesta a punto del entorno común para desarrolladores con todas las partes del Proyecto.
- Puesta a punto de un servidor en la nube con todas las partes del Proyecto.
- Unificación funcional de todos los módulos del Proyecto.
- Unificación de estilos/tecnologías del proyecto integrado y desarrollo de mejora de funcionalidades.
- Mejora en la interfaz del comunicación de los juegos seleccionados.
- Mejora en la interfaz del comunicación de los juegos seleccionados.
Más...
24 años del Proyecto Descartes y 9 de RED Descartes
Escrito por José R. Galo Sánchez
El 1 de junio de 2013 constituimos la organización no gubernamental sin ánimo de lucro denominada "Red Educativa Digital Descartes" (RED Descartes) con el objetivo de dar continuidad y mejorar el proyecto educativo denominado "Proyecto Descartes". Este último surgió en junio de 1998 en torno a la herramienta de autor denominada "Descartes" que introducía la posibilidad de que el profesorado pudiera generar objetos educativos interactivos de manera asequible y que, mediante ellos, el alumnado pudiera lograr su aprendizaje de manera significativa a través de la simulación y de una respuesta automática contextualizada a sus intervenciones. Se contaba con una herramienta que podía promover un cambio metodológico en la enseñanza y aprendizaje de las Matemáticas y que ayudaba a difundir el saber a través de las TIC. Éstas, en aquel momento, comenzaban a extenderse de manera rápida. ¡Haga memoria!, bueno, quien tenga edad para ello, y recuerde que en aquel momento ¡no existía ni Google!, que la velocidad de transferencia de datos era comedida y que los teléfonos inteligentes y tabletas sólo existían como primigenios prototipos de la realidad que se ha alcanzado con posterioridad. ¡Era otro mundo!, pues, aunque ahora nos parezca extraño, esos apéndices que nos han surgido en las manos ¡son artefactos de escasa edad!, meros adolescentes en una analogía temporal humana.
Quienes constituimos y damos soporte a este proyecto hemos de sentirnos satisfechos por habernos mantenido dentro del maremágnum tecnológico cambiante y por la labor educativa realizada. Así pues, debemos de festejar con orgullo este nuevo aniversario, felicitándonos por los logros alcanzados, por los objetivos logrados en este último año y, a la vez, al apagar las velitas expresemos el deseo y la voluntad de poder seguir trabajando altruistamente para la mejora educativa en nuestra aldea global.
Y terminamos, como hicimos hace un año con una manifestación que no nos molesta reiterar:
¡Continuamos...! ¡Con ilusión, iniciamos un nueva vuelta al Sol... con Descartes!
¡Felicidades a todos los cartesianos!

¡Feliz vigésimo cuarto aniversario del Proyecto Descartes! y ¡Feliz noveno cumpleaños de RED Descartes!
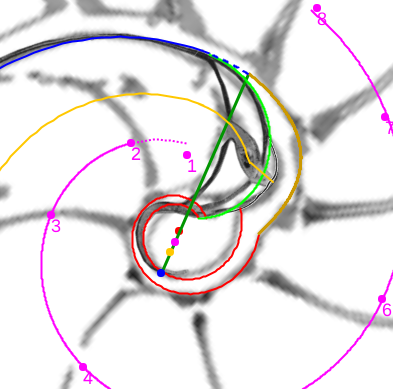
En este nuevo artículo sobre la ontogenia matemática del Nautilus, después de haber modelizado los septos en el segundo y tercer verticilio bajo el invariante de tangencialidad, nos adentramos en la modelización de los septos en el primer verticilo. Esta primera fase de crecimiento vimos que se muestra diversa y con apariencia poco regular, cambiante (menor número de cámaras septales, ocho frente a las dieciséis de la etapa juvenil y adulta, con secciones y amplitudes que cambian como necesidad biológica para alcanzar la flotabilidad) y, ahora, ha llegado el momento de mostrar el modelo matemático que da explicación a esta etapa e introduce la regularidad esperada que parecía no acaecer, pero que queda al descubierto bajo la perspectiva matemática. De nuevo, el hecho de que intervengan dos espirales con diferente polo, en este caso la espiral de la pared ventral y la espiral de los polos de los septos, conduce a proporciones variables entre los radios vectores y consecuentemente a que se formen septos con factores de escala variables. Ello nos conduce y permite determinar las ecuaciones de los septos, los puntos de tangencia con la pared ventral y los de intersección con la pared dorsal (para ello necesitaremos introducir un grosor en el modelo matemático de esa pared, que es lo que físicamente acontece).
Completaremos el contenido de este documento agrupando y relacionando entre sí diferentes puntos que se han ido detectando en este análisis. Unos que denominamos notables, porque matemáticamente son los que establecen el modelo matemático y dan explicación causal al mismo, y que son polos de diferentes espirales. Y otros que catalogaremos como destacables, posible fuente de inspiración matemática futura, y que son centros desde los que algunos objetos se observan con perspectiva angular constante.
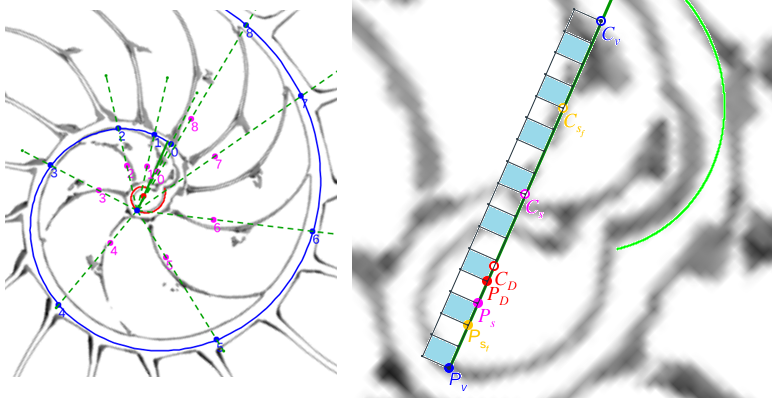 |
|
| Propociones entre los radios vectores de la espiral ventral y los de la espiral de los polos de los septos | Puntos notables y destacables |
Así pues, doy continuidad a los artículos anteriores (I, II, III, IV y V), con un contenido adicional que espero sea de su interés —¡para mí es siempre una satisfacción! ir pudiendo relatarles progresivamente lo que, poco a poco, me cuenta la concha de este animalito—, y he de adelantarles que serán necesarios algunos artículos adicionales porque aún nos quedan secretos que dilucidar en esta ontogenia, en particular lo que acontece en la transición de la fase embrionaria (primera y segunda cámara septal) donde el sifúnculo cambia abruptamente de posición, y en la fase de transición entre el primer y segundo verticilo (cámaras octava, novena y décima) donde al finalizar la primera vuelta se produce el encuentro del fragmacono con la concha embrionaria. Y también habrá que abordar la síntesis o resumen final, es decir, plasmar y reproducir ese modelo ontogénico de la concha del Nautilus.
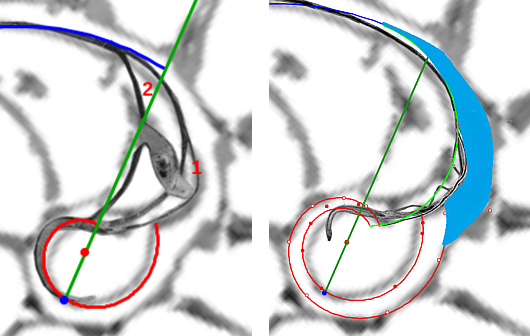 |
|
| El sifúnculo en la segunda cámara septal | Transición entre el pimer y segundo verticilo |
Como observamos, una mirada atenta y un continuo deseo de comprensión nos hace ir visualizando cada vez más detalles que inicialmente pueden parecer nimios, pero que finalmente se han ido mostrando como retos cuya resolución es de interés. Todo ello, a costa de que a ustedes a lo mejor les ocurra como a mi sobrina nieta (Aurora, cerca de los cuatro años) que ayer, al verme una vez más delante de la pantalla de mi ordenador, indagando la imagen de la sección del Nautilus con diversos objetos matemáticos superpuestos, la cual ya ha observado en multitud de ocasiones y quizás hayan sido demasiadas para ella, dijera: "¡Tita!, ¡el tito todavía no ha hecho sus deberes!". Por tanto, espero poder ir finalizando mis deberes, que realmente no son más que satisfacciones aunque requieran esfuerzo y dedicación, y que en el trancurso hacia su final les pueda tener como lectores y juntos podamos desarrollar nuestra vocación como μαθηματικός (mathēmatikós) o amantes del conocimiento.
En el siguiente pdf (o desde este enlace) tienen desarrollados los contenidos de este artículo
Ontogenia matemática del Nautilus VI

Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)








 CONTACTO
CONTACTO
