En este vídeo presentamos una serie de unidades de la Red Descartes para los cursos de la ESO dentro del área de Ciencias de la Naturaleza. Se trata de actividades interactivas y de autoevaluación que se han elaborado partiendo de unidades liberadas del Programa Internacional PISA y que han sido desarrolladas en el proyecto de la RED ASIPISA. Al final del vídeo se indican los pasos a seguir para insertar esta selección de materiales en un espacio web, en este caso en un blog de WordPress.
En concreto se han seleccionado las siguientes actividades:
- Los autobuses: Actividad relacionada con el movimiento de los cuerpos, la inercia y los grados de contaminación de las diferentes energías usadas en el transporte.
- Las Moscas: A partir de un problema de superpoblación de moscas en una determinada granja, se elabora un estudio sobre un determinado producto para la fumigación y su efecto, con una serie de gráficos que indican la eficacia del producto a lo largo del tiempo.
- Detengan ese germen: Se relatan diferentes experimentos de investigación sobre la inmunidad en determinadas enfermedades.
- Luz del día II: Trata aspectos relacionados con el movimiento de rotación de la Tierra, la inclinación de su eje y el movimiento de traslación alrededor del Sol.
EDAD 4ºESO Aplicadas - Funciones elementales
Escrito por Alfonso Saura EspínEste mes vamos a ver la unidad correspondiente de funciones:
En este vídeo hemos tocado los siguientes puntos:
1. Funciones polinómicas
Función de proporcionalidad directa
Funciones afines
Funciones cuadráticas
2. Otras funciones
Función de proporcionalidad inversa
Función exponencial
Funciones definidas a trozos
Función valor absoluto
Publicación de RED Descartes en la revista Epsilon
Escrito por José Antonio Salgueiro GonzálezEn el número 94 de la revista Epsilon de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Sobre la forma y el crecimiento cordobés del Nautilus pompilius". Un detallado trabajo de investigación desarrollado dentro de nuestra RED Descartes, reflejándose así en la autoría, por los socios José R. Galo Sánchez, Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo.
Os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales.
Misceláneas: Lugares geométricos. Epicicloides e Hipocicloides.
Escrito por Ildefonso Fernández TrujilloLugares geométricos: Epicicloides e Hipocicloides.
Continuamos con el estudio de los lugares geométricos y en esta entrada vamos a desarrollar una aproximación al conocimiento genérico de los conocidos como "Epicicloides" e "Hipocicloides" que son un tipo de Epi/Hipo Trocoides que a su vez son una clase de las Ruletas.
Dentro del amplio grupo de cicloides analizaremos los ll.gg. generados por un punto de una circunferencia, o dependiente de ella, cuando dicha circunferencia, a la que llamamos generatriz, gira sin deslizar, de forma tangencial, alrededor de otra circunferencia llamada directriz. Esto es, nuestro estudio se centra en uno de los tipos de las curvas planas cíclicas llamadas Ruletas.
Si la generatriz gira por el exterior de la directriz se genera una Epicicloide, que puede ser: ordinaria, epitrocoide acortada o epitrocoide alargada según la posición del punto generador respecto a la circunferencia generatriz de la que depende. Análogamente, si la generatriz gira por el interior de la directriz el l.g. generado es una hipocicloide que a su vez puede ser: ordinaria, hipotrocoide acortada o hipotrocoide alargada según veremos más adelante.
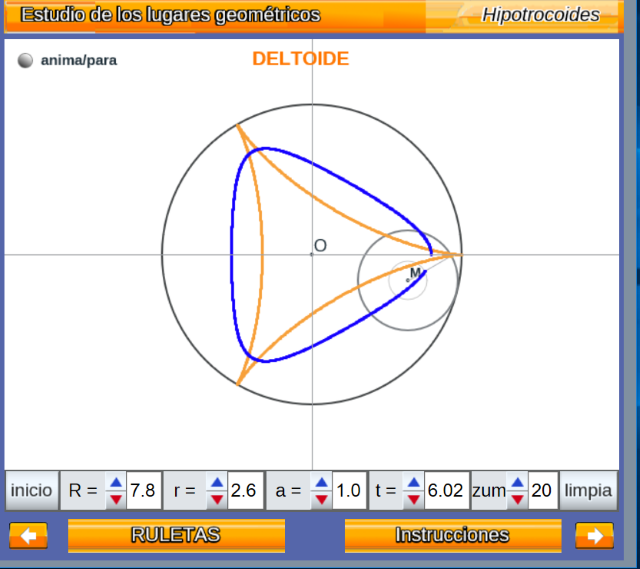
Para llevar a la práctica el estudio se han creado dos escenas: "epitrocoides.html" e "hipotrocoides.html" que se enlazan en la siguiente imagen que muestra como la utilidad "hipotrocoides.html" genera dos ll.gg. uno color rosa conocido como Deltoide (R/r=3) y el otro, de color azul, una hipotrocoide acortada. Esto es así porque se han considerado dos puntos generadores: uno en la circunferencia generatriz y otro, en este caso, interior a la misma. Ver detalles de la escena, dejando repetir la animación, o leer las instrucciones, hasta comprender el proceso de creación de los ll.gg.
Para profundizar en el estudio de los lugares geométricos y en el de uso del editor DescartesJS, hemos elaborado, de forma muy esquemática, las pequeñas utilidades mencionadas anteriormente. Son escenas basadas en la obra del profesor Ricardo Sarandeses Fernández, trabajo que está en proceso de adaptación a las nuevas versiones del editor DescartesJS. A propósito del nuevo editor hemos utilizado, a modo de plantilla, los extraordinarios recursos que la documentación del mismo enlaza en la web de sus creadores. La cantidad de ejemplos-ejercicios ofrecidos hacen que el potencial didáctico y de reutilización de dicha documentación y los ejemplos que la acompañan sea digno de mención ya que con un mínimo esfuerzo, cualquiera de esos abundantes trabajos, puede ser adaptado y servir así de plantilla para un proyecto personal tal como muestran los anteriores y el siguiente enlace.
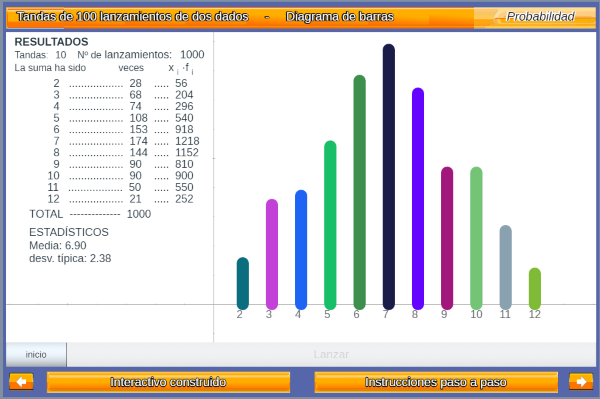
Introducción al concepto de probabilidad
En ambas escenas, de las dos relacionadas con los ll.gg., se ha puesto especial énfasis en el proceso de elaboración de las ecuaciones paramétricas del l.g. lo que se manifiesta al analizarlas. Por otra parte las dos utilidades pueden ser reducidas a una sola muy fácilmente, lo que dejamos como ejercicio.
Indicamos que:
- Si se desea volver a ver la generación del l.g. o la realización de cualquier actividad desde el principio y con la escena despejada es suficiente con pulsar el botón inicio y efectuar las acciones adecuadas.
- Los pulsadores R, r y a definen la forma de los ll.gg. generados. Estos lugares podrian representarse, una vez configurados, mediante sus ecuaciones paramétricas; aunque hemos elegido visualizar su creación dinámica mediante una animación.
Como en anteriores ocasiones notamos que la utilidad es fácilmente adaptable y admite las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
En los siguientes trabajos presentamos una recreación de las escenas anteriores realizadas con el programa GeoGebra con los propósitos de ahondar en el conocimiento de ambas plataformas: GeoGebra y DescartesJS de forma paralela para lograr los objetivos señalados en entradas anteriores.
La siguiente utilidad genera una amplia colección de epicicloides/epitrocoides según los valores que asignemos a los deslizadores. Conviene observar la animación para comprender la influencia que las asignaciones ejercen sobre los gráficos.
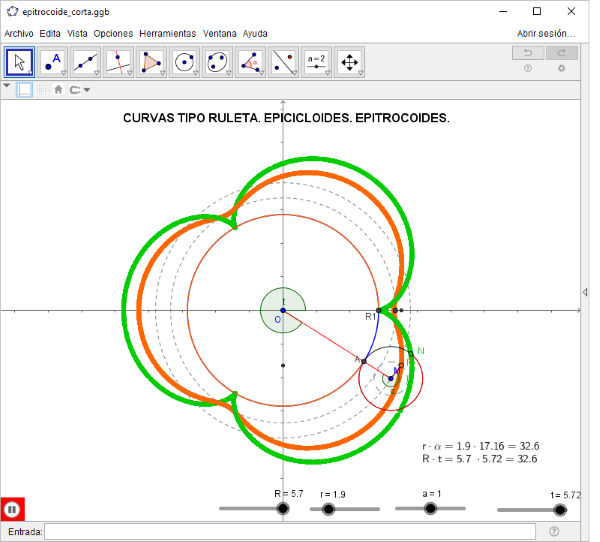
hoja de trabajo de las epicicloides
En la escena que enlaza la siguiente imagen se usa la ecuación de la curva para representarla una vez se conocen los valores que la definen.
Cuando el cociente R/r es un número natural la cicloide se completa en la primera vuelta de la generatriz, en cualquier otro caso es conveniente analizar el cociente anterior para preveer el comportamiento de la curva. La utilidad da un máximo de 10 vueltas, valor que puede modificarse para que se adapte dinámicamente a la situación y así hacer una aplicación más eficiente.
Al igual que en el caso de las epicicloides es conveniente analizar la animación.
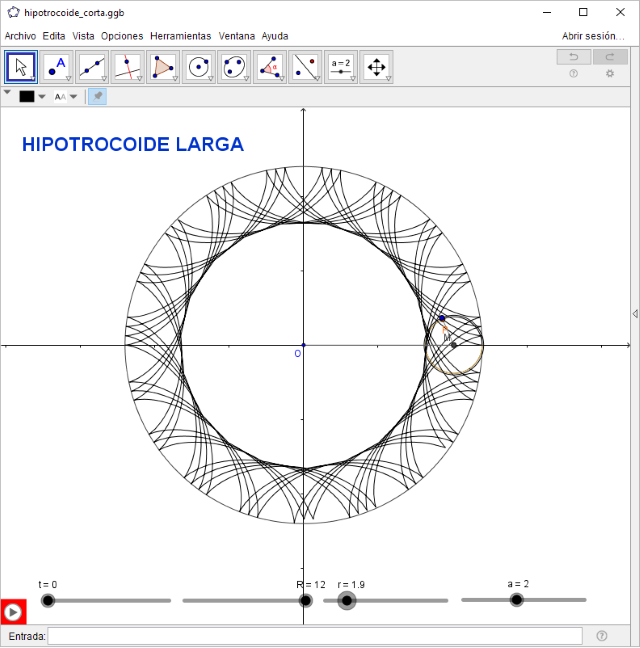
hoja de trabajo de las hipocicloides
Proponemos al lector el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
En esta ocasión en la sección de vídeo hemos elegido de nuevo, debido a su indudable interés, dos de entre las muchas composiciones de Milton Donaire publicadas en YouTube.
La primera trata sobre el teorema de Menelao y la segunda sobre el teorema de Giovanni Ceva. El objetivo es el de apreciar la influencia directa, e indirecta, que el conocimiento del triángulo y de las razones geométricas tiene en el tema que nos ocupa: "Los Lugares Geométricos".
Teorema de Menelao
Teorema de Giovanni Ceva
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- Unidad para el taller de 4º de la E.S.O. "Curvas clásicas en coordenadas paramétricas" del profesor: Ricardo Sarandeses Fernández, que está en proceso de adaptación a la nueva versión del editor DescartesJS.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Más...
Gamificación en el IES Joaquín Turina de Sevilla. Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle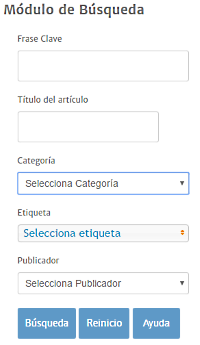 Hace unos días hemos dado por concluida la implementación de un módulo de búsqueda que venía siendo necesario para esta Web de Contenidos.
Hace unos días hemos dado por concluida la implementación de un módulo de búsqueda que venía siendo necesario para esta Web de Contenidos.
Desde las distintas secciones o categorías, Blog, Matemáticas, Física y Química, Otras áreas y Plantillas, se han ido publicando sin pausa, desde la aparición en los medios de RED Descartes, diferentes artículos y ya acumulamos un número importante, ¡sobrepasan los dos mil!
En esta situación es esencial disponer de un buscador que permita acceder a cualquiera de los artículos partiendo de determinados elementos que lo caractericen en función de su categoría, su contenido o su etiquetado. Esto es lo que pretende el Módulo de Búsqueda, para lo cual se han habilitado cinco elementos que actúan de filtro y se rotulan como Frase Clave, Título del artículo, Categoría, Etiqueta y Publicador.
Para mejor comprender la razón de ser de estos cinco elementos podemos decir que cada artículo publicado en la Web de Contenidos lleva, aparte de su contenido literario, metadatos como la fecha de publicación, escrito por (publicador), valoración (de 1 a 5 estrellas) de los lectores, categoría (sección) donde se publica y el etiquetado (conjunto de etiquetas que determinan un perfil para el artículo: temática, proyecto, materia, edad, nivel académico, lenguaje, etc.).
El Módulo de Búsqueda se encuentra en cada una de las secciones, Blog, Matemáticas, Física y Química, Otras áreas y Plantillas y puesto que cada sección se corresponde con una determinada categoría donde los artículos publicados quedan catalogados, el item correspondiente al elemento Categoría queda seleccionado automáticamente al acceder a una determinada sección, pudiendo no obstante desde aquí cambiar a voluntad a cualquier otra categoría.
El Módulo de Búsqueda incorpora un botón de Ayuda que caracteriza a cada uno de los elementos y detalla el formato que tiene el resultado de la búsqueda y las distintas formas como puede ser ordenado. No insistimos más por este lado en este artículo de presentación.
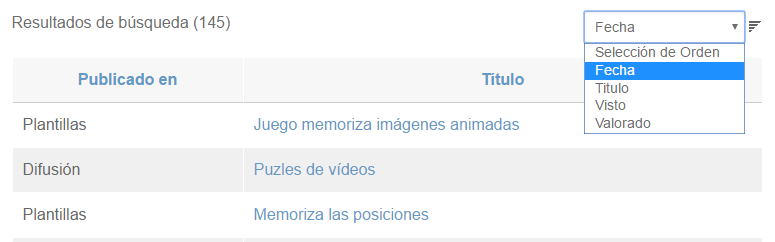
Esperamos haber acertado con esta herramienta y que realmente sea de utilidad a cualquier usuario de la Web de contenidos de RED Descartes.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)








 CONTACTO
CONTACTO
