El movimiento de la pelota. Proyecto Newton
Escrito por Montserrat Gelis BoschEl subproyecto “Problemas” del proyecto Newton, está formado por un conjunto de materiales digitales interactivos que tratan aspectos muy variados del currículo de Física y Química en forma de resolución de un problema.
En este vídeo vamos a mostrar con detalle la unidad de 4º de la ESO, el movimiento de la pelota. En esta escena se considera el movimiento de una pelota lanzada con una determinada velocidad y en una dirección determinada. Se analizan las fuerzas y las ecuaciones del movimiento así como la trayectoria y las variaciones de energía en todo el proceso.
La escena consta de los siguientes apartados:
- Guía del alumno. Se plantea el enunciado del problema y se dan indicaciones para su resolución.
- Escenas interactivas. Dos escenas en las cuales se pueden observar las fuerzas que actúan y la velocidad en cada momento. El alumno puede modificar la masa de la pelota, la velocidad inicial de lanzamiento y el ángulo de la trayectoria
- Evaluación. Este apartado consta de varias preguntas con diferentes respuestas para comprobar lo aprendido.
- Problema resuelto. Se accede a un documento en pdf con el problema resuelto paso a paso.
La radio ficción en el aula de Matemáticas
Escrito por José Antonio Salgueiro GonzálezConviene destacar que el bloque "Procesos, métodos y actitudes en Matemáticas" debe desarrollarse de modo transversal y simultáneamente al resto de bloques, constituyendo el hilo conductor de la asignatura y sustentándose sobre tres pilares básicos: la resolución de problemas, sobre todo; el uso sistemáticamente adecuado de los medios tecnológicos y la dimensión social y cultural de las matemáticas. Además, el estudio del desarrollo y contribución histórica de la disciplina matemática lleva a concebir su saber como una necesidad básica para las personas, que a través del trabajo individual y en equipo pueden obtener las herramientas necesarias para realizar investigaciones, resolver problemas en situaciones reales y tomar decisiones responsables y críticas.
La dimensión histórica, social y cultural de las matemáticas debe programarse de manera cuidada y coordinada para ayudar a la comprensión de los conceptos a través de la perspectiva histórica, así como para contrastar las situaciones sociales de otros tiempos y culturas con la realidad actual, conociendo de manera más humana a los personajes y sus aportaciones, visibilizando las circunstancias personales de mujeres matemáticas y las dificultades que han tenido para acceder a la educación y a la ciencia. Resulta idóneo el uso de Internet y de las herramientas educativas existentes, de vídeos y películas sobre la vida y obra de los personajes matemáticos para lo que es de gran ayuda la pizarra digital, o el tradicional trabajo monográfico que ahora puede crear nuestro alumnado de forma colaborativa haciendo uso de los documentos compartidos. También podemos ir más allá, pues resulta sumamente enriquecedor para la formación competencial crear de forma colaborativa una línea del tiempo con la secuenciación cronológica de descubrimientos matemáticos. Además, debemos enseñar a nuestro alumnado a generar contenido matemático inédito y desarrollar la comunicación audiovisual desde las matemáticas con la creación de un audio o vídeo o poniendo voz a los personajes célebres de ambos géneros, organizando una cadena de radio matemática o un canal de televisión que entreviste de forma ficticia a dichos personajes.
Los dos párrafos anteriores están literalmente extraídos de la Orden de 14 de julio de 2016, por la que se desarrolla el currículo correspondiente a la Educación Secundaria Obligatoria en la Comunidad Autónoma de Andalucía, se regulan determinados aspectos de la atención a la diversidad y se establece la ordenación de la evaluación del proceso de aprendizaje del alumnado, que es la que conozco como docente en activo, pero estoy convencido de que las orientaciones y estrategias metodológicas aportadas serán de gran similitud con las ofrecidas por otras comunidades autónomas en el ámbito de sus competencias.
| ANTECEDENTES |
RED Descartes posee una gran experiencia, reconocida además, en la radio ficción en Matemáticas, gracias a su programa "El personaje misterioso" conducido por Eva Perdiguero y Ángel Cabezudo, con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Pues bien, "La radio ficción en el aula de Matemáticas" es un proyecto del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija con los mismos objetivos que los de Radio Descartes, pero entre discentes en vez de entre docentes, que empieza durante el curso escolar 2015/2016 con un grupo de alumnos de Matemáticas Orientadas a las Enseñanzas Académicas en 3º de ESO, es decir, con 14 y 15 años de edad, que se coordina desde el aula virtual y comprende las fases que se relacionan a continuación.
| ELECCIÓN DEL PERSONAJE MATEMÁTICO Y DIFUSIÓN EN TWITTER |
Cada equipo estará constituido libremente por dos personas que deberán elegir a un personaje matemático para entrevistar en un programa de radio, masculino o femenino garantizando la paridad en el aula, de modo que una persona ejerza de entrevistador y la otra represente al personaje seleccionado.Seguidamente, para información de todos y no repetir personajes, un miembro del equipo publicará un tuit con la composición del mismo, incluyendo el personaje seleccionado con una imagen y el hashtag del curso #MATES3BAJO.
| DOCUMENTACIÓN |
En la segunda fase, cada equipo realizará una búsqueda de información en internet sobre la vida y obra del personaje elegido para entrevistar.
Pueden ser documentos de texto, imágenes con información, presentaciones, infografías, vídeos, audios y cualquier multimedia, en general.
Es fundamental que la información provenga de fuentes fiables, así que se hará una selección de dos o tres recursos y se compartirán en el foro habilitado en el aula virtual las direcciones de cada uno de ellos.
Después, cuando el profesor aprueba los recursos seleccionados, se tendrán que difundir esas direcciones por Twitter con el hashtag del curso #MATES3BAJO.
| ELABORACIÓN DEL GUION |
Cada equipo tiene que elaborar un guion en un documento de texto con la entrevista completa y enviarla al profesor desde la tarea habilitada en el aula virtual, cuidando la expresión, el vocabulario y la escritura.
| INSTRUCCIONES PARA LA GRABACIÓN DE LA ENTREVISTA |
¡Ha llegado el momento! Recuerda que son fundamentales la creatividad e imaginación del equipo, así que, si no tienes experiencia anterior a la hora de protagonizar un programa de radio, te daré algunos consejos:
- Busca un espacio exento de ruidos, internos o externos, y evitarás sorpresas de última hora y pérdida de tiempo.
- Es muy importante ensayar algunas veces y vocalizar perfectamente, haciendo algunas pruebas hasta conseguir el efecto deseado.
- Es muy complicado grabar la entrevista de una sola vez, por ello aconsejamos grabarla por partes, según se estime oportuno.
- Conviene dejar grabando unos segundos de silencio después de cada intervención, lo que facilita la edición y montaje de la entrevista completa.
- Tenéis que hablar con tranquilidad y vocalizando lo mejor posible.
- El protagonista es el entrevistado, es decir, el personaje matemático, no el periodista. No obstante, ambos deben transmitir emociones al público, evitando usar un tono constante.
- Evitar apostillar las respuestas del entrevistado. Conforme el entrevistado va contestando, no debemos decir “ya”, “claro”.
- Como todo programa de radio, deberá contener una presentación, donde se explique el objetivo de la sesión, y una despedida, dando un pequeño resumen de lo tratado y agradeciendo, en nombre de la cadena, la presencia del entrevistado.
La mejor forma de conocer el producto final deseado es oir algunas entrevistas similares.
Encontrarás una docena de entrevistas a personajes matemáticos que te servirán de orientación, sin olvidar que están realizadas por docentes para docentes, mientras que las vuestras son de alumnos para alumnos, y se recomienda que no sobrepasen los cinco minutos de duración.
| EDICIÓN DEL AUDIO |
Una vez grabada la entrevista, te aconsejo hacer una copia de la misma y guardarla en una carpeta llamada copia de seguridad, para evitar posibles problemas, ya que ahora procede editar los distintos archivos para proceder a enriquecer el audio con las uniones correspondientes, incluyendo la presentación, despedida, sintonía del programa de radio, efectos sonoros, etc, para lo que es fundamental la creatividad e imaginación del equipo.
En ningún momento podrás incluir música o sonidos que tengan derechos de autor, es decir, copyright, debiendo usar recursos originales o que tengan licencias que lo permitan, como las Creative Commons. Así que, para ello, te recomiendo que uses el
Descárgate los archivos que sean de tu agrado en formato mp3, preferiblemente.
Abrimos en el aula virtual un foro denominado "Soporte técnico" para que, entre todos, planteemos las dificultades que encontremos y poder compartir soluciones conforme vayamos aprendiendo.
| ENTREGA DEL AUDIO |
Una vez finalizada la edición del audio con los efectos especiales y el equipo considere concluída la entrevista, deberá generar con el software empleado un archivo en formato mp3 para entregarlo desde la tarea habilitada en la plataforma, o bien usar un conversor para pasar su archivo al formato solicitado.
Pues bien, en el marco del proyecto "La radio ficción en el aula de Matemáticas", compartimos en este artículo la entrevista realizada por dos alumnos de 3º ESO al ilustre y prolífico matemático Leonhard Euler.
| ANÁLISIS DE LA EXPERIENCIA |
Con la entrevista al personaje matemático has adquirido, quizás sin darte cuenta, una importante experiencia en comunicación verbal, relacionada con las Matemáticas, que antes no poseías. Estoy convencido de que si tuvieras que grabarlo otra vez no saldría el mismo, porque cambiarías alguna cosa en base a esa experiencia o le darías otro enfoque o incluso usarías otras herramientas.
Has sido pionero y pionera en este aspecto, por ello, tu experiencia debe ser aprovechada para los que te sigan. ¿Y cómo se hace ésto? Pues sencillamente como hacen los científicos, divulgando tus experiencias y conclusiones en las revistas especializadas y en los medios de comunicación del s. XXI.
¿Qué tienes que hacer? Pues sencillamente grabar otro audio, con total libertad, es decir, tú decides sin incluyes o no efectos especiales y música, pero no es necesario, sino que lo importante es oir tu experiencia con absoluta sinceridad, hablando y vocalizando lo mejor posible.
¿Qué temas hay que tratar?
Hay que contar todos los detalles, desde la planificación, redacción del guion, grabación del audio , lugar elegido, recursos usados, osbtáculos que habéis encontrado y cómo los habéis resuelto y vuestras conclusiones finales. Por ejemplo, a modo de guión:
- ¿Conocías al personaje matemático anteriormente?
- ¿Qué te ha llamado la atención de su vida? ¿Y de su obra?
- ¿Crees que esta experiencia contribuye al desarrollo de tu creatividad e imaginación?
- ¿Cómo has planificado la tarea?
- ¿Qué heramientas has empleado? ¿Sabías manejarlas?
- ¿Qué lugar has elegido para la grabación y por qué?
- ¿Qué dificultades has encontrado para realizar todas las tareas que esta acción conlleva y cómo las has resuelto?
- ¿Has tenido que solicitar ayuda externa?
- ¿Qué has aprendido con esta experiencia que antes no sabías?
- ¿Aparece tu personaje matemático en el portal de la RED Descartes? ¿Qué has encontrado?
- ¿Cuáles son tus conclusiones y valoraciones al finalizar esta acción innovadora?
- Puedes añadir cualquier otra pregunta que consideres interesante o hacer la crítica 3x1, es decir, tres cosas que te han gustado y una que cambiarías.
Asamblea general en el IES Isaac Albéniz de Leganés
Escrito por José Antonio Salgueiro GonzálezEl día 5 de julio se celebró, en el IES Isaac Albéniz de Leganés (Madrid), la Asamblea General Ordinaria de Red Educativa Digital Descartes correspondiente al año 2017, con el objetivo de tratar asuntos de gestión y organización como memoria de actividades, cierre económico, renovación de la Junta Directiva, presupuesto y propuesta de proyectos para el próximo ejercicio, entre otros, compaginando la asistencia real con la virtual a través de las herramientas de intercomunicación de nuestra asociación, garantizando así el derecho a voto de todos sus miembros.
Queremos destacar la enorme trascendencia del Proyecto Descartes en estos últimos cuatro años, así como su alcance y repercusión, tanto en España como en todos los países de habla hispana, con una evolución en el número de visitantes que nos ha llevado a 1.200.000 páginas servidas mensualmente, es decir, a una media de 40.000 páginas diarias, una cifra que supone para nosotros el reconocimiento de la calidad de los recursos ofrecidos desde nuestro portal y que nos anima a seguir trabajando altruistamente por la comunidad educativa de la aldea global, así como a mostrar todo nuestro agradecimiento a los usuarios y seguidores de RED Descartes.
Con motivo de esta nueva asamblea nos desplazamos a Leganés desde diversos puntos geográficos: Santiago de Compostela, Valladolid, Zaragoza, Córdoba, Madrid, Burgos, Alcalá de Henares, Móstoles, Arganda del Rey y Lebrija, haciendo posible el reencuentro entre compañeros y amigos que no coincidíamos desde hacía bastantes años.
Al finalizar la fructífera y productiva asamblea pudimos compartir un exquisito almuerzo en el Restaurante Changó, sito en el Parque El Carrascal de la ciudad leganense, aunque con muy corta sobremesa, pues el regreso apremiaba. Por cierto, Josep, nuestro anfitrión, tuvo la cartesiana idea de reunir a este grupo de profesores de matemáticas en la Avda. de la Lengua Española justo en vísperas de la celebración en Madrid del VIII Congreso Iberoamericano de Educación Matemática, que también contará con la representación de RED Descartes ostentada por nuestras compañeras Rita Jiménez, que presenta el taller titulado "El Proyecto Descartes en el aula" y Elena Álvarez con la comunicación que lleva por título "Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automáticas".
Finalmente, desde RED Descartes queremos transmitir nuestro más sincero agradecimiento a D. Juan José Uzquiano Sánchez de Castro, Director del IES Isaac Albéniz, por su cálido recibimiento y atención junto a su Equipo Directivo (Mar Sánchez, Secretaria, Alicia Burgos, Jefa de Estudios, Inmaculada Alonso, Jefa de Estudios Adjunta y Óscar García, Jefe de Estudios de Bilingüismo) así como al personal de administración y servicios.
EDAD 4ºESO Aplicadas Ecuaciones e inecuaciones
Escrito por Alfonso Saura EspínEste mes vamos a ver un vídeo sobre las ecuaciones e inecuaciones de 4ºESO Enseñanzas aplicadas:
Hemos tratado los siguientes puntos:
1.Ecuaciones
Elementos de una ecuación
Solución de una ecuación
2.Ecuaciones de primer grado
Solución
Aplicaciones
3.Ecuaciones de segundo grado
Solución
Incompletas
Número de Soluciones
Aplicaciones
4.Otros tipos de ecuaciones
Bicuadradas
Tipo (x-a)·(x-b)·...=0
Ensayo-error. Bisección
5.Inecuaciones con una incógnita
Definición. Propiedades
Inecuaciones de grado uno
Inecuaciones de grado dos
Más...
Matemáticas para todos con Descartes
Escrito por José Antonio Salgueiro GonzálezLa materia de Matemáticas Orientadas a las Enseñanzas Académicas se distribuye a lo largo de tercero y cuarto de Educación Secundaria Obligatoria en cinco bloques que no son independientes entre sí : Procesos, métodos y actitudes en Matemáticas, Números y Álgebra, Geometría, Funciones y, por último, Estadística y Probabilidad.
Entre los contenidos de este bloque se contempla la utilización de medios tecnológicos en el proceso de aprendizaje, entre otros para:
- la elaboración de informes y documentos sobre los procesos llevados a cabo y los resultados y conclusiones obtenidos.
- comunicar y compartir, en entornos apropiados, la información y las ideas matemáticas.
A su vez, en los criterios de evaluación para este bloque aparece emplear las herramientas tecnológicas adecuadas, de forma autónoma, realizando cálculos numéricos, algebraicos o estadísticos, haciendo representaciones gráficas, recreando situaciones matemáticas mediante simulaciones o analizando con sentido crítico situaciones diversas que ayuden a la comprensión de conceptos matemáticos o a la resolución de problemas. CMCT, CD, CAA.
También se dice utilizar las tecnologías de la información y la comunicación de modo habitual en el proceso de aprendizaje, buscando, analizando y seleccionando información relevante en Internet o en otras fuentes, elaborando documentos propios, haciendo exposiciones y argumentaciones de los mismos y compartiendo éstos en entornos apropiados para facilitar la interacción. CCL, CMCT, CD, CAA.
Más específicos aún son los estándares de aprendizaje evaluables, donde se recoge:
12.1. Elabora documentos digitales propios (texto, presentación, imagen, video, sonido,…), como resultado del proceso de búsqueda, análisis y selección de información relevante, con la herramienta tecnológica adecuada, y los comparte para su discusión o difusión.
12.2. Utiliza los recursos creados para apoyar la exposición oral de los contenidos trabajados en el aula.
12.3. Usa adecuadamente los medios tecnológicos para estructurar y mejorar su proceso de aprendizaje recogiendo la información de las actividades, analizando puntos fuertes y débiles de su proceso académico y estableciendo pautas de mejora.
| DESCRIPCIÓN DE LA EXPERIENCIA |
Esta iniciativa, desarrollada desde el Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, durante el curso escolar 2016/2017 con un grupo de 4º ESO del área de Matemáticas Orientadas a las Enseñanzas Académicas, se ha coordinado desde el aula virtual de Matemáticas, que tiene acceso para invitados, donde se fueron publicando, paulatinamente, las distintas fases con las correspondientes instrucciones para el alumnado. Así, con la pregunta ¿Qué tienes que hacer?, se decía que el reto a superar consiste en generar contenido audiovisual de Matemáticas. Concretamente, tienes que grabar un vídeo en el que se ejecute y explique la resolución de dos ejercicios sobre fracciones polinómicas.
El primero deberá ser simplificar una fracción polinómica, y se extraerá de la página "Para practicar", seleccionando la opción simplificar fracciones. Tienes que escoger una fracción que tenga segundo grado tanto en el numerador como en el denominador.
El segundo tratará sobre operaciones con fracciones polinómicas, pudiendo elegir entre sumar, restar, multiplicar o dividir, y será extraído de la página "Fracciones algebraicas" del libro Descartes.
Para ello, estableceremos distintas etapas o fases.
| PRIMERA FASE |
La clase se organizará en equipos constituidos por dos personas, actuando una de ellas como coordinador o coordinadora del equipo que, además, deberá llevar el nombre de un personaje matemático, hombre o mujer.
Será el coordinador o coordinadora la persona encargada de entregar las tareas en las distintas fases y en los plazos establecidos.
| SEGUNDA FASE |
Comienza la fase de investigación y documentación, así que te propongo algunas sugerencias y te recomiendo espacios y recursos. Por ejemplo:
- Guía rápida para grabar en vídeo. ¡Muy bueno!
Necesitas un guion para tu película, con lo que vas a grabar y a decir, pudiendo alternar planos de lo que se visualiza en el ordenador, tableta o smartphone con planos de la ejecución técnica del ejercicio, es decir, el desarrollo con las fórmulas y operaciones. Puedes realizar los ejercicios en una pizarra, en un cuaderno o folio, con un software que lo permita, grabando en interior o en exterior y, por supuesto, todo lo que se te ocurra. Aquí es donde entra en juego tu creatividad e imaginación.
Recuerda que tú no eres el protagonista de la película, sino la resolución del ejercicio, por lo que no es necesario que aparezcas ni que se te vea.
En cualquier caso, se debe ver y oir cómo se elige el ejercicio desde el libro digital del Proyecto Descartes, comprobando después la solución en el mismo libro y usando, además, una de las dos herramientas que hemos aprendido en clase, es decir, Wiris Calc o Photomath, o incluso ambas.
Recuerda que publicaremos en internet el producto final, así que procura la mejor calidad de imagen y audio posibles.
El lenguaje matemático será primordial para las explicaciones, por eso, me enviaréis, desde el foro "Entrega del guion", el borrador del guion para que yo pueda revisarlo.
No puedes usar ni imágenes ni música con derechos de autor. Para estos casos, te recomiendo:
- Banco de imágenes y sonidos del INTEF.
- Imágenes con licencia Creative Commons, del mismo banco anterior o de Pixabay.
- Jamendo, descarga de música libre y gratis.
En cualquier caso, hay que citar en el vídeo el lugar de procedencia de las imágenes y audios usados.
Deberá aparecer en el vídeo, ya sea al final o al principio, el logotipo del IES Bajo Guadalquivir.
En cualquier caso, hay que dedicar una página de créditos para citar en el vídeo el lugar de procedencia de las imágenes y audios usados.
Si tienes alguna idea y no sabes cómo llevarla a efecto, puedes consultar en el foro del aula virtual denominado "Dudas sobre la segunda fase".
¡Es el momento de la CREATIVIDAD E IMAGINACIÓN!
| TERCERA FASE |
Para entregar el vídeo puedes usar un servicio gratuito para envío de archivos de gran tamaño. Si no conoces ninguno, te recomiendo WeTransfer.
Cuando la página te avise que se ha concluído la transferencia, me envías un mensaje por la plataforma para que me lo descargue. Así quedará constancia de haber entregado el vídeo en su plazo y me llegará un aviso a mi correo para que me descargue vuestra obra.
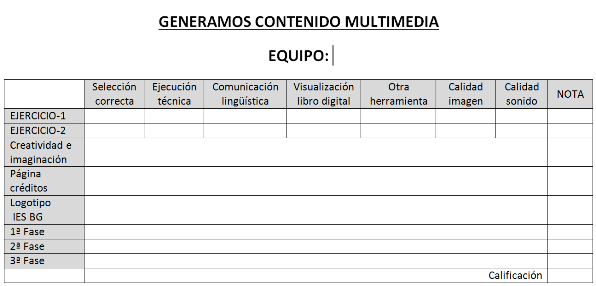
Para evaluar el producto final se tendrán en cuenta las siguientes variables:
La experiencia ha resultado sumamente satisfactoria y quiero felicitar desde el portal de RED Descartes al equipo Sophie Germain por la calidad del producto final conseguido.
Misceláneas. Lugares geométricos: las cónicas II
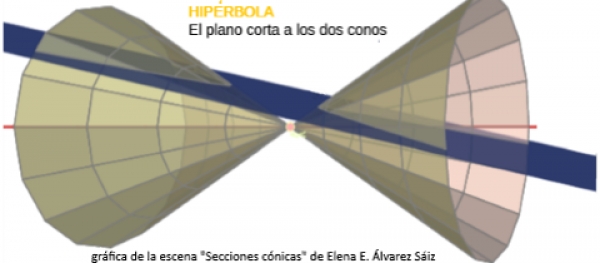
Escrito por Ildefonso Fernández TrujilloLugares geométricos: La Hipérbola.
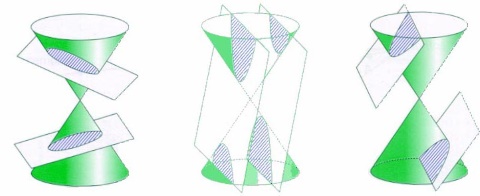
Dentro del estudio de los lugares geométricos tienen un especial interés los relativos a las cónicas por motivos muy diversos y no únicamente cronológicos; si no que también filosóficos, mercantilísticos y geométricos y en esta entrada vamos a continuar la aproximación a su conocimiento genérico analizando algunos aspectos de la Hipérbola considerada como lugar geométrico. Aprovechamos la oportunidad para señalar el aspecto popular, lúdico y funcional que la Geometría clásica ha ejercido sobre las poblaciones cultas: el cono como cucurucho para envolver desde tiempos ancestrales, los niños y niñas jugando con el aro y el yoyo...
Consideramos, por tanto, que el estudio se centra en los ll.gg. generados por puntos que se mueven en el plano de forma que la razón (excentricidad) entre sus distancias a un punto fijo (foco) y a una recta (directriz) se mantiene constante.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- La Hipérbola como lugar geométrico. MB (M. Banasik)
- Construcción de la hipérbola como lugar geométrico, a partir de un circulo y un punto exterior al círculo. La hipérbola que se genera tiene como focos el centro del círculo y el punto exterior al círculo. DORIS ÁLVAREZ QUINTERO
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Curriculum para ESO y Bachillerato.
Ambos trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
- Estudio de la HIPÉRBOLA I. La hipérbola como l.g. generado, la mitad del mismo, por los puntos de intersección de dos circunferencias: una con centro en el foco F y radio k y otra de centro el foco F' y radio r dependiente del pulsador k, de forma que cuando un radio aumenta el otro también. La otra mitad de la hipérbola se genera intercambiando los radios.
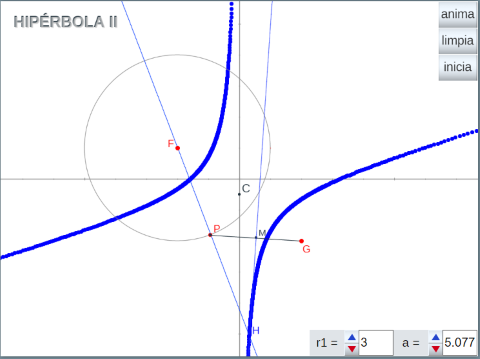
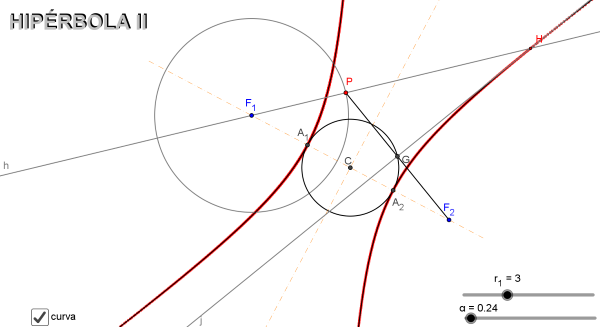
- Estudio de la HIPÉRBOLA II. En esta ocasión se considera la hipérbola como el l.g. generado por un punto, H cuando un punto P gira alrededor de la circunferencia de centro uno de los focos y radio cualquiera r1. El punto H se obtiene de la siguiente forma:
- Los puntos F y G son dos puntos libres que van a ser los focos de la hipérbola.
- Se traza la recta que une el centro de la circunferencia, punto F (uno de los focos), con el punto P.
- Se une el punto P con el otro foco, punto G.
- Se halla el punto medio del segmento PG, punto M y por él se traza la perpendicular al segmento.
- La intersección de las dos rectas trazadas es el punto H.
En ambas escenas los pulsadores k y a o el botón anima, generan el l.g. (hipérbola).
Continuamos animando a conocer el editor DescartesJS. Exponemos, en esta ocasión, la adaptación a DescartesJS de una Unidad realizada por el profesor Antonio Caro Merchante
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Hipérbola, primero como el l.g. creado por los dos puntos intersección de las circunferencias con centro en los focos y radios variables y en segundo lugar el l.g. generado por un punto cuando otro se desplaza por una circunferencia.
La Hipérbola. Método I.
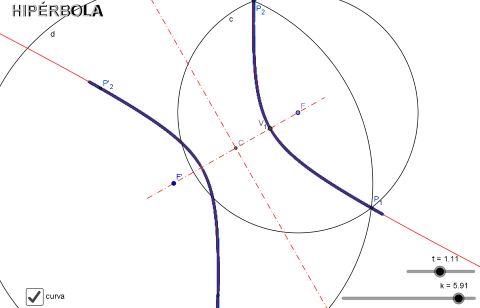
hoja de trabajo de la hipérbola (I)
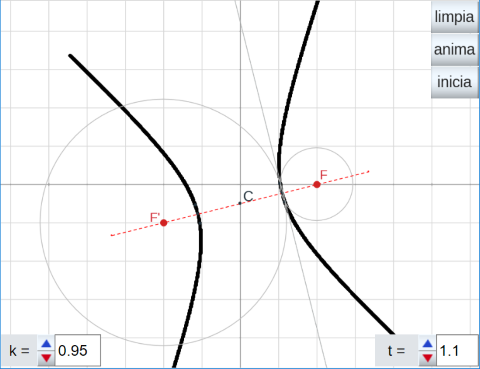
La siguiente imagen es el vínculo a la utilidad que muestra la generación del l.g. por el segundo método.
La Hipérbola. Método II.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la creación, paso a paso, del lugar geométrico que define a la hipérbola.
Las Cónicas como lugares geométricos
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
