Formación en Competencias. PISA 2017
Escrito por Montserrat Gelis BoschEsta semana presentamos una serie de objetos interactivos que forman el grupo PISA 2017 (con algunos objetos diseñados para la modalidad de evaluación con papel y otros con ordenador), patrocinado por el INTEF del Ministerio de Educación de España, para 4º de Educación Secundaria.
Este grupo pertenece al Proyecto Competencias, un proyecto de la RED Descartes con múltiples actividades interactivas para la formación y evaluación competencial. Sus contenidos se basan en las unidades liberadas de PISA y en las Pruebas de Evaluación de Diagnóstico de diferentes Comunidades Autónomas españolas.
Como muestra de las actividades, en el siguiente vídeo, se puede ver con detalle la unidad interactiva meteoroides y cráteres perteneciente a este grupo.
Este mes vamos a ver una unidad de Probabilidad de 4ºESO:
Hemos tratado estos puntos:
1.Experimentos aleatorios
Espacio muestral y sucesos
Operaciones con sucesos
Sucesos compatibles,incompatibles
2.Probabilidad de un suceso
Regla de Laplace
Frecuencia y probabilidad
Propiedades de la probabilidad
3.Experiementos compuestos
Regla de la multiplicación
Extracciones con y sin devolución
Probabilidad condicionada
Probabilidad con diagramas de árbol
Misceláneas: Lugares geométricos. Cuadraturas III.
Escrito por Ildefonso Fernández TrujilloCUADRATURAS III.
Los problemas clásicos de la geometría griega son, por activa o por pasiva, fuente inagotable de inspiración. En esta ocasión el estudio de los lugares geométricos nos llevó a sus orígenes por ende a Hípias, Dinostrato, Arquímedes... e inevitablemente a la cuadratura dinámica del círculo, esto es, a la cuadratura de cualquier polígono regular; o no, con cualquier número de lados. Resultando que, aparentemente, en la base de este proceso está el cuadrado. Motivo por el cual decidimos estudiar este polígono. Ahora bien, al intentar analizar el cuadrado este, en sí mismo, parece desaparecer mostrando como en su interior subyacen infinidad de polígonos: triángulos, cuadrados, rectángulos, trapecios, rombos… y una infinidad de otras formas inexistentes, virtuales, cuya proyección a la realidad tangible proporcionan, probablemente, los objetos y formas más útiles, en todos los sentidos, para el ser humano. Puede comprobarse como el trazo de unas pocas líneas en un cuadrado y a continuación al realizar el teselado del plano con el mismo, aparecen, de manera dinámica, formas que son el resultado de la composición de una traslación y/o de un giro; u otros, y como la visión de conjunto, a veces un palíndromo geométrico bidimensional, sugiere formas, sensaciones y conceptos cambiantes. Este procedimiento constructivo es el que los siguientes enlaces y escenas interactivas pretenden analizar aún cuando sea basándonos en los conceptos teóricos básicos y en los efectos visuales elementales que intervienen en el proceso.
La imagen siguiente está vinculada a la miscelánea que recoge un resumen de las ideas visuales expuestas a lo largo de esta entrada.
Para quien considere necesaria una inmersión en los conceptos básicos relacionados con las teselaciones hemos preparado los siguientes contenidos:
La imagen anterior enlaza con una unidad que, en su día, desarrolló el profesor Ángel Aguirre Pérez y que he comenzado a adaptar a DescartesJS debido a que sus objetivos son similares a los que nos proponemos en este artículo y por tanto nos introduce en el tema de la forma clásica y básica.
Consideramos, por tanto, que el estudio se centra en el problema clásico de la cuadratura del círculo y que nos acercamos a él haciendo, primero, la cuadratura de algunos polígonos regulares y no regulares. No debe olvidarse la idea de círculo como límite, cuando el número de lados tiende a infinito, de los polígonos regulares.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- Rellenado mínimo del plano y del espacio
Autor:

cubo de colores (origen de la imagen) - "Teselas de Escher y otras consideraciones sobre las teselaciones y movimientos en el plano.
Autora: María José Sánchez Quevedo. - Matemáticas mágicas, ingeniosas y... muy serias.
Autora: Therese Eveilleau. - Amplio estudio del plano.
Blog. Varios Autores - Estudio de los frisos, cenefas y celosías.
Autora: Ángela Núñez Castaín
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Currículo para ESO y Bachillerato.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
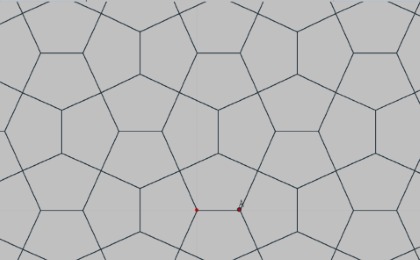
A poco que se observen los trabjos de teselación expuestos o enlazados se evidencia que en cada uno de ellos se reproduce un patrón. Existe un amplio grupo de patrones y entre los más elementales están los conocidos como 'tipo mitad del cuadrado' que son los que se obtienen descomponiendo el cuadrado en dos o más partes diferenciadas, en nuestro caso, por el color, de manera que ambas formas tengan igual área. A continuación se exponen varios ejemplos de estos patrones que aclaran el concepto.
- Estudio de los patrones y sus teselaciones correspondientes tipo "mitad del cuadrado".
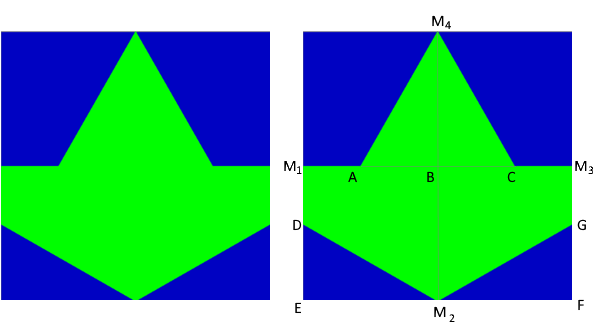
Mitad del cuadrado I.
El gráfico muestra que, por construcción, los triángulos ABM4, BCM4, DEM2 y M2FG son iguales por lo tanto el área de la parte azul es igual al área de la parte verde ya que los puntos: M1, M2, M3 y M4 son los puntos medios de los lados del cuadrado. - Mitad del cuadrado II.
- Mitad del cuadrado III.
- Mitad del cuadrado IV.
- Mitad del cuadrado V.
Debido a la extensión de la entrada las escenas que desarrollan la cuadratura del pentágono regular, tanto con DescartesJS como con GeoGebra, y otras relacionadas con el tema serán expuestas próximamente.
En esta ocasión, en la sección de vídeo, hemos elegido la tercera parte de la colección que muestra la deducción, paso a paso, de la cuadratura del círculo usando el número de oro.
Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos (cuadraturas) estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas."; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Una forma lúdica de teselar es resolver un rompecabezas, esto es un ejercicio para ejercitar la memoria visual y otras habilidades mentales por lo que proponemos, temporalmente, un amplio grupo de puzles para su resolución, uso y disfrute.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- La Mitad del cuadrado. De José Antonio Mora Sánchez: aproximación al estudio de las teselaciones.
- CUADRATURAS. De Ildefonso Fernández Trujillo: aproximación al estudio de las cuadraturas.
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Alumnas de 3º ESO entrevistan a Mary Somerville
Escrito por José Antonio Salgueiro GonzálezLa dimensión histórica, social y cultural de las matemáticas debe programarse de manera cuidada y coordinada para ayudar a la comprensión de los conceptos a través de la perspectiva histórica, así como para contrastar las situaciones sociales de otros tiempos y culturas con la realidad actual, conociendo de manera más humana a los personajes y sus aportaciones, visibilizando las circunstancias personales de mujeres matemáticas y las dificultades que han tenido para acceder a la educación y a la ciencia. Resulta idóneo el uso de Internet y de las herramientas educativas existentes, de vídeos y películas sobre la vida y obra de los personajes matemáticos para lo que es de gran ayuda la pizarra digital, o el tradicional trabajo monográfico que ahora puede crear nuestro alumnado de forma colaborativa haciendo uso de los documentos compartidos. También podemos ir más allá, pues resulta sumamente enriquecedor para la formación competencial crear de forma colaborativa una línea del tiempo con la secuenciación cronológica de descubrimientos matemáticos. Además, debemos enseñar a nuestro alumnado a generar contenido matemático inédito y desarrollar la comunicación audiovisual desde las matemáticas con la creación de un audio o vídeo o poniendo voz a los personajes célebres de ambos géneros, organizando una cadena de radio matemática o un canal de televisión que entreviste de forma ficticia a dichos personajes.
El párrafo anterior están literalmente extraídos de la Orden de 14 de julio de 2016, por la que se desarrolla el currículo correspondiente a la Educación Secundaria Obligatoria en la Comunidad Autónoma de Andalucía, se regulan determinados aspectos de la atención a la diversidad y se establece la ordenación de la evaluación del proceso de aprendizaje del alumnado, que es la que conozco como docente en activo, pero estoy convencido de que las orientaciones y estrategias metodológicas aportadas serán de gran similitud con las ofrecidas por otras comunidades autónomas en el ámbito de sus competencias.
| ANTECEDENTES |
RED Descartes posee una gran experiencia, reconocida además, en la radio ficción en Matemáticas, gracias a su programa "El personaje misterioso" conducido por Eva Perdiguero y Ángel Cabezudo, con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Pues bien, "La radio ficción en el aula de Matemáticas" es un proyecto del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija con los mismos objetivos que los de Radio Descartes, pero entre discentes en vez de entre docentes, que empieza durante el curso escolar 2015/2016 con un grupo de alumnos de Matemáticas Orientadas a las Enseñanzas Académicas en 3º de ESO, es decir, con 14 y 15 años de edad, que se coordina desde el aula virtual y comprende las fases que se relacionan a continuación.
| ELECCIÓN DEL PERSONAJE MATEMÁTICO Y DIFUSIÓN EN TWITTER |
Cada equipo estará constituido libremente por dos personas que deberán elegir a un personaje matemático para entrevistar en un programa de radio, masculino o femenino garantizando la paridad en el aula, de modo que una persona ejerza de entrevistador y la otra represente al personaje seleccionado. Seguidamente, para información de todos y no repetir personajes, un miembro del equipo publicará un tuit con la composición del mismo, incluyendo el personaje seleccionado con una imagen y el hashtag del curso #MATES3BAJO.
| DOCUMENTACIÓN |
En la segunda fase, cada equipo realizará una búsqueda de información en internet sobre la vida y obra del personaje elegido para entrevistar.
Pueden ser documentos de texto, imágenes con información, presentaciones, infografías, vídeos, audios y cualquier multimedia, en general.
Es fundamental que la información provenga de fuentes fiables, así que se hará una selección de dos o tres recursos y se compartirán en el foro habilitado en el aula virtual las direcciones de cada uno de ellos.
Después, cuando el profesor aprueba los recursos seleccionados, se tendrán que difundir esas direcciones por Twitter con el hashtag del curso #MATES3BAJO.
| ELABORACIÓN DEL GUION |
Cada equipo tiene que elaborar un guion en un documento de texto con la entrevista completa y enviarla al profesor desde la tarea habilitada en el aula virtual, cuidando la expresión, el vocabulario y la escritura.
| INSTRUCCIONES PARA LA GRABACIÓN DE LA ENTREVISTA |
¡Ha llegado el momento! Recuerda que son fundamentales la creatividad e imaginación del equipo, así que, si no tienes experiencia anterior a la hora de protagonizar un programa de radio, te daré algunos consejos:
- Busca un espacio exento de ruidos, internos o externos, y evitarás sorpresas de última hora y pérdida de tiempo.
- Es muy importante ensayar algunas veces y vocalizar perfectamente, haciendo algunas pruebas hasta conseguir el efecto deseado.
- Es muy complicado grabar la entrevista de una sola vez, por ello aconsejamos grabarla por partes, según se estime oportuno.
- Conviene dejar grabando unos segundos de silencio después de cada intervención, lo que facilita la edición y montaje de la entrevista completa.
- Tenéis que hablar con tranquilidad y vocalizando lo mejor posible.
- El protagonista es el entrevistado, es decir, el personaje matemático, no el periodista. No obstante, ambos deben transmitir emociones al público, evitando usar un tono constante.
- Evitar apostillar las respuestas del entrevistado. Conforme el entrevistado va contestando, no debemos decir “ya”, “claro”.
- Como todo programa de radio, deberá contener una presentación, donde se explique el objetivo de la sesión, y una despedida, dando un pequeño resumen de lo tratado y agradeciendo, en nombre de la cadena, la presencia del entrevistado.
La mejor forma de conocer el producto final deseado es oir algunas entrevistas similares.
Encontrarás una docena de entrevistas a personajes matemáticos que te servirán de orientación, sin olvidar que están realizadas por docentes para docentes, mientras que las vuestras son de alumnos para alumnos, y se recomienda que no sobrepasen los cinco minutos de duración.
| EDICIÓN DEL AUDIO |
Una vez grabada la entrevista, te aconsejo hacer una copia de la misma y guardarla en una carpeta llamada copia de seguridad, para evitar posibles problemas, ya que ahora procede editar los distintos archivos para proceder a enriquecer el audio con las uniones correspondientes, incluyendo la presentación, despedida, sintonía del programa de radio, efectos sonoros, etc, para lo que es fundamental la creatividad e imaginación del equipo.
En ningún momento podrás incluir música o sonidos que tengan derechos de autor, es decir, copyright, debiendo usar recursos originales o que tengan licencias que lo permitan, como las Creative Commons. Así que, para ello, te recomiendo que uses el
Descárgate los archivos que sean de tu agrado en formato mp3, preferiblemente.
Abrimos en el aula virtual un foro denominado "Soporte técnico" para que, entre todos, planteemos las dificultades que encontremos y poder compartir soluciones conforme vayamos aprendiendo.
| ENTREGA DEL AUDIO |
Una vez finalizada la edición del audio con los efectos especiales y el equipo considere concluída la entrevista, deberá generar con el software empleado un archivo en formato mp3 para entregarlo desde la tarea habilitada en la plataforma, o bien usar un conversor para pasar su archivo al formato solicitado.
Pues bien, en el marco del proyecto "La radio ficción en el aula de Matemáticas", compartimos en este segundo artículo la entrevista realizada por dos alumnas de 3º ESO a Mary Somerville, conocida como "La Reina de las ciencias del siglo XIX".
Por cierto, he de reconocer ante los usuarios y seguidores de RED Descartes que, como profesor de Matemáticas, desconocía la grandeza de la obra de Mary Somerville, por lo que agradezco a María y Julia, o Julia y María, que me ilustraran al respecto desde su estupendo programa "Radio pi al cuadrado", que recomiendo oir en su totalidad y percibir la emoción que transmiten.
Más...
Rectas notables y cálculo del área de un triángulo
Escrito por Montserrat Gelis BoschEntre los diferentes proyectos de la RED Descartes disponemos de múltiples actividades interactivas para el estudio de la geometría. En este vídeo presentamos dos actividades, del proyecto Miscelánea, que tratan diferentes aspectos relacionados con el estudio de los triángulos.
Una vez seleccionadas las actividades vamos a ver cómo se pueden insertar en un curso Moodle mediante el código para abrir en ventana emergente.
Este mes vamos a ver la unidad de sucesiones de 3ºESO:
Hemos tratado las siguientes secciones:
1.Sucesiones
Definición. Regla de formación
Término general
2.Progresiones Aritméticas
Definición
Término general
Suma de n términos
3.Progresiones Geométrica
Definición
Término general
Suma de n términos
Suma de todos los términos
Producto de n términos
4.Aplicaciones
Interpolación
Interés Compuesto
Resolución de problemas
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)















 CONTACTO
CONTACTO
