El objeto dibujar funciones cuya gráfica es una línea recta que presentamos hoy pertenece al proyecto miscelánea de la RED y tiene como objetivo aprender a dibujar funciones reales de variable real cuya representación gráfica es una línea recta.
Los coeficientes de las funciones lineales se modifican aleatoriamente y para su representación se puede elegir dados dos puntos o dado un punto y la pendiente. Una vez seleccionada la función y los datos, se inicia una animación que muestra los pasos a seguir. Al finalizar la animación se puede seleccionar un nuevo ejercicio que se puede resolver en el cuaderno y después activar la animación para comprobar si se ha realizado correctamente.
En este vídeo se muestra también cómo embeber un objeto digital en un espacio web, en este caso un curso Moodle, utilizando el código para embeber:
<iframe style="width: 810px; height: 585px;" src="/descartescms/ https://proyectodescartes.org/miscelanea/materiales_didacticos/dibujar_funciones_con_grafica_una_recta-JS/index.html"></iframe>
EDAD 4ºESO Académicas - Ecuaciones y sistemas
Escrito por Alfonso Saura EspínEste mes vamos a ver un vídeo de 4º ESO académicas sobre las ecuaciones y sistemas:
En este vídeo hemos tratado los siguientes puntos:
1.Ecuaciones de segundo grado
Completas ax²+bx+c=0
Incompletas ax²+c=0, ax²+bx=0
Discriminante y soluciones
2.Otras ecuaciones
Bicuadradas
Racionales
Irracionales
Factorizadas
3.Sistemas de ecuaciones lineales
Solución de un sistema
Sistemas compatibles
Método de sustitución
Método de igualación
Método de reducción
4.Sistemas de segundo grado
Sistema ax+by=c xy=k
Sistema a0x²+b0y²=c0 a1x+b1y=c1
5.Aplicaciones prácticas
Resolución de problemas
En el Proyecto Plantillas hemos dispuesto una sección llamada Puzles, en la cual podemos encontrar puzles de arrastre, de intercambio, giratorios y por desplazamiento. La novedad en estos puzles con respecto a la herramienta de edición Puzles Descartes es el recortado automático de las piezas del puzle, es decir, el usuario sólo se tiene que preocupar por incluir la imagen que desee para el diseño de este tipo de actividad lúdica, evitando la edición de imágenes correspondientes a las piezas del puzle. No obstante esta ventaja, no podemos descartar la herramienta de edición, pues en los puzles tipo Jigsaw aún no tenemos el recortado automático.

Seguramente, algunos diseñadores de escenas quisieran conocer las técnicas utilizadas que, por la brevedad de este post, publicaremos en la sección de documentación de Descartes. Sin embargo, en forma reducida, lo que hemos hecho es aprovechar dos utilidades del editor de Descartes: el uso de capas y los espacios múltiples. El puzle de arrastre mostrado en la imagen anterior, está compuesto de 16 piezas cuadradas, las cuales se corresponden con 16 espacios de igual tamaño. El recortado de imágenes se logra copiando la misma imagen en cada espacio, pero en posiciones diferentes, por ejemplo, en la pieza de la esquina superior izquierda, copiamos la imagen, de tal forma que sólo muestre el 25% de la imagen base, para ello debemos definir la posición de la imagen en el espacio correspondiente. El uso de las capas nos ha permitido incluir controles gráficos invisibles y asociados a cada espacio, pero en una capa superior, de tal forma que al arrastrar el control gráfico se simula el arrastre de la pieza.
Pero, para el público en general estas explicaciones técnicas no son de interés, basta con saber cómo diseñamos nuestros puzles que, como lo dijimos antes sólo es necesario incluir la imagen que deseemos. La buena noticia es que podemos usar vídeos en lugar de imágenes, haciendo más atractivos nuestros puzles.
Presentamos, entonces, dos nuevos puzles que hemos denominado vídeo puzles, el primero de cuatro piezas y el segundo de seis.
Vídeo puzle de cuatro piezas (haz clic en la imagen para abrir el puzle)
Vídeo puzle de seis piezas (haz clic en la imagen para abrir el puzle)
Misceláneas. Lugares geométricos: Cicloide - Trisectriz de Ceva.
Escrito por Ildefonso Fernández Trujillo
Lugares geométricos: Cicloide - Trisectriz de Ceva.
Continuamos con el estudio de los lugares geométricos y en esta entrada vamos a desarrollar una aproximación al conocimiento del l.g. conocido como "Trisectriz o cicloide de Tommaso Ceva". Este l.g. resuelve, a finales del siglo XVII, el problema clásico de la trisección de un ángulo pero no como pretendían los antiguos sabios griegos; aunque sí de una forma muy ingeniosa, extraordinariamente bella, dinámica y funcional.
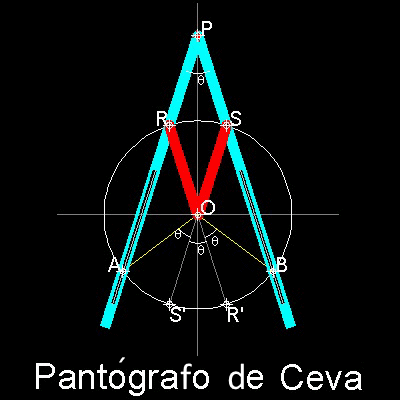
La admiración que el método ideado por Tommaso Ceva despertó en muchos científicos y técnicos propició la creación de numerosos instrumentos mecánicos trisectores de ángulos también llamados Pantógrafos de Ceva la representación gráfica de uno de los cuales se muestra a continuación.
Para profundizar en el estudio del lugar geométrico y en el de uso del editor DescartesJS, hemos elaborado, de forma muy esquemática, las pequeñas utilidades que se muestran a lo largo del capítulo. Son escenas basadas en la obra del profesor Pedro González Enríquez, trabajo que está en proceso de adaptación a las nuevas versiones del editor DescartesJS.
La primera de las escenas muestra la generación dinámica del l.g. conocido como Cicloide-Trisectriz de Ceva de la siguiente manera:
- Establecido un sistema de referencia y considerada una distancia cualquiera, por ejemplo a = 1, se crean los siguientes elementos:
- Con centro en el origen (0,0) y radio r = a se traza una circunferencia.
- Se considera un punto cualquiera, A, de la circunferencia, por ejemplo el (a,0). Este punto es importante pues hará posible, cuando se desplace por la circunferencia, la creación del lugar geométrico.
- Dibujar el punto B que depende de A y cumple dos condiciones: la primera es que debe estar en el eje horizontal y la segunda que su distancia al punto A sea igual a r en nuestro caso a. El punto de coordenadas (2·a·cos(t),0) donde t es el ángulo que la cuerda OA forma con la horizontal, cumple las condiciones. Este punto se mueve en el eje horizontal desde 2·a hasta -2·a y viceversa cada vez que el punto A da una vuelta a la circunferencia según podemos observar en la animación.
- Con centro en el punto B y radio r = a se traza una circunferencia.
- Trazar la cuerda que pasa por el origen de coordenadas y por el punto A. Esta cuerda cortará siempre a ambas circunferencias. Consideramos los puntos de corte A y P.
- El punto P que, solidario con la cuerda, gira alrededor de B y se desplaza por el plano es el punto fundamental ya que genera, en su desplazamiento, el l.g. en estudio.
- Cuando el punto A recorre la circunferencia, el punto P define la Cicloide-Trisectriz de Ceva
- Para observar la generación del l.g. basta con pulsar el botón "anima/para" de la escena.
- Conviene ver, en principio, la generación del l.g. con la curva oculta. También puede ser conveniente ocultar los ángulos pues mostrarlos, durante la primera vuelta del punto P a la circunferencia a la que pertenece, tiene como objetivo comprobar que el l.g. que se está generando es en realidad un trisector.
- Los botones: "ángulos" y "curva" ocultan/muestran, al hacer clic sobre ellos, las gráficas de los ángulos y de la curva y los textos con los valores de los ángulos. La ecuación cartesiana del l.g. es:
(x2 + y2)3 = a2·(3·x2-y2)2
lugar geométricoPara los lectores menos familiarizados con el proceso de creación de escenas DescartesJS indicamos que:
- Si se desea volver a ver la generación del l.g. desde el principio y con la escena despejada es suficiente con pulsar el botón inicio y volver a activar la animación.
- El botón velocidad ajusta la característica que su nombre indica de la animación.
Como en anteriores ocasiones indicamos que la utilidad es fácilmente adaptable y admite las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
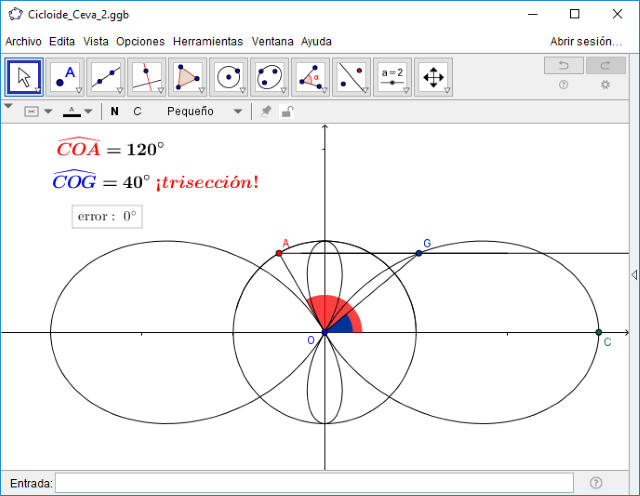
La escena que exponemos a continuación muestra como el lazo mayor de la "Cicloide-Trisectriz de Tommaso Ceva" es en realidad un trisector de ángulos. Esto se evidencia de la siguiente forma:
- En esta ocasión el punto A, que pertenece a la circunferencia de centro el origen y radio a, es un control gráfico que puede desplazarse por dicha circunferencia modificando el valor del pulsador ángulo.
- El ángulo que el radio OA forma con la horizontal puede controlarse con el pulsador ángulo y su valor se muestra en la parte superior izquierda de la escena. Este es el ángulo que vamos a trisecar de la siguiente forma:
- Por el punto A trazamos una semirrecta horizontal tal como muestra la escena.
- En dicha semirrecta colocamos un control gráfico G.
- Se desplaza el control gráfico G hasta que corta al lazo exterior en el punto adecuado (intersección de semirrecta y lazo). Cuando esto ocurre observamos que el segmento OG forma con la horizontal un ángulo que es la tercera parte del ángulo que forma el radio OA, mostrándose esta situación en la parte superior izquierda de la escena debajo del texto existente. Conviene que el desplazamiento se haga lentamente.
- La determinación de la trisección puede ejecutarse de muy diferentes maneras. De hecho en la escena actual se ha contado con una cierta 'holgura', quizás excesiva, para facilitar la interactividad.
Lazo Trisectriz de Ceva.En los siguientes trabajos presentamos una recreación de las escenas anteriores realizadas con el programa GeoGebra con los propósitos de ahondar en el conocimiento de ambas plataformas: GeoGebra y DescartesJS de forma paralela para lograr los objetivos señalados en entradas anteriores.
La siguiente utilidad genera la trisectriz al desplazar el punto A por la circunferencia.
creación del l.g.En la escena que enlaza la siguiente imagen se usa el lazo de la curva de Ceva como trisector de ángulos.
Proponemos al lector el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido dos composiciones de Milton Donaire publicadas en YouTube.
La primera trata sobre el teorema de Menelao y la segunda sobre el teorema de Giovanni Ceva. El objetivo es el de apreciar la influencia directa, e indirecta, que el conocimiento del triángulo y de las razones geométricas tiene en el tema que nos ocupa: "Los Lugares Geométricos".Teorema de Menelao
Teorema de Giovanni Ceva
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos y analizando el subproyecto Misceláneas.Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:- Parte de la Unidad creada por el profesor Pedro González Enríquez que se encuentra en fase de adaptación a DescartesJS.
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Más...
Versión 1.0 del editor en javascript de Descartes
Escrito por José R. Galo Sánchez¡Descartes cuenta con un nuevo editor de escenas!
Con la versión 1.0 de este editor, desarrollado con javascript, se inicia una nueva andadura que da continuidad al editor de Descartes en Java, y al proyecto Descartes, adaptándonos a las nuevas tendencias tecnológicas: compatibilidad HTML5, multidispositivo (ordenadores, tabletas y smaprtphones) y multisistema operativo.
Con este paso Descartes deja de usar Java tanto en la interpretación de las escenas, lo cual lleva haciéndolo desde el año 2013, como en la edición de las mismas. Durante un periodo de seis meses se ha mantenido en fase beta a este nuevo editor DescartesJS, en ese tiempo ha sido ampliamente probado por los socios de RED Descartes y se han ido subsanando los errores detectados.
El editor DescartesJS ha sido programado por Joel Espinosa Longi miembro del equipo dirigido por el Dr. José Luis Abreu León y su desarrollo ha sido patrocinado por el Instituto de Matemáticas de la Universidad Nacional Autónoma de México (UNAM), basándose en el editor de Descartes anterior.
Como se especifica en los créditos, la herramienta es software libre con licencia LGPLv3

Cuenta con una página específica desde la que se puede descargar la versión deseada según el sistema operativo: Windows, macOS o Linux (32 0 64 bits). La dirección es http://descartes.matem.unam.mx/.
DescartesJS incorpora una nueva interfaz, si bien la funcionalidad es similar a la del editor anterior, mantiene las características básicas de poder reproducirse en cualquier dispositivo y ser de uso libre y gratuito, e incluye nuevas posibilidades que incentivan la creatividad de los desarrolladores y potencian su carácter como herramienta multipropósito de aplicación a cualquier área de conocimiento científica y literaria.
Aunque la edición de escenas se efectúa en un entorno propio, ajeno al navegador que después elija el usuario para ver e interactuar con dichas escenas, la funcionalidad y el aspecto es exactamente el mismo al pasar de un contexto al otro pues en ambos casos se está utilizando el mismo intérprete de Descartes. Con el editor en Java había algunas diferencias como consecuencia de usarse dos intérpretes diferentes: el de edición en Java y el de interpretación en javascript, pero ahora es el mismo. Sí puede observarse alguna particularidad entre navegadores en aspectos muy específicos, pero eso es causado por el diferente nivel de compatibilidad HTML5 que tenga cada uno de ellos y no es debido a Descartes.
Descartes, como se indica en el logotipo actual de esta herramienta y como se indicaba en logotipo inicial, son "matemáticas interactivas" que cimentan y sustentan el desarrollo de recursos para compartir el saber y el saber hacer. Saber al estilo global clásico griego y saber compartido a nivel global gracias a las TIC y a Internet. Descartes es un medio que ayuda a conformar a sus usuarios como matemáticos, pero en su sentido etimológico (μαθηματικóς , mathematikós: amante del conocimiento).

En la página de descarga indicada también puede consultarse la documentación técnica en formato pdf. Ésta ha sido desarrollada por Alejandro Radillo Díaz, José Luis Abreu León y Joel Espinosa Longi.
La herramienta contempla compatibilidad hacia atrás, es decir, las escenas desarrolladas con el editor de Descartes en Java son editables por DescartesJS, pero hay que señalar que una vez una escena sean guardada con el editor DescartesJS, ésta no será ya editable con la versión del editor Java.
Con esta herramienta se incluye una nueva imagen identificadora, un nuevo logotipo basado en una familia de óvalos de Descartes.
Desde RED Descartes agradecemos públicamente el patrocinio del Instituto de Matemáticas de la UNAM mediante el que ha sido desarrollada esta herramienta. Agradecimiento que transmitimos también a José Luis Abreu como director de este desarrollo que actualiza y da continuidad a la labor que se inició en 1998 con la versión 1 de Descartes, a Joel Espinosa que ha realizado su programación y a Alejandro Radillo que ha abordado con los anteriores la actualización de la documentación a la nueva versión. ¡Muchas gracias a todos por vuestra dedicación y logro! y por aportar la base tecnológica que permite continuar catalizando la ilusión por innovar en la educación con y gracias a Descartes.
Nota bene 1: Este artículo sólo tiene como objetivo dar a conocer esta nueva herramienta y animar a todos los usuarios de RED Descartes a iniciarse en su aprendizaje, si son noveles en ella, o a profundizar, si son usuarios habituales. En futuros artículos iremos describiendo detalles de la misma y también las herramientas de geometría dinámica conGeo2D y conGeo3D desarrolladas con DescartesJS.
Nota bene 2: Cualquier comentario u observación sobre DescartesJS, sobre algún posible mal funcionamiento o error que detecte sera bien recibido con objeto de optimizar su funcionamiento. Puede comentarlo bien en este blog o bien puede escribirnos a la dirección de correo Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
Proyecto "Aplicación de juegos didácticos en el aula"
Escrito por Jesús Manuel Muñoz Calle"Aplicación de juegos didácticos en el aula" es uno de los proyectos de la Red Educativa Digital Descartes que están presentes en la misma desde su fundación. Como otros proyectos de Descartes, aplicación de juegos didácticos se inició en el INTEF (Ministerio de Educación) y ha seguido creciendo y ampliándose en Descartes. En la ampliación y difusión de este proyecto han participado varios compañeros a los que me gustaría citar expresamente: Enric Ripol, Santos Mondejar, Juan Carlos Collantes, Luis Ramírez, Joaquín Recio, Pepe Galo, Carlos Palacios, Antonio Vázquez, Paco Ruiz, José Luis San Emeterio, David Benito, Enrique Pescador, Luisa Muiño, Trino Grau, Ángel Velasco, Miguel Ángel Garcés y María Hijano.
En este proyecto se propone la inclusión de juegos didácticos en el aula, basados en escenas de Descartes, como herramienta dinamizadora, motivadora, de cambio metodológico, interdisciplinar, transversal, integradora, personalizable y fácil de utilizar.
Los contenidos de este proyecto se estructuran en base a los siguientes elementos: web, blog, DVD y canal de YouTube. La web es el sitio principal del proyecto, en ella se encuentran clasificados todos los juegos y materiales relacionados (ficheros de contenidos, cursos, tutoriales, enlaces, etc). En el blog se presentan experiencias de utilización práctica de juegos, ideas y orientaciones sobre el funcionamiento de los juegos, noticias y materiales relacionados con el proyecto, etc. El DVD, descargable desde el apartado de descargas de la web del proyecto, contiene los juegos y materiales del proyecto para su uso off-line. El canal de YouTube incluyen todos los vídeos y tutoreiales reazionados con el mismo.
A partir de ahora y mensualmente se realizará una publicación mensual en el Blog de Descartes sobre el proyecto de juegos didácticos. Agradeceré cualquier contribución, aportación, comentario o intervención que se realice al respecto. Finalmente incluyo el último vídeo de presentación realizado sobre los juegos de este proyecto.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)










 CONTACTO
CONTACTO
