Progresiones geométricas. Aplicaciones
Escrito por Montserrat Gelis BoschEsta semana presentamos una unidad interactiva del proyecto misceláneas que contiene actividades de aplicación de las progresiones geométricas. Ha sido creada a partir de unidades liberadas PISA y en ella se plantean tres actividades distintas en las cuales aplicar conocimientos sobre progresiones.
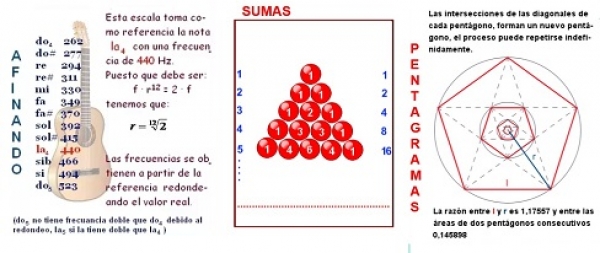
En la primera actividad, a partir de una imagen del triángulo de Pascal y la sucesión de los primeros términos, el alumnado deberá calcular la suma de un número determinado de filas.
En la segunda actividad, pentagramas, se presenta la imagen de una serie de pentágonos inscritos y se pide la suma de las áreas de los infinitos pentágonos.
Finalmente, en la actividad escala temperada, a partir de una frecuencia inicial dada y la razón, se debe calcular la frecuencia de una nota determinada.
Comunicación audiovisual en Matemáticas con Descartes
Escrito por José Antonio Salgueiro GonzálezCompartimos un nuevo multimedia correspondiente al proyecto "Matemáticas para todos con Descartes", desarrollado desde el Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, durante el curso escolar 2016/2017 con un grupo de 4º ESO del área de Matemáticas Orientadas a las Enseñanzas Académicas, coordinado desde el aula virtual de Matemáticas, que tiene acceso para invitados, donde se fueron publicando, paulatinamente, las distintas fases con las correspondientes instrucciones para el alumnado. Así, con la pregunta ¿Qué tienes que hacer?, se decía que el reto a superar consiste en generar contenido audiovisual de Matemáticas. Concretamente, tienes que grabar un vídeo en el que se ejecute y explique la resolución de dos ejercicios sobre fracciones polinómicas.
La experiencia ha resultado sumamente satisfactoria y quiero felicitar desde el portal de RED Descartes al equipo Mary Somerville por la calidad técnica del producto final conseguido. Agradecimiento extensivo a su familia por autorizar la publicación y difusión de este vídeo en internet y las redes sociales, conscientes de lo beneficioso para la formación de sus hijos.
Gracias a nuestra integración en Cero en conducta y en la Tribu 2.0, tuvimos constancia de la existencia del curriculum para docentes sobre Alfabetización Mediática e Informacional, como parte de una estrategia integral para auspiciar que las sociedades sean alfabetizadas en medios e información y promover la cooperación internacional, constituyendo un gran aporte para la innovación y mejora en todas las etapas educativas.
A su vez, fuimos conscientes de la necesidad de formarnos en comunicación audiovisual y de iniciar un Plan de Alfabetización Audiovisual en las aulas para lograr una buena formación del futuro espectador. Para ello, creamos un grupo de trabajo en el CEP de Lebrija con la denominación "Elaboración y desarrollo del Plan de Alfabetización Audiovisual para el IES Bajo Guadalquivir, en el marco del proyecto Cine y Educación".
En consecuencia, son ya bastantes años de experiencia con satisfacciones por lo conseguido, aunque nos queda un camino por delante en el que hay que ir insistiendo en esta línea y mejorando paulatinamente. Dejamos aquí enlace a lo más significativo, por si puede servir de orientación y ayuda a los docentes que se inicien en este ámbito. Añadir que cada audiovisual generado por el alumnado es completamente diferente, cual película enfocada por distintos directores de cine, demostrando así su creatividad e imaginación y sacando parte de esas capacidades ocultas que poseen nuestros alumnos y alumnas.
| TRIGONOMETRÍA EN 1º BACHILLERATO |
- Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes
- Comunicación audiovisual con iCartesiLibri
- Resolución de problemas y comunicación audiovisual y multimedia con Descartes
- ¡Diviértete! aprendiendo con Descartes
- El ángulo de depresión y la comunicación audiovisual con Descartes
- Giros: una unidad PISA en comunicación audiovisual
- ¿La Trigonometría?, pero si es muy fácil con Descartes
- Alumnos explican el cálculo del ángulo de elevación con Descartes
| RESOLUCIÓN DE PROBLEMAS EN 4º ESO |
- Aprendemos a resolver problemas con Descartes y Wiris
- Resolvemos problemas con Descartes y Photomath y comunicamos y compartimos usando medios tecnológicos
- Aprendemos a resolver problemas con Descartes, a desarrollar nuestra comunicación audiovisual y a compartir usando medios tecnológicos
| FRACCIONES POLINÓMICAS EN 4º ESO |
- Matemáticas para todos con Descartes
- Comunicación audiovisual en Matemáticas con Descartes
Este mes vamos a ver un vídeo de 2ºESO correspondiente a la Semejanza.
En él hemos tratado los siguientes puntos:
1.Teorema de Tales
Enunciado y posición de Tales
Aplicaciones
2.Semejanza de figuras
Figuras semejantes
Semejanza de triángulos
Aplicaciones
Relación entre áreas
3.Ampliación y reducción de figuras
Ampliación, reducción y escala
4.Teorema de Pitágoras.
Enunciado
Aplicaciones
Misceláneas. Lugares geométricos: las cónicas III
Escrito por Ildefonso Fernández TrujilloLas cónicas como lugares geométricos: La Parábola.
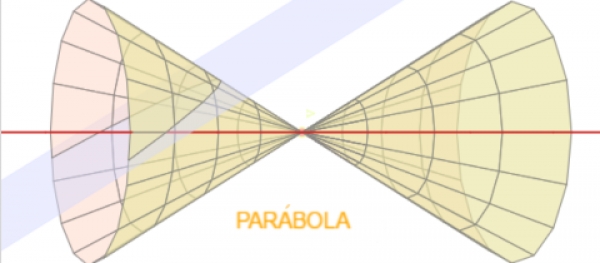
Dentro del estudio de los lugares geométricos tienen un especial interés los relativos a las cónicas por motivos muy diversos, fundamentalmente geométricos, físicos y filosóficos. Esta es la razón por la que en esta entrada vamos a continuar la aproximación a su conocimiento genérico analizando algunos aspectos de la Parábola considerada como lugar geométrico. Aprovechamos la oportunidad para señalar el aspecto popular, lúdico y funcional que la Geometría clásica ha tenido en las poblaciones cultas: el cucurucho con sus múltiples aplicaciones, los niños y niñas jugando con el aro, la peonza, el yoyo...
Consideramos, por tanto, que el estudio se centra en los ll.gg. generados por puntos que se mueven en el plano de forma que la razón (excentricidad) entre sus distancias a un punto fijo (foco) y a una recta (directriz) se mantiene constante.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- La Parábola como lugar geométrico.
- Generación de la Parábola como lugar geométrico.
Trabajo muy detallado de la creación del l.g. Ignacio Larrosa Cañestro (Grupo XeoDin)
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Curriculum para ESO y Bachillerato.
Ambos trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
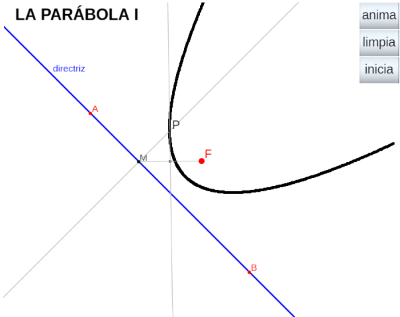
- Estudio de la PARÁBOLA I. La parábola como l.g. generado por el método, basado en la definición, del triángulo isósceles.
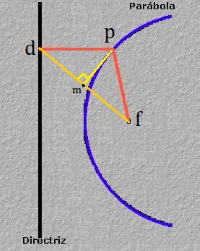
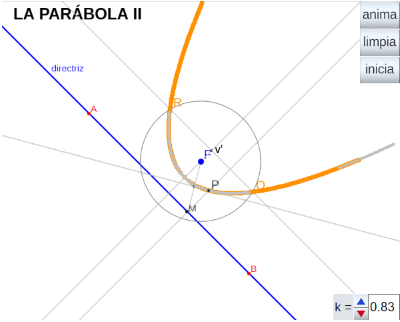
A partir de una recta d (directriz) y de un punto F (foco) consideramos que un punto del plano, P, pertenece a la parábola (F,d) si la distancia de P a M (ver imagen) es igual a la distancia de P a F. Esto es, el triángulo PMF es isósceles y por lo tanto la altura de dicho triángulo trazada desde P corta al lado FM en su punto medio. O bien que la intersección de la perpendicular a la directriz por un punto M de la misma con la perpendicular por el punto medio de FM es un punto de la parábola. Haciendo que M recorra la directriz obtendremos la parábola (F,d). - Estudio de la PARÁBOLA II. En esta ocasión se considera la parábola como el l.g. generado por los puntos, Q y R, intersección de la circunferencia c(F,r) con la paralela a la directriz por el vértice cuando el vértice, como punto virtual v', se desplaza por el eje focal desde su posición original hasta el infinito alejandose de la directriz (ver la animación completa), el radio de la circunferencia, r es igual a la distancia del vértice virtual v' a la directriz.
Es trivial comprobar que los puntos Q y R siempre son puntos de la parábola.
Se ha construido el l.g. por este segundo método sobre la construcción anterior por motivos didácticos.
En la primera escena el botón anima y en la segunda el pulsador k y el botón anima, generan el l.g. (parábola).
Continuamos animando a conocer el editor DescartesJS. Volvemos a exponer la adaptación a DescartesJS de la Unidad realizada por el profesor Antonio Caro Merchante debido a su relación con los conceptos en estudio.
Como en anteriores ocasiones notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Parábola, primero por el método del triángulo isósceles y a continuación por el método clásico de la intersección de recta y circunferencia.
La Parábola. Método I.
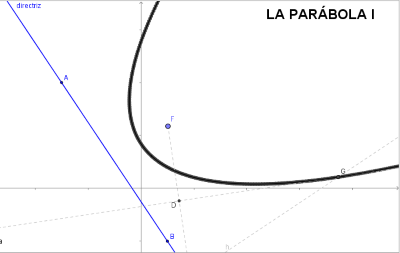
hoja de trabajo de la parábola (I)
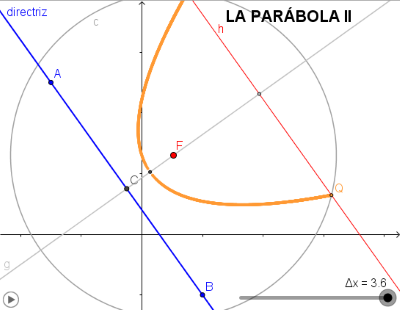
La siguiente imagen es el vínculo a la utilidad que muestra la generación del l.g. por el segundo método, intersección de paralela a la directriz con la circunferencia de centro el foco y radio variable..
La Parábola. Método II.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido uno que muestra la deducción, paso a paso, de la ecuación del lugar geométrico que define a una curva cónica.
Las Cónicas como lugares geométricos
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Más...
El alumnado como generador de contenido multimedia con Descartes JS
Escrito por José Antonio Salgueiro GonzálezLos alumnos y alumnas del s. XXI utilizan los ordenadores personales, y sobre todo sus dispositivos móviles, para comunicarse, jugar, buscar información, estar conectados y generar contenido multimedia para el ocio y relaciones en sociedad a través, básicamente, de sus redes sociales habituales. Pero, ¿cómo utilizar este potencial tecnológico para que nuestros alumnos y alumnas generen contenido multimedia destinado al aprendizaje de sus áreas o materias? ¿Debemos los docentes asesorar, orientar, proponer y evaluar tareas y pruebas encaminadas a este fin?
En el desarrollo curricular del Bachillerato se recoge que los contenidos de esta materia se organizan en cinco bloques que se desarrollarán de forma global, pensando en las conexiones internas de la materia tanto dentro del curso como entre las distintas etapas. Así, el bloque de contenidos "Procesos, métodos y actitudes en Matemáticas" es común a la etapa y transversal ya que debe desarrollarse de forma simultánea al resto de bloques de contenidos y es el eje fundamental de la materia. Se articula sobre procesos básicos e imprescindibles en el quehacer matemático como la resolución de problemas, proyectos de investigación matemática, la matematización y modelización, las actitudes adecuadas para desarrollar el trabajo científico y la utilización de medios tecnológicos.
En las estrategias metodológicas se dice que el profesorado debe actuar como orientador, promotor y facilitador del aprendizaje y del desarrollo competencial del alumnado, fomentando su participación activa y autónoma. Asimismo, debe despertar y mantener la motivación, favoreciendo la implicación en su propio aprendizaje; promover hábitos de colaboración y de trabajo en grupo para fomentar el intercambio de conocimientos y experiencias entre iguales; provocar una visión más amplia de los problemas al debatirlos y cuestionar las soluciones, con la posibilidad de plantear nuevos interrogantes o nuevos caminos de resolución y de aprender de los errores.
Entre los contenidos de este bloque encontramos la elaboración de informes y documentos sobre los procesos llevados a cabo y los resultados y conclusiones obtenidos, así como comunicar y compartir, en entornos apropiados, la información y las ideas matemáticas. Finalmente, en los criterios de evaluación se mencionan:
- Emplear las herramientas tecnológicas adecuadas, de forma autónoma, realizando cálculos numéricos, algebraicos o estadísticos, haciendo representaciones gráficas, recreando situaciones matemáticas mediante simulaciones o analizando con sentido crítico situaciones diversas que ayuden a la comprensión de conceptos matemáticos o a la resolución de problemas. CMCT, CD, CAA.
- Utilizar las tecnologías de la información y la comunicación de modo habitual en el proceso de aprendizaje, buscando, analizando y seleccionando información relevante en Internet o en otras fuentes, elaborando documentos propios, haciendo exposiciones y argumentaciones de los mismos y compartiendo éstos en entornos apropiados para facilitar la interacción. CCL, CMCT, CD, CAA.
| DESCRIPCIÓN DE LA EXPERIENCIA |
Esta iniciativa, desarrollada desde el Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, durante el curso escolar 2016/2017 con un grupo de 1º Bachillerato Ciencias, se ha coordinado desde el Aula virtual de Matemáticas-1, que tiene acceso para invitados, donde se fueron publicando, paulatinamente, las distintas fases con las correspondientes instrucciones para el alumnado. Así, con la pregunta ¿Qué tienes que hacer?, se decía que el reto a superar consiste en generar contenido multimedia e interactivo con Descartes JS, que tiene compatibilidad HTML5, es multidispositivo (ordenadores, tabletas y smartphones) y multisistema operativo.
Concretamente, tienes que diseñar y crear una autoevaluación interactiva similar a la denominada "Ecuaciones de la recta en el plano", que encuentras enlazada aquí y en los recursos.
Para ello, estableceremos distintas etapas o fases.
| PRIMERA FASE |
La clase se organizará en equipos constituidos por dos personas, actuando una de ellas como coordinador o coordinadora del equipo que, además, deberá llevar el nombre de un personaje matemático, hombre o mujer.
Será el coordinador o coordinadora la persona encargada de entregar las tareas en las distintas fases y en los plazos establecidos.
La persona que coordina comunicará en el foro denominado "Constitución y nombre del equipo" la composición del mismo y el nombre del matemático o matemática elegido, con una pequeña explicación del motivo de esa elección.
En caso de coincidencia en el nombre del equipo, tendrá que cambiar su decisión el último equipo que haya intervenido en el foro, según la fecha y hora que muestra el aula virtual.
Autoevaluación-1, generada por el equipo Juan de Ortega.
| SEGUNDA FASE |
Cada equipo deberá elaborar una prueba final con 10 ejercicios o problemas, distribuidos de la siguiente forma:
- 2 sobre trigonometría superior
- 2 sobre logaritmos
- 2 sobre vectores y sus aplicaciones (1ª parte de geometría analítica plana)
- 2 sobre rectas, circunferencias y distancias (2ª parte de geometría analítica plana)
- 2 sobre funciones reales de variable real
En la cabecera de un folio escribirás el nombre del equipo y los de sus componentes.
Redactarás, con letra clara, la selección de ejercicios o problemas incluyendo debajo de cada uno la solución, es decir, solo el resultado final, sin el desarrollo.
Escaneas el folio y el coordinador o coordinadora del equipo lo adjunta al foro denominado "Nuestra selección de ejercicios", para compartilo con toda la clase, evitar que tengamos excesivos ejercicios o problemas repetidos y garantizar que la solución es la correcta. En este sentido, se podrá comenzar con la siguiente fase cuando el profesor otorgue el visto bueno.
En caso de repeticiones en exceso, deberá modificar y buscar nuevos ejercicios el equipo que los presente con posterioridad, según la fecha y hora que muestra el aula virtual.
Autoevaluación-2, generada por el equipo Eratóstenes
| TERCERA FASE |
Ha llegado el momento de organizar y preparar los recursos necesarios para generar nuestro multimedia.
Utilizaremos el Plantillero Descartes-JS, una herramienta que permite a cualquier usuario, con mínimos conocimientos de los entornos digitales, crear contenidos interactivos de acuerdo a sus necesidades.
Para editar la plantilla, sólo se requiere de las siguientes herramientas básicas:
- Un editor de texto. Puede ser el bloc de notas de Windows, el TextEdit de Mac o, en forma general, cualquier editor de texto que no incluya formatos. No obstante, recomendamos el editor Notepad++, que se puede descargar libremente desde https://notepad-plus-plus.org/
- Un editor de imágenes. No se trata de tener una herramienta sofisticada de edición de imágenes, basta con un Paint de Windows o un Paintbrush de Mac, pues lo único que haremos es redimensionar (resize) algunas imágenes.
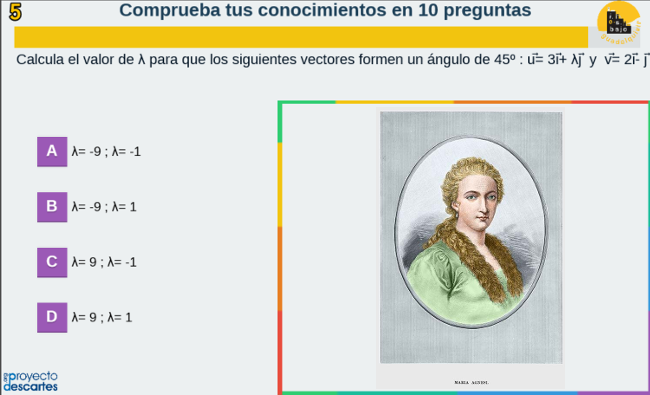
Autoevaluación-3, generada por el equipo María Gaetana Agnesi
Descarga los recursos necesarios y organiza todo el material en tu ordenador. Para ello, crea una nueva carpeta con el nombre de tu equipo y descarga en ella el tutorial o manual de instrucciones, en formato PDF, así como el archivo comprimido que contiene la plantilla para, seguidamente, proceder a descomprimirlo y poder acceder a su contenido.
Por último, te recomiendo descargar e instalar en tu equipo el editor gratuito Notepad++.
- Tutorial o manual de funcionamiento
- Archivo comprimido con la plantilla
- Descarga Notepad++
- Ejemplo de autoevaluación
Si tienes alguna duda, puedes plantearla en el foro del aula virtual denominado "Consulta tus dudas", que fomentará el aprendizaje y trabajo colaborativo en la distancia, a través de internet, como tendrás casi con toda seguridad que desarrollar tu profesión en un futuro.
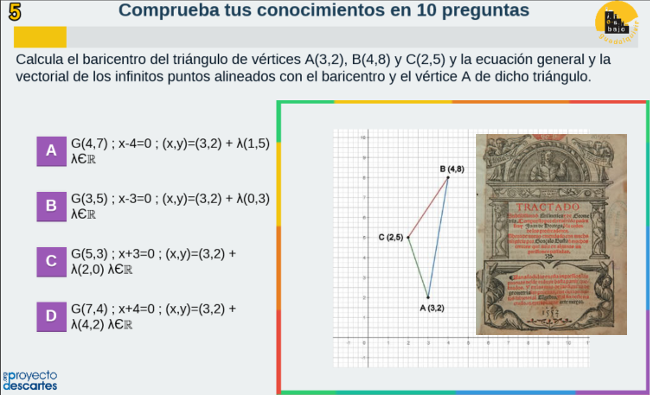
Autoevaluación-4, generada por el equipo Descartes
| FASE FINAL |
Finalizadas las tres fases en las que hemos dividido este proyecto, llega el momento de entregar la autoevaluación digital que has creado.
Antes de proceder a su entrega, y con objeto de conseguir la máxima calificación posible, te recomiendo que revises la redacción de las preguntas, por si hubiera alguna falta de ortografía, así como las fórmulas y expresiones matemáticas.
Debes entregar la autoevaluación en las mismas condiciones que te descargaste la plantilla, es decir, en un archivo comprimido de extensión .zip o .rar, conteniendo las carpetas audio, css, fonts, images, js, lib, textos y los archivos index e indexb, es decir, todo el contenido original una vez modificado.
El archivo deberá denominarse equipo_nombreequipo, donde nombreequipo corresponde, obviamente, al del personaje matemático elegido en su momento, y se entregará a través de la tarea habilitada en el aula virtual a tal efecto.
Autoevaluación-5, generada por el equipo Hipatia de Alejandría
| A MODO DE CONCLUSIÓN |
En primer lugar, quiero felicitar a todos mis alumnos y alumnas porque no cesan de sorprenderme con su creatividad, imaginación, estrategias y capacidades para superar los retos que les planteo, proporcionando productos finales de calidad, no sin esfuerzo, dedicación, trabajo colaborativo e investigación.
Agradecimientos, también a Juan Guillermo Rivera, presidente de ColDescartes, la RED Descartes de Colombia, por su ayuda y personalización de la plantilla para el desarrollo del proyecto, así como a todos mis compañeros cartesianos que me animan, apoyan y proporcionan el soporte técnico para materializar en realidad una idea.
A todos nuestros usuarios y seguidores, recordar que RED Descartes ofrece de forma completamente gratuita una amplia y variada gama de modelos en el Proyecto Plantillas para que los alumnos y alumnas de cualquier etapa educativa puedan generar y difundir contenido multimedia en HTML5, para todos los dispositivos, para cualquier área o materia y, además, pueden publicarlos, si lo desean, en nuestros espacios, sin más que contactar con nosotros en Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Autoevaluación-6, generada por el equipo Alan Turing
El Proyecto Descartes en el aula. Taller presentado en el VIII CIBEM
Escrito por José Antonio Salgueiro GonzálezDel 10 al 14 de julio de 2017 se celebró, en las facultades de Ciencias Matemáticas, Ciencias Físicas y Medicina de la Universidad Complutense de Madrid, el VIII Congreso Iberoamericano de Educación Matemática que, con el lema "Miramos con ilusión hacia el futuro de la educación matemática", congregó a 1600 docentes de todas las etapas educativas que mantienen viva la llama de la ilusión por esta maravillosa tarea que es la educación matemática de nuestros alumnos, según palabras de Concepción Toboso Nieto, presidenta del comité organizador, integrado por la Sociedad Madrileña de Profesores de Matemáticas "Emma Castelnuovo", con el apoyo de la Federación Española de Sociedades de Profesores de Matemáticas y por delegación de la Federación Iberoamericana de Sociedades de Educación Matemática.
La Red Educativa Digital Descartes estuvo representada por Rita Jiménez Igea y Elena Álvarez Sáiz, que aportaron, respectivamente, el taller titulado "El Proyecto Descartes en el aula" y la comunicación "Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automática".
El objetivo del taller es dar a conocer el portal de Red Educativa Digital Descartes (RED Descartes) a los profesores y profesoras de Matemáticas, mostrando los recursos educativos accesibles desde cualquier dispositivo para las etapas de Infantil, Primaria, Secundaria, Bachillerato y Universidad, que pueden usarse libre y gratuitamente y se encuentran disponibles en los dominios ProyectoDescartes.org, REDDescartes.org y DescartesJS.org.
Se presentaron los diversos subproyectos del Proyecto Descartes y se hizo un recorrido por distintas unidades didácticas digitales y objetos interactivos, pudiendo los asistentes interactuar con las escenas entrando en esas unidades de modo dirigido y de forma libre. Se expusieron, de manera práctica, distintas formas de incorporar al aula estos materiales en función de las posibilidades tecnológicas de cada centro, concluyendo con unos ejercicios para mostrar la posibilidad de crear nuevos recursos usando los ya existentes o adaptarlos a las necesidades del alumnado.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)









 CONTACTO
CONTACTO
