Misceláneas. Lugares geométricos: Cuadraturas II
Escrito por Ildefonso Fernández TrujilloCUADRATURAS II
Adentrarse en el estudio de los lugares geométricos, las cuadraturas, las teselaciones y las particiones de un polígono en otros más pequeños con la intención de teselar, en general el espacio plano, y en particular otros polígonos de diferente forma es estar, literalmente, predispuesto a perderse dentro de la espiral del tiempo en un ir y venir por las manifestaciones más sobresalientes de las diferentes culturas y épocas. Esta es la razón por la que en esta entrada vamos a continuar la aproximación al conocimiento genérico de los ll.gg. analizando algunos aspectos de las Cuadraturas, asuntos estos tan íntimamente ligados que, a veces, es difícil discernir cuál es la causa y cuál el efecto.
Recordamos que el estudio de las cuadraturas, los ll.gg. y la descomposición de un polígono en otros más pequeños que lo recubren completamente con objeto de, con ellos, recubrir otro polígono diferente, están ligados, también, al estudio de las teselaciones.
Aprovechamos la oportunidad para señalar el aspecto popular, lúdico, espiritual, económico, agrario y funcional que la Geometría clásica, la Cosmología, la Astronomía y en general el conocimiento ha tenido en las poblaciones cultas.
Consideramos, por tanto, que el estudio se centra en el problema clásico de la cuadratura del círculo y que nos vamos a aproximar a él haciendo, primero, la cuadratura de algunos polígonos regulares y no regulares. No debe olvidarse la idea de círculo como límite, cuando el número de lados tiende a infinito, de los polígonos regulares.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- Teselaciones
- Mosaico de Escher
Autor: Enrique Martínez Arcos. Adaptación a DescartesJS: Mª José García Cebrian. Publicado por: Ángel Cabezudo Bueno - Salamandra de Escher
Fernándo Pavez Peñaloza. - Descubierto un nuevo pentágono que tesela el plano
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Currículo para ESO y Bachillerato.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
- Estudio de la Cuadratura y Teselación de un Triángulo Equilátero.
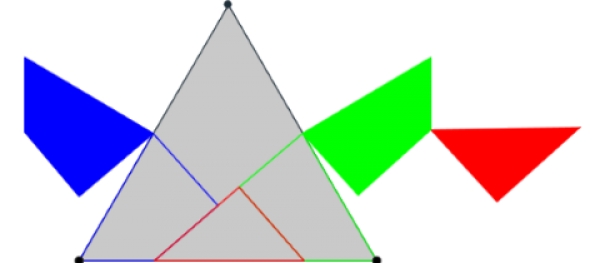
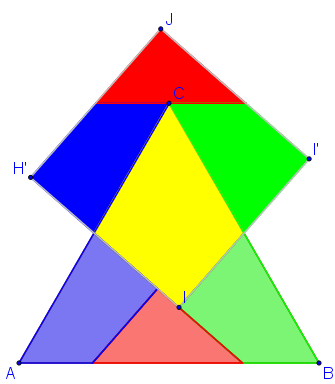
Supongamos que el triángulo equilátero ABC (ver la siguiente figura), se descompone en los polígonos: AFEM3, FHI, IHBM2 y EM2CM3.
Con los polígonos anteriores podemos formar muchas figuras, además del triángulo equilátero ABC, según coloquemos los polígonos en el plano. Una de las maneras de situar los polígonos es la que muestra la escena que enlaza la imagen anterior. En dicha escena: activando el botón anima o pulsando en el control alfa se observa como se recolocan los polígonos para formar el rectángulo EE2E3E4, visible cuando alfa = 3.14, que evidentemente es un cuadrado con el mismo área que el triángulo equilátero ABC.
Con la misma intención y con objeto de practicar con las animaciones y diferentes formas de lograr un objetivo se ha creado la escena que enlaza la imagen siguiente.
Analizadas las dos escenas anteriores, conviene pulsar el botón ver aux. o aux, vamos a elaborar una nueva escena para obtener infinitas teselaciones del triángulo equilátero ABC y con dichas teselaciones recubrir un rectángulo y/o un cuadrado.
En esencia la escena es la misma que las anteriores pero simplificada en extremo. Hemos procedido de la siguiente manera:
- dibujamos el triángulo equilátero ABC: A(0,0), B(6,0) y C(3, 6·sen(60º)).
- particionamos el lado horizontal de la siguiente forma:
- segmento AD controlado por el pulsador t
- segmento DE de longitud igual a la mitad del lado AB
- segmento EB tal que AD+EB=DE
- situamos los puntos medios de los lados AC y BC, M3 y M2.
- unimos, mediante una recta, uno de esos puntos medios con el punto más alejado de él entre D y E
- desde el otro punto medio y desde el punto intermedio de la partición que no se ha usado se trazan segmentos perpendiculares a la recta anterior.
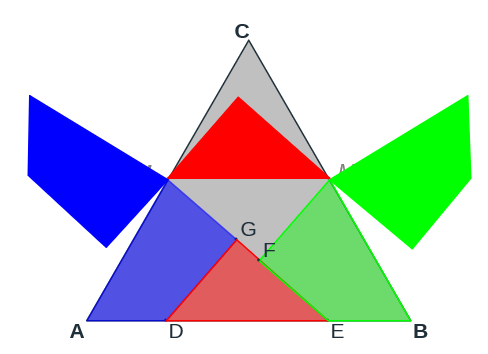
- así se obtienen (por ejemplo) los polígonos: ADGM3, DEG, FEBM2 y FM2CM3 que teselan al triángulo. (ver escena enlazada con la imagen anterior)
- en la escena mencionada al pulsar el botón anima o llevar el pulsador ang a 3.14, se construye el rectángulo FF2F3F4 de igual área que el triángulo ABC y que cuando t vale 0.97 es un cuadrado.
- por lo tanto para cada valor de t tenemos una teselación diferente y para ciertos valores, además, la cuadratura.
- debe indicarse que la construcción está aproximada a las centésimas y que para cualquier otro grado de precisión habría que reajustar los valores.
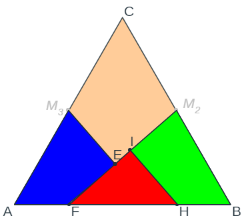
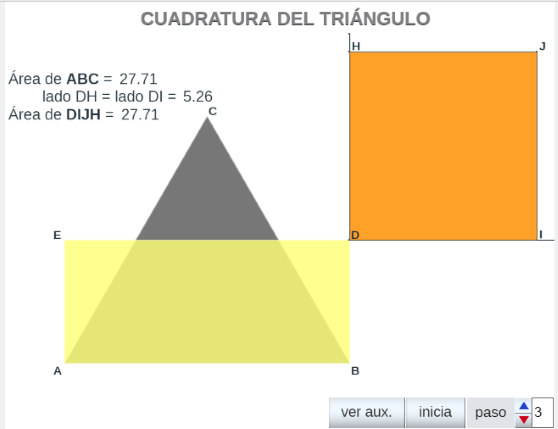
- Cuadratura estándar de un triángulo. El método estándar de cuadrar un triángulo consiste en hallar el rectángulo con la misma área que él y a continuación cuadrar dicho rectángulo como muestra la escena que enlaza la siguiente imagen.
Construcción de la escena:
- paso 0
- Representamos el triángulo, en esta ocasión equilátero, ABC y los puntos médios de los lados: AC y BC.
- paso 1
- El rectángulo ABDE, obviamente, tiene la misma superficie que el triángulo ABC.
- El botón comprobar muestra una animación que evidencia la afirmación anterior.
- paso 2
- Prolongamos los lados BD y ED como apoyo a la construcción.
- Con centro en D y radio DB se traza la circunferencia que junto a la extensión del lado ED definen el punto F.
- Se determina G, punto medio del segmento EF.
- Con centro en G y radio EG se traza la circunferencia que en su intersección con la prolongación de BD determina el punto H.
- En la escena (paso 2) se observa que el segmento DH es medía geométrica de ED y DF, pero DF = BD, por lo tanto AB·BD = DH2.
- Construimos el cuadrado DIJH.
- paso 3
- SABC=SABDE=SDIJH
- paso 0
Enlazamos a continuación otros ejemplos relacionados con el cuadrado y su partición en dos partes iguales o en dos/tres partes de forma que el área de una de las partes es siempre igual a la mitad de la superficie del cuadrado.
Escena 1

Partición dinámica del cuadrado en dos/tres partes.
Escena 2

Partición dinámica del cuadrado en dos partes iguales
Las escenas anteriores muestran la intima relación del cuadrado con el triángulo, el rectángulo y los trapecios para conformar teselas de indudable belleza.
Notamos que las utilidades mostradas son fácilmente adaptables y admiten las modificaciones y/o ampliaciones que se consideren convenientes para los propósitos particulares de uso.
Las siguientes imágenes enlazan con pequeñas herramientas realizadas con el programa GeoGebra en las que se recrean los procesos de generación de la Cuadratura del Hexágono, por el método estándar o clásico y la descomposición de un triángulo equilátero de infinitas formas diferentes en cuatro polígonos para teselar rectángulos e incluso el cuadrado .
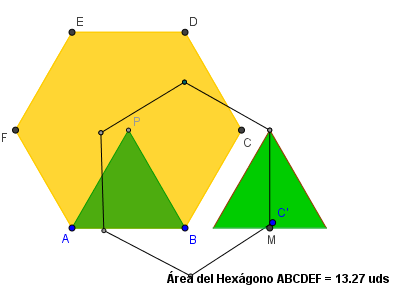
La siguiente imagen es el vínculo a la utilidad que muestra la generación de la Cuadratura del Hexágono por el método estándar.
Cuadratura del Hexágono. Método clásico.
Descomposición de un triángulo equilátero.
La siguiente utilidad es copia de la ya analizada anteriormente.
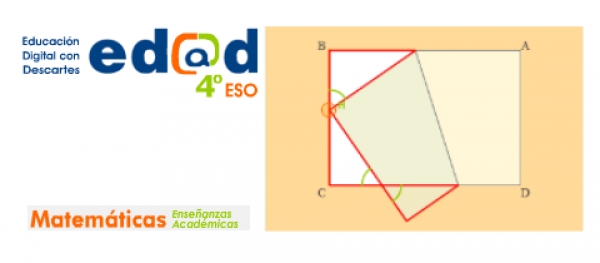
También, en esta introducción elemental al estudio de las cuadraturas, puede ser de interés el estudio de este otro trabajo sobre la cuadratura de un triángulo cualquiera.
Proponemos el análisis de las utilidades anteriores, su modificación y mejora con objeto de lograr un profundo conocimiento de ambas plataformas y así potenciar la inclusión del cálculo simbólico en escenas DescartesJS de forma eficaz.
Esta vez en la sección de vídeo hemos elegido la segunda parte de la colección que muestra la deducción, paso a paso, de la cuadratura del círculo usando el número de oro.
Continuando con la creación de la miscelánea "Las Espirales sugerimos completar su elaboración extrayendo el contenido relacionado con los lugares geométricos estudiados para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografia:
- La Mitad del cuadrado. De José Antonio Mora Sánchez: aproximación al estudio de las teselaciones.
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Tablas y expresiones algebraicas
Escrito por Montserrat Gelis BoschEl proyecto Unidades Didácticas de la RED está formado por una serie de unidades independientes que cubren el currículo de Matemáticas y Física y Química de la Enseñanza Secundaria Obligatoria.
En este vídeo presentamos la unidad Tablas y expresiones algebraicas que consta de una serie de ejercicios y actividades para afianzar la lectura e interpretación de gráficas y su relación con las expresiones algebraicas.
Finalmente, para trabajar en el aula, se muestran los pasos a seguir para insertar esta unidad en un curso moodle.
¡La vuelta al cole con Descartes en 2017/2018!
Escrito por José Antonio Salgueiro GonzálezEDAD 4º ESO Académicas - Semejanza
Escrito por Alfonso Saura EspínEl vídeo de este mes es también de semejanza pero de 4ºESO Académicas:
Los epígrafes tratados han sido los siguientes:
1.Semejanza
Figuras semejantes
Teorema de Tales
Triángulos semejantes
2.Triángulos rectángulos. Teoremas
Teorema del Cateto
Teorema de la Altura
Teorema de Pitágoras generalizado
3.Razón de semejanza
Razón de semejanza en longitudes
Razón de semejanza en áreas
Razón de semejanza en volúmenes
Más...
Misceláneas. Lugares geométricos. Cuadraturas.
Escrito por Ildefonso Fernández TrujilloCUADRATURAS.
Adentrarse en el estudio de los lugares geométricos es estar, literalmente, predispuesto a perderse dentro de la espiral del tiempo en un ir y venir por las expresiones artísticas, religiosas, estructurales y técnicas de las diferentes culturas y épocas. Los conceptos, fundamentalmente los geométricos, físicos y filosóficos aparentan una evolución-involución atractiva y armónica que fascina. Esta es la razón por la que en esta entrada vamos a continuar la aproximación al conocimiento genérico de los ll.gg. analizando algunos aspectos de las Cuadraturas, asuntos estos tan íntimamente ligados que, a veces, es difícil discernir cuál es la causa y cuál el efecto.
Recordamos que el estudio de las cuadraturas, los ll.gg. y la descomposición de un polígono en otros más pequeños que lo recubren completamente con objeto de, con ellos, recubrir otro polígono diferente, están ligados, también, al estudio de las teselaciones.
Aprovechamos la oportunidad para señalar el aspecto popular, lúdico, espiritual y funcional que la Geometría clásica, la Cosmología, la Astronomía y en general el conocimiento ha tenido en las poblaciones cultas.
Consideramos, por tanto, que el estudio se centra en el problema clásico de la cuadratura del círculo y que nos vamos a aproximar a él haciendo, primero, la cuadratura de algunos polígonos regulares y no regulares. No debe olvidarse la idea de círculo como límite, cuando el número de lados tiende a infinito, de los polígonos regulares.
Ejercicios interactivos con tutorización automática. Una experiencia de aula
Escrito por Elena Álvarez SáizComo se informó desde este blog, durante la celebración del VIII Congreso Iberoamericano de Educación Matemática (CIBEM) en julio del 2017 en Madrid, la Red Educativa Descartes participó con el taller “El Proyecto Descartes en el aula” y la comunicación “Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automática”. El objetivo del taller dirigido por Rita Jiménez Igea fue dar a conocer el portal de la Red Educativa Digital Descartes a los profesores y profesoras de Matemáticas, mostrando los recursos educativos generados en el Proyecto Descartes para todas las etapas del sistema educativo.
En la comunicación presentada por Elena Álvarez Sáiz y Mª Reyes Ruiz Cobo, se expuso una experiencia de aula desarrollada durante el curso 2016-2017 en dos asignaturas que se imparten en el primer curso de los Grados de Ingeniería de la E.T.S.I. Industriales y Telecomunicación de la Universidad de Cantabria. Su diseño y desarrollo ha formado parte de un Proyecto apoyado por esta universidad dentro de la III Convocatoria de Innovación Docente.
Teniendo en cuenta la problemática específica de las asignaturas de Matemáticas en los primeros cursos de Grado respecto a la heterogeneidad del alumnado y las dificultades de su adaptación a la universidad, el Proyecto se planteó como primer objetivo la creación de actividades de autoevaluación que favoreciesen la evaluación continua formativa y tutorizada. Para su diseño se adoptó como estrategia didáctica la gestión de errores de forma que, mediante la intervención docente, se pudiera llegar a un fortalecimiento de los contenidos de más difícil comprensión.

En el desarrollo de estas actividades se ha utilizado la herramienta DescartesJS y su posibilidad de comunicación con páginas html. Gracias a las potentes funcionalidades de esta herramienta se han podido construir actividades de evaluación multimedia que incorporan, entre otros elementos, videos interactivos, animaciones, representaciones gráficas, controles numéricos y gráficos así como evaluación de resultados por un sistema de álgebra computacional (CAS). Las características más destacables de estas actividades son:
- Se adaptan a cada alumno.
- Contemplan distintos niveles de aprendizaje.
- Incluyen asistencia personalizada y retroalimentación inmediata a la actuación del estudiante utilizando para ello botones de acción, menús de navegación y diálogos multimedia que hacen sentir al estudiante que está ayudado en todo momento.
- Sitúan al estudiante en el centro del proceso de aprendizaje.
- Se integran en un entorno de aprendizaje virtual estando disponibles en abierto.
El material generado se puso a disposición de los estudiantes al finalizar los temas seleccionados en cada asignatura como actividad voluntaria a realizar dentro de la evaluación continua. La participación del alumnado en esta experiencia ha sido alta y su satisfacción ha sido muy positiva valorando la utilidad del material en el aprendizaje de los contenidos abordados.
El guión de la presentación que se realizó en el VIII CIBEM muestra los aspectos destacados de esta experiencia.
Puede obtenerse más información accediendo al texto de la comunicación presentada en el VIII CIBEM: Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automática .
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)










 CONTACTO
CONTACTO
