Guía rápida de uso de juegos del Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle
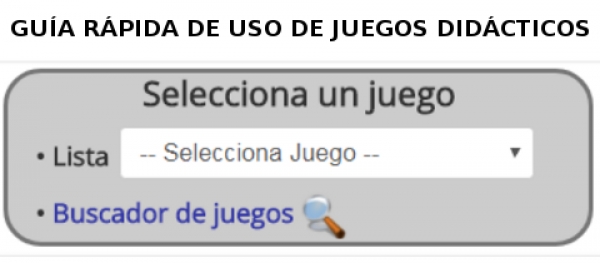
1. Buscar y elegir el juego que se desee.
Elige un juego del menú "Selecciona un juego", situado en la esquina superior izquierda de la web del proyecto. Al pulsar se mostrará una descripción del juego. (También se puede usar los buscadores de la web, especialmente el de juegos).
Para entrar en el juego pulsa el botón rojo, "ACCEDER AL JUEGO" que aparece en la descripción del mismo.
3. Seleccionar la modalidad de introducción de preguntas el juego.
Éstas pueden introducirse de forma escrita, oral o no contener preguntas. (Si el juego sólo presenta una modalidad este paso se omite).
4. Elegir la configuración o parámetros iniciales del juego.
Introduce los nombres de los jugadores, opciones específicas y generales del juego, carga de ficheros de preguntas para juegos con esta modalidad, etc.
5. Pulsar en el botón JUGAR.
6. Comenzar la partida.
Introducción al cálculo. Primeras actividades con Canals.
Escrito por Montserrat Gelis BoschEsta semana vamos a ver algunas unidades del Proyecto Canals con actividades de introducción al cálculo. Pertenecen al Proyecto Canals una serie de materiales interactivos que han sido diseñados a partir de los materiales que ha ido elaborando y compilando la professora Maria Antònia Canals durante su extenso periodo docente.
En el siguiente vídeo y a modo de ejemplo se han seleccionado tres actividades de sumas y restas y se muestran también los pasos a seguir para insertar dichas actividades en un curso de Moodle.
Las actividades seleccionadas son:
- Actividades para iniciar el cálculo escrito. Una recopilación de actividades con imágenes para empezar a aprender el significado de las operaciones.
- Ábaco para restar con unidades, decenas y centenas. Se utiliza un ábaco para realizar operaciones que requieran el paso de unidades de un orden, a las del orden siguiente.
- Operaciones. Tres escenas con juegos numéricos para practicar la operaciones con números naturales.
En este artículo se pone de manifiesto la conveniencia y utilidad de contar con una herramienta, la calculadora de la Normal, que nos permita dar respuesta de manera cómoda y rápida a múltiples y rutinarios problemas de probabilidad que surgen en estudios con poblaciones que se ajustan a cualquier distribución normal. Se evita el paso de tipificación a la N(0, 1) y se mejora la precisión usual obtenida.
LA DISTRIBUCIÓN NORMAL
Pensemos en voz alta:
- ¿Me gustan los problemas de probabilidad?
- ¿Es difícil plantear y resolver situaciones en las que se requiere contar y recontar casos utilizando técnicas de combinatoria?
- ¿Se parecen mucho algunos problemas de probabilidad a otros?
- ¿Puede pensarse que resolver muchos problemas de probabilidad consiste en realidad en medir de forma aproximada áreas de un aspecto muy determinado?

- Cuando resuelvo un problema de probabilidad siempre tiendo a "dudar" de mi respuesta… y es que siempre he tenido mala "pata" con eso de la suerte.
La estructuración, orden, entendimiento y control en ese escurridizo e inestable mundo, parece llegar en el momento que las Matemáticas clásicas intervienen en el azar con toda su “potencia de fuego” y cuando también, por qué no, se adentran en él con todo su rigor. La introducción del concepto de variable aleatoria —que no es más que el de función— y su ubicación en este contexto con un carácter protagonista supone un primer paso básico y fundamental que conviene tener presente.
Variable aleatoria, funciones de probabilidad y de distribución
El concepto de variable aleatoria como función numérica y su aplicación en la Estadística y la Probabilidad supone un extraordinario avance en estas dos disciplinas. Muchos problemas y situaciones prácticas procedentes de experimentos aparentemente muy diferentes se pueden modelar en un mismo marco teórico mediante variables aleatorias con sus respectivas funciones de probabilidad y de distribución.
- En los casos en que la variable aleatoria sea discreta ―valores aislados―, existen modelos teóricos como la distribución Binomial, la distribución Hipergeométrica, la distribución Geométrica, la Binomial Negativa , la Multinomial,… que permiten la adaptación y estudio de muchos problemas relacionados con experimentos aleatorios procedentes de situaciones muy distintas.
- En los casos en los que la variable aleatoria sea continua ―que pueda tomar, al menos teóricamente, cualquier valor de un intervalo―, sin duda es el modelo de la distribución Normal el que se adapta a un mayor número de situaciones. Caracteres morfológicos como peso, estatura, diámetros, perímetros de la mayoría de especies tanto animales como plantas, errores cometidos en la medición de la mayoría de las magnitudes, caracteres fisiológicos, psicológicos o aquellos que se obtengan en general como suma de otros factores, se distribuyen siguiendo un modelo cuya función de densidad adopta una particular forma y que se conoce como modelo de la distribución Normal.
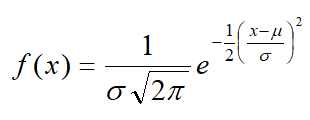
Función de densidad de la distribución normal de media µ y desviación típica σ
Cada modelo de distribución normal va a depender numéricamente de dos parámetros fundamentales que son la media aritmética μ y la desviación típica σ. Es decir, hay una infinidad de distribuciones normales. Por ejemplo:
- Se dice que el cociente intelectual de las personas sigue una distribución normal de media 100 y desviación típica 15. ¿Cuál sería la probabilidad de que una persona tenga un cociente entre…?
- La estatura de los varones de entre 35 y 55 años en España sigue una distribución normal de media 172,9 cm y desviación típica 3,55 cm. ¿Cuál sería la probabilidad de que un varón…?
- La distribución de las notas de selectividad en la asignatura de matemáticas sigue una distribución normal de media 5,85 y desviación típica 2,25. ¿Cuál sería la probabilidad de que un alumno…?
- La distribución de pesos de una ganadería sigue una distribución normal de media 540 kg y desviación típica 15 kg. ¿Cuál sería la probabilidad de que en un grupo de 20 reses al menos la mitad…?
Por otro lado, en Estadística Inferencial el modelo de distribución normal aparece en resultados tan importantes como el Teorema Central del Límite, en las distribuciones en el muestreo de algunos parámetros como las medias muestrales o las proporciones muestrales, así como en aproximaciones de otros modelos teóricos como la distribución binomial o la de Poisson.
Así pues, con la distribución Normal, estamos ante un tema estratégico clave sobre el que se fundamentan y desarrollan otros muchos y que, por tanto, conviene cuanto menos familiarizar a cualquier persona que se "asome" al mundo de la estadística y probabilidad y, por supuesto, que han de conocer y entender todos aquellos que intenten profundizar en él en un futuro.
La distribución normal N(0, 1)
Aunque hay una infinidad de distribuciones normales, tantas como valores toman los dos parámetros anteriores, µ y σ, obviamente todas se corresponden a un único tipo de función o familia de funciones con propiedades comunes en las que µ genera una traslación y σ un cambio de escala. Por ello, dentro de todas las posibles distribuciones normales se considera la que tiene por media cero y desviación típica uno, que usualmente se denota como N(0, 1), y que se establece como referente para hacer manejable este tipo de distribución. Todas las demás podrán relacionarse con la N(0, 1) y, por tanto, basta centrarse en el análisis de ésta y posteriormente trasladar su conocimiento al resto.
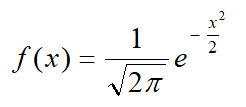
Función de densidad de la distribución normal de media 0 y desviación típica 1, la N(0, 1)
Por tanto, es la N(0, 1) es objeto de minucioso y pormenorizado estudio cuando se busca investigar las diferentes probabilidades que toma su función de distribución.

Probabilidad para valores menores o iguales que zα
La integral anterior no es elemental, es decir no existe una primitiva que pueda expresarse como un conjunto finito de operaciones de funciones elementales y consecuentemente no puede calcularse mediante la aplicación de la regla de Barrow. Por ello, usualmente lo que se aborda es la construcción de una tabla de valores aproximados ―la tabla de la normal cero uno― en la que se refleja el valor de p(z ≤ zα ) para un conjunto de valores de zα.
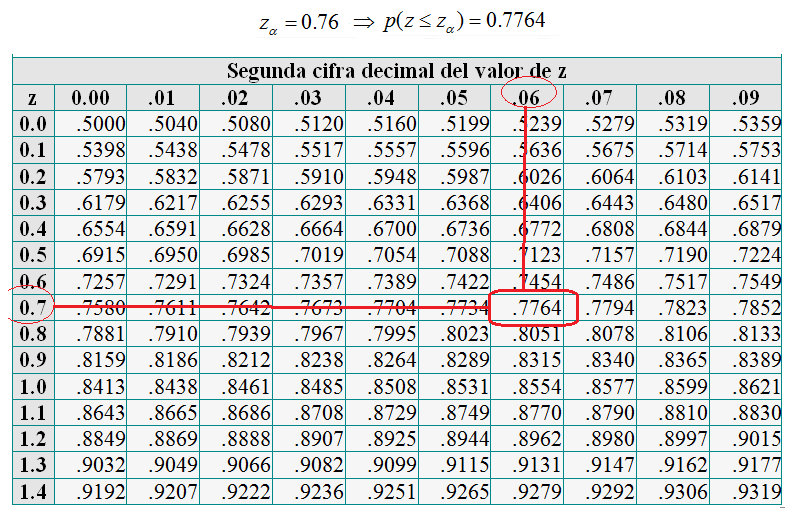 Fragmento de la Tabla de la N(0, 1)
Fragmento de la Tabla de la N(0, 1)
En la primera columna de la tabla se refleja el valor de desde 0 a 3,9 con incrementos de una décima (el extremo superior depende de la precisión empleada en el cálculo de valor de p(z ≤ zα )), y en la primera fila se consideran diez columnas etiquetadas desde 0,00 hasta 0,09, de manera que si zα = 0,76 entonces la p(z ≤ zα ) queda reflejada en la fila de etiquetada como 0,7 y en la columna 0,06 (0,76=0,7+0,06). Generalmente el valor de esta probabilidad se refleja con cuatro cifras decimales y cuando éstas no son suficientes hay tablas en la que se consideran cinco decimales. Indiquemos, de nuevo, que el cálculo de esa integral definida no es inmediato y, por ello, la precisión del valor reflejado en la tabla será dependiente del método de cálculo aproximado usado. Para valores de zα del orden de las milésimas o inferior puede considerarse una interpolación, por ejemplo si zα = 0,752 se realizaría una interpolación entre los valores correspondientes a zα = 0,75 y zα = 0,76, es decir, una interpolación posiblemente lineal (aunque no sería la más ajustada) entre los correspondientes valores que son 0,7734 y 0,7764.
Construida la tabla, también es posible plantearse el problema inverso, es decir, dada una probabilidad identificar el valor de zα correspondiente. Para ello se localiza el valor de dicha probabilidad en la tabla, y una vez encontrado entonces la fila y columna donde se ubica nos aporta dicho zα = fila+columna, pudiéndose abordar también una interpolación en caso de que la probabilidad dada no se localice exactamente en la tabla, sino que se encuentre entre dos elementos de la misma.
Para valores negativos de zα, para probabilidades asimilables a barridos a la derecha p(z > zα ) o franjas de probabilidad determinadas entre dos valores p(z-α ≤ z ≤ zα ), se recurre a ciertas estrategias sencillas basadas en razonamientos más o menos directos que utilizan como elementos fundamentales la simetría de la curva y el valor unitario del área global bajo la misma.
Tipificación
Lo obtenido para esa distribución normal particular, la N(0, 1), es muy significativo y extrapolable a cualquier otra distribución normal, pues mediante una fácil transformación en la variable aleatoria ―Tipificación― convertiremos cualquier pregunta directa o inversa sobre una normal cualquiera en una cuestión planteada sobre la N(0, 1) con su correspondiente respuesta rápida.
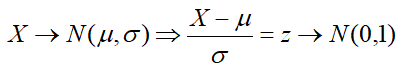 Tipificación de una variable aleatoria
Tipificación de una variable aleatoria
Consecuentemente la importancia de la N(0,1), de la tabla de valores asociada y de la tipificación es evidente. Las técnicas y estrategias que permiten la localización de cualquier valor de probabilidad de manera directa o las que se utilizan para la localización de valores críticos que dejan una determinada probabilidad a la izquierda, a la derecha o en una franja central ―manejo inverso―, deben ser comprendidas y utilizadas perfectamente por los alumnos de bachillerato o de primeros cursos de estudios universitarios. Pero, esto no es óbice para preguntarse: ¿la vigencia de la tabla de la N(0,1) es incuestionable?
Preguntémenos y respondamos:
- ¿Cántas veces realizamos el mismo tipo de razonamiento y estrategia en problemas de distribuciones normales?
- ¿Cuántas veces repetiremos el procedimiento hasta automatizarlo?
- ¿Cuántas veces llegaremos a cansarnos de tipificar y consultar la tabla, e interpolar valores?
La respuesta puede ser variable dependiendo de las circunstancias, del número de problemas y de preguntas que desee o necesite responder, pero estamos seguros de que si trabaja o estudia en este contexto la cuantificación será elevada. Por tanto, ¿no estima necesario y conveniente evitar este proceso? y simplemente ¿no desea proceder a realizar una consulta rápida y automática? Posiblemente esté pensando o diciendo ¡Sí! y aquí trataremos de dar satisfacción a su deseo con "La calculadora de la Normal". Quienes ya tengan cierta edad, recordarán lo imprescindibles que también eran las tablas de logaritmos o las tablas trigonométricas hace no mucho tiempo y quienes tengan menos edad podrán indagar por su cuenta y riesgo o en el enlace anterior.
La calculadora de la Normal
La calculadora de la Normal es una escena desarrollada con DescartesJS y lo que pretendemos es que cualquiera con conocimientos teóricos básicos, disponga de una herramienta fácil, directa y rápida que le permita abordar y resolver problemas relacionados con la distribución normal.
Somos conscientes que las calculadoras de gama alta con cierto nivel científico disponen de la posibilidad de cálculo de valores de probabilidad de cualquier distribución normal e incluso en algunos casos de cálculo de valores críticos, (z-valores). Sin embargo el interfaz o la secuencia de cálculo no suelen ser naturales y a menudo muy diferentes de unos modelos a otros. A nuestro entender no se produce esa estrecha comunión entre el modelo teórico que proporcionan el profesor o el libro y el escueto y solitario número con que responde la calculadora. Es por esto, entre otras cosas, por lo que decidimos emprender el desarrollo de una escena sencilla y útil, rápida y con aspectos muy elementales, tanto gráficos como algebraicos que mantengan al menos una mínima conexión ―necesaria en nuestra opinión― con el desarrollo teórico clásico. Y aquí la tienen a su disposición:
El manejo es intuitivo y sencillo, no obstante puede consultar las indicaciones.
Finalmente, sólo nos queda indicaros que esperamos que la utilización de esta escena, de esta calculadora de la Normal, os resulte interesante desde el punto de vista didáctico y útil desde el punto de vista técnico y, en particular, para nuestros colegas docentes que les ayude a implementar el aprendizaje significativo de este tema que consideramos estratégico en Estadística y Probabilidad.
Nota bene técnica
Para aquellos interesados en las consideraciones y criterios matemáticos adoptados en el desarrollo de esta herramienta ―y sólo para ellos por ser cuestiones que, posiblemente, no interesen al usuario habitual― indiquemos algunos detalles técnicos:
- El usuario establece la media y desviación típica y la calculadora realiza la tipificación a la N(0, 1) o viceversa. Aunque no sería necesario mostrar esta tipificación, se refleja por cuestión metodológica en entornos de aprendizaje donde conviene que ésta quede explicitada. Es una calculadora para cualquier media y desviación típica, por lo que representa una mejora respecto a lo habitual.
- Internamente se contruye una tabla para la N(0,1) en la que se ha considerado como intervalo significativo [-4, 4], es decir, p(z<=-4)=0 y p(z<=4)=1.
- En el intervalo [-4, 4] se considera un partición regular de paso una diezmilésima, es decir los valores zα aportados por el usuario o determinados por la calculadora tienen una precisión de cuatro cifras decimales. Esto representa una mejora respecto a la tabla usual que suele estar restringida a dos decimales. Puede ampliarse a más cifras, pero en esta versión se ha ajustado a esta precisión buscando que la necesidad computacional no ralentice el tiempo de respuesta y sea adecuado para la mayoría de dispositivos actuales.
- El cálculo de p(z ≤ zα ), para los valores de zα de esa partición comprendidos en [-4, 0], se realiza calculando la integral definida correspondiente mediante integración numérica aplicando la regla de Simpson compuesta que en este caso tiene una cota de error inferior a 1·10-19. En las escena se reflejan sólo 9 cifras decimales, pero podrían incluirse más (al menos hasta doce correspondientes a la precisión de cálculo interna de Descartes). Esto representa una mejora respecto a lo usual en las tablas que son cuatro o cinco cifras decimales.
- El cálculo de p(z ≤ zα ), para los valores de zα de esa partición comprendidos en (0, 4] se determinan por simetría con los del intervalo [-4, 0] como 1-p(z ≤ -zα ).
- En Inferencia Estadística, por ejemplo en intervalos de confianza o en contraste de hipótesis, es fundamental el manejo inverso de la tabla de la normal. En esta escena se ofrece la posibilidad de localización directa de valores que determinan ciertas probabilidades, tanto franjas de áreas entre dos valores (zα/2) como barridos a la izquierda o a la derecha (zα). La precisión es de cuatro cifras decimales, lo que representa una mejora respecto a lo usual.
Este mes vamos a ver un vídeo de Matemáticas Aplicadas de 4ªESO sobre Polinomios:
Hemos tratado los siguientes epígrafes:
1. Expresiones algebraicas
De enunciados a expresiones
Valor numérico
Expresión en coeficientes
2. División de Polinomios
División
División con coeficientes
Regla de Ruffini
Teorema del resto
3. Descomposición factorial
Factor xn
Polinomios de 2º grado
Regla de Ruffini reiterada
Identidades notables
Más...
Quince millones de páginas servidas en 2017
Escrito por José R. Galo SánchezSí, en el pasado año 2017 son más de quince millones de páginas las que hemos servido desde nuestro dominio proyectodescartes.org y casi mil setecientos Gigabytes los que, a través de ellas, han sido distribuidos hacia nuestros usuarios. Estos son sólo dos parámetros que dan una pincelada del alcance de la RED Descartes.
El final y comienzo de año suele asociarse a periodos de reflexión, valoración de objetivos y propuesta de nuevas acciones. Ubicándonos en este contexto, en este artículo, buscamos analizar y divulgar algunos parámetros que nos permitan determinar el alcance de nuestra organización no gubernamental RED Descartes. Obviamente una adecuada valoración ha de contemplar aspectos tanto cuantitativos como cualitativos, pero, aun siendo conscientes de esto, aquí únicamente vamos a tratar de realizar una observación parcial, meramente cuantitativa, y para ello vamos a fijarnos exclusivamente en la información que podemos obtener a partir de las estadísticas que se generan automáticamente en nuestro servidor proyectodescartes.org con la herramienta Webalizer. En la ayuda de esta herramienta se describen los caracteres estadísticos que se registran: accesos (hits) , archivos (files), páginas (pages), visitas (visits), clientes (sites) y kbytes. Reflejaremos y pondremos accesibles todos ellos dejando al lector interesado la posibilidad de abordar su propio estudio, pero aquí nosotros pondremos el foco sólo en tres de ellos.
La siguiente tabla refleja el resumen mensual y anual de este año 2017:
En la primera columna de esta tabla se cuenta con un enlace que da acceso a un desglose detallado por días y horas para cada uno de los meses.
En la columna de páginas podemos observar el dato relativo al número de páginas servidas, el cual es el que hemos destacado en el título de este artículo. Son más de quince millones de páginas las que han sido requeridas por nuestros usuarios y que han sido servidas desde nuestro servidor, una media mensual aproximada de un millón doscientas cincuenta mil páginas (1.250.000), más de cuarenta y una mil diarias, mil setecientas a la hora, casi veintinueve cada minuto, 1 página aproximadamente cada dos segundos.
El siguiente diagrama de barras muestra ese desglose mensual de páginas servidas.
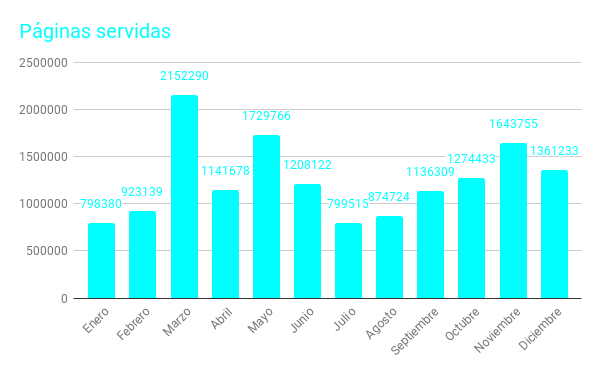
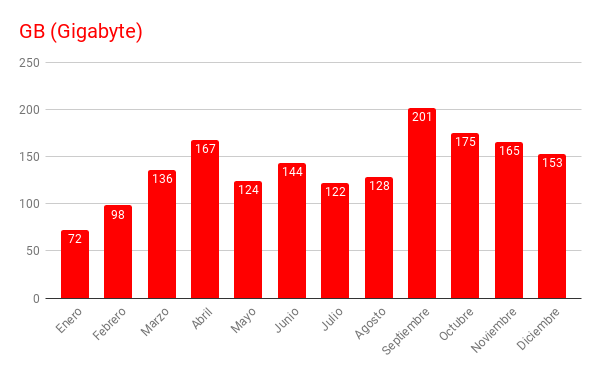
En la columna "kB F" se reflejan el número de kbytes transferidos desde el servidor hacia los usuarios a través de las páginas solicitadas. Aquí no se contabilizan, no se incluyen, los bytes correspondientes a las descargas que se realizan de nuestras publicaciones anuales en DVD (Vol. I y Vol. II) ya que los archivos de estos DVD están alojados en otros servidores. Son unos mil setecientos Gigabytes los transferidos en este año, lo que equivale a haber replicado el contenido de nuestro servidor en la red unas cincuenta veces a lo largo de este año, casi una vez cada semana.
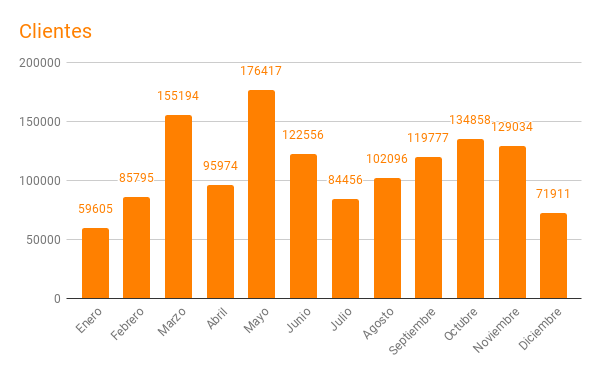
La columna de "clientes" o "sites" refleja la cantidad de direcciones IP diferentes que realizan solicitudes al servidor y es como un indicador aproximado de la cantidad de visitantes recibidos en nuestro servidor. La media mensual alcanzada es de unos ciento diez mil y diariamente serían unos tres mil seiscientos.
La procedencia de estos visitantes también queda reflejada en el control estadístico del servidor y estos proceden principalmente de toda iberoamérica encabezados, generalmente, por España, Colombia, México, Argentina y Ecuador, pero no siempre en ese orden siendo claramente dependiente del periodo lectivo en cada país.
Nuestro agradecimiento a todos los que, accediendo a nuestro dominio proyectodescartes.org, han ido contribuyendo página a página a incrementar estos y cada uno de los caracteres estadísticos que perfilan el nivel de utilidad de nuestro servicio y, así, estiman y valoran nuestra dedicación altruista en pro de la comunidad educativa de la aldea global.
¡Feliz 2018! y ¡A aprender con Descartes!
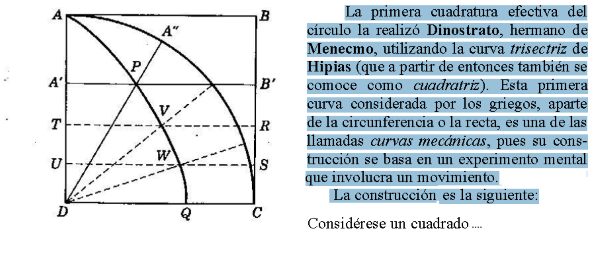
Misceláneas. Lugares geométricos. Cuadraturas V. La cuadratura del círculo I.
Escrito por Ildefonso Fernández Trujillo
Misceláneas. Lugares geométricos. Cuadraturas V. La cuadratura del círculo.
Como prólogo a un breve estudio sobre la cuadratura del círculo, hemos analizado la manera de cuadrar algunos polígonos y hecho una breve reflexión sobre los teselados. En particular se ha visto, entre otros asuntos, el método general de cuadrar los polígonos regulares y referente a las teselaciones se ha mostrado, entre otras, la manera de teselar un triángulo cordobés con una sucesión de triángulos cordobeses.
Dentro del tema que nos ocupa: los Lugares geométricos también, en su día, estudiamos las Trisectrices de Hipias y Nicomedes y en otros artículos se han expuesto misceláneas y escenas que desarrollan la espiral de Arquímedes y la cuadratriz de Dinostrato; no obstante en la presente entrada volvemos a insistir en el estudio de las primeras curvas mecánicas o lugares geométricos creados por estos autores por su evidente interés y para animar a la conversión en misceláneas de las escenas que aún no lo son.
Anteriormente hemos enlazado el extraordinario trabajo del profesor Fernando Bombal sobre la cuadratura del círculo, volvemos a hacerlo y en el leemos:
Recomendamos la lectura completa del documento así como el análisis de su extensa bibliografía.
También en entradas anteriores hemos enlazado con el blog de Miguel Ángel Morales Medina, en esta ocasión lo hacemos al básico pero minucioso artículo sobre la cuadratura del círculo: ¿Quién dijo que la cuadratura del círculo era imposible?.
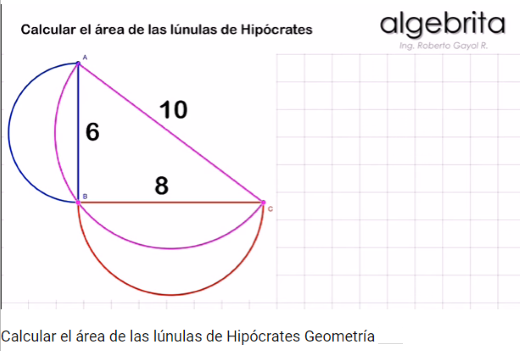
A continuación y también como prolegómeno al estudio de la cuadratura del círculo enlazamos con dos pequeños trabajos sobre la cuadratura de las lúnulas: el primero de ellos creado con DescartesJS y el segundo con el programa GeoGebra.
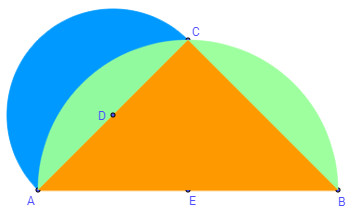
- Cuadratura de una lúnula I: Con la ayuda de dos semicírculos creamos una lúnula y aplicando el teorema de Hipócrates de Chios encontramos, según se muestra en la siguiente escena interactiva, un triángulo de igual área que dicha lúnula. Cuadrando el triángulo obtenemos la cuadratura de la lúnula.
Escena desarrollada con DescartesJS.
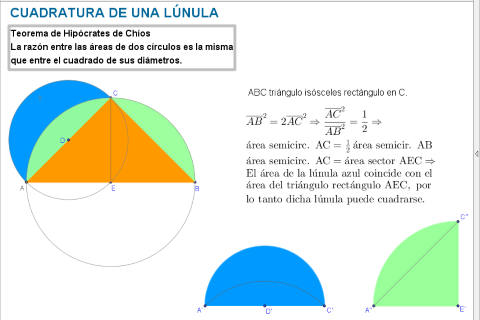
- Cuadratura de una lúnula II: actuando de forma análoga a como hemos hecho en la escena anterior obtenemos la cuadratura de una lúnula con el programa GeoGebra
Las escenas que se exponen a continuación son recreaciones de otras ya expuestas en este blog y tienen como objetivo refrescar la memoria sobre las curvas mecánicas mencionadas anteriormente.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
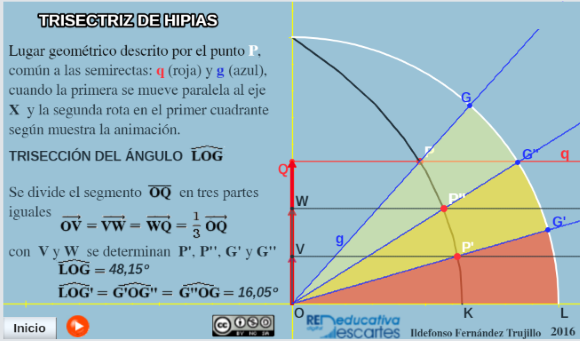
La trisectriz de Hípias
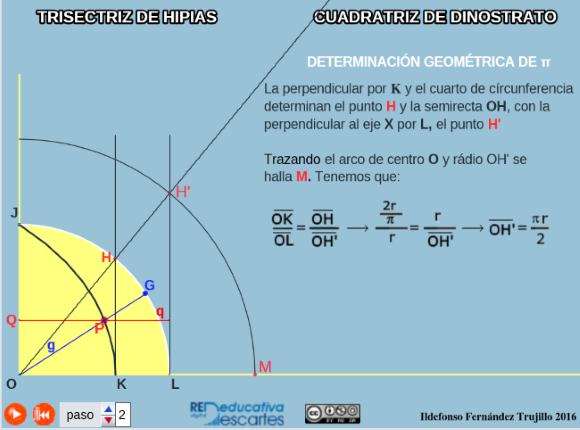
La trisectriz - cuadratriz de Hípias - Dinostrato
En la siguiente escena se determina un segmento relacionado directamente con el número π utilizando la trisectriz - cuadratriz de Hípias - Dinostrato
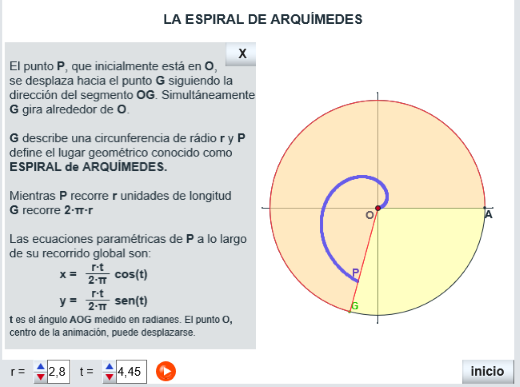
Las siguientes utilidades muestran: la primera, además de las ecuaciones paramétricas de la espiral, la manera como se genera el lugar geométrico conocido como espiral de Arquímedes y la otra la determinación de un segmento de longitud raiz cuadrada de π, en esta ocasión mediante la mencionada espiral de Arquímedes y la ecuación cartesiana de dicho lugar geométrico.
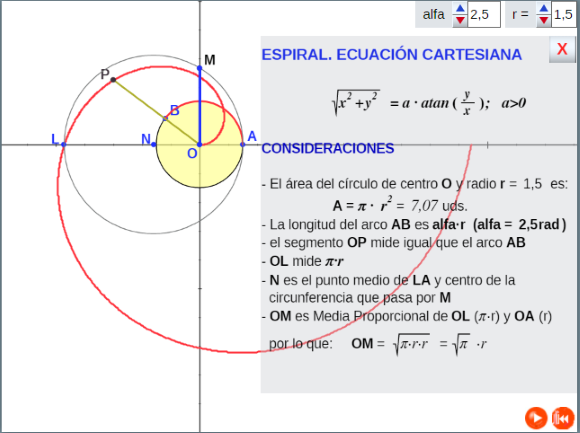
deducción de raiz de π con la espiral de Arquímedes
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la deducción, paso a paso, del área de las lúnulas de Hipócrates.
,Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con las cuadraturas estudiadas para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
