Nuevo impulso del Grupo IC a la Educación del s. XXI
Escrito por José Antonio Salgueiro GonzálezUn año más, el Grupo Empresarial IC S.L., prestigiosa Institución Comercial especializada en la ejecución integral de grandes proyectos de interior que abarcan la construcción, las instalaciones, el mobiliario y el mantenimiento, ofrece su apoyo al mundo de la Educación y la difusión del conocimiento, como base de cualquier actividad humana, patrocinando sesenta y nueve unidades didácticas interactivas generadas con Descartes JS, que son funcionales en cualquier tipo de dispositivo (ordenador, tableta o smartphone). Concretamente, llevan el sello del Grupo IC, los libros interactivos del Proyecto ED@D correspondientes al currículo de Matemáticas orientadas a las Enseñanzas Académicas y Matemáticas orientadas a las Enseñanzas Aplicadas en el curso de 3º ESO, respectivamente en castellano, catalán y gallego.
Grupo IC trabaja en exclusiva para grandes marcas de los sectores retail, hoteles, lujo, sanitario, oficinas y restauración, siendo cuatro las empresas que conforman el grupo:
- IC Construction.- Es la constructora del grupo especializada en construcción integral de interiores.
- Efficentre.- Es la instaladora del grupo especializada en soluciones de eficiencia energética.
- Ekipashop.- Empresa del grupo dedicada a la fabricación y montaje de mobiliario a medida realizado con maderas ecológicas certificadas PEFC o FSC®.
- Servishop.- Dedicada a la gestión integral del mantenimiento con un call center técnico 24h/365d.
Aunque Grupo IC construye grandes proyectos de interior para importantes y conocidas empresas en cualquier lugar del mundo, es posible que sea Primark Gran Vía Madrid el más conocido, pues con sus 12.300 metros cuadrados de superficie de ventas es la mayor tienda que esta firma posee en España.
Feliz Navidad con Descartes
Escrito por Juan Guillermo Rivera BerríoDesde RED Descartes Colombia y desde la Institución Universitaria Pascual Bravo os deseamos una Feliz Navidad para todos los cartesianos y pascualinos.
Actualización completa del Proyecto "Aplicación de Juegos didácticos en el aula"
Escrito por Jesús Manuel Muñoz CalleDurante 2017 se ha trabajado intensamente en la renovación y actualización del Proyecto "Aplicación de juegos didácticos en el aula", proyecto que promueve la inclusión de juegos didácticos basados en escenas de Descartes en la práctica docente. Las principales cambios e innovaciones introducidas son las siguientes:
- Renovación y reoorganización por completo del diseño de la web, blog y DVD del proyecto.
- Diseño y puesta en funcionamiento de un canal de YouTube para el proyecto.
- Mejora en el diseño, programación y funcionamiento de todos los juegos didácticos.
- Inclusión de nuevos juegos hasta llegar a la cifra de 414.
- Diseño y puesta en funcionamiento de un nuevo generador de ficheros de preguntas para juegos.
- Rediseño de la sección de video-tutoriales y de sus contenidos.
- Renovación y actualización del curso "Aplicación de juegos didácticos en el aula".
- Renovado y actualización del curso "Creación de animaciones y juegos interactivos para el aula". Adaptación del curso al nuevo editor de escenas basado en javascript.
- Realización de una nueva guía rápida de utilización de juegos didácticos.
- Actualización de las presentaciones y documentos del proyecto.
Recordamos que los contenidos del proyecto se encuentran en su: web, blog, DVD y canal de YouTube. En el siguiente vídeo se presentan las secciones de este renovado proyecto.
Aviso en el supermercado es una unidad didáctica interactiva que pertenece al apartado de Comprensión lectora del grupo PISA 2017. Las unidades de este grupo forman parte del Proyecto Competencias de la RED y han sido elaboradas a partir de unidades liberadas PISA.
Para facilitar su consulta, están agrupadas cinco grandes bloques: ciencias, comprensión lectora, finanzas, matemáticas y resolución de problemas.
Más...
Este mes vamos a ver el resumen de fracciones de 1ºESO:
Hemos tratado los siguientes puntos en nuestro vídeo:
1.Concepto de fracción.
Las fracciones en nuestra vida.
Elementos de una fracción.
Cómo se lee una fracción.
El valor de una fracción.
Pasar una fracción a un decimal.
2.Fracciones equivalentes.
Fracciones equivalentes.
Productos cruzados.
Simplificar una fracción.
3.Operaciones con fracciones.
Paso a común denominador.
Suma de fracciones.
Suma y resta de fracciones.
Multiplicación de fracciones.
Fracción inversa de una fracción.
División de fracciones.
Operaciones combinadas
4.Aplicaciones
Problemas con fracciones
Misceláneas: Lugares geométricos. Cuadraturas IV
Escrito por Ildefonso Fernández TrujilloCUADRATURAS IV.
La cantidad de patrones de teselado, por lo tanto la cantidad de teselados, es infinita e inagotable. También lo es la cantidad de no teselados. Los alarifes que hicieron posible la habitación de retiro de la reina y sus alrededores, en la alhambra de Granada, hicieron realmente, poesía geométrica viva, dinámica, sensorial, placentera, evocativa…
Hacemos hincapié en el estudio de los patrones más elementales del grupo de los básicos con objeto de analizar como una sutil variación en la forma o el color produce efectos anímicos y visuales muy diferentes y así facilitar el proceso de análisis y creación de las teselaciones más complejas.
Además de nuevos enlaces volvemos a mostrar, por su interés, algunos de los ya expuestos en entradas anteriores:
Para quien considere necesaria una inmersión en los conceptos básicos relacionados con las teselaciones hemos preparado los siguientes contenidos:
La imagen anterior enlaza con una unidad que, en su día, desarrolló el profesor Ángel Aguirre Pérez y que he comenzado a adaptar a DescartesJS debido a que sus objetivos son similares a los que nos proponemos en este artículo y por tanto nos introduce en el tema de la forma clásica y básica.
Consideramos, por tanto, que el estudio se centra en el problema clásico de la cuadratura del círculo y que nos acercamos a él haciendo, primero, la cuadratura de algunos polígonos regulares y no regulares. No debe olvidarse la idea de círculo como límite, cuando el número de lados tiende a infinito, de los polígonos regulares.
Dentro del amplio grupo de trabajos relacionados con el tema destacamos, además de los que se muestran en la bibliografía, los que se enlazan a continuación.
- teselado del plano y del espacio
Wikipedia - "Teselas de Escher y otras consideraciones sobre las teselaciones y movimientos en el plano.
Autora: María José Sánchez Quevedo. - Matemáticas mágicas, ingeniosas y... muy serias.
Autora: Therese Eveilleau. - Amplio estudio del plano.
Blog. Vaios Autores - Estudio de los frisos, cenefas y celosías.
Autora: Ángela Núñez Castaín
Tomando como base, fundamentalmente, la documentación anterior hemos elaborado, con DescartesJS, las escenas que se exponen a continuación. Queremos notar que en dichos trabajos se hace uso de gran parte de los conceptos elementales de Geometría del Currículo para ESO y Bachillerato.
Todos los trabajos dejan, para quien tenga interés en el tema, una buena cantidad de opciones de ampliación y mejora.
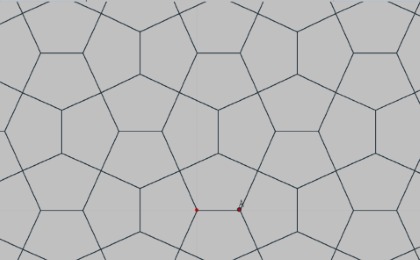
A poco que se observen los trabjos de teselción expuestos o enlazados se evidencia que en cada uno de ellos se reproduce un patrón. Existe un amplio grupo de patrones y entre los más elementales están los conocidos como 'tipo mitad del cuadrado' que son los que se obtienen descomponiendo el cuadrado en dos o más partes diferenciadas, en nuestro caso, por el color, de manera que ambas formas tengan igual área. A continuación se exponen varios ejemplos de estos patrones que aclaran el concepto.
- Estudio de los patrones y sus teselaciones correspondientes tipo "mitad del cuadrado".
Mitad del cuadrado I. - Mitad del cuadrado II.
- Mitad del cuadrado III.
Este patrón ya ha sido expuesto en entradas anteriores, en la actual enlazamos con un ejemplo de las teselaciones a que da lugar. - Mitad del cuadrado IV.
- Mitad del cuadrado V.
A continuación exponemos los trabajos que desarrollan la cuadratura del pentágono regular, tanto con DescartesJS como con GeoGebra.
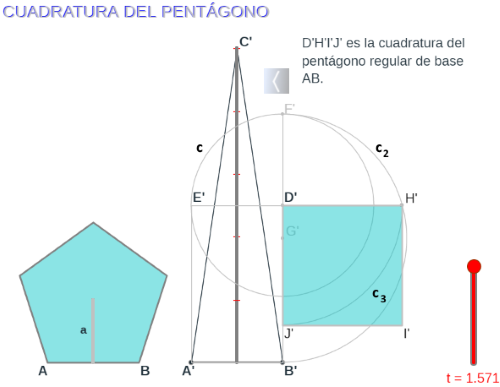
- Cuadratura de un pentágono regular de lado AB. La miscelánea Pentágono regular: Cuadratura. Método clásico detalla más explícitamente la misma escena.
Recordamos que:
- La circunferencia c tiene de centro el punto D' y radio A'B'.
- El arco c2 tiene de centro el punto G' (punto medio de B'F') y radio G'B'.
- El arco c3 tiene de centro el punto D' y radio D'H'.
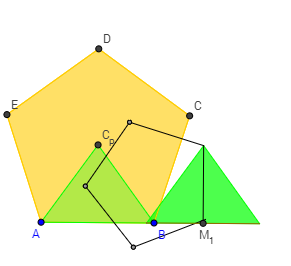
- La misma cuadratura realizada con el programa GeoGebra
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la creación, paso a paso, de una tesela reutilizando un "cede (CD)".

Interesante manualidad sobre teselación.
Continuando con la creación de la miscelánea "Las Espirales" sugerimos completar su elaboración extrayendo el contenido relacionado con las cuadraturas estudiadss para añadir dichos contenidos a una nueva miscelánea que podemos nombrar como "Lugares Geométricos. Cuadraturas"; o bien continuar con la anterior incorporando los nuevos contenidos en el apartado adecuado.
Una forma lúdica de teselar es resolver un rompecabezas, esto es un ejercicio para ejercitar la memoria visual y otras habilidades por lo que proponemos, temporalmente, un amplio grupo de puzles para su resolución, uso y disfrute.

Juegos para entrenar la memoria visual.
En próximas entradas continuaremos el estudio de los lugares geométricos, su aplicación en las cuadraturas y analizando el subproyecto Misceláneas.
Animamos a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:
- CÓNICAS. De Francisco Orti, profesor del IES Las Fuentezuelas: amplio estudio de las secciones cónicas.
- "Secciones cónicas " de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación reducida de una elipse" de la profesora: Elena E. Álvarez Sáiz.
- "Ecuación matricial de una cónica " de la profesora: Elena E. Álvarez Sáiz.
- Las cónicas como lugares geométricos. Extraordinaria, completa y muy instructiva página elaborada por los profesores de la Universidad de Valladolid e Instituto de Investigación en Matemáticas: M. Teresa Pérez García y Oscar Arratia García
- Web de Robert FERRÉOL con mucha y muy interesante información sobre diversos lugares geométricos.
- Caracol de Pascal
- Departamento de Matemáticas. Instituto Rey Pastor. Madrid. Amplio estudio sobre curvas planas
- Geometría Diferencial de Curvas en el Plano de J. Lafuente (ucm)
- La cuadratura del círculo: Historia de una obsesión.
XIV Programa de Promoción de la Cultura Científica y Tecnológica.
Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol. 105, Nº 2 (2012), 241-258
Fernando Bombal - Cuadraturas
Prof. Esteban Rubén Hurtado Cruz. Facultad de Ciencias UNAM. Cálculo Diferencial e Integral II - Páginas en GeoGebra de Vicente Martín Torres López
- La abundante información encontrada en la Wikipedia
Ildefonso Fernández Trujillo. 2017
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)



















 CONTACTO
CONTACTO
