Los números enteros con iCartesiLibri
Escrito por Montserrat Gelis BoschEn el vídeo de esta semana presentamos dos libros dinámicos interactivos con actividades para el aprendizaje y la práctica de las operaciones con números enteros.
Estas unidades forman parte del proyecto iCartesiLibri, un proyecto de la Red que se basa en el desarrollo de materiales para el aprendizaje en diversas áreas de conocimiento, promoviendo la autonomía del estudiante y su formación en competencias.
En el primer libro digital, Cuaderno para practicar con los números enteros, primera parte, se introducen los números enteros y las operaciones de la suma y la resta. En el segundo libro digital, Cuaderno para practicar con los números enteros, segunda parte, se definen el producto y sus propiedades, la división y las potencias.
En estos materiales encontramos muchas actividades autocorrectivas que se generan aleatoriamente, permitiendo la realización de los ejercicios tantas veces como se precise. Para ampliar y consolidar los conceptos trabajados, se proponen diversos cuadrados mágicos de cálculo con enteros.
Para su aplicación en el aula, se muestran los pasos a seguir para insertar estas unidades en un aula virtual moodle.
GEOdiver: nueva sección del subproyecto GEOgráfica
Escrito por José R. Galo SánchezBuscando experimentar con nuevos formatos de recursos interactivos e integrar las escenas interactivas de Descartes en soportes que puedan resultar atractivos para nuestro alumnado, hemos abierto una nueva sección dentro del subproyecto GEOgrafica a la que hemos denominado GEOdiver.
Como indica su nombre, tiene como objetivo el aprendizaje de la Geografía de manera divertida y, para ello, se plantean diversas actividades lúdicas mediante las cuales el alumnado aprende jugando, es decir, lo que actualmente se encuadra en el término "gamificación" (transcripción fónetica al castellano del término inglés gamification) o también con un término de raíz más próxima a nuestra lengua: "ludificación".
Actualmente en GEOdiver hemos incluido siete minilibros cuya temática se centra en los cinco continentes habitados (África, América, Asia, Europa y Oceanía) y en dos países (Colombia y España). Estos recursos han sido elaborados por cartesianos colombianos y españoles siguiendo un esquema y patrón común.

El soporte simula un libro clásico en el que se puede pasar de una hoja a otra bien con las flechas laterales o bien seleccionando el borde de la hoja y desplazándola como es habitual en un libro de papel.

También se dispone de un índice, ubicado en la esquina superior derecha, desde el que puede desplazarse de manera rápida a una página concreta sin necesidad de pasar por las intermedias.
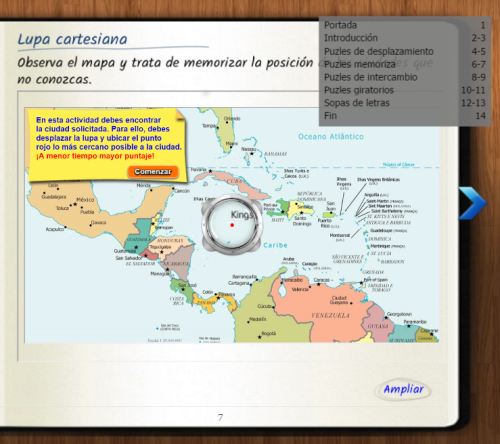
En las diferentes páginas nos encontramos actividades basadas en el clásico juego del ahorcado, puzles de desplazamiento, de emparejamiento, de intercambio y giratorios, sopas de letras y búsqueda con lupa.
¡Puedes empezar a jugar!
En el "Encuentro del Profesorado de Sevilla"
Escrito por José Antonio Salgueiro González"Matemáticas con arte" fue el lema del VI Encuentro Provincial del Profesorado de Matemáticas, que se celebró durante los días 11, 12 y 13 de noviembre de 2015 en la Universidad Pablo de Olavide de la capital hispalense. Este encuentro, que tiene carácter bienal, está organizado por los Centros del Profesorado de la provincia de Sevilla y la Sociedad Andaluza de Educación Matemática "Thales", y pretende ser un lugar de reflexión compartida sobre qué matemáticas enseñamos y cómo, de intercambio de experiencias, de miradas y acercamientos diferentes a la enseñanza de las matemáticas.
EDAD 3ºESO Figuras planas. Relaciones métricas
Escrito por Alfonso Saura EspínEste mes vamos a ver la unidad de 3ºESO correspondiente a "Figuras planas. Propiedades métricas":
En este video hemos tratado los siguientes apartados:
1.Ángulos en la circunferencia
Ángulo central y ángulo inscrito
2.Semejanza
Figuras semejantes
Semejanza de triángulos. Criterios
3.Triángulos rectángulos
El teorema de Pitágoras
Aplicaciones del T. de Pitágoras
4.Lugares geométricos
Definición y ejemplos
Más lugares geométricos: Cónicas
5.Aplicaciones
Áreas de figuras planas
Publicación en DVD de los "Recursos educativos interactivos de RED Descartes"
Escrito por José R. Galo Sánchez
Nuestra asociación "Red Educativa Digital Descartes" (RED Descartes) acaba de editar y publicar el volumen primero de la nueva publicación periódica titulada
Recursos educativos interactivos de RED Descartes
Este volumen consta de tres números: Vol. I-Núm 1, Vol. I-Núm. 2 y Vol. I- Núm. 3.
La referencia oficial y administrativa es:
ISSN: 2444-9180 Dep. Legal: CO-2079-2015
y pueden descargarse desde los siguientes enlaces.
| Vol. I, enero de 2016 | |||||||||||||
 |
 |
 |
|||||||||||
| Vol. I - Núm. 1 (3,7 GB) | Vol. I - Núm. 2 (4,7 GB) | Vol. I - Núm. 3 (4,3 GB) | |||||||||||
| Incluye los materiales de los subproyectos @prende.mx, Pizarra interactiva, Proyecto Canals, Unidades didácticas, Comperetencias, ASIPISA, Misceláneas, iCartesiLibri, Ingeniería y Tecnología, Un_100, Problemas, Estudio Europeo de Comunicación Lingüística y GEOgráfica. | Incluye los materiales del Proyecto ED@D Matemáticas (1º, 2º y 3º de Secundaria) y Aplicaciones de juegos didácticos en el aula. | Incluye los materiales del Proyecto ED@D Matemáticas (4º de Secundaria) y Proyecto ED@D Ciencias Naturales y Física y Química de Secundaria. | |||||||||||
| Carátulas | Carátulas | Carátulas | |||||||||||
|
|
|
Todas y todos los socios de RED Descartes están de enhorabuena por esta nueva iniciativa que ayudará a la difusión de todo el trabajo altruista que realizan en pro de la Educación en la aldea global, gracias a las TIC.
Escenas con DescartesJS: Técnicas y trucos (B02)
Escrito por Ángel Cabezudo Bueno Muchas gracias por la atención que ha recibido nuestro primer artículo de nivel básico de “Escenas con DescartesJS: Técnicas y trucos”. Esperamos seguir manteniendo vuestro interés por la ayuda que os podamos prestar desde aquí.
Muchas gracias por la atención que ha recibido nuestro primer artículo de nivel básico de “Escenas con DescartesJS: Técnicas y trucos”. Esperamos seguir manteniendo vuestro interés por la ayuda que os podamos prestar desde aquí.
Cuando Eduardo Barbero Corral me proporcionó una lista de títulos de entre su colección de recursos de cosecha propia, enseguida me fijé en este que hoy os presentamos para dar continuidad a la serie: no me cabe duda que os va a gustar. La redacción de este artículo mantiene el mismo método de trabajo con el anterior; he utilizado las ideas de Eduardo, la descripción que él me hace de este recurso según su técnica de programación y las anotaciones en cada etapa para el proceso de elaboración de la escena: Botones, Espacio, Controles, Auxiliares, Cálculos y Gráficos.
La mejor forma de entender su proceso y darlo a conocer a través de este artículo es seguir sus pautas de una forma práctica: me pongo manos a la obra, genero la escena, voy anotando mis propias observaciones en aquellas partes que requieren alguna explicación más amplia, saco imágenes sobre los materiales, la escena y los paneles de configuración del Editor de Escenas para que sirvan de ayuda al lector interesado… Después de un intercambio de opiniones con su autor para la mejora didáctica procedo a la redacción del artículo.
Este trabajo trata los controles numéricos tipo campo de texto para escribir sobre ellos palabras (contenido alfanumérico).
Veremos cómo podemos programar escenas en las que el alumno debe contestar escribiendo una palabra en un control numérico tipo campo de texto.
Los controles numéricos se emplean en muchas escenas; en un principio en ellos solamente se podían escribir números, pero actualmente, la herramienta Descartes también permite que se utilice un control numérico para que el alumno escriba en él una expresión alfanumérica y que se pueda interpretar como texto. Esto nos posibilita crear escenas tipo test.
¡No confundir un control numérico tipo campo de texto con un control texto al manipular el panel Controles o si se consulta la Documentación técnica!
Cuando tratemos más adelante el panel de Controles para programar la escena si el lector lo considera necesario puede consultar el artículo sobre Controles numéricos en la Documentación técnica.
Idea del proyecto
|
Escena_B02: En esta escena el alumno debe de escribir los nombres de las partes de una montaña con letras minúsculas. Se ha buscado la imagen de una montaña donde se pueden observar estas partes, se trata del archivo monte.jpg
Figura 1 El tamaño de la escena por defecto tiene que modificarse para que coincida con el de la imagen, 530x296 píxeles, que debe de verse como fondo de la escena. En la escena el alumno dispone de sendos campos de texto junto a las partes de la montaña y debe de escribir en ellos la respuesta. Se considera respuesta correcta para la parte más alta "cima", "cumbre" o "pico", para la parte intermedia "falda" o "ladera" y solo se aceptará "pie" para la parte más baja. El programa debe de responder según estos dos casos posibles:
|
La siguiente Figura 2 lleva un enlace a la escena ya elaborada a partir de la idea expuesta. Interaccionad con ella para comprender la funcionalidad y después explicaremos los recursos de DescartesJS que se emplean utilizando el Editor de Escenas.
Figura 2

Figura 3
Primeros pasos, herramientas y recomendaciones
Ya dijimos en el artículo anterior cuales son los primeros pasos que hay que dar antes de empezar a programar la escena, las herramientas que se necesitan y algunas recomendaciones para quienes se inician con DescartesJS.
Remitimos a estos preliminares, explicados con detalle y ahora solo hacemos un recordatorio esquemático:
- El Gestor de escenas de Descartes, denominado Descartes.jar, debe de haberse descargado y disponer de un acceso directo (recomendable) en el escritorio de Windows. Además, es conveniente un editor de texto como Notepad++ que dispone de un modo particular para presentar las líneas de código y facilitar la lectura y edición de los archivos HTML.
- Crear la carpeta de contenidos. En este trabajo la hemos denominado escena_B02
- Incluir la subcarpeta lib que contiene el archivo intérprete descartes-min.js.
- El archivo index.html incluye el código de la escena encerrado entre etiquetas <ajs> </ajs> y la referencia al interprete, <script type='text/javascript' src='lib/descartes-min.js'></script>, delante de la etiqueta de cierre </head>.
- Los pasos 2 a 4 se pueden realizar desde el mismo Gestor de Escenas.
El procedimiento preliminar consiste:
- Abrir el Gestor de Escenas
- Seleccionar en el menú Opciones > Librería portable > Sólo para JS (verificando esta elección en la línea de estado, línea inferior en la ventana del Gestor)
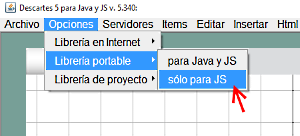 Figura 4
Figura 4 - Seleccionar en el menú Archivo > Guardar como, especificando la carpeta destino (creándola en ese momento si no existe) y el nombre que damos al archivo portador de la escena index.html
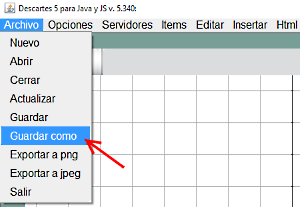
Figura 5
De esta manera disponemos ya del archivo index.html que contiene el código necesario para poder ver una escena básica que por defecto ha creado el Gestor. La Figura 6 muestra el código del archivo así creado visto desde el editor Notepad++
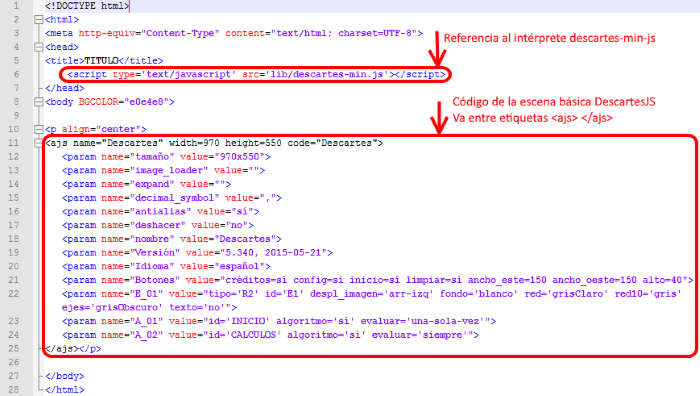 Figura 6
Figura 6
Para continuar, no olvidar incluir en la carpeta de contenidos escena_B02 el archivo monte.jpg.
Iremos describiendo paso a paso la trasformación de esta escena básica, utilizando el Editor de Escenas del Gestor Descartes.jar hasta culminar el proyecto.
Es importante que las explicaciones que aquí damos se acompañen, si fueran insuficientes, con la consulta puntual del concepto que se esté aportando en la "documentación técnica", sin pretender conocerlo todo desde un principio y solo para entender la aplicación en esta escena en concreto.
Apertura del Editor de Escenas y cambio de las dimensiones de la escena
La escena por defecto tiene un botón básico en cada esquina: créditos (arriba-izq), config (arriba-dcha), inicio (abajo-izq), limpiar (abajo, dcha).
Con la escena básica en la ventana del Gestor, accedemos a configurarla con el Editor de Escenas, de dos formas alternativas:
- Pulsando el botón E (editar) al lado derecho, fuera de la ventana.
- Pulsando el botón config (configurar) en la esquina superior derecha de la escena.
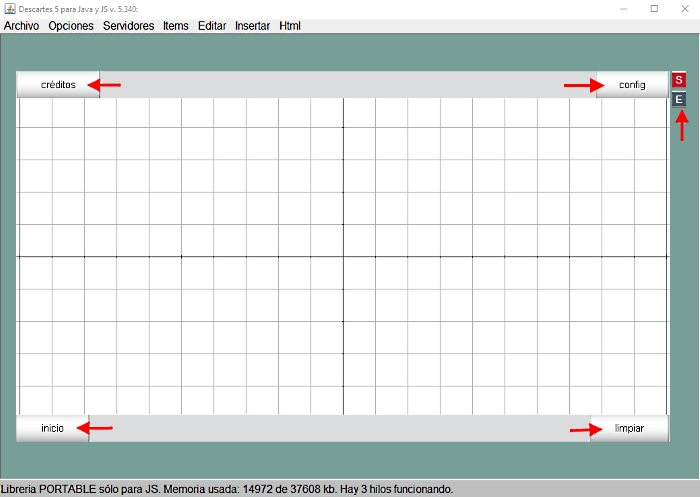
Figura 7
Estos botones pueden desactivarse posteriormente (todos o solo alguno), si creemos que no son necesarios que se muestren en la escena, pero podemos en cualquier momento acceder a ellos haciendo clic derecho sobre cualquier parte de la escena como se muestra en la Figura 8
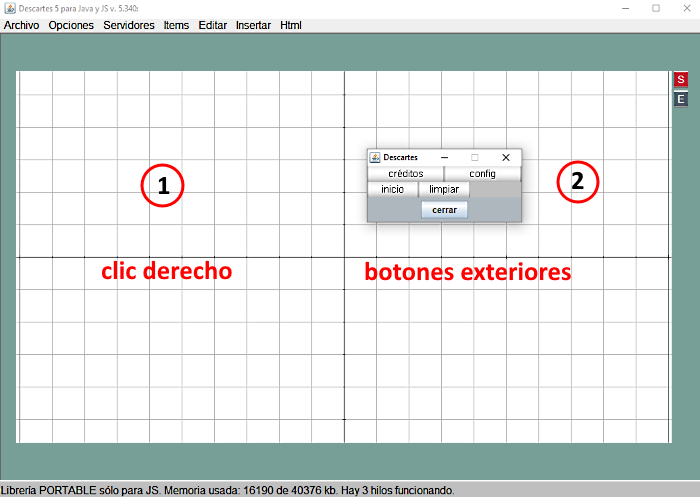
Figura 8
La figura siguiente muestra el panel Botones del Editor con todos ellos desactivados. Así es como vamos a configurarlo en este proyecto.
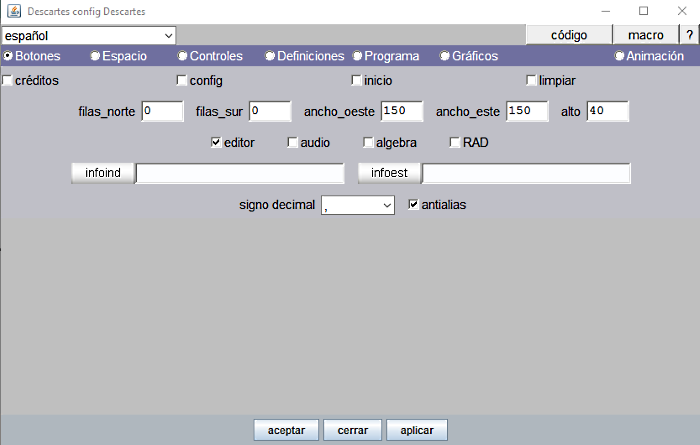
Figura 9
Para cambiar el tamaño de la escena, que por defecto es 970x550 píxeles, recordemos que hay que hacerlo desde el código de la escena. Al pulsar el botón código (arriba a la derecha) accedemos al código fuente de la escena y escribimos el ancho (530px) y el alto (296px) especificado para este proyecto
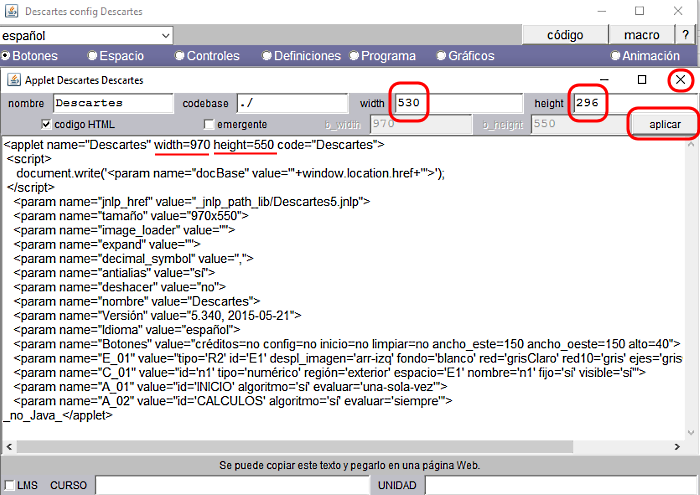
Figura 10
Para proceder con este cambio habrá que aplicar y cerrar (X) la ventana de código para regresar al panel de configuración del Editor de Escenas.
Cambios en el panel Espacio
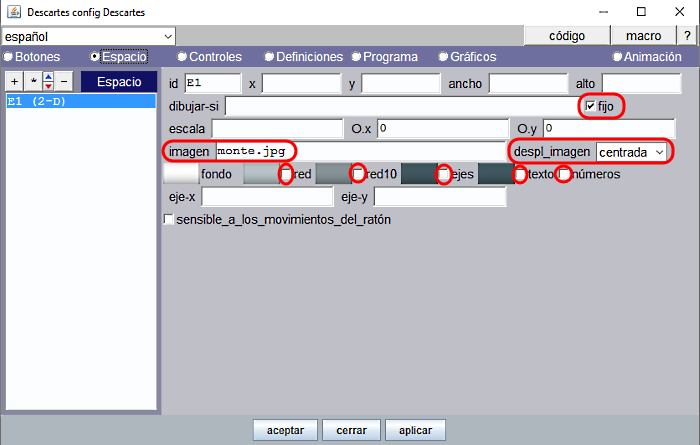
Figura 11
- En el campo “imagen”, escribimos el nombre del archivo, monte.jpg, incluyendo su trayectoria respecto del archivo index.html, que lleva el código de la escena.
- Elegimos la opción centrada en el campo “despl_imagen” (desplazamiento de la imagen).
- La red, los ejes y los números están desactivados.
- La escala cuando no lleva valor es por defecto 48 píxeles.
Cambios en el panel Controles
Iremos añadiendo (+) sucesivamente los controles numéricos identificados internamente (id) como n1, n2 y n3, seleccionando el tipo “campo de texto” y que utilizamos respectivamente para dar respuesta a cada una de las tres partes de la montaña: cima, cumbre o pico, ladera o falda y pie. Estos controles hay que definirlos como “interiores” y así podremos situarlos donde mejor convenga dentro de la escena. El control tiene forma rectangular.
Las posiciones respectivas sobre la escena serán las siguientes:
- Para la respuesta n1, la posición junto a la cima es (244,10, 70,30)
- Para la respuesta n2, la posición junto a la ladera es (386,100,70,30)
- Para la respuesta n3, la posición junto al pie es (310,210,70,30)
Los cuatro números, leídos ordenadamente y encerrados entre paréntesis, (x, y, w, h), significan:
- x: Distancia horizontal en píxeles del vértice superior izquierdo del control al lado izquierdo de la escena
- y: Distancia vertical en píxeles del vértice superior izquierdo del control al lado superior de la escena.
- w: ancho del control
- h: alto del control
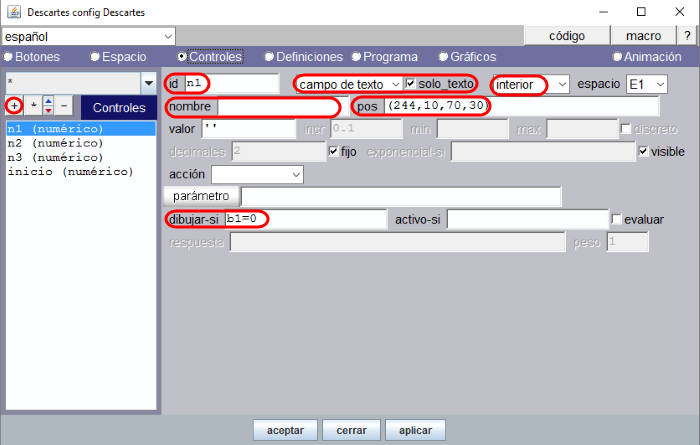
Figura 12
En la Figura 12 se muestra los parámetros del control n1. No mostramos las figuras correspondientes a n2 y n3 dado que son similares a n1 diferenciándose en el campo “pos” y en el auxiliar para la condición “dibujar-si” (b2=0 en el control n2 y b3=0 en el control n3).
El campo “nombre” es el nombre externo que tiene el control, a modo de etiqueta, a la izquierda del control. Si no ponemos nombre la etiqueta en un control numérico de campo de texto, la etiqueta no va a aparecer y solo se muestra el área rectangular del control para recibir el texto como respuesta.
También es posible indicar que el “nombre” es vacío con las expresiones _._, _nada_ o _void_. Estas fórmulas son en cambio necesarias en los controles numéricos tipo pulsador (que trataremos en otros proyectos) pero no en los de tipo campo de texto.
Es importante marcar la opción “solo texto” para que se interprete la entrada como un dato no numérico y escribir el “valor” inicial como cadena vacía, abriendo y cerrando apóstrofos '' (acentos simples) o abriendo y cerrando barras verticales ||. Si no iniciamos el control con cadena vacía, aparecerá el valor 0 por defecto, antes de que podamos escribir un texto: cuando pedimos al alumno que escriba una palabra preferimos que el rectángulo esté totalmente en blanco.
Queremos que los controles desaparezcan cuando el alumno ha contestado bien, por eso en el control n1 se ha puesto la condición dibujar-si='b1=0'. Es decir, desaparecerá cuando el auxiliar b1 toma valor distinto de 0. De esa manera el alumno puede corregir hasta dar una respuesta correcta. Cuando la respuesta es correcta el control desaparece, pero en su lugar debemos hacer que aparezca la palabra que ha escrito el alumno. Para ello, más adelante en el panel de Gráficos añadimos un gráfico tipo texto con el contenido de n1 que se dibuja cuando la respuesta es correcta, ahora con la condición dibujar-si=’b1’
Hemos añadido un cuarto control para que la escena se reinicie y se pueda practicar con ella cuantas veces se quiera desde el principio. En este caso en vez de utilizar el botón básico, seleccionado desde el panel Botones, hemos incluido un control numérico tipo botón interior para configurar a nuestro gusto su posición y tamaño en la escena x=0, x=266, w=80, h=30. El tamaño de la fuente con que se escribe el nombre externo del control, que funciona como etiqueta, es de 20 puntos.
Obsérvese que se ha vinculado la “acción=inicio”, fundamental para nuestro propósito, cuando se pulsa el control tipo botón.
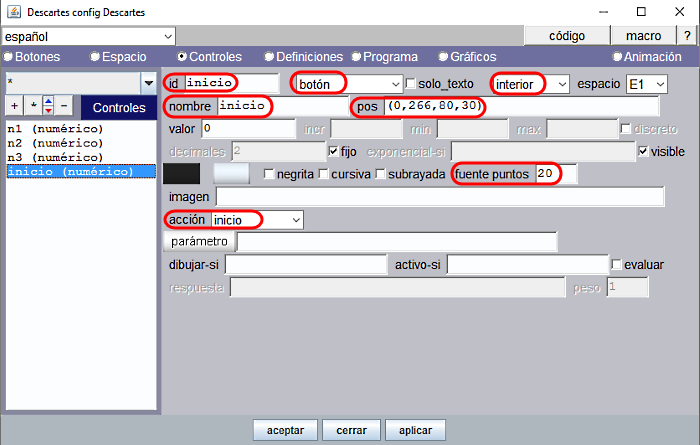
Figura 13
Cambios en el panel Programa
Debemos de definir los valores de las respuestas que vamos a considerar acertadas. Para ello disponemos del panel Programa.
La respuesta que se proporcione a través del control tiene que ser perfectamente coincidente con la palabra que hemos programado, pero a veces nos interesa permitir que también se considere válido si contesta con una palabra sinónima o si esa palabra tiene tilde y el alumno no lo ha puesto.
En la parte más alta de una montaña es válido poner “cima”, “cumbre” o “pico”. Para la parte intermedia, generalmente inclinada, es válido “falda” o “ladera”. Solo aceptaremos “pie” como respuesta correcta de la parte más baja.
Los cálculos deben de evaluarse siempre que se realicen cambios al escribir las respuestas. La figura 14 muestra estos cálculos que se explican en los siguientes dos puntos:
- Auxiliares de respuestas correctas. Una respuesta está bien cuando coincide con cualquiera de las respuestas válidas.
Utilizamos las variables b1, b2 y b3 para registrar cada una de las tres respuestas, para que sean correctas. El valor resultante de cada variable podrá ser 1 o 0. Así pues, b1 valdrá 1 si n1=’cima’ O n1=’cumbre’ O n1=’pico’ y b1 se expresa como una suma de las tres expresiones. Dicho esto, es fácil entender las definiciones que escritas en este panel para b1, b2 y b3. Observar que toda expresión de la forma (A) = (B) tiene un valor booleano {0,1}. - Auxiliares de respuestas incorrectas. Una respuesta está mal cuando la respuesta es diferente de todas las posibles respuestas válidas y también es diferente de no haber puesto nada.
Utilizaremos las variables m1, m2 y m3 para registrar la respuesta de cada parte de la montaña cuando es incorrecta o falsa. La variable m1 tomará el valor 1 si ninguna de las respuestas que se den para la parte más alta de la montaña es la convenida: n1#'cima', n1#'cumbre' y n1#'pico'. Es condición necesaria para que se registre una respuesta como incorrecta si además se contesta escribiendo algo, luego también ha de cumplirse que n1#''. Por tanto, m1 se expresa como producto de las cuatro expresiones anteriores. Procedemos análogamente para definir los cálculos de m2 y m3.
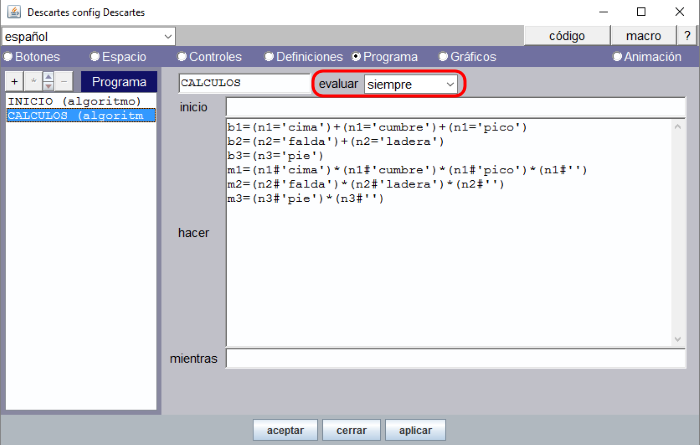
Figura 14
Observación:
Para indicar que dos expresiones (A) y (B) toman distinto valor lo expresaremos con el operador binario desigualdad que puede escribirse como # o bien !=. Ver operadores en la Documentación técnica. Por tanto (A) # (B) o (A) != (B) tienen un valor booleano {0, 1}.
Cambios en el panel Gráficos
En las figuras 2 y 3 donde se presenta la idea del proyecto, vemos que hay tres clases de gráficos de tipo texto:
- El texto para el título de la escena: “Partes de una montaña”
- Los tres textos [n1], [n2] y [n3] que contienen las respuestas correctas que reemplazarán a sus respectivos controles n1, n2 y n3
- Los textos con los que el programa responde: “¡Muy bien!” cuando las tres respuestas son correctas y “nombre incorrecto” cuando al menos una de las respuestas es incorrecta.
El texto para el título de la escena (Figura 15)
Escribimos el título de la escena “Partes de una montaña” en el lado izquierdo y más o menos centrado verticalmente, expresión= [10,110].
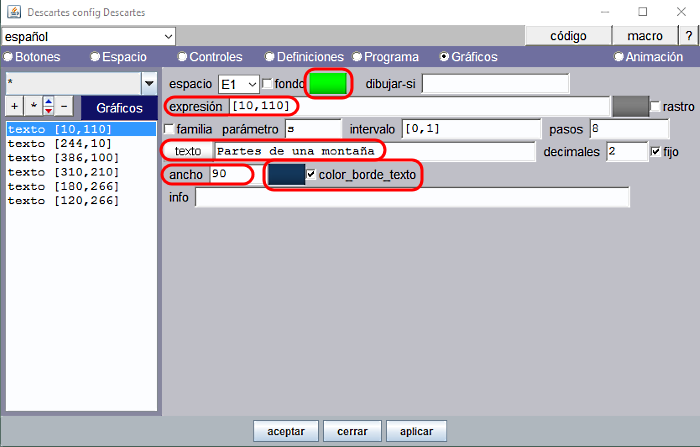
Figura 15
Observemos en la Figura 2 que el texto está dividido en tres líneas: como consecuencia de haber especificado ancho=90 puntos el texto se tiene que acomodar a este ancho y se ve obligado a saltar 2 veces de línea. Para que esto funcione así hay que escribir el texto con la opción texto simple. El formato elegido es SansSerif, Negrita y 20.
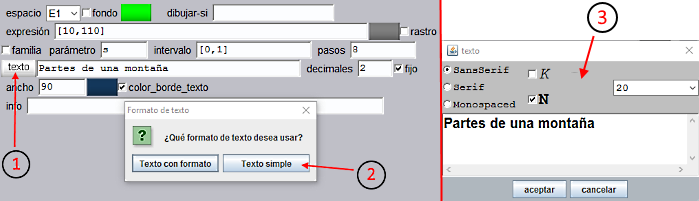
Figura 16
El color del texto es verde estándar (R=00, V=ff, A=00) y se adorna con un borde obscuro de color aditivo Rojo=14, Verde=38, Azul=5C. Este color se ha obtenido mediante una herramienta Cuentagotas seleccionando la zona de sombra producida en los huecos de la ladera de la montaña.
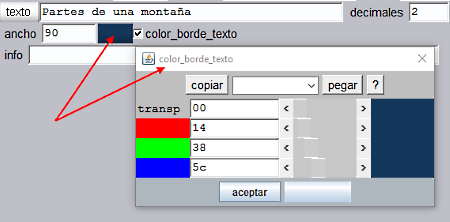
Figura 17
Queremos que los controles desaparezcan cuando el alumno ha contestado bien (Figura 18), por eso en el control n1 se ha puesto la condición dibujar-si='b1=0' Es decir, desaparecerá cuando el auxiliar b1 toma valor 1. De esa manera el alumno puede corregir sobre el control hasta dar una respuesta correcta.
Cuando la respuesta es correcta el control desaparece, pero en su lugar debemos hacer que aparezca la palabra que ha escrito el alumno en la misma posición, expresión= [244,10].
Observar que hay que escribir con la opción texto simple el contenido de la variable [n1] y no el nombre de la variable n1. El formato del texto es SanSerif, 20 y en color blanco (R=ff, V=ff, A=ff).
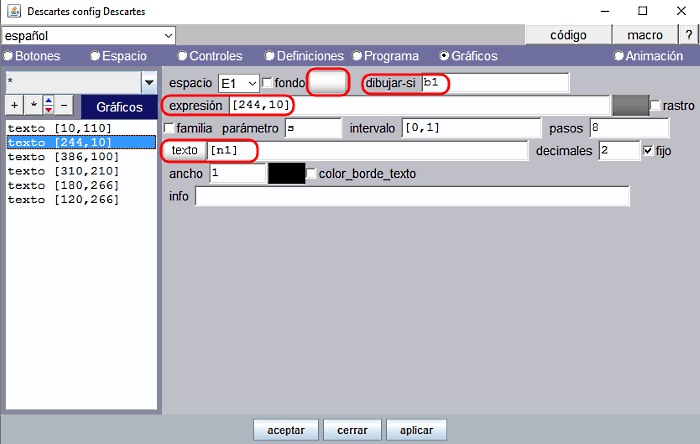
Figura 18
Análogamente escribiremos con el mismo formato y color que [n1] las respuestas correctas [n2] en la posición expresión= [386,100] con la condición dibujar-si ='b2' y [n3] en la posición expresión= [310,210] con la condición dibujar-si = 'b3'
Texto de respuesta del programa cuando se contesta bien (Figura 19)
El texto “¡Muy bien!” se dibuja cuando se cumple la condición b1*b2*b3=1 >0 por lo que basta escribir dibujar-si=b1*b2*b3 es decir cuando b1=1, b2=1 y b3=1.
Este texto se dibuja en la posición [180,266], con la opción Texto simple y el formato siguiente: SansSerif, Negrita, 28. Color amarillo estándar (R=ff, V=ff, A=00) y borde negro (R=00, V=00, A=00).
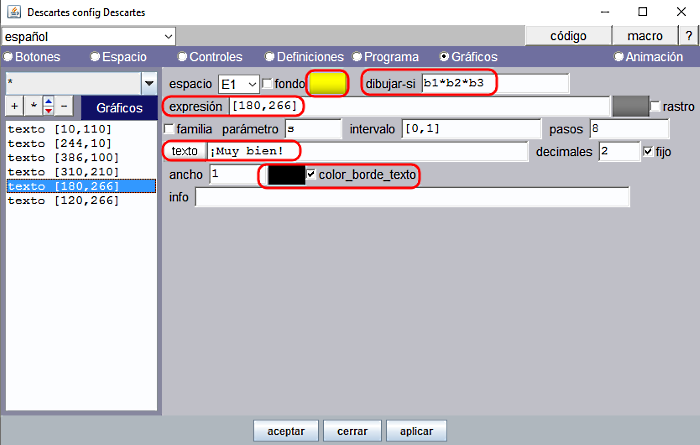
Figura 19
Texto de respuesta del programa cuando se contesta incorrectamente (Figura 20)
El texto “nombre incorrecto” se dibuja cuando se cumple la condición m1+m2+m3>0 por lo que basta escribir dibujar-si= m1+m2+m3 es decir cuando m1=1 o m2=1 o m3=1 (alguno de los nombres es incorrecto).
Este texto se dibuja en la posición [180,266], Texto simple con el formato siguiente: SansSerif, Negrita, 28. Color rosa estándar (R=ff, V=af, A=af) y borde negro (R=00, V=00, A=00).
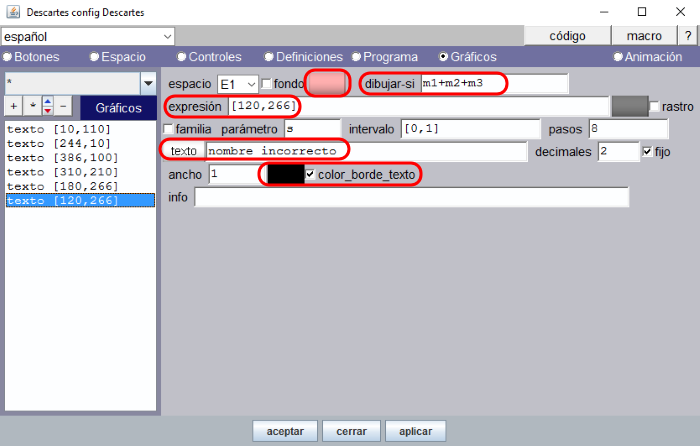 Figura 20
Figura 20
La condición dibujar-si y propuesta alternativa para dibujar texto con el gráfico tipo punto
La condición dibujar-si
Tanto para dibujar los controles como para dibujar los textos que aparecen en la escena de este proyecto hemos utilizado la condición expresada en el campo dibujar-si. Es oportuno explicar cómo funciona este campo dependiendo de los valores que puede tomar.
- Si el campo se deja vacío (valor por defecto) siempre se dibuja
- Si el campo tiene valor 0 o es negativo no se dibuja.
- Si el campo es mayor que 0 se dibuja.
- Si el campo lleva la condición A = B, se dibujará si A = B es una expresión verdadera y tiene valor lógico 1 (punto 3), en caso contrario es una expresión falsa, tiene un valor lógico 0 y no se dibuja (punto 2).
Escribir texto con el tipo gráfico punto vs tipo gráfico texto
En el primer artículo correspondiente al proyecto Escena_B01 utilizamos el gráfico tipo punto para dibujar texto.
En este artículo hemos utilizado el tipo gráfico texto, cuya expresión para el posicionamiento en la escena es (x, y), donde x=distancia en píxeles al borde izquierdo de la escena e y=distancia en píxeles al borde superior de la escena.
Recordemos que el punto como elemento gráfico tiene la posibilidad de asociar un texto que se escribe próximo. El recurso para escribir solo el texto consiste en dar un tamaño 0 al punto, con lo cual éste no se dibuja.
La posición del punto como elemento gráfico se expresa en coordenadas cartesianas (x, y), no en píxeles y la longitud de la unidad cartesiana es el valor que asignemos a la escala que por defecto es 48 píxeles.
La siguiente imagen es utilizada de fondo del espacio en la escala de nuestro actual proyecto Escena_B02. Se dibujan ahora los ejes, la red y los números para facilitar la localización del punto de tamaño 0 que deberíamos dibujar asociando los textos de contenido [n1], [n2] y [n3]
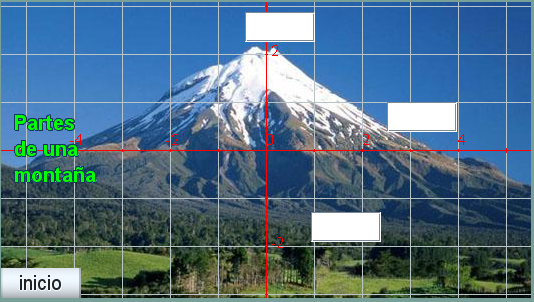
Figura 21
Proponemos al lector verificar que la posición de los tres puntos para dibujar los textos [n1], [n2] y [n3] asociados podrían ser respectivamente (-0.5, 2.5), (2.5, 0.5) y (1, -1.8) y si está interesado en ver los resultados que elabore una segunda escena donde las respuestas se dibujen como textos de gráficos tipo punto en vez de gráficos tipo texto.
Determinación del espacio:
- Ancho= 530 píxeles, alto=296 píxeles, Escala=48 píxeles.
- Unidades representadas en el eje OX=530/48=11.04, unidades representadas en el eje OY=296/48=6.17
Autoría:
Eduardo Barbero Corral (Idea del proyecto y técnicas de programación DescartesJS)
Ángel Cabezudo Bueno (Interpretación, edición de la escena, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
El proyecto @prende.mx es una iniciativa de la Secretaría de Educación Pública de México. Está formado por materiales interactivos para primaria, diseñados para su uso en tabletas usando la herramienta DescartesJS. En su desarrollo han participado el Instituto de Matemáticas de la Universidad Autónoma de México y el Laboratorio de Tecnologías de la Educación (LITE)
En el siguiente vídeo analizamos la unidad Unidades de masa, con actividades para introducir la masa y sus medidas en primaria.
Todas las unidades pertenecientes al proyecto @prende.mx constan de cuatro fases: observa, explora, aprende y prueba. En el apartado observa de la unidad Unidades de masa se pueden ver diferentes imágenes. Situando el ratón sobre cada una de ellas aparece un mensaje indicando la masa del objeto que representa y la unidad en que se mide.
En el apartado explora el alumnado debe completar una tabla de equivalencias entre unidades de masa. Para ello se dispone de una balanza que se debe equilibrar.
En los apartados aprende y prueba, se proponen varios ejercicios de conversiones entre diferentes unidades de masa. Una vez completado el ejercicio, el alumno puede verificar si la respuesta es correcta o no.
Se trata de actividades interactivas autocorrectivas que se pueden realizar tantas veces como se precise ya que se van generando aleatoriamente.
Libros interactivos con Descartes embebido en "Moleskine notebook"
Escrito por Juan Guillermo Rivera BerríoEn este artículo se describe cómo se pueden elaborar libros interactivos donde la interactividad la aporta Descartes y el soporte visual y de navegación viene dado por "Moleskine notebook".
A continuación tienes un ejemplo de libro interactivo diseñado con estas herramientas. Puedes navegar en él.
(Puedes descargar este libro desde este enlace y para verlo en otra pestaña pulsa aquí)
Este nuevo recurso de la Red Educativa Digital Descartes lo hemos definido con el término LIBRO, fundamentado en las siguientes razones:
- Diseño. Su presentación gráfica simula la cubierta y hojas de un libro.
- Animación. La transición entre las páginas es una animación que simula el desplazamiento de natural de una página a otra.
- Interactividad. Según la UNESCO, un libro debe tener 50 o más páginas. Esta afirmación la consideramos válida para libros estáticos; sin embargo, en los libros digitales interactivos, una página no es “una simple página”, en tanto que factores como la interactividad y la aleatoriedad, la convierten en un número indefinido de páginas. La siguiente imagen, que hace parte del libro ejemplo de este tutorial, valida la afirmación anterior.
Si aceptamos los argumentos anteriores, diseñar un libro digital interactivo será algo sencillo para cualquier desarrollador de escenas Descartes. Veamos, entonces, cuál es el procedimiento para ello.
RECURSOS A UTILIZAR
Este tutorial viene acompañado de un libro ejemplo, sobre el cual haremos todas las explicaciones. Los recursos necesarios para diseñar nuestro libro son los siguientes:
- Moleskine Notebook. Hemos realizado una adaptación de este recurso, ampliando el tamaño de las páginas, ajustando fuentes y tamaño de imágenes. El recurso original, se puede descargar desde este enlace: http://tympanus.net/codrops/2010/12/14/moleskine-notebook/.
- Escenas Descartes. Es importante, de acuerdo al tercer argumento planteado para validar nuestro concepto de “Libro”, que las escenas que incluyamos en nuestro libro tengan algo de aleatoriedad. En caso contrario, se podría optar por diseñar 50 páginas, o definirlo simplemente como un folleto.
- Editor de textos. Podría bastar con un editor simple (bloc de notas de Windows, por ejemplo); sin embargo, es recomendable utilizar un editor como Notepad (https://notepad-plus-plus.org/), que presenta las líneas de código en una forma más comprensible para su edición.
Los tres recursos son de acceso y uso libre, lo que facilita el diseño de nuestro libro.
CONTENIDO DEL LIBRO
El modelo que acompaña este tutorial, contiene los siguientes elementos:
- Seis archivos tipo html. Sólo son útiles los archivos index.html e indexb.html, los otros cuatro se han dejado para que el usuario, si lo desea, los consulte o modifique desde el editor de Descartes, pues son las escenas que se incorporarán en el libro. Se pueden eliminar.
- Carpeta audio. Hace parte de la última escena del libro. Para otros diseños no es necesaria, se puede eliminar.
- Carpeta "imagenes". Incluye las imágenes usadas en las escenas Descartes.
- Carpeta "images". Incluye las imágenes usadas por Moleskine.
- Carpeta css. Contiene el archivo style.css, que intervendremos en el diseño.
- Otras carpetas. Todas necesarias, no las intervendremos.
ESCRITORIO
Iniciamos el diseño de nuestro libro con la elección del escritorio. Para darle más realismo a la presentación, Moleskine usa una imagen de fondo que muestra una superficie (escritorio) sobre el que está apoyado el libro. Además de la imagen original, hemos incluido otras que puedes elegir o, si lo prefieres, incluir otra que desees (ver carpeta images).
 Para cambiar el escritorio, abrimos con el editor de textos el archivo style.css, que se encuentra en la carpeta css. Luego cambiamos el nombre de la imagen en la línea seis:
Para cambiar el escritorio, abrimos con el editor de textos el archivo style.css, que se encuentra en la carpeta css. Luego cambiamos el nombre de la imagen en la línea seis: 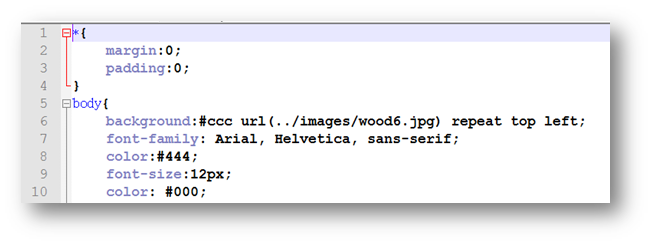 TIPO DE FUENTE
TIPO DE FUENTE
Hemos incluido nueve tipos de fuente, diferentes a la original de Moleskine, que aceptan los caracteres del español. 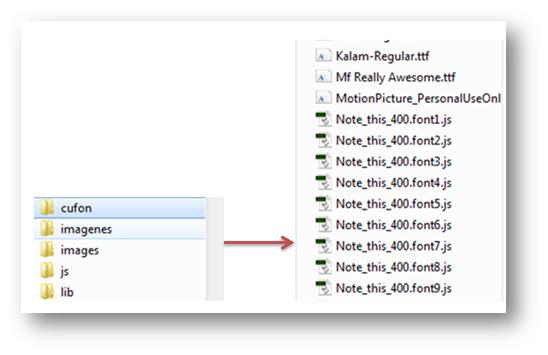 Puedes ensayar varios de ellos, modificando la línea 20 del archivo indexb.html:
Puedes ensayar varios de ellos, modificando la línea 20 del archivo indexb.html: 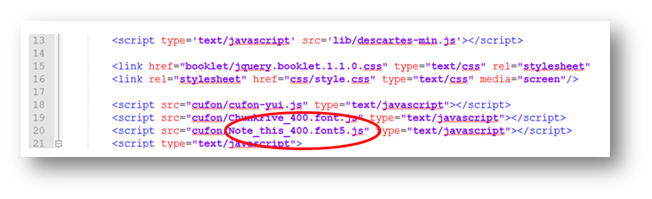 Nosotros, hemos usado la fuente Note_this_400.font5.js.
Nosotros, hemos usado la fuente Note_this_400.font5.js.
PRIMERA PÁGINA
 Por defecto, Moleskine deja en blanco la página de la contraportada. Nos ocuparemos, entonces, de diseñar la primera página. Antes de iniciar con la primera página, es importante que sepas que cada página está incluida en un bloque <div>. Nuestra primera página podemos crearla de dos formas. La primera, puede ser una imagen de un texto que diseñemos en un editor gráfico (PowerPoint, por ejemplo), un ejemplo de ello lo veremos en la segunda página. La segunda, es usar las etiquetas de HTML, así:
Por defecto, Moleskine deja en blanco la página de la contraportada. Nos ocuparemos, entonces, de diseñar la primera página. Antes de iniciar con la primera página, es importante que sepas que cada página está incluida en un bloque <div>. Nuestra primera página podemos crearla de dos formas. La primera, puede ser una imagen de un texto que diseñemos en un editor gráfico (PowerPoint, por ejemplo), un ejemplo de ello lo veremos en la segunda página. La segunda, es usar las etiquetas de HTML, así: 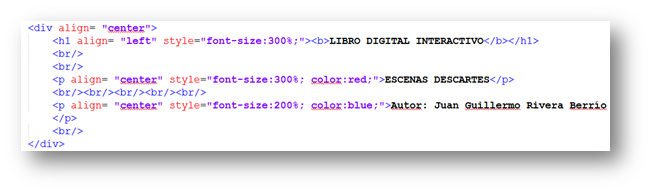 En el diseño hemos usado:
En el diseño hemos usado:
- Centrado de página: <div align= "center">.
- Etiqueta <h1>. Moleskine incluye, para esta etiqueta, un subrayado informal (ver imagen). Por ser la primera página, hemos aumentado tres veces el tamaño de la fuente usando style="font-size:300%;" y alineado el texto a la izquierda.
- Etiqueta <p>. Tiene el mismo efecto de <h1>, pero sin el subrayado. Aquí hemos usado diferentes tipos de color de fuente.
- Salto de línea <br/>.
Si no deseas usar el tipo de fuente, puedes combinar con las etiquetas <h2>, <h3>,… Si no deseas usar ninguna etiqueta, siempre te queda la opción de la imagen, como veremos a continuación.
PÁGINA CON IMAGEN
 Se trata de una imagen, que podemos incorporar así:
Se trata de una imagen, que podemos incorporar así:  Es importante tener en cuenta que su ancho y alto no puede ser superior a 450 pixeles.
Es importante tener en cuenta que su ancho y alto no puede ser superior a 450 pixeles.
PÁGINAS CON ESCENAS DESCARTES
Aquí terminamos nuestro tutorial, explicando cómo insertamos una escena Descartes. 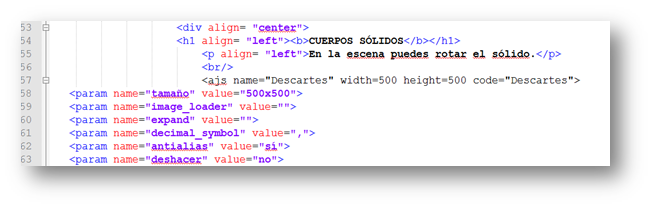 Nuestra escena debe tener un tamaño no superior a los 500x500 pixeles. Ocasionalmente, en escenas ya diseñadas, podríamos extendernos a 550x550, sacrificando un poco las márgenes de la página. Para incluir nuestras escenas al libro, seguimos este procedimiento:
Nuestra escena debe tener un tamaño no superior a los 500x500 pixeles. Ocasionalmente, en escenas ya diseñadas, podríamos extendernos a 550x550, sacrificando un poco las márgenes de la página. Para incluir nuestras escenas al libro, seguimos este procedimiento:
- Abrimos con el editor de textos el archivo de la escena Descartes.
- Copiamos el código comprendido entre las etiquetas <ajs> y </ajs>.
- En un bloque <div> pegamos este código y… listo.
Sugerencias de diseño:
- Centrar la escena. Para ello, usamos <div align=”center”>.
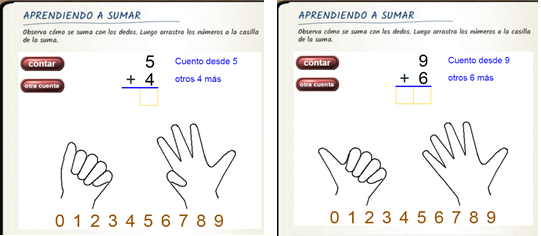
- Incluir título de la página. Podemos usar: <h1 align= "left"><b>APRENDIENDO A SUMAR</b></h1>.
- Incluir un texto introductorio. Algo así como: <p align= "left">Observa cómo se suma con los dedos. Luego arrastra los números a la casilla de la suma. </p>.
- Incluir los créditos. Además del reconocimiento al autor del libro, recomendamos incluir los créditos a la herramienta Descartes y a http://tympanus.net/codrops/2010/12/14/moleskine-notebook/, además de la licencia.
Pulsa sobre la siguiente imagen para acceder a otro libro interactivo diseñado con estas herramientas y que está publicado en el subproyecto iCartesiLibri
(Puedes descargar este libro desde este enlace)
En este artículo se muestra el proceso de comunicación entre una escena de Descartes y una página web que integra un mapa de Google Maps. Google Maps es un servidor de aplicaciones de mapas en la web que pertenece a Google. Ofrece imágenes de mapas desplazables, así como fotografías por satélite del mundo e incluso la ruta entre diferentes ubicaciones o imágenes a pie de calle con Google Street View. La interacción entre la escena de Descartes y la página web aprovecha el manejador de eventos propuesto en el artículo "Comunicación escena-html usando DescartesJS" y la API de Google Maps Javascript para controlar las acciones del usuario.
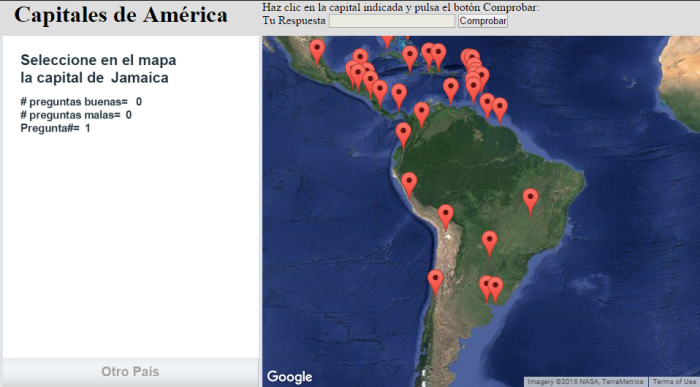
En el siguiente objeto interactivo, usado para afianzar el conocimiento de las capitales del continente americano, se propone localizar en un mapa de Google Maps la capital de un determinado país. Dicho objeto está formado por una página html que sostiene dos grandes contenedores: el primer bloque soporta una escena de Descartes embebida mediante un iframe (ubicado a la izquierda) y el segundo, un mapa de Google Maps (ubicado a la derecha).
Autor: Diego Luis Feria Gómez Red Educativa Digital Descartes Colombia
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
(Puedes descargar esta escena desde este enlace)
La comunicación entre la escena de Descartes y la página html tiene lugar en 3 momentos:
- Envío de la pregunta desde la escena de Descartes
- Gestión de la pregunta y envío de las respuesta desde el archivo html hasta la escena de Descartes.
- Administración de respuestas desde la escena de Descartes.
En la primera fase, internamente la escena de Descartes (incluida en el archivo comunicacion_Descartes.html) carga las capitales, configura las variables que controlan las respuestas del usuario y ordena los países de manera aleatoria, y después envía una pregunta a la página html en la que está embebida como iframe y que se denomina indexb.html. Este proceso es controlado por el código javascript incluido en comunica.js.
En la segunda etapa, la página indexb.html administra la interacción del usuario con el mapa y envía la respuesta a la escena de Descartes a través de el código javascript externo incluido en mapa.js. Este documento también es responsable de la construcción y configuración del mapa.
Finalmente, en la fase tercera, la escena de Descartes valida los resultados, controla los aciertos y desaciertos, y a continuación reinicia el ciclo con una nueva pregunta.
Este mes vamos a comentar una unidad de 1ºESO correspondiente a Múltiplos y divisores
en este video hemos tratado estos apartados:
1.Múltiplos y divisores
Múltiplos de un número
La división exacta
Divisores de un número
Criterios de divisibilidad
2.Números primos
Números primos y compuestos
Obtención de números primos
Descomposición factorial
3.m.c.m. y m.c.d.
El mínimo común múltiplo
Obtención del m.c.m.
El máximo común divisor
Obtención del m.c.d.
4.Aplicaciones
Problemas de divisibilidad
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)






 CONTACTO
CONTACTO
