Misceláneas. Proporcionalidad: Las Espirales V
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales V
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes y gracias al convenio trilateral entre la Facultad de Ciencia y Tecnología de la Universidad Autónoma de Entre Ríos (FCyT-UADER) en la provincia de Entre Ríos en Argentina, la Red Educativa Digital Descartes Colombia (colDescartes) y la Red Educativa Digital Descartes (RED Descartes), están: el libro Opúsculo sobre la función lineal y afín, la recta en el plano creado por las profesoras Irma Manuela Benitez - Alicia Elena Carbonell y María Alicia Gemignani, la siguiente imagen enlaza con dicho libro
y la integración de los mapas de Google en una escena DescartesJS realizada por Diego Feria Gómez, que abre un amplio abanico de posibilidades al proyecto GEOGráfica según muestra la escena que enlazamos a continuación.
También cabe destacar la aportación de la profesora Montserrat Gelis Bosch que ha adaptado al catalán el material sobre planos de simetría en 3D creado por el profesor José R. Galo Sánchez que puede consultarse en los siguientes vínculos,
y el Opúsculo sobre los complejos de María José García Cebrian que se enlaza a continuación y que, encarecidamente, aconsejamos visitar y utilizar en el tema de Complejos por su completitud y potencial didáctico.
De la espléndida colección de libros dinámicos, interactivos y multimedia del subproyecto iCartesiLibri que los profesores: Juan Jesús Cañas Escamilla, José R. Galo Sánchez, Juan Guillermo Rivera Berrío, Irma Manuela Benitez, Alicia Elena Carbonell y María Alicia Gemignani han creado sobre algunos temas de Estadística y Análisis enlazamos, por su indudable interés, el libro de estadística.
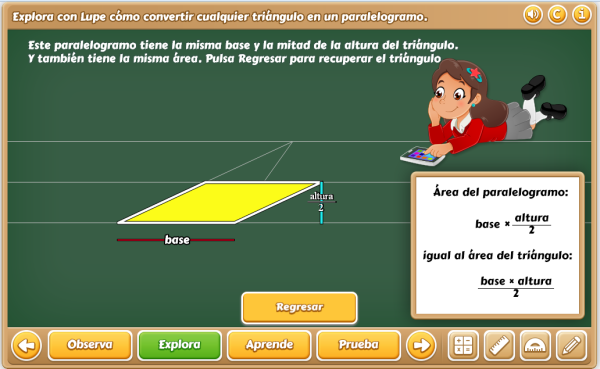
La extraordinaria acogida a los materiales del proyecto @prende, recientemente elaborado por: José Luis Abreu León (Instituto de Matemáticas), Joel Espinosa Longi (Instituto de Matemáticas), Deyanira Monroy Zariñán (LITE) y equipo para Primaria, comentada ampliamente en los foros hace que no sea necesario reiterar los elogios a tan meritotia creación, en la imagen siguiente enlazamos el recurso dedicado a las áreas.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información sobre las animaciones y la construcción, paso a paso, de algunas escenas ejemplo, elaborada por el profesor Juan Guillermo Rivera Berrío.
Antes de comenzar con el análisis de como hemos incluido en la miscelánea que estamos creando las escenas de la espiral de Teodoro y las espirales de tres a veinte centros, vamos a mostrar un vídeo de la presencia de la espiral en el organismo con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior terminamos de estudiar el proyecto de miscelánea, tal y como estaba hasta aquella fecha, indicando que íbamos a integrar en el mismo el contenido de la escena de la espiral de Teodoro.
También hemos añadido al proyecto el contenido de la siguiente escena sobre como dibujar las espirales de 3, 4, 5 ... 20 centros
La escena de la espiral de n centros, que vemos a continuación
está formada por:
- dos controles tipo pulsador
- un control gráfico de color rojo que es la referencia para la construcción de la gráfica.
- un texto.
- dos familias de puntos (los vértices y sus trasladados)
- dos familias de segmentos (los lados y sus prolongaciones).
- una familia de arcos.
Los pulsadores controlan, respectivamente, la cantidad de centros de la espiral y la longitud del lado del polígono regular sobre cuyos vértices se encuentran dichos centros. Inicialmente es visibles la espiral de tres centros.
Con objeto de que puedan verse todas las espirales, la escala del espacio donde se representan tiene un valor de 16 en lugar de 48 que es el valor por defecto. Aunque para ver bien las espirales de más de 9 centros es conveniente poner la longitud del lado a 1. Esto se ha hecho así para que se practique con el cambio de escala. Puede conseguirse el mismo efecto poniendo un control en la escena que modifique la escala; o reduciendo - aumentando el tamaño del lado del polígono base.
Para poder dibujar la colección de centros y los segmentos de los lados y sus prolongaciones, hemos definido:
- Cuatro vectores de tamaño dinámico para albergar las coordenadas de los vértices y sus trasladados que harán posible la gráfica de los segmentos de la escena.
- Un algoritmo que calcula las coordenadas de los vértices y sus trasladados.
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Teodoro y las espirales de n centros incluidas, se puede observar que el nombre del archivo ha cambiado respecto al original, es así para que se puedan comparar los códigos y ver los cambios realizados. Aconsejamos, a quienes comienzan a crear escenas fundamentalmente, y a cualquiera que visite el Blog, leer detenidamente el extraordinario artículo creado por el profesor Ángel Cabezudo Bueno sobre las Escenas con DescartesJS: Técnicas y trucos, donde se detalla con rigor el significado y uso de los componentes que pueden intervenir en una escena aportando una buena colección de atajos y utilidades que agilizan la creación y dotan a las escenas de funcionalidades extraordinarias.
La escena del proyecto puede verse a continuación:
Como aplicación de la proporción Humana hemos elaborado la siguiente escena.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como teselar un triángulo cordobés con triángulos cordobeses.
Acceso al recurso en GeoGebraTube
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral Cordobesa, la de Durero, la de Fibonacci y otras más entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
En el siguiente vídeo vamos a ver cómo crear un libro digital de moodle con unidades de la Red Educativa Digital Descartes, utilizando el código para embeber.
<iframe style="width: …px; height: …px;" src="/descartescms/dirección web de la escena"></iframe>
Se han seleccionado las unidades de estadística del Proyecto Pizarra Interactiva (PI).
- En la primera unidad, azar, se introduce la idea de suceso seguro, probable e imposible.
- En la unidad frecuencia, a partir de la simulación del lanzamiento de un dado se introduce el cálculo de la frecuencia absoluta y relativa así como la organización y clasificación de datos en tablas.
- En la tercera unidad, de forma visual y amena, nos acercamos al concepto de media y moda.
- Finalmente, para el estudio de las probabilidades, se proponen diferentes experimentos aleatorios observando los casos posibles y los casos favorables de un suceso y su relación para el cálculo de la probabilidad.
EDAD 3ºESO Ecuaciones de segundo grado
Escrito por Alfonso Saura EspínEsta semana vamos a ver el contenido de 3ºESO de ecuaciones de segundo grado
el índice seguido ha sido el siguiente:
1.Expresiones algebraicas
Identidad y ecuación
Solución de una ecuación
2.Ecuaciones de primer grado
Definición
Método de resolución
Resolución de problemas
3.Ecuaciones de segundo grado
Definición. Tipos
Resolución de ax²+bx=0
Resolución de ax²+c=0
Resolución de ax²+bx+c=0
Suma y producto de las raíces
Discriminante de una ecuación
Ecuación (x-a)·(x-b)=0
Resolución de problemas
Misceláneas. La Proporcionalidad
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales IV
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes y gracias al convenio de colaboración con la Facultad Regional Santa Fe de la Universidad Tecnológica Nacional de Argentina, está la miscelánea: Simulador de Sistemas diferenciales autónomos y no autónomos creada por la profesora Valeria Bertossi. La siguiente imagen enlaza con la miscelánea.
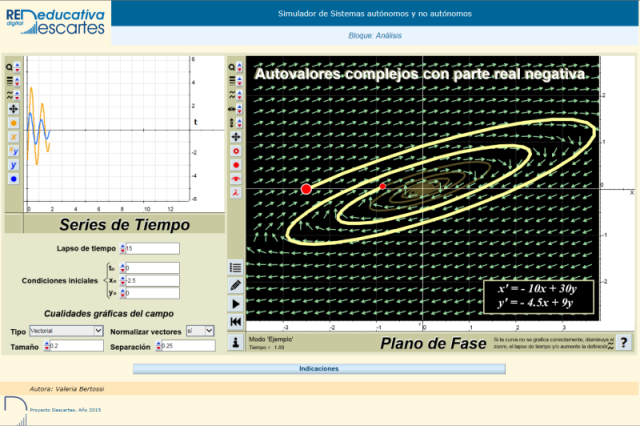
También cabe destacar la aportación del profesor José R. Galo Sánchez con su trabajo sobre Geometría tridimensional, también disponible en catalán gracias a la profesora Monserrat Gelis Bosch, que enlazamos a continuación.
En próximos artículos comentaremos y/o enlazaremos la espléndida colección de libros dinámicos, interactivos y multimedia del subproyecto iCartesiLibri que los profesores: Juan Jesús Cañas Escamilla, José R. Galo Sánchez, Juan Guillermo Rivera Berrío, Irma Manuela Benitez, Alicia Elena Carbonell y María Alicia Gemignani han creado sobre algunos temas de Estadística y Análisis. Por su indudable interés se aconseja visitar dicho subproyecto al igual que el recientemente elaborado por: José Luis Abreu León (Instituto de Matemáticas), Joel Espinosa Longi (Instituto de Matemáticas), Deyanira Monroy Zariñán (LITE) y equipo para Primaria, y que con el nombre @prende proporciona a los alumnos un material lúdico e interactivo que facilitará de forma notable la asimilación de conceptos matemáticos.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información sobre las familias 3D, elaborada por el profesor Juan Guillermo Rivera Berrío.
Antes de comenzar con el análisis de la escena de la espiral de Teodoro para incluirla en la miscelánea sobre las espirales en estudio, vamos a mostrar un vídeo que relaciona la música y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior terminamos de estudiar el proyecto de miscelánea tal como está en la actualidad, indicando que íbamos a integrar en el mismo el contenido de la escena de la espiral de Teodoro.
La escena de la espiral de Teodoro, que vemos a continuación
Está formada por:
- dos controles tipo pulsador
- un texto
- un punto rojo de referencia
- una familia de 139 puntos
- otra de 138 segmentos.
Los pulsadores controlan, respectivamente, la cantidad de puntos y segmentos que están presentes en la escena. Inicialmente son visibles 0 segmentos y 29 puntos.
Con objeto de que puedan verse varias vueltas de la espiral, la escala del espacio donde se representa tiene un valor de 15 en lugar de 48 que es el que viene por defecto.
Para poder dibujar la colección de puntos, y posteriormente los respectivos segmentos, hemos definido:
- Un vector de 140 de tamaño para albergar los arcos que los segmentos que unen los sucesivos puntos con el de referencia forman con la horizontal.
- Una función, x1, para controlar la abscisa de los puntos.
- Otra función, y1, para controlar la ordenada de los puntos.
Los gráficos siguientes muestran como se ha hecho lo anterior.
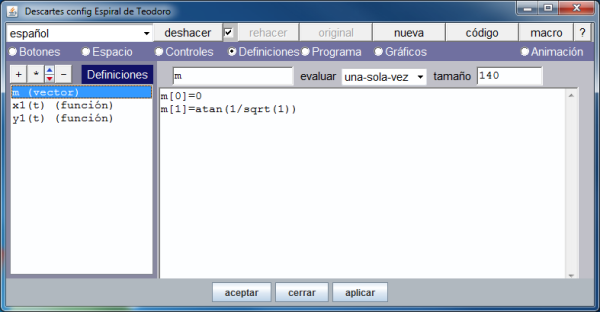
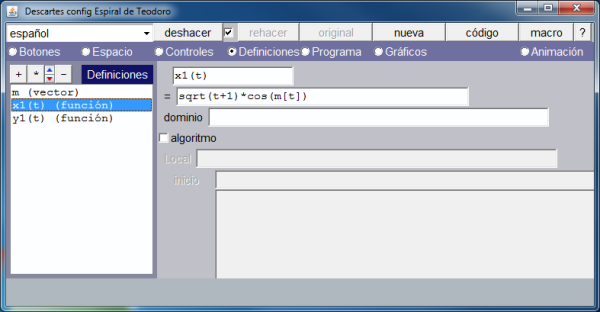
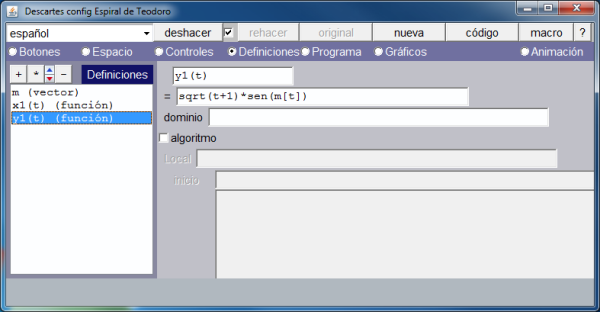
En la imagen que muestra la definición del vector se ve que únicamente se asignan valores a sus dos primeras componentes. Activando la opción de menú: Programa, vemos, en la siguiente imagen, como se han definido el resto de los arcos.
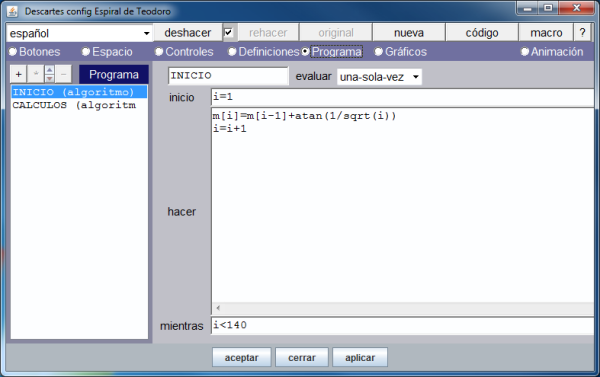
La siguiente imagen muestra los gráficos de la escena, en concreto despliega la forma en que se ha definido la colección de puntos.
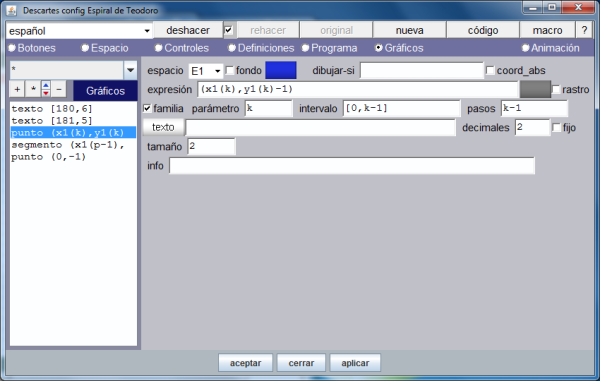
Observamos que los 139 puntos de la espiral se han definido mediante una familia que depende del parámetro k (identificador del pulsador de nombre: puntos presente en la pantalla).
La cantidad de puntos en pantalla depende del valor de este pulsador, el cual podemos manipular a nuestra conveniencia.
Analizada la escena de la espiral de Teodoro podemos pasar a incluirla en la miscelánea que estamos elaborando, acción que dejamos para el siguiente artículo. Aunque, insistimos, es conveniente que, para practicar con el editor de escenas, cada cual lo intente por su cuenta ya que disponiendo de las escenas se puede analizar cada uno de los cambios que se hagan y observar el efecto de cualquier modificación y así aprender a configurar escenas con el editor.
Como aplicación de la proporción Humana hemos elaborado la siguiente escena donde se hace una breve introducción al estudio del Triángulo Cordobés.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como teselar un cuadrado con triángulos cordobeses.
Acceso al recurso en GeoGebra
Conviene desplazar el deslizador tesela con las flechas del teclado.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral Cordobesa entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Escenas con DescartesJS: Técnicas y trucos.
Escrito por Ángel Cabezudo Bueno
Abrimos esta nueva sección del Blog que hemos titulado genéricamente "Escenas con DescartesJS: Técnicas y trucos" con una escena propuesta por nuestro compañero cartesiano Eduardo Barbero Corral y contamos con él para que nos siga mostrando sus técnicas y trucos en sucesivas ediciones de esta sección del blog. Una muestra de sus habilidades para el desarrollo de escenas de Descartes puede ser consultada en el siguiente enlace al artículo "Recomendaciones, indicaciones y elementos prefabricados" que está publicado en la "Documentación técnica y de usuario de Descartes 5" (en lo sucesivo "Documentación técnica").
Las "técnicas y trucos" que se irán explicando en sucesivos artículos tendrán dos niveles, uno básico y otro avanzado. Con el nivel básico pretendemos acercar la herramienta DescartesJS a quien le pueda interesar iniciarse en la programación de escenas. El nivel avanzado estará orientado a quien ya tiene cierto dominio de la herramienta y facilitará la interpretación de las instrucciones que se incluyen en los diferentes paneles del Editor de Escenas y que nadie ignora, a veces resultan difíciles de comprender sin la correspondiente documentación del programa.
otro avanzado. Con el nivel básico pretendemos acercar la herramienta DescartesJS a quien le pueda interesar iniciarse en la programación de escenas. El nivel avanzado estará orientado a quien ya tiene cierto dominio de la herramienta y facilitará la interpretación de las instrucciones que se incluyen en los diferentes paneles del Editor de Escenas y que nadie ignora, a veces resultan difíciles de comprender sin la correspondiente documentación del programa.
Pretendemos que esta sección esté abierta a cualquier "cartesiano" que quiera comunicar alguna "técnica o truco" para resolver escenas con DescartesJS. Siempre estamos dispuestos a aprender y a recibir el estímulo de los demás.
En este supuesto poneros en contacto conmigo y acordaremos las condiciones para su publicación en este blog.
Un primer contacto con DescartesJS: Programación de una escena paso a paso
Eduardo me entregó la idea de esta escena y el proceso que él sigue en su realización que seguidamente vamos a documentar. También puso unas notas sobre lo que considera necesario preparar de antemano y los retoques y mejoras que cabe hacer con la escena.
Con todo esto, mi trabajo como redactor de este artículo ha consistido en elaborar la escena siguiendo sus pautas e interpretar sus propuestas de mejora. He ido observando todo lo que sería conveniente añadir, explicaciones e imágenes tomadas directamente de la escena o de las herramientas de trabajo, para facilitar la comprensión a quien se anime a emularlo y aprender a programar.
Quizá a alguien le pueda resultar excesivo el detalle en algunas ocasiones pero hay que pensar que se trata de la primera escena para el nivel básico y pretende que el neófito o el que ha experimentado muy poco con DescartesJS tenga la orientación suficiente para dar los primeros pasos, no se despiste demasiado y le estimule a seguir practicando. Espero haber acertado en mi pretensión.
Es importante que las explicaciones que aquí damos se acompañen, si fueran insuficientes, con la consulta puntual del concepto que se esté aportando en la "documentación técnica", sin pretender conocerlo todo desde un principio y solamente para entender la aplicación en esta escena en concreto.
Una nueva escena elaborada desde cero
Solamente comenzaremos desde cero si pretendemos elaborar una escena totalmente nueva y diferente de las que tenemos. Cuando elaboramos escenas parecidas a otras es más fácil actuar sobre la escena antigua, quitando y poniendo lo que interese, nos ahorraremos mucho trabajo.
En este caso vamos a hacer una escena totalmente nueva.
Las herramientas que se necesitan
| 1. | Un editor de texto plano (uno recomendable es Notepad++). Importante para poder consultar y si fuera el caso editar el código HTML del archivo que lleva la escena de DescartesJS. La escena se reconoce porque va entre etiquetas <ajs> y </ajs>. |
| 2. |
El Gestor de Escenas de Descartes (Descartes.jar) y la carpeta lib conteniendo el archivo intérprete descartes-min.js. |
El Gestor de Escenas está desarrollado en la "Documentación técnica" y puede descargarse desde http://arquimedes.matem.unam.mx/Descartes5/distribucion/
Crea una carpeta y nómbrala p.e. "Descartes5" para guardar esta descarga. Para abrir el Gestor de Escenas basta hacer doble clic en el nombre del archivo Descartes.jar. Es práctico tener un acceso directo a este archivo desde el Escritorio de Windows, cada vez que se quiera trabajar con él. Este es el aspecto que tiene la ventana del Gestor de Escenas cuando se abre en pantalla, mostrando por defecto una escena básica nueva.
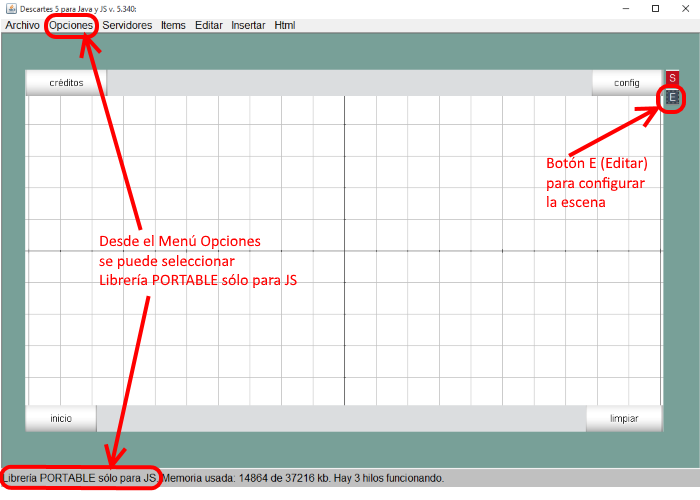
Figura 1
Una de las herramientas que nos interesa por ahora del Gestor de Escenas es el Editor de Escenas que facilita la escritura del código de la escena a través de un determinado número de paneles de configuración: Botones, Espacio, Controles, Definiciones, Programa, Gráficos y Animación.
Las escenas que vamos a explicar en esta serie de artículos son escenas de DescartesJS. El sufijo JS viene a señalar que el intérprete está escrito en JavaScript. Una escena escrita en DescartesJS necesita la referencia a un archivo llamado descartes-min.js para que pueda ser interpretada cuando se abra el archivo HTML que la contiene y se visualice en un navegador Web como Google Chrome, Mozilla Firefox o Safari de Apple. Este archivo puede ser descargado desde
http://arquimedes.matem.unam.mx/Descartes5/lib.
La imagen siguiente muestra la estructura de carpetas que va a tener nuestro proyecto.
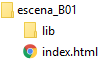
Figura 2
Para el caso de la escena que vamos a desarrollar en este artículo el archivo descartes-min.js debe de estar en la carpeta llamada lib. Esto se consigue simplemente seleccionando desde el Menú Opciones, Librería portable y solo para JS. Puede observarse que este modo está seleccionado si aparece escrito en la línea de estado de la ventana del Gestor de Escenas (Figura 1)
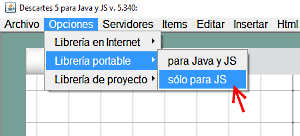
Figura 3
El archivo index.html lleva el código de la escena y la referencia al intérprete descartes-min.js (ver más adelante el apartado Preparar lo Necesario)
Idea del proyecto
|
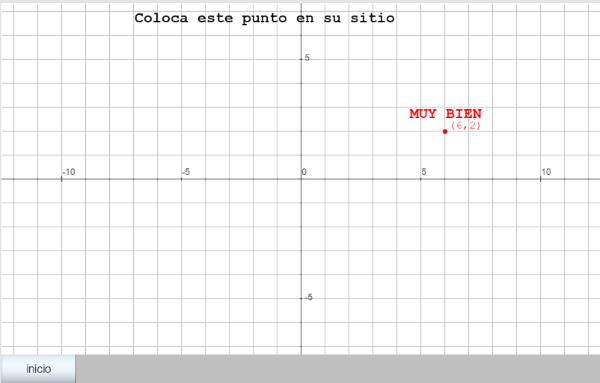
Escena_B01: Se trata de una escena para que el alumno aprenda a situar puntos sobre el plano cartesiano. Será una escena de tipo actividad, es decir que el alumno debe contestar actuando sobre la escena y el ordenador le indicará si lo hace bien o mal. Es conveniente que primero dibujemos en un papel nuestro proyecto. En la escena solamente aparecerán los ejes de coordenadas y la frase "Coloca este punto en su sitio:" Continuando la frase aparecerá el punto y entre paréntesis sus coordenadas cartesianas, empleando números enteros. Esos valores de las coordenadas serán números aleatorios para que cada vez que se inicia la escena sean diferentes. El alumno deberá mover ese punto con el puntero hasta colocarlo adecuadamente en su lugar. Cuando ese punto esté en su sitio aparecerá el mensaje "MUY BIEN ". |
La siguiente imagen lleva un enlace a la escena ya elaborada a partir de la idea expuesta. Interaccionar con ella para comprender su funcionalidad y después veremos cómo se crea el programa en DescartesJS utilizando el Editor de Escenas.
Figura 4
Preparar lo necesario
Crear una carpeta, p.e. escena_B01, que contendrá archivo HTML que se va a elaborar, p.e. index.html. En ella también debe estar la subcarpeta lib con el archivo intérprete descartes-min.js.
Esta operación puede realizarse completamente desde el Gestor de Escenas tal como indicamos seguidamente.
Una vez abierto el Gestor y seleccionada la opción Librería portable > solo para JS, se guarda desde el menú Archivo seleccionando Guardar como, que permite seleccionar la carpeta escena_B01 si ya existe o crearla en su caso y poner nombre al archivo que portará la escena p.e index.html.
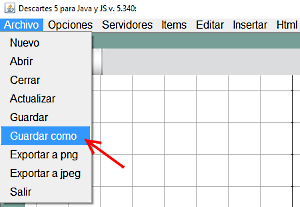
Figura 5
Dentro del archivo index.html que contiene la escena por defecto entre etiquetas <ajs> y </ajs>, el Gestor de Escenas ha colocado la línea de código <script type='text/javascript' src='lib/descartes-min.js'></script> delante de la etiqueta de cierre </head>
Para familiarizarse con estos conceptos conviene consultar el código HTML del archivo index.html para la escena básica abriéndolo con un editor de texto plano como Notepad++.
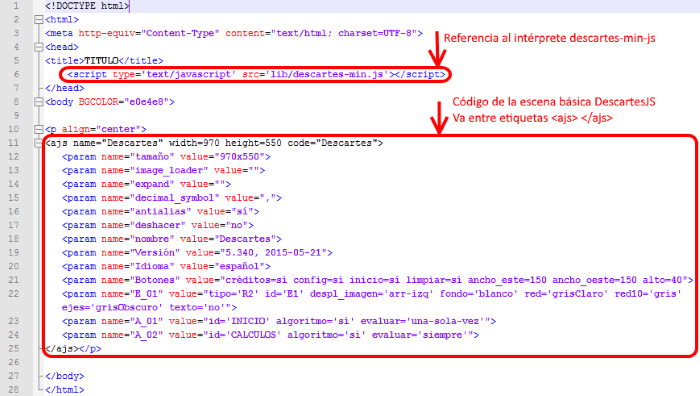
Figura 6
La escena ocupará un espacio rectangular de 800x510 píxeles. Con una unidad coordenada de 32 píxeles van a poderse ver con cierta holgura puntos (x,y), x entre -10 y 10 e y entre -5 y 5.
Al abrir el Gestor nos muestra una escena por defecto (escena básica) de dimensiones 970x550 píxeles (Figura 1). Éstas se cambian pulsando el botón E (edición) o Config y después, en el Editor de Escenas, el botón código (Figura 7) modificando los valores width (ancho) y height (alto) (Figura 8)
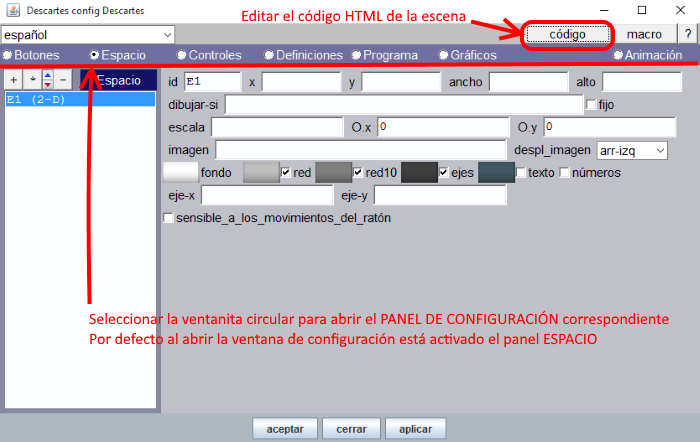
Figura 7
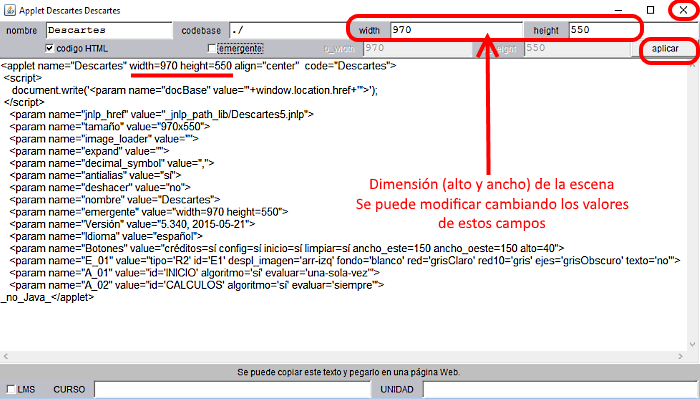
Figura 8
Para fijar el cambio se pulsa aplicar y se cierra (X) la ventana de código. Pueden verse estos cambios si pulsamos aplicar/aceptar en la ventana Descartes Config (Figura 7)
Proceso a seguir en el Editor de Escenas
| 1. |
Desde el Gestor de Escenas se accede al Editor de Escenas. Se selecciona el panel Botones y se desmarcan las casillas de créditos, config y limpiar, dejando solamente marcada la de inicio. Para que surta los efectos de este cambio hay que pulsar aplicar y aceptar para salir del editor aceptando los cambios. El botón Inicio aparecerá en el ángulo inferior izquierdo de la escena (Figura 4) y cuando se pulse repondrá la escena en condiciones iniciales del programa. |
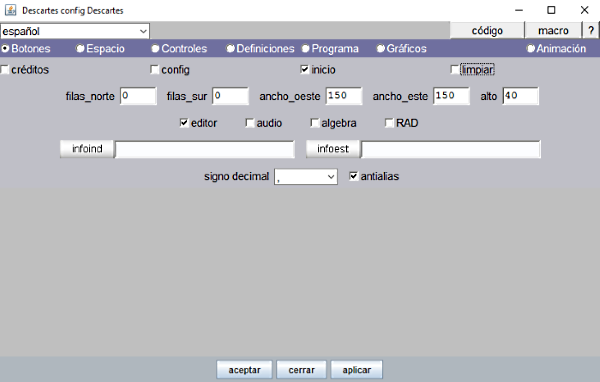
Figura 9
| 2. | En el panel Espacio, se fija una escala a 32 y se marcan únicamente las casillas para que se vea red, ejes y números. La escala es el número de píxeles que contiene la unidad coordenada. La casilla fijo, si está marcada, consigue que el espacio quede fijo y no se podrá desplazar cuando se arrastra el puntero sobre el mismo |
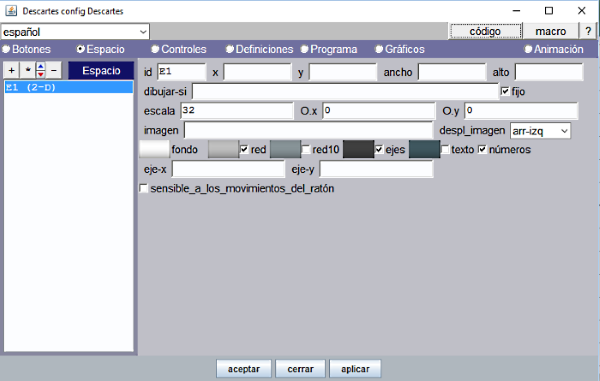
Figura 10
| 3. |
Para situar en escena la frase "Coloca este punto en su lugar" se selecciona el panel Gráficos y se añade un gráfico tipo punto de tamaño 0 y en la ventana texto se escribe esa frase. Se cambian sus coordenadas (0, 0) en la ventana expresión por (-7, 6.5) o hasta que la frase quede en el lugar que interese. Se pulsa aplicar y se comprueba que aparece en la escena. La Figura 11 siguiente, muestra el panel Gráficos con el primer punto añadido. Para añadir un gráfico en la escena hay que pulsar el botón (+) y seleccionarlo de una lista ofrecida con los diferentes tipos. Si queremos que solo aparezca este texto basta indicar que el tamaño del punto sea 0. El gráfico tipo texto en cambio situaría el texto según una expresión encerrada entre corchetes [x,y] donde x e y vienen dados en píxeles siendo el origen [0,0] el vértice superior izquierdo de la escena. |
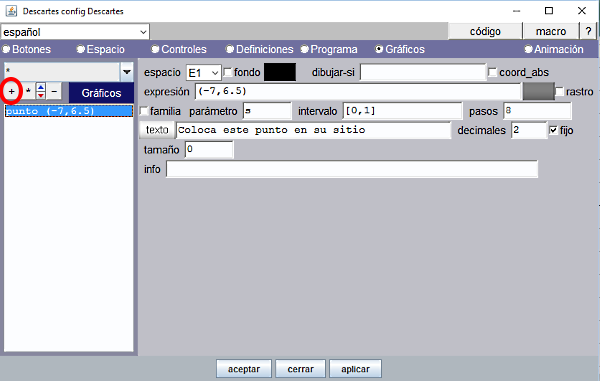
Figura 11
| 4. |
Ahora es necesario crear un control gráfico para poder referenciar sobre él un punto que podamos mover arrastrándolo con el puntero. |
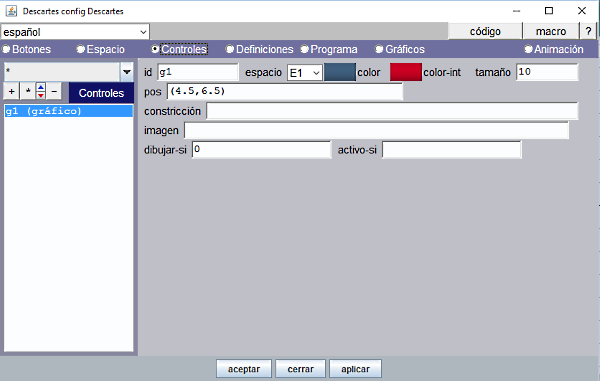
Figura 12
|
Pero el disco del control no tiene que verse, por eso debe de figurar dibujar-si=0. Esta es una condición lógica que debe de verificarse para que se dibuje el control. Al asignar el valor 0 o FALSO no se dibujará. Las coordenadas x e y del control gráfico como el g1 se pueden referenciar en cualquier parte del programa escribiendo g1.x y g1.y como vemos en el siguiente paso. |
| 5. |
En el panel Gráficos se añade un nuevo gráfico tipo punto. |
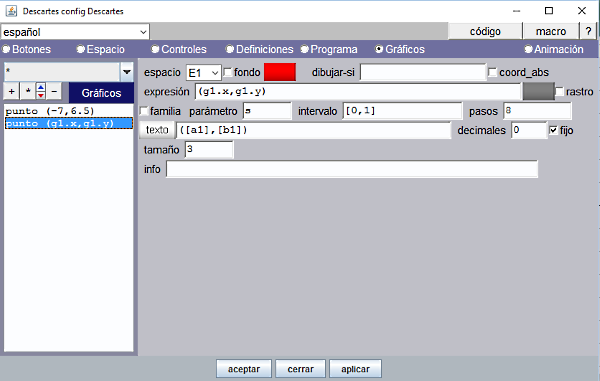
Figura 13
|
Observar que para que se escriban los valores de las variables a1 y b1 y no estos nombres hay que encerrarlos entre corchetes [a1] y [b1]. Para que no se escriban estos valores con coma decimal hay que poner 0 en la ventana de decimales. |
| 6. |
Estos valores auxiliares a1 y b1 se definen en el panel Programa. Puede hacerse en el algoritmo INICIO que se calcula solo una vez, escribiendo en el campo hacer, a1=ent(rnd*21)-10 En a1 se obtiene un valor aleatorio entero comprendido entre -10 y +10. Observar que rnd es una función interna de Descartes que genera un valor dentro del intervalo [0, 1). |
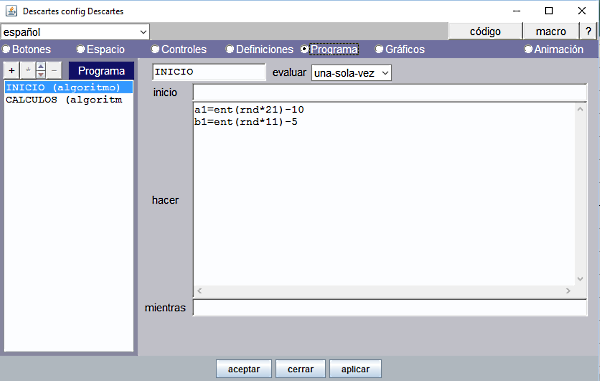
Figura 14
|
Es conveniente Guardar desde el menú Archivo cada vez que hemos completado un proceso, para que no se pierda nuestro trabajo en caso de que surja algún problema con el ordenador. |
| 7. |
Queremos que el programa compruebe que el alumno, cuando interacciona con la escena, coloca el punto en su sitio y que entonces aparezca un mensaje indicando que está bien. Para ello debemos definir un auxiliar en el panel Programa, en el algoritmo CÁLCULOS y que se evalúe siempre: bien1= (abs(a1-g1.x)<0.1)*(abs(b1-g1.y)<0.1) bien1 es el resultado de multiplicar 2 expresiones que únicamente pueden valer 0 ó 1. Es necesario darle un pequeño margen 0.1 porque sino sería muy difícil acertar. Esta fórmula comprueba que las coordenadas en que se coloca el punto son las mismas que las del control gráfico, (g1.x, g1.y). Si el punto está en el lugar adecuado, entonces bien1 valdrá 1. |
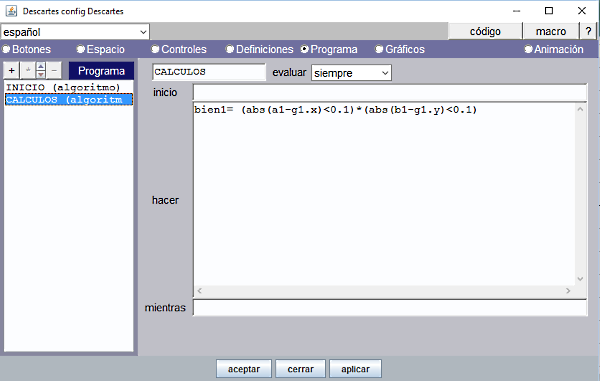
Figura 15
| 8. |
Falta añadir en el panel Gráficos un tercer punto, de tamaño 0, con el texto "MUY BIEN"; poniendo la condición dibujar-si=bien1. Es decir el texto se escribe cuando bien1 toma el valor 1 o VERDADERO. |
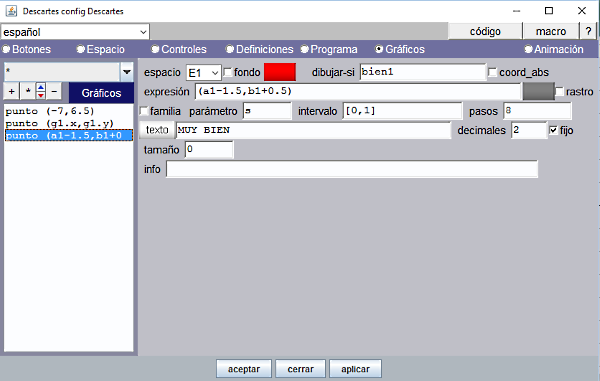
Figura 16
|
Conforme se ha ido elaborando la escena se comprueba que todo funciona y aparece lo que se quiere. |
| 9. |
Finalmente, hay que Guardar y Cerrar desde el menú Archivo del Gestor de Escenas. |
Retoques y mejoras
Todas excepto la última de las que se indican se han tenido en cuenta al describir el proceso anterior.
| 1. | El tamaño de la escena por defecto es muy grande. Para modificar el tamaño de la escena, se hace desde el código fuente, cambiando los números que aparecen inicialmente y que indican el ancho y el alto de la escena. |
| 2. |
Modificaciones en el panel espacio. Conviene que la escala sea la deseada y que no se pueda arrastrar el espacio con el puntero, por ello en el panel espacio se marca la casilla fijo. No deben de verse las coordenadas del puntero al hacer clic izquierdo, para ello se deja desmarcada la casilla texto. |
| 3. | Es conveniente que el color, el tipo y el tamaño de la letra sea lo adecuado. En este trabajo se da formato a los textos utilizando la opción Texto simple
, al pulsar el botón texto,
que permite cambiar algunos atributos básicos, tales como el tipo de letra, tamaño, negrita y cursiva. La otra opción Texto con formato dispone de un repertorio más amplio y se podrá ver en sucesivos trabajos. |
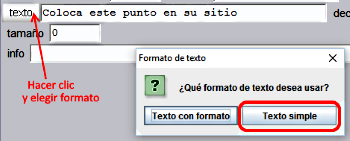 Figura 17 Figura 17
|
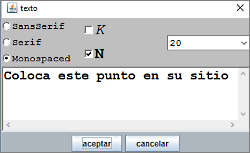 Figura 18 Figura 18
|
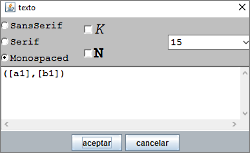 Figura 19 Figura 19
|
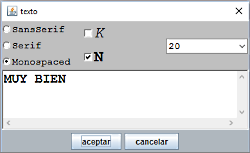 Figura 20 Figura 20
|
| Se habrá podido observar como el color del punto que debe ser movido y el texto "MUY BIEN" llevan color rojo. Hemos visto que la opción Texto simple no dispone del atributo color; en este caso el color del texto puede modificarse utilizando el botón de color (1) que figura en el panel Gráficos. Al pulsar el botón de color (1) se abre una ventana que facilita le selección del color, bien a través de un listado de colores estándar (2), o mediante una combinación cualquiera de valores hexadecimales desde 00 a FF para cada uno de los tres colores básicos rojo verde y azul. |
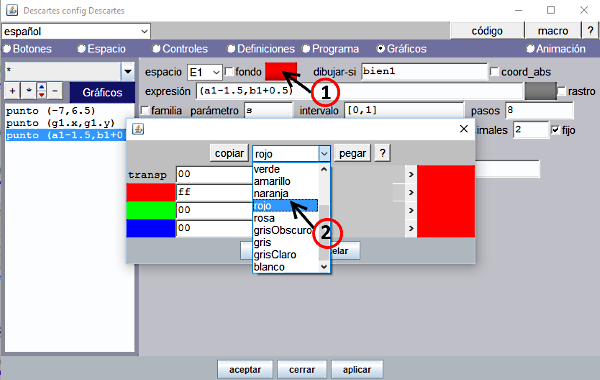
Figura 21
| 4. | En la frase del principio "Coloca este punto en su sitio" y en "MUY BIEN " no interesa que se vea el punto del texto, por eso ponemos tamaño=0. |
| 5. | Una posible mejora se consigue poniendo en la escena varios puntos para situar correctamente en el plano cartesiano en vez de uno solo y también los auxiliares necesarios para ello. No obstante, es mejor que la escena no quede recargada y que todo ello tenga un aspecto simple. |
Autoría:
Eduardo Barbero Corral (Idea del proyecto y técnicas de programación DescartesJS)
Ángel Cabezudo Bueno (Interpretación, edición de la escena, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
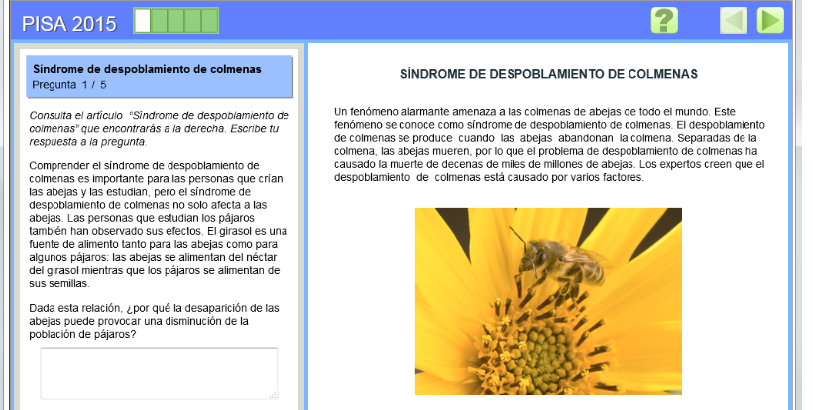
Hoy os vamos a presentar un pequeño subproyecto dentro del proyecto Competencias, se trata de PISA con ordenador.
Se emplea la interacción para evaluar en base a la recreación de una situación que permite al alumno contextualizar el problema.
Estos objetos de aprendizaje san desarrollado con Descartes por lo que son ejecutables desde cualquier sistema operativo y dispositivo móvil.
Centrándonos ya en los recursos, disponemos de 19 objetos que podemos descargar de forma individual o todos en un fichero comprimido. Por supuesto también disponemos de enlaces a los objetos publicados en la web de la Red Descartes.
Las actividades propuestas provienen de preguntas aparecidas en las pruebas de evaluación PISA y cada recurso consta de varias preguntas sobre el mismo tema. También tienes disponibles los recursos antes de la adaptación.
Encontramos una serie de datos en forma de textos, tablas de datos o gráficos de los que los alumnos deben extraer la información para responder las preguntas. Éstas cuestiones son de varios tipos, elegir la respuesta correcta, redactarla, seleccionar enunciados para completar la frase correcta, seleccionar varias respuestas válidas…Esta variedad en la forma de responder permite detectar mejor las capacidades del alumnado.
Una vez se han contestado las preguntas se ofrece la opción de revisarlas para que puedan asegurarse de hacerlo bien.
Al terminar encontramos cuatro posibilidades:
- Ver las respuestas correctas, una corrección automática instantánea de las contestaciones exceptuando las preguntas de redacción que deben ser evaluadas por el profesor
- Descargarlas respuestas, esta opción permite al profesor recogerlas y poder calificarlas después
corregidas
- Enviarlas por correo al profesor, los alumnos deben poner su nombre y el correo del profesor para poder indentificarlos y que sea posible el envío
- Imprimirlas, también permite la corrección con la ventaja de mostrar con facilidad al alumnado las pruebas
En todos los casos el alumno verá las respuestas correctas después de realizar la acción elegida
Os dejamos un vídeo en el que repasamos la web y comentamos uno de los recursos: Síndrome de despoblamiento de colmenas
Dispones de muchos más recursos en la web de la Red Descartes
Operando con enteros. Una lección interactiva
Escrito por Montserrat Gelis BoschEn el vídeo de esta semana se presenta una selección de actividades para introducir en 1º de ESO las operaciones con enteros.
Se trata de actividades pertenecientes a la unidad los números enteros, del Proyecto ED@D y para su aplicación en el aula se propone embeber las escenas en un curso de moodle mediante el recurso Lección.
El recurso Lección de moodle, ofrece muchas posibilidades, desde la edición de páginas de contenido con diferentes ramificaciones hasta las páginas de preguntas. En este caso se han creado una serie de páginas de contenido, pero se puede ampliar la lección con otras actividades en función de las preferencias de cada uno.
Las escenas Descartes se insertan en páginas de contenido utilizando la siguiente línea de código:
<iframe style="width: 600px; height: 400px;" src="https://proyectodescartes.org/EDAD/materiales_didacticos/EDAD_1eso_numeros_enteros-JS/1q3_ejercicios_resueltos_2a.htm"></iframe>
Si se trata de una actividad de la cual no se dispone de la dirección web, se puede copiar todo el código de la escena y pegar en la página de la lección.
Misceláneas. Las Espirales III
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales III
Entre las innovaciones producidas en el ámbito de la Red Educativa Digital Descartes caben destacar, entre otras, la creación del subproyecto Pisa con ordenador por parte de Mª José García Cebrian y José R. Galo Sánchez, documentado en este Blog por Santos Mondéjar López y la herramienta creada por el profesor Ángel Cabezudo Bueno que nos ha dotado de la posibilidad de analizar un crecimiento espiral y hallar la expresión matemática que mejor lo ajusta. La siguiente imagen enlaza con la miscelánea que explica el proceso de creación de dicha herramienta y el uso de la misma.
En el proceso de recuperación y adaptación de materiales de la Red Descartes que habían quedado obsoletos y en el de creación de nuevos recursos son varios los trabajos que merecen mención especial que ya está reflejada en el Blog, no obstante animamos a los socios y visitantes de nuestra web a usar y estudiar dichos trabajos y emprender tareas de adaptación-creación de: Unidades, Misceláneas, Discursos... para recuperar todo el esfuerzo e ilusión que en su día se invirtió y dotar a la aldea global de herramientas útiles para la enseñanza y el aprendizaje.
Seguimos insistiendo en la necesidad de estar al día de las posibilidades operativas y de uso de los materiales y escenas de la Red Educativa Digital Descartes. Aconsejamos acudir a los foros y contenidos de la Documentación técnica de la herramienta de autoría DescartesJS, en especial a estos, que llevan a la información de las funciones matemáticas disponibles para la construcción de escenas.
Antes de comenzar con el análisis de los gráficos incluidos en la escena en estudio vamos a mostrar un vídeo que relaciona los fractales y las espirales con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Los siguientes enlaces nos llevan a páginas donde puede ampliarse el conocimiento de las espirales y el concepto, significado y enfoque del estudio de las mismas.
- Espirales de Antonio Pérez Sanz
- Real Sociedad Matemática Española
- Espirales, fractales, Fibonacci,...
- Visión más espiritual
- Espirales y Laberintos
Continuamos con la creación de la miscelánea que con el título Las Espirales va a contener una serie de escenas donde se introducirán, estudiarán y representarán algunas espirales.
En el artículo anterior nos quedamos estudiando los gráficos introducidos en la escena: puntos, segmentos, líneas, polígonos, textos... etc. Para lo cual abrimos la opción de menú Gráficos y observamos los 26 objetos creados y que muestra la siguiente imagen.
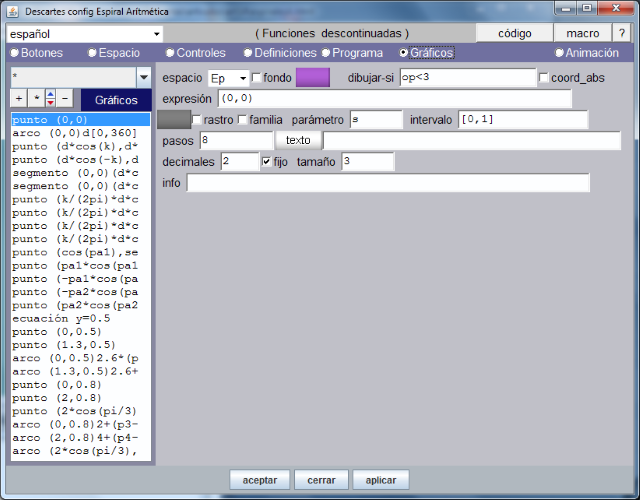
Insistimos en la conveniencia de descargar la escena, abrirla con el editor DescartesJS y analizar detenidamente las propiedades de cada gráfico. Si en este punto se tiene alguna duda el autor o la administración del Blog atenderán las consultas.
El código que corresponde a los gráficos se puede examinar y modificar, abriendo el archivo descargado "espiralesA.html", con un editor de texto plano. Las líneas que corresponden a dichos gráficos son las que comienzan por: <param name="G_x" que en nuestro caso llegan hasta <param name="G_26". Recordamos que se debe tener mucha precaución al editar directamente el código.
Observando la imagen vemos que, en primer lugar, se ha definido un punto en el origen de coordenadas (0,0) que, en esta ocasión, está centrado en la escena. Conviene, si no se tiene práctica, estudiar y probar las diferentes maneras de situar el origen de coordenadas de un espacio y el espacio en si mismo, dentro de la escena. También vemos el espacio donde se representará el punto, su color, tamaño y otra serie de parámetros autoexplicativos y de facil uso.
De los parámetros que ayudan a manejar un punto en la escena uno muy interesante es el de 'familia' que mediante un parámetro (variable) que se introduce en la/s coordenada/s y que se declara en el cuadro de texto "parámetro" (o se acepta el ofrecido por el editor 's') permite introducir simultáneamente tantos puntos como se precise en los lugares definidos por las coordenadas.
La siguiente imagen muestra como se han definido la colección de puntos azules que dibujan la espiral de Aquímedes según la definió el geómetra griego, donde se usa el parámetro global 'familia' con el parámetro o variable 'k '. Recordamos que en su momento definimos el control 'k ' y le asignamos un valor inicial y un valor final. Esta manera de proceder hace que la escena sea interactiva ya que el conrol k puede manipularse al estar presente en la escena en forma de pulsador.
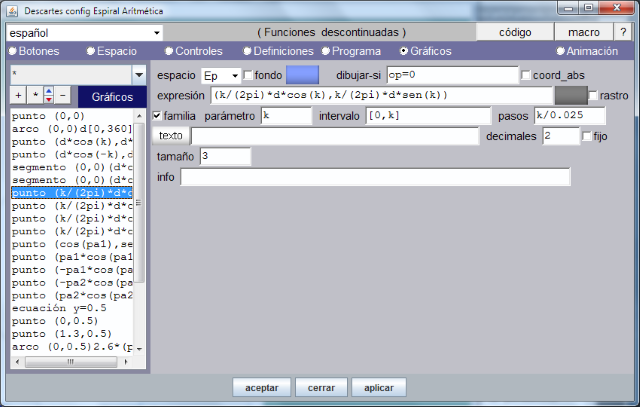
Puesto que disponemos de la escena podemos analizar cada uno de los gráficos cambiando los valores de sus parámetros y observando el efecto de las modificaciones para así aprender a configurar escenas con el editor de código.
Con objeto de practicar con los condicionales hemos elaborado la siguiente escena para su análisis. Es una pequeña aplicación donde se hace una breve introducción al estudio de la distribución de la proporción humana en superficies lisas mediante triángulos, rectángulos, rombos y otras figuras derivadas.
También, en la misma dirección, hemos creado, con el programa GeoGebra, una breve aplicación que muestra como obtener dos triángulos cordobeses a partir de un folio DIN A4.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo la espiral de Teodoro entre sus funcionalidades, analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
EDAD 4º ESO Opc. A Números enteros y racionales
Escrito por Alfonso Saura EspínEste mes vamos a ver el siguiente vídeo sobre la unidad correspondiente a enteros y racionales:
Los temas tratados han sido:
1.Números enteros
Representación y orden
Operaciones
Problemas
2.Fracciones y decimales.
Fracciones equivalentes.
Expresión decimal. Clasificación
3.Números racionales
Representación y orden
Suma y resta
Multiplicación y división
Potencias de exponente entero.
Operaciones con potencias.
Problemas.
4.Notación científica
Definición
Operaciones
Proyecto Canals. Objetos interactivos para Educación Primaria 5º
Escrito por Xosé Eixo BrancoEl Proyecto Canals, subproyecto del Proyecto Descartes de la asociación no gubernamental Red Educativa Digital Descartes (http://ProyectoDescartes.org), está constituido por 375 objetos interactivos que tratan diversos aspectos de la matemática y que están pensados fundamentalmente para Educación Primaria. Estas unidades didácticas interactivas están desarrolladas a partir de los materiales que diseñó durante su vida docente la profesora Mª Antonia Canals.
En este vídeo se muestran, a modo de ejemplo, algunos de los 85 objetos digitales que, para el curso de 5º de Educación Primaria, se pueden ver en la página de este proyecto y que pueden ser usados en cualquier dispositivo, ordenador, tableta o smartphone.
En próximos vídeos veremos materiales de este mismo proyecto para otros cursos.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)








 CONTACTO
CONTACTO
