Título de la obra:
¡No!, ¡no soy áureo! ¡Soy cordobés! Firmado: Nautilus
Autor:
JOSÉ R. GALO SÁNCHEZ
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-18834-89-9
A Pepe y a Cristi
Hace algunos cientos de años que el canon de belleza va ligado a la razón áurea. Todo lo que es bello es observado buscando este patrón y su beldad es sublimada cuando se sigue esta pauta. Y de manera recíproca, cuando se busca construir algo que llegue a ser bello y sea atractivo, se diseña para que sea el reflejo de la admirada razón. Ello ha acontecido con la concha del Nautilus, una bellísima concha en su exterior que queda esplendorosamente magnificada al observar su arquitectura y forma interior. Es tal la atracción que provoca su observación que pocos son los que no quedan embelesados o al menos algo extasiados con ella, y ¡cómo no! si provoca esa sensación rápidamente surgen augures, vaticinadores y oráculos que proclaman que ¡el Nautilus es áureo! y divulgan imágenes proclamando su afirmación. Esto acontece en legos, con los que hay que ser condescendientes porque en su arrebato no reparan en verificar su aserto, pero también en versados e ilustrados quienes, de manera explícita, usan la imagen del Nautilus como medio llamativo que capte la atención de posibles lectores de sus documentos sobre la proporción áurea, canalizando y generando una asociación entre ambas que las deja implícitamente identificadas e incluso hay quienes lo verbalizan y transcriben. Son multitud quienes han reproducido esta divulgación, quienes lo han enseñado y quienes lo han aprendido así, e incluso algunos han aprobado sus exámenes afirmando que el Nautilus es áureo, ¿es usted uno de ellos?
No vamos adentrarnos aquí sobre el porqué acontece reiteradamente la divulgación de afirmaciones erróneas cuando es fácil verificar su no cumplimiento, pero sí indicamos que mucha literatura matemática de divulgación lo que se hace es una reproducción sucinta de resultados que llamen la atención, pero sin una justificación o invitación a comprobarlo, y se suele enlazar con aspectos geométricos que aparecen en la Naturaleza como una
muestra fehaciente del reflejo del mundo matemático en nuestro entorno vital, como una justificación de que las matemáticas son útiles, cuando el camino real es el inverso, es decir, las matemáticas surgen al tratar de explicar el entorno y precisamente al lector, entendemos, hay que invitarle a verificar que el modelo matemático se ajusta al ser vivo modelado y no exponerlo como un axioma que ha de creer a pies juntillas. Precisamente en la geometría, cuando se rompió la axiomática euclidiana fue cuando se abrieron universos que estaban ocultos a nuestro intelecto. No vamos a sentar nosotros que la negación del carácter áureo del Nautilus, que hacemos aquí, sea el germen de la apertura de otros mundos desconocidos, pero sí indicaremos que nuestro objetivo será el abordar y el lograr una divulgación de conceptos matemáticos bajo una perspectiva en la que el lector pueda ver reflejado el porqué, o algunos de los porqués, de por qué se exponen, se reiteran y aprenden algunos resultados matemáticos, de dónde surgen, cuál puede ser su valor intelectual y su aplicabilidad material, cómo se le pudo ocurrir a sus descubridores aunque en algún momento podamos adentrarnos en el ámbito de la hipótesis y no de la constancia histórica cierta ―en los descubrimientos matemáticos no hay un historiador leyendo la mente del investigador, ni en general los investigadores dejamos pistas de cómo llegamos a ellos―, pero será una hipótesis con una base plausible, un camino que bien pudo ser uno de los posibles conducentes a ese resultado.
Ya lo hemos indicado, o tratemos de expresarlo de mejor forma, el Nautilus lleva millones de años siguiendo un mismo patrón de crecimiento, lleva bastante tiempo diciéndonos de manera ortegasiana “yo soy yo y mis circunstancias”, escuchadme bien y me reconoceréis. Pero desde algunos cientos de años o menos (tampoco son relativamente muchos) se le ha ubicado, se le ha trasladado e incluso encarcelado en un mundo áureo que le es ajeno. ¡Sí, ajeno!, pero afortunadamente (estimamos que para él, y lo afirmamos para
nosotros) fuimos capaces de escuchar su llamada de auxilio, su petición de rescate para llevarlo a su ubicación exacta, a aquella en la que sí encaja cual pieza de un puzle que sólo se diluye en el mismo cuando sus bordes se ubican en el sitio preciso y adecuado. Ahora sí, podemos trasladarles el escueto escrito que el Nautilus nos ha hecho llegar:
¡No!, ¡no soy áureo!
¡Soy cordobés!
Firmado: Nautilus
Pero en este libro no vamos sólo a restringirnos a mostrar el porqué de esa afirmación nautiliana. No, ésta es la motivación o el punto atractor con el que queremos animarle a que nos acompañe en un camino que queremos sea de aprendizaje mutuo, en el que trataremos algunos temas clásicos muchas veces trillados, pero en gran parte ni aventados, ni desbrozados, en los que se nos muestra el grano todavía escondido entre la paja, donde vemos el resultado de una acción sin la exposición del proceso a él conducente. Nuestra línea va a ser tratar de motivarles a aventar y a desbrozar y ¡ya comprobaremos si, juntos, lo hemos logrado!
El lector interesado en el contenido de este libro podrá pasear a lo largo de cinco capítulos donde se combinaran secciones divulgativas, a las que se puede acceder sin un conocimiento matemático especial, con secciones que buscan dar fundamento o formalización matemática a lo observado y experimentado en las que sí será necesario adentrarse en el lenguaje matemático para una total compresión, pero quien inicialmente no lo desee puede centrarse en lo descrito y obviar el detalle técnico. Aquellos que opten por esta última alternativa vaticinamos que quedarán satisfechos del tiempo invertido en la lectura y aprendizaje sobre el fundamento de la belleza del Nautilus porque conocerán la causa o causas de su belleza, y los más técnicos tendrán adicionalmente respuestas al qué, el cómo y el porqué de la misma.
Y hemos citado lo experimentado por el lector, no de manera metafórica o como traslación a través de la lectura de la experimentación realizada por el autor, sino que la incluimos porque esa experimentación individual y personal es posible dado que este libro se caracteriza por ser interactivo, es decir, que el lector si lo desea puede dejar de ser un ente pasivo y puede convertirse en actor, en co-investigador con el autor, y reproducir las situaciones que se describen en el texto gracias a los recursos u objetos interactivos que se embeben y enlazan. Escenas interactivas que, al estar desarrolladas con la herramienta de software libre "Descartes" son editables y pueden servir de base para profundizar en la investigación aquí desglosada y descrita o para abrir otras investigaciones relacionadas. A esas escenas hay que añadir también animaciones y vídeos que muestran y amplían lo narrado.
En el primer capítulo se introduce al lector en el objeto de estudio, el Nautilus, describiendo sus diferentes especies. Este animal se ha venido a llamar "fósil viviente" porque se encuentra rastro vital del mismo desde hace más de 400 millones de años, pero sin detectar un cambio esencial, como si la evolución no hubiera intervenido en él, si bien para algunos autores lo que puede acontecer es que sufren pequeños cambios evolutivos que se deshacen una y otra vez y consecuentemente generan a lo largo del tiempo un cambio morfológico neto pequeño. Simplificando, podríamos interpretar que su forma le aporta una funcionalidad vital que es muy difícil de mejorar y cualquier cambio es deshecho para no desviarse de esa perfección. Y, ciertamente, adentrándose un poco en la morfología de su concha se llega a ese convencimiento porque si bien en nuestro caso llegamos al Nautilus por la atractiva forma de su concha, interiormente dividida en cámaras con un pequeño canal de comunicación entre ellas, al realizar una breve incursión en cómo éstas son las que aportan la flotabilidad al conseguir el equilibrio hidroestático o al analizar las diferentes y periódicas fases que han
de acaecer a medida que va creciendo el animal para no romper ese equilibrio y lograr mantener esa flotabilidad neutra en todo momento, o al comprender la necesidad de tener y desarrollar un órgano específico —el sifúnculo— que vacia esas cámaras y aprender el mecanismo químico mediante el que se logra ese vaciado... todo ello, hace que uno quede gratamente impresionado, bueno más bien embelesado. Y comprendida esa flotabilidad neutra, tampoco quedaremos defraudados al descubrir los mecanismos mediante los que cubre su movilidad en su entorno vital. Para su desplazamiento horizontal cuenta con el sifón, órgano mediante el que expulsa chorros de agua aplicando el principio newtoniano de acción y reacción, y el movimiento vertical queda cubierto al introducir pequeños cambios de presión que generan un sorpresivo desplazamiento fruto de una composición o combinación de los principios de Pascal y de Arquimedes los cuales pueden visualizarse y modelarse con el denominado diablillo o buzo cartesiano. Así pues, si la belleza de la forma motiva nuestra mirada matemática, es obvio que la arquitectura físico-química que la soporta logra sublimarla, dejando anonado a todo el que se detiene en ella. Vaticino que no podrá obviar su lectura y que la hará pausadamente para no perder ningún detalle.
Una vez anudados esos mimbres biológicos y físico-químicos, procede comenzar a introducir alguna urdimbre matemática con fundamento aristotélico para poder explicar el crecimiento autosemejante en base a la adición de un gnomon, lo que se denomina crecimiento gnomónico. Éste es el que se observa en el Nautilus donde al añadir una nueva cámara, incrementa su volumen manteniendo la forma. En el segundo capítulo se aborda el planteamiento matemático de esta autosemejanza, que obviamente tiene su base en el Teorema de Thales. Se inicia con el modelo matemático bidimensional con el que se simula el crecimiento continuo de diferentes conchas desde una perspectiva cenital,
determinando el polo y la forma de la línea en base a los cuales se produce su crecimiento. Pero también nos adentramos en en el crecimiento gnomónico discreto que nos permite matemáticamente detallar ciertas pautas particulares que ayudan a comprender situaciones de crecimiento discreto o de aparente crecimiento discreto, pues éstas pueden plantearse como instancias concretas de un crecimiento continuo. Se analiza el crecimiento gnomónico de un triángulo, de un rectángulo y de ciertos polígonos en general. Adicionalmente se introduce el modelo tridimensional de las conchas y cómo plantear el crecimiento gnomónico de las mismas.
En el tercer capítulo nos centraremos en las razones y proporciones y en los cánones de belleza asociadas a ellas. Entre todas, la más conocida es la que actualmente se nombra como "proporción áurea" (que es citada en el título de este libro). Ésta se referencia en los "Elementos" de Euclides y la primera pregunta que surge es por qué, de las infinitas razones existentes, Euclides encuentra su exclusiva aguja en el pajar a la que denomina “extrema y media razón” y relacionada con el pentágono. Pero es Pacioli, en su toma de contacto renacentista con los "Elementos", quien la magnifica llevándola a su caracter divino, y es dorada y armónica para Durero y Da Vinci, y así hasta nuestros días como sumum de la preciosidad. No obstante, hay otras hermosuras y, en particular la asociada a un polígono que es constructivamente más simple, casi trivial, que es el octógono del que se obtiene la proporción denominada cordobesa, por ubicación histórico-geográfica, o humana por contraposición a la anterior. Aquí, estimamos que realizará un agradable paseo en el que la matemática se hará arte y el arte se leerá matemáticamente. Y le auguro un nuevo destino al que tendrá que viajar y que, por múltiples motivos, no le defraudará.
Y para avanzar en el conocimiento de la forma nautiliana es imprecindible profundizar en la curva hipnótica plana que se denomina "espiral" y que, en una formalización expositiva imprecisa, Durero describía como:
"Se puede imaginar una línea eterna que, en continuo desarrollo en torno a un centro y describiendo con su otro extremo espiras cada vez más amplias, nunca tenga fin. Esta línea no se puede hacer a mano por lo infinito de sus magnitudes grandes y pequeñas. Su principio y final no existen, ni se pueden encontrar, salvo en el entendimiento."
Sin embargo, las espirales son diversas y en el capítulo cuarto, como bocado introductorio o aperitivo, se le adentra al lector en la clásica espiral de Arquímedes o espiral aritmética, pero rápidamente se le oferta el plato principal: la espiral cartesiana, geométrica, logarítmica, equiangular, armoniosa, maravillosa... equiparable en admiración a la antes alabada proporción. Y sublimando lo sublime ¡¿qué puede ser más óptimo que una espiral logarítmica áurea?! Sí, ante este anuncio, ha de ponerse tenso y receptivo porque tal oferta no puede obviarla y, como ya hemos adelantado, inefablemente se realizan múltiples asociaciones, cómo no, entre el Nautilus y esa espiral logarítmica áurea..., pero nosotros, también, de la infinidad de espirales equiangulares existentes, le invitamos a conocer a la espiral logarítmica ¡cordobesa! Y como postre, aunque ningún comensal está obligado a tomar postre, es decir, sólo para los lectores más hambrientos e interesados en aspectos más matemáticos el capítulo cuarto se completa analizando cómo, gracias al caracter equiangular, estas espirales pueden aproximarse por espirales discretas (poligonales) inscritas y circunscritas e igualmente cómo la región comprendida entre los arcos de la espiral que se diferencia una vuelta se aproxima por polígonos inscritos y circunscritos semejantes con gnomon poligonal definible por el usuario.
Al llegar al quinto y último capitúlo contamos con todas las herramientas necesarias y los moldes bien pergeñados para su aplicación al Nautilus. Basta usar hábilmente las primeras y ajustar los segundos para vestirlo adecuadamente y obtener un patrón
fidedigno para su especie. La manifiesta forma espiral encaja con la espiral cordobesa, el sifúnculo es la misma espiral cordobesa (salvo traslaciones y giros ―cambio de escala― hay una única espiral cordobesa), los septos son arcos de esa espiral trasladándose por el fragmacono y el polo al trasladarse traza la misma espiral. No hay duda: ¡tu traje es cordobés! y el patrón del mismo queda reflejado en las ecuaciones matemáticas que permiten reproducir a cualquiera tu forma y tu crecimiento.
No obstante, ¡gracias Nautilus! por ser condescendiente y no protestar al haber proscrito aquí tu infancia y ñiñez y por haber camuflado tu rastro de esa época inmadura, pero también muy bella, en un único traje uniforme de juventud y madurez. Así suele ser la estrategia humana ante los problemas difíciles, los convertimos en otros más fáciles y nos convencemos de que habrá un tiempo ulterior en el que con lo aprendido, y si las musas nos acompañan, podremos retomar las metas dejadas. Pero en este caso, te adelanto, que tu prudencia, recato y discreción se verá recompensada dado que Urania, la celestial musa de las ciencias exactas, ha querido premiarnos con la inspiración suficiente para modelar tu concha desde tu génesis, distinguiendo las fases de tu ontogenia. En un próximo libro (Galo, 2024)
Y... ¡sí!, no te pongas ahora impaciente, que soy consciente que el mundo de planilandia en el que encaja la sección sagital analizada de tu concha, te/nos queda muy aplastado, que hay que dar volumen a lo que es tridimensional y en otro libro (Galo 2024b)
¡Quizás usted, intrépido lector, pueda aportar la luz suficiente!
Pero, no todo lo que parece fácil lo es ―al menos para el ignorante―, y ha sido mucho el tiempo dedicado a escuchar lo que susurraba el Nautilus y a tratar de vislumbrar los patrones matemáticos de la concha de este magnificente arquitecto. Tanto tiempo, que mi sobrina-nieta, Aurora, al verme una y otra vez delante de la pantalla de mi ordenador observando la reiterada imagen de la concha del Nautilus comentaba a su tía ―a Conchi, mi mujer―:
¡Tita!, ¡qué el tito no ha acabado sus deberes!
Tenía y tiene la razón, pero al menos espero que, con lo detallado en este libro, cuando ella tenga la edad suficiente para poder leerlo y verlo con la mirada de una científica ―si es su elección― o la de una inquieta observadora de su entorno ―como ahora ya lo es― quede satisfecha y recompensada por quien ¡le hacía rabiar! Y, quizás, su hermano pequeño, Nico, podrá disfrutar centrando sus grandes ojos en la mecánica nautiliana, pues ahora esa temática es la que más le atrae.
Y a usted, lector, le invito no sólo a leer, sino a interactuar con las escenas y deseo que, al menos, encuentre algunos detalles con los que quede agradado ¡Gracias por compartir su tiempo conmigo!
Córdoba (España), marzo de 2024.
El Nautilus es un animalito que lleva haciendo matemáticas desde hace 500 millones de años. Aunque, para ser más precisos, conceptualmente, deberíamos plantearnos la alternativa entre si es la Naturaleza la que hace matemática o si realmente somos nosotros los que matematizamos la Naturaleza.
Al mirar nuestro entorno observamos patrones que se repiten o se asemejan, de hecho esa capacidad de mirar dos objetos, compararlos y extraer las propiedades que comparten o en las que discrepan es lo que permite ubicarnos en nuestro lugar, desplazarnos en él y, en definitiva, poder dar transcurso a nuestro acotado intervalo vital dentro de la aparente continua línea existencial. Así pues, desde esta perspectiva somos nosotros los que abstraemos las formas y distinguimos y catalogamos las diferentes figuras que vemos e incluso, en un paso más de nuestra capacidad imaginativa, nos inventamos algunas que nunca podremos ver por carecer de dimensión ―los puntos―, o por tener sólo una ―las líneas―, pero que nos permiten construir modelos sobre los que razonar y deducir propiedades adicionales. Desde ese punto de vista puede defenderse el hecho de que somos nosotros los que matematizamos la Naturaleza, que trasladamos nuestro ver a un mundo abstracto intangible que modela nuestro ser. Pero en general esas formas que nosotros distinguimos han sido creadas de manera inconsciente, o más bien digamos de una manera programada por un código genético en simbiosis con unas propiedades físicas que restringen las posibilidades de crecer y la forma de hacerlo, por lo que denominamos Naturaleza y consecuentemente es ésta la que construye la Matemática que nosotros llegamos a descubrir. No obstante, independientemente de cuál fuera la alternativa cierta —si alguna lo es, o si no lo fuera ninguna de ellas, o si lo son ambas— lo que sí parece obvio es que basta observar nuestro entorno para
reconocer atractivas formas naturales y asimilarlas a modelos matemáticos que recíprocamente se mimetizan, estableciendo un hipertúnel entre la concreción y la abstracción, entre el mundo real y el virtual. Sin embargo, en contraposición, a este planteamiento dual en el que se muestran o exponen dos mundos diferentes con un cordón umbilical que permite la transición bidireccional, la imagen que más nos gusta exponer es que nuestro mundo vital es el mundo matemático, pero tenemos limitaciones físicas que hacen que nuestros sentidos no nos permitan percibir todo lo existente en nuestro alrededor, únicamente captamos una realidad discreta del mismo, una realidad muy burda que progresivamente hemos ido ampliando, afinando, con dispositivos ópticos o electrónicos como los microscopios y los telescopios, pero con unos límites que se ubican en lo que en 2016 nosotros (Galo et al., 2016
Cuando sublimamos nuestra percepción a través de la mente es cuando, pasamos a ser conscientes que el mundo en el que vivimos realmente es el mundo matemático y la yocto-yotta realidad es la visión pixelada que captan nuestros sentidos amplificados con recursos tecnológicos.
Según WoRMS (2024d
Son los únicos cefalópodos existentes que tienen verdaderas conchas externas, pues la hembra del Argonauta () que es un cefalópodo octópodo de la subclase Coleoidea y no de la Nautilodea lo que produce es una cáscara calcárea semejante a una concha que sujeta con sus tentáculos y que le sirve como habitáculo para la puesta e incubación de los huevos; vulgarmente se les suele denominar “nautilos de papel”.

Aunque profundizaremos posteriormente indiquemos que las conchas de los nautilos se caracterizan porque internamente están divididas en compartimentos o cámaras que están unidas por un tubo orgánico denominado sifúnculo. Con este órgano extrae el líquido cameral por ósmosis y así consigue una flotabilidad neutra en el agua en la que habita. En el Si lo necesita puede configurar la traducción automática de los subtítulos. podemos tomar un primer contacto y conocer suscintamente algunos aspectos de interés que nos invitarán a adentrarnos en el conocimiento de esta familia de animales que habitan en el Indo-Pacífico.
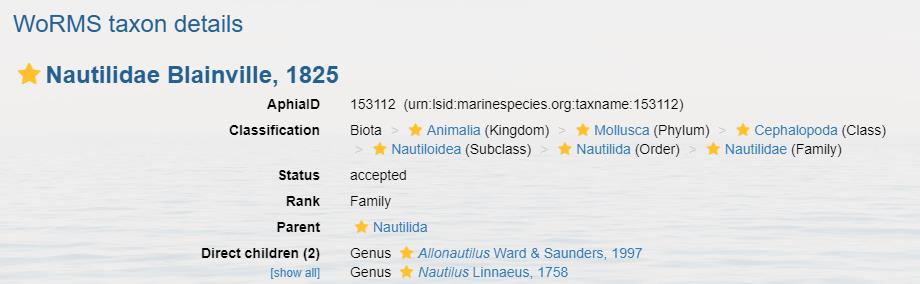
En 1997, ver , la familia de los Nautilidae se subdividió en dos géneros: los Nautilus y los Allonautilus, como consecuencia de las diferencias anatómicas significativas que pusieron de manifiesto Ward & Saunders (1997)
Siguiendo lo detallado por Jereb (2005)
Se caracteriza por su ombligo abierto, con una profunda concavidad aproximadamente del 15 al 16% del diámetro de la concha en el punto más ancho y con los verticilos interiores visibles. No hay capa espesa (callo) presente.
El diámetro máximo de la concha es alrededor de 160 mm. Ver .

De ombligo pequeño, cerrado y visible como un parche plateado y negro. Con callo generalmente presente. Los vórtices o bobinas internas no son visibles. Los patrones de color de la concha son variables: de rayas marrones irregulares a marrón rojizo que irradian desde el ombligo al vientre en la coloración habitual, pero este rayado se puede reducir a varios grados dejando el ombligo e incluso gran parte de los flancos en blanco. Tamaño típico entre 170 y 180 mm en el entorno de Fiji y Filipinas y mayores (una media de 222 mm) en el oeste de Australia.

Basándose en el estudio de los tipos existentes del Nautilus pompilius realizado por Nikolaeva (2015)
Muy parecido al pompilius con el que comparte el tener ombligo cerrado y cubierto con una callosidad. Se diferencian en la base de la rádula. Diámetro de la concha hasta 226 mm. Ubicación en la isla de Palaos. Ver .

Muy similar en tamaño y peso al Nautilus pompilius, pero sin callo y la coloración se presenta reducida faltando en la región del ombligo. Adicionalmente la capucha está cubierta por unas papilas elevadas en un patrón muy característico. Ver .

Fue inicialmente considerada como la especie Nautilus scrobiculatus dentro de los Nautilus y desde 1997 (Ward & Saunders)

Concha muy similar a la del Allonautilus scrobiculatus y comparte el ombligo abierto. Se desconoce si posee la capa protectora (periostracum). Sólo es conocida por las conchas que arrastra la corriente. Jereb (2005)
Aunque nuestro objetivo principal se centra en la forma de la concha de los nautilos y la fundamentación matemática de la misma, consideramos de interés la contextualización y conocimiento básico
de esta familia de animales, en lo que respecta a su anatomía básica, porque pensamos que cuando se introduce una visión científica global, interdisciplinar, es cuando se consigue un salto cualitativo esencial al aportarse no sólo la parte descriptiva ―el qué― sino también la explicativa o justificativa ―el por qué―. En esa línea, en la imagen siguiente () aportada por Jereb (2005
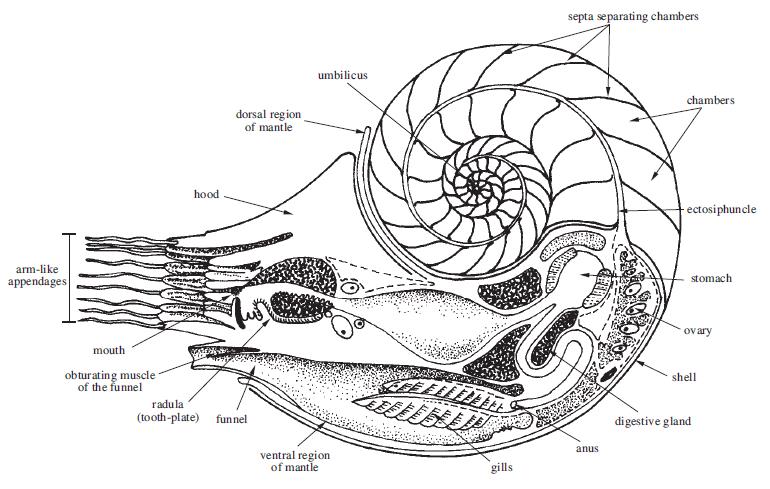
Según indica esta autora el animal se localiza en la última cámara, denominada cámara habitacional, uniéndose a los lados de la misma por los músculos aductores. La cámara habitacional está unida con el resto de cámaras mediante el tubo sifuncular que contiene al sifúnculo que como veremos posteriormente es un órgano que permite lograr y mantener su flotabilidad neutra en el fluido marino en el que habita.
También podemos destacar los tentáculos sin ventosas, que como ya indicamos se denominan cirros, de los que tiene 47 pares y cuenta con una caperuza que le sirve para cerrar la entrada de la cámara habitacional cuando al sentirse amenazado se repliega en su interior para protegerse. Para desplazarse cuenta con un sifón que le permite expeler agua y por el principio de acción y reacción obtiene un impulso que lo mueve en sentido retrógrado.
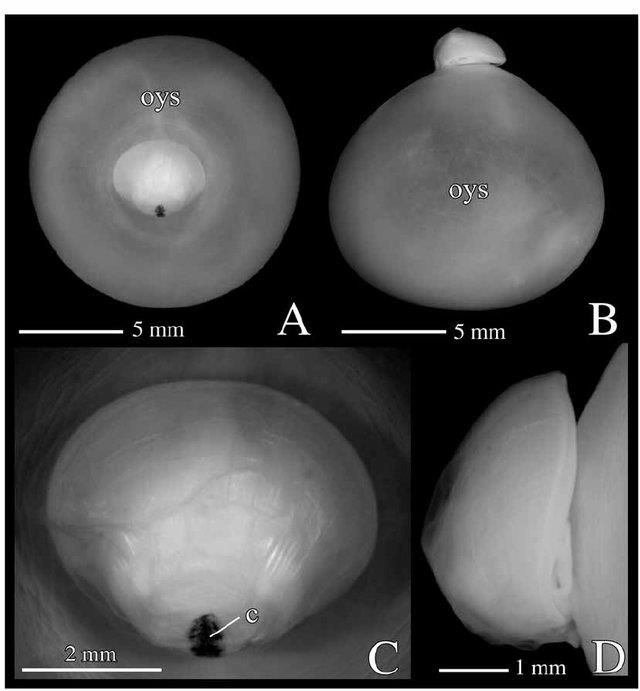
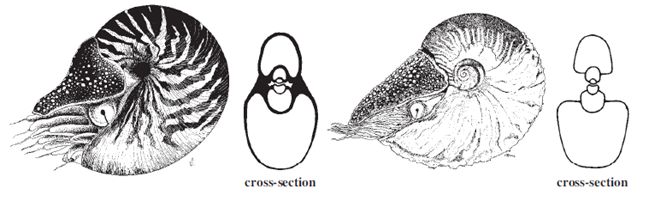
La concha es de tipo discoidal, es decir, crece manteniéndose en un mismo plano y su sección tiene una forma de espiral en la que se puede contabilizar el número de vueltas o verticilos. La protoconcha se corresponde con la parte de la misma que se forma en la vida embrionaria y larvaria (ver ) y la teleoconcha es la que construye en su vida juvenil y adulta. La parte que presenta cámaras se denomina fragmacono y los tabiques que las separan son los septos.
En el exterior de la concha pueden observarse las líneas de crecimiento y a la última se le denomina peristoma. La cabeza del animal emerge de la abertura y se dice que ésa es la parte anterior de la concha y la opuesta la posterior; la que está por encima del cuerpo es la parte dorsal y la inferior es la ventral (Hendricks, 2018
Cephalopod: Nautilus pompilius (PRI 70573) by Digital Atlas of Ancient Life on Sketchfab
En Barroso-Barcenilla (2008)
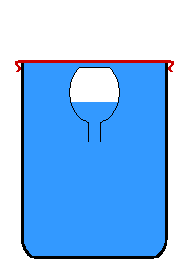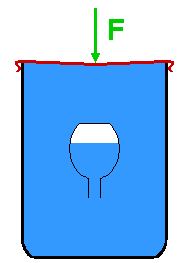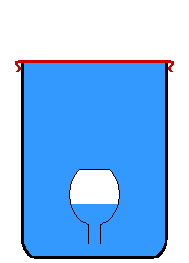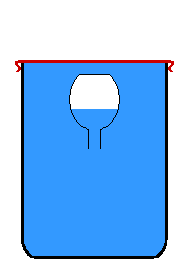
El principio de Arquímedes (Walker, 2015
“todo cuerpo sumergido en un fluido experimenta un empuje vertical y hacia arriba igual al peso de fluido desalojado”
Como consecuencia de este empuje $E$ el peso de un cuerpo es diferente en el aire o en el agua. Si denominamos peso real $P_{real}$ al que tiene un cuerpo en el aire y $P_{fluido}$ al peso del fluido desalojado al introducirlo en él, dicho cuerpo tendrá un peso aparente $P_{aparente}$ dado por:
$$\begin{aligned} P_{aparente} &=P_{real}-P_{fluido} \\ &=m_{cuerpo}g-d_{fluido}V_{fluido}g \\ &=d_{cuerpo}V_{cuerpo}g-d_{fluido}V_{fluido}g \end{aligned}$$ donde $g$ es la aceleración de la gravedad.
Analicemos las posibilidades que pueden acontecer considerando dos situaciones: que el cuerpo esté completamente sumergido (caso aplicable a los nautilos) en un único fluido o que se tengan dos fluidos entre los que puede desplazarse.
La flotabilidad neutra es un logro evolutivo y, como hemos indicado, para conseguirla ha de equipararse la densidad del agua con la densidad global del animal, de su concha y su interior, y en ello es esencial la estructura interna cameral del Nautilus. Las cámaras van incrementando el volumen global de la concha y al sustituir el líquido cameral por otro fluido gaseoso ―nitrógeno, oxígeno y dióxido de carbono principalmente― que tiene menor densidad que el agua que le rodea se consigue una flotabilidad positiva la cual, a su vez, se contrarresta con el incremento de peso del animal al crecer y con el correspondiente a la nueva parte de la concha que se va generando. La obtención continua de este equilibrio es una labor que quedará reflejada en la siguiente sección.
Greenwald y Ward (2010)
El conocido experimento conocido como el "Diablillo de Descartes" visualiza cómo pequeños cambios de densidad en un cuerpo ubicado dentro de un fluido generan un descenso o ascenso del mismo. Ver y
En el se puede interactuar con un modelo tridimensional de la sección de la concha de un Nautilus en el que pueden verse en detalle las cámaras que componen el fragmacono. Este modelo se ha construido mediante un proceso de digitalización de un ejemplar del museo de zoología D'Arcy Thompson.
Para conocer el proceso de formación de las cámaras de los nautilos vamos a fijarnos en lo estudiado y analizado por Ward, Greenwald y Magnier (1981)

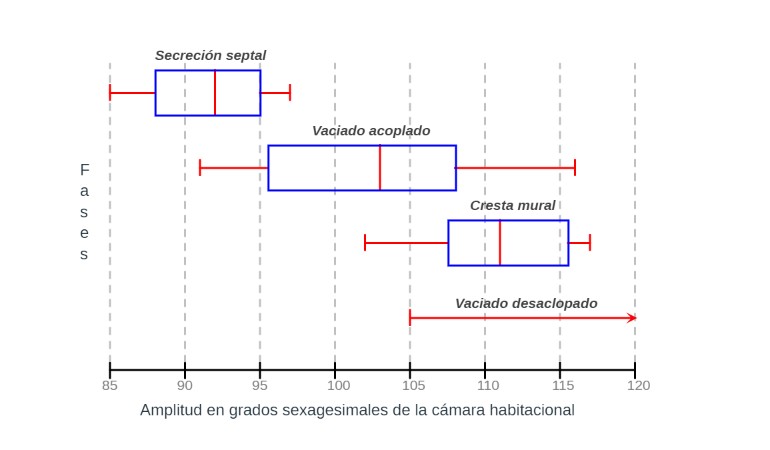
Dichos autores basan su estudio en la observación radiográfica (ver ) de diferentes ejemplares, en distintos momentos, y así pueden analizar las variaciones que acontecen y también realizar mediciones que les lleva a plantear un crecimiento periódico que comprende tres fases:
Durante el ciclo de formación de una cámara, el crecimiento de la concha exterior parece ser que es continuo, pero hay una correlación inversa entre el porcentaje de líquido que se ha vaciado en la última cámara construida y la amplitud angular de la cámara habitacional. A medida que la cámara septal está más vacía la cámara habitacional es mayor y viceversa. Esta relación logra mantener la flotabilidad ya que cuando la nueva cámara está más llena de líquido el peso de la concha en la zona habitacional es menor y a medida que decrementa el líquido aumenta la amplitud de la zona habitacional. El inicio de cada cámara representa un punto crítico para la flotabilidad global, pero esto se compensa con el vaciado desacoplado que sigue aconteciendo en las cámaras anteriores.
En base a las mediciones efectuadas por dichos autores se obtienen los siguientes datos:
En el diagrama de la se reflejan los datos anteriores.
Con posterioridad veremos que:
En ambas situaciones los valores teóricos se ubican en los intervalos empíricos aportados por Ward, Greenwald y Magnier (1981)
Cuando se forma una nueva cámara ésta queda rellena con un líquido cameral que se parece bastante al agua del mar, pero que presenta suficientes diferencias en la concentración de iones con respecto a ella. Adicionalmente no hay un camino claro por el que pudiera introducirse agua del mar en esa nueva cámara, por ello Ward y Greenwald (1982)
El sifúnculo es una extensión orgánica del cuerpo que lo une con las diferentes cámaras que va construyendo y es un órgano característico de los cefalópodos. Su desarrollo puede marcarse como un elemento clave en la evolución de estos moluscos ya que fue la que les permitió emanciparse de la vida ligada al fondo marino, una situación que puede compararse con el desarrollo de las alas en los insectos. Kröger (2003)
En el vaciado interviene un proceso fisiológico de las células epiteliales conocido como ATPase. El esquema de este proceso puede consultarse en el vídeo de youtube enlazado en la .
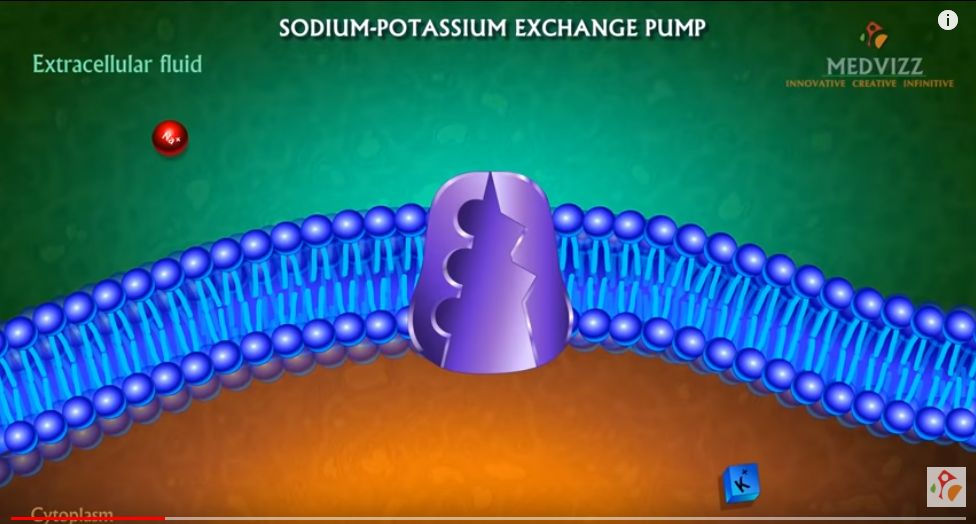
Fuente: Acceso al vídeo de youtube.
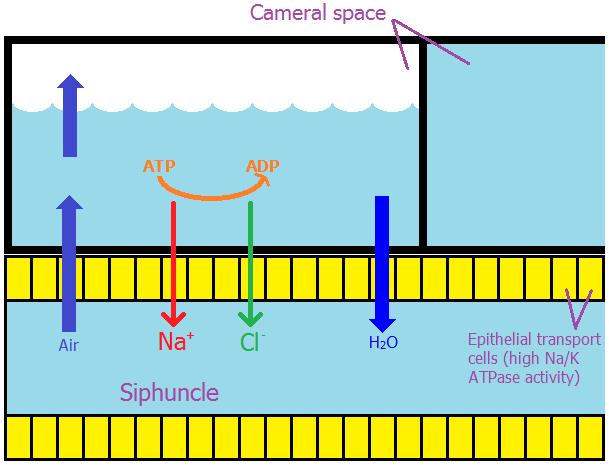
En este proceso, esquematizado en la , las células activan el vaciado de iones Na+ y CL- desde el líquido cameral al sifúnculo y generan un gradiente osmótico entre ambos. Como consecuencia el agua pasa desde la cámara al sifúnculo y el aire (oxígeno y dióxido de carbono) penetra desde el sifúnculo al espacio vacío producido en el espacio cameral. Partiendo de una composición del líquido cameral casi isotónica con el agua del mar, la salinidad baja rápidamente en la cámara alcanzando su valor mínimo cuando se está próximo a la mitad de su vaciado, lo que coincide con el momento de desacoplamiento del líquido con el sifúnculo. Después de este instante el volumen del líquido cameral sigue disminuyendo, pero pasa a incrementarse la salinidad volviendo a ser casi isotónica con el agua del mar cuando la cámara está casi vacía (Ward, 1979)
El Nautilus como todo ser vivo: nace, crece, se reproduce y muere. Y en su devenir vital va escribiendo un cuaderno de bitácora que queda reflejado y muestra en la parte exterior de su concha, pero realizando una radiografía, un escáner o una sección de la misma nos encontramos con otra bitácora secreta que incrementa aún más su belleza geométrica, una belleza que es consecuencia y está al servicio de sus necesidades vitales. Pero ¿por qué se produce un crecimiento de ese tipo? ¿qué principio conceptual lo modela?

Para tratar de dar respuesta a la pregunta anterior quizás proceda acudir, inicialmente, a ejemplos que al menos aparentemente pueden ser más sencillos. Así pues, observemos las conchas de otros moluscos como los bivalvos (WoRMS, 2024a. Bivalvia)


Sachs (1995)
«Hay ciertas cosas que cuando crecen no sufren alteración salvo en magnitud»
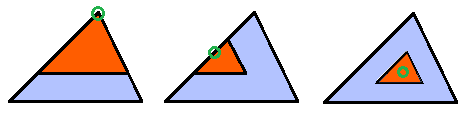
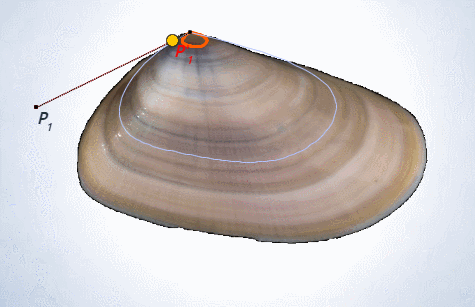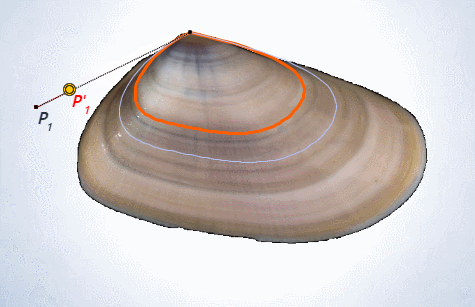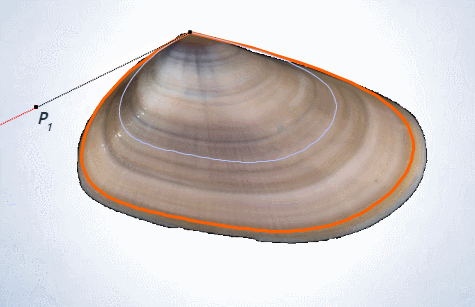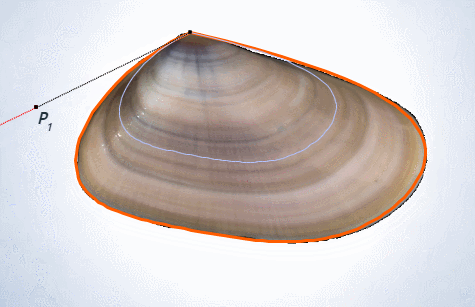
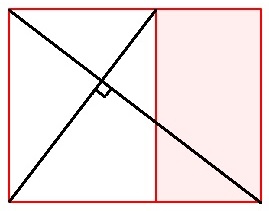
y definió el gnomon como toda figura cuya yuxtaposición a una dada produce otra que es semejante a la inicial. Este crecimiento autosemejante se produce en los seres vivos —el Nautilus de la es un claro ejemplo de ese tipo de crecimiento a nivel tridimensional—, pero en aras de sistematizar el proceso fijémonos inicialmente en las conchas incluidas en la , y , las cuales desde una perspectiva cenital y como proyección bidimensional, se caracterizan por observar un crecimiento lineal, radial, a partir de un punto central o polo.
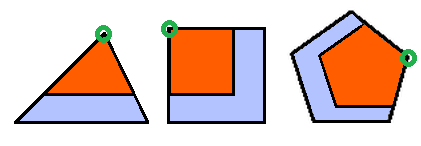
En el supuesto de un recinto bidimensional, el crecimiento autosemejante puede conceptualmente abstraerse y reflejarse en la figura geométrica 2D más sencilla, el triángulo, y extenderse a cuadriláteros, pentágonos, etc., como los dibujados en la donde el gnomon considerado se ha coloreado en azul grisáceo. Todo en base y gracias al Teorema de Thales (624 a. C.- 546 a. C.) que tres siglos después de su formulación quedó incluido en la proposición 2 del Libro VI de "Los elementos de Euclides" (Euclides ca. 325 a. C.-ca. 265 a. C.) (consultad Joyce, 2013
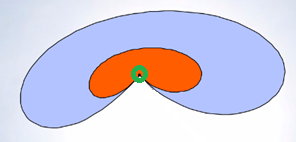
Esta situación puede aplicarse no sólo a polígonos convexos, sino también a aquellos cóncavos que tengan al menos un punto interior o en la frontera desde el que se puede contruir una familia de triángulos con área disjunta que conformen una partición de dicho polígono. Todos los triángulos tendrán ese vértice común que se
configura como el polo. Ver la , en la imagen de la izquierda el polo está en la frontera, en concreto un vértice, y en la imagen de la derecha en su interior.
Y, en general, es ampliable a recintos planos, en las que se pueda distinguir un polo desde el que todos los segmentos trazados desde él a los puntos de su frontera sean interiores a dicho recinto. Ver la .
Así pues, la base del modelo matemático puede reducirse a un triángulo. No obstante hay que considerar las posibles ubicaciones del polo en dicho polígono: bien como un vértice, bien en un lado o bien en el interior, ya que esa posición permite o impide diferentes direcciones de crecimiento (). Si el polo es un vértice, el crecimiento está acotado por los lados que determinan ese vértice. Si está en un lado, éste se configura como una frontera. Y si está en el interior, crece en todas las direcciones.
Obviamente la aplicación de este modelo requiere el establecimiento de un triángulo inicial (u otra figura genérica que fija el patrón) que se configura como el germen o embrión que de manera autosemejante irá creciendo.
En la Naturaleza los organismos están sujetos a diversas causas o limitaciones físicas, químicas o bioquímicas que influyen en su forma y crecimiento, y en este amplio contexto se configura la forma germinal y el polo director de la autosemejanza. Por señalar un contraste evidente, indiquemos que no es lo mismo el crecimiento básico conceptual del cuerpo humano que el del un caracol o cualquier molusco con concha. En el primero no hay a priori ninguna limitación en las direcciones de crecimiento, fruto de un teórico polo interior, y en el segundo la concha limita esas direcciones, correspondiéndose con un polo en el vértice o ápice. No obstante, el
último caso requiere una aclaración específica ya que la concha es el resultado de la segregación que realiza el animal y, por tanto, es la segregación la que se adapta a su forma y no al contrario. En todas estas consideraciones la fuente clásica y obligada se encuentra en "On the Growth and Form" de Thompson (1917
El modelo matemático anterior es aplicable, por ejemplo, a las conchas de los tres moluscos que antes hemos citado bajo la perspectiva bidimensional considerada hasta ahora, posteriormente las analizaremos como objetos tridimensionales que son. En las imágenes de la puede observarse, para cada concha, cuál es el polo, la forma de las líneas de crecimiento que definen el recinto que va aumentando y su gnomon.

En la se presenta una animación que modela el crecimiento gnomónico de la coquina. Y en la se observa el detalle de la poligonal utilizada para modelar las líneas de crecimiento mediante curvas de Bézier y el crecimiento gnomónico de las mismas (Galo, 2019
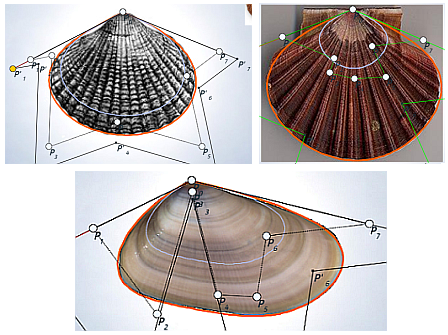
Todo lo anterior queda sintetizado en la donde puede experimentarse con todas las situaciones descritas y donde el lector puede diseñar su recinto preferido y observar su crecimiento gnomónico.
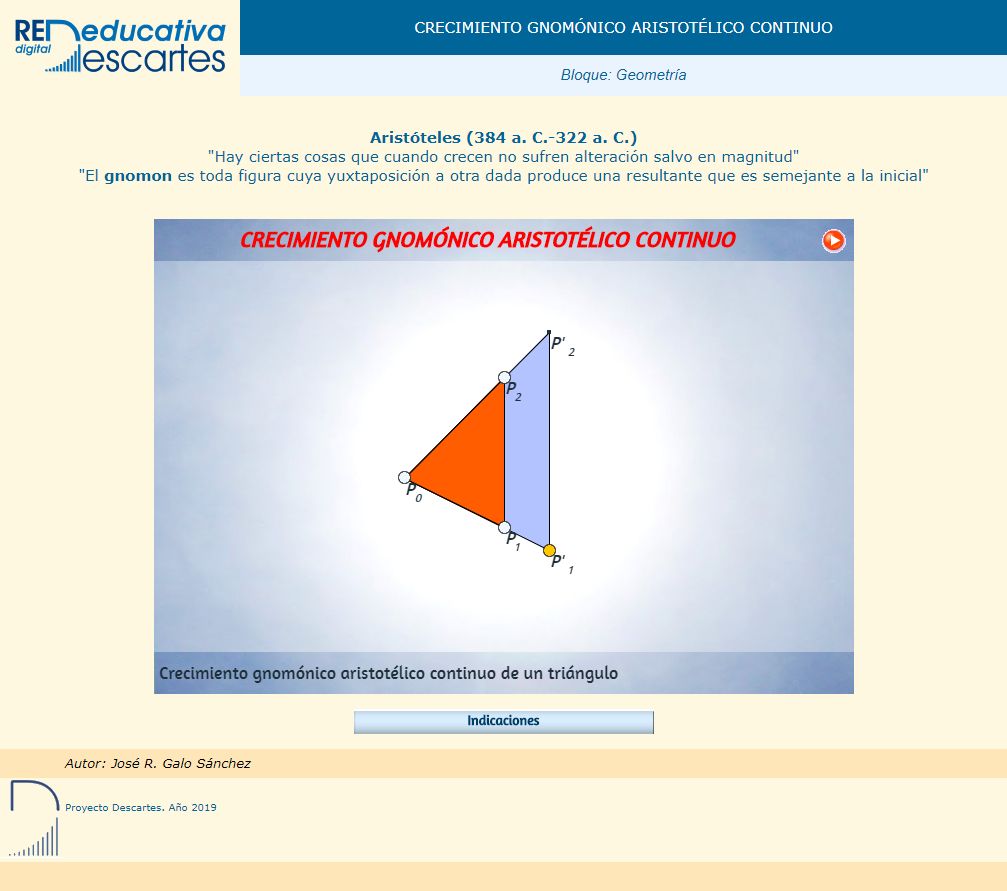
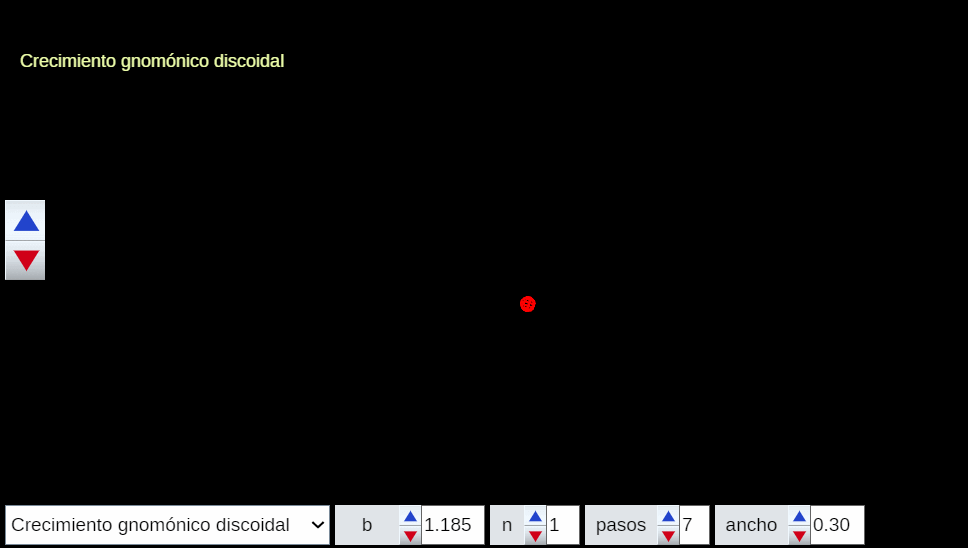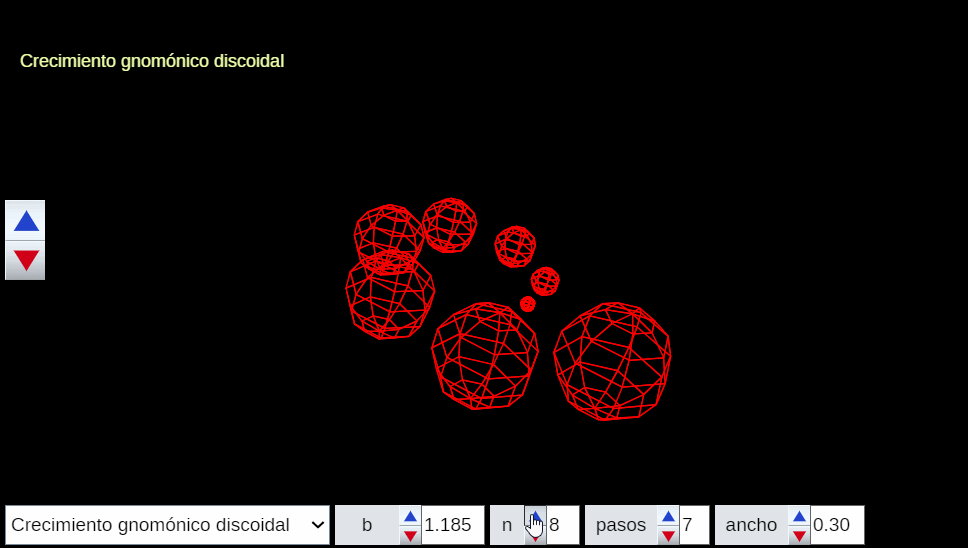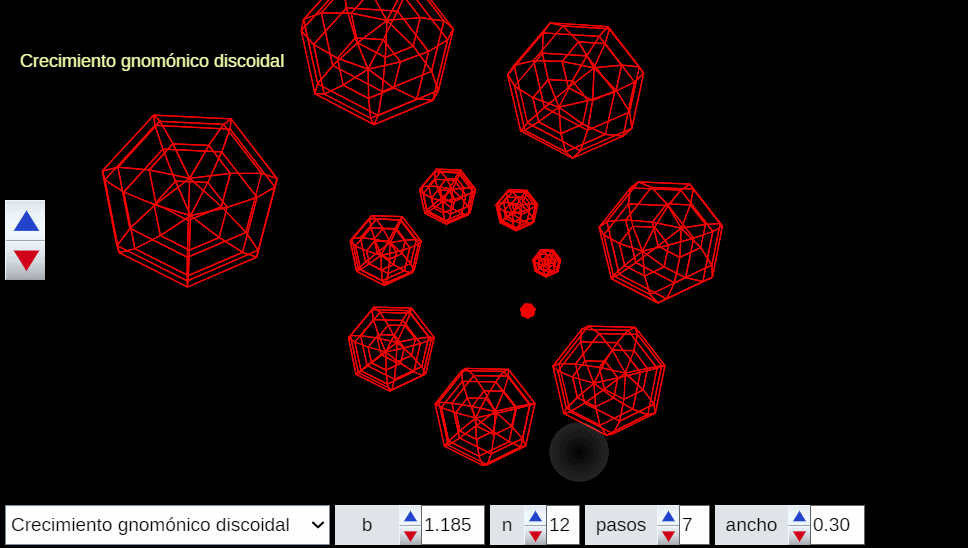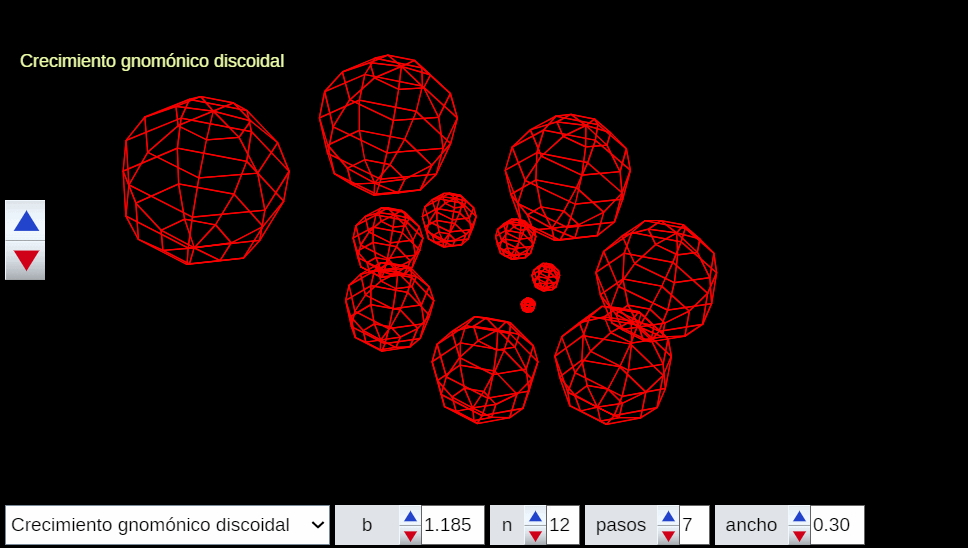
Si bien con lo descrito hasta ahora ya disponemos del modelo y fundamento matemático del crecimiento gnomónico aristotélico hemos de remarcar y detallar algunas pautas particulares que nos ayuden a comprender situaciones de crecimiento discreto o de aparente crecimiento discreto, pues pueden plantearse como instancias concretas de un crecimiento continuo.
Esas situaciones teóricas se puede observar en la Naturaleza (mirar las imágenes en la ) donde, por ejemplo, podemos ver cómo las marcas en el fósil o las cámaras de flotación del Nautilus, o las hojas del cactus o las estrías en los los cuernos marcan una pauta discreta, si bien nuestra mente construye, transmite y visualiza ese carácter discreto inmerso en una continuidad.

Las cámaras interseptos son gnómones discretos en el crecimiento gnomónico del fragmacono del Nautilus, se generan cada cierto intervalo temporal, pero entre septo y septo se observa mentalmente el crecimiento continuo.
Según Ghyca (1953
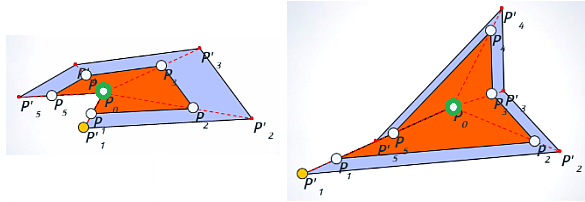
Dado un triángulo cualquiera siempre se puede construir uno semejante que lo contenga, quedando determinado su gnomon.
Proposición que podemos visualizar en la construcción realizada en la imagen izquierda de la . Ahí, partiendo de un triángulo $ABC$ y tomando un punto $A'$ de la recta $BC$ en el que se cumpla que $\hat{A'} = \hat{A}$Para que ese punto $A'$ sea exterior al segmento $BC$ tiene que ser $\hat{A} \lt \hat{B}$ en crecimiento dextrógiro y $\hat{A} \lt \hat{C}$ en levógiro, por ello en la , la y se considera siempre el ángulo menor de los tres. , se obtiene que el triángulo $ABC$ de partida es semejante al nuevo $A'B'C'$ obtenido. En esa figura, el gnomon del triángulo de color azul se ha representado en color amarillo.
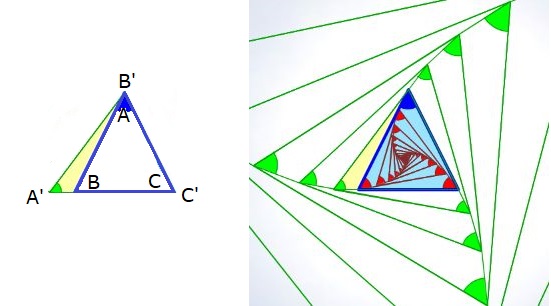
Y, en la imagen de la derecha de esa se ha reiterado esa construcción incrementando el tamaño del triángulo y también decrementando el mismo. El sentido creciente que se ha seguido es el levógiro. De manera alternativa podría plantearse en sentido dextrógiro.
Así pues, dado un triángulo se construye uno semejante. Pero con este procedimiento no es posible construir otro también semejante con dimensiones intermedias. De ahí nuestra denominación de crecimiento gnomónico discreto. No obstante, parece vislumbrarse que estos triángulos no son más que instancias puntuales de un crecimiento continuo. En esa imagen puede intuirse una curiosa ubicación de los vértices en tres espirales. Como posteriormente indicaremos la espiral logarítmica es el referente o guía de la autosemejanza y una de sus propiedades es la de ser equiángular, por tanto, lo casual realmente puede ser y será causal.
En la se modela lo sintetizado en los párrafos anteriores de esta sección. En ella disponemos de un control tipo pulsador etiquetado como "Paso":
Este planteamiento discreto podemos realizarlo también con rectángulos, es decir, podemos parafrasear a Aristóteles y afirmar que:
Dado un rectángulo cualquiera siempre se puede construir uno semejante que lo contenga, quedando determinado su gnomon.
Para la construcción de ese rectángulo semejante nos basamos en el concepto de rectángulos semejantes recíprocos, es decir, dos rectángulos semejantes en los que el lado menor del primero es el mayor del segundo o viceversa y en la propiedad que verifican de tener sus diagonales perpendiculares (consultad
En la podemos observar cómo a partir del rectángulo de fondo blanco, podemos determinar su gnomon (rectángulo con fondo rojo) y con él queda construido el rectángulo recíproco que contiene al inicial. Y con igual base constructiva se puede realizar el proceso inverso, es decir, cortar un rectángulo para obtener el recíproco contenido en él. Este procedimiento conduce a un crecimiento gnomónico discreto ya que la construcción queda limitada a cuatro direcciones (derecha, arriba, izquierda y abajo, donde usamos estos términos en base a la posición del rectángulo que hemos representado) y, por tanto, no podemos obtener un rectángulo semejante con dimensiones intermedias a los ahí obtenidos en esas direcciones.
Con este crecimiento gnomónico discreto trabajamos en su momento en el recurso "Las Matemáticas en la belleza y la belleza de las Matemáticas" (Galo, 2005
En la podemos trabajar con estas construcciones, interactuando mediante los siguientes controles:
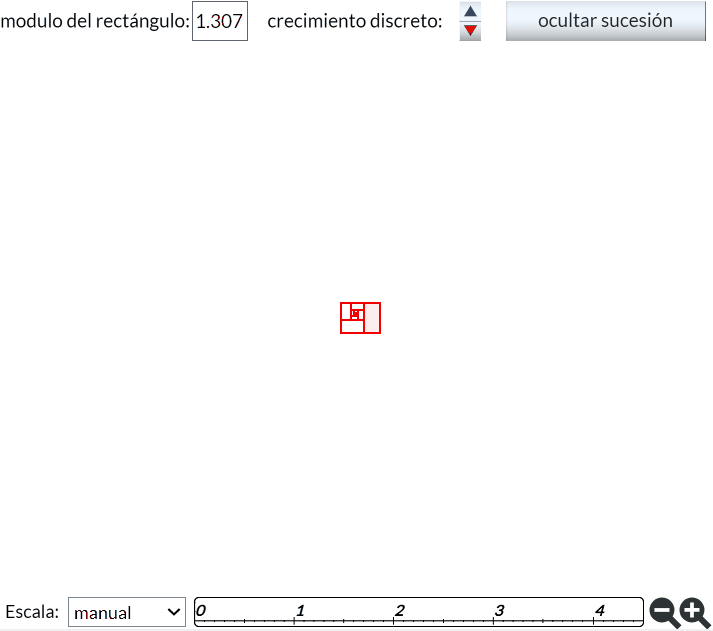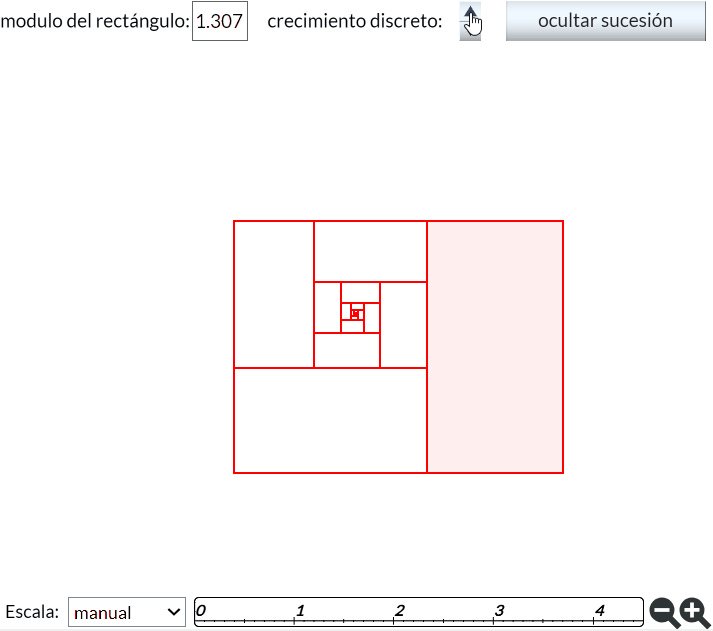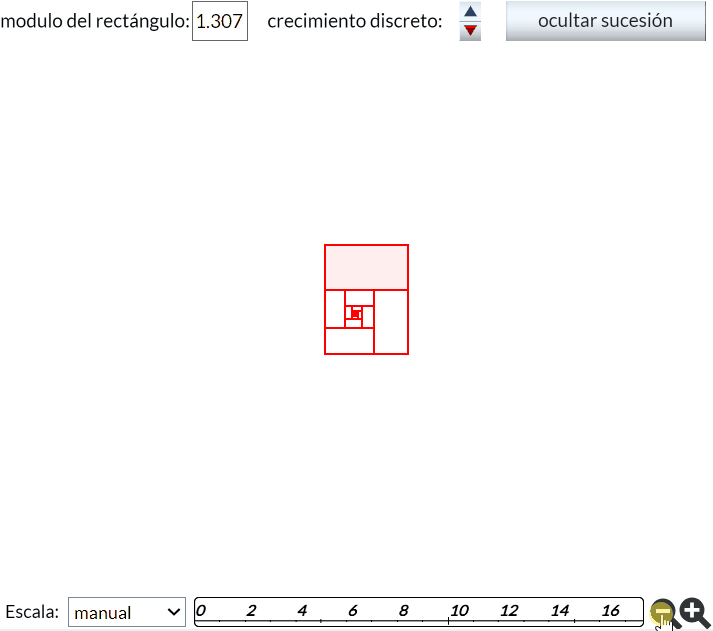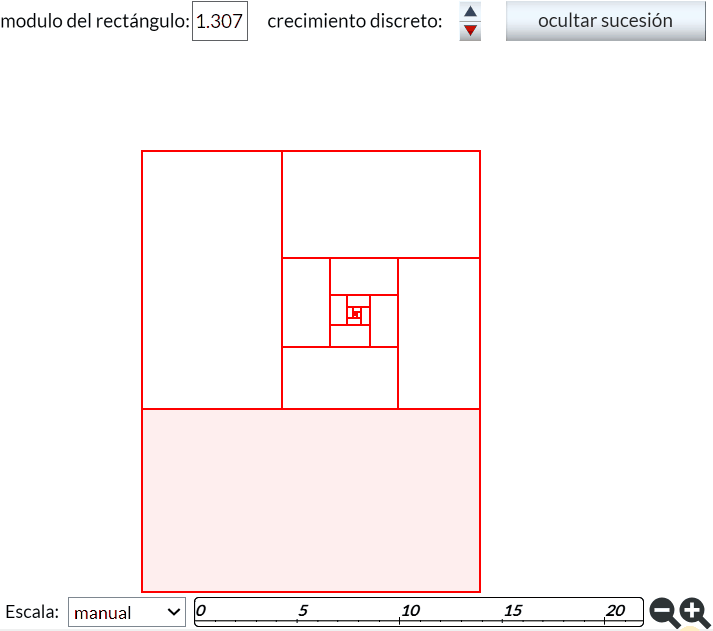
Detengámonos en este caso para visualizar cómo este crecimiento gnomónico discreto está inmerso en el crecimiento gnomónico continuo. Y ello podemos lograrlo en el momento que el procedimiento constructivo que usemos no quede restringido por las únicas cuatro direcciones admisibles en la construcción de rectángulos recíprocos. Observemos e interactuemos con la y podremos ver el crecimiento continuo de los rectangulos semejantes y que sus vértices son puntos de dos espirales logarítmicas de igual base y que el crecimiento gnomónico discreto son instantes correspondientes a ángulos que se diferencian en $\frac{\pi}{2}$. Ver también la animación incluida en la
En la disponemos de los controles descritos en la escena y además tenemos:
Análogamente este crecimiento gnomónico discreto es ampliable a pentágonos, hexágonos y polígonos de $n$ lados en general, si bien estos han de tener una forma adecuada (ver e interactuar con la ). En todos los casos se observa un crecimiento discreto en espiralEn el capítulo IV se analizan las aproximaciones gnomónicas discretas a una espiral logarítmica. de paso $\frac{2\pi}{n}$. Puede observarse cómo al disminuir el paso el crecimiento discreto converge al continuo (espiral logarítmica).
En la animación de la se refleja un resumen de lo que puede experimentar al interactuar con la escena anterior.

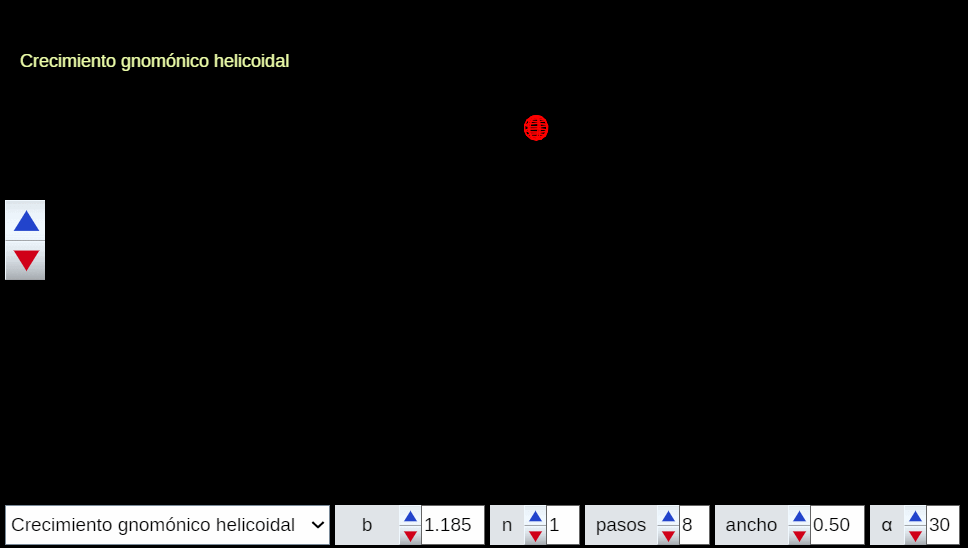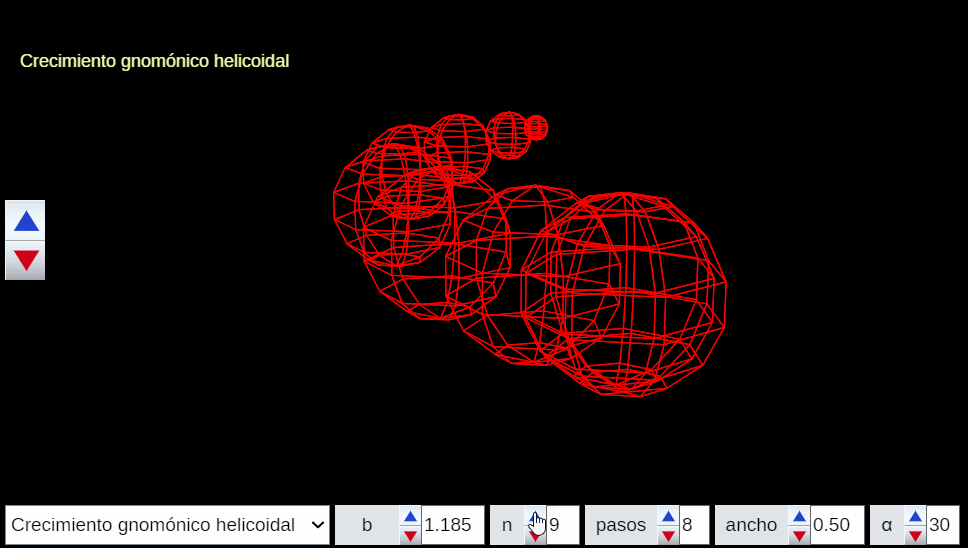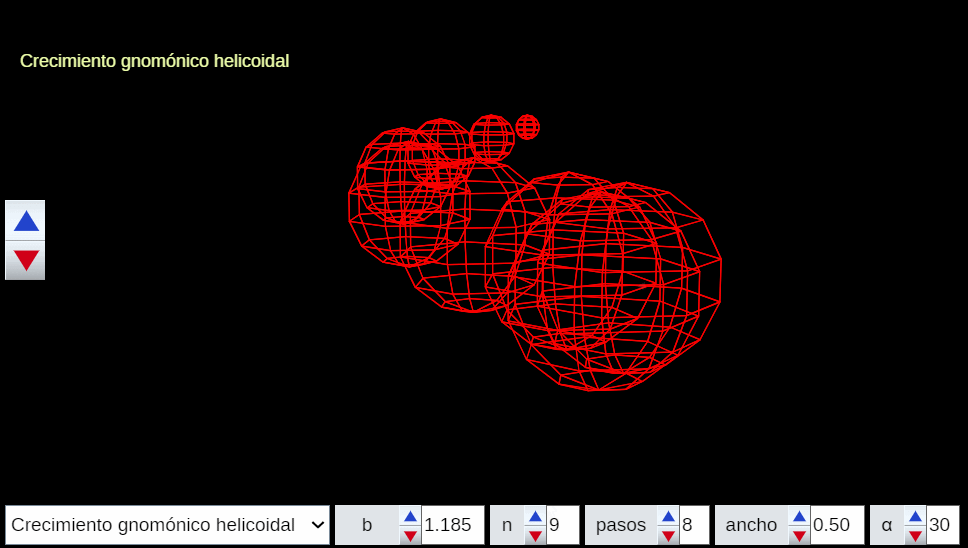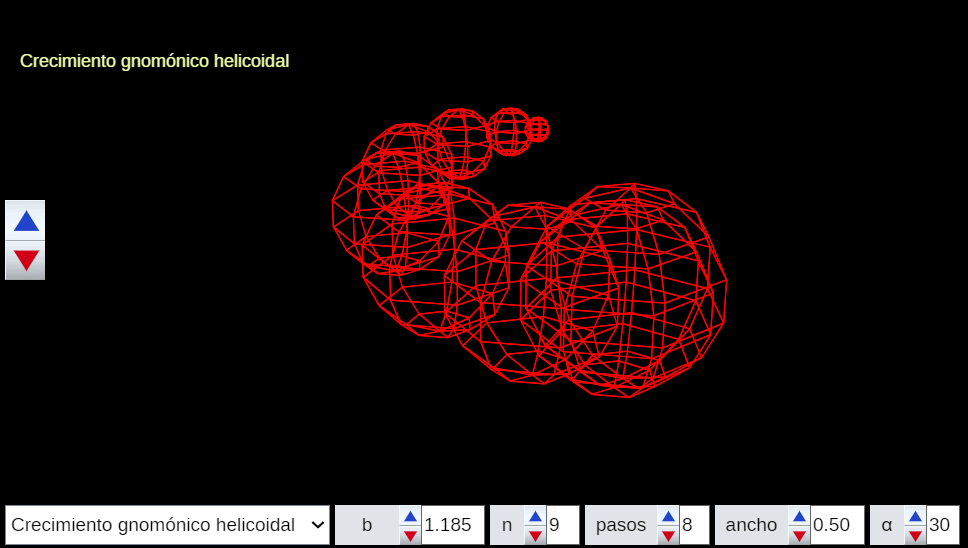
El control etiquetado como b veremos que tiene relación con el factor de crecimiento en una espiral logarítmica y el valor que se muestra por defecto $b\simeq 1,186$ veremos que tiene relación con la espiral que modela la sección sagital de la concha del Nautilus.
Progresivamente iremos experimentando como la aparente sencillez de la concha del Nautilus se sustenta en propiedades matemáticas de gran enjundia.
Un caso particularDetenerse en un caso particular, históricamente posterior a la definición aristotélica, tiene como único objetivo el contextualizar este concepto de crecimiento en el compendio geométrico básico de la Geometría: "Los Elementos" de Euclides, al que acudiremos con posterioridad y en el que surge la extrema y media razón, divina proporción o razón áurea.
del crecimiento gnomónico aristotélico es el que plantea Euclides (325 a. C.-ca. 265 a. C.) en “Los Elementos” (Euclides, 1991, p.265
En toda área de paralelogramo se llama gnomon a uno cualquiera de los paralelogramos situados en torno a su diagonal junto con los dos complementos.
Siguiendo lo comentado por Joyce (2013
Euclides, en base a esta definición de gnomom, procede a introducir en ese mismo libro II de sus Elementos la actualmente denominada razón áurea, que es la explícitamente citada en el título de este libro. La undécima proposición afirma:
Cortar una línea recta dada de modo que el rectángulo contenido por el todo y uno de los segmentos sea igual al cuadrado del segmento restante.
No obstante, como tal proporción aparecerá en la definición tercera del libro VI:
Dícese que una línea recta queda dividida en razón extrema y media cuando la parte entera es a la mayor, como ésta lo es a la menor.
Pero seamos pacientes...
Anteriormente planteamos el crecimiento gnomónico de la almeja, de la vieira y de la coquina relizando una simplificación de su forma al verlas desde una perspectiva bidimensional, como si fueran planas. Pero, realmente, somos conscientes que el crecimiento de esas conchas acontece en el espacio tridimensional y en la mostramos una animación que simula el crecimiento gnomónico tridimensional de una almeja.

En la se puede reproducir ese crecimiento y analizar cómo afectan en él los diversos controles que están a disposición del lector y que parametrizan el modelo. En particular, si se incrementa el "ángulo característico" se puede observar cómo el crecimiento de una almeja no es más que un caso similar al crecimiento de un Nautilus que posteriormente catalogaremos como crecimiento discoidal.
En el modelo bidimensional ya observamos que la forma germinal se reproduce a mayor tamaño formando las diferentes líneas de crecimiento, las cuales son una reprodución homotética, a escala, de la inicial teniendo como centro el polo de la transformacion.
En el modelo tridimensional son dos los elementos necesarios para su parametrización: el perfil de la boca y la inclinación o ángulo en el que éstas se ubican. En la escena, como ejemplo, se ha considerado como perfil una elipse de semiejes mayor y menor en proporción 4:3 y el usuario puede interactuar cambiando el ángulo entre $5º$ y $85º$ y pasar del propuesto ($20º$) que modela la almeja a uno mayor (por ejemplo 80º) que asemeja al Nautilus.
En esa escena el usuario cuenta también con controles auxiliares que permitem abordar un zum, simular el crecimiento y visualizar un corte o sección donde se evidencia la reiterada espiral.
En los moluscos podemos encontrar esencialmente tres tipos de conchas, no obstante pueden observarse otras conchas hetereomorfas que se obtienen como variaciones o combinaciones de éstas formas básicas:
se corresponde con la concha helicoidal de un gasterópodo, en concreto, el Buccinum undatum.

Thompson (1942, p. 798

En la se puede experimentar con los tres tipos descritos y modificando los parámetros obtener diferentes situaciones.
Si en el modelo anterior incluimos la sección de la boca de la concha () podemos simular cómo se generaría una concha discoidal como la del Nautilus (), donde esa boca es la curva generatriz que incrementa sus dimensiones, pero manteniendo la semejanza y el plano de giro.


Y análogamente, definida la curva generatriz, simular el crecimiento helicoidal de una concha como la de un caracol (). En la puede observarse ese crecimiento homotético, pero en en este caso combinado con un desplazamiento perpendicular al plano de giro.


En la puede experimentar, sintiéndose como un experto constructor de conchas discoidales y helicoidales, manipulando varios párametros y en particular definiendo la curva generatriz que determina la concha deseada.
Como generatriz puede considerarse cualquier sección plana de la concha, bien conteniendo al eje de giro o con cualquier inclinación respecto a él. Usualmente se considera la sección transversal obtenida por el corte con un plano que contenga al eje de giro y suele coincidir con la forma de la boca de la concha siempre que ésta se ubique en un plano.
Si seleccionamos un punto de esa generatriz, o bien un punto cualquiera de la región que delimita, y unimos todos los puntos homólogos a él obtenemos otra curva que traza la dirección de crecimiento. En el caso discoidal esa curva directriz adopta la forma de una espiral y en el helicoidal es de una hélice cónica, así pues el conocimiento de ambas curvas es básico en la comprensión del crecimiento de las conchas y en particular la del Nautilus.
Imagen generada por la IA Designer de Microsoft
Cualquiera que tome en sus manos una cuerda o una cinta se encontrará con el hecho que al asirla por un punto intermedio quedará fraccionada en dos cabos que invitarán a ser comparados, es decir, verificar si son iguales, o si uno el doble o el triple del otro, o en general cuánto cabe uno en el otro. Surge de manera natural el concepto de proporción o razón entre dos partes comparablesAl decir comparables evitamos introducirnos en el concepto de conmensurabilidad de magnitudes que llevó a los griegos a denominar como ¡irracional! la inconmensurabilidad existente entre la diagonal y el lado de un cuadrado. En este libro consideraremos que esa razón podrá venir dada por un número irracional. .
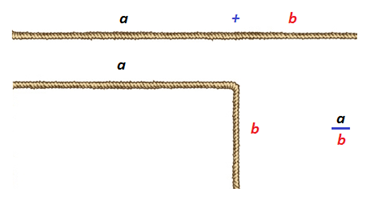
Con una simple flexión de uno de esos cabos surgirá un ángulo. Y si repetimos la construcción —gracias a la aplicación del quinto postulado de Euclides— podremos construir un paralelogramo. O mejor, en particular (ver ), consideremos un rectángulo porque nuestra propia naturaleza al estar condicionada por la gravedad nos marca intuitiva y experimentalmente esa dirección privilegiada que llamamos perpendicular.
Así pues, a todo rectángulo podemos asociarle un número al que denominaremos su módulo y que vendrá dado por la razón entre la medida de sus lados (ver ). Y en concreto, para que el módulo quede determinado de manera unívoca, realizaremos la razón entre el lado mayor y el menor, y consecuentemente el módulo será siempre mayor o igual que la unidad.
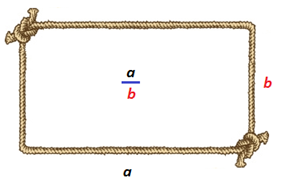
Si un rectángulo se obtiene añadiendo a otro un gnomon euclidiano, ambos tendrán igual módulo (ver ). Basta aplicar el Teorema de Thales que se demuestra en el libro VI de “Los elementos”.
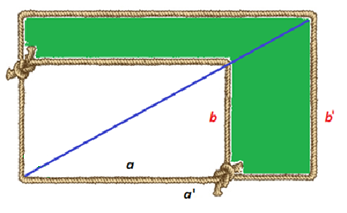
Consecuentemente:
Todos los rectángulos semejantes tienen el mismo módulo .
Pero también, de manera recíproca, se verifica que:
Todos los rectángulos con igual módulo son semejantes.
El módulo de un rectángulo coincide con la cotangente del ángulo que forma la diagonal con el lado mayor, por tanto, en ambos rectángulos dicho ángulo coincide y consecuentemente son semejantes (ver ).
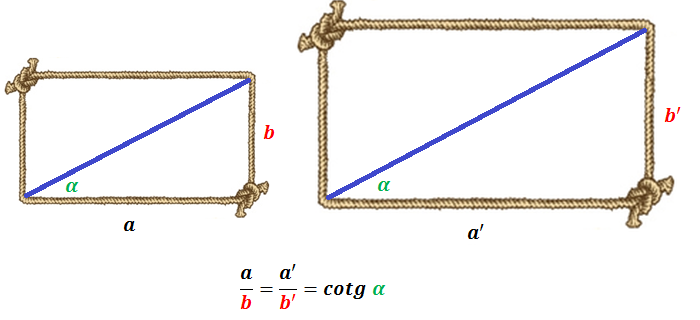
El ángulo que forma la diagonal con el lado mayor (o menor) es una característica o invariante de todos los rectángulos semejantes. Esta es la base teórica que lleva a la construcción y uso de cartabones en las artes y oficios, pues mediante una mera comparación con esta herramienta se puede identificar cuándo un rectángulo tiene igual módulo que el cartabón o bien construir con él uno con esa proporción.
Dado un rectángulo diremos que uno semejante a él es su recíproco si el lado mayor del primero es el lado menor del segundo o viceversa.
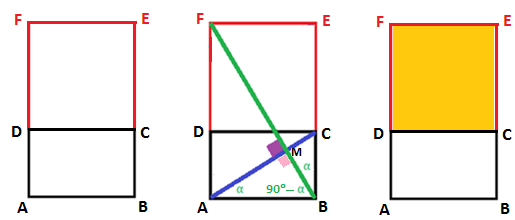
Se verifica que:
Las diagonales de los rectángulos recíprocos son perpendiculares.
En la el lado mayor del rectángulo $ABCD$ coincide con el lado menor del rectángulo $ABEF$, y para que el primero sea recíproco del segundo es necesario que sean semejantes, es decir, que se cumpla la siguiente relación:
$$\frac{AB}{BC}=\frac{BE}{AB}$$Por tanto, los ángulos $\widehat{BAC}$ y $\widehat{EBF}$ son iguales ya que tienen igual cotangente. Y dado que $\widehat{ABC}$ es un ángulo recto, entonces $\widehat{ABM}$ es el complementario del $\widehat{MAB}$ y consecuentemente $\widehat{AMB}$ es también recto, es decir, las dos diagonales son perpendiculares.
El gnomon del rectángulo $ABCD$ es el $CEFD$ (en color naranja en la figura ), rectángulo que al añadirlo al anterior nos determina su recíproco $ABEF$.
En la definición tercera del libro sexto de "Los Elementos", Euclides sublimó el planteamiento de la división de un segmento en dos partes al señalar:
Un segmento se dice que está dividido en extrema y media razón si
el segmento entero es a la parte mayor como ésta es a la menor.
Ahí (ver la ), se establece una proporción a la que Luca Paccioli (
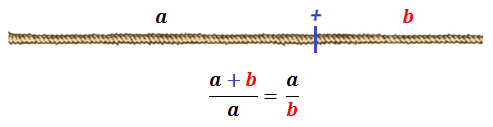
Este planteamiento puede parecer artificioso y, a priori, lo es. Pero no queramos pedir a Euclides, paradigma y ejemplo de sistematización y formalización, que actuara de manera diferente a como tantísimas
veces, demasiadas, procedemos los matemáticos a esconder en nuestros trabajos cuál fue el origen y germen de lo que analizamos y estudiamos. Es usual que en la divulgación de nuestras investigaciones solemos centrarnos en lograr un correcto y preciso planteamiento académicoPlatón, 427-347 a. C., fundó la Academia y fue maestro de Aristóteles 384-322 a. C.; Euclides vivió del 325 al 265 a. C. que suele conducir a la típica pregunta y exclamación de nuestros discentes: ¡¿Y esto, a quién se le ocurre?!
Pero ¿dónde radica la importancia de esa proporción? ¿por qué tanto interés es una proporción entre una infinidad de ellas? Euclides no lo indica, pero podemos inicialmente realizar algunas conjeturas y después, también, hacer un análisis en "Los Elementos" y tratar de inducir su porqué.
Comencemos con las conjeturas. Pudiera haber acontecido por:
Si en esa construcción exigimos que el rectángulo inicial y el nuevo sean semejantes surge la relación indicada en .
Adicionalmente, obsérvese que el gnomon que relaciona a ambos rectangúlos es un cuadrado.
Podemos plantear la situación recíproca de la anterior (ver ), es decir, partir de un cuadrado y en base a él proceder a construir dos rectángulos recíprocos cuyo gnomon sea justamente ese cuadrado, con lo que obtendríamos los rectángulos recíprocos que tienen el gnomon más sencillo posible.
¿Cuál es la proporción de los rectángulos recíprocos así obtenidos? En la se ha obtenido esa proporción y efectivamente es la extrema y media razón. Puede observarse también en la .
Ghyca, (1953
$$\frac{a}{\color{red}b},\quad \frac{\color{red}b}{\color{blue}c},\quad \frac{\color{blue}c}{a},\quad \frac{\color{red}b}{a},\quad \frac{\color{blue}c}{\color{red}b},\quad \frac{a}{\color{blue}c}\quad $$
Y si se igualan dos a dos se tienen quince posibles combinaciones que dan lugar a sendas proporciones. Si de ellas excluimos aquellas que no son posibles y a las que podemos considerar triviales, es decir, cuando $\color{blue}c= a$, o $\color{blue}c=\color{red}b$, o $a =\color{red}b$, restan sólo dos situaciones:
$$\frac{a}{\color{red}b}=\frac{a+\color{red}b}{a},\quad \frac{a}{\color{red}b}=\frac{\color{red}b}{a+\color{red}b}$$
que realmente corresponde a la misma situación porque basta cambiar el papel de $a$ y $\color{red}b$ o bien establecer de partida que $a$ sea mayor que $\color{red}b$. Consecuentemente la única proporción asimétrica posible es la correspondiente a la extrema y media razónSi en $\frac{a}{\color{red}b}=\frac{a+\color{red}b}{a}$ hacemos $x=\frac{a}{b}$ obtenemos la ecuación $x=\frac{x+1}{x}$ cuya raíz positiva es $\frac{1+\sqrt{5}}{2}\simeq{}1,61803398875...$ que es el denominado número áureo..
Así pues, aunque inicialmente sorprende lo de "la extrema y media razón" parece ser que no es difícil llegar a ella cuando alguien está trabajando con proporciones y semejanzas. Pero, quizás, el interés de Euclides se vea amplificado si profundizamos más y vemos donde aplica o usa Euclides esta específica razón, es decir, analizar la posible causa y, con ello, eliminando esa primera impresión de casualidad.
Siguiendo el orden deductivo euclidiano, hemos de retroceder a la proposición undécima del libro segundo (ver ). En el libro

VI ya indicamos que aparece la definición, pero ahí lo único que se hace es denominarla. En esta proposición se establece el objetivo de:
dividir una línea de manera que el rectángulo formado por ella y una de sus partes sea igual al cuadrado de la parte que resta.
que no es más que la división en extrema y media razón.
Pero no es hasta el libro cuarto, que es el que trata sobre figuras inscritas y circunscritas en una circunferencia, cuando nos encontramos una aplicación de la "extraña" partición anterior. En la proposición décima (ver ), Euclides plantea:
Hacer un triángulo isósceles que tenga cada uno de los ángulos iguales el doble del desigual .
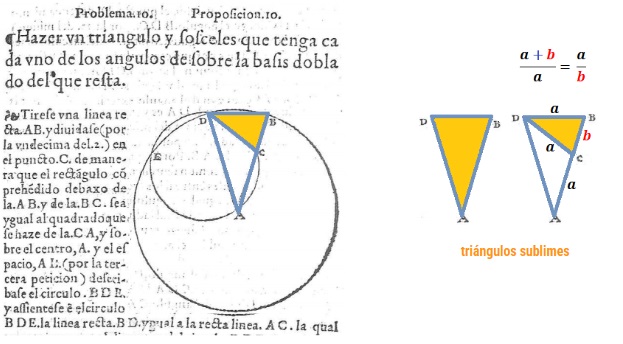
Ese triángulo ¡cómo no! se denominó posteriormente ¡triángulo sublime! —¡qué no baje el nivel de exaltación en los calificativos!—. Y en su construcción se requiere de esa partición en extrema y media razón. Los lados de ese triángulo siguen esa proporción.
Tenemos ya al menos una motivación: "la extrema y media razón es necesaria para obtener este triángulo sublime", aunque aún no conozcamos el interés final de este logro Reiteremos que esto es lo que acontece al seguir la sistematización y formalización que introdujo Euclides en sus libros y que desde entonces se sigue repitiendo en los ambientes académicos, donde se aborda una exposición progresiva de menor a mayor dificultad y se oculta la motivación inicial y las líneas de trabajo seguidas realmente por el investigador, tanto las productivas como las abandonadas por alguna decisión personal o por no haber sabido llevarlas a buen término. Siguiendo esa línea expositiva se obtiene una narracción unidireccional académica, organizada, precisa, pautada y aséptica, pero que, en general, queda descontextualizada en sus motivaciones y causas para el lector. .
Pero afortunadamente, en este caso, Euclides no tarda en manifestar la utilidad que perseguía ya que en la siguiente proposición, la undécima del libro cuarto (ver ), usa el triángulo sublime para construir el pentágono regular en el que dos diagonales consecutivas se cortan ¡en extrema y media razón!
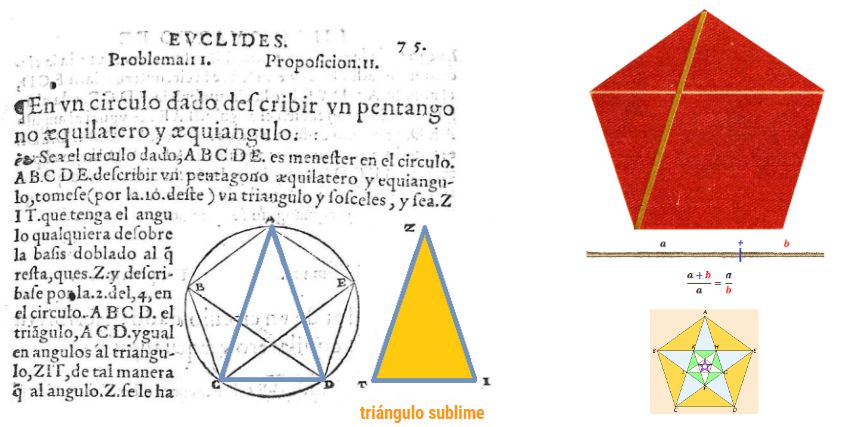
Previamente en ese libro se ha construido de manera sencilla el triángulo equilateral y equiangular e igualmente el cuadrado y en la
siguiente construcción, la del pentágono, se ve que surgieron las dificultades y requirió toda esta artillería matemática para su logro. Todo gran esfuerzo produce excitación y gozo y no es de extrañar que este logro se magnificara a lo largo de los siglos. Y que los pentagramas que surgen en la construcción de esta proposición se hayan usado como iconos identificadores de grupos o sectas, si bien éste icono ya era propio de los pitágóricos y Pitágoras (c. 570, c. 490 a. C.) es antecesor de Platón, de Aristóteles y de Euclides, es decir, que éste último se permite la licencia de divulgar ese oculto saber previo.
Y aún más importancia le darían si constatamos que la alegría constructiva se les acabó pronto ya que, aunque la construcción del hexágono regular es elemental a partir del triángulo equilátero pues construido un polígono regular es trivial la construcción del polígono que tiene el doble de lados, el heptágono seguro que les supuso una indigestión al igual que el eneágono y endecágono... ¡qué gracias a Gauss ahora bien sabemos que no son construibles con regla y compás! Seguro que pasaron un mal rato al no saber construir esos polígonos regulares, lo cual se lo callaron, y consecuentemente en esto podemos encontrar la justificación de ese enardecimiento del pentágono y de esta excelsa razón que se magnifica y a la que se le da nombre propio: ¡Extrema y media razón!Omitimos explicar el porqué de la denominación "extrema y media razón", baste recordar que en una proporción $\frac{a}{b}=\frac{c}{d}$, $a$ y $d$ son los extremos y $b$ y $c$ los medios. Si $b=c$ se dice que la proporción es continua y este valor es la media geométrica de $a$ y $d$ que viene dada por $c=\sqrt{a d}$. Además $a$, $b$ y $d$ están en proporción geométrica.
Ante lo detallado en la sección anterior, y como ahí adelantamos, no es de extrañar que cuando Luca Pacioli tiene alcance a los resultados citados y a los de “Los elementos” en general, su estudio le catapulte
a escribir el libro que tituló “La divina proporción”

La primera que es una y nada más que una, al igual que Dios es uno y sólo uno. La segunda es que en la proporción intervienen tres términos al igual que la Santísima Trinidad son tres sustancias en una sola. La tercera es que es inconmensurable, irracional, no es expresable en cantidad racional, al igual que Dios no puede ser entendido por nosotros con palabras. La cuarta es que como Dios no puede cambiar y está en todas partes. La quinta que lo mismo que Dios es la quinta esencia del universo, la que da el ser a los cuatro elementos: tierra, agua, aire y fuego, la proporción divina lo es para los cinco poliedros regulares que los representan y sin ella no puede relacionarse e inscribirse en una esfera. Y, Pacioli, en su euforia,
asigna a la proporción divina diversos efectos. Entre ellos el efecto noveno lo cataloga como excelso el cual es el hecho antes citado de que dos diagonales consecutivas de un pentágono regular se cortan en media y extrema razón. Y continúa hasta el efecto decimotercero o dignísimo efecto porque sin su ayuda no podría construirse el pentágono. Y ahí detiene su descripción por reverencia a Nuestro Salvador Jesucristo y sus doce apóstoles.
Parece obvio que esa extrema pasión de Pacioli es el pilar sobre el que se basa y el que provoca en la Edad Moderna y Contemporánea la inmensa admiración por su divina proporción. Y más, teniendo en consideración que este efecto se ve ponderado por su amigo Leonardo da Vinci que ilustra su trabajo y también por Alberto Durero

Pero no puedo dejar de comentar que a esta euforia pacioliana, indirectamente y directamente, ¡también contribuimos los cordobeses!El autor es oriundo de la provincia de Córdoba (España) y la proporción cordobesa toma su nombre de este topónimo. "Los Elementos" de Euclides, al igual que gran parte
del saber científico griego, nos ha llegado a través de traducciones al árabe de manuscritos en griego, lo cual acontece en torno a la época del Califato de Córdoba (siglos X y XI), luego fue traducido del árabe al latín (siglo XII) y ampliada su difusión mediante su impresión a finales del XV. La primera edición impresa es de 1482 (época de Luca Pacioli) y se basó en versiones árabes y, en particular, en una versión latina atribuida a Adelhard de Bath quien estuvo en Córdoba a principios del siglo XII. A él se le atribuye el primer caso de espionaje científico porque se infiltró en la escuela matemática cordobesa y además del cero, que le debió de saber a poco o nada, llevó consigo un ejemplar de "Los Elementos".
Posiblemente éste fue el camino a través del cual Fibonacci en el siglo XII tuvo conocimiento y difundió el sistema de numeración posicional gracias a ese cero indo-arábigo. Y también cómo, posteriormente, Luca Pacioli pudo construir su eufórica exaltación de la “proporción divina”.
¡Euclides se hizo cordobés!

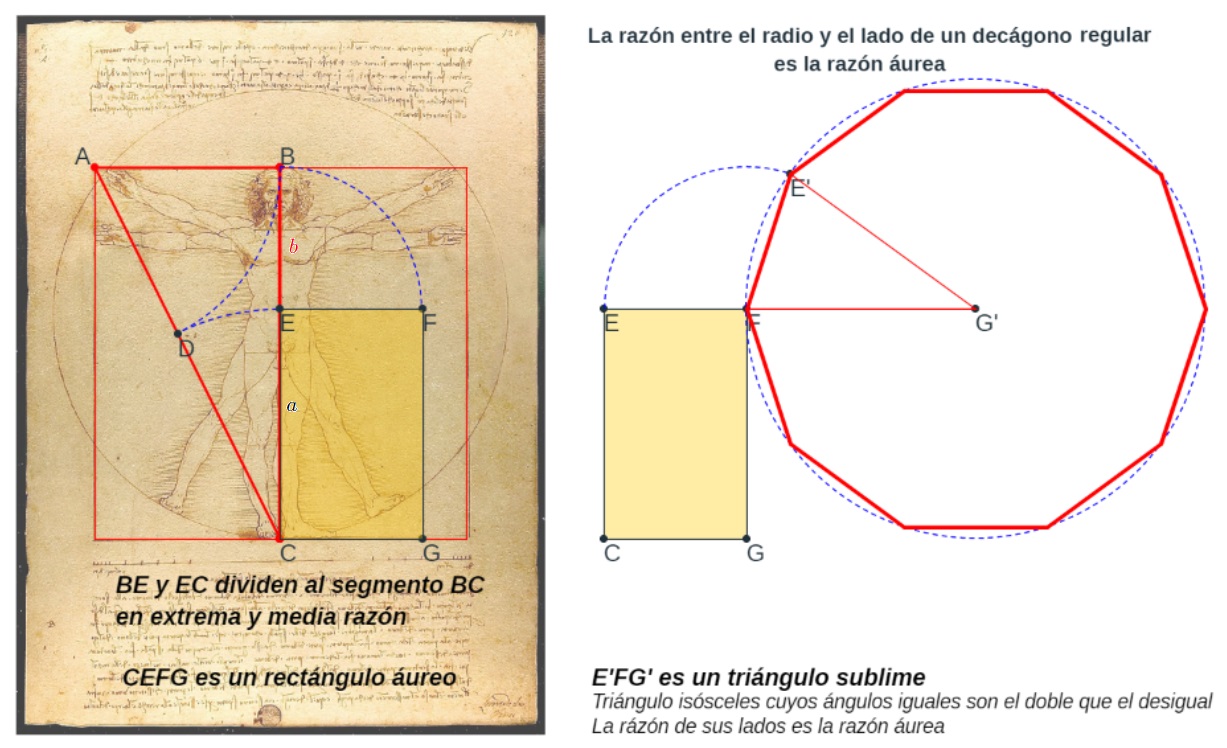
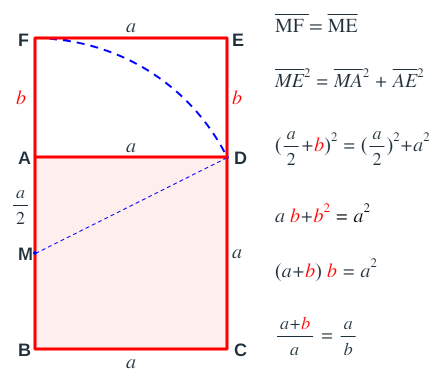
Leonardo da Vinci adoptó esta proporción divina como pauta para la elaboración del canon de belleza humano y lo reflejó en su dibujo del hombre de Vitrubio. En la podemos ver como equipara la altura de un hombre a la longitud entre sus brazos. Partiendo del cuadrado que determinan estas dos magnitudes y apoyándose en el eje de simetría del mismo, que es eje de la figura humana, procede a dividir este segmento en extrema y media razón, donde el ombligo es el punto que determina esta partición En la imagen se tiene que $\overline{CE}=a, \overline{EB}=\color{red}b$ y según la construcción realizada, aplicando el teorema de Pitágoras en el triángulo rectángulo $ABC$ tendríamos que $\overline{AB}^2+\overline{BC}^2=\overline{AC}^2$ , es decir, $(\frac{a+\color{red}b}{2})^2+{\footnotesize(a+{\color{red}b})^2}=(\frac{a+\color{red}b}{2}+a)^2$, de donde se obtiene que ${\footnotesize(a+{\color{red}b}) {\color{red}b}=a^2}$, es decir, $\frac{a+\color{red}b}{a}=\frac{a}{\color{red}b}$. . La proporción divina queda reflejada en el cuerpo humano y el ombligo se configura como el centro armónico de esta belleza. De ahí surge también la denominación de proporción armónica y ¡la belleza davinciana queda ligada a esta proporción!
Adicionalmente, en esa figura , si se flexiona el cuerpo por la cintura a la altura del ombligo (las líneas que lo representan), se obtiene un rectángulo que guarda esa proporción al que lógicamente se nombra como rectángulo armónico, áureo o dorado. E igualmente los lados de ese rectángulo también se corresponden con los lados del triángulo sublime y con diez triángulos sublimes se construye un decágono regular, es decir, tenemos que la razón entre el radio y el lado del decágono regular es la razón divina. En la se hace una descripción visual y textual de estas relaciones.
Consecuentemente, comprobamos cómo esta belleza davinciana puede abstraerse y representarse mediante un rectángulo y un polígono regular: el decágono. Y ello, nos induce a plantearnos cuáles son las bellezas ligadas a otras proporciones, a otros rectángulos y, en particular a otros polígonos regulares porque parece que es evidente
buscar el conocimiento de la belleza a través de la búsqueda de las proporciones, pero lo que no es tan obvio es que esa búsqueda se convierta en una obsesión por encontrar la proporción divina en todas las cosas. Para que algo sea bello ¿ha de seguir a la fuerza la proporción divina? (ver ).
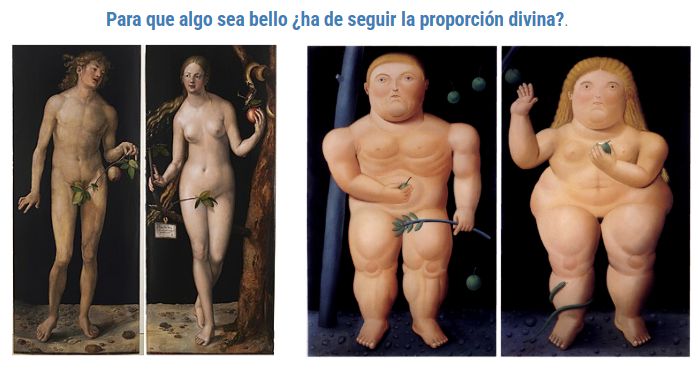
La fijación de Pacioli por la divina proporción y análogamente la de Da Vinci por la belleza divina, al igual que Durero y un ingente número de grandes artistas que desde el siglo XV hasta nuestros días la han seguido a pie juntillas (ver por ejemplo la ), nos deja un camino amplio de elección de otras bellezas. Quizás demasiado extenso, pues tendríamos por delante una muestra infinita que analizar y, además, sería excesivamente arriesgado si esto llegara a interpretarse como un intento de rebatir a tan excelsos personajes, por ello, de partida remarquemos con firmeza que no es ésa la intención.
 |
 |
 |
Si en la búsqueda de nuevos cánones de belleza seguimos el camino de Leonardo Da Vinci, podemos modelar la belleza mediante la razón entre la distancia desde los pies al ombligo y desde éste hasta la cabeza, asociándola a la proporción de un rectángulo. Pero, para restringir las posibilidades busquemos que también esa proporción coincida con la relación entre el radio y el lado de un polígono regular (ver la animación de la e interactuar con la ). Y adicionalmente, a nivel teórico y ubicándonos en el purismo euclidiano excluyamos aquellos polígonos que no son construibles con regla y compás, es decir, que consideraremos sólo los polígonos regulares cuyo número de lados son 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96,... que sigue siendo una infinidad, pero que en este contexto, en la práctica, realmente quedará reducido a un pequeño conjunto de posibilidades ya que se observa cómo la razón crece y para el dodecágono esta razón es próxima a dos y, como comprobaremos, ello se corresponde con una belleza bastante atípica.
Si trasladamos esto al hombre de Vitrubio, que ahora lo convertimos en polifacético pues adopta todas las caras o formas que deseemos sin más que cambiar la posición del ombligo. Podemos observar (ver animación en la ) que para polígonos de doce lados o más su traslación al hombre de Vitrubio conduce más a una desproporción que a una armonía, una situación de hombres patilargos, es decir, con un largo de piernas mayor al usual y, al contrario, paticortos para polígonos de de seis o menos lados.

En la disponemos de un control gráfico que al seleccionarlo y desplazarlo nos permite cambiar la posición del ombligo y así observar cómo varían las proporciones en la imagen. Y si dejamos de seleccionarlo, pulsando sobre cualquier otro punto de la escena, se activa un campo de texto donde podemos elegir el rectángulo y razón asociada a cada polígono regular y comprobar el canon de belleza asociado a dichos polígonos.
En la se realiza una comparativa del hombre de Vitrubio correspondiente a la razón asociada a los seis primeros polígonos regulares construibles. Tenemos que los tres casos primeros se corresponden con situaciones de hombres con menor largo de las piernas que del tronco y cabeza, iguales en el caso del hexágono y mayor largo de piernas en el octógono y decágono, sin llegar a ese carácter patilargo indicado para valores superiores. El caso del decágono y el octógono son los más frecuentes y asumibles en el contexto de una población gausiana normal y quizás también, aunque algo menos, el caso del hexágono.

Así pues, entre las diversas alternativas parecen surgir dos posibles cánones de belleza procedentes de razones poligonales. La primera es la belleza armónica davinciana ligada a la proporción divina y otra una belleza ligada al octógono. Y por contraposición al canon divino diremos que tenemos el canon humano y a la razón correspondiente al cociente entre el radio y el lado del octógono la denominaremos razón humanaAsí la denominó Rafael de la Hoz Arderius (Hoz, 1973

En la podemos realizar una comparativa personalizada, elegir nuestro canon y compararlos con otros.
Llegados a este punto podemos abordar el dar respuesta a cuestiones en la que subjetividad toma parte, pero en las que el apoyo matemático antes analizado introduce cierta razón a través de la razón matemática. Así pues, observando la podemos preguntarnos:
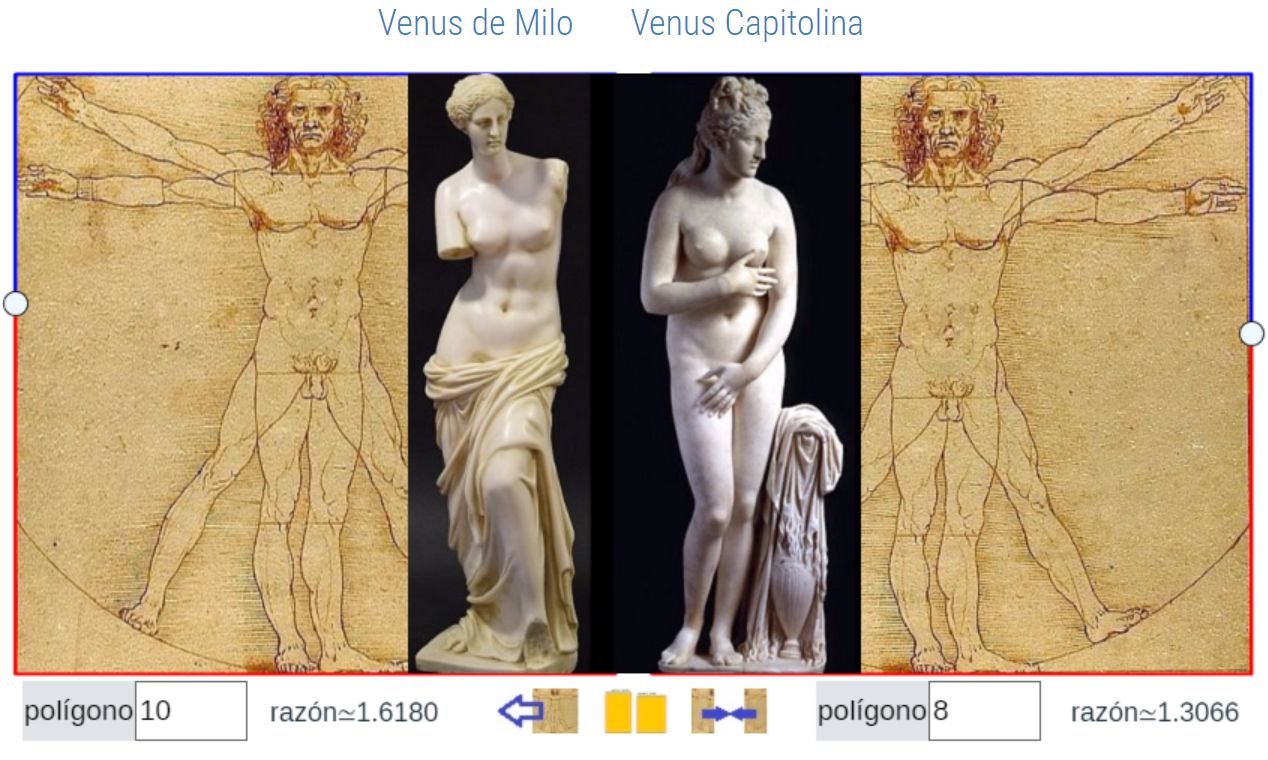
¿Cuál es más bella? ¿La venus de Milo o la venus Capitolina?
Pacioli lo tendría claro, tomaría su compás áureo y seleccionaría la Venus de Milo. Pero ¿cuál es su elección?
Y si nos ha gustado el reto anterior, procede abordar otra comparativa y posicionamiento igual de difícil. Observemos ahora la y respondamos:
¿Cuál les parece más bello? ¿El Apoxiómeno de Lísipo o el David de Miguel Ángel?

La elección es personal y nadie la va a cuestionar. Pero aquí, sí vamos a destacar y poner de manifiesto que la comparativa compuesta en la resulta irónica e incluso graciosa, pues en ella hemos contrapuesto al hombre de Vitrubio de Leonardo con el David de su gran rival Miguel Ángel y, en ella, parece detectarse una prolongación de la inquina que se profesaron. Y más, si a la vista de esa comparación señalamos, incluyendo cierta inventiva por nuestra parte, que Miguel Ángel parece que diseñó a su majestuoso David como "humano" tratando de obviar a toda costa el modelo "divino" de Leonardo. No es más que mera especulación, pero… la imagen habla por sí sola, ¿verdad?
Es obvio, o al menos lo parece, que de manera lógica surge el canon humano, ligado al octógono y al rectángulo cordobés. Pero ¿por qué cordobés?

Quizá convendría una visita a Córdoba en Andalucía (España) y a uno de sus más singulares edificios. En la tenemos una vista aérea de la mezquita-catedral con el patio de abluciones o patio de los naranjos, las naves, el muro de la quibla y las bóvedas de la macsura y del mihrab... y embebida en ella la catedral de Córdoba, realmente la catedral nueva y también la antigua (sí, una catedral en una mezquita o una mezquita que acoge a una catedral). Y a la derecha una de las puertas laterales, la de Alhaken II por la que el califa accedía directamente desde su alcázar a la macsura. La mezquita de Córdoba es patrimonio de la humanidad y Córdoba es la ciudad que más nombramientos patrimonio de la humanidad acumula: la mezquita, el casco histórico, los patios como patrimonio inmaterial y Medina Azahara, ciudad califal efímera del siglo X de la era actual (936-1013).
En la animación de la podemos adentrarnos en la mezquita de Córdoba, ubicarnos en sus naves configuradas por un
bosque de columnas y de arcos de medio punto y de herradura con inconfundibles y únicos colores identitarios, esos alternantes blancos y rojos de la piedra y el ladrillo que los componen. Y les adentro en este entorno porque aquí, con seguridad, estuvo nuestro espía científico. Sí el que se llevó el cero junto a los Elementos de Euclides, pero no lo cito de nuevo para reprender su hurto, no, los cordobeses y los andaluces en general somos desprendidos, por algo el lema de nuestra comunidad es: “Andalucía por sí, por España y la Humanidad”, lo mismo que el de la Red Educativa Digital Descartes de la que soy socio es: “trabajando altruistamente por la comunidad educativa de la aldea global”.

Les recuerdo a nuestro espía porque, con seguridad, cuando penetró en la mezquita quedaría tan empequeñecido, perdido, sorprendido, asombrado, maravillado desconcertado, obnubilado, estupefacto,... y ¡paro! porque me estoy pareciendo a Pacioli al describir no los efectos de la proporción divina, sino los efectos de esa singular belleza humana en un pobre ser humano.
 |
 |
En la imagen de la izquierda de la podemos ver los arcos polilobulados que dan acceso a la macsura —recinto reservado donde se sitúa el califa o el imán durante las oraciones públicas— y en ella el mihrab (imagen de la derecha) con su arco de herradura que sirve de guía de orientación para que los creyentes dirijan su rezo hacia La Meca. Es la puerta simbólica de acceso a dicha ciudad. No obstante, el mihrab de la mezquita de Córdoba no está orientado hacia La Meca, diversas causas pueden apuntarse desde la más simple de ajustarse al terreno disponible cuando se inició su construcción, pasando por su coincidencia con la orientación de las mezquitas de Damasco origen de la dinastía omeya que constituyó el Al-Andalus, pero la que para mí no es admisible es la que lo achaca a una falta de conocimiento a quienes, como hemos indicado, fueron el canal de comunicación del saber antiguo, más cuando la mezquita de Medina Azahara si está orientada hacia La Meca.
Pero ése es otro tema que siendo muy interesante no vamos a detenernos en él, pues largo es el camino en el que nos hemos embarcado. Pero ello, no es óbice, para pararnos a contemplar detalles de esta zona ricamente embellecida con mosaicos bizantinos (ver animación en la ) y regocijarnos en su belleza que podemos acompañar de un canto más moderno, un siglo posterior, pero que transmite la espiritualidad eterna de este lugar (Canto al amanecer de Carlos Cano, en "Crónicas granadinas", 1978).

Y en la podemos admirar el interior del mihrab de planta ¡OC-TO-GO-NALl! y curiosa bóveda en forma de concha. Pero aquí no pudo estar nuestro espía, pues es el sanctasanctórum. Pero en su atolondramiento y desconcierto tuvo que dejar escapar a su vista otro elemento arquitectónico intrínseco en la mezquita de Córdoba: ¡La bóveda cordobesa! la cual tiene como base matemática el OC-TÓ-GO-NO. Si nuestro espía la hubiera contemplado ¡también se habría llevado consigo el saber matemático que contiene! y Luca Pacioli habría tenido un dilema al tener que elegir entre el decágono y el octógono y entre las dos proporciones asociadas a los mismos.

Nuestro espía, obnubilado por el entorno, no repararía que en la parte más lujosa de la mezquita, en la denominada ampliación de Alhahen II, hay cuatro bóvedas que por su características constructivas permiten abrir huecos que proporcionan ventilación y luz, los denominados lucernarios. La mezquita original de Abderramán I, ampliada posteriormente por Abderramán II recibía su luz natural por los vanos del muro de entrada, pero la extensa ampliación de Alhaken II queda bastante alejada de esa entrada y difícilmente la luz podría llegar a romper las tinieblas en las que quedaría sumergida esta nueva zona. Consecuentemente se plantearían una solución arquitectónica para aportar esa necesaria claridad. ¡Y la lograron! y fue y ha sido un referente aplicado en multitud de obras posteriores. Surgió la bóveda de nervios cruzados o bóveda cordobesa.
En la imagen de la vemos el lucernario de la denominada "Capilla de Villaviciosa" que es donde estuvo el mihrab de la mezquita de la ampliación de Abderramán II y después de la reconquista cristiana estuvo ubicado el altar mayor de la primera catedral, por ello el nombre actual que recibe de capilla. Los elementos constructivos son arcos entrecruzados, nervios, que se caracterizan porque no comparten una clave común. En este caso se entrecruzan de tres en tres y esa unión es la parte con más dificultad de la edificación. Con esta estructura Desde este enlace (wikiarquitectura) se accede a un esquema constructivo del lucernario de la capilla de Villaviciosa. Para el análisis de esta bóveda y las que veremos posteriormene consultar también el artículo de Fuentes (2019)
Matemáticamente, si describimos la proyección de la bóveda sobre un plano paralelo al suelo, el esquema es simple: una sucesión de tres cuadrados inscritos uniendo los puntos medios de cada lado. Pero realmente, la planta de esta capilla es rectangular ocupando tres espacios entre columnas los cuales suman una longitud superior al ancho de la nave que ocupa que, en concreto, es la nave central que se diferencia del resto de naves por tener mayor anchura. Así pues, sobre una base rectangular, por un lado se trazan cuatro arcos que unen los puntos medios de los lados formando su proyección sobre
esa base un rombo y por otro desde los lados del rectángulo se trazan dos parejas de arcos paralelos que se entrecruzan con los anteriores creando su proyección un cuadrado central inscrito en el rombo anterior, junto a cuatro rectángulos en las esquinas y doce triángulos de diferente tamaño. Los vértices de ese cuadrado son los de mayor dificultad constructiva porque se forman al intersecarse tres arcos.

Tenemos una primera muestra constructiva, pionera, que por su origen se denomina "bóveda cordobesa" y por su componentes "bóveda de nervios cruzados". Pero ésta es una de las diversas posibilidades que pueden plantearse según el número de arcos que se utilicen, según la ubicación relativa de los mismos y/o el cruce que se genera entre ellos. A continuación, veremos cómo evoluciona este modelo y cómo mejora a medida que se construyen otros lucernarios en la propia mezquita cordobesa.
El hueco central se rellena truncando las esquinas y obteniendo un octógono sobre el que se eleva una cúpula gallonada dodecagonal.
(a)
 |
(b) |
(c)
 |
(d)
 |
Las esquinas son rectangulares y, por ello, las figuras que conforman estas pequeñas bóvedas no son regulares.
Pegando un salto temporal desde el califato cordobés a la época de la reconquista cristina de Al-Ándalus podemos fijarnos en la zona anexa a la capilla de Villaviciosa que se denomina como capilla real por haber sido tumba de dos reyes castellanos. En ella podemos observar
una reproducciónde la bóveda de Villaviciosa, pero en este caso la obra está realizada sobre planta cuadrada y usando como elemento constructivo la madera. Aunque la planta base es rectangular (ocupa el espacio de los tres mismos huecos intercolumnas de la de Villaviciosa, pero en la nave colindante), introdujeron dos arcos muy anchos en la nave en la dirección del Mihrab y así en la parte superior se parte de una base que es cuadrada (ver la ). Este es un ejemplo de la influencia constructiva de la bóveda cordobesa.

Las dos bóvedas que se ubican a ambos lados de la macsura son gemelas e introducen, al menos desde el punto de vista matemático, un salto cualitativo estético que alcanza su sumun en la bóveda central de este lugar reservado al imán y al califa. Ver la .

Las formas geométricas que se identifican al realizar la proyección de la bóveda sobre el plano horizontal son las siguientes: un cuadrado inicial al que se le truncan las esquinas obteniendo un octógono regular. Con los vértices de éste se construye un octógono estrellado de paso 3, es decir, moviéndose por el octógono inicial se traza el segmento que une un vértice con el tercer vértice después de él; que también puede verse como dos cruces griegas giradas una repecto a otra 45º, recordemos que un octógono se puede obtener intersecando un cuadrado con otro girado 45º, luego es una propiedad que se hereda aquí, y que se visualiza en el nuevo octógono regular que el polígono estrellado determina en su centro. Éste queda coronado por una bóveda con ocho nervios con clave central común.
En este esquema los arcos se entrecruzan dos a dos, es decir, es constructivamente parece más sencilla que la bóveda de Villaviciosa, pero a costa de tener un mayor número de intersecciones; también
los arcos alcanzan mayor altura, si bien el hueco central tiene menor superficie. Desde este enlace se accede a un esquema constructivo y puede compararse con el indicado anteriormente de la capilla de Villaviciosa.
Comprobamos que aparece de manera recurrente el óctogono, que vimos que es el polígono asociado a la proporción humana y que, según lo que hemos empezado a observar, comienza a pedir ser denominada como proporción cordobesa. Pero si nos parece poco fundamentado, continuemos visitando la Mezquita cordobesa.

En la bóveda central de la macsura (ver ), se construye un octógono inicial truncando las esquinas y ahora se unen los vértices alternos construyendo un polígono estrellado de paso 2, que equivale a dos cuadrados uno girado 45º respecto al otro y configurando de
nuevo un octógono central. Los arcos se entrecruzan también dos a dos, pero en este caso la ventaja de esta construcción respecto a la anterior es que el octógono obtenido tiene más superficie. Desde este enlace se accede a un esquema constructivo de esta bóveda. Adicionalmente toda ella se adorna con mosaico bizantino. ¡La bóveda cordobesa alcanza su esplendor! El canón de belleza octogonal queda puesto de manifiesto ¿verdad?
Y en este lugar hemos de detenernos en el Mihrab (ver las imágenes en la ) donde volvemos a encontrarnos con el octógono, pues la planta del este lugar tiene esa forma y sobre esa base octogonal en el techo se ubica una cúpula con forma de venera.
Es difícil en este espléndido monumento el que la mirada no encuentre un detalle atractivo y bello, pero es obvio que al acumularse estos de manera armoniosa se logra verificar el dicho aristotélico de que el todo es más que la suma de las partes. Ello se hace obvio, por ejemplo, al mirar la portada del mihrab en la macsura, si bien no es fácil de ver el conjunto porque las columnas y arcos polilobulados la tapan parcialmente cuando se observa a distancia y al acercarse su extensa superficie supera al ángulo de visión humano. No obstante, gracias a la técnica artística desde hace tiempo disponemos de dibujos y litografías que nos la muestran en toda su grandeza o posteriormente innumerables fotografías y, ahora con tecnologías digitales contamos con imagenes 3D y con la posibilidad de realizar visitas virtuales. En las imágenes de la tenemos accesibles dos muestras de este conjunto.
Pero al observar dicha portada, la pregunta que podemos hacernos es: ¿Por qué nos atrae y nos gusta esa composición?
 |
 |
Aparte de la bellísima decoración con diversas técnicas que llena majestuosamente nuestro sentido visual, la abstracción matemática nos lleva a recordar la importancia de las proporciones en la belleza (Galo, 2005
Para abordar este análisis proporcional nos apoyaremos en las imágenes de la y en la , donde disponemos de la posibilidad de activar cartabones/rectángulos que siguen la proporción humana, tanto en orientación vertical como horizontal (también ahí se pueden usar cartabones/rectángulos divinos) y desplazándolos o escalándolos poder detectar sobre dichas imágenes la ocurrencia de la proporción humana (o la divina).
Obviamente no vamos a aseverar al respecto, sino marcar ciertas tendencias o relaciones que puedan ser objeto de mayor profundización por quienes puedan disponer de los datos precisos necesarios sobre los que poder contrastar estas observaciones, de manera similar a lo realizado por Cantizani et al. (2022)
(a)
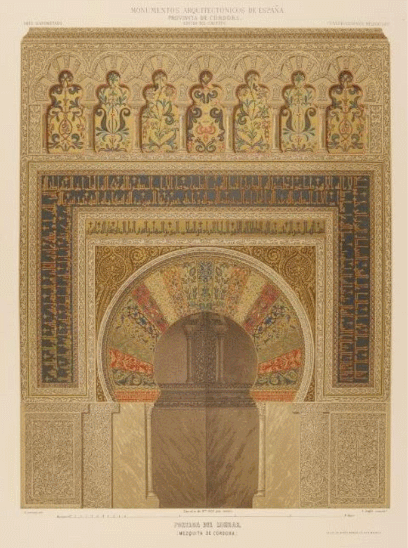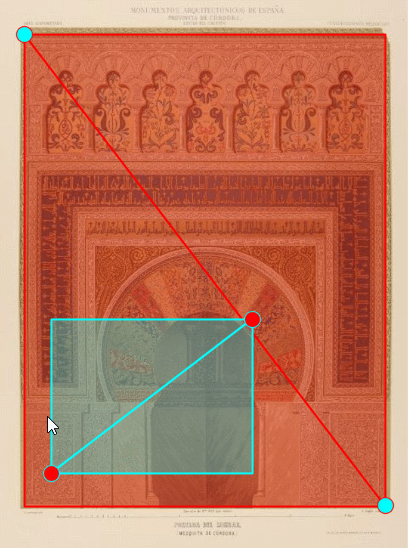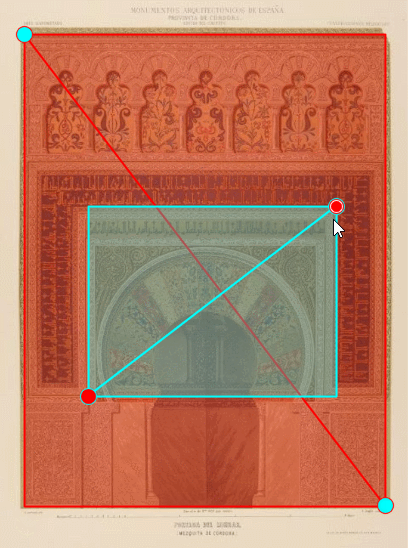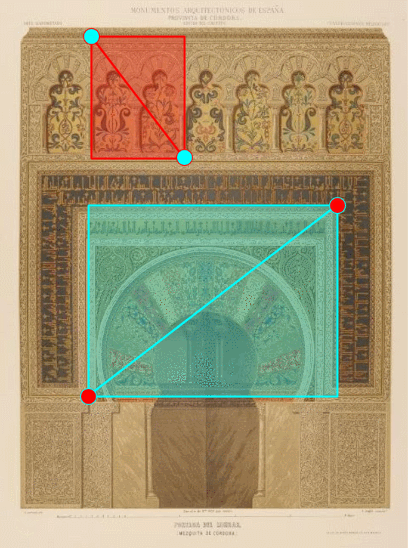
|
(b)
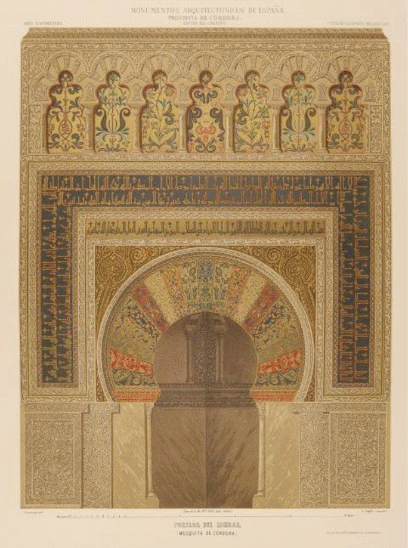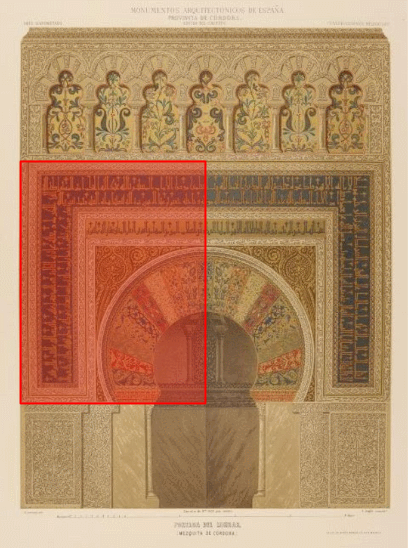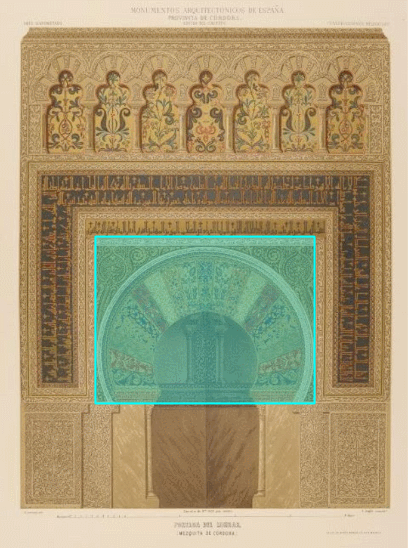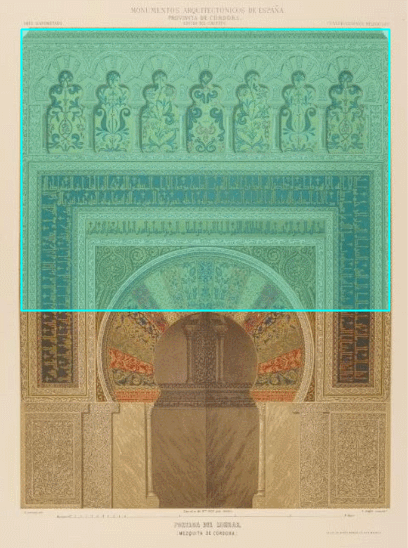
|
(a) Uso del cartabón/rectángulo humano en la . (b) Algunos rectángulos humanos. |
|

|
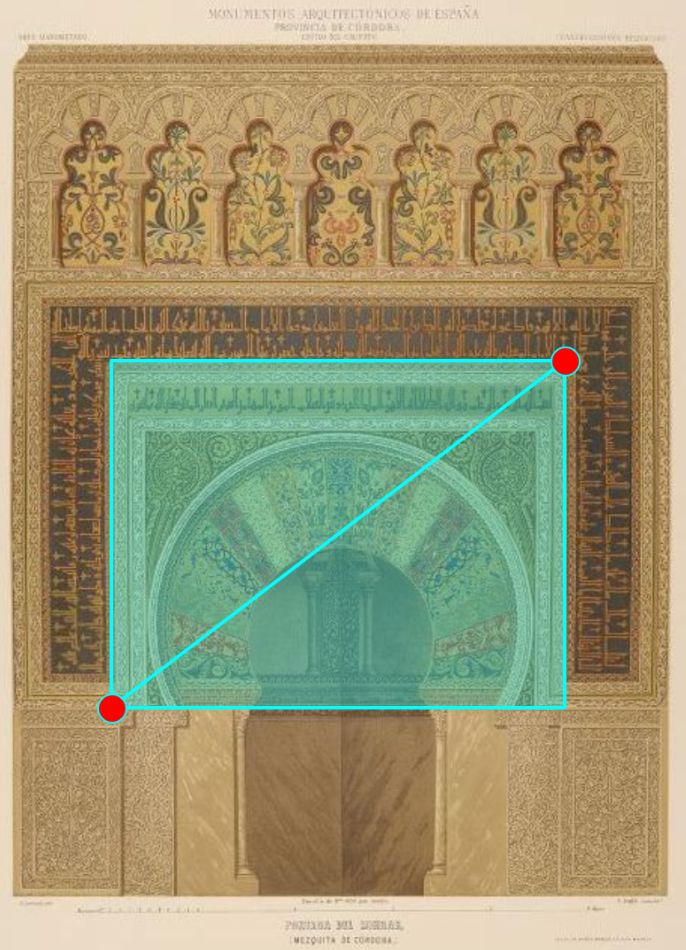
|
En la animación (a) de la observamos cómo manejar los cartabones disponibles en la y en la animación (b) de esta figura observamos algunas zonas de la portada que siguen la proporción humana. Y en las imágenes de la se muestras dos instancias de dos de esos rectángulos humanos. Uno se ajusta a la globalidad de la portada y otro está ubicado en la parte central comprendiendo la zona del arco de herradura y la leyenda ubicada encima de él.
Así pues, el diseño de este frontal aparenta seguir el canon de la razón entre el radio y el lado del octógono, es decir, en los diseñadores de esta portada hay plena conciencia del uso de la que hemos estado denominando proporción humana y que, a partir de ahora, en base a todo lo que hemos indicado en esta sección podemos y hemos de llamar, con toda propiedad, proporción cordobesa. Fue R. de la Hoz (1973)
Pero ya les decía que los andaluces somos abiertos mentalmente y si algo es útil y bello por qué no usarlo. Si conocíamos los rectángulos áureos y los cordobeses ¿por qué no combinar ambos? Les invito a que accedan a la y usen los cartabones o rectángulos áureos sobre la portada e indaguen sobre su ocurrencia en la misma.
De nuevo lo que estamos es tratando de detectar posibles tendencias o posturas abordadas en el diseño, intuir posibles pinceladas gruesas
en las que poder reconocer la intencionalidad de sus autores.
En la se incluye una animación donde se reflejan algunos rectángulos áureos sobre la portada del Mihrab.

Pero no queremos limitar la imaginación del lector y le invitamos a investigar en esta portada otras posibles proporciones que han sido analizadas por Cantizani et al. (2022)
O podrían aplicarse otras posibles alternativas como la que se indica, aunque sin haber encontrado la fuente documental que lo respalde, en el Paseo matemático de la Fundación Descubre. Se puede encontrar en la información que hay incluida cuando se visita virtualmente la portada del Mihrab. En este caso se establecen rectángulos en proporción 3/2 junto a cuadrados trivialmente obtenidos en base a esa proporción decimal exacta.
Pero nuestro objetivo es sólo poner de manifiesto el extenso conocimiento de los autores de esa bella portada y que ha quedado cripticamente oculto a pesar de estar literalmente ante nuestros ojos. Aquí nos quedamos, por el contenido de este libro y por opinión personal, con la mixtura del canon cordobés y el canon áureo. La amalgama de ambos cánones de belleza es la que posiblemente logra sublimar su majestuosidad. Como ya hemos indicado, la belleza no
tiene por qué seguir un único patrón o canon, sino que la combinación hábil de dos o más de ellos dan razón a Aristóteles al verificar que el todo es más que la suma de las partes.
En línea con lo indicado en la sección anterior, en general, estamos acostumbrados a adaptar y combinar esas proporciones. ¿Qué es si no la transformación que conseguimos cuando nos subimos a unos tacones o plataformas? Alargamos la distancia desde los pies al ombligo y de esta forma logramos pasar de la proporción humana a la proporción divina (ver la animación de la ).

¡La proporción áurea vs. la proporción cordobesa!
Puesto de manifiesto la coexistencia de la proporción divina y de la proporción humana, o bien con la terminología paralela de la proporción áureaAunque ya hemos usado estas denominaciones múltiples, concretemos aquí que la "extrema y media razón" de Euclides, es denominada por Pacioli como "divina", es "armónica" en el hombre de Vitrubio de Da Vinci y "áurea, dorada o de oro" según término introducido por Martin Ohm en el siglo XIX y que parece predominar en nuestros días. y de la proporción cordobesaEn este caso lo de "humana" es confrontándola frente a la divina de Pacioli, y "cordobesa" por el contexto de su descubrimiento y posible impulso arquitectónico de la misma. Ambos términos introducidos por Rafael de la Hoz Arderius. , procedamos a determinar las constantes de proporcionalidad respectivas, los denominados número áureo y número cordobés.
Para determinar la constante de proporcionalidad correspondiente a la proporción divina o áurea basta considerar un rectángulo áureo de lados $1$ y $x$, es decir, que verifique que:
$$\frac{x+1}{x}=\frac{x}{1}$$ lo que equivale a determinar $x$ en la ecuación polinómica de segundo grado
Actualmente a los números que verifican las ecuaciones $x^2-n \, x-1=0$ con $n \in \mathbb{N}$ se le denominan metálicos= oro, plata, bronce, cobre, níquel,... introducidos y estudiados por Vera de Spinadel $$x^2-x-1=0$$ que tiene por raíz positiva $x=\dfrac{1+\sqrt{5}}{2}$.
A este número se le denomina áureo y suele representar con la letra griega $\Phi$ (en honor a Fidias arquitecto del Partenon donde se prodiga esta proporción), siendo su valor aproximado $1,618033...$.
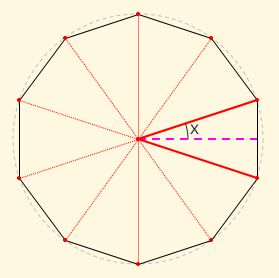
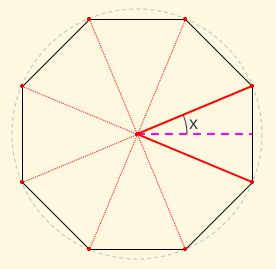
El número cordobés, que vamos a denotarLa elección de esta letra es algo personal por su parecido a la letra c, inicial de cordobés.
$$\varsigma = \frac{1}{2 \, sen \, 22,5º}$$
Para calcular el valor del $sen \, 22,5º$ basta considerar las razones trigonométricas que relacionan el ángulo mitad con el total y tenemos que:
$$sen \, 22,5º=\sqrt{\frac{1-cos \, 45º}{2}}=\frac{\sqrt{2-\sqrt{2}}}{2}$$
y consecuentemente
$$\varsigma=\frac{1}{\sqrt{2-\sqrt{2}}}$$
cuyo valor aproximado es $1,306562...$
El número cordobés está relacionado con el número de plata, número metálico que también está ligado al octógono (Fernandes y Reyes, 2003
En una sección anterior ya citamos al triángulo sublime o triángulo áureo, sobre el que ahora nos detendremos un poco más, y en este paralelismo corresponde también analizar el triángulo cordobés.
Como ya indicamos, la proposición décima del libro cuarto de Los Elementos de Euclides aborda la construcción de un triángulo isósceles en el que el lado igual y desigual sigan la extrema y media razón, el triángulo sublime (ver la ).
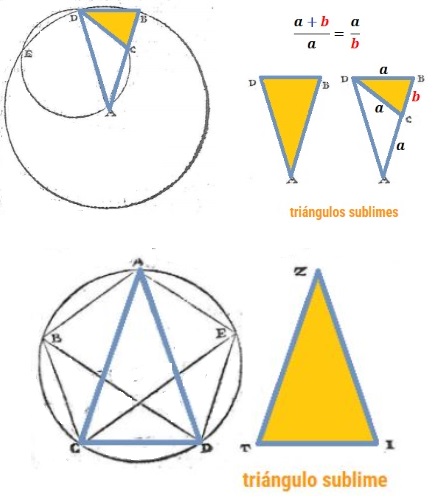
Como triángulo central que es del decágono tenemos que el ángulo desigual del triángulo áureo mide 36º y los dos iguales 72º, o también el ángulo desigual puede verse como el ángulo inscrito que abarca un lado del pentágono. Y su gnomon es un triángulo obtusángulo isósceles de ángulo desigual 108º y ángulos iguales de 36º.
De manera análoga, el triángulo cordobés es un triángulo isósceles en el que el lado igual y desigual están en proporción cordobesa (ver la ).
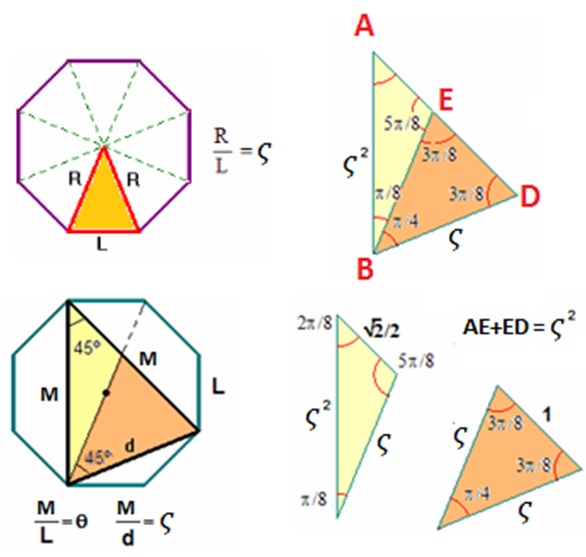
Imagen generada por la IA Designer de Microsoft
Desde la Grecia clásica ha existido la inquietud de estudiar algunas curvas que se enrollan sobre sí, sin intersecarse —también podríamos decir que se desenrollan, ya que es una mera interpretación dinámica según el recorrido que se opte realizar sobre la curva, que es algo estático— .
Entre todas ellas aquí destacaremos dos: la espiral de Arquímedes y la espiral logarítmica.


Cardona Suárez (2006, p.38
"Se puede imaginar una línea eterna que, en continuo desarrollo en torno a un centro y describiendo con su otro extremo espiras cada vez más amplias, nunca tenga fin. Esta línea no se puede hacer a mano por lo infinito de sus magnitudes grandes y pequeñas. Su principio y final no existen, ni se pueden encontrar, salvo en el entendimiento."
No obstante, entendemos que ha de ubicarse sólo en una formalización expositiva imprecisa, siendo realmente Descartes (1596-1650) quien, como posteriormente veremos, precisa su definición en base a su carácter equiangular como extensión de lo que acontece con todas las rectas tangentes en una circunferencia.
Descartes y Torricelli (1608-1647) abordaron el estudio de las propiedades de la espiral logarítmica, pero fue Bernoulli (1654-1705) el auténtico modelador matemático y quien la denominó Spira mirabilis «la espiral maravillosa», y quiso que figurara en el epitafio de su tumba esculpida con el lema Eadem mutata resurgo o "Mutante y permanente, vuelvo a resurgir siendo el mismo", pero el cantero bien en su ignorancia o bien en su etéreo saber actuó siguiendo una espiral atemporal unificadora del antes y después, cual agujero negro, y reflejó la originaria espiral arquimediana en su lugar.

La imagen que permite visualizar la espiral de Arquímedes es la de una cuerda enrollada alrededor de ella misma rozando cada vuelta con la anterior. La separación entre cada espira es siempre la misma y viene dada por el ancho de la cuerda en sí. Por tanto, la distancia al
polo (centro u origen de la espiral) desde los puntos situados en linea recta con dicho polo siguen una progresión aritmética de diferencia el ancho de la cuerda. Esa es una propiedad característica de esta espiral y de ahí que se denomine también como espiral aritmética. Geométricamente equivale al enrollamiento topológico de un rectángulo o a nivel tridimensional el de la superficie lateral de un cilindro manteniendo invariable la sección circular que lo define.
En la se aborda de manera constructiva la obtención de esta espiral mediante la simulación de la posición de una hormiga que se desplaza en línea recta con velocidad constante sobre una superficie que a su vez gira con velocidad angular
constante alrededor de un punto ubicado en la trayectoria rectilínea citada, y se realiza el análisis matemático de ella. En cada panel se incluye un botón informativo en el que se detalla lo reflejado en cada simulación, pero adicionalmente se pueden consultar las instrucciones en este hiperenlace y en el documento donde se describen los detalles de dicho análisis.
En resumen tenemos:

Si al igual que antes queremos formarnos una imagen que nos permita visualizar esta espiral cartesiana (conocida principalmente como logarítmica), tendremos que pensar en una cuerda enrollada pero en la que cada vez la separación entre espiras es mayor. Por tanto, la distancia al polo (centro u origen de la espiral) desde los puntos situados en linea recta con dicho polo es cada vez más amplia, en particular para la espiral logarítmica veremos que estarán en progresión geométrica. Esa es una propiedad característica de esta espiral y de ahí que se denomine también con este calificativo: espiral geométrica. Geométricamente equivale al enrollamiento topológico de un triángulo o tridimensionalmente el de la superficie lateral de un cono.
Es bien conocido que la circunferencia es una curva equiangular, es decir, que en cualquier punto de la misma el ángulo que forma el radio con la tangente es siempre constante e igual a un ángulo recto (ver ).
Descartes se planteó la determinación de una curva que también fuera equiangular, pero que en todo punto el ángulo que formara el radio vector con la recta tangente fuera el que previamente se deseara, es decir, buscaba una generalización de lo que acontece en la circunferencia. Un plantemiento simple que conduce, como analizaremos a continuación, a la espiral que es la más admirada por muchos: la espiral logarítmica, o espiral geométrica o espiral equiángular o espiral armoniosa o espiral maravillosa... multiplicidad nominativa ante tanta admiración y cúmulo de propiedades que iremos detallando.
En la se aborda de manera constructiva la obtención de esta espiral mediante la simulación de la posición de un grillo que se desplaza en línea recta con velocidad no uniforme, la cual se incrementa de manera exponencial, sobre una superficie que
a su vez gira con velocidad angular constante alrededor de un punto ubicado en la trayectoria rectilínea citada, y se realiza el análisis matemático de ella.

Abordando el análisis matemático de esta situación, podemos afirmar que esta espiral se caracteriza porque:
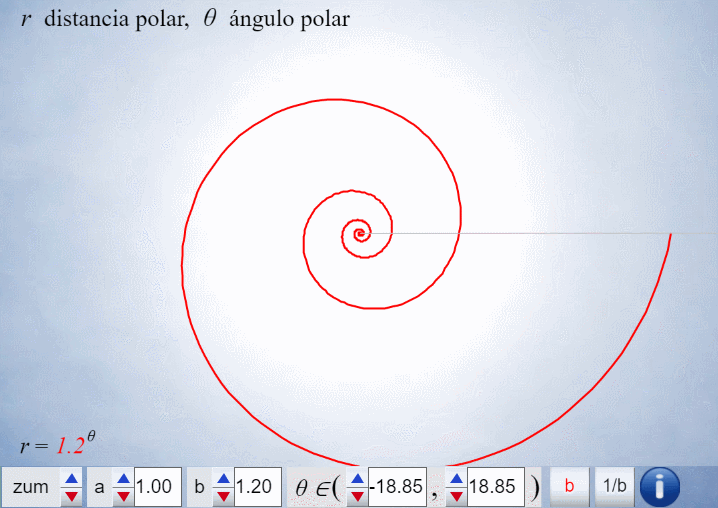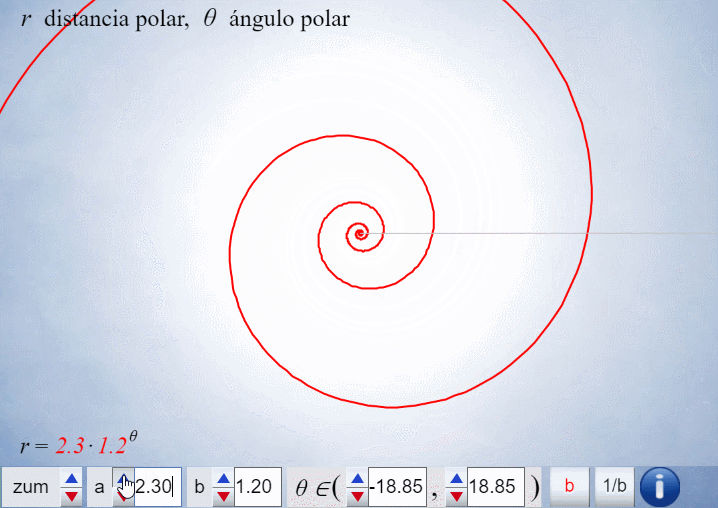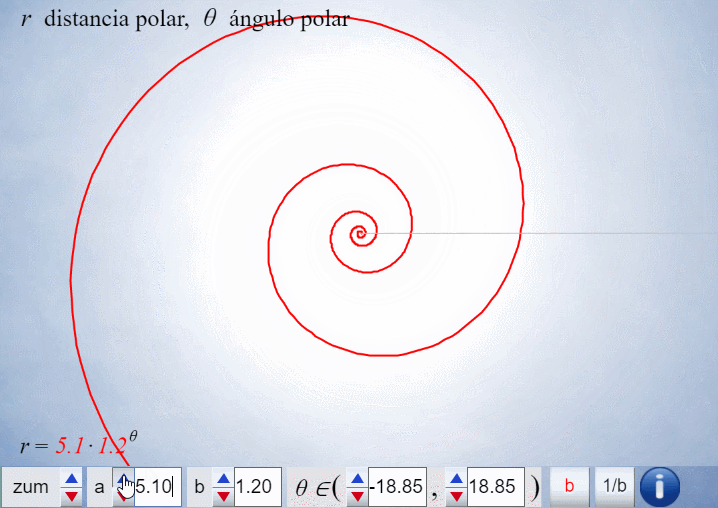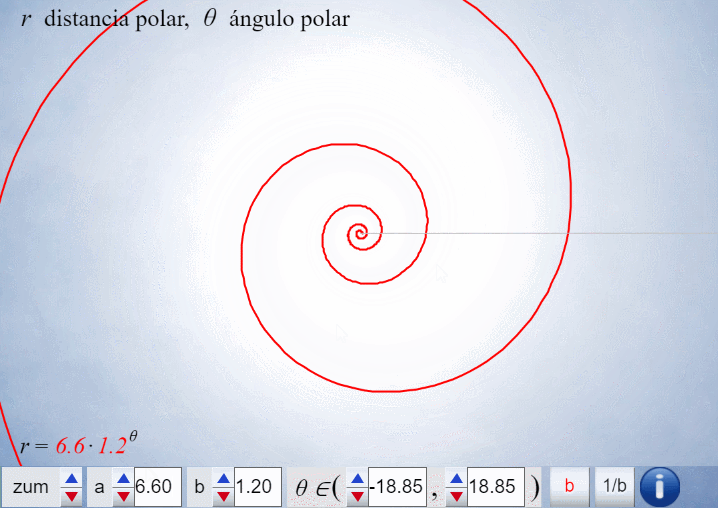
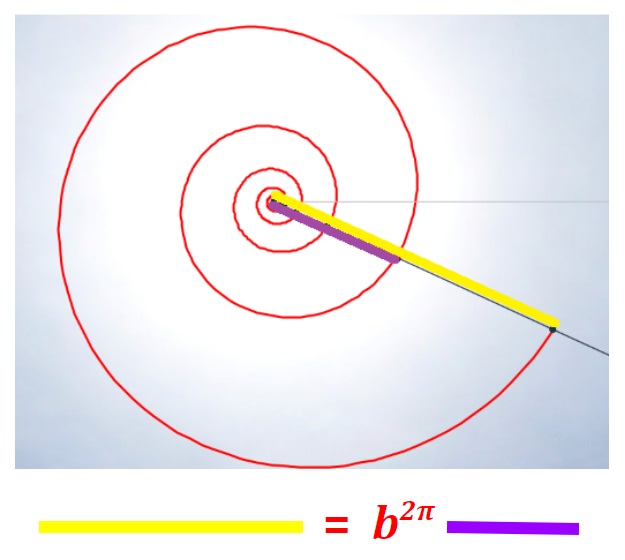
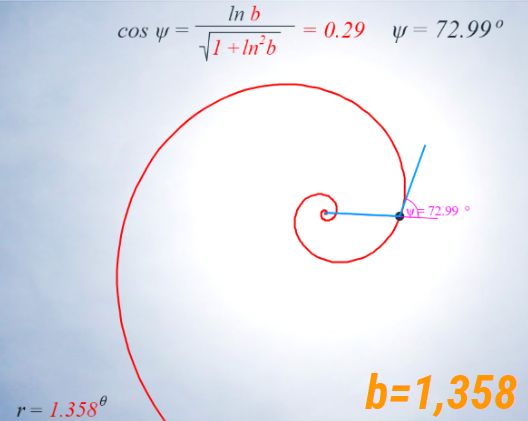
|
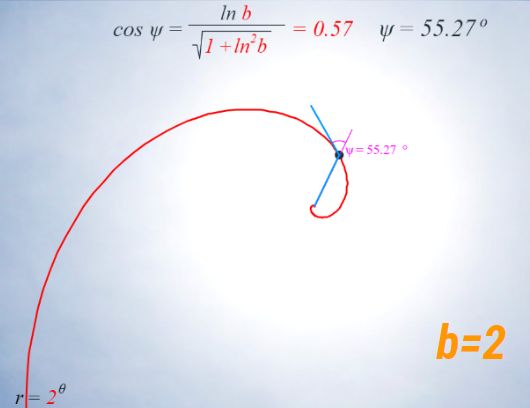
|
| $$\begin{cases} x=a \, b^\theta cos \, \theta \\ y=a \, b^\theta sen \, \theta \end{cases} $$ | $$\begin{cases} x'=a \, b^\theta \, ln \, b \, cos \, \theta - a \, b^\theta \, sen \, \theta \\ y'=a \, b^\theta \, ln \, b \, sen \, \theta + a \, b^\theta \, cos \, \theta \end{cases} $$ |
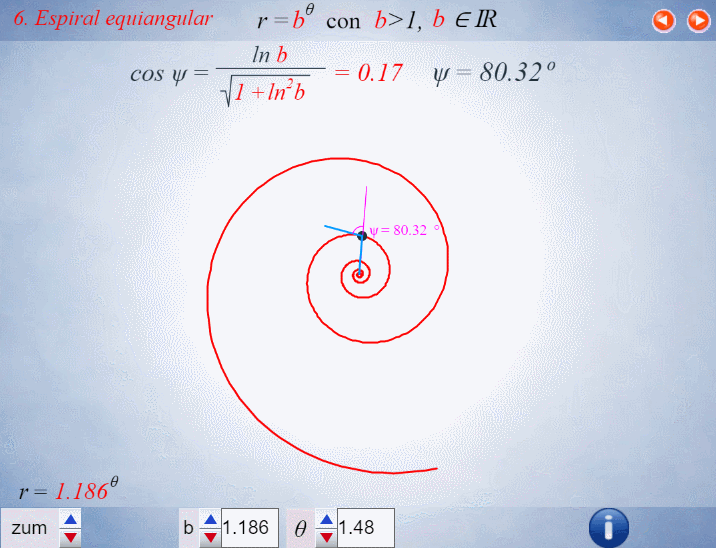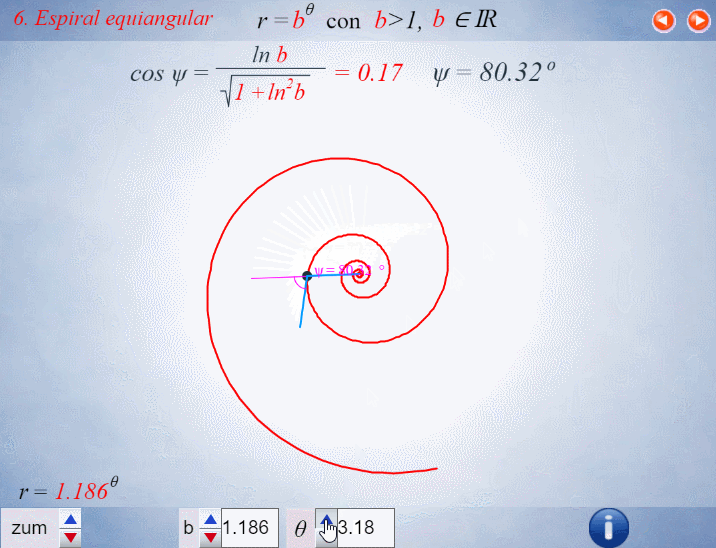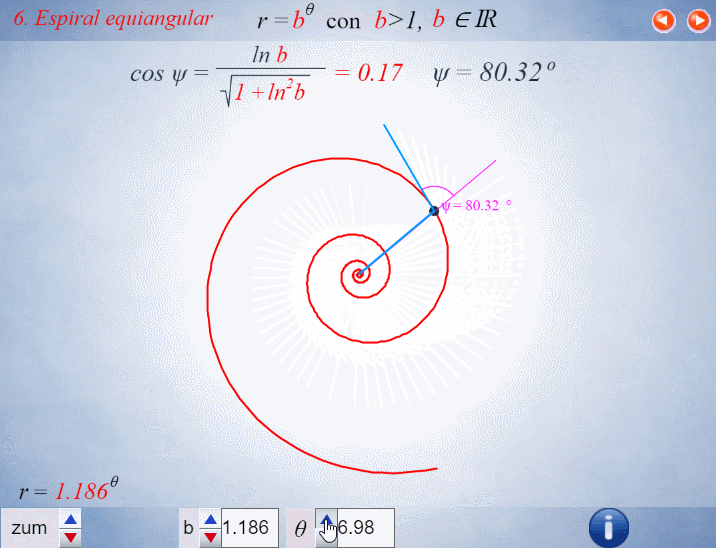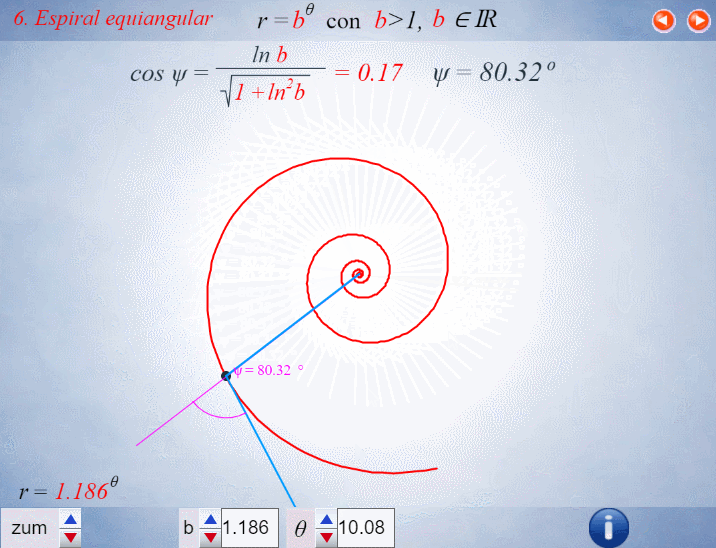
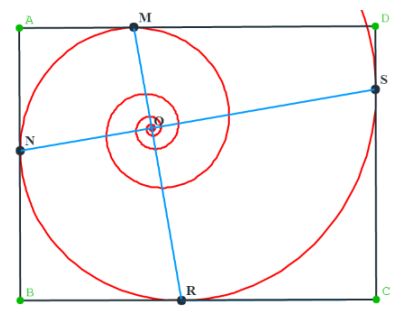
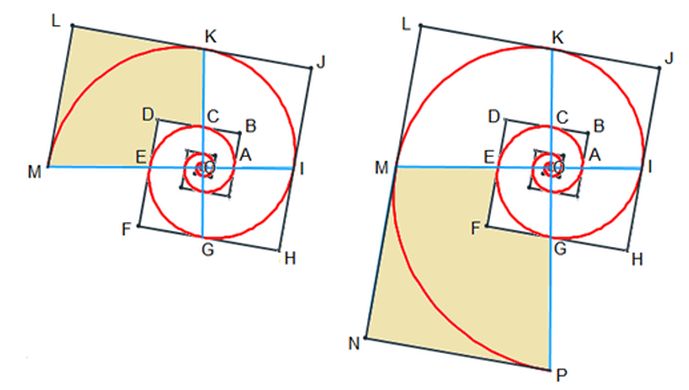
En la , el hexágono $CKLMED$ es el gnomon del hexágono $CDFHJK$, pues al añadirlo a éste el hexágono $EFHJLM$ obtenido es semejante al $CDFHJK$ con razón de semejanza $b^{\frac{\pi}{2}}$. Análogamente un nuevo gnomon es $EMNPGF$ y además esos dos gnómones son a su vez semejantes, con igual razón. Así pues, el factor de crecimiento en cada paso de esta aproximación discreta sería $b^{\frac{\pi}{2}}$.
Éste es un caso particular de las aproximaciones poligonales que se detallan en la sección 4.3, que , a su vez, son una extensión de la propiedad reflejada en la página 777 de Thompson (1942)
En la siguiente figura $Q,Q',Q''$ están en una espiral semejante a la dibujada.
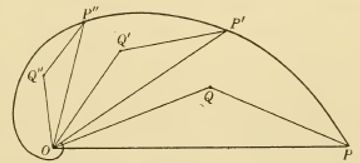 La demostración es sencilla ya que al ser los triángulos semejantes entonces:
$$\frac{OQ}{OP}=\frac{OQ'}{OP'}=\frac{OQ''}{OP''}=k$$
De donde $OQ=k OP$, y dado que $OP$ es el radio vector de una espiral logarítmica $r= a b^θ$, entonces $OP=a b^θ$ y por tanto $OQ=k a b^θ$, es decir los puntos $Q$ pertenecen a una espiral logarítmica de ecuación $r=k a b^θ$ semejante a la anterior y con igual razón de semejanza que la existente entre los triángulos.
La demostración es sencilla ya que al ser los triángulos semejantes entonces:
$$\frac{OQ}{OP}=\frac{OQ'}{OP'}=\frac{OQ''}{OP''}=k$$
De donde $OQ=k OP$, y dado que $OP$ es el radio vector de una espiral logarítmica $r= a b^θ$, entonces $OP=a b^θ$ y por tanto $OQ=k a b^θ$, es decir los puntos $Q$ pertenecen a una espiral logarítmica de ecuación $r=k a b^θ$ semejante a la anterior y con igual razón de semejanza que la existente entre los triángulos.
Esta propiedad se puede generalizar a cualquier otra figura o curva construida sobre un radio vector y así se muestra evidente cómo se reproducen las mismas formas al crecer la espiral.
.
De manera general puede aproximarse mediante gnómones obtenidos con paso $\frac{2\pi}{n}$ con $n \in \mathbb{N}, \, n \ge 3$, y con factor de crecimiento en cada paso $b^{\frac{2 \pi}{n}}$ (ver la ).
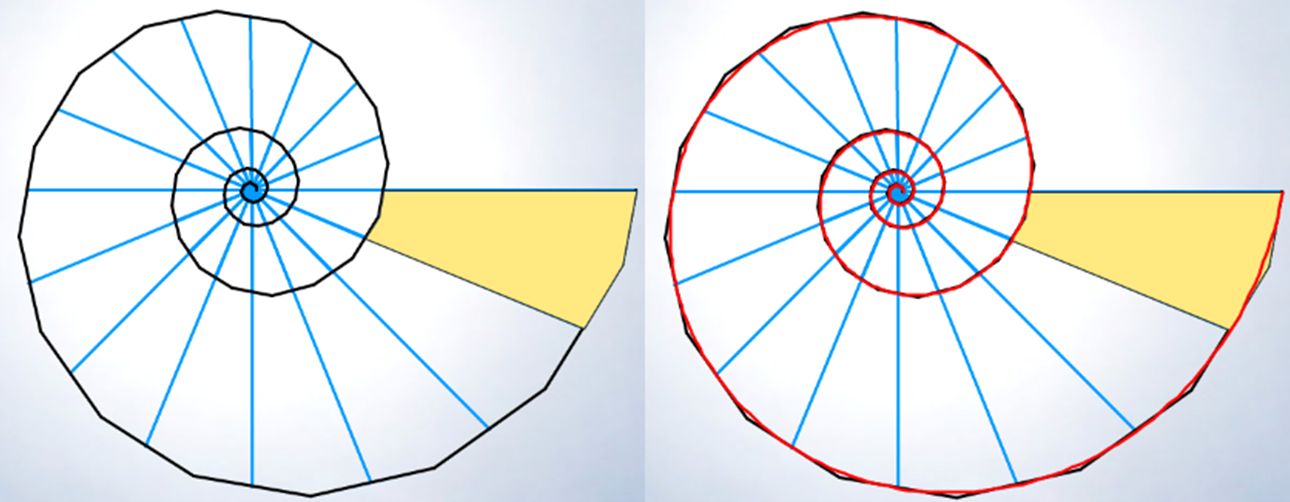
Y en el caso límite en el que $n \rightarrow \infty$ el factor de crecimiento sería $$\lim_{n \to{\infty}}{b^{\frac{2 \pi}{n}}}=1$$es decir, que el factor de crecimiento instantáneo es la unidad. Esto puede considerarse como una explicación al emblema empleado por Jakob Bernoulli (citado en la página
entre los puntos $P$ y $Q$ correspondientes a $r=a \, b^\beta$ y $r=a \, b^\gamma$ respectivamente es: $$l=\frac{\sqrt{1+ln^2 b}}{ln \, b} \, a \,(b^\gamma-b^\beta) $$
Diremos que una espiral logarítmica es áurea (ver la ) si su rectángulo circunscrito asociado es áureo, es decir, que el módulo o proporción de este rectángulo se corresponde con el número áureo $\Phi = \frac{1+\sqrt{5}}{2}$. Por tanto, dado que ha de ser $b^{\frac{\pi}{2}}=\Phi$ o bien $b=\Phi^{\frac{2}{\pi}}$, tenemos que:

De manera análoga, diremos que una espiral logarítmica es cordobesa si su rectángulo circunscrito asociado es cordobés (ver la ), es decir, que el módulo o proporción de este rectángulo se corresponde con el número cordobés $\varsigma=\frac{1}{\sqrt{2-\sqrt{2}}}$. Por tanto, dado que ha de ser $b^{\frac{\pi}{2}}=\varsigma$ o bien $b=\varsigma^{\frac{2}{\pi}}$, tenemos que:
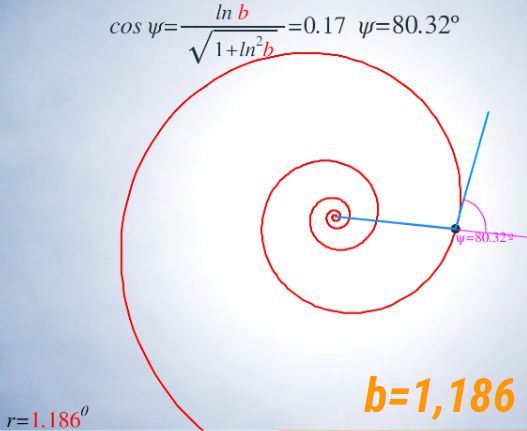
Apoyándonos en el caracter equiangular de toda espiral logarítmica podemos verificar que fijado un punto de ella se puede construir un rectángulo circunscrito, tangencial en cuatro puntos, y otro inscrito. Todos esos rectángulos tienen igual módulo (cociente entre el lado mayor y el menor) siendo su valor $b^{\frac{\pi}{2}}$. Por tanto, conceptualmente cada espiral tiene asociado un rectángulo que la caracteriza y viceversa (ver la y esta animación).
En base a esos rectángulos inscritos y circunscritos equimodulares, si partimos de un punto cualquiera $M_0$ de una espiral logarítmica $r=b^\theta$, por ejemplo: $M_0 (b^\theta_0, \theta_0)$ en coordenadas polares, podemos construir una poligonal abierta inscrita en esa espiral y otra circunscrita () a las cuales nombraremos como espirales discretas inscrita y circunscrita, respectivamente.
Los vértices $M_i$ de la espiral discreta inscrita son puntos de la espiral logarítmica considerada: $M_i (b^{\theta_0+i\frac{\pi}{2}}, \theta_0+i\tfrac{\pi}{2}), i \in \mathbb Z$ y los vértices $A_i$ de la espiral circunscrita están en otra espiral, que vamos a denominar como "espiral gemela de paso $\tfrac{\pi}{2}$" dado que es la misma al tener la misma base $b$, pero con un retardo $\delta-\beta$ (), es decir, su ecuación es: $$r=b^{\delta-\beta} b^\theta$$
Donde se tiene que:
$\space b^{\delta}=\dfrac{sen \medspace\alpha}{sen(\alpha+\beta)}$, $\space \alpha$ es el ángulo suplementario del ángulo $\psi$ (característico de la espiral) y $\beta$ el ángulo que forma el radio vector $\overrightarrow{OM_i}$ con el $\overrightarrow{OA_i}$. Adicionalmente, se tiene que $sen \space \alpha = \dfrac{1}{\sqrt{1+ln^2 b}}$, $sen(\alpha+\beta) = \dfrac{1}{\sqrt{1+b^\pi}}$, $cotg(\alpha+\beta) = -b^{\frac{\pi}{2}}$ y de estos valores se obtiene que $$cotg \space \beta= \dfrac{1+b^{\frac{\pi}{2}} ln \space b}{b^{\frac{\pi}{2}}-ln \space b}$$
$$A_i (b^{\delta-\beta} b^{\theta_0+\beta+i\frac{\pi}{2}}, \theta_0+\beta+i\tfrac{\pi}{2}), \quad i \in \mathbb Z$$
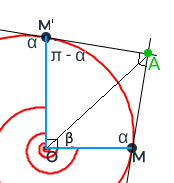
Para obtener las relaciones anteriores podemos apoyarnos en la . En ella, $M(b^\theta,\theta)$ y $M'(b^{\theta+\frac{\pi}{2}},\theta+\frac{\pi}{2})$ son dos nodos de la espiral discreta inscrita correspondiente a la espiral logarítmica $b^\theta$ y $A$ el nodo de la espiral discreta circunscrita obtenido por la intersección de las tangentes a la espiral en $M$ y $M'$. Consideremos, en coordenadas polares, que $A(l,\theta+\beta)$, es decir, $\beta$ es el ángulo $OM$ con $OA$.
Aplicando el teorema del seno en los triángulos $OMA$ y $OAM'$ se tiene que
$$\frac{l}{sen \alpha} = \frac{b^\theta}{sen (\alpha+\beta)} = \frac{b^{\theta+\frac{\pi}{2}}}{sen (\alpha+\beta-\frac{\pi}{2})}$$
y, por tanto, de esas igualdades se tiene:
$$l= \frac{sen \alpha}{sen (\alpha+\beta)} \space b^\theta = \frac{sen \alpha}{sen (\alpha+\beta)} \space b^{-\beta} \space b^{\theta+\beta} = b^{\delta-\beta} \space b^{\theta+\beta}$$
y $cotg(\alpha+\beta) = - b^\frac{\pi}{2}$. Y dado que $\space sen \space\alpha = sen \space \psi = \dfrac{1}{\sqrt{1+ln^2 b}}$, aplicando relaciones trigonométricas se obtienen las expresiones indicadas para $cotg \space\beta$ y $b^\delta$.
Así pues, $A(b^{\delta-\beta} \space b^{\theta+\beta},\theta+\beta)$ y pertenece a la espiral $r = b^{\delta-\beta} \space b^{\theta}$.
Los resultados anteriores, obtenidos para rectángulos y espirales discretas de paso $\frac{\pi}{2}$, podemos generalizarlos para polígonos de cualquier número $n$ de lados y espirales discretas de paso $\frac{2\pi}{n}$. Construyamos primero las espirales discretas y, posteriormente, en base a ellas abordemos las diferentes posibilidades que acontecen con los polígonos.
Dado $n \in \mathbb N$, si partimos de un punto cualquiera $M_0$ de una espiral logarítmica $r=b^\theta$, por ejemplo: $M_0 (b^\theta_0, \theta_0)$ en coordenadas polares, podemos construir una poligonal abierta inscrita en esa espiral y otra circunscrita en la que cada dos segmentos consecutivos forman un ángulo de amplitud $\frac{(n-2)\pi}{n}$ y son proporcionales con razón de propocionalidad $b^{\frac{2 \pi}{n}}$ (ver ).
Los vértices $M_i$ de la espiral discreta inscrita son puntos de la espiral logarítmica considerada :
$$M_i (b^{\theta_0+i\frac{2\pi}{n}}, \theta_0+i\tfrac{2\pi}{n}), \quad i \in \mathbb Z$$
y los vértices $A_i$ de la espiral circunscrita están en otra espiral, su espiral gemela de paso $\tfrac{2\pi}{n}$ (ver ), de igual base $b$, pero con un ángulo de retardo $\delta-\beta$, es decir, de ecuación:
$$r=b^{\delta-\beta} b^\theta$$
donde se tiene que: $b^{\delta}=\dfrac{sen \medspace\alpha}{sen(\alpha+\beta)}$, $\space \alpha$ es el ángulo suplementario del ángulo $\psi$ (característico de la espiral) y $\beta$ el ángulo que forma el radio vector $\overrightarrow{OM_i}$ con el $\overrightarrow{OA_i}$, $sen \alpha = \dfrac{1}{\sqrt{1+ ln^2 b}}$, $sen (\alpha+\beta) = \dfrac{1}{\sqrt{1+ ct^2}}$ con
$ct= cotg (\alpha+\beta) = \dfrac{cos {\frac{2 \pi}{n}-b^{\frac{2 \pi}{n}}}}{sen \frac{2 \pi}{n}}$ y de estos valores se obtiene que $cotg \medspace \beta= \dfrac{ct \medspace ln \medspace b - 1}{ct+ln \medspace b}$.
$$A_i (b^{\delta-\beta} b^{\theta_0+\beta+i\frac{2\pi}{n}}, \theta_0+\beta+i\tfrac{2\pi}{n}), \quad i \in \mathbb Z$$
De la relación anterior se concluye que ambas espirales discretas son la misma, pero una girada respecto a la otra y, por ello, en ambos casos el ángulo $\frac{(n-2) \pi}{n}$ y la proporcionalidad $b^{\frac{2 \pi}{n}}$ de cada pareja de segmentos consecutivos es la misma.
La demostración es análoga al caso anterior, pues aquel no es más que un caso particular de éste para $n=4$, y para ello podemos apoyarnos en la . En ella, $M(b^\theta,\theta)$ y $M'(b^{\theta+\frac{2\pi}{n}},\theta+\frac{2\pi}{n})$ son dos nodos de la espiral discreta inscrita correspondiente a la
espiral logarítmica $b^\theta$ y $A$ el nodo de la espiral discreta circunscrita obtenido por la intersección de las tangentes a la espiral en $M$ y $M'$. Consideremos, en coordenadas polares, que $A(l,\theta+\beta)$, es decir, $\beta$ es el ángulo que forma $OM$ con $OA$.
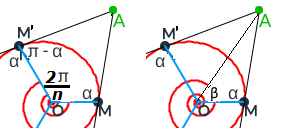
Aplicando el teorema del seno en los triángulos $OMA$ y $OAM'$ se tiene que
$$\frac{l}{sen \alpha} = \frac{b^\theta}{sen (\alpha+\beta)} = \frac{b^{\theta+\frac{2\pi}{n}}}{sen (\alpha+\beta-\frac{2\pi}{n})}$$
y, por tanto, de la primera y segunda igualdad se tiene:
$$l= \frac{sen \alpha}{sen (\alpha+\beta)} \space b^\theta = \frac{sen \alpha}{sen (\alpha+\beta)} \space b^{-\beta} \space b^{\theta+\beta} = b^{\delta-\beta} \space b^{\theta+\beta}$$
y de la segunda y tercera obtenemos el valor que hemos indicado para $cotg(\alpha+\beta)$ y denotándolo como $ct$ también tenemos el de $sen(\alpha+\beta)$.
Igualmente, al ser $\space sen \space\alpha = sen \space \psi = \dfrac{1}{\sqrt{1+ln^2 b}}$, tenemos que $cotg \space \alpha = -ln \space b$ y aplicando que $cotg \space \beta = \dfrac{1+ cotg(\alpha+\beta) cotg \space \alpha}{cotg \space \alpha-cotg(\alpha+\beta)}$ obtenemos ésta en función de $b$ y $n$.
El valor del $\hat{A}=\tfrac{(n-2)\pi}{n}$ es consecuencia de ser la espiral equiangular y $\overline{MA}$ y $\overline{AM'}$ segmentos de tangentes de esa espiral (ver imagen izquierda de la ) y, por tanto es el mismo para todos los $\hat{A_i}$ en la espiral circunscrita y para los $\hat{M_i}$ en la inscrita por ser congruentes mediante un giro.
La proporcionalidad entre cada dos segmentos consecutivos de ambas espirales discretas se obtiene sin más que partir, por ejemplo en la inscrita, de que: $$\overline{OM_i}=b^{\theta+i\frac{2\pi}{n}}$$ calcular $\overline{M_i M_{i+1}}^2=\overline{OM_i}^2+\overline{OM_{i+1}}^2-2 \space \overline{OM_i} \space \overline{OM_{i+1}} \space cos \space \frac{2\pi}{n} \space$ y de ahí se obtiene que: $$\dfrac{\overline{M_{i+1} M_{i+2}}}{\overline{M_i M_{i+1}}}= b^{\frac{2\pi}{n}}$$ e igual valor para la espiral discreta circunscrita por congruencia.Como indicamos, basándonos en estas espirales discretas podemos construir polígonos inscritos en la espiral original con cualquier número de lados y, a partir de uno de ellos, obtener una familia de polígonos semejantes encajados que representan el crecimiento gnomónico discreto del poligono inicial. Y análogamente puede plantearse con polígonos circunscritos, pero dado que, como ya hemos reiterado con antelación, las espirales discretas inscritas y circunscritas son coincidentes sin más que realizar una rotación, basta analizar un caso. Abordaremos, por ejemplo el inscrito, y lo tendremos para el circunscrito.
Pero la construcción de esos polígonos puede abordarse de diversas formas y así lo haremos. Inicialmente nos plantearemos que los polígonos sean convexos, después consideraremos la posibilidad de ser cóncavos y finalmente adaptaremos estos últimos para que puedan ajustarse a la forma de las conchas discoidales que es el objeto final de nuestro estudio.
Dada la espiral $r = b^\theta$ consideremos $n+1$ puntos de ella $M_i, 0 \leq i \leq n$ que forman parte de la espiral discreta inscrita de paso $\gamma = \frac{2\pi}{n}$, es decir, $M_i \equiv (b^{\theta_i},\theta_i), \theta_i = \theta_0+i \gamma $ donde $\theta_0$ es un ángulo cualquiera que fija el punto inicial $M_0$ de la construcción.
Si para $b \gt 1, n \geq 3$ y $l \geq 0$, consideramos la función:
$$\begin{aligned}
k(b,n,l) = & \hspace{1mm} sen \gamma +b^{(n-1-l)\gamma}sen((n-2-l)\gamma)\\& -b^{(n-2-l)\gamma}sen((n-1-l)\gamma)
\end{aligned}
$$
entonces se verifica:
En la puede observarse el resultado anterior y en este hiperenlace puede consultarse la funcionalidad de cada uno de los controles ahí usados.
En la se ha reflejado un hexágono circunscrito (imagen de la izquierda) y otro inscrito (imagen a la derecha) con sus gnómones respectivos (cuadriláteros en color azul y rojo). Puede observarse como uno puede obtenerse del otro sin más que realizar un giro.
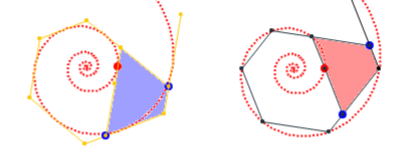
La elección indicada para el punto $P$ que completa los vértices del polígono inscrito es sólo una de otras muchas posibles, sin más limitación que su homólogo $Q$ en el gnomon se obtenga con el mismo procedimiento a partir de los vértices de la espiral discreta.
La libertad de elección del punto final de la poligonal, permite abordar construcciones de polígonos cóncavos que aproximan mejor la simulación de las conchas discoidales de la Naturaleza.
Por ejemplo, en la se ha reflejado una posible alternativa donde los vértices del polígono de n+1 lados para la espiral $r = b^\theta$ con paso $\gamma = \frac{2\pi}{n}$ serían, al igual que en el caso anterior,
$M_i, 0 \leq i \leq n$, siendo $M_i \equiv (b^{\theta_i},\theta_i), \theta_i = \theta_0+i \gamma $, donde $\theta_0$ es un ángulo cualquiera que fija el punto inicial $M_0$. Y en este caso el gnomon correspondiente es el cuadrilátero $M_0 M_n M_{n+1} M_1$. (instrucciones de la escena).
En la se muestra un eneágono cóncavo inscrito con su gnomon (cuadrilátero rojo). Puede observarse su parecido al perfil de la sección sagital de una concha discoidal. La semejanza entre el polígono inicial y el obtenido al añadir su gnomon se demuestra, de nuevo, en base a que los segmentos del polígono son segmentos de la espiral logarítmica y por tanto proporcionales.
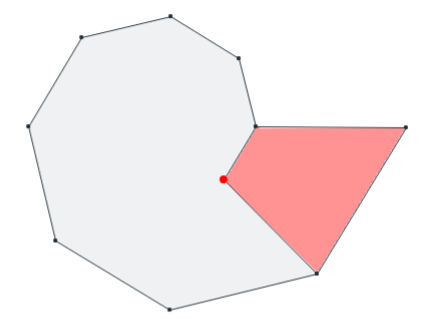
El ajuste anterior puede mejorarse si el segmento de cierre $\overline{M_0 M_n}$ lo sustituimos por una poligonal $M_0 P_1 ... P_l M_n$, o en general una curva, que permita simular lo que sería el perfil de la boca de la concha. Pasemos a describir dicha poligonal y el gnomon del polígono obtenido.
Previamente observemos que fijada una espiral logarítmica $r=b^\theta$ todo punto del plano está en otra espiral del mismo tipo, es decir, con la misma base y un ángulo de retardo o factor de escala. Este resultado es trivial, dado que si ese punto en coordenadas polares es $(r_\delta,\delta$), si $\sigma=\log_b r_\delta$, entonces $r_\delta=b^\sigma=b^{\sigma-\delta}\thinspace b^{\delta}$, es decir está en la espiral $r=b^{\sigma-\delta} b^\theta$ que es la espiral indicada, pero con un ángulo de retardo $\sigma-\delta$ o con factor de escala $b^{\sigma-\delta}$.
Así pues, partiendo de la poligonal de la sección anterior de nodos $M_i \equiv (b^{\theta_i},\theta_i), \theta_i = \theta_0+i \gamma $, $0 \leq i \leq n$, consideremos $l$ puntos $P_j, 1 \leq j \leq l \space$ de coordenadas polares $(r_{\delta_j},\delta_j)$, tales que $b^{\theta_0} \lt r_{\delta_1} \lt \cdots \lt r_{\delta_1} \lt b^{\theta_0+2\pi}$, y que son puntos ubicados en la zona intermedia de la espiral entre $M_0$ y $M_n$. Cada uno de los $P_j$ está en una espiral $r=b^{\sigma_j-\delta_j} b^\theta$ y $M_0 P_1 \cdots P_l M_n$ forman una poligonal que sustituye al segmento $M_0M_N$ del poligono inicial y sirve de cierre del mismo. Tomando como puntos homólogos de los $P_j$ a los $Q_j$ definidos por $Q_j(b^{\sigma_j-\delta_j} b^{\delta_j+\gamma},\delta_j+\gamma)$, y por la tanto verificándose que cada pareja de puntos $P_j, Q_j$ están ubicados en una misma espiral, pero con un desfase angular $\gamma$, tendremos que se verifica que:
$$\frac{\overline{Q_j Q_{j+1}}}{\overline{P_j P_{j+1}}}=b^{\frac{2\pi}{n}}$$
que es la misma proporción de los lados del polígono y consecuentemente $M_0 P_1 \cdots P_l M_n M_{n+1} Q_l \cdots Q_1 M_1 M_0$ es un gnomon del polígono inicial $M_0 M_1 \cdots M_n P_l \cdots P_1 M_0$.
En la podemos observar el polígono inscrito con vértices en la espiral logarítmica, que está dibujada de color rojo, y la poligonal de cierre cuyos vértices están en espirales del mismo tipo dibujadas en color gris. También se refleja la poligonal de cierre homóloga y el gnomon que forman, el cual está sombreado en rojo.
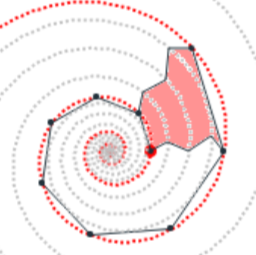
En la podemos interactuar modificando la poligonal de cierre. En este caso se ha limitado a tres vértices controlados por tres pulsadores etiquetados como p1, p2 y p3.
Después del amplio y detallado recorrido que hemos abordado sobre los aspectos básicos de la biología del Nautilus, una vez abordada la fundamentación teórica matemática a la que se ajusta el crecimiento gnomónico aristotélico, habiendo profundizado en la hipnótica curva espiral cartesiana o logarítmica y explicitadas las propiedades que le dan su ser y que le hacen ser una curva maravillosa, y comprobado cómo ésta se ajusta a ese tipo de crecimiento, después de haber ubicado la formalización de la Belleza en base a las proporciones aritméticas y confrontado el ideal clásico de la proporción divina con una proporción más humana, parece que contamos con las herramientas suficientes para tratar de alcanzar el objetivo primordial y final de la investigación realizada y que se busca plasmar en este libro. Así pues, no dilatemos más el esperado desenlace.
Regresemos a nuestro Nautilus y tratemos de leer detenidamente su bitácora vital e intentar interpretarla lo más adecuadamente posibleLos resultados incluidos en este capítulo fueron publicados inicialmente en Galo et al. (2016)
Apoyándonos en lo descrito en la sección "
Como generatriz puede considerarse cualquier sección de la concha, bien sea ésta paralela, normal o con cualquier inclinación respecto al eje de giro. Usualmente se considera la sección transversal obtenida por el corte con un plano que contenga al eje de giro y suele coincidir con la forma de la abertura o boca de la concha siempre que ésta se ubique en un plano (ver la ), pero se detectan diferenciasEn una nota al pie en Thompson (1942) p. 813

|

|
Observando la sección sagital del Nautilus (ver la y la ) podemos abordar la descripción de algunos detalles morfológicos de esta concha:

|

|

|
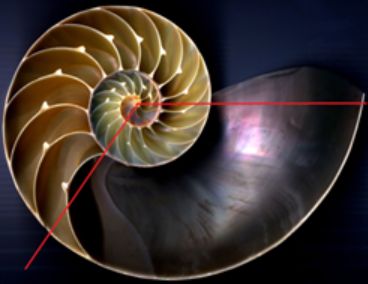
|
En la literatura biológica están documentadas diferentes fases de crecimiento postembrionario distinguiendo un estadio neánico, uno juvenil y otro adulto lo cual puede asociarse en este caso respectivamente a las primeras ocho cámaras en el primer verticilo, a las dieciséis siguientes en el segundo y a las ocho últimas en el tercero. En el análisis matemático a realizar se podría reproducir sin dificultad este comportamiento diferenciado, sin embargo nuestro objetivo principal aquí es la obtención del modelo matemático a partir de lo observado en la quecto-quetta realidad, pero sin necesidad de proyectarlo de nuevo en ésta Como hemos indicado, en Galo (2021-2023)
todo el modelo. Por tanto, abordamos y nos centramos exclusivamente en el que denominamos modelo uniforme del Nautilus.
Del análisis realizado por Thompson (1942)
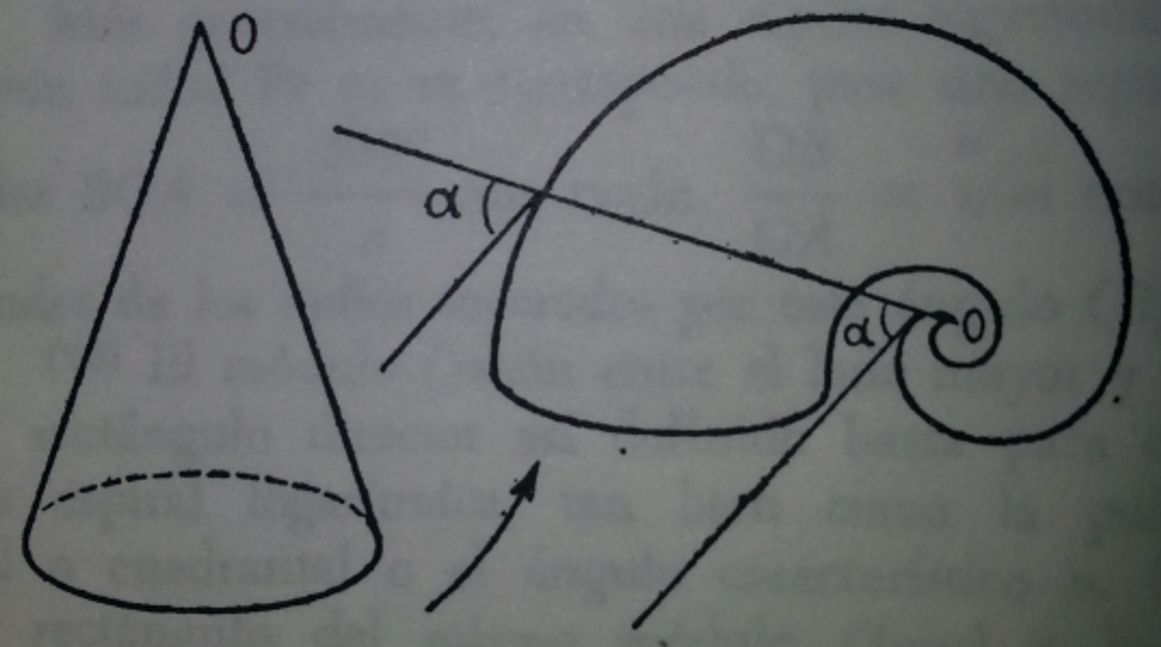
Según lo especificado en
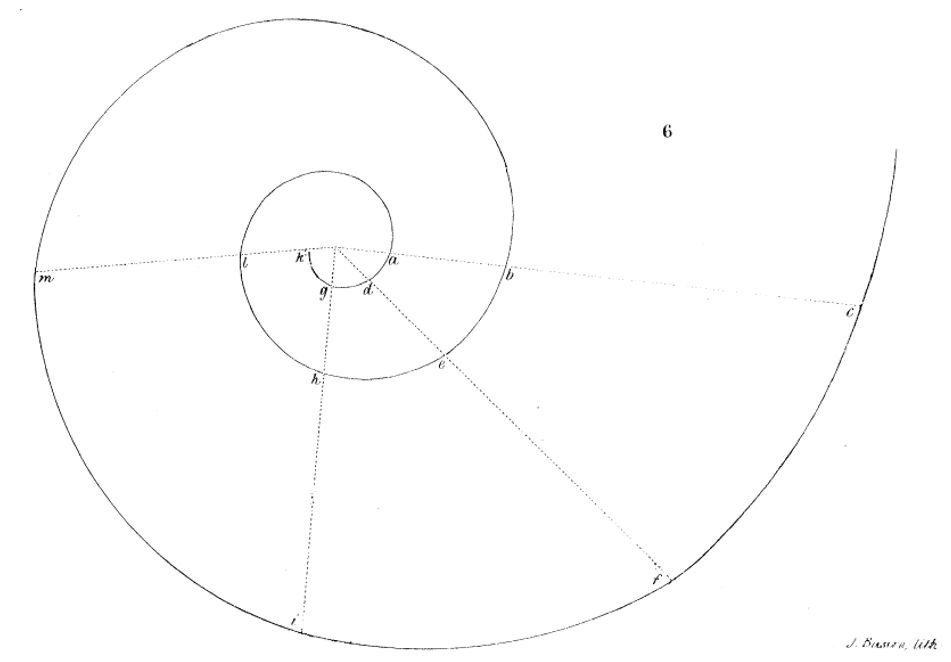
Pero en nuestro caso, este análisis ha sido sustituido por la utilización de la (en concreto el panel: 1. Ajuste de la concha por una espiral logarítimica) en la que podemos dibujar diferentes espirales logarítmicas, superponiéndolas con la imagen de la sección del Nautilus, y entre ellas seleccionar aquella que mejor se ajusta.
En este caso estamos sustituyendo el anterior procedimiento que puede decirse que es local, pues se efectúa en base a mediciones puntuales y a su vez es dependiente de la elección del polo, por uno global ya que el ajuste se realiza a la vez en todos y cada uno de los puntos de la espiral de la concha dado que se procede a una comparación entre dos curvas, una la correspondiente a la sección de la concha y otra la aportada por la escena. A su vez el polo queda determinado explicitamente.
Interactuando en la escena anterior o bien observando la animación de la obtenemos el ajuste descrito. Ahí se representa la espiral logarítmica de ecuación $r=b^{\theta}$ dibujada en color rojo y mediante el control numérico $b$ se modifica el valor de la base de esa potencia hasta detectar la mejor aproximación que se alcanza con $b \simeq 1.186$. Este valor se corresponde con la espiral logarítmica cordobesa analizada en la
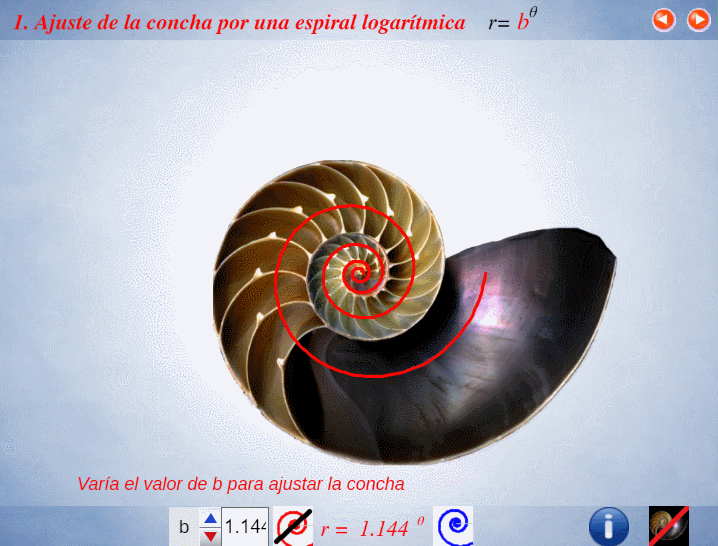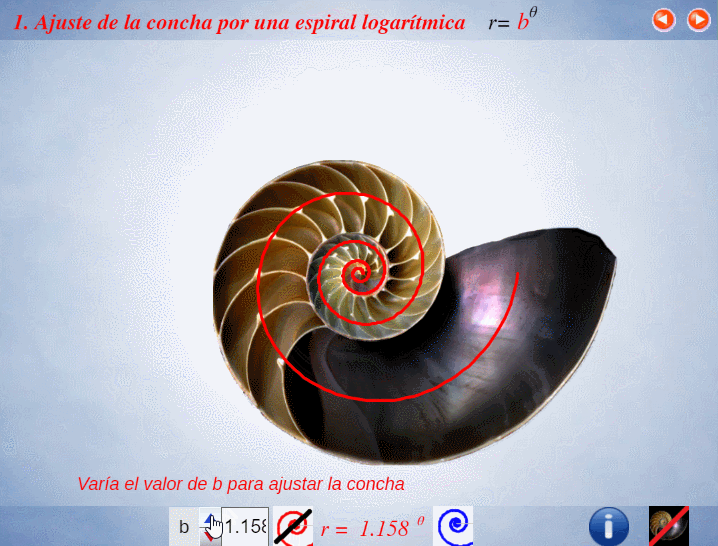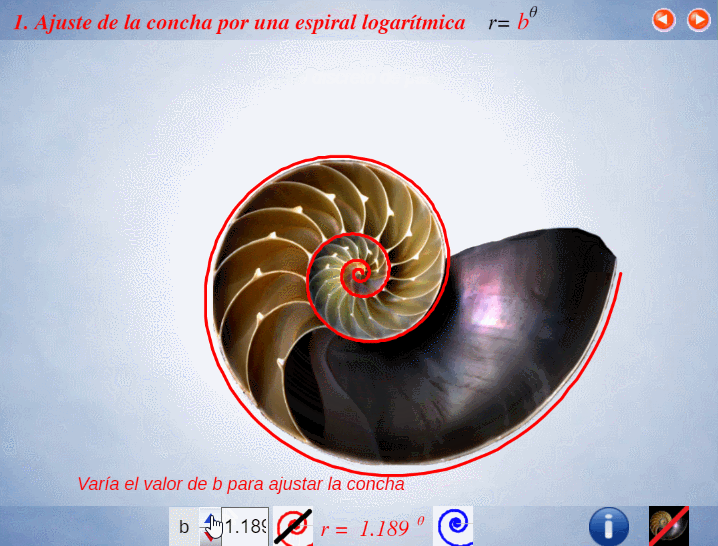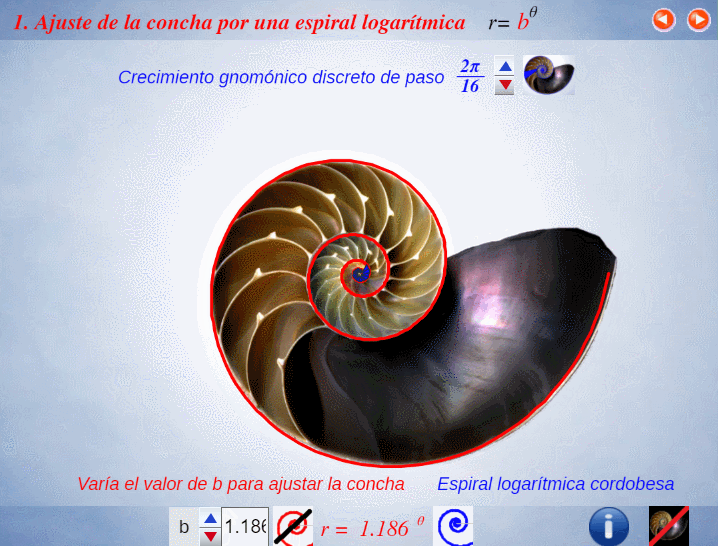
Surge nuestra primera asociación entre el Nautilus y la proporción cordobesa, pero adelantemos que todo girará alrededor de ella ―lo cual a priori es lo lógico, pues es de esperar un único patrón de crecimiento, que es lo que confirmaremos a posteriori―.
Así pues, en base a esta observación, el factor de crecimiento que se obtiene es $\kappa^{2 \pi}=2,914214…$. Este factor está próximo al calculado por MoseleySon de admirar las mediciones realizadas por Moseley y pienso que el valor exacto de $3,00$ fue un redondeo que él realizó a conciencia al, posiblemente, interpretar que la Naturaleza debía de haber elegido un valor entero para la belleza generada por este animal. Sin embargo, en nuestro caso, el factor de crecimiento $2,914214...$ es por el que abogamos por su relación con el caracter cordobés. de $3,00$, cuya espiral asociada es la que tiene de base $b=1,191067...$ para que $b^{2 \pi}=3,00$. En la imagen izda. de la se refleja la comparativa de la espiral de Moseley con el perfil del Nautilus. Sin embargo ese factor difiere bastante del correspondiente a la espiral logarítmica áurea, determinado en la
¡No!, el Nautilus ¡no puede ser y no es áureo!
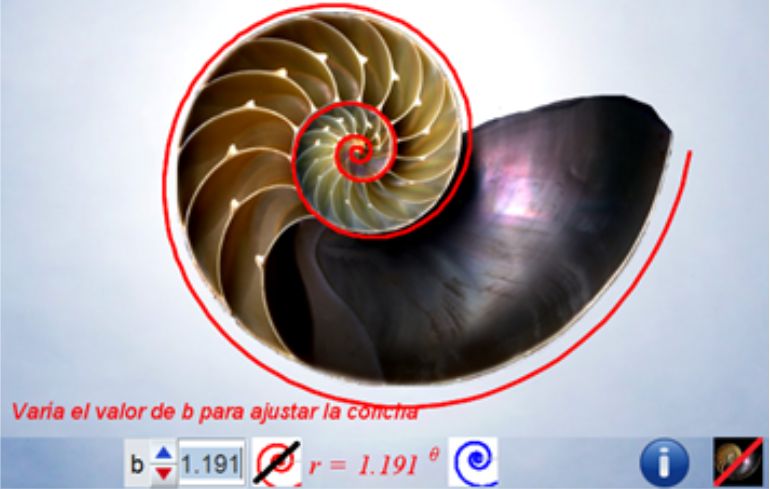
|
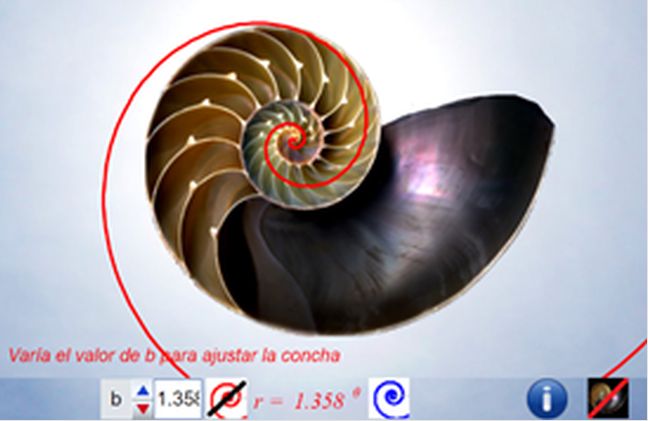
|
Espiral con factor de crecimiento $3,00$, según el cálculo de Moseley (izqda.) Espiral áurea con factor de crecimiento $6,854104...$ (dcha.) |
|
El factor de crecimiento, o en definitiva el valor de $b$ en la espiral logarítmica es clave en la forma de la concha. En la imagen de la podemos ver algunos ejemplos en función de ese valor. Al crecer $b$ el factor de crecimiento aumenta y el ángulo formado por el radio vector y la tangente disminuye.

En la podemos aprender a clasificar conchas y a asociar forma, factor de crecimiento y ángulo característico.
En los septos puede observarse los restos del canal sifuncular y los orificios que permiten el paso del sifúnculo por las cámaras. Estos, visualmente, siguen un patrón espiral y es de esperar que sea una espiral logarítmica $r=b^{\theta}$, pero si utilizamos la (panel 1) para su aproximación, de manera análoga a como hemos hecho con la sección de la concha, podemos comprobar que no hay ninguna espiral que se ajuste bien al sifúnculo. Conceptualmente parece más lógico intuir que cualquier punto ubicado en el interior de la concha habrá surgido como consecuencia de un crecimiento análogo al de la propia concha, si bien afectado por un factor de escala, es decir, todo punto debería pertenecer a una espiral logarítmica cordobesa de ecuación $r=a \kappa^{\theta}$. Y eso puede verificarse en esa misma escena, en el panel "2. Ajuste del sifúnculo por una espiral logarítmica" y verse en la animación de la .

Por tanto, variando el valor de $a$ en la expresión de la espiral $r=a \kappa ^{\theta}$ comprobamos que todos los puntos del interior de la sección de la concha forman parte de espirales cordobesas con $0,34 \le a \le 1$. En particular, podemos comprobar que los puntos del sifúnculo están ubicados en una espiral de este tipo en la que aproximadamente $a$ toma valores en el intervalo: $0,65 \le a \le 0,7$. Y de esta observación surge la cuestión: ¿A qué valores teóricos se corresponden esos valores experimentales?

|

|
Imagen de la sección de un ejemplar (izqda.) Representación gráfica (dcha.) |
|
Aunque, en nuestro mundo matemático, hemos aproximado la sección de la concha como una única curva, realmente el crecimiento del Nautilus se produce siguiendo ese cono topológico que hemos reflejado en la ―pero en este caso curvándose lo suficiente para que haya un solapamiento―, es decir, al crecer podemos ver cómo lo que era el exterior de la concha pasa a ser el interior y ello acontece superponiéndose una nueva capa sobre la anterior, una capa diferenteLa necesaria distinción de estas capas, para poder abordar la medición necesaria que conduce a la obtención del factor de crecimiento, era manifestada por Moseley (1838)
reflejado esa distinción utilizando dos espirales logarítmicas cordobesas próximas, diferenciándo ambas capas con dos colores, azul y rojo. Matemáticamente podemos expresarlo como dos espirales de ecuaciones:
$$r=\kappa^{\theta} \quad \text{y} \quad r=\kappa^{\theta-2\pi}$$
o bien
$$r=\kappa^{\theta} \quad \text{y} \quad r=\kappa^{-2\pi}\kappa^{\theta}=0,3431... \, \kappa^{\theta} $$
surgiendo ese valor cercano a $0,34$, que antes hemos detectado, y que podemos interpretar como que la velocidad o razón de crecimiento entre la capa interior y la exterior es de $0,3431...$ a $1$, o bien que la capa exterior crece $\frac{1}{0,3431…}=2,914214...$ veces más rápido que la interior (en definitiva el factor de crecimiento), o bien según lo indicado en la página
Consecuentemente, la sección del Nautilus es una región del plano de ecuación: $$r=a \kappa^\theta \quad \text{con} \quad \begin{cases} \kappa^{-2 \pi} \le a \le 1 \\ \theta_0 \lt \theta \le \theta_0 + 2 \pi n\end{cases}$$ donde $n$ es el número de ciclos o verticilos.
Pero, de las infinitas espirales que determinan el fragmacono nautiliano ¿cuál se corresponde con el sifúnculo? Si consideramos la espiral intermedia entre la interior y la exterior ―lo cual sería consistente con el hecho de que el sifúnculo fuera el eje del cono topológico citado― entonces tendría que ser que:
$$ a=\frac{\kappa^{-2 \pi}+1}{2}=\frac{0,3431...+1}{2}=0,6715...$$
valor que está en el rango de valores experimentales obtenidos para el sifúnculo en la , lo cual da fundamento al modelo teórico construido.
Consecuentemente el sifunculo se ajusta a una espiral cordobesa que tiene un ángulo de retardo aproximado de $\frac{3 \pi}{4}$ respecto a la espiral de la concha ventral, pues $$log_\kappa 0,6715...= -2,3394... \simeq -\frac{3 \pi}{4}$$
En línea a lo analizado en la sección sobre las espirales discretas asociadas a una espiral logarítmica" de la página
Ajustada la forma global de la sección de la concha fijémonos en el rastro dejado por el Nautilus en su crecimiento. Lo más ostensible son las diferentes cámaras que presenta, delimitadas por los septos, y la conexión entre ellas correspondiente al paso del sifúnculo. Centrémonos y analicemos inicialmente dichas cámaras que, como hemos indicado, en el último verticilo se contabilizan en un número de dieciséis. Por tanto, dentro del crecimiento continuo de la concha, podríamos decir que los septos surgen como consecuencia de un crecimiento discreto de paso $\frac{2 \pi}{16}=\frac{\pi}{8}$, que casualmente o más bien por causalidad tiene una connotación en la proporción cordobesa pues como vimos en la sección "El triángulo cordobés" de la página
escaleno de ángulos $\frac{5\pi}{8}$, $\frac{2\pi}{8}$ y $\frac{\pi}{8}$
Apoyándonos en la espiral logarítimica discreta de paso $\frac{2 \pi}{16}$ obtenemos una primera aproximación que podemos reproducir en la En el panel 1.º cuando se ha ajustado la pared ventral se activa un botón que permite reproducir esta aproximación. y verla en la animación de la .

Para mejorar la aproximación discreta podemos apoyarnos también en la espiral discreta de igual paso $\frac{2 \pi}{16}$, asociada a la espiral del sifúnculo y abordar una aproximación análoga en cada una de las zonas que éste subdivide al fragmacono. De nuevo podemos reproducirlo en el panel 2.º de la y verla en la animación de la .

Siguiendo la línea de mejorar la aproximación, procede considerar una familia de espirales discretas de igual paso $\frac{2 \pi}{16}$ que aproximan a una famila análoga de espirales cordobesas que cubren al fragmacono. Esta situación puede reproducirse en el panel 3.º de la . Pero adicionalmente podemos mejorar, tanto como deseemos a nivel teórico esa aproximación, ampliando el número de espirales en la familia antes considerada y, a su vez, considerando que las espirales discretas sean de paso $\frac{2 \pi}{m 16}$, es decir fraccionando cada cámara en $m$ partes. Eso es lo que se puede reproducir en el panel 4.º de dicha escena. Obviamente, de esta forma, haciendo que $n \rightarrow \infty$ convergemos al modelo continuo.
En la animación de la y en la podemos ver estas aproximaciones.


La proporción cordobesa se ha manifestado como patrón único en la morfología y crecimiento del Nautilus. Pero siguiendo la misma pauta, posiblemente no nos equivocaremos si formulamos la conjetura de que los septos deberían seguir también un patrón cordobés. Para iniciar su verificación usaremos el recurso interactivo "Sobre el crecimiento gnomónico del Nautilus" () y , en concreto, el panel 5.º de esa escena que por comodidad para el lector ubicamos en esta página (Consultad en las indicaciones de la escena la fase 5 y la información de este panel en el boton i de la escena o pulsando aquí). En el modelo uniforme, no ontogénico, que estamos considerando el total de septos considerado es 40 (16 en el primer y segundo verticilo, y 8 en el tercero) para un paso interseptos constante de $\frac{2 \pi}{16}$. ). Abordaremos una comparación de dichos septos, al igual que hicimos con la sección de la concha, con espirales logarítmicas y en particular con la espiral logarítmica cordobesa.
En la animación de la se reflejan los pasos seguidos para determinar la forma de los septos:

En la vemos un detalle del encaje del arco de la espiral cordobesa con uno de los septos.
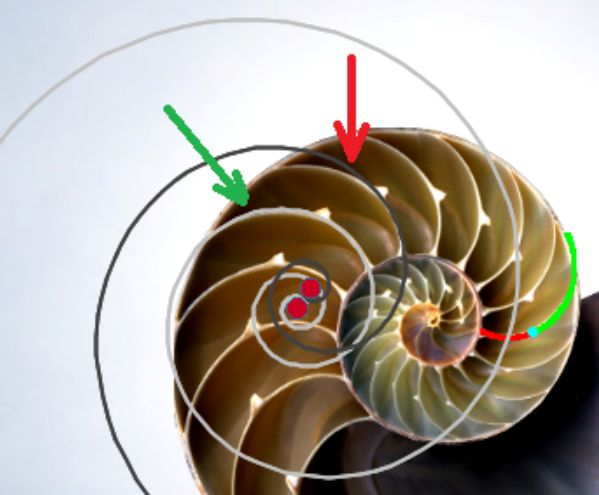
Pero, si ha reproducido ese ajuste en la escena interactiva (o al menos observado en la animación anterior) habrá experimentado que una vez ha encajado un septo, para encajar el siguiente es necesario trasladar el polo de esa espiral y que la curva que van describiendo dichos polos parece estar situada:
¡¿en una espiral?!
Esto pone nervioso a cualquier investigador o lector interesado, ¿verdad? Y, para remate o colmo de nerviosismo:
¡¿será esa espiral cordobesa?!
En la animación de la observamos:

Para verificar que la espiral que forman los polos de los septos es cordobesa podemos hacerlo con la . Primero dibujamos esa espiral (botón con la espiral magenta) y después seleccionando el botón con la espiral gris oscura, ponemos $b=1,185$ que se corresponde con la espiral cordobesa y finalmente hay que ajustar el coeficiente $a$, que se comprueba que está próximo a $0,5$.

Esta espiral de los polos () parece que se ubica en una posición media entre la espiral dorsal y la espiral del sifúnculo. El coeficiente de la primera determinamos que era $0,3431...$ y el de la segunda es 0,6715... y, por tanto el coeficiente de la intermedia sería:
$$\dfrac{0,3431...+0,6715...}{2}=0,5073...$$ que está en el entorno del valor de $0,5$ hallado experimentalmente.
Adicionalmente al pasar de un septo a otro, el arco de la espiral con el que coteja es uno que se obtiene como consecuencia de un desplazamiento en esa espiral, es decir, si el paso de un septo a otro equivale a incrementar el ángulo en la espiral de los polos de los septos en $\frac{2 \pi}{16}$, el arco del segundo septo es una traslación en la espiral del septo anterior en ese mismo ángulo. Para verificar esta circunstacia y todo lo anterior hemos de proceder a construir el modelo matemático que se deduce de todas las observaciones realizadas. Pero previo a la formalización procede hacer una síntesis.
La pauta observada y explicitada hasta ahora se reitera y prolonga, todo encaja en un patrón único cimentado en la proporción cordobesa:
Todo en el Nautilus se muestra concordante con la proporción cordobesa. Y llegado este momento (ver la ) escuchamos al Nautilus que nos decía:
“He vivido en un mundo áureo que me era ajeno, pero me habéis escuchado y ahora sí puedo cantar..."

|
|

|
|
A partir de todo lo analizado estamos en situación de poder establecer un modelo matemático global que reproduce globalmente la morfología y el crecimiento continuo y uniforme del Nautilus. Este modelo puede observarse en la y en el panel 6.º de la .

También puede verse la simulación del crecimiento del Nautilus en la animación de la .

Procedamos a realizar la formalización de dicho modelo mediante la especificación de sus ecuaciones en base a las cuales se han realizado las representaciones gráficas previas.
En el instante de crecimiento de la concha correspondiente a un ángulo $\lambda $, el fragmacono es la región del plano: $$r=a \kappa^\theta \quad \text{con} \quad \begin{cases} \kappa^{-2 \pi} \le a \le 1 \\ \theta_0 \le \theta \le \lambda \end{cases} \tag{$1$}$$ donde $\kappa=1,185580...$ es el número cordobés y $r=a \kappa^\theta$ es una espiral cordobesaPor simplificación, el polo común de todas esas espirales se ha posicionado en el origen de coordenadas $O(0,0)$. para cada valor de $a$.
El número de verticilos, hasta ese instante $\lambda$, viene dado por $\frac{\lambda-\theta_0}{2 \pi}$.
Así pues, todo puntoEn lo sucesivo, mediante el uso del subíndice $_F$ indicamos que ese valor depende del punto $\color{green} F$ que se considere. $\color{green}F (r_F, \theta_F) $ del fragmacono, el cual verifica que $\color{green} \theta_0 \le \theta_F \le \lambda$ y $\color{green} \kappa^{\theta_0-2 \pi} \le r_F \le \kappa^{\lambda}$, pertenece a una espiral cordobesa
$$\color{green} r_F=a_F \kappa^{\theta_F} \tag{$2$}$$ que denominaremos “longitudinal” (ver la espiral en color verde oscuro en la y pulsad los pulsadores inferiores "movimiento lateral" y "movimiento transversal" para desplazar el punto $\color{green} F$ en el fragmacono).
A su vez, ese punto $\color{green}F$ también pertenece a un arco de una espiral logarítmica cordobesa “transversal”Estos arcos bien son septos o bien son arcos interseptos semejantes. (ver la espiral en color rojo oscuro en la ). Su ecuación paramétricaDe la ecuación se deduce que todos estos arcos no son más que traslaciones de vector $\overrightarrow{OP_F}$ de arcos de la espiral logarítmica cordobesa de ecuación $r=d \, \kappa^\theta$.
es :
$$\color{IndianRed} \begin{cases} x_F
=P_{x_F}+d \, \kappa^{\varphi_F} cos({\varphi_F}) \\ y_F=P_{y_F}+d \, \kappa^{\varphi_F} sen({\varphi_F}) \end{cases} \quad {\varphi_F} \in [\alpha_F, \beta_F] \tag{$3$}$$
donde $d \simeq 0,5$ es independiente de $\color{green} F$ y $\color{IndianRed} P_F (P_{x_F}, P_{y_F})$ es su polo. La amplitud de este arco viene dada por el intervalo determinado por los ángulos $\color{IndianRed} \alpha_F$ y $\color{IndianRed} \beta_F$, ambos dependientes de $\color{green} F$, pero como consecuencia del crecimiento gnomónico se verifica que ésta es angularmente constante en todos esos arcos y en el modelo se tasaEn el libro "El modelo ontogénico matemático del Nautilus" (Galo, 2024)
También acontece que todos esos polos $\color{IndianRed} P_F$ de las espirales transversales son puntos de la espiral longitudinal, que denominamos espiral de los polos de los septos, cuya ecuación es:
$$\color{magenta} r=d \kappa^\theta \tag{$4$}$$
es decir,
$$\color{magenta} \begin{cases} P_{x_F}=d \, \kappa^{\theta_P} \, cos({\theta_P}) \\ P_{y_F}=d \, \kappa^{\theta_P} \, sen({\theta_P}) \end{cases} \tag{$5$}$$
Si $\color{magenta} P_F$ y $\color{magenta} P_{F'}$ son dos puntos de esa espiral de los polos que se diferencian un ángulo $\color{magenta} \Delta \theta_P$ entonces los arcos transversales asociados verifican que $$\color{IndianRed} \alpha_{F'} = \alpha_{F} + \color{magenta} \Delta \theta_P \tag{$6$}$$ y, por tanto, una traslación "longitudinal" en el fragmacono genera un traslación "transversal" en el arco septal asociadoEsto formaliza lo descrito en las secciones "Modelando los septos" y "La espiral de los polos de los septos" y que está reflejado en la animación de la ..
Adicionalmente, tenemos que si $\color{magenta} \theta_P$ es el ángulo asociado a $\color{magenta} P_F$, entonces $\color{IndianRed} \alpha_{F}$ en (3) cumple queEl desfase angular $\frac{51 \pi}{64}$ está próximo a $\frac{3 \pi}{4}$ y ha sido objeto de revisión en el modelo ontogénico (Galo 2021-2023)
El fragmacono está delimitado por:
Y el sifúnculo es el eje del fragmacono (ver la espiral en color turquesa en la ):
$$\color{turquoise} r= \frac{1+\kappa^{\theta-2 \pi}}{2}\kappa^{\theta} \quad 0 \lt \theta \le \lambda - \frac{3 \pi}{4} \tag{10}$$
Después de una extensa trayectoria investigadora queda uno sorprendido de que todo pueda resumirse en una única espiral, la espiral logarítimica cordobesa, de ecuación:
$$r=\kappa^\theta$$
sobre la que se realizan traslaciones, mediante desplazamiento de su polo, y giros o cambios de escala —que en este caso son transformaciones equivalentes—.
Todo el modelo ha quedado resumido en las diez expresiones matemáticas recogidas en las páginas
Ciertamente, al Nautilus, hay que reconocerle su ardid de sintésis. Y el meollo o quid de su ser o más bien de su rastro calcáreo lo hemos detectado. Sin embargo, siendo su locuacidad escasa o bien estando nuestra capacidad de escucha limitada, es obvio que hemos tenido
que acomodarle en el modelo expuesto, realmente ha sido un corsé con el que se logra esa simplicidad explicativa que cubre satisfactoriamente la comprensión de su devenir juvenil y de su madurez, pero su etapa embrionaria y neánica queda claramente tapada, desdibujada. No obstante, el reconocimiento de estas limitaciones no es más que un acicate, un trampolín sobre el que tomar consciencia y proceder a la adaptación del traje nautiliano a esas estapas primigenias y a ajustarlo con puntadas más precisas a las etapas posteriores. En esencia procede pasar del modelo uniforme, considerado en este libro, al modelo ontogénico que será objeto de detallado desarrollo en uno próximo a publicar (Galo, 2024b)

Imagen generada por la IA Designer de Microsoft
El contenido de este libro se ha escrito en base a investigaciones y trabajos publicados previamente y, también, en otros hasta ahora inéditos. Algunos de ellos fueron realizados en colaboración con mis colegas Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo († 2023
Los recursos interactivos publicados en los proyectos unidades didácticas y miscelánea de RED Descartes son los siguientes:
 |
Las matemáticas en la Belleza y la belleza de las Matemáticas José R. Galo Sánchez 2005 Versión adaptada a DescartesJS del recurso original (resolución 800×600) realizado inicialmente en "Descartes Java" premiado por la Junta de Andalucía |
|
| Proporcionalidad. Rectángulo Cordobés Ildefonso Fernández Trujillo 2015 |
||
 |
La espiral logarítmica y el crecimiento gnomónico Ángel Cabezudo Bueno 2015 |
|
| Espirales generalizadas de Durero Ángel Cabezudo Bueno, Ildefonso Fernández Trujillo y José R. Galo Sánchez 2019 |
||
 |
Triángulo, Rectángulo y Diamante Cordobés. Tesela. Ildefonso Fernández Trujillo 2015 |
|
 | Sobre el crecimiento cordobés del Nautilus Pompilius José R. Galo Sánchez, Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo 2016 |
|
 |
Rectángulo asociado a un polígono regular José R. Galo Sánchez 2019 |
|
 | El hombre de Vitrubio y la razón áurea José R. Galo Sánchez 2019 |
|
 | El hombre de Vitrubio polifacético José R. Galo Sánchez 2019 |
|
 | Comparador de cánones de belleza José R. Galo Sánchez 2019 |
|
 | Rectángulos cordobeses y áureos en el frontal del Mihrab de la Mezquita de Córdoba José R. Galo Sánchez 2019 |
 | Crecimiento gnomónico aristotélico continuo José R. Galo Sánchez 2019 |
Artículo "Sobre la forma y crecimiento cordobés del Nautilus Pompilius. Epsilon, 2016, Vol. 34 (3), nº 94.


Portada de la revista donde se publicó este artículo y enlace a ella.
En noviembre de 2019 accedí a un artículo publicado en "divulgaMAT", portal dependiente de la Real Sociedad Matemática Española, titulado "Una regla para dibujar espirales logarítmicas y deshacer mitos" (Giraldo y Maestre, 2019)
Artículo publicado y enlace a él en divulgaMAT.
En ese artículo, basándose en lo explicado por Martin Gardner (2018) 

La parte izquierda de esa regla (ver ) sirve para dibujar una espiral discreta que aproximaObviamente, si lo que se está trazando es una poligonal lo que se obtiene es una espiral discreta que aproxima a la espiral logarítmica deseada y esa aproximación, como veremos posteriormente, depende de la razón entre la longitud del segmento que se traza y el radio polar inicial considerado, mejorando la aproximación a medida que ese valor tiende a cero. a la espiral áurea. Sobre ella se refleja explícitamente su crecimiento diametral $1:\phi^2$ y, por tanto, implícitamente queda indicado que el crecimiento radial correspondiente es $1:\phi^4$, que es lo que concluimos en la

Y la parte derecha (ver la ) permite aproximar la espiral logarítmica de factor de crecimiento diametral $1:\phi$.

Sobre ella, los autores indican que es la "Espiral del Nautilus" lo cual, como se argumenta en este libro, no es correcto. Por tanto, he procedido a tachar dicha denominación en esta figura.
La discrepancia entre el crecimiento nautiliano diametral $1:\varsigma^2$ y el $1:\phi$ ahí indicado es lo que me llevó a adentrarme en disquisiciones con uno de los autores de ese artículo, las cuales quedarán reflejadas a continuación pues considero que ayudan a desembrollar la confusión que reiteradamente ya hemos manifestado y que claramente se especifica en el título de este libro.
Analizado en detalle el citado artículo 
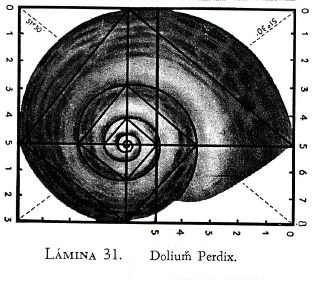
La respuesta no tardó en llegar (). En ella se notaba cierta pesadumbre al haber errado, hecho lógico, pues es algo básico en todo investigador revisar y revisar las conclusiones y estar convencido de ellas, bien por tener referencias que lo apoyen o bien por haber madurado las reflexiones realizadas hasta alcanzar un completo convencimiento personal antes que buscar el ajeno.
En ese correo podemos destacar la insinuación de una variabilidad en el crecimiento del Nautilus que no tiene referencia científica y que no está fundamentada, pues la cita "Sea Shell Spirals" no muestra ninguna base fiable. Y, sin embargo, como veremos a continuación el factor de crecimiento radial del Nautilus lleva más de doscientos años (Moseley, 1838)
También se nos pide la base informativa sobre la que hemos realizado el estudio, si sólo se ha usado la imagen que se muestra en nuestro artículo (Galo et al., 2016)
Finalmente indican que incluirán una corrección en sus artículos en base a lo que le hemos señalado.
En la lectura de la respuesta se captaba cierta resignación, dentro del reconocimiento, y a la vez la búsqueda de alguna posible línea de trabajo en la que poder sustentar sus conclusiones sobre la espiral $1:\phi$ y conocer la solidez de las nuestras al requerir fuentes y datos adicionales sobre los que hubiéramos trabajado, junto a una explicación adicional nuestra. Por ello, di acuse de recibo y le informé sobre la preparación de un documento que pudiera solventar sus inquietudes y observaciones (ver la ).
Dicho documento informativo lo envié día y medio después (ver la ).

El documento adjuntado fue el siguiente:
Sin afán de reproducir el contenido de este documento, el cual puede leer detenidamente, sino buscando sintetizar las conclusiones ahí expuestas indiquemos:
| Áurea | crecimiento 3 | cordobesa | Divermates | |
|---|---|---|---|---|
| pulsación cuadrantal | $\phi=1,61803...$ | $r=1,31607...$ | $\varsigma=1,3065...$ | $\sqrt{\phi}=1,2720...$ |
| pulsación diametral | $\phi^2=2,61803...$ | $r^2=1,73205...$ | $\varsigma^2=1,7071...$ | $\phi=1,61803...$ |
| pulsación radial | $\phi^4=6,85410...$ | $r^4=3$ | $\varsigma^4=2,9142...$ | $\phi^2=2,61803...$ |
| ángulo característico | 72,97º | 80,08º | 80,32º | 81,29º |
Con la respuesta recibida (ver la ) cerraban las disquisiciones que yo había abierto.

Y por mí parte también quedaba finalizado (ver la ).

Los autores incluyeron una nota informativa al pie de su artículo
Ese mismo artículo en la web de dichos autores sí incluye la posibilidad de descargar la plantilla corregida y también la de descargar una plantilla con la regla cordobesa ().
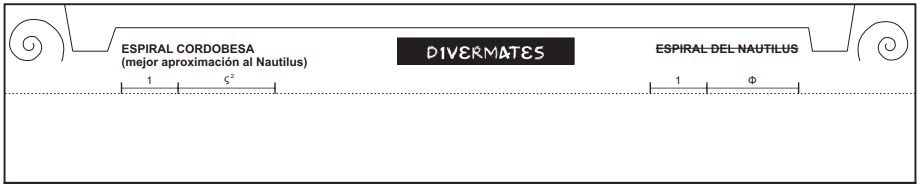
Habiendo llegado a estas reglas, que sirven para aproximar por una poligonal a espirales logarítmicas, no me he resistido a profundizar un poco más en ellas y aportar el fundamento matemático de las mismas y cómo construirlas.
La poligonal en espiral que se obtiene se realiza en base a la propiedad equiangular de toda espiral logarítmica, y lo que se hace es dibujar segmentos que forman un ángulo constante respecto al radio polar (ver la ). Para ello, en la plantilla de la regla se recorta la región marcada en color ocre (ver la ). La línea pintada en rojo es la que marca la dirección de los radios polares y el segmento inclinado respecto a esta línea, que en la imagen está destacado como más grueso, en color negro y con el punto medio pintado en rojo, es el segmento de la poligonal que se dibuja en cada momento.

El ángulo que forman estas dos líneas es el ángulo característico de la espiral logarítmica aproximada (ver ángulo "a" en la ) y, en este caso, para la espiral de pulsación radial 3 (pulsación diametral 1,73205...) aproximadamente es de $80,08º$.
Consecuentemente, lo que se hace es dibujar supuestos segmentos tangenciales a la espiral aproximada formando entre ellos ese ángulo característico.
El punto pintado en rojo es la intersección de la prolongación del radio polar (línea roja) con el segmento de la poligonal (línea negra gruesa) y, consecuentemente, es el punto teórico de tangencia con la espiral que se desea aproximar, pero realmente en general no lo será.
Remarquemos que las espirales discretas aquí obtenidas son claramente diferentes de las analizadas en la
Ese punto de tangencia teórica puede variarse, obteniendo así reglas alternativas, sin más que modificar la posición de la línea que marca la dirección del radio polar (ver en la la línea morada y la verde y los puntos de tangencia asociados con igual color).

Igualmente si variamos la inclinación del segmento tangencial, es decir, el ángulo característico, obtenemos otras reglas alternativas en este caso para aproximar diferentes espirales logarítmicas. Ver en la la línea inclinada naranja que se corresponde con un factor de crecimiento mayor que el áureo, línea negra para el áureo, y la inclinada azul turquesa en la que el factor es menor.

Todas estas posibilidades están contempladas en la donde podemos analizar cómo se comporta el modelo al variar los parámetros que intervienen en él.
Los parámetros son:
Adicionalmente se tienen elementos auxiliares configurables, pero que no afectan al modelo matemático:
Y, finalmente, un botón con la imagen  para acceder a la representación gráfica de la regla correspondiente a los parámetros indicados y que detallaremos posteriormente.
para acceder a la representación gráfica de la regla correspondiente a los parámetros indicados y que detallaremos posteriormente.
Fijada la espiral logarítmica a aproximar mediante el ángulo característico $\Psi$, en la animación de la podemos observar cómo influye el parámetro $k$ en el modelo, estando fijo $l$ y $r$.
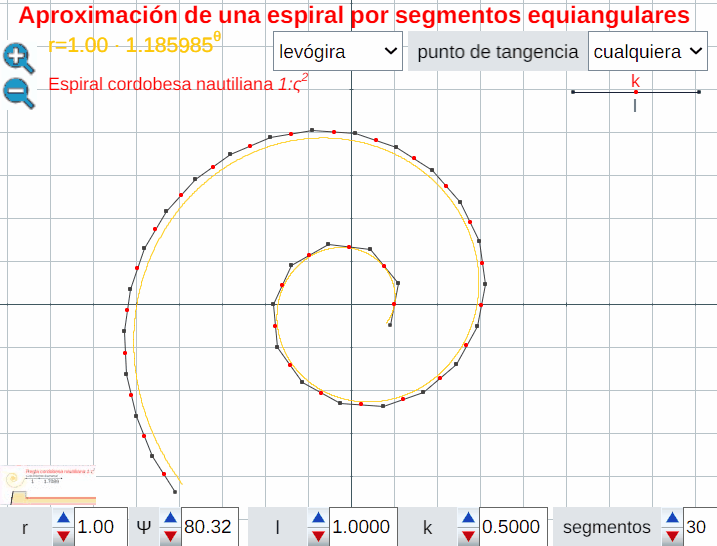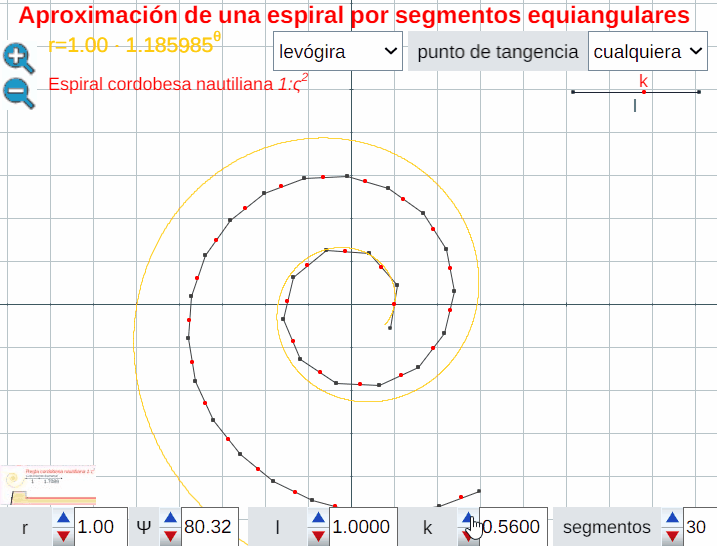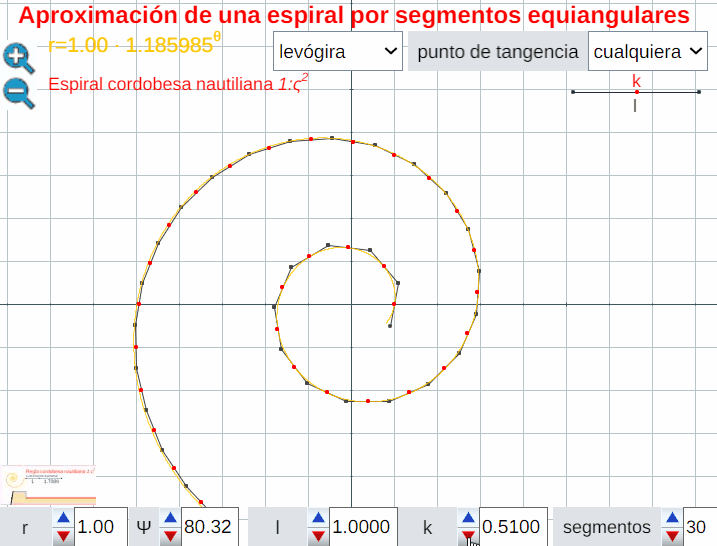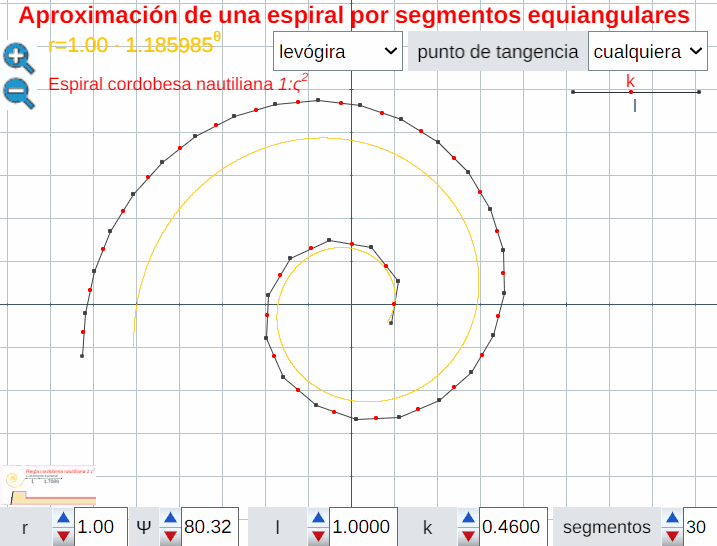
Las situaciones anteriores recuerdan a lo que acontece con las diferencias finitas centradas, regresivas y progresivas en la aproximación de la derivada en un punto que, en esencia, es lo que aquí se está aplicando.
Por otra parte, si mantenemos fijos los parámetros $l$ y $k$, en la animación de la podemos observar como al aumentar el valor de $r0$ mejora la aproximación. Pero precisando mejor lo que acontece, tenemos que $r0$ lo que genera es un cambio de escala en la espiral, pero al aumentar su valor lo que ocurre es que la razón $\frac{l}{r0}$ tiende a cero, es decir, la longitud relativa del segmento tangencial aproximador es menor y, por tanto, se ajusta mejor a la espiral.
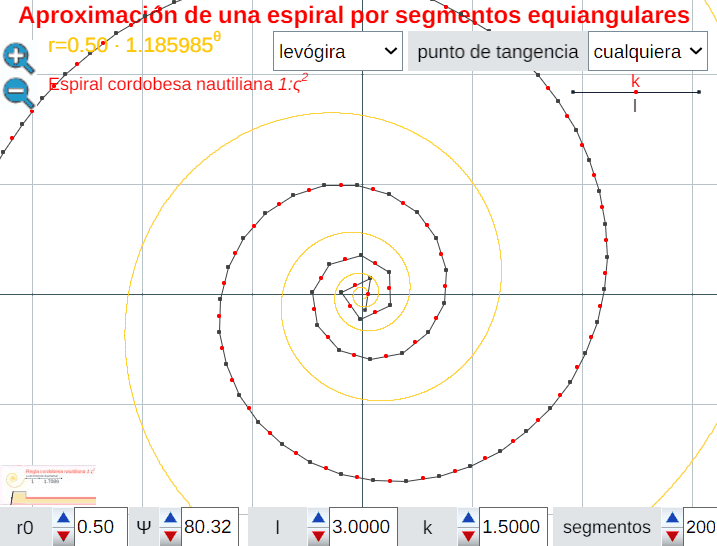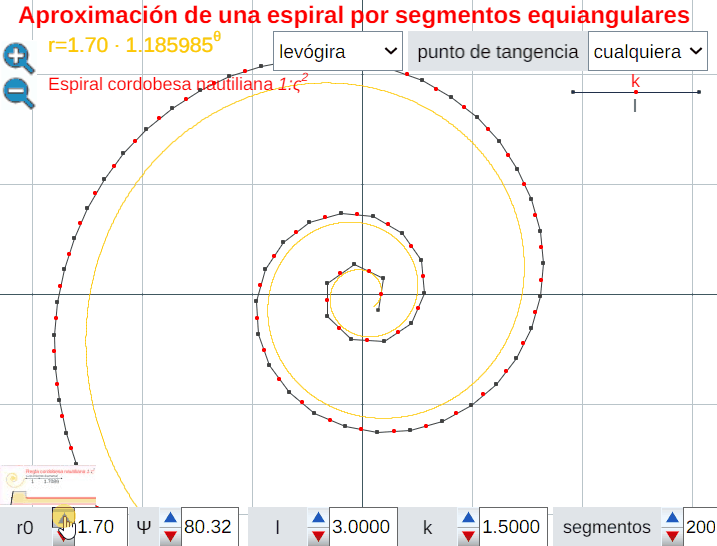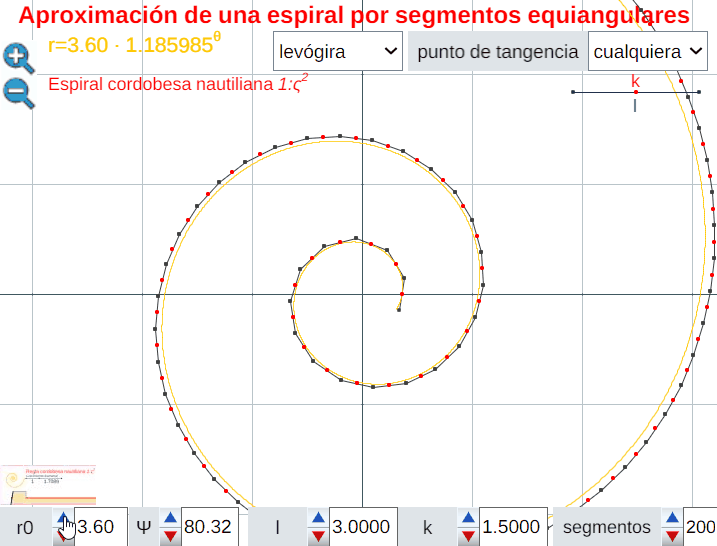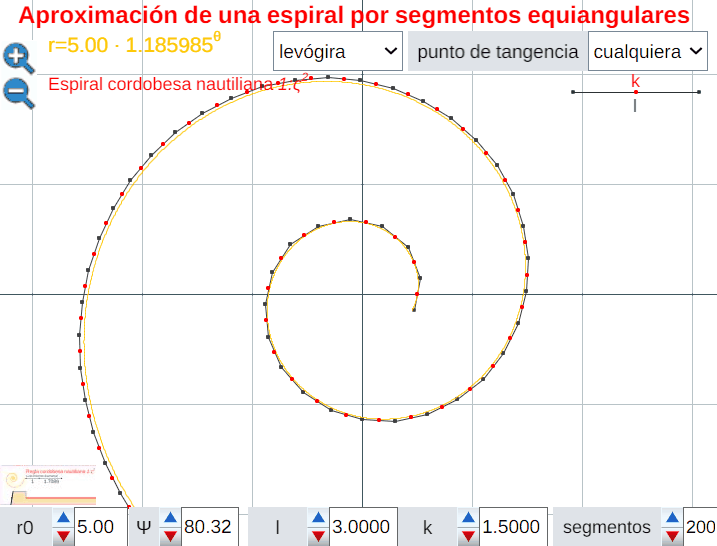
A nivel de dibujo manual con la regla y con el objetivo de que el número de segmentos a dibujar no sea excesivo y que tampoco sean relativamente pequeños, basta considerar $l=r0$ y que el punto de tangencia esté en torno al punto medio. Esa es la propuesta que por defecto se oferta en la .
Al pulsar en esa escena sobre el botón con la imagen  se abre un espacio en el que está representada la regla correspondiente a los parámetros $\Psi$, $l$ y $k$ considerados por el usuario (puede modificarlos también ahí, si lo desea) y, sobre ella, se superpone la gráfica de la espiral logarítmica que aproxima (ver la ).
se abre un espacio en el que está representada la regla correspondiente a los parámetros $\Psi$, $l$ y $k$ considerados por el usuario (puede modificarlos también ahí, si lo desea) y, sobre ella, se superpone la gráfica de la espiral logarítmica que aproxima (ver la ).
Aquí se dispone del botón  con el que se puede proceder a la impresión de esa regla bien en un pdf o bien en papel. Y para regresar a la representación de la espiral y de la poligonal ha de pulsarse en el botón
con el que se puede proceder a la impresión de esa regla bien en un pdf o bien en papel. Y para regresar a la representación de la espiral y de la poligonal ha de pulsarse en el botón  .
También puede elegirse si la regla es levógira o dextrógira, si bien si la regla está impresa basta usar una cara o la opuesta para conseguir ese efecto.
.
También puede elegirse si la regla es levógira o dextrógira, si bien si la regla está impresa basta usar una cara o la opuesta para conseguir ese efecto.
Finalmente, en un menú, puede elegirse entre las opciones:
La primera regla se destaca por ser la espiral áurea ¡la obtusamente asociada al Nautilus!, la de crecimiento radial 3 de Moseley
En la animación de la se realiza una comparación entre estas cuatro reglas. Se presentan una detrás de otra para que se pueda observar como cambia el segmento tangencial inclinado de cada una de ellas al pasar de una a otra. Ese cambio es bastante ostensible al pasar de la áurea a la de Moseley (de 72,97º a 80,08º, hay más de 7º de diferencia), la cordobesa (de 80,08º a 80,32º, casi imperceptible) y algo menor, pero detectable visualmente, al pasar de la cordobesa a la $1:\phi$ (de 80,32º a 81,29º, casi 1º de diferencia).

En la abordamos una comparativa de la espirales logarítmicas antes citadas y las superponemos sobre la sección de la concha del Nautilus.
En ella, el botón  permite ocultar o mostrar la comparación y
permite ocultar o mostrar la comparación y  ocultar o mostrar la sección de Nautilus. En el menú superior puede selecionarse entre las cuatro espirales que hemos distinguido y verificar cómo la espiral nautiliana se ajusta a la cordobesa, lo cual es ya reiterativo en este libro, pero es que la búsqueda del parecido áureo es empecinado.
ocultar o mostrar la sección de Nautilus. En el menú superior puede selecionarse entre las cuatro espirales que hemos distinguido y verificar cómo la espiral nautiliana se ajusta a la cordobesa, lo cual es ya reiterativo en este libro, pero es que la búsqueda del parecido áureo es empecinado.
En Bogotá (Colombia), en la sede del Instituto Pedagógico Nacional y organizado por la Universidad Pedagógica Nacional, la Escuela Colombiana de Ingeniería Julio Garavito y la Universidad Distrital Francisco José de Caldas se celebró el "24 Encuentro de Geometría y sus Aplicaciones" desde el 19 hasta el 21 de junio de 2019.

En este congreso internacional, que se celebra desde el año 1990, el autor participó como invitado internacional impartiendo la conferencia inaugural, titulada:
El Nautilus: referente del crecimiento gnomónico cordobés
En ella, se detalla cómo el Nautilus pompilius, un animalito que lleva haciendo matemáticas desde hace más de 400 millones de años, sigue un modelo de crecimiento gnomónico aristotélico que se encuadra en el canon de belleza humana o cordobesa y, de manera colateral, se desmiente el ampliamente extendido bulo (fake new) de que la concha de este molúsco cefalópodo sigue la proporción divina o áurea.

El contenido de la conferencia transcurre en varios bloques:

Presentación con Google Slides usada en la conferencia.
Versión en pdf con las notas del autor y versión en Powerpoint.
En la barra de herramientas inferior puede gestionar manualmente el paso de las diapositivas
y pulsando el icono ⋮ se tiene acceso a las notas del conferenciante.
Resumen publicado en las memorias del Encuentro pp. 28-32.
En el mismo "24 Encuentro de Geometría y sus Aplicaciones" se desarrolló un Taller de edición de escenas con Descartes.

Este taller está planificado como un aprendizaje centrado en el desarrollo de escenas que tiene un contenido relacionado con la conferencia inaugural del 24 Encuentro "El Nautilus: referente del crecimiento gnomónico cordobés" y todo está englobado en un espacio web específico.

En esta web se desglosan los siguientes apartados:
Cada práctica cuenta con:
Resumen publicado en las memorias del Encuentro pp. 70-77.
Imagen generada por la IA Designer de Microsoft