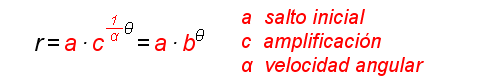La espiral equiangular, logarítmica o geométrica fue estudiada por Descartes al plantearse la búsqueda de una curva con comportamiento análogo a de la circunferencia, en el sentido de que en cada punto el ángulo que forme el radio vector con la tangente sea siempre constante. Benouilli la denominó "Spira mirabilis" o espiral maravillosa. Puede definirse de manera dinámica como el resultado de la composición de un movimiento rectilíneo no uniforme (exponencial) y de un movimiento circular uniforme. Este procedimiento constructivo es el que se refleja en esta escena interactiva.

A partir de la construcción dinámica o dependiente del tiempo, puede obtenerse la relación algebraica que verifican todos los puntos de esa curva. Ésta queda representada de una manera simple al usar coordenadas polares.

El nombre de logarítmica es porque en una expresión equivalente el ángulo queda determinado en función del logaritmo de la distancia polar, es decir del módulo del radio vector.

OBJETIVOS

• Construir la espiral logarítmica como composición de movimientos.
• Analizar algunas propiedades de esta espiral.
• Es logarímica porque el ángulo polar es un logaritmo de la distancia polar o radio, o bien el radio es una exponencial del ángulo.
• Es geométrica porque las distancias polares de todos los puntos situados en una semirrecta están en progresión geométrica.
• Es equiangular porque el ángulo que forma el radio vector de un punto con la tangente en ese punto es siempre constante.
• Introducir el crecimiento gnomónico euclídeo y el crecimiento gnomónico discreto en la aproximación de la espiral logarítmica por poligonales.
• Verificar como la naturaleza se ajusta al uso de esta espiral.
• Introducir el crecimiento gnomónico instantáneo o continuo como límite del crecimiento discreto.
• Verificar que la razón de crecimiento en la espiral logarítmica es la unidad.
  

INSTRUCCIONES

El objeto se desglosa en varias fases que se corresponden con diferentes escenas que pueden recorrerse con los botones de desplazamiento ubicados en la esquina superior derecha:

• Fase 0. Se muestra una imagen de Descartes y Bernoulli y de la espiral maravillosa junto a la ecuación algebraica que la define en coordenadas polares, donde se manifiesta que es una familia de espirales dependientes de dos parámetros reales positivos a y b. Podría considerarse a<0 y en este caso hay que considerar que r es una distancia dirigida, en este supuesto la gráfica de la espiral es simétrica respecto al polo con respecto a la espiral en la que el coeficiente es |a|.
  
• Fase 1. Se plantea la determinación de la posición de un grillo, un móvil, en un movimiento rectilíneo no uniforme consistente en un salto inicial de longitud a y sucesivos saltos en línea recta, de manera que en cada salto la distancia a la que se encuentra del punto inicial es c veces mayor que la distancia anterior. Es decir, se parte de una situación dinámica y por tanto dependiente del tiempo. Puedes interactuar para realizar las siguientes acciones:
• Abordar un zum, es decir, un cambio de escala en la representación.
  
• Establecer la posición inicial del grillo en ese salto inicial (sólo cuando t=0), para ello posiciona el ratón sobre él y desplázalo. Esa longitud quedará reflejada en la linea inferior.
  
• Indicar la constante c que marca el factor de amplificación (c>1), estabilizacion (si c=1) o contracción (si c<1). Ver las diferentes situaciones.
  
• El tiempo se refleja automáticamente, una vez inicies el movimiento. No puedes cambiarlo.
• Cuentas con tres botones: uno informativo, otro que permite regresar a la situación inicial y un tercero que permite la activación o la parada del movimiento.
  
• Fase 2. En este caso se plantea el movimiento circular uniforme. Una nueva situación dinámica dependiente del tiempo y en la que puedes interactuar de manera análoga al paso anterior. En este caso lo que podrás cambiar es la velocidad angular antes de iniciar el movimiento y la posición del grillo si lo deseas.
  
• Fase 3. Aquí se aborda una composición de movimientos, el lineal y el angular. Podrás interactuar de manera similar a las situaciones anteriores y en el botón de información se obtiene, a partir del planteamiento dinámico, una relación -- digamos estática o atemporal-- entre la distancia y el ángulo polar. Ésta es la ecuación algebráica en coordenadas polares de la espiral logarítmica y nos permite identificar el significado de los dos parámetros a y b específicos de la misma:



• Fase 4. Representamos gráficamente la curva correspondiente a la espiral logarítmica a partir de la relación algebraica obtenida en función de los parámetros que denotamos a y b.
  • Dado que r viene dado como a por una función, a es un factor de escala.  Puede variarse el parámetro a y observar ese cambio de escala, por ello equivale al zum que puede realizarse con el botón etiquetado con ese nombre.
  • Cuando a=0 o b=0 degenera a un punto, el polo.
  • Cuando b=1 es una circunferencia de radio a.
  • Si se cambia el valor de b por su inverso las espirales son simétricas respecto al eje polar, es decir, lo que cambia es el sentido de giro. Así pues, por ello, bastaría analizar las espirales en las que b>1. Se dispone también de dos botones etiquetados como b y 1/b que permiten mostrar u ocultar la espiral correspondiente a esos valores y observar la relación citada. Al pulsar el botón de información se explicita este hecho.
  • Se tienen también dos controles que permiten definir el intervalo de variación del ángulo en el que se representará la espiral.
    
• Fase 5. En base a lo indicado en el paso anterior, consideramos la dependencia sólo del parámetro b y cuando b>1. Puede cambiarse el valor de este parámetro y el intervalo de variación del ángulo en el que se representará la espiral. 
• Pulsando el botón de información se muestra la relación entre dos puntos cualesquiera de la espiral y, en particular, la que acontece entre los situados en la misma semirrecta. Estos puntos están posicionados según una progresión geométrica, de ahí que a la espiral logarítmica se le denomine también como "espiral geométrica". 
• Pulsando el botón inferior derecho se dibuja una semirrecta y los puntos de ésta que pertenecen a la espiral.  En esa semirrecta se dispone de un control gráfico con el que se puede variar dicha semirrecta.
  
• Fase 6. La espiral logarítmica se denomina también equiangular debido a que el ángulo que determina el radio vector de un punto de la espiral con la recta tangente en ese punto es siempre el mismo , es decir, es un invariante ligado a cada espiral.
• Pulsando el botón de información se explicitan las componentes del radio vector y del vector tangente, y se calcula el ángulo que forman ambos. Éste depende sólo del parámetro b y es independiente del ángulo polar. Por tanto, en cada espiral este ángulo es constante en todos sus puntos, de ahí que sea equiangular.
  
• Puede cambiarse el valor de b y comprobar como también cambia ese ángulo. Pero manteniendo b fijo, dicho ángulo permanece constante al variar el ángulo polar. En el caso particular en que b=1 (el control permite que pongas este valor), como ya indicamos, la espiral degenera en una circunferencia y este ángulo constante es recto --la espiral generaliza a la circunferencia según buscaba Descartes--, y a medida que b tiende a infinito el ángulo tiende a cero, el radio vector tiende a coincidir con la recta tangente, --la espiral degenera en una recta--.
• En el control de infomacion se detalla el cálculo de dicho ángulo.