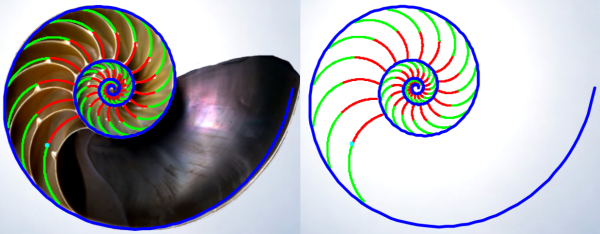
En esta escena se observa el modelo matemático de aproximación de los septos y la modelación de su crecimiento.
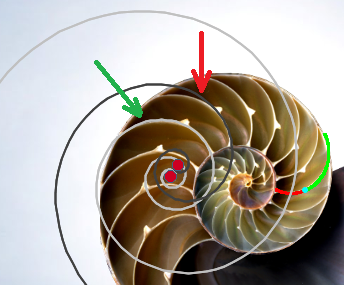
En una observación del interior de la concha podemos contabilizar un primer verticilo con ocho cámaras (marcadas en la imagen siguiente con un punto rojo), uno segundo con dieciséis (color azul) y medio verticilo final con otros ocho (en magenta). La cámara habitacional ocupa un espacio aproximadamente de 135º. El diferente ritmo de crecimiento se corresponde a diferentes fases que están descritas en la documentación técnica enlazada en las indicaciones.

En el modelo matemático tomamos un paso angular fijo y para ello consideraremos las ocho primeras cámaras subdivididas en dos con lo que contabilizaremos un total de 40 (2*8+16+8) y los septos que las determinan los numeraremos desde el cero al cuarenta. Obviamente, si se deseara, es trivial contemplar el crecimiento más rápido en el primer verticilo. Cada septo se puede seleccionar mediante el control etiquetado como "septo".
En la escena, inicialmente, se presenta la aproximación del septo trigésimo segundo mediante dos arcos concatenados, uno rojo y otro verde, que contactan en un punto turquesa el cual se corresponde con el punto de corte del septo con el sifúnculo. Y en la parte inferior se dispone de varios controles que nos permitirán visualizar y comprender el modelo matemático.
En la parte izquierda de la siguiente imagen, y en la escena, podemos observar que la aproximación es bastante buena hasta el trigésimo segundo septo y a partir de él el modelo inicia cierta desviación respecto a la foto que nos sirve de base al estudio --esa variación acontece en el paso discreto de crecimiento y no en la forma del septo modelado--. La divergencia entre el carácter matemático de la Naturaleza y la matematización de la misma se pone aquí de manifiesto. El modelo matemático sigue unas pautas fijas invariables y la Naturaleza no siempre manifiesta tal exactitud dado que los condicionantes son múltiples y diversos y desde el punto de vista biológico están documentadas diversas fases en el crecimiento. El resultado de aplicar el modelo matemático queda reflejado en la parte derecha de esta imagen.