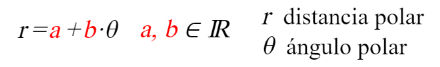La espiral de Arquímedes fue estudiada y descrita por éste en su libro "Sobre las espirales" en torno al 225 a.C. Puede definirse de manera dinámica como el resultado de la composición de un movimiento rectilíneo uniforme y de un movimiento circular uniforme. Este procedimiento constructivo es el que se refleja en esta escena interactiva.

A partir de la construcción dinámica o dependiente del tiempo, puede obtenerse la relación algebraica que verifican todos los puntos de esa curva. Ésta queda representada de una manera simple al usar coordenadas polares.

OBJETIVOS

• Construir la espiral de Arquímedes como composición de movimientos.
• Analizar las propiedades de esta espiral.

INSTRUCCIONES

El objeto se desglosa en varios pasos o fases que se corresponden con diferentes escenas que pueden recorrerse con los botones de desplazamiento ubicados en la esquina superior derecha:

• Paso 0. Se muestra una imagen de Arquímedes y de la espiral que lleva su nombre (fuente wikipedia) y la ecuación algebraica que la define en coordenadas polares, donde se manifiesta que es una familia de espirales dependientes de dos parámetros reales a y b.
• Paso 1. Se plantea la determinación de la posición de una hormiga, un móvil, en el movimiento rectilíneo uniforme. Es decir se parte de una situación dinámica y por tanto dependiente del tiempo. Puedes interactuar para realizar las siguientes acciones:
• Abordar un zum, es decir, un cambio de escala en la representación.
  
• Establecer la posición inicial de la hormiga (sólo cuando t=0), para ello posiciona el ratón sobre ella y desplázala.
• Indica la velocidad constante a la que deseas se desplace.
• El tiempo se refleja automáticamente, una vez inicies el movimiento. No puedes cambiarlo.
• Cuentas con tres botones: uno informativo, otro que permite regresar a la situación inicial y un tercero que permite la activación o la parada del movimiento.
  
• Paso 2. En este caso se plantea el movimiento circular uniforme. Una nueva situación dinámica dependiente del tiempo y en la que puedes interactuar de manera análoga al paso anterior. En este caso lo que podrás cambiar es la velocidad angular antes de iniciar el movimiento.
  
• Paso 3. Aquí se aborda una composición de movimientos, el lineal y el angular. Podrás interactuar de manera similar a las situaciones anteriores y en el botón de información se obtiene, a partir del planteamiento dinámico, una relación -- digamos estática o atemporal-- entre la distancia y el ángulo polar. Ésta es la ecuación algebráica en coordenadas polares de la espiral de Arquímedes y nos permite identificar el significado físico de los dos parámetros específicos de la misma. El primero es la posición inicial y el segundo la relación entre la velocidad lineal y la angular:



• Paso 4. Representamos gráficamente la curva correspondiente a la espiral de Arquímedes a partir de la relación algebraica obtenida denotándola con los parámetros a y b.
  
  
  • Puede variarse el parámetro a y observar que el efecto que produce es un giro.  En este paso el parámetro b se ha dejado fijo.
  • Se observan dos ramas, una simétrica de la otra. Puede ocultarse o mostrarse con el botón "Una rama/Dos ramas".
  • Al pulsar el botón de información se justifica por qué se produce ese giro y, por tanto, que para el análisis de esta función basta considerar sólo el parámetro b.
    
• Paso 5. Si consideramos el caso particular en el que b=0, observaremos que la espiral degenera en una circunferencia de radio a y en punto si a=0.
• Paso 6. En base a lo indicado en el paso cuarto, consideramos la dependencia sólo del parámetro b. Puede cambiarse el valor de este parámetro y el intervalo de variación del ángulo. 
• se observa que para valores opuestos de b las espirales correspondientes son simétricas respecto del eje polar.
  
• Pulsando el botón de información se muestra la relación entre dos puntos cualesquiera de la espiral y, en particular, cómo todos los situados en la misma semirrecta son equidistantes. Esa distancia  común es la separación entre cada dos espiras consecutivas.
  
• Pulsando el botón inferior derecho se dibuja una semirrecta y los puntos de ésta que pertenecen a la espiral.  En esa semirrecta se dispone de un control gráfico con el que se puede variar ésta, y también se cuenta con un segmento que puede desplazarse y así observar cómo todos los puntos son equidistantes, es decir, esa distancia es un invariante característico de esta espiral. Esos puntos, por tanto, están posicionados según una progresión aritmética, de ahí que se le denomine también como "espiral aritmética". Por claridad en el gráfico se representa sólo una de las ramas.

En el documento aquí enlazado puede consultarse algo más detallado el análisis matemático de esta escena y de la espiral de Arquímedes.