
Curvas clásicas en coordenadas paramétricas
PARTE I
ÍNDICE:
(Evolvente de la circunferencia)
Realiza la siguiente experiencia:
Observa que dibujas una especie de espiral que recibe el nombre de evolvente o desarrollada de la circunferencia.
La evolvente a la circunferencia puede considerarse engendrada desarrollando un hilo, mantenido tenso, que se supone previamente enrollado a la circunferencia.
|
|
Actividad 1:
|
|
|
Actividad 2:
|
|
|
Curvas de LISSAJOUS (Siglo XIX)
Las curvas de Lissajous fueron descubiertas por el físico francés Julio Antoine Lissajous (1822 a 1880). Lissajous estaba interesado en poder visualizar las vibraciones. Estudió las vibraciones transversales de las láminas elásticas y la composición de varios movimientos vibratorios por un procedimiento óptico. Sus experimentos más famosos implicaron diapasones y espejos. Por ejemplo, uniendo un espejo a un diapasón y enfocando una luz sobre él, Lissajous podía observar, ayudado por otro par de espejos, la luz reflejada que se torcía y daba vuelta en los espejos, al tiempo de las vibraciones del diapasón. Cuando él instaló dos diapasones perpendicularmente, con uno vibrando al doble de la frecuencia del otro, Lissajous encontró que las líneas curvadas en la pantalla se combinaban para dar lugar a una de estas curvas que hoy llevan su nombre.
Las curvas de Lissajous fueron utilizadas para determinar las frecuencias de sonidos o de señales de radio. Estas curvas permiten el estudio de los movimientos vibratorios y, particularmente, la comparación de los sonidos dados por dos instrumentos.
|
osciloscopio El osciloscopio se emplea en todos los procesos que abarca la electrónica y en muchas áreas de la técnica.
|
Medida de frecuencia La frecuencia de una señal se puede medir con un osciloscopio por dos métodos:
F(Hz) = 1/T(sg)
En este caso el osciloscopio se hace trabajar en régimen X/Y (Deflexión exterior). Aplicando cada una de las señales, a las entradas "X" e "Y" del osciloscopio y en el caso de que exista una relación armónica completa entre ambas, aparece en la pantalla una de las llamadas "figuras de Lissajous", a la vista de la cual se puede averiguar el número de veces que una frecuencia contiene a la otra y por lo tanto deducir el valor de la frecuencia desconocida. |
||
|
Medida de
fase El sistema anterior de medida de frecuencia mediante el empleo de las "curvas de Lissajous", se puede utilizar igualmente para averiguar el desfase en grados existente entre dos señales distintas de la misma frecuencia.
Hacemos trabajar el osciloscopio con deflexión horizontal exterior, aplicando a sus entradas horizontal y vertical (X/Y) las dos señales que se desean comparar.
Mediante esta conexión se formará en la pantalla una "curva de Lissajous" que debidamente interpretada nos dará la diferencia de fase existente entre las dos formas de onda que se comparan.
En los siguientes dibujos, se dan algunos ejemplos de este sistema de aplicación. |
|||
 |
 |
 |
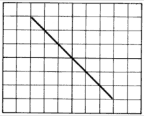 |
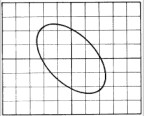
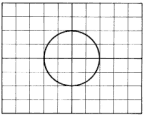
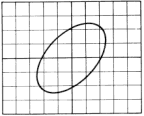
| Curva de Lissajous. Señales desfasadas 30º (o bien 330º). | Curva de Lissajous. Señales desfasadas 90º (o bien 270º). | Curva de Lissajous. Señales desfasadas 110º (o bien 250º) | Curva de Lissajous. Señales desfasadas 180º. |
|
|
Actividad 3: Al final de cada uno de los siguientes puntos pincha en "Inicio". Mantén los valores iniciales excepto el que se indica en cada caso:
|
|
|
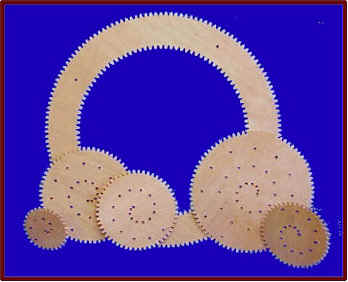
Son curvas que se pueden obtener con un Spirograph
 |
Spirograph
Una curva espirográfica se puede obtener con un Spirograph, haciendo rodar un círculo interior o exterior sobre otro círculo, que permanece fijo, y colocando un bolígrafo en cualquier punto (agujero) del círculo que rueda. |
 |
Si el radio del círculo fijo es R, el radio del círculo móvil es r, y módulo del vector de posición del punto P respecto al centro del círculo móvil es a, la ecuación de la curva que resulta se define :
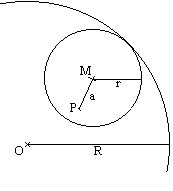
El punto P(x,y) describe la curva espirográfica |
|
|
|
|
|
|
Actividad 4:
|
|
|
|
||||||||||||||||||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.