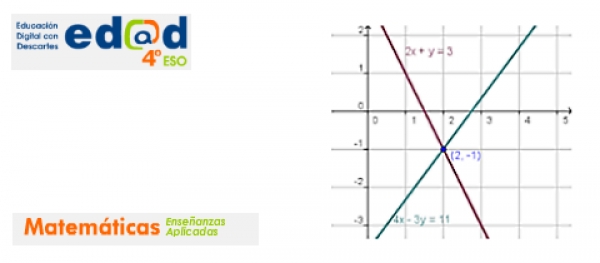
EDAD 4º ESO Aplicadas - Sistemas de ecuaciones
Escrito por Alfonso Saura EspínEste mes vamos a ver la unidad de "Sistemas de ecuaciones" de 4ºESO Aplicadas:
De forma muy breve hemos tratado los siguientes temas:
1.Sistemas de ecuaciones lineales
Ecuación lineal con dos incógnitas
Sistemas de ecuaciones lineales
Clasificación de sistemas
2.Métodos de resolución
Reducción
Sustitución
Igualación
3.Aplicaciones prácticas
Resolución de problemas
4.Sistemas de inecuaciones con una
incógnita
Resolución
Subproyecto Misceláneas.
El subproyecto Misceláneas está de enhorabuena, que se recuerde, pocas veces, en tan poco tiempo, un grupo tan reducido de personas ha aportado tanta cantidad de objetos de tan elevada calidad y tan alto potencial educativo a cualquiera de los subproyectos de la Red Descartes. Y no es la intención desmerecer al resto, muy al contrario; si no la de dar merecida notificación de un hito tan memorable. La excepcionalidad se justifica a si misma nada más visualizar cualesquiera de las últimas escenas incorporadas al subproyecto, lo que ya ha sido posible gracias a las reseñas que tanto José R. Galo Sánchez como Ángel Cabezudo Bueno han expuesto recientemente en el apartado Últimos materiales del blog y al artículo que el primero de ellos acaba de publicar, también en este blog, donde justifica el proceso de creación, creando a su vez nuevas escenas relacionadas con el tema de proporcionar una ayuda inestimable a la capacidad de visualización de las transformaciones dinámicas en el espacio tridimensional. Por otro lado la buena salud del subproyecto también se debe a la infatigable tarea de adaptación de materiales obsoletos, al nuevo editor DescartesJS, de las profesoras Elena E. Álvarez Sáiz y María José García Cebrian, los profesores ya mencionados y otros/as que aunque no se indican están en la mente de todos los usuarios del portal. Relativo a las aportaciones más recientes caben destacar:
- De la profesora Rita Jiménez Igea, quien nos ha sorprendido con un nuevo diseño de las escenas, más funcional, interactivo, armonioso y desde luego con un potencial instructivo y didáctico encomiable, seleccionamos una muestra de sus aportaciones:
De las que destacamos:

Matemáticas, joyería y mezclas.
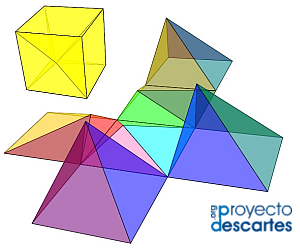
- Seleccionar parte de las aportaciones del profesor José R. Galo Sánchez al subproyecto Misceláneas o casi a cualquier otro subproyecto es una tarea ardua, así que seleccionaré cronológicamente las siete últimas aportaciones relacionadas con el desarrollo del cubo y de entre ellas destacaré las tres más recientes; no obstante quisiera aprovechar la ocasión para documentar la génesis de la creación de las siete últimas y extraordinarias aportaciones de nuestro presidente para dar valor al ejercicio de la colaboración entre socios a tenor de los frutos obtenidos.
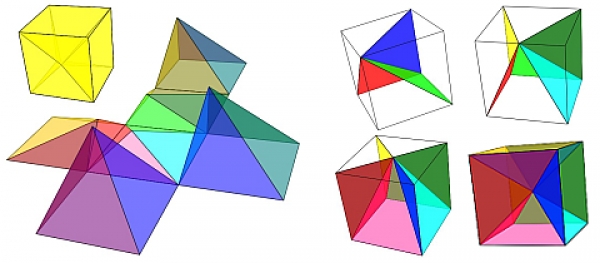
En el año 2001 la profesora Ángela Nuñez Castaín publicó la miscelánea Partición de un cubo en seis pirámides triangulares iguales, en el año 2017 se adaptó a DescartesJS dicha miscelánea, la adaptación fué realizada conjuntamente por la profesora y nuestro presidente. A continuación se muestra el resultado obtenido. Las misceláneas más recientes que se han publicado sobre el tema han sido:- Partición de un cubo en pirámides de base cuadrada. Caso general.
- Partición de un cubo en 4 pirámides cuadradas iguales dos a dos
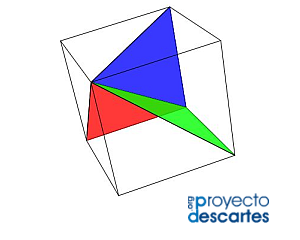
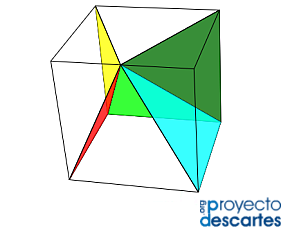
- Partición de un cubo en seis pirámides triangulares congruentes
- Partición de un cubo en cinco pirámides triangulares
- Partición de un cubo en seis pirámides cuadradas iguales
- Partición de un cubo en cinco pirámides cuadradas
- Partición de un cubo en tres pirámides cuadradas iguales
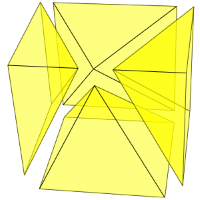
- A la hora de cerrar este artículo nos vemos sorprendidos por una nueva y brillante aportación del profesor José R. Galo Sánchez que aunque aún no hemos tenido tiempo de analizar en profundidad consideramos de interés prioritario su exposición. Partición no prismática de un cubo en seis pirámides triangulares equivalentes
De las anteriores destacamos:
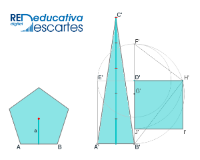
- A continuación, también a modo de resumen, exponemos tres misceláneas: la primera, que muestra la cuadratura de un polígono regular, elaborada por el profesor Ángel Cabezudo Bueno y el autor de este artículo y las otras dos, de este último, relativas a los patrones de teselación tipo mitad del cuadrado.
- Pentágono regular: Cuadratura. Método clásico
- Teselas del plano. Patrones: Mitad del cuadrado
- Teselas del plano. Patrones: Mitad del cuadrado II
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra una presentación de los cuerpos platónicos diferente a lo habitual.
Ildefonso Fernández Trujillo. 2018
Descripción de los juegos didácticos del Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle- Carátula del juego. Al pulsar sobre la misma se muestra una captura de pantalla del juego.
- Reglas del juego. Se presenta la descripción, dinámica y objetivo del juego.
- Documentos de registro. Apartado en el que se pueden descargar formularios de registro de respuestas y de resultado de los jugadores.
- Tabla con las principales características del juego.
- Autoría y licencia de uso.
- En la primera ventana se selecciona la modalidad de introducción de preguntas en el juego: mediante fichero, oral, a mano al principio del juego, generadas por el juego y sin preguntas. Esta ventana no aparecerá si el juego dispone de una sola modalidad de introducción de preguntas.
- En la segunda ventana se deben introducir los datos de los jugadores y las opciones de configuración del juego. Estas opciones pueden ser específicas del juego tales como: número de jugadores, orden de aparición de las preguntas, tiempo, sorteo de orden de participación de los jugadores, etc., o opciones generales (se encuentran en un menú superior visible durante todo el trascurso del juego) y son del tipo: reinicio del juego, sonido, idioma, registro de resultados, etc.
- Si se ha elegido la modalidad de introducción de preguntas a través de ficheros, se mostrará una tercera ventana para cargar el fichero de preguntas de distintas formas: arrastrando el fichero, seleccionando el archivo a través del explorador del navegador, escribiendo su nombre o URL o a través de listas desplegables de repositorios.
- A continuación y tras pulsar en el botón Jugar comienza el juego con la dinámica propia del mismo.
Particiones del cubo en pirámides (parte I)
Escrito por José R. Galo SánchezEl estudio y búsqueda de regularidades o propiedades en cualquier objeto puede abordarse desde diferentes perspectivas. Una de ellas es proceder a la disección o descomposición buscando desentrañar el interior o lo particular para comprender el exterior o la globalidad. La máxima aristotélica de que el todo es más que la suma de sus partes no queda contradicha por acudir al hecho de realizar una partición —matemáticamente descomponer un conjunto como unión de subconjuntos cuyas intersecciones tienen medida nula—, sino que metodológica o procedimentalmente es un medio humanamente asequible con el que dar un primer paso a través del cual buscar y tratar de abarcar, en un posterior análisis global, ese todo a partir de sus partes. En esta línea, en este artículo, mostraremos con recursos interactivos algunas particiones usuales de un cubo en pirámides con base cuadrada y comprobaremos como todos esos casos son situaciones particulares de una partición general basada en nueve puntos (los vértices del cubo y un adicional).
El motivo para elegir una determinada partición de la infinidad de particiones posibles y hacerla distinguible del resto puede sustentarse en diversos criterios u objetivos, pero usualmente suelen marcarse pautas como que la partición tenga el menor número de elementos o que sea lo más regular posible, es decir, que las partes sean iguales o congruentes —que coincidan mediante una composición de isometrías (traslaciones, giros o simetrías)— o equivalentes —con igual medida— o cualquier otro parámetro que sea atractivo para quien busque adentrarse en este contexto. Pero la elección también podría estar marcada por criterios opuestos o diferentes a los anteriores. Si pensamos en que la reconstrucción del cubo a partir de las piezas de una partición es un entretenimiento usual, catalogado como rompecabezas o puzle, el diseñador del mismo puede perseguir que todas las piezas sean iguales o plantarse en la situación opuesta de que todas sean diferentes. La dificultad o sencillez, la mayor o menor belleza del modelo obtenido tiene más componente subjetivo que objetivo; pero la belleza matemática siempre estará implícita en todos y cada unos de los planteamientos realizados, al ser medios y soportes conducentes a la extracción y obtención del conocimiento.
En este artículo analizaremos la partición de un cubo en pirámides de base cuadrada y en un artículo posterior nos adentraremos en la partición en pirámides de base triangular (tetraedros aunque no necesariamente regulares).
Particiones de un cubo en pirámides de base cuadrada
Posicionándonos y atendiendo al criterio de que la partición tenga cardinal mínimo o que sea lo menor posible y adicionalmente que sus componentes sean regulares o que sean lo más similares entre sí, podemos encontrar cuatro situaciones, que son las que usualmente se muestran y divulgan, y que reflejaremos en sendos recursos interactivos. En ellos se conjugará la virtualidad digital con la posibilidad de contruir el modelo respectivo de forma tangible, a lo que animamos e invitamos a todos.
1. Tres pirámides cuadradas iguales.
Este caso se corresponde con la partición con cardinal mínimo. Las tres pirámides comparten la misma cúspide y son iguales. Esta partición suele tomarse como base para mostrar que el volumen de una piramide es la tercera parte del área de su base por su altura, pero no nos adentraremos en ese objetivo.
Haz clic en la imagen para acceder al recurso interactivo
2. Cuatro pirámides cuadradas iguales dos a dos.
Esta partición se caracteriza porque las cuatro pirámides también comparten la misma cúspide y son iguales dos a dos.
Haz clic en la imagen para acceder al recurso interactivo
3. Cinco pirámides cuadradas, cuatro iguales y una desigual que es regular.
Aquí las cinco pirámides vuelven a tener la misma cúspide.
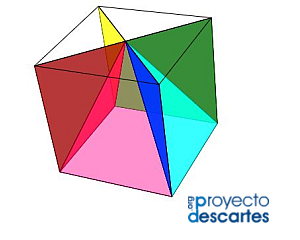 Haz clic en la imagen para acceder al recurso interactivo
Haz clic en la imagen para acceder al recurso interactivo
4. Seis pirámides cuadradas regulares e iguales.
Todas las pirámides comparten la misma cúspide y todas son regulares e iguales (congruentes).
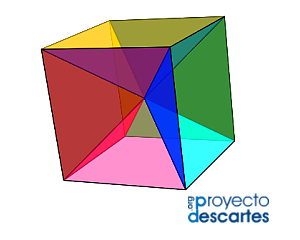 Haz clic en la imagen para acceder al recurso interactivo
Haz clic en la imagen para acceder al recurso interactivo
Todos los casos anteriores son los ejemplos que usualmente se suelen mostrar en múltiples contextos por su simplicidad y belleza. Pero, como hemos indicado, la belleza también puede alcanzarse a través de un análisis global en el que los casos anteriores no sean más que un caso particular de una situación general, y donde la diversidad y la diferencia sean la pauta a lograr. En ese empeño, a continuación, mostraremos de manera razonada y constructiva cómo abordar una partición del cubo en pirámides de base cuadrada, y adicionalmente se podrá observar digital y analógicamente apoyándonos en un nuevo recurso interactivo.
Generalización de la partición del cubo en pirámides cuadradas
Para construir una partición del cubo en pirámides cuadradas es necesario, obligatorio, utilizar los ocho vértices del cubo y las doce aristas del mismo, y adicionalmente hay que seleccionar o marcar cuál o cuáles serán las cúspides de las pirámides a construir. La introducción de puntos adicionales a los vértices hará que aumente el número de combinaciones de cinco puntos que pueden realizarse y consecuentemente podrá incrementarse el número de pirámides de la partición (no todas las combinaciones posibles de vértices son viables para obtener una partición del cubo). Así pues, analicemos diferentes alternativas:
- No incluir ningún punto adicional.
Esta elección obliga a que la cúspide de cada pirámide sea uno de los vértices del cubo y si además imponemos que todas las pirámides compartan la misma cúspide entonces obviamente obtendremos la partición de cardinal mínimo. Este plantemiento es viable pues basta seleccionar un vértice del cubo y desde él trazar segmentos a cada uno de los otros siete vértices, ello conduce a la partición en tres pirámides que ha sido reflejada en el primer caso descrito en este artículo. La partición es única pues, se elija el vértice que se elija, todas las particiones son congruentes mediante giros. - Añadir un punto adicional.
Este punto sería la cúspide común de todas las pirámides a construir para que así el número de éstas sea lo menor posible y constructivamente se procede igual que en el caso anterior trazando segmentos desde la cúspide común a los vértices del cubo. Dicho punto adicional ha de pertenecer al cubo, bien a su interior o a la frontera y por tanto podemos distinguir las siguientes situaciones:- Punto perteneciente a una arista. Aquí obtendremos una partición compuesta por cuatro pirámides. En general las cuatro son distintas, pero entre dos de ellas se da siempre una congruencia (una es simétrica de la otra). Y hay un caso particular en el que las pirámides son iguales dos a dos, que es el segundo caso expuesto en la sección anterior, y que acontece cuando el punto adicional considerado es el punto medio de la arista.
La arista a la que pertenezca el punto no introduce ninguna variación. Todas serán situaciones congruentes. - Punto perteneciente a una cara. Este caso conduce a la partición en cinco pirámides y de las infinitas posibilidades la situación con más regularidad es cuando el punto elegido es el punto donde se intersecan las diagonales de la cara. Es el tercer caso expuesto con anterioridad.
La partición, salvo isometrías, es independiente de la cara seleccionada - Punto perteneciente al interior del cubo. Esta situación hace que sean seis pirámides las que forman la partición. De las infinitas particiones posibles, cuando el punto seleccionado es el punto de intersección de las diagonales del cubo se tiene que las seis pirámides son iguales y regulares, éste es el cuarto caso mostrado antes.
- Punto perteneciente a una arista. Aquí obtendremos una partición compuesta por cuatro pirámides. En general las cuatro son distintas, pero entre dos de ellas se da siempre una congruencia (una es simétrica de la otra). Y hay un caso particular en el que las pirámides son iguales dos a dos, que es el segundo caso expuesto en la sección anterior, y que acontece cuando el punto adicional considerado es el punto medio de la arista.
En el siguiente objeto interactivo puede experimentarse y verse todo lo indicado.
Haz clic en la imagen para acceder al recurso interactivo
En un próximo artículo nos adentraremos en la partición de un cubo en pirámides triangulares.
Más...
Hoy presentamos la unidad Operaciones con números racionales, perteneciente al proyecto Miscelánea de la RED.
Se trata de un objeto didáctico interactivo con una serie de actividades para practicar las operaciones con números racionales. Las actividades de esta unidad son adecuadas para los primeros cursos de la ESO y facilitan el aprendizaje y consolidación de dichos cálculos ya que en cada ejercicio el alumno puede comprobar si su respuesta es correcta o no y seguir así la evolución de su aprendizaje.
El siguiente vídeo consta de dos partes, en primer lugar se analizan las actividades que forman parte de dicha unidad y, en segundo lugar, se propone la inserción de este objeto en un curso Moodle para el trabajo en el aula, mediante el código para embeber.
Día Internacional de la Mujer y la Niña en la Ciencia
Escrito por José Antonio Salgueiro González"En la actualidad, las mujeres y niñas encuentran barreras de muchos tipos, a veces muy sutiles, que dificultan su presencia en la ciencia. Esta desigualdad es patente en la elección de los estudios por parte de las niñas y se va agudizando al avanzar en las carreras científicas y tecnológicas. Con el objetivo de lograr el acceso y la participación plena y equitativa en la ciencia para las mujeres y las niñas, la igualdad de género y el empoderamiento de las mujeres y las niñas, el 15 de diciembre de 2015, la Asamblea General de las Naciones Unidas proclamó el 11 de febrero de cada año como el Día Internacional de la Mujer y la Niña en la Ciencia".
El párrafo ha sido extraído literalmente del sitio web 11 de febrero, donde puedes encontrar toda la información relativa a esta importante fecha, a la que RED Descartes se suma animando a celebrar dicha efemérides, programando y realizando actividades en las aulas y aportando los recursos y experiencias disponibles en nuestros dominios.
Desde RED Descartes se difunde la enorme labor desarrollada, a lo largo de la historia, por la mujer en la ciencia, y muy especialmente en las ciencias matemáticas, físicas y químicas. Además, promovemos en nuestras aulas y divulgamos la ciencia que realizan nuestras alumnas desde los diversos proyectos que abordamos y que compartimos en este artículo para apoyar los objetivos del 11 de febrero.
| LA MUJER EN LA CIENCIA |
"El personaje misterioso" es un programa de Radio Descartes conducido por Eva Perdiguero y Ángel Cabezudo con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Concretamente, tras la entrevista del invitado, que no se desvela, el escuchante debería conocer su nombre o bien tomar los datos que se aportan en la dramatización y tomarse un tiempo para averiguarlo consultando en la múltiple documentación que hoy día se encuentra disponible, principalmente en Internet o en libros divulgativos de Historia de las Matemáticas o de Matemáticos célebres, pasando a responder en un comentario del blog de nuestro portal. Pues bien, de este proyecto hemos seleccionado las siguientes entrevistas a mujeres matemáticas de la historia, cuyas voces son interpretadas por mujeres científicas del ámbito educativo. Así, aportamos los siguientes recursos:
- Entrevista a Hipatia de Alejandría, interpretada por Eva Mª. Perdiguero Garzo, profesora de matemáticas.
- Entrevista a Sofía Kovalévskaya, interpretada por Marta Macho Stadler, matemática y divulgadora científica.
- Entrevista a Emmy Noether, interpretada por Elena Vázquez Abal, matemática y divulgadora científica.
- Entrevista a Ada Lovelace, interpretada por Montse Gelis Bosch, profesora de matemáticas.
- Entrevista a María Gaetana Agnesi, interpretada por Elena Ramírez Ezquerro, profesora de matemáticas.
Para descubrir al personaje misterioso, se publica un puzle creado con Descartes JS que incluye imágenes alusivas, alegóricas o de efemérides que descubren al personaje:
- Puzle dedicado a Hipatia de Alejandría
- Puzle dedicado a Sofía Kovalévskaya
- Puzle dedicado a Emmy Noether
- Puzle dedicado a Ada Lovelace
- Puzle dedicado a María Gaetana Agnesi
| CONTRIBUCIONES DE ALUMNAS A LA CIENCIA |
Son varios los proyectos difundidos desde el portal de RED Descartes donde las alumnas son protagonistas y divulgadoras de la ciencia, especialmente de la matemática. Así, del proyecto para el "desarrollo de la comunicación audiovisual a través de las matemáticas con Descartes", hemos seleccionado con motivo del día 11 de febrero las siguientes contribuciones y aportaciones de alumnas a la ciencia:
- María, divulga la resolución de triángulos rectángulos
- Claudia y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Rocío, divulga la resolución de una unidad liberada de PISA
- Margarita y María, divulgan la simplificación de expresiones trigonométricas de cociente
- Virginia, María y Laura, divulgan una técnica de resolución de problemas
- María del Castillo e Irene, divulgan las operaciones con fracciones algebraicas
- Carmen, divulga la simplificación de fracciones algebraicas y la suma de las mismas
"La radio ficción en el aula de matemáticas" es otro de los proyectos difundidos en el portal de RED Descartes, del que hemos seleccionado las siguientes contribuciones de alumnas a la ciencia:
- María y Julia, entrevistan y divulgan la vida y obra de Mary Somerville
- Ángela y Alejandro, entrevistan y divulgan la vida y obra de Euclides
Finalmente, del proyecto "El alumnado como generador de contenido multimedia con Descartes JS" hemos realizado la siguiente selección de producciones en las que participan alumnas:
- Ana y Virginia, ponen a prueba tus conocimientos de Matemáticas-1
- María y Alba, ponen a prueba tus conocimientos de Matemáticas-1
- Lucía e Ismael, ponen a prueba tus conocimientos de Matemáticas-1
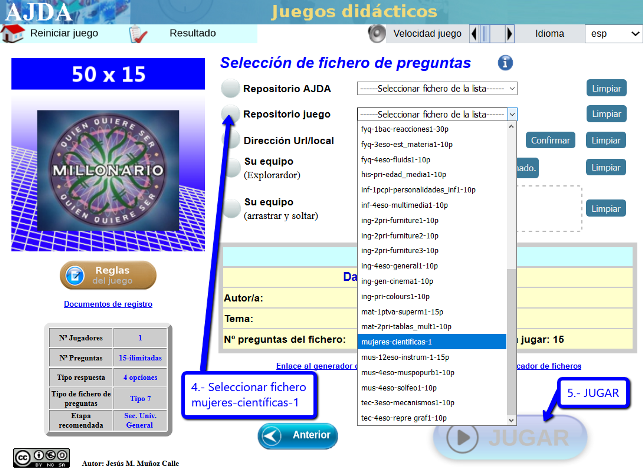
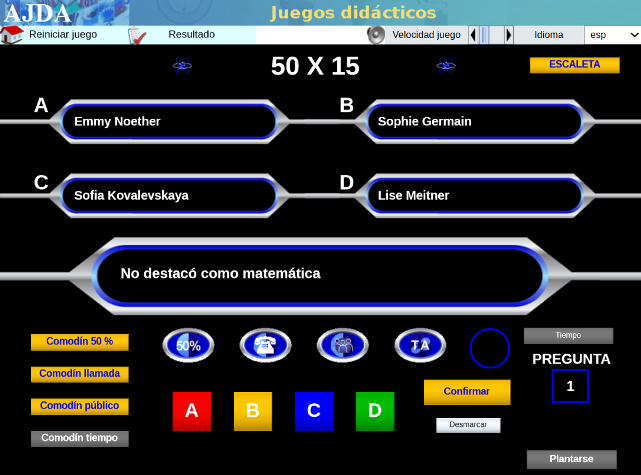
| JUEGO DIDÁCTICO SOBRE MUJERES CIENTÍFICAS |
El juego es una de las estrategias didácticas de gran valor que motiva a nuestro alumnado y que se potencia con las tecnologías de la información y la comunicación. Así que os dejamos el que ha creado nuestro compañero Jesús M. Muñoz Calle, del proyecto Aplicación de Juegos Didácticos en el Aula, para difundir algunos de los decubrimientos y avances científicos gracias a la mujer, con algunas capturas de pantalla por si fueran necesarias.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)










 CONTACTO
CONTACTO
