Hay una tendencia a tratar de asociar o encontrar en todo aquello que es bello la proporción áurea o divina, o a construir objetos a partir de esta razón porque se presuponen serán apreciados como bellos por el simple hecho de seguir dicha pauta. Esto, como no, también ha acontecido con la modelación matemática de la concha del Nautilus pompilius sobre la que suele afirmarse que su forma y crecimiento es áureo. Sin embargo, en este artículo se muestra y se analiza en detalle cómo dicha concha lo que realmente sigue es un patrón ubicado en la denominada proporción cordobesa o humana. Con apoyo en un recurso interactivo desarrollado con la herramienta Descartes se motiva el análisis y comportamiento y se procede a partir de la yocto-yotta realidad observada a construir el modelo matemático, el cual se detalla ampliamente.

Pulsando sobre la siguiente imagen se accede a dicho recurso interactivo que se aborda o plantea en seis fases:

1. 1. 1. Ajuste de la concha por una espiral logarítmica.
      2. Ajuste del sifúnculo por una espiral logarítmica.
      3. Ajuste global por una familia de espirales cordobesas.
      4. Mejora del modelo discreto.
      5. Aproximación de los septos.
      6. Modelo matemático del Nautilus pompilius.

Y en el botón de indicaciones se aborda una introducción, los objetivos, las instrucciones de uso en cada fase y finalmente se enlaza un artículo donde se detalla el análisis matemático realizado.  Este artículo está embebido a continuación o bien puede abrirse y/o descargarse desde este enlace.

 En las conclusiones del artículo anterior afirmamos:

A través del detallado y progresivo análisis realizado hemos ido construyendo la base teórica o modelo matemático que soporta a la bella morfología del Nautilus Pompilius y hemos tratado del encontrar el modelo de crecimiento que conduce a poder explicar y a comprender por qué adquiere esa forma.  Desde su inicio la espiral logarítmica cordobesa tomó presencia y a medida que la mirada se deslizaba hacia algún nuevo detalle esta espiral ha vuelto a imponer su presencia marcándonos y alumbrándonos el camino del descubrimiento y de la adquisición del conocimiento. La belleza del Nautilus pompilius se sustenta en la proporción cordobesa o humana y todo punto de su concha o del interior ha quedado determinado por la intersección de dos espirales cordobesas. El germen o base inicial matemática que explica el por qué acontece todo lo observado, se ha ubicado en el crecimiento gnomónico de un triángulo cordobés, las propiedades de éste se trasladan al desarrollo y comportamiento global detectado y modelado.

Deseamos que nuestro trabajo de investigación satisfaga tu curiosidad y te animamos a interactuar con nosotros bien realizando algún comentario en este blog (los comentarios no se publicarán directamente sino que pasan por una moderación previa a su publicación) o bien escribe al correo de nuestra RED Descartes: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.. 

Proporcionalidad. Las Espirales XIII

Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca la continua aportación de nuevas unidades a los subproyectos: TELESECUNDARIA, GEOgráfica-GEOevaluación y PLANTILLAS.

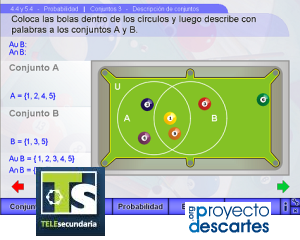
Como muestra enlazamos la unidad sobre Probabilidad, del subproyecto TELESECUNDARIA,

la GEOevaluación de Francia.

y los cinco ejemplos de plantillas transparentes, de los que enlazamos el primero.

Dentro de nuestro ámbito local destacan, entre otras, la permanente actualización del Proyecto ED@D en particular los materiales de 2º y 4º LOMCE y LOE y la experiencia: Aprendemos a resolver problemas con Descartes y Wiris
Aprendemos a resolver problemas con Descartes es una iniciativa del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, realizada con alumnos y alumnas de 4º ESO durante el curso escolar 2015/2016, basada en la experiencia para el "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes"

Continuando con el estudio de los l.g. y sus utilidades se expone a continuación una escena con el primero de los métodos para duplicar un cubo, esto es, dado un cubo de arista a y volumen V halla, mediante la Duplicatriz de Hipócrates, un segmento de longitud a'= a·2^1/3 que será la arista del cubo de volumen V' = 2·V.

La escena, en primer lugar, construye dinámicamente la curva duplicatriz pulsando en el botón , en el momento en que la recta MA corta a la recta PO (M = C y A = B) se activa el botón de información que al pulsarlo deja ver un breve texto con la definición del l.g. y una demostración, que usa la construcción de Platón, del hecho de la duplicidad. En cualquier instante puede detenerse la animación mediante el botón .

La escena es facilmente adaptable y admite las modificaciones y/o ampliaciones que el usuario considere convenientes para su uso personal.

En el siguiente trabajo se muestra la forma en que se genera el l.g. conocido como Cisoide de Diocles y la manera de encontrar con dicha curva el segmento que sirva de arista al cubo que doble en volumen a uno inicial dado.

En esta ocasión, en la sección de vídeo, hemos elegido la primera parte del que se ha mostrado en las últimas entradas. El objetivo de este vídeo es el de apreciar distintas formas de enfocar el tema que nos ocupa: "Las Espirales.

Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Cornu" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:

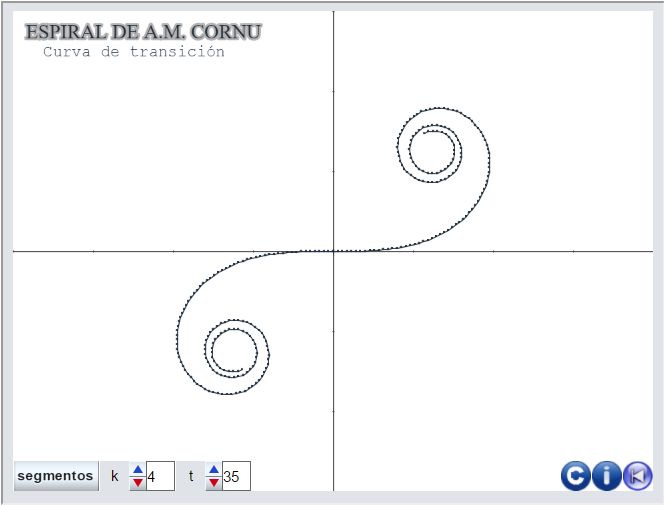
• Hemos creado la siguiente escena: Espiral de Cornu (pulsad sobre la imagen para acceder a ella). Debemos advertir que, tal y como hemos procedido, esta realiza cálculos intensivos con números extremadamente grandes y pequeños, lo que hace que la ejecución de la misma sea muy lenta. Esta manera de proceder tiene la intención de hacer visible la sensibilidad de las aproximaciones polinómicas y sus efectos secundarios según muestra el trabajo posterior realizado con GeoGebra y que puede reproducirse con la escena actual con unas pocas modificaciones.

• Inclusión de parte del código de la escena anterior en el de la miscelánea en proyecto.

La escena del proyecto puede verse a continuación:

Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Cornu incluida.

En el siguiente trabajo realizado con GeoGebra, al activar la animación puede observarse como se genera el lugar geométrico conocido como curva Duplicatriz. En primer lugar se obtienen las dos medias proporcionales, propuestas por Hipócrates, entre dos segmentos de longitudes a y 2·a, donde a es la longitud de la arista del cubo inicial. A continuación la curva determina el segmento que se usará de arista del cubo de volumen doble al primero. Para la demostración se usa la composición de triángulos rectángulos semejantes atribuida a la escuela platónica.

De los recursos de la web de GeoGebra hemos tomado como origen para el análisis de las características de la aproximación polinómica de las integrales de Fresnel el "material-956849" y entre otras hemos encontrado ocurrencias como las que se exponen a continuación, que se ponen en evidencia pulsando el botón 'GO'.

En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.

Animamos a los lectores a colaborar elaborando contenidos o aportando ideas y sugerencias.
Bibliografía:

• Documentación de Yuli Andrea Rodríguez Rodríguez y Benjamin R. Sarmiento Lugo
• El problema de la Duplicación del cubo de Juana Contreras S. y Claudio del Pino O. Instituto de Matemática y Física. Universidad de Talca.
• Una aproximación a la curva de transición Clotoide vista desde Mathematica de:
  Luís Blanch, Emilio Checa, Josefa Marín
  Universitat Politecnica de Valencia
  Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
• Problema de la duplicación del cubo de Juan Pablo Mora.
• Y otros documentos buscados en Internet.

Ildefonso Fernández Trujillo

Proyecto Descartes estuvo invitado al programa Boulevard de Radio Euskadi en su emisión del día 25 de agosto, para tratar el tema de la radio ficción en la divulgación de personajes matemáticos.

Boulevard es un programa que reúne, desde las 6:00, información y análisis de la información de Euskadi y el mundo, mientras que a partir de las 10:00 el espacio se dedica a la actualidad más cercana y a los temas que nos interesan.

En la imagen superior hay un enlace a la página del programa en su totalidad, mientras que compartimos el audio con la entrevista dedicada a la asociación Red Educativa Digital Descartes o Proyecto Descartes, agradeciendo a Radio Euskadi y al programa Boulevard su difusión y la posibilidad de acceder a su contenido.

Recordamos que "El personaje misterioso" es un programa de Radio Descartes conducido por Eva Perdiguero y Ángel Cabezudo con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Concretamente, tras la entrevista del invitado, que no se desvela, el escuchante debería conocer su nombre o bien tomar los datos que se aportan en la dramatización y tomarse un tiempo para averiguarlo consultando en la múltiple documentación que hoy día se encuentra disponible, principalmente en Internet o en libros divulgativos de Historia de las Matemáticas o de Matemáticos célebres, pasando a responder en un comentario del blog de nuestro portal. A la semana siguiente, se publica un puzle creado con Descartes JS que incluye imágenes alusivas, alegóricas o de efemérides que descubren al personaje.

Hasta la fecha se han realizado un total de doce entrevistas ficticas a personajes matemáticos, que enlazamos junto a su intérprete:

1. Personaje misterioso - 1, interpretado por Ángel Cabezudo Bueno
2. Personaje misterioso - 2, interpretado por Eva Perdiguero Garzo
3. Personaje misterioso - 3, interpretado por José Antonio Salgueiro González
4. Personaje misterioso - 4, interpretado por Ricardo Alonso Liarte
5. Personaje misterioso - 5, interpretado por Antonio Pérez Sanz
6. Personaje misterioso - 6, interpretado por Marta Macho Stadler
7. Personaje misterioso - 7, interpretado por Elena Vázquez Abal
8. Personaje misterioso - 8, interpretado por José María Sorando Muzás
9. Personaje misterioso - 9, interpretado por Montse Gelis Bosch
10. Personaje misterioso - 10, interpretado por Xosé Eixo Blanco
11. Personaje misterioso - 11, interpretado por Elena Ramírez Ezquerro
12. Personaje misterioso - 12, interpretado por Bernat Ancochea Millet

Hay que recordar también que "El personaje misterioso" resultó finalista en la categoría de Mejor Iniciativa Educativa a los V Premios Asociación Podcast, entregados en Barcelona en 2014.

Por último, y como anunciamos al final de la entrevista del programa Boulevard de Radio Euskadi, añadir que esta iniciativa se ha extrapolado al entorno educativo de Secundaria, de manera que son ya alumnos y alumnas de 3º ESO los encargados de realizar entrevistas a personajes matemáticos, como iremos difundiendo en próximos artículos donde las divulgaremos.

Ya puedes "pinear" los recursos digitales interactivos y seguir los tableros de RED Descartes en Pinterest, pudiendo acceder desde el enlace que te proporcionamos o, mejor aún, desde el menú de redes sociales que encontrarás en la zona superior derecha de nuestro portal.

Si no eres usuario habitual de esta red social, te indicamos que debes estar registrado y con la sesión abierta en Pinterest para poder visitar los diferentes tableros que hemos creado, así como para recorrer la variedad de recursos que los componen, cuya descripción te informará sobre el proyecto de RED Descartes al que pertenecen y sobre su contenido u objetivos.

Si desconoces Pinterest, puedes tomar contacto rápidamente con el vídeo del canal TEC titulado "¿Qué es y cómo se usa Pinterest?

Guardar

Guardar

Guardar

Guardar

Guardar

“Cuadrilateralia es una aplicación informática de carácter didáctico que pretende aprovechar a tendencia natural de manipular objetos concretos para, a través de la visualización, la observación, la composición y descomposición, el diseño y la construcción virtual, descubrir y estudiar las propiedades de carácter matemático de los cuadriláteros. Sus actividades han sido programadas teniendo en cuenta los principios de interactividad, brevedad en los textos, aleatoriedad y corrección o evaluación automática.”

Ése es el resumen descriptivo que Javier de la Escosura Caballero y María Antolina Muñoz Huertas hacen del recurso educativo del que son autores y que desarrollaron en el año 2006 usando Descartes. Fueron premiados por el Ministerio de Educación de España con el segundo premio a materiales educativos convocado por el Instituto de Tecnologías Educativas en el año 2006. Es un contínuum del recurso “Geometría dinámica del triángulo” que divulgamos en este blog y que igualmente hemos procedido a adaptarlo a DescartesJS permitiendo así que pueda utilizarse tanto en ordenadores como en tabletas y smartphones.

Los contenidos curriculares de Cuadrilateralia han sido vertebrados en torno a nueve capítulos o ejes temáticos:

• • Definición, clasificación y obtención
  • Ángulos y lados
  • Diagonales y ejes de simetría
  • Áreas
  • Perímetros
  • Cuadraturas
  • El rectángulo áureo
  • Construcción de los paralelogramos
  • Construcción de trapecios y trapezoides

En la guía didáctica, los autores, nos indican que:

“Las actividades guiadas e interactivas tales como: estudiar definiciones, fórmulas y clasificaciones; analizar propiedades de los lados, ángulos y diagonales; deducir las fórmulas del área o la cuadratura de los cuadriláteros utilizando puzles; usar regla y compás para resolver problemas de construcción; calcular áreas y perímetros tomando las medidas necesarias para ello; y encontrar los ejes de simetría o descubrir, doblando papel, cuándo un rectángulo es áureo, etc., favorecen la motivación y la comprensión y solución de los problemas relacionados con el tema.”

Y nos manifiestan que:

“Hemos realizado esta aplicación pensando en los alumnos y en las alumnas. Contando esencialmente con su participación activa. Ellos van a ser los/las protagonistas que con la ayuda del profesor han de tratar de llevar a buen puerto las actividades propuestas.

Ojalá que esta tarea os resulte a todos tan interesante, divertida y apasionante como para nosotros ha sido su elaboración.”

Todo lo expuesto concuerda con lo reflejado en el recurso y ciertamente es un medio eficaz para el aprendizaje activo e interactivo de los cuadriláteros.

¡Os invitamos a comprobarlo!

Este artículo tiene como objetivo el difundir un recurso interactivo desarrollado por Javier de la Escosura Caballero en el año 2002, utilizando Descartes, y que obtuvo tres premios:

1. 1. Tercer premio a Materiales Educativos del Instituto de Tecnologías Educativas del Ministerio de Educación de España en el 2002
   2. Primer premio en el "First European Contest of Mathematics Teaching Actions" TeachMath Excellence 2002.
   3. Accésit en la "XVIII Convocatoria de Premios de Investigación Pedagógica y Experiencias Didácticas". Geometría dinámica del triángulo: Una experiencia en el área de Matemáticas.

Descartes acaba de alcanzar en este mes de junio de 2016 su mayoría de edad, dieciocho años. Al ir creciendo, progresivamente, ha ido confirmando y asentando su potencial como herramienta de autor multipropósito mediante la que el profesorado y los desarrolladores de recursos educativos pueden plasmar su experiencia de aula, y su creatividad, obteniendo materiales que catalizan el aprendizaje de un alumnado que, gracias a Internet, se ubica en cualquier punto o lugar de nuestro pequeña “Gaia”o “Pachamama”.

Y como ejemplo de ese potencial cartesiano, más bien de esta realidad, hemos adaptado a DescartesJS la unidad “Geometría dinámica del triángulo”. 

Una unidad didáctica que en la permanente voracidad informática y sólo por haberse desarrollado hace catorce años, quizás, alguien podría equivocadamente verse tentado a catalogarla como una antigualla —en esa línea, ¿cómo catalogaría a “Los Elementos de Euclides”?—, pero que mantiene inalterable su objetivo educativo promoviendo un encuadre meramente euclidiano, ubicado en la Geometría sintética. Con la adaptación a DescartesJS se logra que el aprendizaje se pueda alcanzar usando cualquier tipo de dispositivo, es decir, tanto ordenadores como tabletas o smartphones con cualquier sistema operativo. Se mantiene el diseño, los objetivos y contenidos del recurso original, pero se actualiza el soporte que pasa a ser compatible HTML5.

Las “nuevas” tecnologías —¡¿hasta cuándo seguiremos denominándolas nuevas?!— han permitido dinamizar la Geometría y ese es planteamiento que aborda Javier de la Escosura según lo describe en la introducción a esta unidad, donde aboga por potenciar la capacidad visual y constructiva del alumnado, dando igual importancia tanto al concepto como a su plasmación física. Y para ello, conjuga tanto el entorno virtual que le aporta Descartes (en el que se observa y aprende) como la manipulación de los objetos en papel al plantear proyectos de trabajo (aportando plantillas imprimibles que facilitan su realización) en los que el plegado del papel, la construcción de puzles y la utilización de regla y compás es algo intrínseco al aprendizaje.

Los contenidos, que como indica el título se centran en la geometría del triángulo, se desarrollan en cinco bloques:

1. 1. Ángulos. Mediante plegado se demuestra que la suma de los ángulos de un triángulo en el plano es un ángulo llano y también que un ángulo exterior es la suma de los otros dos interiores no adyacentes.
   2. Construcción. Dibujo con regla y compás de triángulos conocidos sus lados, un ángulo y los lados adyacentes y dos lados y el ángulo comprendido, pudiendo deducir cuando los datos aportados permiten la construcción y consecuentemente el descubrimiento de algunas propiedades del triángulo.
   3. Área. Se abordan tres construcciones que permiten deducir el área de un triángulo en base a la del rectángulo.
   4. Rectas y puntos notables. Análisis de las mediatrices, medianas, bisectrices y alturas.
   5. Triángulos rectángulos. Se aborda la demostración de Teorema de la altura, del cateto y de Pitágoras con puzles.

En esencia un completo aprendizaje del triángulo que se verá complementado con otro recurso, denominado “Cuadrilateralia”, que fue también premiado y que presentaremos en un próximo artículo en este blog. Y más adelante lo ampliaremos con “Poligonalia”.

Este es el nombre del nuevo subproyecto de RED Descartes.

Telesecundaria es una modalidad de los estudios de educación secundaria en el Sistema Educativo de México dirigido a estudiantes adolescentes de 12 a 15 años que viven en comunidades dispersas que carecen de escuela de secundaria.

Se utilizan para ello los avances en tecnologías de la información y comunicación (TIC) como recurso para acercar esta formación a los jóvenes y puedan concluir su educación básica.

En este subproyecto de RED Descartes se han recogido objetos de la Telesecundaria desarrollando los correspondientes materiales con la herramienta Descartes. Las asociaciones de Colombia y España han sido las encargadas de preparar la adaptación a DescartesJS y en consecuencia todos podrán ser consultados en cualquier dispositivo con sistema operativo que admita un navegador compatible con HTML5.

Los materiales, que se irán integrando en el subproyecto corresponde a los tres cursos o grados en que se divide la Secundaria en el Sistema Educativo de México, trata los contenidos de Matemáticas, Física y Química.

En el momento en que se redacta este artículo se pueden consultar ya los 24 recursos del segundo grado de Física (13-14 años). En un corto espacio de tiempo iremos viendo aparecer publicados los restantes hasta un total de 123, con la siguiente distribución:

• 28 de Matemáticas 1º
• 38 de Matemáticas 2º
• 29 de Matemáticas 3º
• 24 de Física 2º
• 4 de Química 3º

Destaca la alta calidad de estos materiales y son perfectamente válidos para ser utilizados complementariamente a los contenidos curriculares de nuestro sistema educativo tanto por alumnos como por profesores. 

Enhorabuena y muchas gracias por el esfuerzo y el mérito de quienes han estado vinculados a esta producción.

Un grillo está sobre una superficie, que gira a una velocidad angular constante, y se está desplazando dando saltos siguiendo una línea recta que pasa por el centro de giro. Ha dado un salto inicial y posteriormente cada salto es c veces mayor que el anterior. ¿En qué posición está en cada instante? ¿Cuál es la trayectoria que sigue?

Este planteamiento dinámico conduce a una curva, ampliamente estudiada, la cual es el objeto de este artículo de difusión. En la miscelánea que hemos publicado en nuestro servidor de contenidos puedes ver el camino que sigue nuestro grillo saltarín, pudiendo seleccionar el salto y la velocidad de giro que desees y observando en qué influye tu elección.

Es bien conocido que la circunferencia es una curva equiangular, es decir, que en cualquier punto de la misma, el ángulo que forma el radio con la tangente es siempre constante e igual a un ángulo recto.

Inicialmente René Descartes (1596-1650) fue quien se planteó la determinación de una curva que también fuera equiangular, pero que el ángulo fuera el que previamente se deseara, es decir, una generalización de lo que acontece en la circunferencia. Jakob Bernoulli (1654-1705) también la analizó y la denominó “Spira mirabilis” o espiral maravillosa, y de acuerdo con sus propiedades, en su epitafio hizo poner “Eadem mutata resurgo”, es decir, “Mutante y permanente vuelvo a resurgir siendo el mismo”. En este recurso podrás comprobar el significado de esta expresión y experimentar que:

¡Ciertamente es maravillosa!

Para ello, planteamos un camino en varias fases, un total de doce, y en cada una de ellas se avanza en el análisis de esta espiral, en sus propiedades. Pulsa sobre la imagen siguiente para acceder al recurso.

En las tres primeras fases se aborda su construcción dinámica —dependiente del tiempo— y se inicia su análisis con la obtención de la relación —digamos estática o atemporal— entre la distancia y el ángulo polar. Ésta, es la ecuación algebraica en coordenadas polares de la espiral y nos permite identificar el significado físico de los parámetros específicos de la misma.

La expresión justifica su denominación como espiral logarítmica, pues se observa que el ángulo polar se puede expresar en función del logaritmo del radio polar. Y en la fase cuarta del recurso se observa y justifica que a es un factor de escala, que para b=1 obtenemos como caso particular la circunferencia y que las espirales de base b y 1/b son simétricas respecto del eje polar.

Una quinta fase permite ver y justificar por qué también se le denomina espiral geométrica ya que los puntos de ella situados sobre una misma semirrecta siguen la relación de una proporción geométrica (aquí se aplica una analogía con la que acontece en la espiral de Arquimedes o espiral aritmética). Y en la sexta se visualiza y demuestra el carácter equiangular que motivó a Descartes.

El hecho de ser equiangular es lo que le confiere a esta espiral su carácter tan especial. Y en base a ello, las últimas fases del recurso se centran en mostrar y demostrar el carácter maravilloso que marcó Bernoulli y que sintetizó en la citada expresión: “Eadem mutata resurgo”. Para una circunferencia es fácil de intuir y ver que su forma es tal que siempre surge o resurge siendo la misma, crece y crece siempre siendo la misma. Y lo maravilloso es que este surgir y resurgir siendo la misma se verifica también en esta “circunferencia generalizada” o espiral logarítmica, es decir, la razón de su crecimiento instantáneo es la unidad. Sintetizando el planteamiento que se realiza en el recurso, pues el detalle lo puedes comprobar interactuando con él, tenemos que:

• Inicialmente el análisis del crecimiento se aproxima mediante rectángulos semejantes circunscritos a la espiral, que siguen un patrón de crecimiento gnomónico en el sentido euclídeo (según lo definido en “Los elementos de Euclides”), que puede interpretarse como el patrón de crecimiento en pasos discretos de π radianes.
• Posteriormente se aborda el crecimiento, pero en el sentido establecido por Aristóteles cuando decía: «Hay ciertas cosas que no sufren alteración salvo en magnitud, cuando crecen...».

Y aquí, esto se aborda planteando el crecimiento con polígonos semejantes construidos sobre radios vectores, correspondientes a puntos de la espiral, que difieren:

• • En π/2 radianes, lo que conduce a una razón de semejanza b^(π/2): 

• • O, en general, con paso 2π/n y razón de semejanza b^(2π/n):

 Como ejemplo, sobre la concha del Nautilus pompilius, se muestra un crecimiento gnomónico discreto de paso 2π/16 en una espiral logarítmica cordobesa (b=1.186):

• Finalmente cuando el crecimiento es instantáneo, es decir, si n->infinito y el paso entre radios vectores es por tanto 2π/n->0, la razón de semejanza b^(2π/n) tiende a la unidad: “Eadem mutata resurgo”.

¡Te deseamos un buen aprendizaje siguiendo a nuestro grillo!

Éste es el título de un nuevo subproyecto de la Red Educativa Digital Descartes (RED Descartes) de Colombia y España, junto a la Institución Universitaria Pascual Bravo de Medellín (Colombia), que tiene como objetivo fundamental centrar al docente en el desarrollo de su labor y evitar, en lo posible, su reconversión en un técnico informático. Podríamos subtitularlo como "Descartes para no cartesianos", si bien ello no impide que estos también obtengan bastante ventaja de su uso. 

El aprendizaje de Descartes como herramienta y medio didáctico no es difícil, pero como todo recurso requiere una dedicación, un tiempo de práctica y de una maduración para poder integrar ágilmente en el desarrollo de nuestros materiales todo el potencial y las posibilidades que pueden contemplarse, obviamente buscando la consecución de recursos que sean atractivos para nuestros críticos nativos digitales, es decir, nuestro alumnado. Ello, a veces, puede conllevar cierto alejamiento de la tarea docente y centrar la dedicación más en la técnica, en el soporte, que en el contenido. El objetivo de este proyecto es mostrar cómo es posible generar atractivos juegos, puzles, actividades y test de memoria, de arrastre y asociación, sin más que realizar simples y usuales tareas de edición de imágenes y de ficheros de texto “plano”. Para ello se usan escenas, previamente desarrolladas, como cajas negras que recibiendo como entrada un conjunto de datos preparados por el profesor o profesora aportan una actividad interactiva que pueden utilizarse e incorporarse en el proceso de enseñanza-aprendizaje.

A continuación podemos observar un ejemplo de los diversos recursos que pueden elaborarse:

El profesorado no necesita conocer cómo elaborar la escena de Descartes sino que la utiliza como soporte para la consecución de su objetivo educativo, su tarea se centra en el diseño y elaboración de los medios auxilares (textos, imágenes) que se usan como datos de entrada. Se aprovecha el potencial educativo y la interactividad intrínseca de Descartes sin necesidad de desarrollar escenas de Descartes.

Los materiales que pueden elaborarse tienen encuadre en cualquier nivel educativo y materia, ya que es el contenido en sí el que marca su ubicación. Por ejemplo, un test de asociación puede establecerse entre poliedros regulares y sus denominaciones o bien entre imágenes de animales y sus nombres en castellano o en otro idioma; o en un test de memoria es posible identificar figuras geométricas con igual o análoga forma o bien animales de la misma especie, o palabras sinónimas. En definitiva la creatividad docente es la que mueve la herramienta en la consecución de los logros educativos.

Las actividades que son necesarias realizar para el desarrollo de estos materiales se encuadran en tres tipos de acciones:

• Manipulación y transformación de imágenes.
• Edición de textos sin formato, tipo txt.
• Preparación de los datos necesarios para el recurso.

Sencillas tareas que permitirán la construcción rápida y fácil de recursos didácticos sin necesidad de estudiar ni conocer la herramienta de edición de Descartes. Todo va acompañado de su correspondiente guía o tutorial para, a partir de la plantilla, abordar y lograr el recurso deseado.

Las plantillas

Seleccionando la opción del menú de este proyecto etiquetada como "Materiales" accederemos al conjunto de plantillas disponibles agrupadas en diferentes bloques o secciones. Para cada plantilla dispondremos de una línea en la que se refleja su título, una imagen del mismo y un icono (un ojo) que dan acceso a ver un modelo del recurso que se quiere construir, y además se cuenta con un enlace a la guía o tutorial en pdf y un zip para su descarga.

A continuación tenenemos una de estas líneas sobre las que se puede interactuar y comprobar las acciones antes descritas:

Selección múltiple - Identifica imágenes

Así pues, podemos concluir afirmando que la herramienta Descartes permite la elaboración de escenas genéricas que pueden ser reutilizadas por el profesorado para generar actividades educativas sin necesidad de conocer dicha herramienta. En base a las plantillas de este proyecto los usuarios podrán generar diferentes actividades sin más que manipular adecuadamente imágenes y ficheros, y aportar una información estructurada siguiendo el adecuado instructivo.

Descartes aporta su potencial como herramienta y el profesorado su creatividad y buen saber hacer docente.

Os invitamos a compartir con la Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo., tanto los recursos que elaboréis con estas plantillas, como las plantillas que elaboréis.