Obtención de fichero de resultados de un juego
Escrito por Jesús Manuel Muñoz Calle- Son específicos para cada juego, recogiendo los datos más relevantes de los mismos.
- Se puede generar en cualquier momento del juego. Los datos que se recogerán en el fichero serán los que existan en el juego en el momento de crearse.
- El fichero de texto es editable y se puede guardar con el nombre que se desee.
Más de diecisiete millones de páginas servidas en 2018
Escrito por José R. Galo SánchezEn 2018 hemos servido más de diecisiete millones de páginas (casi dieciocho millones) desde nuestro dominio proyectodescartes.org y a través de ellas han sido distribuidos hacia nuestros usuarios más de dos mil quinientos Gigabytes. Estos son sólo dos parámetros que dan una pincelada del alcance logrado por nuestra organización no gubernamental "Red Educativa Digital Descartes" (RED Descartes).
Como ya indicamos en el artículo que publicamos el pasado año nuestra reflexión como asociación, al inicio de este año 2018, no puede limitarse a analizar aspectos meramente cuantitativos, pero estos sí nos pueden servir como base informativa del alcance conseguido y también para ver la evolución acaecida entre el año 2017 y el de 2018. De partida adelantamos que hemos incrementado un 20% las páginas servidas y un 50% en los GB transmitidos.
Tomamos como base la información que podemos obtener a partir de las estadísticas que se generan automáticamente en nuestro servidor proyectodescartes.org con la herramienta Webalizer. En la ayuda de esta herramienta se describen los caracteres estadísticos que se registran: accesos (hits) , archivos (files), páginas (pages), visitas (visits), clientes (sites) y kbytes.
La siguiente tabla refleja el resumen mensual y anual de este año 2018:
En la primera columna de esta tabla se cuenta con un enlace que da acceso a un desglose detallado por días y horas para cada uno de los meses.
En la columna de páginas podemos observar el dato relativo al número de páginas servidas, el cual es el que hemos destacado en el título de este artículo. Son más de diecisiete, casi dieciocho, millones de páginas las que han sido requeridas por nuestros usuarios y que han sido servidas desde nuestro servidor, una media mensual aproximada de un millón quinientas mil páginas, más de cuarenta y ocho mil diarias, dos mil a la hora, casi treinta y cuatro cada minuto, 1 página aproximadamente cada dos segundos.
El siguiente diagrama de barras muestra ese desglose mensual de páginas servidas.
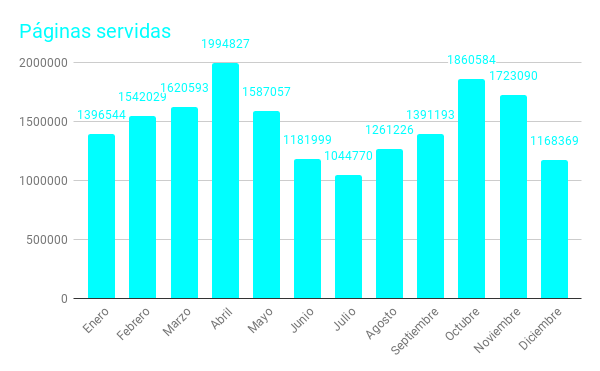
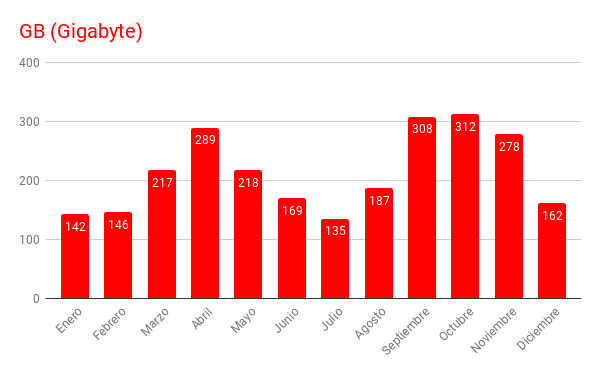
En la columna "kB F" se reflejan el número de kbytes transferidos desde el servidor hacia los usuarios a través de las páginas solicitadas. Aquí no se contabilizan, no se incluyen, los bytes correspondientes a las descargas que se realizan de nuestras publicaciones anuales en DVD (Vol. I, Vol. II y Vol. III) ya que los archivos de estos DVD están alojados en otros servidores. Son más de dos mil quinientos Gigabytes los transferidos este año, lo que equivale a haber replicado el contenido de nuestro servidor en la red unas noventa veces a lo largo de este año, casi dos veces cada semana.
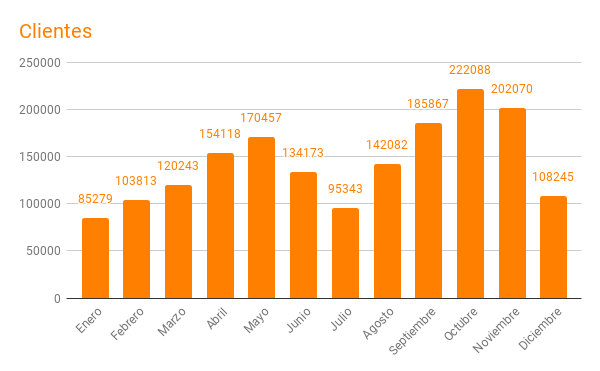
La columna de "clientes" o "sites" refleja la cantidad de direcciones IP diferentes que realizan solicitudes al servidor y es como un indicador aproximado de la cantidad de visitantes recibidos en nuestro servidor. La media mensual alcanzada es de unos ciento cuarenta mil y diariamente serían unos cuatro mil ochocientos.
La procedencia de estos visitantes también queda reflejada en el control estadístico del servidor y estos proceden principalmente de toda iberoamérica encabezados, generalmente, por España, Colombia, México, Argentina y Ecuador, pero no siempre en ese orden siendo claramente dependiente del periodo lectivo en cada país. En los meses vacacionales en España es Colombia quien ha estado liderando esta procedencia. Desde aquí felicitamos a nuestros colegas de RED Descartes Colombia por la labor que realizan y que queda reflejado en todos los datos aquí expuestos y en particular en este liderazgo.
Comparación 2017 y 2018
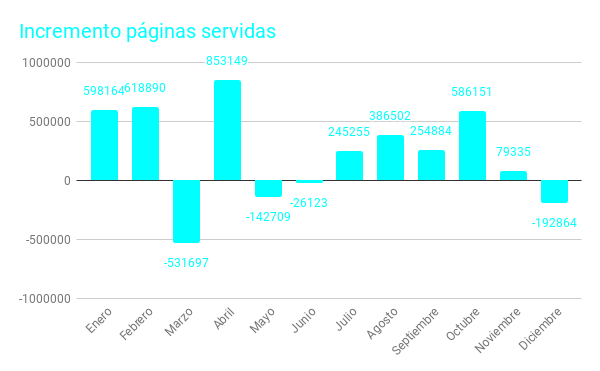
Realizando una comparación entre el año 2017 y 2018 podemos observar el incremento de páginas servidas. Globalmente han sido casi tres millones más de páginas las servidas en 2018, respecto a 2017. Pero en marzo se ve un decremento sustancial, quizás causado porque en 2017 la Semana Santa (periodo vacacional) cayó en Abril en 2017 y sin embargo en 2018 fue en marzo. También hay decrementos en mayo, junio y diciembre, pero obviamente todos compensados por el incremento acaecido en otros meses, en especial el ocurrido en abril de 2018. Porcentualmente ha acontecido un incremento del 20% anual.
En lo relativo a los GB servidos se ha producido un sustancial incremento en todos los meses, y globalmente en 2017 fueron 1687 GB y en 2018 un total de 2563. Un 50% más. Al ser este porcentaje superior al acontecido con el de páginas podríamos intuir que nuestros usuarios han procedido a realizar un mayor número descargas de nuestros recursos para su uso en local.
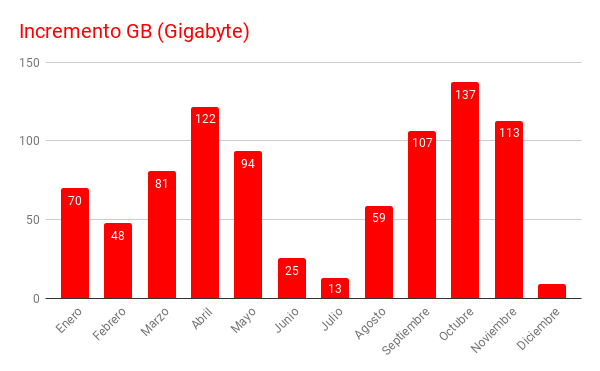
Y en lo que respecta a clientes en 2017 fueron algo más de un millón trescientos mil y en 2018 se paso a un millón ochocientos mil, un 40% adicional.
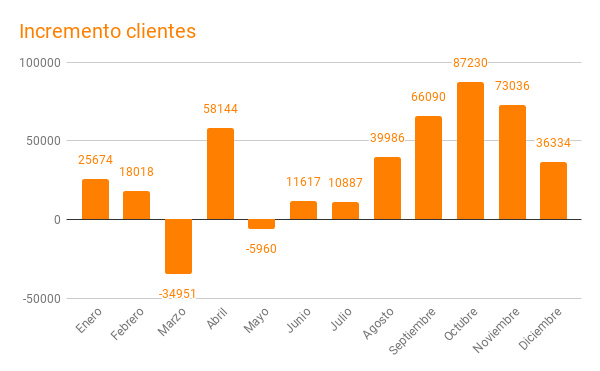
Nuestro agradecimiento a todos los que, accediendo a nuestro dominio proyectodescartes.org, han ido contribuyendo página a página a incrementar estos y cada uno de los caracteres estadísticos que perfilan el nivel de utilidad de nuestro servicio y, así, estiman y valoran nuestra dedicación altruista en pro de la comunidad educativa de la aldea global.
¡Feliz 2019! y ¡A aprender con Descartes!
Guardado y continuación de partidas de juegos del Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle- Pas partidas cuya duración sea grande pueden ser fraccionadas.
- Se puede guardar la partida en diferentes puntos y se podrá continuar desde el punto que se desee.
- Se puede empezar una partida de un juego en una modalidad y continuarse en otra. Por ejemplo, se puede empezar en la modalidad de introducción de preguntas mediante un fichero, continuarla en la modalidad de preguntas orales y terminarla en una sin preguntas.
- Se guardar una partida nada más cargar los nombres y las opciones iniciales y guardarla. De esta forma se puede llevar preparada una partida directamente para empezar a jugar.
- Se puede guardar una partida tras finalizar y servir así para tener registrado el resultado que se haya producido.
- Si se quiere hacer una modificación en los jugadores, opciones del juego, fichero de preguntas, etc., se puede guardar la partida y continuarla con los nuevos datos que deseemos.
- Si se desea cambiar de equipo o navegador, también se puede utilizar este procedimiento.
- Las partidas se podrán guardar cuando el control del menú superior Guardar partida esté activo. Estará activo siempre al comenzar y al terminar una partida y en otras ocasiones según la dinámica del juego.
- Al pulsar el botón Guardar partida se abrirá una ventana de exploración de archivos para indicar el nombre y la ubicación del fichero que contiene los datos y estado de la partida que se guarda.
- En algunos navegadores se producen errores al guardar ficheros. Se debe verificar que se ha guardado correctamente y si no es así se debe repetir el proceso de guardado.
- El nombre por defecto de un fichero para guardar una partida será partida-nombre del juego, pero se puede guardar con el nombre que se desee.
- Una partida guardada en una modalidad de introducción de preguntas de un juego se podrá continuar en cualquier modalidad del propio juego, pero no en otro juego diferente.
- Una partida guardada podrá continuarse cargando el fichero con los datos y estado de una partida guardada a través del control Continuar partida que aparece al principio del juego (en la ventana de introducción de los nombres de los jugadores).
- Al pulsar el botón Continuar partida se abrirá una ventana de exploración de archivos que permitirá buscar y seleccionar el fichero de continuación de una partida anteriormente guardada.
- Si el fichero cargado es correcto dicho botón se pondrá de color azul oscuro con el nombre Partida cargada. Además se podrá ver se han cargado los nombres y las opciones específicas de la partida que se continua.
- En general y salvo que no lo permita la dinámica del juego, una vez cargada una partida guardada, se pueden modificar os nombres y las opciones del juego si se desea.
- Si una vez cargado el fichero de continuación de una partida se carga otro, la partida cargada será la del último fichero válido introducido.
- Si se carga el fichero de continuación de una partida y se quiere anular, se debe utilizar el control de la esquina superior izquierda Reiniciar juego.
- Si se carga un fichero no válido, el botón de Continuar partida se volverá rojo e indicará Fichero no válido. Las cargas de los ficheros no válidos no serán tenidas en cuenta y se considerará cargado el último fichero correcto y si no se ha cargado ninguno correcto el juego comenzará sin considerar continuación alguna de partida.
Ejemplo de uso de tres juegos del Proyecto AJDA (I)
Escrito por Jesús Manuel Muñoz CalleBatalla naval. Es un juego original del proyecto AJDA en el que dos jugadores o equipos se enfrentan en una "guerra de preguntas" que gana el equipo que hunde el barco del adversario alcanzándole cinco veces.
Libro interactivo para formarse en Descartes JS
Escrito por José R. Galo SánchezEl Fondo editorial de la Institución Universitaria Pascual Bravo de Medellín (Colombia) ha publicado un libro interactivo de formación en la herramienta de autor “Descartes JS”.
Los autores son Juan Guillermo Rivera Berrío --vicerrector de dicha institución--, Joel Espinosa Longi y Alejandro Radillo Díaz --técnicos académicos del Instituto de matemáticas de la Universidad Autónoma de México--.
El libro como se indica en su título “Descartes JS nivel I” tiene como objetivo introducir a sus lectores-actores en el desarrollo con esta herramienta de escenas interactivas para alcanzar un primer nivel de capacitación, estando previsto darle continuidad en próximos libros complementarios. No se presuponen conocimientos previos en Descartes y su contenido está configurado para el aprendizaje autónomo mediante la elaboración de proyectos en los que se acompaña al discente en su elaboración. Mira esta escena:
Como puedes observar, la catalogación como nivel I o introductorio no debe de llevar a la presunción de que los proyectos elaborados sean muy básicos, muy al contrario podrá experimentarse el potencial de Descartes y cómo pueden conseguirse recursos educativos muy interesantes con un coste formativo asumible. Por ejemplo, la actividad del capítulo sexto en la que se desarrolla un vídeo interactivo que embebemos aquí:
O la elaboración de secuencias temporales como ésta:
¡Ánimo! ¡Aprende con este interesante libro interactivo y desarrolla tus recursos educativos con DescartesJS!
(Pulsa sobre la imagen para acceder al libro interactivo)
Publicación de RED Descartes en el Open Journal "Matemáticas, Educación y Sociedad"
Escrito por Ángel Cabezudo BuenoEn el Vol. I, Núm. 2 del Open Journal "Matemáticas, Educación y Sociedad" (ISSN: 2603-9982) se ha publicado el artículo titulado "Partición prismática de un cubo en seis pirámides triangulares equivalentes". Un detallado trabajo de investigación que, como se refleja en la autoría, ha sido desarrollado dentro de nuestra RED Descartes por nuestro socio José R. Galo Sánchez.
Os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales.
NOTA: En este pdf hay numerosos enlaces externos a recursos interactivos desarrollados con Descartes y que están publicados en nuestro servidor de contenidos. Os aconsejamos que la apertura de cada uno de estos enlaces la realicéis posicionando el ratón sobre el enlace y pulsando Ctrl+clic, de esta manera el recurso enlazado se abre en una nueva pestaña y permite realizar una lectura del pdf sin necesidad de tener que volver a posicionarse en el punto desde el que se produjo el salto.
Uso de dirección URL de ficheros de preguntas para cargarlos en el juego (AJDA)
Escrito por Jesús Manuel Muñoz Calle- Crear el fichero de preguntas, se recomienda usar el generador de ficheros.
- Subir el fichero a Internet. Se puede enviar para ser publicados en la web del Proyecto AJDA o a cualquier otra.
- Copiar la dirección Url del juego (barra de direcciones del navegador).
- Se entra en el juego y en su apartado "Selección de ficheros de preguntas", se pega la dirección Url del juego en el campo "Dirección Url/local". Si el proceso se ha realizado correctamente se mostrarán los datos del fichero cargado.
¡La vuelta al cole con Descartes en 2018/2019!
Escrito por José Antonio Salgueiro GonzálezMisceláneas: Probabilidad. Inferencia II.
Escrito por Ildefonso Fernández TrujilloMisceláneas: Probabilidad. Inferencia. Fundamentos II.
Incertidumbre.
De la pérdida de la incertidumbre en el acto de decidir sobre cualquier asunto son responsables los estudiosos de la Probabilidad y la Estadística. Un estudio, bien fundamentado y realizado, sobre prácticamente cualquier tema, desvelará el desarrollo futuro de un proceso económico, sanitario, social...y si, un puñado de herramientas inmateriales: teoremas, lemas, hipótesis, tesis, etc. cada vez más sofisticadas y eficaces, hacen las veces de bola de cristal de los auténticos videntes actuales, aunque a decir verdad la incertidumbre no desaparece del todo y está en función del dinero a invertir y/o las características propias del tema en estudio pero por lo general suele ser inferior al 5%. O dicho de otra manera el nivel de confianza en los resultados del estudio suele ser superior al 95%.
En la entrada anterior en este blog incrustamos una escena del libro digital: Estadística, Probabilidad e Inferencia, en la que se mostraba el cálculo práctico de los intervalos de confianza en una simulación teórica que permite manipular el tamaño de la muestra, el nivel de confianza exigido y el valor del parámetro en estudio. En esta ocasión, en principio, hemos creído conveniente insistir en la fundamentación elemental teórica de la Inferencia para lo cual proponemos que al introducir (difundir) este tema debemos garantizar el conocimiento de la distribución Normal, sus propiedades y el uso de la tabla para el cálculo de probabilidades de los valores de la variable X cuando esta variable tiene una distribución normal de media µ = 0 y una desviación típica σ = 1. X con distribución N(0,1). Así como el procedimiento de tipificación de variables normales con cualquier media y desviación.
Todo lo anterior queda completamente cubierto en la unidad didáctica dinámica e interactiva INFERENCIA ESTADÍSTICA
Que se complementa con la útil "Calculadora de la Distribución Normal" del profesor Juan Jesús Cañas Escamilla
Ambas utilidades y el resto de las mencionadas constituyen una muy completa documentación para uso personal y como herramientas didácticas para la explicación del tema. Como consecuencia del análisis del material expuesto y de la bondad de los métodos numéricos finitos hemos desarrollado la siguiente utilidad que consiste en una escena que muestra la probabilidad de que una variable que se distribuye según una distribución Normal(0,1) tome un valor menor o igual que otro dado. La escena pretende ser una utilidad simple y eficaz para la introducción al estudio de las distribuciones de probabilidad.
Todo lo expuesto anteriormente además del resto de conocimientos teóricos necesarios para afrontar el estudio de los intervalos de confianza y de los contrastes de resultados se encuentra en los materiales enlazados en esta y en entradas anteriores; no obstante volvemos a mostrar algunos de ellos por su indudable interés:
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra una clase sobre las distribuciones de probabilidad.
Ildefonso Fernández Trujillo. 2018
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
