1. Buscar y elegir el juego que se desee.

Elige un juego del menú "Selecciona un juego", situado en la esquina superior izquierda de la web del proyecto. Al pulsar se mostrará una descripción del juego. (También se puede usar los buscadores de la web, especialmente el de juegos).

2. Acceder al juego elegido.

Para entrar en el juego pulsa el botón rojo, "ACCEDER AL JUEGO" que aparece en la descripción del mismo.

3. Seleccionar la modalidad de introducción de preguntas el juego.

Éstas pueden introducirse de forma escrita, oral o no contener preguntas. (Si el juego sólo presenta una modalidad este paso se omite).

4. Elegir la configuración o parámetros iniciales del juego.

Introduce los nombres de los jugadores, opciones específicas y generales del juego, carga de ficheros de preguntas para juegos con esta modalidad, etc.

5. Pulsar en el botón JUGAR.

6. Comenzar la partida.

Durante los días 3 y 4 de noviembre de 2017 se celebraron, en el aulario de la Universidad Pública de Navarra, las V Jornadas de Enseñanza de las Matemáticas en Navarra, organizadas conjuntamente por la Sociedad Navarra de Profesores de Matemáticas "TORNAMIRA", el CAP de Pamplona y la UPNA, con el objetivo de lograr un lugar de encuentro para docentes desde la etapa de educación infantil hasta la universitaria, constituir un foro de comunicación de trabajos, experiencias e inquietudes del profesorado de matemáticas en la Comunidad Foral de Navarra, así como un elemento más que contribuya a transmitir y a hacer visible la cultura matemática en la sociedad navarra.

La RED Descartes estuvo representada por Rita Jiménez Igea, profesora de matemáticas en el IES Tomás Mingot de Logroño, quien presentó el taller titulado "¿A qué jugamos hoy en clase de Mates?", un REA (Recurso Educativo Abierto) con sugerencias didácticas para usar en el aula escenas de Descartes que contienen un juego o pasatiempo y trabajar conceptos y contenidos del currículo de Matemáticas,  principalmente  de  secundaria, aunque también aplicables en primaria. Todas las escenas permiten jugar y/o simular el juego tantas veces como se desee, pertenecen al Proyecto Descartes y están publicadas en el enlace superior.

Podemos encontrar escenas interactivas que son un juego y al usarlas se están trabajando los contenidos, escenas a partir de las cuales se sugiere cómo crear puzzles que permiten a los alumnos trabajar algunos conceptos, escenas que recrean un juego conocido y al plantear preguntas podemos descubrir las matemáticas que contiene ese juego y usarlas para ganar, etc...

Debemos tratar de encontrar y llevar al aula materiales y recursos que estimulen al alumno. Las Tics, los pasatiempos, los juegos, los materiales manipulativos son buenas opciones que hacen que salgamos de la monotonía de la pizarra, el cuaderno y los ejercicios de lápiz y papel. Este recurso pretende dar ideas y sugerencias de cómo llevar al aula estas escenas y juegos. No es un trabajo completo y cerrado. Es una primera vía de trabajo porque seguro que cada profesor conseguirá enfoques nuevos, plantear otro tipo de preguntas y utilizar estas escenas de otra forma.

Para generar el REA se ha utilizado eXeLearning (software libre) que permite incluir actividades interactivas tipo rellenar huecos, actividades tipo test, de verdadero o falso, etc. con autocorrección y/o retroalimentación, además permite incrustar páginas web, escenas de Descartes o Geogebra, applets de Java, imágenes , videos etc…

También podemos encontrar este Recurso Educativo Abierto compartido en el espacio Procomún.

Finalmente, compartimos en nuestro portal la presentación y el texto íntegro de la comunicación presentada por Rita Jiménez Igea.

Sí, en el pasado año 2017 son más de quince millones de páginas las que hemos servido desde nuestro dominio proyectodescartes.org y casi mil setecientos Gigabytes los que, a través de ellas, han sido distribuidos hacia nuestros usuarios. Estos son sólo dos parámetros que dan una pincelada del alcance de la RED Descartes.

El final y comienzo de año suele asociarse a periodos de reflexión, valoración de objetivos y propuesta de nuevas acciones. Ubicándonos en este contexto, en este artículo, buscamos analizar y divulgar algunos parámetros que nos permitan determinar el alcance de nuestra organización no gubernamental RED Descartes. Obviamente una adecuada valoración  ha de contemplar  aspectos tanto cuantitativos como cualitativos, pero, aun siendo conscientes de esto, aquí únicamente vamos a tratar de realizar una observación parcial, meramente cuantitativa, y para ello vamos a fijarnos exclusivamente en la información que podemos obtener a partir de las estadísticas que se generan automáticamente en nuestro servidor proyectodescartes.org con la herramienta Webalizer. En la ayuda de esta herramienta se describen los caracteres estadísticos que se registran: accesos (hits) , archivos (files), páginas (pages), visitas (visits), clientes (sites) y kbytes. Reflejaremos y pondremos accesibles todos ellos dejando al lector interesado la posibilidad de abordar su propio estudio, pero aquí nosotros pondremos el foco sólo en tres de ellos.

La siguiente tabla refleja el resumen mensual y anual de este año 2017:

En la primera columna de esta tabla se cuenta con un enlace que da acceso a un desglose detallado por días y horas para cada uno de los meses.

En la columna de páginas podemos observar el dato relativo al número de páginas servidas, el cual es el que hemos destacado en el título de este artículo. Son más de quince millones de páginas las que han sido requeridas por nuestros usuarios y que han sido servidas desde nuestro servidor, una media mensual aproximada de un millón doscientas cincuenta mil páginas (1.250.000), más de cuarenta y una mil diarias, mil setecientas a la hora,  casi veintinueve cada minuto, 1 página aproximadamente cada dos segundos.

El siguiente diagrama de barras muestra ese desglose mensual de páginas servidas.

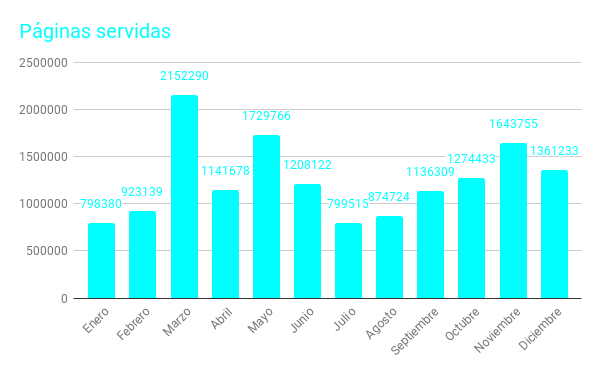
 En la columna "kB F" se reflejan el número de kbytes transferidos desde el servidor hacia los usuarios a través de las páginas solicitadas. Aquí no se contabilizan, no se incluyen, los bytes correspondientes a las descargas que se realizan de nuestras publicaciones anuales en DVD (Vol. I y Vol. II) ya que los archivos de estos DVD están alojados en otros servidores. Son unos mil setecientos Gigabytes los transferidos en este año, lo que equivale a haber replicado el contenido de nuestro servidor en la red unas cincuenta veces a lo largo de este año, casi una vez cada semana.

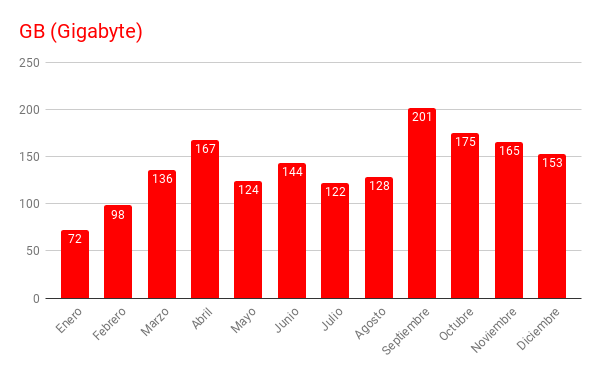
La columna de "clientes" o "sites" refleja la cantidad de direcciones IP diferentes que realizan solicitudes al servidor y es como un indicador aproximado de la cantidad de visitantes recibidos en nuestro servidor. La media mensual alcanzada es de unos ciento diez mil y diariamente serían unos tres mil seiscientos.

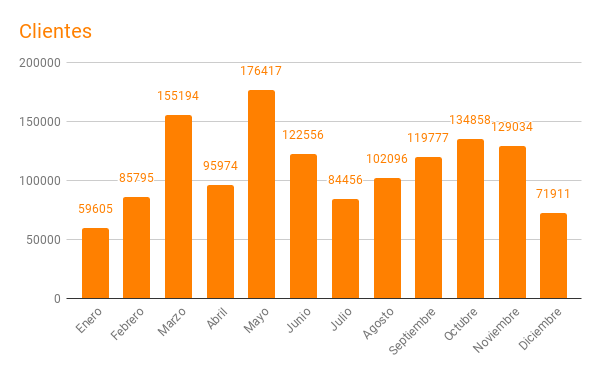
La procedencia de estos visitantes también queda reflejada en el control estadístico del servidor y estos proceden principalmente de toda iberoamérica encabezados, generalmente, por España, Colombia, México, Argentina y Ecuador, pero no siempre en ese orden siendo claramente dependiente del periodo lectivo en cada país. 

Nuestro agradecimiento a todos los que, accediendo a nuestro dominio proyectodescartes.org, han ido contribuyendo página a página a incrementar estos y cada uno de los caracteres estadísticos que perfilan el nivel de utilidad de nuestro servicio y, así, estiman y valoran nuestra dedicación altruista en pro de la comunidad educativa de la aldea global.

¡Feliz 2018! y ¡A aprender con Descartes!

Un año más, el Grupo Empresarial IC S.L., prestigiosa Institución Comercial especializada en la ejecución integral de grandes proyectos de interior que abarcan la construcción, las instalaciones, el mobiliario y el mantenimiento, ofrece su apoyo al mundo de la Educación y la difusión del conocimiento, como base de cualquier actividad humana, patrocinando sesenta y nueve unidades didácticas interactivas generadas con Descartes JS, que son funcionales en cualquier tipo de dispositivo (ordenador, tableta o smartphone). Concretamente, llevan el sello del Grupo IC, los libros interactivos del Proyecto ED@D correspondientes al currículo de Matemáticas orientadas a las Enseñanzas Académicas y Matemáticas orientadas a las Enseñanzas Aplicadas en el curso de 3º ESO, respectivamente en castellano, catalán y gallego.

Grupo IC trabaja en exclusiva para grandes marcas de los sectores retail, hoteles, lujo, sanitario, oficinas y restauración, siendo cuatro las empresas que conforman el grupo:

• IC Construction.- Es la constructora del grupo especializada en construcción integral de interiores.
• Efficentre.- Es la instaladora del grupo especializada en soluciones de eficiencia energética.
• Ekipashop.- Empresa del grupo dedicada a la fabricación y montaje de mobiliario a medida realizado con maderas ecológicas certificadas PEFC o FSC®.
• Servishop.- Dedicada a la gestión integral del mantenimiento con un call center técnico 24h/365d.

Aunque Grupo IC construye grandes proyectos de interior para importantes y conocidas empresas en cualquier lugar del mundo, es posible que sea Primark Gran Vía Madrid el más conocido, pues con sus 12.300 metros cuadrados de superficie de ventas es la mayor tienda que esta firma posee en España.

Guardar

Guardar

Guardar

Guardar

Durante 2017 se ha trabajado intensamente en la renovación y actualización del Proyecto "Aplicación de juegos didácticos en el aula", proyecto que promueve la inclusión de juegos didácticos basados en escenas de Descartes en la práctica docente. Las principales cambios e innovaciones introducidas son las siguientes:

• Renovación y reoorganización por completo del diseño de la web, blog y DVD del proyecto.
• Diseño y puesta en funcionamiento de un canal de YouTube para el proyecto.
• Mejora en el diseño, programación y funcionamiento de todos los juegos didácticos.
• Inclusión de nuevos juegos hasta llegar a la cifra de 414.
• Diseño y puesta en funcionamiento de un nuevo generador de ficheros de preguntas para juegos.
• Rediseño de la sección de video-tutoriales y de sus contenidos.
• Renovación y actualización del curso "Aplicación de juegos didácticos en el aula".
• Renovado y actualización del curso "Creación de animaciones y juegos interactivos para el aula". Adaptación del curso al nuevo editor de escenas basado en javascript.
• Realización de una nueva guía rápida de utilización de juegos didácticos.
• Actualización de las presentaciones y documentos del proyecto.

Recordamos que los contenidos del proyecto se encuentran en su: web, blog, DVD y canal de YouTube. En el siguiente vídeo se presentan las secciones de este renovado proyecto. 

Del 10 al 14 de julio de 2017 se celebró, en las facultades de Ciencias Matemáticas, Ciencias Físicas y Medicina de la Universidad Complutense de Madrid, el VIII Congreso Iberoamericano de Educación Matemática que, con el lema "Miramos con ilusión hacia el futuro de la educación matemática", congregó a 1600 docentes de todas las etapas educativas que mantienen viva la llama de la ilusión por esta maravillosa tarea que es la educación matemática de nuestros alumnos, según palabras de Concepción Toboso Nieto, presidenta del comité organizador, integrado por la Sociedad Madrileña de Profesores de Matemáticas "Emma Castelnuovo", con el apoyo de la Federación Española de Sociedades de Profesores de Matemáticas y por delegación de la Federación Iberoamericana de Sociedades de Educación Matemática.

La Red Educativa Digital Descartes estuvo representada por Rita Jiménez Igea y Elena Álvarez Sáiz, que aportaron, respectivamente, el taller titulado "El Proyecto Descartes en el aula" y la comunicación "Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automática".

El objetivo del taller es dar a conocer el portal de Red Educativa Digital Descartes (RED Descartes) a los profesores y profesoras de Matemáticas, mostrando los recursos educativos accesibles desde cualquier dispositivo para las etapas de Infantil, Primaria, Secundaria, Bachillerato y Universidad, que pueden usarse libre y gratuitamente y se encuentran disponibles en los dominios ProyectoDescartes.org,  REDDescartes.org y DescartesJS.org.

Se presentaron los diversos subproyectos del Proyecto Descartes y se hizo un recorrido por distintas unidades didácticas digitales y objetos interactivos, pudiendo los asistentes interactuar con las escenas entrando en esas unidades de modo dirigido y de forma libre. Se expusieron, de manera práctica, distintas formas de incorporar al aula estos materiales en función de las posibilidades tecnológicas de cada centro, concluyendo con unos ejercicios para mostrar la posibilidad de crear nuevos recursos usando los ya existentes o adaptarlos a las necesidades del alumnado.

Guardar

Guardar

El día 5 de julio se celebró, en el IES Isaac Albéniz de Leganés (Madrid), la Asamblea General Ordinaria de Red Educativa Digital Descartes correspondiente al año 2017, con el objetivo de tratar asuntos de gestión y organización como memoria de actividades, cierre económico, renovación de la Junta Directiva, presupuesto y propuesta de proyectos para el próximo ejercicio, entre otros, compaginando la asistencia real con la virtual a través de las herramientas de intercomunicación de nuestra asociación, garantizando así el derecho a voto de todos sus miembros.

Queremos destacar la enorme trascendencia del Proyecto Descartes en estos últimos cuatro años, así como su alcance y repercusión, tanto en España como en todos los países de habla hispana, con una evolución en el número de visitantes que nos ha llevado a 1.200.000 páginas servidas mensualmente, es decir, a una media de 40.000 páginas diarias, una cifra que supone para nosotros el reconocimiento de la calidad de los recursos ofrecidos desde nuestro portal y que nos anima a seguir trabajando altruistamente por la comunidad educativa de la aldea global, así como a mostrar todo nuestro agradecimiento a los usuarios y seguidores de RED Descartes.

Con motivo de esta nueva asamblea nos desplazamos a Leganés desde diversos puntos geográficos: Santiago de Compostela, Valladolid, Zaragoza, Córdoba, Madrid, Burgos, Alcalá de Henares, Móstoles, Arganda del Rey y Lebrija, haciendo posible el reencuentro entre compañeros y amigos que no coincidíamos desde hacía bastantes años. 

Al finalizar la fructífera y productiva asamblea pudimos compartir un exquisito almuerzo en el Restaurante Changó, sito en el Parque El Carrascal de la ciudad leganense, aunque con muy corta sobremesa, pues el regreso apremiaba. Por cierto, Josep, nuestro anfitrión, tuvo la cartesiana idea de reunir a este grupo de profesores de matemáticas en la Avda. de la Lengua Española justo en vísperas de la celebración en Madrid del VIII Congreso Iberoamericano de Educación Matemática, que también contará con la representación de RED Descartes ostentada por nuestras compañeras Rita Jiménez, que presenta el taller titulado "El Proyecto Descartes en el aula" y Elena Álvarez con la comunicación que lleva por título "Diseño y desarrollo online de ejercicios interactivos de matemáticas con estrategias de tutorización automáticas".

Finalmente, desde RED Descartes queremos transmitir nuestro más sincero agradecimiento a D. Juan José Uzquiano Sánchez de Castro, Director del IES Isaac Albéniz, por su cálido recibimiento y atención junto a su Equipo Directivo (Mar Sánchez, Secretaria, Alicia Burgos, Jefa de Estudios, Inmaculada Alonso, Jefa de Estudios Adjunta y Óscar García, Jefe de Estudios de Bilingüismo) así como al personal de administración y servicios.

Guardar

Guardar

Guardar

Guardar

Guardar

En el número 94 de la revista Epsilon de la Sociedad Andaluza de Educación Matemática Thales se ha publicado el artículo titulado "Sobre la forma y el crecimiento cordobés del Nautilus pompilius". Un detallado trabajo de investigación desarrollado dentro de nuestra RED Descartes, reflejándose así en la autoría, por los socios José R. Galo Sánchez, Ángel Cabezudo Bueno e Ildefonso Fernández Trujillo.

Os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales.

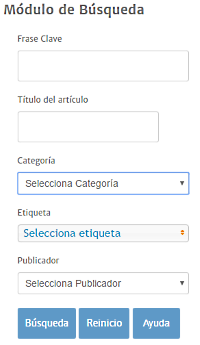Hace unos días hemos dado por concluida la implementación de un módulo de búsqueda que venía siendo necesario para esta Web de Contenidos.

Desde las distintas secciones o categorías, Blog, Matemáticas, Física y Química, Otras áreas y Plantillas, se han ido publicando sin pausa, desde la aparición en los medios de RED Descartes, diferentes artículos y ya acumulamos un número importante, ¡sobrepasan los dos mil!

En esta situación es esencial disponer de un buscador que permita acceder a cualquiera de los artículos partiendo de determinados elementos que lo caractericen en función de su categoría, su contenido o su etiquetado. Esto es lo que pretende el Módulo de Búsqueda, para lo cual se han habilitado cinco elementos que actúan de filtro y se rotulan como Frase Clave, Título del artículo, Categoría, Etiqueta y Publicador.

Para mejor comprender la razón de ser de estos cinco elementos podemos decir que cada artículo publicado en la Web de Contenidos lleva, aparte de su contenido literario, metadatos como la fecha de publicación, escrito por (publicador), valoración (de 1 a 5 estrellas) de los lectores, categoría (sección) donde se publica y el etiquetado (conjunto de etiquetas que determinan un perfil para el artículo: temática, proyecto, materia, edad, nivel académico, lenguaje, etc.).

El Módulo de Búsqueda se encuentra en cada una de las secciones, Blog, Matemáticas, Física y Química, Otras áreas y Plantillas y puesto que cada sección se corresponde con una determinada categoría donde los artículos publicados quedan catalogados, el item correspondiente al elemento Categoría queda seleccionado automáticamente al acceder a una determinada sección, pudiendo no obstante  desde aquí cambiar a voluntad a cualquier otra categoría.

El Módulo de Búsqueda incorpora un botón de Ayuda que caracteriza a cada uno de los elementos y detalla el formato que tiene el resultado de la búsqueda y las distintas formas como puede ser ordenado. No insistimos más por este lado en este artículo de presentación.

Esperamos haber acertado con esta herramienta y que realmente sea de utilidad a cualquier usuario de la Web de contenidos de RED Descartes.