Ejercicios y problemas (Vol. II)
Título de la obra:
Álgebra Lineal Interactiva. Ejercicios y problemas. (Vol. II)
Autor:
Augusto Spela
Universidad tecnológica Nacional - FRBA
Buenos Aires (Argentina)
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS, WebSim, GeoGebra.
Fuentes: Lato y UbuntuMono
Imagen de portada: ilustración generada por Lexica
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-10368-17-0

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Este libro interactivo continúa la senda trazada en el Volumen 1, el cual fue muy bien recibido por la comunidad educativa. En esta nueva entrega, abordamos más temas que continúan desarrollando los conceptos esenciales de la materia, ampliando y profundizando la comprensión adquirida previamente. De hecho, fue la solicitud de los propios alumnos lo que impulsó la creación de este segundo tomo, motivados por el interés y entusiasmo generado en el primero.
Al igual que su predecesor, no pretende ser un libro de referencia exhaustivo, apenas un complemento interactivo enfocado en el "hacer", que apoya a los buenos recursos que existen en la actualidad sobre Álgebra Lineal. Una lista sugerida de los mismos se ofrece en la
Especial mención y agradecimiento a la UDB Matemática de la Universidad Tecnológica Nacional FRBA, que una vez más me permitió utilizar parte del excelente material disponible en su sitio web de Álgebra y Geometría Analítica https://aga.frba.utn.edu.ar
Del mismo modo quiero expresar mi más sincero reconocimiento a la labor de los académicos Juan Guillermo Rivera Berrío, Ramiro Antonio Lopera Sánchez, Joel Espinosa Longi y demás desarrolladores del Proyecto iCartesiLibrihttps://proyectodescartes.org/iCartesiLibri/, por su invaluable ayuda y aporte de recursos y conocimientos, siempre ofrecidos de manera desinteresada y generosa.
En esta oportunidad hemos seguido trabajando con adaptaciones de recursos y applets disponibles en Geogebra. En cada caso compartimos la información sobre la autoría de los diseñadores de los mismos.
También hemos utilizado videos y algunas escenas interactivas realizadas en DescartesJS; pero la novedad en este volumen es el uso de las inteligencias artificiales generativas que han permitido realizar cuestionarios (aparecen al final de cada capítulo); diseñar páginas web como las nuevas secciones "¿Y esto para qué sirve?" y la "Herramienta IA con Pollinations.AI" inspiradas en trabajos del Dr. Juan Guillermo Rivera Berrío.
Por primera vez también habrá secciones que requerirán de conexión a internet, hemos propuesto un juego de "sala de escape" realizado en Genially, que no podrá concretarse sin conexión. Igualmente necesitaremos conectarnos para utilizar el interactivo "Herramienta IA". Además hay varios enlaces que complementan información que requerirán de dicha conexión.
El script que acompaña el inicio de cada capítulo es obra de Dan Margalit y Joseph Rabinoff, quienes junto a Larry Rolen han escrito el maravilloso libro interactivo Interactive Linear Algebra que ha sido fuente de inspiración conjuntamente con los libros de la colección iCartesiLibri para quien esto escribe. Gracias a ChatGPT he podido diseñar una página para que pueda correr dicho script, adaptada a nuestro libro y con todas las funcionalidades disponibles.
Para quienes gusten de la lectura más cruda, todos los temas "teóricos" del libro pueden leerse descargándolo en un dispositivo digital, así como el 99% del contenido interactivo.
Confío en que el enfoque de este libro sea una fuente de inspiración y aprendizaje, y que disfrute el usuario de cada paso del camino en su exploración del álgebra lineal. ¡Que esta obra los acompañe y los motive a seguir creciendo en su conocimiento!
En primer lugar, una transformación lineal es una función. Por ser función, tiene su dominio y su codominio, con la particularidad de que éstos son espacios vectoriales. Tenemos dos espacios vectoriales \(V\) y \(W\), y una función que va de \(V\) a \(W\). O sea una regla de asignación que transforma vectores de \(V\) en vectores de \(W\). Pero no toda función que transforme vectores de \(V\) en vectores de \(W\) es una transformación lineal. Debe cumplir ciertas condiciones:
\(F:V \to W\) es una transformación lineal si y sólo si:
La imagen del vector nulo del dominio \({0_V}\) es el vector nulo del codominio \({0_{W\;}}\):
\[T\left( {{0_V}} \right) = {0_W}\]
\[T\left( {{0_V}} \right) = T\left( {0\,v} \right) = 0\,T\left( v \right) = 0\,w = {0_W}\]
Donde hemos expresado a \({0_V}\) como el producto del escalar \(0\) por cualquier vector del espacio vectorial \(V\), hemos usado la segunda condición que debe cumplir una transformación lineal, y finalmente hemos vuelto a usar la propiedad de espacios vectoriales sobre el producto del escalar 0 por cualquier vector.
La imagen del vector \( -\, v\) es igual al opuesto de la imagen de \(v\):
\[T\left( { - \, v} \right) = - \; T\left( v \right)\]
\[T\left( { - v} \right) = T\left( { - 1\,v} \right) = - 1\,T\left( v \right) = - \, T\left( v \right)\]
La justificación de los pasos dados en la demostración es similar a la anterior.
Consideremos \(r\) vectores del espacio vectorial \(V\):
\[{v_1},{v_2}, \ldots ,{v_r} \in V\]
Tomemos una combinación lineal en el dominio:
\[{\alpha _1}{v_1} \, + \,{\alpha _2}{v_2} + \,{\alpha _3}{v_3} \,+ ..{\rm{\;}}.{\rm{\;}} + {\alpha _r}{v_r}\]
Donde \({\alpha _i} \in \mathbb{R}\).
Si aplicamos la transformación lineal \(F\) de \(V\) a \(W\), teniendo en cuenta las propiedades enunciadas en la definición, resulta:
\[ \small{F\left( {{\alpha _1}{v_1} + {\alpha _2}{v_2}\,\; + ...{\rm{\;}}.{\rm{\;}} + \; {\alpha _r}{v_r}} \right) = {\alpha _1}F\left( {{v_1}} \right) + {\alpha _2}F\left( {{v_2}} \right) + \ldots + {\alpha _r}F\left( {{v_r}} \right){\rm{\;}}}\]
Es decir que una transformación lineal «transporta» combinaciones lineales de \(V\) a \(W\), conservando los escalares de la combinación lineal.
Ejemplo 1
Analizar si la siguiente función es una transformación lineal:
\[T:\mathbb{R}^3\to \mathbb{R}^2/ \: T\left ( \underbrace{x,y,z}_{\in \; \mathbb{R}^3} \right )=\left ( \underbrace{x+z,y-2z}_{\in \;\mathbb{R}^2} \right )\]Resolución
Controlemos primero que el transformado del \({0_V}\) sea el \({0_W}\). Ésta es una condición necesaria: si no se cumpliera, no sería transformación lineal. Como \(T\left( {\left( {0,0,0} \right)} \right) = \left( {0,0} \right)\), la función dada es «candidata» a ser transformación lineal. Para demostrar que es una transformación lineal tenemos que comprobar las condiciones dadas en la definición.Veamos si \( \:\, T\left( {u + v} \right) = T\left( u \right) + T\left( v \right)\)
Primero hacemos la suma de \(u\) y \(v\):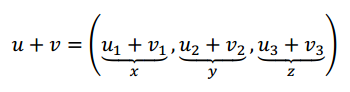
Y ahora aplicamos \(T\):
\[T\left( {u + v} \right) = \left( {{u_1} + {v_1} + {u_3} + {v_3}{\rm{\;}},{\rm{\;}}{u_2} + {v_2} - 2{u_3} - 2{v_3}} \right)\]
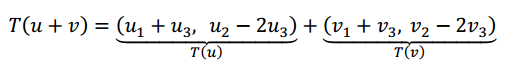
\[T\left( {u + v} \right) = T\left( u \right) + T\left( v \right)\]
En conclusión: se cumple la primera de las condiciones.
Nos faltaría la otra propiedad.
Condición 2: \(\;\;T\left( {k\,v} \right) = k\,T\left( v \right){\rm{\;\;\;}}\forall v \in V,{\rm{\;}}\forall k \in \mathbb{R}\)
\[T\left( {k\,v} \right) = T\left( {\left( {k{v_1},k{v_2},k{v_3}} \right)} \right) = \left( {k{v_1} + k{v_3},{\rm{\;}}k{v_2} - 2k{v_3}} \right)\]
\[ = k \, \left( {{v_1} + {v_3},{v_2} - 2{v_3}} \right) = k \, T\left( v \right)\]
Como \(T\) cumple las dos condiciones, es una transformación lineal.
Ejemplo 2
Analizar si la siguiente función es una transformación lineal:
\[F:{P_2} \to \mathbb{R}\;\;\;|\;\;F\left( p \right) = p\left( 0 \right)\]
Observación: con \({P_2}\) se designa al conjunto de todos los polinomios de grado menor o igual que dos, con el polinomio nulo.
Entonces a un polinomio \(p\) de grado menor o igual que dos, le aplicamos la función \(F\) y obtenemos un número real que proviene de evaluar el polinomio en \(x = 0\).
$$ p\in {P_2}\to p\left( 0 \right)\in \mathbb{R}$$ Por ejemplo evaluemos la transformación en \({x^2} - 1\):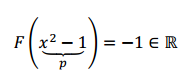
Veamos si el vector nulo del espacio vectorial \({P_2}\) va al \(0 \in \mathbb{R}\) (es condición necesaria).
El polinomio cero es:
\[{0_{{P_2}}} = {\rm{\;}}0{x^2} + 0x + 0\]
¿Cuánto vale el polinomio nulo evaluado en \(0\,\)? \(\,0\)
\[{0_{{P_2}}}\left( 0 \right) = {0 \; 0^2} + 0 \; 0 + 0 = 0\]
Entonces la condición necesaria para este ejercicio se cumple, porque \(F\left( {{0_{{P_2}}}} \right) = 0\)
Primera condición \(\;F\left( {u + v} \right) = F\left( u \right) + F\left( v \right){\rm{\;\;}}\forall u,v \in V\)
Para que sea transformación lineal se debe cumplir la primera condición. Veamos qué pasa con el transformado de la suma:
\[\left( {p + q} \right) \in {P_2}\]
\[F\left( {p + q} \right) = \left( {p + q} \right)\left( 0 \right) = p\left( 0 \right) + q\left( 0 \right)\]
Observación: evaluar una suma de funciones en \(0\), es evaluar cada una en \(0\) y sumarlas. Esto no es una particularidad de los polinomios, sino que se corresponde con la definición de suma de funciones:
Para cualquier función: \(\left( {f\; + \;g} \right)\;\left( x \right)\; = \;f\left( x \right)\; + \;g\left( x \right)\), para todo \(x\) perteneciente al dominio de \(f\) y de \(g\).
Otra forma de pensar la misma propiedad. Si consideramos
\(p\left( x \right) = a{x^2} + bx + c\) y \(q\left( x \right) = d{x^2} + ex + f\)
\[p{\rm{\;}} + {\rm{\;}}q{\rm{\;}} = {\rm{\;}}\left( {a + d} \right){x^2}{\rm{\;}} + {\rm{\;}}\left( {b + e} \right){\rm{\;}}x{\rm{\;}} + {\rm{\;}}\left( {c + f} \right)\]
\[F\left( {p + q} \right){\rm{\;}} = {\rm{\;}}c{\rm{\;}} + {\rm{\;}}f{\rm{\;}} = {\rm{\;}}F\left( p \right){\rm{\;}} + {\rm{\;}}F\left( q \right)\]
Por los dos caminos arribamos a la misma conclusión.
Segunda condición \(F\left( {k \, v} \right) = k \, F\left( v \right){\rm{\;\;\;}}\forall v \in V,{\rm{\;}}\forall k \in \mathbb{R}\)
Veamos si se cumple la segunda condición. Para esto podemos recordar que dada una función \(f\left( x \right)\) y un escalar \(k\), la función \(\left( {kf} \right)\left( x \right)\) se define como \(k \, f\left( x \right)\). De esta forma podemos decir:
Otra forma de verlo es escribir a un polinomio \(p \in {P_2}\) de forma genérica y aplicar la transformación sobre \(k\,p\,\):
\[p\left( x \right) = a{x^2} + bx + c\]
\[F\left( {k\,p} \right) = F\left( {k\left( {a{x^2} + bx + c} \right)} \right) = F\left( {ka{x^2} + kbx + kc} \right) \] $$ F\left( {k\,p} \right) = F\left( {k\,a\,{0^2} + k\,b\,0 + k\,c} \right)= kc = k\;F\left( p \right)$$Ejemplo 3
Consideremos la transformación lineal: \[T:{R^3} \to {R^3}{\rm{\;\;}},{\rm{\;\;\;}}T\left( v \right) = v \times {w_0}{\rm{\;}}\] Siendo \({w_0}\) un vector fijo y \(\;v\) un vector cualquiera de \({R^3}\). Veamos que se trata de una transformación lineal.Condición 1: \(\quad T\left( {u + v} \right) = T\left( u \right) + T\left( v \right){\rm{\;\;}}\forall u,v \in V\)
Para ver que se cumple esta condición usaremos la propiedad distributiva del producto vectorial respecto de la suma de vectores:
\[{v_1},{v_2} \in {R^3},{\rm{\;\;\;\;}}T\left( {{v_1} + {v_2}} \right) = \left( {{v_1} + {v_2}} \right) \times {w_0} =\] \[={v_1} \times {w_0} + {v_2} \times {w_0} = T\left( {{v_1}} \right) + T\left( {{v_2}} \right)\]
Condición 2: \(\quad T\left( {k\,v} \right) = k \, T\left( v \right){\rm{\;\;\;}}\forall v \in V,{\rm{\;}}\forall k \in \mathbb{R}\)
Para ver que se cumple esta condición podemos extraer el escalar:
\[T\left( {k\,v} \right) = \left( {kv} \right) \times {w_0} = k\,\left( {v \times {w_0}} \right) = k\,T\left( v \right)\]
Ejemplo 4
Consideremos las siguientes transformaciones:
\[{T_1}:{\mathbb{R}^2} \to {\mathbb{R}^2}{\rm{}},{\rm{\;\;\;}}{T_1}\left( {\left( {x,y} \right)} \right) = \left( {2x - 1,y} \right)\]
\[{T_2}:{\mathbb{R}^2} \to {\mathbb{R}^2}{\rm{}},{\rm{\;\;\;\;}}{T_2}\left( {\left( {a,b} \right)} \right) = \left( {{a^2},b} \right)\]
¿Cómo analizamos si son o no son transformaciones lineales?
Para la primera transformación basta con ver que la imagen de \(\left( {0,0} \right)\) es \(\left( { – 1,0} \right)\). No se cumple una de las propiedades de las transformaciones lineales, entonces no es una transformación lineal. La segunda transformación no cumple con la segunda condición ya que:
Luego, como no se cumple que \(T\left( {k\,v} \right) = k\,T\left( v \right)\) podemos afirmar que \({T_2}\,\) no es una transformación lineal.
Sea \(F:V \to W\;\) una transformación lineal. Llamamos núcleo de \(F\) al conjunto de vectores del dominio cuya imagen por \(F\) es el \(0_{W}\)
Llamamos imagen de \(F\) al conjunto de vectores de \(W\) que son imagen de algún vector de \(V\).

El teorema de las dimensiones establece una relación aritmética sencilla entre la dimensión de \(V\) y la dimensión del núcleo y de la imagen.
Sea \(F:V \to W \,\)una transformación lineal\(.\)
Si \(dim\left( V \right) = n\) (finita) entonces:

Sea \(F:V \to W \;\) una transformación lineal, y \(B = \left\{ {{v_1}, \ldots ,{v_n}} \right\}\) una base de\(\;V.\;\) Entonces: \[w \in Im\left( F \right) \Leftrightarrow {\rm{\;}}w = F\left( v \right),{\rm{\;}}v \in V \Leftrightarrow {\rm{\;}}w = F\left( {{a_1}{v_1} + \ldots + {\alpha _n}{v_n}{\rm{\;}}} \right)\] \[ \Leftrightarrow {\rm{\;}}w = {\alpha _1}F\left( {{v_1}} \right) + \ldots + {\alpha _n}F\left( {{v_n}} \right){\rm{\;}}\]
Hemos demostrado que:
O sea, aplicando la transformación lineal a los vectores de una base (cualquiera) del dominio, se obtiene un conjunto de generadores de la imagen: \[\left\{ {F\left( {{v_1}} \right),F\left( {{v_2}} \right),F\left( {{v_3}} \right), \ldots ,F\left( {{v_n}} \right)} \right\}{\rm{\;}}generan{\rm{\;}}Im\left( F \right)\] No estamos diciendo que constituyan una base de la imagen, sino que la generan. Veremos dos ejemplos sobre cómo se aplica esto:

En el último ejemplo resuelto de la página anterior nos preguntábamos si se podría haber pensado geométricamente. ¿Cuál es el conjunto de vectores que se obtiene al hacer el producto vectorial de cualquier vector \(v \in {\mathbb{R}^3}\) con \(\left( {0,0,1} \right)\)? ¿Cómo generalizaríamos para un \({w_0}\) cualquiera, no nulo?
En el siguiente applet de GeoGebra se puede explorar la situación. Hay tres vectores:
Te proponemos que muevas el vector verde y veas que se va obteniendo cómo el conjunto de vectores que se obtienen de los sucesivos productos vectoriales:
Recordemos que una función \(F:A \to B\;\) es inyectiva si verifica la siguiente propiedad: \[F\left( {{x_1}} \right) = {\rm{\;}}F\left( {{x_2}} \right) \Rightarrow {x_1} = {x_2}{\rm{\;\;\;}}\forall {x_1},{x_2} \in A\] En el caso particular de las T.L., puede demostrarse que:
Sea \(F:\;V \to \;W\) una transformación lineal,
Consideremos la siguiente transformación lineal \[T:{\mathbb{R}^2} \to {\mathbb{R}^3}/\;\;T\left( {\left( {x,y} \right)} \right) = \left( {x + y,\;x - y,\;2x} \right)\] Saquemos el núcleo de la transformación: \[\left( {x,y} \right) \in Nu\left( T \right) \Leftrightarrow T\left( {\left( {x,y} \right)} \right) = \left( {0,0,0} \right)\] \[\left( {x + y,\;x - y,\;2x} \right) = \left( {0,0,0} \right){\rm{\;\;}} \Rightarrow {\rm{\;\;}}x = 0 \wedge y = 0\] Entonces por la propiedad enunciada anteriormente podemos decir que \(T\) es un monomorfismo. Por el teorema de las dimensiones resulta: \[\dim \left( {Im} \right) = \dim \left( {{\mathbb{R}^2}} \right) - \dim \left( {Nu} \right) = 2 - 0 = 2\] Como la dimensión de la imagen es 2, entonces no es un epimorfismo (sobreyectiva). Conclusión: \(T\) es un monomorfismo.
Consideremos la transformación lineal \[F:{\mathbb{R}^{2 \times 2}} \to {\mathbb{R}^2}{\rm{\;}}/{\rm{\;\;}}F\left( {\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)} \right) = \left( {a + b, - d} \right)\] Busquemos su imagen:
Consideremos la siguiente transformación lineal \[G:{\mathbb{R}^2} \to {P_1}\;/{\rm{\;\;}}G\left( {\left( {a,b} \right)} \right) = 2a - bx\] Busquemos su núcleo: \[2a - bx = 0 + 0.x{\rm{\;}} \Rightarrow a = 0{\rm{\;}} \wedge {\rm{\;}}b = 0 \Rightarrow Nu\left( G \right) = \left\{ {\left( {0,0} \right)} \right\} \Rightarrow\] \[ \Rightarrow \dim \left( {Nu\left( F \right)} \right) = 0\] Por la propiedad enunciada anteriormente, podemos afirmar que \(G\) es un monomorfismo.
Veamos cuál es la imagen: \[2a.\left( 1 \right) + b.\left( { - x} \right){\rm{\;}} \Rightarrow Im\left( G \right) = gen\left\{ {1, - x} \right\} \Rightarrow \dim \left( {Im\left( G \right)} \right) = 2\] Por lo tanto la imagen es \({P_1}\) y la transformación es un epimorfismo (sobreyectiva).
Como es monomorfismo y epimorfismo, entonces es un isomorfismo.
¿Habrá alguna TL que no sea ni monomorfismo, ni epimorfismo? ¿Que no sea ni inyectiva ni sobreyectiva? Consideremos la siguiente TL que analizamos en el ejemplo 2 de "Imagen de una TL": \[F:{\mathbb{R}^3} \to {\mathbb{R}^{2 \times 2}}\;/{\rm{\;\;}}F\left( {\left( {x,y,z} \right)} \right) = \left( {\begin{array}{*{20}{c}}{x + y}&{x - z}\\0&{y + z}\end{array}} \right)\] Vimos que \({B_{Nu}} = \left\{ {\left( {1, - 1,1} \right)} \right\}\), así que no es un monomorfismo.
Vimos que \({B_{Im}} = \left\{ {\left( {\begin{array}{*{20}{c}}1&1\\0&0\end{array}} \right),\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)} \right\}\), así que no es un epimorfismo.
Conclusión: existen TL que no son ni monomorfismos ni epimorfismos.
Sea \(F:\;V \to W\) una TL., \(\;dim\left( V \right) = \;dim\left( W \right) = \;n\)
Puede afirmarse que:
Sugerimos al lector demostrar esta propiedad, teniendo en cuenta que:
\(F\) es inyectiva \( \Leftrightarrow \) \(Nu\left( F \right) = \left\{ {{0_V}} \right\}{\rm{\;}}\) \( \Leftrightarrow {\rm{\;\;}}dim\left( {Nu} \right){\rm{\;}} = {\rm{\;}}0\)
Dada la TL \[T:{\mathbb{R}^3} \to {\mathbb{R}^3}/\;\; T\left( {x,y,z} \right) = \left( {x + y + z\;,\;\;2y + z,\;\;3y + kz} \right)\] encontrar todos los valores de \(k\) para los cuales \(T\) es biyectiva (isomorfismo).
Como la TL va de \({\mathbb{R}^3}\) a \({\mathbb{R}^3},\,\) es suficiente analizar para qué valores de \(k\,\) es inyectiva (o sobreyectiva).
Por inyectividad:
Si pensamos en la inyectividad, tenemos que buscar que el núcleo sea \(\left\{ {\left( {0,0,0} \right)} \right\}\). Es decir que el sistema \[\left\{ {\begin{array}{*{20}{c}}{x + y + z = 0}\\{2y + z = 0}\\{3y + kz = 0}\end{array}} \right.\] tiene que ser compatible determinado. Hemos visto que un sistema de ecuaciones \(A.X = b\) es compatible determinado \( \Leftrightarrow \) \(\det \left( A \right) \ne 0\), así que planteamos esta condición para hallar los valores de \(k\): \[\left| {\begin{array}{*{20}{c}}1&1&1\\0&2&1\\0&3&k\end{array}} \right| = 1.\left( {2k - 3} \right) \ne 0 \Rightarrow k \ne \frac{3}{2}\] Luego \(\;\forall k \in \mathbb{R},\;\;k \ne \dfrac{3}{2}\;\;\) la transformación lineal \(T\) es biyectiva.
Por sobreyectividad
Si pensamos en la sobreyectividad, tenemos que buscar que la dimensión de la imagen sea 3 (o sea que la imagen sea \({\mathbb{R}^3}\)). Recordemos que los transformados de una base del dominio generan la imagen: \[T\left( {1,0,0} \right){\rm{\;}} = \left( {1,0,0} \right)\] \[T\left( {0,1,0} \right){\rm{\;}} = \left( {1,2,3} \right)\] \[T\left( {0,0,1} \right){\rm{\;}} = \left( {1,1,k} \right)\]
Como queremos que sea sobreyectiva, los tres vectores que se obtuvieron deben generar todo \({\mathbb{R}^3}\), así que deben ser LI. Recordemos que: \[det\left( A \right) \ne 0 \Leftrightarrow rango\left( A \right) = n \Leftrightarrow las\;filas\;\left( {columnas} \right)de\;A\;son\;LI\] Apliquemos esta propiedad: \[\left| {\begin{array}{*{20}{c}}1&0&0\\1&2&3\\1&1&k\end{array}} \right| = 2k -3 \ne 0 \Rightarrow k \ne \frac{3}{2}\] Así que hemos llegado a la misma conclusión: si \(k \ne \frac{3}{2}\) la transformación lineal \(T\) es biyectiva.
Resumiendo: no es necesario analizar inyectividad y sobreyectividad separadamente, ya que una de ellas implica la otra y por lo tanto, que se cumpla una de ellas implica que la transformación lineal es biyectiva. Esto sólo ocurre cuando el dominio y el codominio tienen la misma dimensión.
Si las dimensiones del dominio y del codominio son distintas, ¿la TL puede ser biyectiva? Para responder, les sugerimos que consideren dos casos:
i) \(dim\left( V \right) > dim\left( W \right)\)
ii) \(dim\left( V \right) < dim\left( W \right)\)
Dada la transformación lineal \[T:{\mathbb{R}^3} \to {\mathbb{R}^3}/ \;T\left( {x,y,z} \right) = \left( {x + y + z,\;x + ky - z,\;3y - kz} \right)\] Hallar en cada caso los valores de \(k\) para los cuales:
a) \(T\) es biyectiva.
b) \(T\) no es biyectiva y \(\left( {0,1, - 1} \right)\) pertenece a la imagen de \(T\).

Consideremos el siguiente triángulo en \({\mathbb{R}^2}\):
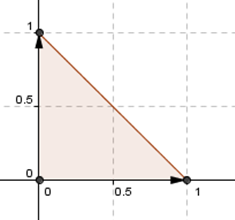
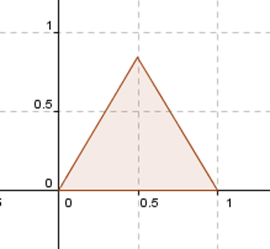
¿Existirá alguna transformación lineal que permita modificar de cierta manera este triángulo? Por ejemplo, una \(F\) que transforme el triángulo dado en este otro:
O alguna que lo transforme así:
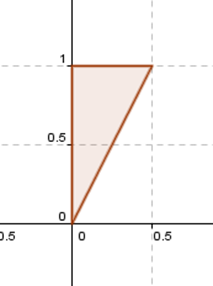
O un movimiento como éste:
El triángulo 4 no contiene al (0,0), por lo tanto no puede obtenerse aplicando una transformación lineal al triángulo 1.
¿Por qué?
¿Los otros podrán obtenerse mediante una transformación lineal? ¿Existe alguna herramienta teórica que permita asegurarlo?
Sí, es el teorema fundamental de las transformaciones lineales.
Este teorema, conocido también como "Teorema de existencia y unicidad de una transformación lineal", dice lo siguiente:
Para demostrarlo habría que demostrar que esa transformación existe, que es única, y que es lineal. Una demostración se puede encontrar en el texto recomendado de Ana María Kozak y otros autores, Nociones de Geometría Analítica y Algebra Lineal. Se puede hallar en página 561 y siguientes.
Sean \(V = {\mathbb{R}^2}\;\) y \(W = {\mathbb{R}^3}\).
Consideremos la base \(B = \left\{ {\left( {1,0} \right),\left( {1,1} \right)} \right\}\), y sean
\({w_1} = {w_2} = \left( {0,1,0} \right).\) De acuerdo con el teorema, existe una única transformación lineal \(T:{\mathbb{R}^2} \to {\mathbb{R}^3}\;\) que verifica: \[T\left( {\left( {1,0} \right)} \right) = \left( {0,1,0} \right)\] \[T\left( {\left( {1,1} \right)} \right) = \left( {0,1,0} \right)\] ¿Cómo buscamos la fórmula de la transformación lineal? Tomamos un vector genérico de \({\mathbb{R}^2}\) y lo escribimos como combinación lineal de la base, o sea buscamos sus coordenadas respecto de B: \[\left( {x,y} \right) = \alpha \left( {1,0} \right) + \beta \left( {1,1} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = \alpha + \beta }\\{y = \beta }\end{array}} \right. \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{\alpha = x - y}\\{\beta = y}\end{array}} \right.\] Los escalares \(\alpha ,\beta \) son las cordenadas del vector \(\left( {x,y} \right)\) en la base \(B\):\[{\left[ {\left( {x,y} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}{x - y}\\y\end{array}} \right)\] Donde recordemos que la escritura \({\left[ {\left( {x,y} \right)} \right]_B}\) significa "las coordenadas del vector \(\left( {x,y} \right)\) en la base \(B\;\)".
\[\left( {x,y} \right) = \alpha \left( {1,0} \right) + \beta \left( {1,1} \right)\]
Vamos a ver si podemos transformar el triángulo del esquema de la izquierda, en el triángulo del esquema que está a la derecha:
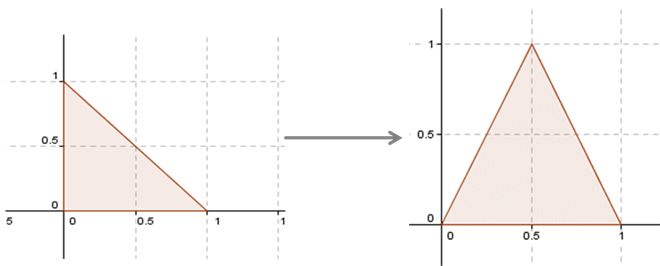
Nosotros tenemos que dar una base de \({\mathbb{R}^2}\) y asignarle sus transformados.
Por ejemplo consideremos los versores canónicos que definen al primer triángulo:
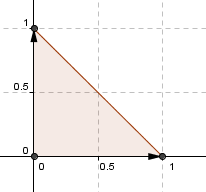
Entonces podríamos hacer la siguiente asignación:
\[F\left( {\left( {1,0} \right){\rm{\;}}} \right) = \left( {1;0} \right)\] \[F\left( {\left( {0,1} \right){\rm{\;}}} \right) = \left( {\frac{1}{2};1} \right)\]
Como \(\left( {1,0} \right),\;\left( {0,1} \right)\) constituyen una base del dominio, el teorema fundamental permite afirmar que existe una única transformación lineal que verifica esto:
 Para encontrar la fórmula de esta trasformación vamos a escribir a un vector genérico de \({\mathbb{R}^2}\) como combinación lineal de los vectores de la base dada: \[\left( {x,y} \right) = \alpha \left( {1,0} \right) + \beta \left( {0,1} \right) \; \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{x = \alpha }\\{y = \beta }\end{array}} \right.\;\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{\alpha = x}\\{\beta = y}\end{array}} \right.\]
Ahora aplicamos la transformación lineal sobre ese vector genérico, y resolvemos para llegar a una expresión analítica de la transformación lineal: \[F\left( {\left( {x,y} \right)} \right) = F\left( {\alpha \left( {1,0} \right) + \beta \left( {0,1} \right)} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \alpha \,F\left( {\left( {1,0} \right)} \right) + \beta \,F\left( {\left( {0,1} \right)} \right)\] \[F\left( {\left( {x,y} \right)} \right) = x\left( {1,0} \right) + y\left( {\frac{1}{2};\;1} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {x,0} \right) + \left( {\frac{1}{2}y;\;y} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {\frac{1}{2}y + x;\;y} \right)\]
Para encontrar la fórmula de esta trasformación vamos a escribir a un vector genérico de \({\mathbb{R}^2}\) como combinación lineal de los vectores de la base dada: \[\left( {x,y} \right) = \alpha \left( {1,0} \right) + \beta \left( {0,1} \right) \; \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{x = \alpha }\\{y = \beta }\end{array}} \right.\;\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{\alpha = x}\\{\beta = y}\end{array}} \right.\]
Ahora aplicamos la transformación lineal sobre ese vector genérico, y resolvemos para llegar a una expresión analítica de la transformación lineal: \[F\left( {\left( {x,y} \right)} \right) = F\left( {\alpha \left( {1,0} \right) + \beta \left( {0,1} \right)} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \alpha \,F\left( {\left( {1,0} \right)} \right) + \beta \,F\left( {\left( {0,1} \right)} \right)\] \[F\left( {\left( {x,y} \right)} \right) = x\left( {1,0} \right) + y\left( {\frac{1}{2};\;1} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {x,0} \right) + \left( {\frac{1}{2}y;\;y} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {\frac{1}{2}y + x;\;y} \right)\]
Hallar la expresión analítica de cada una de las siguientes transformaciones de \( \mathbb{R}^2 \to \mathbb{R}^2 \):
a) Simetría respecto de la recta \(y = 3x\)
La clave para resolver este ejercicio es elegir una base conveniente para definir la simetría. Grafiquemos la recta \(y = 3x\):
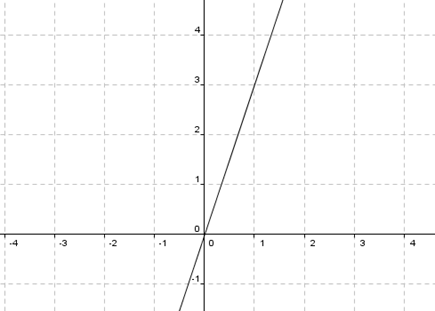
Primero hay que entender qué significa una reflexión respecto de una recta. Supongamos que nos piden una simetría respecto del eje \(x\).
Si tenemos un cuadrado así como el rojo, se transforma en un cuadrado como el violeta:
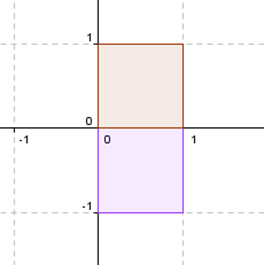
Todos los puntos que pertenecen al eje \(x\) quedan idénticos. Y los puntos que están sobre el eje \(y\) se transforman en su opuesto. Entonces: \[\left\{ {\begin{array}{*{20}{c}}{F\left( {\left( {1,0} \right)} \right) = \left( {1,0} \right)}\\{F\left( {\left( {0,1} \right)} \right) = \left( {0, - 1} \right)}\end{array}} \right.\] Considerando estas ideas sobre simetría, en nuestro caso tomamos un vector que esté sobre el eje de simetría y otro perpendicular a él:
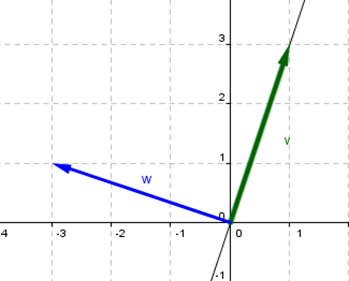
\[v = \left( {1,3} \right){\rm{\;}},{\rm{\;}}w = \left( { - 3,1} \right)\] ¿Cuál es el transformado del vector \(\left( {1,3} \right)\) que está sobre el eje de simetría? ¿Cuál es el transformado del vector \(\left( { - 3,1} \right)\) que es perpendicular al eje de simetría? Entonces: \[\left\{ {\begin{array}{*{20}{c}}{F\left( {\left( {1,3} \right)} \right) = \left( {1,3} \right)\;\;porque\;está \;sobre\;el\;eje\;de\;simetría}\\{F\left( {\left( { - 3,1} \right)} \right) = \left( {3, - 1} \right)\;\;porque\;es\;perpendicular\;al\;eje\;de\;simetría}\end{array}} \right.\]
Ahora queda el problema técnico de buscar la fórmula de esta transformación lineal: \[(x,y) = \alpha (1,3) + \beta (- 3,1) \Rightarrow \left\{\begin{matrix} x = \alpha - 3\beta\\y = 3\alpha + \beta \end{matrix}\right.\] \[\Rightarrow \beta = \frac{{y - 3x}}{{10}} \wedge \; \alpha = \frac{{x + 3y}}{{10}} \]
Podemos ver en GeoGebra cómo opera la transformación:
El propósito de este ejercicio es destacar cuándo es posible aplicar el teorema fundamental de las transformaciones lineales. Sugerimos una lectura cuidadosa de cada uno de los casos presentados a continuación:
Analizar si existe y es única la transformación lineal \(T:{\mathbb{R}^3} \to {\mathbb{R}^3}\) que verifica:
Caso A \[\left\{ {\begin{array}{*{20}{c}}{T\left( {\left( {1,0,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {0,1,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {1,1,1} \right)} \right) = \left( {0,0,0} \right)}\end{array}} \right.\]
Caso B \[\left\{ {\begin{array}{*{20}{c}}{T\left( {\left( {1,0,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {0,1,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {1, - 1,0} \right)} \right) = \left( {1,0,0} \right)}\end{array}} \right.\]
Caso C \[\left\{ {\begin{array}{*{20}{c}}{T\left( {\left( {1,0,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {0,1,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {1, - 1,0} \right)} \right) = \left( {0,0,0} \right)}\end{array}} \right.\]
¿Cuál es la hipótesis del teorema? O sea, ¿qué debe cumplirse para que el teorema tenga validez?
Los vectores del dominio deben ser una base, es decir que debemos prestar atención en cada caso a los vectores señalados:
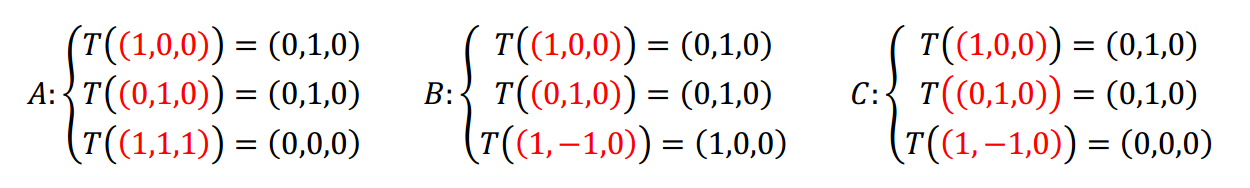
Caso A
En el caso A los tres vectores son base de \({\mathbb{R}^3}\;\) y entonces podemos aplicar el Teorema Fundamental de las Transformaciones Lineales. Como lo establece el teorema, se puede afirmar que existe una única transformación lineal que verifica las condiciones dadas. ¿Cuál es el mecanismo para buscar la fórmula? Consideramos un vector \(\left( {x,y,z} \right)\) y buscamos sus coordenadas respecto de la base de partida: \[\left( {x.y,z} \right) = \alpha \left( {1,0,0} \right) + \beta \left( {0,1,0} \right) + \gamma \left( {1,1,1} \right)\] \[\left\{ {\begin{array}{*{20}{c}}{x = \alpha + \gamma }\\{y = \beta + \gamma }\\{z = \gamma }\end{array}} \right.{\rm{\;\;}} \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{\alpha = x - z}\\{\beta = y - z}\\{\gamma = z}\end{array}} \right.\] Aplicamos la transformación lineal a ambos miembros: \[T\left( {\left( {x,y,z} \right)} \right) = \alpha\, T\left( {\left( {1,0,0} \right)} \right) + \beta\, T\left( {\left( {0,1,0} \right)} \right) + \gamma\, T\left( {\left( {1,1,1} \right)} \right)\]
Caso B
En el caso B, el conjunto de vectores de partida es linealmente dependiente, no es base de \({\mathbb{R}^3}\). Si no se cumplen las hipótesis de un teorema, éste no puede aplicarse. ¿Cómo podemos determinar si existe una transformación lineal que verifique estas condiciones?
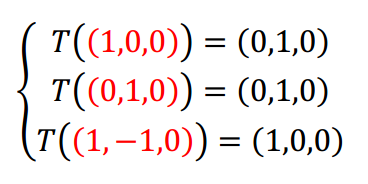
Lo que define a una transformación lineal es la conservación de las combinaciones lineales. ¡Esto es lo que debemos controlar! Veamos la diferencia entre el caso B y el C: Observamos que el tercer vector se puede obtener como combinación lineal de los primeros dos: \[\left( {1, - 1,0} \right) = \left( {1,0,0} \right) -\left( {0,1,0} \right)\] Entonces entre sus transformados debería cumplirse la misma relación:
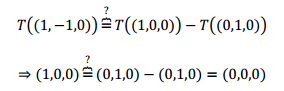
No se conserva la combinación lineal, entonces no existe una transformación lineal que cumpla las condiciones dadas.
Caso C
En el caso C tenemos la siguiente información: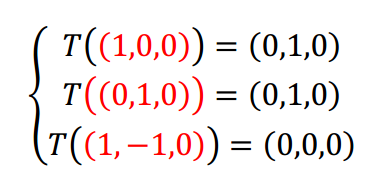
Tampoco se puede aplicar el TFTL, porque el conjunto de vectores de partida es linealmente dependiente. Igualmente podemos preguntarnos: ¿Se conserva la combinación lineal? Notemos que el tercer vector es la diferencia del primero con el segundo: \[\left( {1, - 1,0} \right) = \left( {1,0,0} \right) - \left( {0,1,0} \right)\] Aplicamos la transformación lineal suponiendo que se conservan las combinaciones lineales:
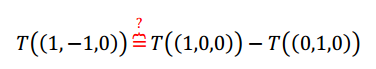 Reemplazando:
Reemplazando:
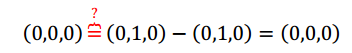
Lo cual es verdadero. Entonces podemos concluir que existe la transformación lineal aunque no quede unívocamente determinada por la información disponible. Para definir una TL bastaría con establecer cuáll es el transformado de un tercer vector LI con \(\left( {1,0,0} \right)\) y \(\left( {0,1,0} \right)\). Agreguemos un dato nuevo para que quede bien definida: \[T\left( {\left( {0,0,1} \right)} \right) = \left( {0,0,1} \right)\] ¿Existe una TL que cumpla con las condiciones iniciales más ésta que acabamos de agregar? Llamemos: \[\left\{ {\begin{array}{*{20}{c}}{{T_1}\left( {\left( {1,0,0} \right)} \right) = \left( {0,1,0} \right)}\\{{T_1}\left( {\left( {0,1,0} \right)} \right) = \left( {0,1,0} \right)}\\{{T_1}\left( {\left( {0,0,1} \right)} \right) = \left( {0,0,1} \right)}\end{array}} \right.\] Ahora \({T_1}\) queda bien definida y podríamos hallar su fórmula. ¿Cómo podrían definir una transformación \({T_2}\) distinta de \({T_1}\) que también cumpla con las condiciones iniciales? Resumamos lo que obtuvimos analizando estos tres casos:
Halle la expresión analítica de cada una de las siguientes transformaciones de \({\mathbb{R}^3} \to {\mathbb{R}^3}\):
a) Reflexión respecto del plano \(x = y\)
Este ejercicio requiere elegir una buena base. Una gráfica del plano \(x = y\;\) se puede ver a continuación:
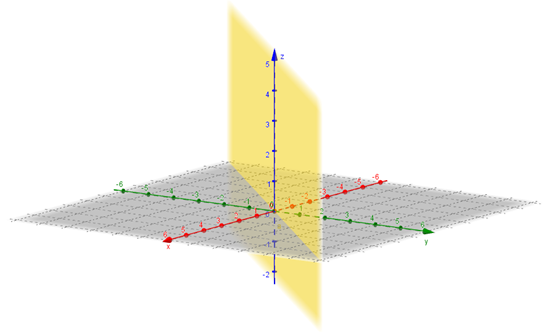
El arte para resolver este ejercicio es elegir tres vectores linealmente independientes que sepamos en qué se transforman.
¿Cuál es el simétrico de un vector que esté sobre el plano? El mismo vector. Entonces podemos elegir dos vectores no paralelos incluidos en el plano: \[T\left( {{v_1}} \right) = {v_1}\] \[T\left( {{v_2}} \right) = {v_2}\] ¿Y si tomamos un vector perpendicular al plano, digamos \({v_3}\), en que se transforma? \[T\left( {{v_3}} \right) = - {v_3}\] Ahora debemos elegir \({v_1}\), \({v_2}\) y \({v_3}\) de acuerdo con el plano dado. Proponemos: \[{v_1} = \left( {1,1,0} \right)\] \[{v_2} = \left( {0,0,1} \right)\] \[{v_3} = \left( {1, - 1,0} \right)\] Donde los vectores \({v_1}\) y \({v_2}\) están en el plano y el vector \({v_3}\) es perpendicular al plano. De esta forma sabemos cómo se transforman: \[\left\{ {\begin{array}{*{20}{c}}{T\left( {\left( {1,1,0} \right)} \right) = \left( {1,1,0} \right)}\\{T\left( {\left( {0,0,1} \right)} \right) = \left( {0,0,1} \right)}\\{T\left( {\left( {1, - 1,0} \right)} \right) = \left( { - 1,1,0} \right)}\end{array}} \right.\] Ya queda definida la transformación lineal sobre una base del dominio. Dejamos a cargo del lector encontrar la fórmula de la TL.
Les proponemos que definan la TL sobre otra base con las mismas características: dos vectores del plano y uno perpendicular a él. Luego busquen la expresión analítica, ¿coincide con la anterior? Los vectores no son únicos: \({v_1}\) y \({v_2}\) son dos vectores cualesquiera (LI) del plano y \({v_3}\) es un vector perpendicular cualquiera. No importa cuáles elijamos, obtendremos la misma transformación lineal.
Definir una transformación lineal \(F\) de \({\mathbb{R}^3} \to {\mathbb{R}^{2 \times 2}}\) que verifique las dos condiciones que siguen:
i) \(Nu\left( F \right)\; = \;gen\;\left\{ {\left( {1,1,0} \right)} \right\}\)
ii) \(Im\left( F \right) \subseteq \;S = \left\{ {A \in {\mathbb{R}^{2×2}}\;/\;\;A = {A^t}\;} \right\}\)
Obtener la fórmula de la transformación definida.
Observación: este ejercicio no es de respuesta única.

Sea \(T\;\) la siguiente transformación lineal: \[T:{\mathbb{R}^2} \to {\mathbb{R}^3}{\rm{\;}}|{\rm{\;\;}}T\left( {\left( {x,y} \right)} \right) = \left( {x + 2y,\;x - y,\;y} \right)\] ¿Existirá una matriz \(A\) que multiplicada por \(\left( {x,y} \right)\) dé por resultado \(\left( {x + 2y,\;x - y,\;y} \right)\)? Para esto vamos a escribir los vectores como columna: \[A.\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{x + 2y}\\{\begin{array}{*{20}{c}}{x - y}\\y\end{array}}\end{array}} \right)\]
¿Cuál debería ser el tamaño de la matriz?
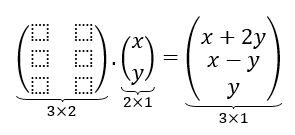 Efectuando el producto de matrices, podemos obtener los coeficientes de \(A\) :
Efectuando el producto de matrices, podemos obtener los coeficientes de \(A\) :
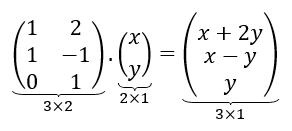
Encontramos una matriz que realiza la transformación lineal. Se conoce como la matriz estándar de la transformación lineal.
Notemos que la transformación va de \({\mathbb{R}^2}\) a \({\mathbb{R}^3}\), y que el orden de la matriz es \(3 \times 2\).
Ahora consideremos la siguiente transformación lineal:
\[F:{\mathbb{R}^3} \to {\mathbb{R}^2}{\rm{\;}}|{\rm{\;}}F\left( {\left( {x,y,z} \right)} \right) = \left( {x + 2z, - y} \right)\]
Queremos buscar una matriz \(B\) tal que:
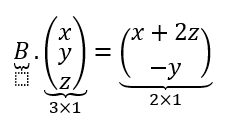
Pensando el orden de la matriz y el valor de sus elementos llegamos a:
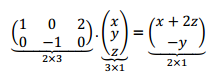
Hemos hallado de manera intuitiva la matriz estándar de la transformación lineal. Notemos que la transformación va de \({\mathbb{R}^3}\) a \({\mathbb{R}^2}\) y que el orden de la matriz asociada a la transformación lineal es \(2 \times 3\).
Hemos visto ejemplos de cómo surge a partir del producto de matrices, la matriz estándar de una transformación lineal de \({\mathbb{R}^n}\) a \({\mathbb{R}^m}\). En lo que sigue intentaremos generalizar para cualquier espacio vectorial de dimensión finita, el concepto de matriz asociada a una transformación lineal. Aunque en el caso de TL en \({\mathbb{R}^n}\), veremos que no siempre la matriz estándar es la más conveniente para trabajar.
Sea \(T:V \to W\;\) transformación lineal, y
\[\operatorname{dim}(V) = n, \quad\;\;\; \operatorname{dim}(W) = m\] \[B = \left\{ {{v_1},{v_2}, \ldots ,{v_n}} \right\}{\rm{\;}}base{\rm{\;}}de{\rm{\;}}V\] \[B\,' = \left\{ {{w_1}, \ldots ,{w_m}} \right\}{\rm{\;}}base{\rm{\;}}de{\rm{\;}}W\]
Designamos:
\(M{\left( T \right)_{BB\,'}}\) a la matriz asociada a la transformación lineal \(T\) respecto de las bases \(B\) y \(B\,'\).
Esta matriz se construye por columnas transformando los vectores de la base \(B\) (del dominio), y expresando los transformados en sus coordenadas en la base \(B\,'\):
La matriz asociada tiene \(n\) columnas porque la base \(B\) tiene \(n\) vectores, y tiene \(m\) filas porque las coordenadas en \(B\,'\) se escriben con \(m\) componentes.
O sea que si \(dim\left( V \right){\rm{\;}} = {\rm{\;}}n\) y \(dim\left( W \right){\rm{\;}} = {\rm{\;}}m,\;\) \(M{\left( T \right)_{BB\,'}} \in {\mathbb{R}^{m \times n}}\)
La matriz asociada a una transformación lineal cumple la siguiente propiedad:
Retomemos la transformación lineal:
\[T:{\mathbb{R}^2} \to {\mathbb{R}^3}{\rm{\;}}|{\rm{\;\;}}T\left( {\left( {x,y} \right)} \right) = \left( {x + 2y,\;x - y,\;y} \right)\] Consideremos las siguientes bases para el dominio y codominio:
\[B = \left\{ {\left( {0,1} \right),\left( {1,1} \right)} \right\}{\rm{\;}}\] \[B\,' = \left\{ {\left( {1,0,0} \right),\left( {1,1,0} \right),\left( {0,1,1} \right)} \right\}\]
Construyamos la matriz asociada a la transformación \(T\) de la base \(B\) a la base \(B\,',\;\) es decir \(M{\left( T \right)_{BB\,'}}\;\):
Dado un vector cualquiera, aunque no conozcamos la fórmula, conociendo la matriz y las dos bases podemos calcular su transformado. Vamos a tomar un vector cualquiera de \({\mathbb{R}^2}\) y lo transformamos… sin mirar la fórmula. Hallemos \(T\left( {\left( {3,5} \right)} \right)\) mediante la matriz asociada \(M{\left( T \right)_{BB\;'}}\) : \[M{\left( T \right)_{BB\;'}}{\left[ v \right]_B} = {\left[ {T\left( v \right)} \right]_{B\;'}}\] No podemos operar con \(\left( {3,5} \right)\) porque la matriz asociada opera con coordenadas. Debemos buscar las coordenadas de \(\left( {3,5} \right)\) en la base \(B\). \[\left( {3,5} \right) = \alpha \left( {0,1} \right) + \beta \left( {1,1} \right) \Rightarrow \beta = 3{\rm{\;}},{\rm{\;}}\alpha = 2\]
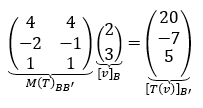
El vector obtenido no es el transformado del vector (3,5) sino que son sus coordenadas en la base \(B\;'\).
Para hallar \(T\left( {3,5} \right)\) debemos multiplicar las coordenadas obtenidas por los vectores de la base \(B\;'\):
\[T\left( {\left( {3,5} \right)} \right) = 20\left( {1,0,0} \right) - 7\left( {1,1,0} \right) + 5\left( {0,1,1} \right)\] \[T\left( {\left( {3,5} \right)} \right) = \left( {13, - 2,{\rm{\;}}5} \right)\]Ahora en lugar de tomar estas bases, tomemos las bases canónicas de \({\mathbb{R}^2}\;\) y de \({\mathbb{R}^3}\).
Busquemos \(M{\left( T \right)_{{E_2}{E_3}}}\) donde:
\[{E_2} = \left\{ {\left( {1,0} \right),\left( {0,1} \right)} \right\}{\rm{\;}}\] \[{E_3} = \left\{ {\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {0,0,1} \right)} \right\}{\rm{\;}}\]
El procedimiento es el mismo pero las cuentas son más fáciles
\[T\left( {\left( {1,0} \right)} \right) = \left( {1,1,0} \right) = \alpha \left( {1,0,0} \right) + \beta \,\left( {0,1,0} \right) + \gamma \, \left( {0,0,1} \right)\] \[ \Rightarrow {\rm{\;}}\left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1\\1\end{array}}\\0\end{array}} \right){\rm{\;}}1^\circ {\rm{\;}}columna\]Estos vectores hay que expresarlos en coordenadas respecto de la base canónica de \({\mathbb{R}^3}\), pero justamente por tratarse de la base canónica, el vector y sus coordenadas son iguales. Entonces resulta:
\[M(T)_{E_2E_3}=\begin{pmatrix} 1 & & 2 \\ 1 & & -1 \\ 0 & & 1 \end{pmatrix}=A\]¡Qué es la matriz estándar de la TL! Es decir que la matriz estándar es la que trabaja con las bases canónicas.
Consideremos la siguiente transformación lineal: \[F:{\mathbb{R}^2} \to {P_1}\;/\;\;M{\left( F \right)_{BB\;'}} = \left( {\begin{array}{*{20}{c}}1&2\\1&2\end{array}} \right)\] \[B = \left\{ {\left( {1,0} \right),\left( {1,1} \right)} \right\}\] \[B\;' = \left\{ {\color{blue}{1},{\rm{\;}}\color{blue}{1 - x}} \right\}\]
Ítem a
No tenemos la fórmula. Tenemos que trabajar con la matriz asociada. ¿Qué propiedad tiene la matriz asociada? \[M{\left( F \right)_{BB\,'}}\;{\left[ v \right]_B} = {\left[ {F\left( v \right)} \right]_{B\;'}}\]
Donde:
Las matrices asociadas no operan con los vectores, sino con las coordenadas de los vectores en alguna base. Entonces no podemos multiplicar la matriz por el vector \(\left( {2,1} \right)\).
Para operar, tenemos que encontrar las coordenadas de \(\left( {2,1} \right)\) en la base \(B\):
\[\left( {2,1} \right) = \alpha \left( {1,0} \right) + \beta \left( {1,1} \right){\rm{\;\;}} \Rightarrow {\rm{\;\;}}\alpha = 1 \wedge \beta = 1{\rm{\;\;}} \Rightarrow {\rm{\;\;}}{\left[ {\left( {2,1} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right)\]
Ahora multiplicamos por la matriz y obtenemos las coordenadas en \(B\,'\) del transformado de \(\left( {2,1} \right)\):
\[{\left[ {F\left( {\left( {2,1} \right)} \right)} \right]_{B\,'}} = \left( {\begin{array}{*{20}{c}}1&2\\1&2\end{array}} \right)\left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}\color{#F05}{3}\\\color{#F05}{3}\end{array}} \right)\]
¿Qué objeto esperamos obtener como imagen de esta transformación?
¿Un vector de \({\mathbb{R}^2}\)? No, esperamos obtener un polinomio de grado menor o igual que uno.
Para obtener \(F\left( {\left( {2,1} \right)} \right)\) debemos multiplicar estas coordenadas por los vectores de la base \(B\,'\):
\[F\left( {\left( {2,1} \right)} \right) = \textcolor{#F05}{3}.\textcolor{blue}{1} + \textcolor{#F05}{3}.\left( {\textcolor{blue}{1-x}} \right) = 6 - 3x\]
Ítem b
En el ítem (a) buscamos la imagen del vector \(\left( {2,1} \right)\). Ahora nos proponemos obtener la fórmula de la transformación, esto significa encontrar la imagen de cualquier vector \(\left( {x,\;y} \right)\) de \({\mathbb{R}^2}\). Teniendo en cuenta que en el polinomio usamos la variable \(x\), llamaremos \(\left( {a,b} \right)\) a los vectores de \({\mathbb{R}^2}\).
Busquemos \(F\left( {\left( {a,b} \right)} \right)\) tal como buscamos \(F\;\left( {\left( {2,1} \right)} \right)\): \[\left( {a,b} \right) = \alpha \left( {1,0} \right) + \beta \left( {1,1} \right) \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{a = \alpha + \beta }\\{b = \beta }\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\alpha = a - b}\\{\beta = b}\end{array}} \right.\] \[{\left[ {\left( {a,b} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}{a - b}\\b\end{array}} \right)\]
\[\left[F((a,b))\right]_{B^{\prime}}=\begin{pmatrix} 1 & 2 \\ 1 & 2 \\ \end{pmatrix}\begin{pmatrix} a-b \\ b \end{pmatrix}=\begin{pmatrix}{\color{#F05} a+b} \\ {\color{#F05} a+b} \end{pmatrix}\]Éstas son las coordenadas del vector que estamos buscando. Falta multiplicar por los vectores de la base B\,':
\[F\left( {\left( {a,b} \right)} \right) = \left( {\textcolor{#F05}{a + b}} \right) \,\textcolor{blue}{1} + \left( {\textcolor{#F05}{a + b}} \right)\left( {\textcolor{blue}{1-x}} \right) = 2a + 2b - \left( {a + b} \right).x\]
Ésta es la fórmula de la transformación lineal.
Ahora podemos hallar base y dimensión de núcleo e imagen.
Ítem c
La definición de núcleo dice que son los vectores del dominio que se transforman en el vector nulo del codominio.
\[ - \left( {a + b} \right)x + 2\left( {a + b} \right) = {0_{{P_1}}} = 0x + 0\] \[ \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{a + b = 0}\\{a + b = 0}\end{array} \;\;\Rightarrow \;\; a = - b} \right.\]
\[ \Rightarrow Nu(F) = \left\{ {({a, - a}) \in {\mathbb{R}^2}} \right\} \Rightarrow {B_{Nu}} = \left\{ {\begin{pmatrix} -1 \\ 1 \end{pmatrix}} \right\}\]
\[ \Rightarrow \dim ({Nu(F)}) = 1\]Ítem d
Por el teorema de las dimensiones:
\[\dim \left( {Im\left( F \right)} \right) = \dim \left( {{\mathbb{R}^2}} \right) - \dim \left( {Nu\left( F \right)} \right) = 1\]Queremos una base de la imagen. ¿En qué espacio vectorial está la imagen? En \(\,P_{\,1}\).
Recordemos que los transformados de una base (cualquiera) del dominio, generan la imagen de la transformación lineal: \[F\left( {\left( {1,0} \right)} \right) = 2 - x\] \[F\left( {\left( {0,1} \right)} \right) = 2 - x\]
Entonces ¿Cuál es una base de la imagen de la transformación lineal?
\[{B_{Im}} = \left\{ {2 - x} \right\}\]Veamos que la imagen no depende de la base del dominio que elijamos. Por ejemplo tomemos la base \(B\):
\[F\left( {\left( {1,0} \right)} \right) = 2 - x\] \[F\left( {\left( {1,1} \right)} \right) = 4 - 2x\]\(\left\{{2 - x\; , \; 4 - 2x} \right\}\) generan \(Im\left( F \right)\)
\[\Rightarrow\;\;{B_{Im}} = \left\{ {2 - x} \right\}\]Ítem e
No es necesario buscar la fórmula para obtener la imagen. Las columnas en la matriz nos dan las coordenadas en la base \(B\,'\) de los transformados de una base del dominio:
\[M{\left( F \right)_{BB\,'}} = \left( {{{\left[ {F\left( {{v_1}} \right)} \right]}_{B\,'}}{\rm{\;\;\;\;}}{{\left[ {F\left( {{v_2}} \right)} \right]}_{B\,'}}{\rm{\;}}} \right) = \left( {\begin{array}{*{20}{c}}1&2\\1&2\end{array}} \right)\]Entonces:
\[F\left( {\left( {1,0} \right)} \right) = 1\;\textcolor{blue}{1} + 1\;\left( {\textcolor{blue}{1 - x}} \right) = 2 - x\] \[F\left( {1,1} \right) = 2\;\textcolor{blue}{1} + 2\left( {\textcolor{blue}{1 - x}} \right) = 4 - 2x\]Luego:
\[Im\left( F \right) = gen\left\{ {2 - x{\rm{\;}},{\rm{\;}}4 - 2x} \right\}\]
Como \(4 - 2x\) es combinación lineal de \(2 - x\) podemos quedarnos con la siguiente base: \[{B_{Im\left( F \right)}} = \left\{ {2 - x} \right\}\]
Ítem f
¿Y para el núcleo sin la fórmula? Queremos hallar los \(v \in {\mathbb{R}^2}\) tales que al aplicarles la transformación den por resultado el polinomio nulo:
\[F\left( v \right) = {0_{{P_1}}}\]
Éstas son las coordenadas en la base \(B\) de una base del núcleo:
\[v=2 \, (1,0)-(1,1)=\underbrace{(1,-1)}_{B_{Nu}}\]Vamos a retomar el ejemplo 3, ítem a, de la página 40 que decía:
Hallar la expresión analítica de la siguiente transformación de \( \mathbb{R}^2 \to \mathbb{R}^2\;:\; \) Simetría respecto de la recta \(y = 3x\)
En ese ejemplo habíamos obtenido la fórmula de la transformación lineal:
\[T\left( {\left( {x,y} \right)} \right) = \left( { -\, \frac{4}{5}x + \frac{3}{5}y; \;\;\frac{3}{5}x + \frac{4}{5}y} \right)\]
La matriz estándar (referida a la base canónica de\({\;\mathbb{R}^2}\,\)), \(M{\left( T \right)_{EE}}\;\) es la siguiente:
\[M\left( T \right) = \left( {\begin{array}{*{20}{c}}{ - \dfrac{4}{5}}&{\dfrac{3}{5}}\\{\dfrac{3}{5}}&{\dfrac{4}{5}}\end{array}} \right)\]
Observación: cuando se trata de las bases canónicas para simplificar la notación se escribe \(M\left( T \right)\) en lugar de \(M{\left( T \right)_{EE}}\).
Veamos si podemos hallar una representación matricial más sencilla para esta simetría.
¿Qué significa una simetría respecto de la recta \(y = 3x\,\)? Recordemos que el transformado de un vector que esté sobre la recta es el mismo vector, y el transformado de un vector perpendicular a la recta es su opuesto.

Armemos una base de \({\mathbb{R}^2}\) formada por un vector \(\vec v\) sobre la recta \(y = 3x\) y un vector \(\vec w\) perpendicular a dicha recta. Por ejemplo:
¿Cuál es la matriz asociada a la transformación lineal en esta nueva base?
\[M{\left( T \right)_{BB}} = \left( {\begin{array}{*{20}{c}}1&0\\0&{ - 1}\end{array}} \right)\]
Eligiendo una base conveniente, pudimos caracterizar la simetría mediante una matriz diagonal. Continuaremos desarrollando este tema en el próximo capítulo (autovalores y autovectores).
Dada la transformación lineal \(F\) de \({\mathbb{R}^3}\) a \({P_1}\) cuya matriz asociada es:
\[M{\left( F \right)_{BE}} = \left( {\begin{array}{*{20}{c}}1&0&1\\{ - 1}&0&0\end{array}} \right)\]
siendo \(B = \left\{ {\left( {1,0,0} \right)\;,\;\left( {1,1,0} \right)\;,\;\left( {1,0,1} \right)} \right\}\) y \(E = \left\{ {1,\;x} \right\}\) bases de \({\mathbb{R}^3}\) y \({P_1}\) respectivamente.

Recordemos que:
Para obtener una base de \(Im\left( T \right)\) tenemos que determinar cuántos son LI. Se puede demostrar que en \(\left\{ {T\left( {{v_1}} \right), \ldots ,T\left( {{v_n}} \right)} \right\}\) habrá tantos vectores LI como columnas LI en la matriz. Dado que el rango de una matriz es el número de columnas LI, entonces el rango de la matriz asociada a la transformación lineal respecto de las bases \(B\) y \(B\,'\) es igual a la dimensión de la imagen de la trasformación lineal.
Observación: La dimensión de la imagen no depende de las bases elegidas, por esto el rango tampoco depende de ellas.
Sea \(T:{\mathbb{R}^2} \to {\mathbb{R}^3}\) una transformación lineal tal que su matriz estándar es: \(M\left( T \right) = \left( {\begin{array}{*{20}{c}}1&2\\1&a\\0&{ - 1}\end{array}} \right) \in {\mathbb{R}^{3 \times 2}}\)

Sean \(F\) y \(G\,\) dos transformaciones lineales tales que: \[F:U \to V;{\rm{\;\;\;\;\;}}G:V \to W\]
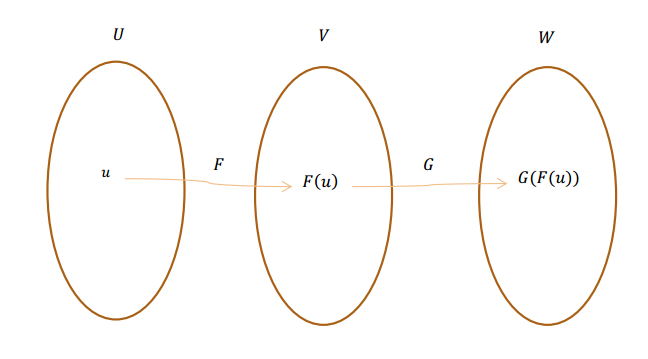
\[\exists \; GoF:U \to W{\rm{\;}}|{\rm{\;}} \left(GoF\right) \left( u \right) = G\left( {F\left( u \right)} \right){\rm{\;\;}}\forall u \in U\] Propiedad: la composición de transformaciones lineales, es una transformación lineal.
\[F:{\mathbb{R}^2} \to {\mathbb{R}^3}{\rm{\;}}|{\rm{\;}}F\left( {\left( {x,y} \right)} \right) = \left( {x - y,\;x + y,\;2x} \right)\] \[G:{\mathbb{R}^3} \to {\mathbb{R}^2}{\rm{\;}}|{\rm{\;}}G\left( {\left( {x,y,z} \right)} \right) = \left( {x - z,{\rm{\;}}y + z} \right)\]
Hallar la fórmula de \(GoF\) y \(Fo\,G\), indicando en cada caso dominio y codominio. \[GoF:{\mathbb{R}^2} \to {\mathbb{R}^2},{\rm{\;\;\;}}Go\,F\left( {\left( {x,y} \right)} \right) = G\left( {\left( {x - y,\;x + y,\;2x} \right)} \right)\] \[ = \left( {x - y - \left( {2x} \right){\rm{\;}},{\rm{\;\;\;}}x + y + 2x} \right) = \left( { - x - y,{\rm{\;}}3x + y} \right)\] \[Fo\,G:{\mathbb{R}^3} \to {\mathbb{R}^3},{\rm{\;}}Fo\,G\left( {\left( {x,y,z} \right)} \right) = F\left( {\left( {x - z,\; y + z} \right)} \right)\] \[ =\left(x - z - (y + z), \, x - z + (y + z),\, 2x - 2z \right)\; \Rightarrow\] \[\left(Fo\,G\right)(x,y,z) = ({x - y - 2z,\; x + y,\; 2x - 2z})\] ¿Con qué operación de matrices se relaciona la composición de transformaciones lineales?
Busquemos las matrices estándar: \[M\left( F \right) \in {\mathbb{R}^{3 \times 2}},{\rm{\;\;}}M\left( F \right) = \left( {\begin{array}{*{20}{c}}1&{ - 1}\\1&1\\2&0\end{array}} \right)\] \[M\left( G \right) \in {\mathbb{R}^{2 \times 3}},{\rm{\;\;\;\;\;}}M\left( G \right) = \left( {\begin{array}{*{20}{c}}1&0&{ - 1}\\0&1&1\end{array}} \right)\] Recuerden que cuando no colocamos subíndices, significa que es la matriz estándar, referida a las bases canónicas.
Calculemos los productos: \[M\left( F \right).M\left( G \right) = \left( {\begin{array}{*{20}{c}}1&{ - 1}\\1&1\\2&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&0&{ - 1}\\0&1&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&{ - 1}&{ - 2}\\1&1&0\\2&0&{ - 2}\end{array}} \right)\]Sean \(F\) y \(G\) dos transformaciones lineales tales que: \[F:U \to V;{\rm{\;\;\;\;\;}}G:V \to W\] Y sean \({B_1},{B_2},{B_3}\) bases de \(U,V\) y \(W\) respectivamente, entonces
se puede demostrar que:
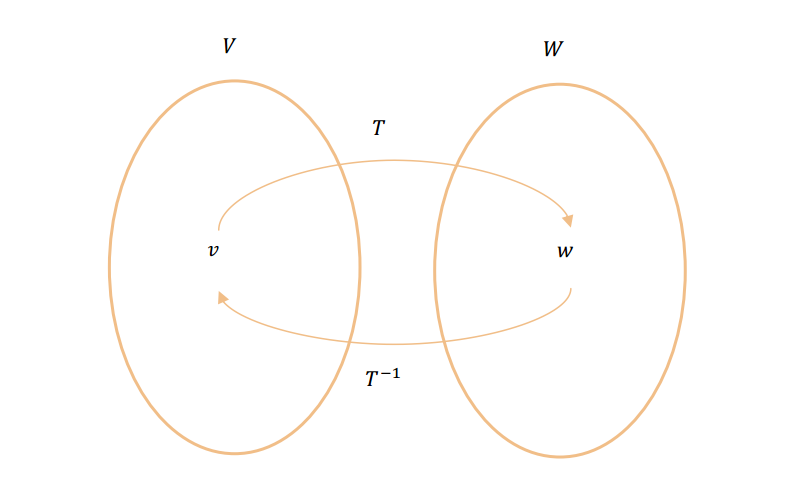
\({T^{ - 1}}\) también es una transformación lineal biyectiva: \[{T^{ - 1}}o\,T = I{d_V}\] \[To\,{T^{ - 1}} = I{d_w}\] Observación: Para que exista una transformación lineal biyectiva entre dos espacios vectoriales, éstos deben tener la misma dimensión. ¿Por qué?
Sea la transformación lineal \(T:{\mathbb{R}^2} \to {\mathbb{P}_1}\), \(T\left( {\left( {a,b} \right)} \right) = a - b + 2ax\)
¿Cuál es el núcleo de \(T\)?
\[a - b + 2ax = 0x + 0 \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{a - b = 0}\\{2a = 0}\end{array}{\rm{\;}}} \right. \Rightarrow a = 0 = b\] \[Nu\left( T \right) = \left\{ {\left( {0,0} \right)} \right\}\] ¿Cuál es la imagen de \(T\)? \[T\left( {\left( {1,0} \right)} \right) = 2x + 1\] \[T\left( {\left( {0,1} \right)} \right) = - 1 + 0x\] Estos dos polinomios ¿son LI o LD? Son LI, y por lo tanto la dimensión de la imagen es 2. La imagen ‘vive’ en \({\mathbb{P}_1}\), entonces: \[Im\left( T \right) = {\mathbb{P}_1}\]
¿Está bien definida \({T^{ - 1}}\)? Sí, porque \(\left\{ {2x + 1, - 1} \right\}\) es una base de \({P_1}\) (por
Sea \(T:V \to W\) isomorfismo, \(\dim \left( V \right) = \dim \left( W \right) = n\), y \(M{\left( T \right)_{BB\,'}} \in {\mathbb{R}^{n \times n}}\;\) la matriz asociada a \(T\,\) respecto de las bases \(B\) y \(B\,'\).
Recordemos que el rango de la matriz asociada es igual a la dimensión de la imagen.
Como \(T\) es isomorfismo, \(Im\left( T \right)\; = \;W\) y por lo tanto: \(rg\left( {M{{\left( T \right)}_{BB\,'}}} \right) = n\).
Entonces\(\;\;\;M{\left( T \right)_{BB\,'}}\) es inversible y su inversa es la matriz de \({T^{ - 1}}\) respecto de las bases \(B\,'\) y \(B\):
En el siguiente esquema se puede observar cómo operan las matrices \(M{\left( T \right)_{BB\,'}}\) y \(M{\left( {{T^{ - 1}}} \right)_{B\,'B}}\,\):
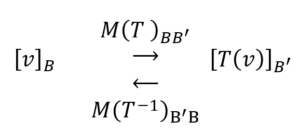
Caso particular: \(V = W = {\mathbb{R}^n}\),
Sea \(T:{\mathbb{R}^3} \to {\mathbb{R}^3}\) una TL, tal que \(\;T\left( {x,y,z} \right) =\left( {x + y,\;x - z,\;z} \right)\), hallar la fórmula de \({T^{ - 1}}\).
Construyamos la matriz asociada a la TL en las bases canónicas: \[M\left( T \right) = A = \left( {\begin{array}{*{20}{c}}1&1&0\\1&0&{ - 1}\\0&0&1\end{array}} \right)\]
Sabemos que \({A^{ - 1}}\) será la matriz asociada a la TL inversa: \[M\left( {{T^{ - 1}}} \right) = \;{A^{ - 1}} = \left( {\begin{array}{*{20}{c}}0&1&1\\1&{ - 1}&{ -1}\\0&0&1\end{array}} \right)\]
Y a partir de la matriz estándar de la TL inversa podemos hallar la fórmula de la TL inversa:
\[{T^{ - 1}}:{\mathbb{R}^3} \to {\mathbb{R}^3},\;\;\;{T^{ - 1}}\left( {\left( {x,y,z} \right)} \right) = \left( {y + z,\;x - y - z,\;z} \right)\]Dadas las transformaciones lineales: \(F\) de \({\mathbb{R}^3} \to {\mathbb{R}^2}\), \(F\left( {x,y,z} \right)\; = \left( {x - y\;,\;y + z} \right)\) y \(G\) de \({\mathbb{R}^2} \to {\mathbb{R}^3}\), \(G\left( {a,b} \right)\; = \;\left( {a + b\;,\;0,\;2a + kb} \right)\)
a) Determinar todos los valores de \(k\) para los cuales \(F \circ G\) es biyectiva (isomorfismo).
b) Para \(k = 1\), obtener \({\left( {F \circ G} \right)^{ - 1}}\left( {1,0} \right)\).

Queremos construir una matriz que nos permita cambiar las coordenadas de un vector en una base por las coordenadas del mismo vector en otra base.
Consideremos en un espacio vectorial \(V\) la función identidad, que transforma cada vector en sí mismo. Dejamos a cargo del lector demostrar que es una T.L. \[Id:V \to V{\rm{\;}}|{\rm{\;}}Id\left( v \right) = v\]
Observación: Si \(V = \mathbb{R}\), la función identidad es \(f\left( x \right) = x\). Tomemos un par de bases del mismo espacio vectorial \(V\): \[B = \left\{ {{v_1}, \ldots ,{v_n}} \right\}\] \[B\,' = \left\{ {{w_1}, \ldots ,{w_n}} \right\}\] Construyamos ahora la
¿Qué efecto produce esta matriz? Cambia las coordenadas, o sea el sistema de referencia. No transforma el vector pues \(Id\left( v \right) = v\).
\[M{\left( {Id} \right)_{BB\,'}}\;\text{se denomina matriz de cambio de base de}\; B \;a\; B\,'. \]¿Qué rango tiene esta matriz? Tiene rango \(n\) ya que sus columnas son LI por ser coordenadas de vectores de una base de \(V\).
Por ser \(M{\left( {Id} \right)_{BB\,'}} \in {\mathbb{R}^{n \times n}}\) de rango \(n\), es inversible.
¿Qué efecto produce la matriz inversa? Nos permite volver a la primera base, como lo indica el siguiente esquema:
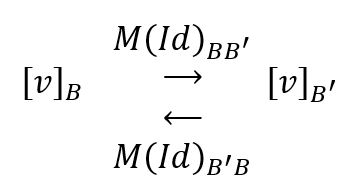
Consideremos las siguientes bases de \({\mathbb{R}^2}\): \[{B_1} = \left\{ {\left( {1,0} \right),\;\left( {1,3} \right)} \right\}\] \[{B_2} = \left\{ {\left( {0,1} \right),\left( {1,1} \right)} \right\}\] \[E = \left\{ {\left( {1,0} \right),\left( {0,1} \right)} \right\}\]
a) Hallar \(M{\left( {Id} \right)_{{B\displaystyle_{1}}{B\displaystyle_2}}}\)
b) Hallar \(M{\left( {Id} \right)_{{B\displaystyle_1}E}}\)
c) Hallar \(M{\left( {Id} \right)_{E{B\displaystyle_1}}}\)
Ítem a
Se construye la matriz de cambio de base buscando las coordenadas en la base \({B\displaystyle_2}\) de los vectores de la base \({B\displaystyle_1}\).
\[M{\left( {Id} \right)_{{B\displaystyle_1}{B\displaystyle_2}}} = \left( {{{\left[ {{v_1}} \right]}_{{B\displaystyle_2}}}\;\;\;\;{{\left[ {{v_2}} \right]}_{{B\displaystyle_2}}}} \right)\]
Busquemos las coordenadas de \(\left( {1,0} \right)\) en la base \({B\displaystyle_2}\;\):
\[\left( {1,0} \right) = \alpha \left( {0,1} \right) + \beta \left( {1,1} \right)\] \[ \Rightarrow \alpha = \; - 1\;\; \wedge \;\;\beta = 1\] \[ \Rightarrow {\left[ {\left( {1,0} \right)} \right]_{{B\displaystyle_2}}} = \left( {\begin{array}{*{20}{c}}{ - 1}\\1\end{array}} \right)\] Busquemos las coordenadas de \(\left( {1,3} \right)\) en la base \({B\displaystyle_2}\;\): \[\left( {1,3} \right) = \alpha \left( {0,1} \right) + \beta \left( {1,1} \right)\] \[ \Rightarrow \alpha = 2\;\; \wedge \;\beta = 1\] \[ \Rightarrow {\left[ {\left( {1,3} \right)} \right]_{{B_2}}} = \left( {\begin{array}{*{20}{c}}2\\1\end{array}} \right)\]
Ítem b
Se construye la matriz de cambio de base buscando las coordenadas en la base \(E\) de los vectores de la base \({B\displaystyle_1}\). \[M{\left( {Id} \right)_{{B\displaystyle_1}E}} = \left( {{{\left[ {{v_1}} \right]}_E}\;\;\;\;{{\left[ {{v_2}} \right]}_E}} \right)\] Pero las coordenadas en base canónicas son las mismas componentes del vector. Podemos verificarlo para \(\left( {1,0} \right)\): \[\left( {1,0} \right) = \alpha \left( {1,0} \right) + \beta \left( {0,1} \right) \Rightarrow \alpha = 1,\;\beta = 0\] Entonces las coordenadas de \(\left( {1,0} \right)\) en la base canónica son justamente \(\left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right)\): \[{\left[ {\left( {1,0} \right)} \right]_E} = \left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right)\] Para el vector \(\left( {1,3} \right)\) podemos escribir: \[{\left[ {\left( {1,3} \right)} \right]_E} = \left( {\begin{array}{*{20}{c}}1\\3\end{array}} \right)\] Así que la matriz de cambio de base resulta: \[M{\left( {Id} \right)_{{B\displaystyle_1}E}} = \left( {\begin{array}{*{20}{c}}1&1\\0&3\end{array}} \right)\]
Que podemos decir que se construyó ubicando a los vectores de la base \({B_1} = \left\{ {\left( {1,0} \right),\left( {1,3} \right)} \right\}\) como columnas de la matriz.
Ítem c
Se pide que hallemos \(M{\left( {Id} \right)_{E{B\displaystyle_1}}}\), pero según hemos visto esta matriz es la inversa de \(M{\left( {Id} \right)_{{B\displaystyle_1}E\;}}\): \[M{\left( {Id} \right)_{E{B\displaystyle_1}}} = \dfrac{1}{3}\left( {\begin{array}{*{20}{c}}3&{ - 1}\\0&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&{ - \frac{1}{3}}\\0&{\frac{1}{3}}\end{array}} \right)\]
Sean \({B_1}\) y \({B_2}\) bases de \({\mathbb{R}^2}\) tales que \(P = \left( {\begin{array}{*{20}{c}}1&1\\0&{ - 3}\end{array}} \right)\) es la matriz de cambio de base de \({B_1}\) a \({B_2}.\)
a) Si \({\left[ u \right]_{{B\displaystyle_1}}} = \left( {\begin{array}{*{20}{c}}{ - 1}\\4\end{array}} \right)\) calcular \({\left[ u \right]_{{B\displaystyle_2}}}\)
b) Si \({\left[ v \right]_{{B\displaystyle_2}}} = \left( {\begin{array}{*{20}{c}}3\\5\end{array}} \right)\) calcular \({\left[ v \right]_{{B\displaystyle_1}}}\)
c) Si \({B_1} = \left\{ {\left( {1,3} \right),\left( {0,4} \right)} \right\}\), obtener la base \({B_2}\). ¿Es única?
Ítem a
Según la propiedad de la matriz de cambio de base:
¿Podemos determinar cuál es el vector \(u\)? No, porque no tenemos información sobre las bases.
Ítem b
Ahora es en sentido contrario: \[{\left[ v \right]_{{B\displaystyle_2}}} = \left( {\begin{array}{*{20}{c}}3\\5\end{array}} \right) \to {\left[ v \right]_{B\displaystyle_1 \;}} = \;?\] \[P.{\left[ v \right]_{{B\displaystyle_1}}} = {\left[ v \right]_{{{\rm{B}}\displaystyle_2}}} \Rightarrow \left( {\begin{array}{*{20}{c}}1&1\\0&{ - 3}\end{array}} \right){\left[ v \right]_B} = \left( {\begin{array}{*{20}{c}}3\\5\end{array}} \right){\rm{\;}} \Rightarrow {\left[ v \right]_B} = \left( {\begin{array}{*{20}{c}}{\dfrac{{14}}{3}}\\{ - \dfrac{5}{3}}\end{array}} \right)\]
Ítem c
En este punto nos dan la base \({B_1}\): \[{B_1} = \left\{ {\left( {1,3} \right),\left( {0,4} \right)} \right\}\] ¿Puede determinarse \({B_2}\)? Sabemos que: \[Id\left( {\left( {1,3} \right)} \right) = \left( {1,3} \right)\] \[Id\left( {\left( {0,4} \right)} \right) = \left( {0,4} \right)\] \[{v_1} = \left( {1,3} \right){\rm{\;\;}}{v_2} = \left( {0,4} \right)\]
Queremos obtener: \[{B\displaystyle_2} = \left\{ {{w\displaystyle_{1{\rm{\;}}}},{\rm{\;}}{w\displaystyle_2}} \right\}\] \[\left( {1,3} \right) = 1\,{w\displaystyle_1} + 0\,{w\displaystyle_2} \Rightarrow {w\displaystyle_1} = \left( {1,3} \right)\] \[\left( {0,4} \right) = 1\,{w\displaystyle_1} + \left( { - 3} \right)\,{w\displaystyle_2} \Rightarrow {w\displaystyle_2} = \frac{{\left( {0,4} \right) - \left( {1,3} \right)}}{{ - 3}} = \left( {\frac{1}{3}, - \frac{1}{3}} \right)\] Quiere decir que si tenemos como dato la matriz de cambio de base, podemos determinar la base \({B\displaystyle_2}\;\)a partir de la base \({B\displaystyle_1}\) y viceversa.
En este apartado nos interesa estudiar cuál es la relación entre dos matrices asociadas a una misma transformación lineal, pero que están expresadas en bases diferentes.
Sean:
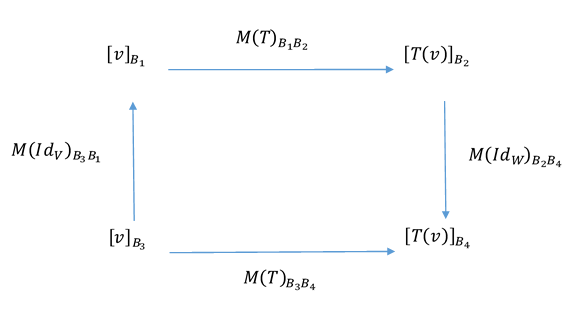
¿Qué relación existe entre \(M{\left( T \right)_{{B\displaystyle_1}{B\displaystyle_2}}}\) y \(M{\left( T \right)_{{B\displaystyle_3}{B\displaystyle_4}}}\;\)? ¿Cómo se podría a partir de una de ellas calcular la otra?
Por las propiedades de las matrices asociadas a una TL, puede afirmarse que: \[M{\left( T \right)_{{B\displaystyle_1}{B\displaystyle_2}}}{\left[ v \right]_{{B\displaystyle_1}}} = {\left[ {T\left( v \right)} \right]_{{B\displaystyle_2}}}\] \[M{\left( T \right)_{{B\displaystyle_3}{B\displaystyle_4}}}{\left[ v \right]_{{B\displaystyle_3}}} = {\left[ {T\left( v \right)} \right]_{{B\displaystyle_4}}}\] \[M{\left( {I{d_V}} \right)_{{B\displaystyle_3}{B\displaystyle_1}}}{\left[ v \right]_{{B\displaystyle_3}}} = {\left[ v \right]_{{B\displaystyle_1}}}\] \[M{\left( {I{d_W}} \right)_{{B\displaystyle_2}{B\displaystyle_4}}}{\left[ {T\left( v \right)} \right]_{{B\displaystyle_2}}} = {\left[ {T\left( v \right)} \right]_{{B\displaystyle_4}}}\] Si el lector leyó cuidadosamente las igualdades anteriores, estará convencido de que son válidas. Las relaciones enunciadas pueden verse convenientemente en el siguiente esquema:
Nos interesa especialmente el caso de las TL \(T:{\mathbb{R}^n} \to {\mathbb{R}^n}\), y la relación entre la matriz estándar y otra matriz asociada \(M{\left( T \right)_{BB}}\) , con \(\;B\) base de \({\mathbb{R}^n}\). Volvamos a construir el esquema para este caso particular:
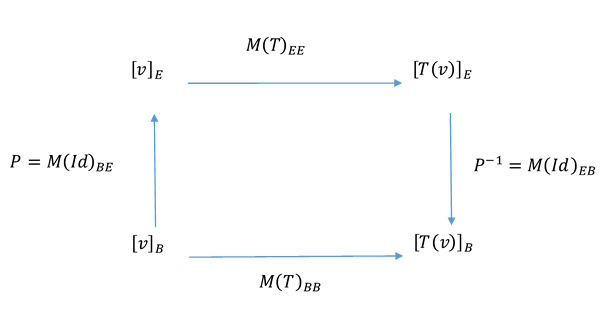
Por lo tanto:
Queremos encontrar \(M{\left( T \right)_{BB}}\) . Calculamos la matriz de cambio de base: \[P = M{\left( {Id} \right)_{BE}} = \left( {\begin{array}{*{20}{c}}1&3\\1&{ - 2}\end{array}} \right)\] Buscamos su inversa: \[{P^{ - 1}} = M{\left( {Id} \right)_{EB}} = - \, \frac{1}{5}\left( {\begin{array}{*{20}{c}}{ - 2}&{ - 3}\\{ - 1}&1\end{array}} \right)\] Entonces resulta: \[M{\left( T \right)_{BB}} = {P^{ - 1}}\,M{\left( T \right)_{EE}}\,P = \left( {\begin{array}{*{20}{c}}4&0\\0&{ - 1}\end{array}} \right)\]
Observemos que en esta base \(B\), la matriz asociada es diagonal. Dada una TL en \({\mathbb{R}^n}\), ¿cuándo es posible hallar una base \(B\) de modo que la matriz asociada en esa base resulte diagonal? La respuesta la encontraremos en el próximo capítulo.
a) Eligiendo una base adecuada, definir una transformación lineal \(T:{\mathbb{R}^3} \to {\mathbb{R}^3}\) que represente la simetría (reflexión) respecto del plano \(\pi :\;\;x - z = 0\) .
b) Hallar si es posible, una base \(B\) de \({\mathbb{R}^3}\) de modo que la matriz asociada a \(T\) sea: \[M{\left( T \right)_{BB}} = \left( {\begin{array}{*{20}{c}}1&0&0\\0&1&0\\0&0&{ - 1}\end{array}} \right)\] Sugerencia: si \(B = \left\{ {{v_1},{v_2},{v_3}} \right\}\), ¿cuáles son los transformados de los vectores de \(B\,\)? (Tener en cuenta cómo se construye \(M{\left( T \right)_{BB}}\)).
c) Obtener la matriz de \(T\) respecto de la base canónica de \({\mathbb{R}^3}\).

Muchos cuestionan la utilidad de las matemáticas, y los propios matemáticos a veces las defendemos más como un arte que por sus aplicaciones, que consideramos propiedad privada de los ingenieros. Sin embargo, están presentes en todo lo que nos rodea: desde la seguridad en internet hasta los gráficos de los videojuegos y la compresión de imágenes. En una era tan tecnológica, ¿no deberíamos saber más matemáticas?
Veamos algunas aplicaciones (información que hemos obtenido gracias a la IA Gemini 2.0)
Cliquea en el botón superior derecho del interactivo para tener el recurso abierto de forma independiente y navega por las distintas pestañas.
En la siguiente página podemos observar algunas transformaciones lineales asociadas a movimientos geométricos conocidos: homotecias de razón positiva, reflexiones (simetrías axiales), cizallamientos respecto de cada uno de los ejes de coordenadas, rotaciones, rotaciones compuestas con escalados y un sexto movimiento que llamamos "Ejemplo".
¿Puedes interpretar que tipos de movimientos son los que se producen en el "Ejemplo"?
Sugerimos que pruebes con distintos valores del parámetro. Por ejemplo:
Si el elemento variable de la matriz es 2, el determinante de la matriz es \(-3\), Como \(\det(A) \neq \pm1\), la transformación no es una isometría (no conserva distancias). Además, \( \det(A) < 0 \) implica que la transformación "invierte la orientación", lo que sugiere que podría ser una reflexión combinada con otro tipo de transformación.
Los autovalores nos ayudan a entender la transformación en términos de direcciones invariantes. Los autovalores son: \(\;\lambda_1 = 3, \quad \lambda_2 = -1.\)
Un autovector asociado a \( \lambda_1 = 3 \) es \( v_1 = (1,1), \, \) mientras que uno asociado a \( \lambda_2 = -1 \) es \( v_2 = (1,-1) \).
En esta animación podemos mover el cuadrado de área 1 moviendo el vértice inferior izquierdo. Una vez que decidimos donde localizarlo, podemos transformar los versores de la base canónica arrastrando sus extremos. ¿Cómo se refleja este movimiento en las columnas de la matriz?
Podemos tildar la casilla "Cuadrícula" pudiendo observar cómo se transforma todo el espacio. Para ello, una vez marcada dicha casilla, usamos el botón "Animar".
Para restablecer el plano y el cuadrado original cliqueamos en "Comenzar". El botón "Ortogonal" permite visualizar dos vectores ortogonales como referencia.
En el siguiente interactivo te proponemos que explores 5 transformaciones y trates de describir que tipo de movimiento producen. Luego dirígete a la herramienta de IA de la página siguiente y te proponemos que utilices un prompt similar a: "¿Qué tipo de movimiento geométrico representa la transformación lineal dada por la matriz:
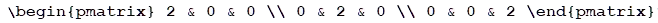 Ten especial cuidado al escribir la matriz en el formato sugerido (latex) para que la IA interprete correctamente los datos ingresados. Puedes cambiar los valores numéricos de manera de usar los de cada ejemplo.
Ten especial cuidado al escribir la matriz en el formato sugerido (latex) para que la IA interprete correctamente los datos ingresados. Puedes cambiar los valores numéricos de manera de usar los de cada ejemplo.
Introduce el prompt sugerido: "¿Qué tipo de movimiento geométrico representa la transformación lineal dada por..."
En caso de utilizar valores decimales recuerda que el separador decimal es "." (debemos escribir 0.5 si queremos referirnos al número "un medio".)
Consideremos la matriz: \[A = \left( {\begin{array}{*{20}{c}}3&2\\1&4\end{array}} \right)\] Queremos ver cuál es el efecto que provoca esa matriz al multiplicarla por los vectores de \({\mathbb{R}^2}\). ¿Qué pasa cuando uno multiplica esa matriz A por un vector? \[A.\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}3&2\\1&4\end{array}} \right).\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{3x + 2y}\\{x + 4y}\end{array}} \right)\] Pensemos para que sea sencillo que tomamos el cuadrado con vértice en el origen de lado 1 y que está en el primer cuadrante:
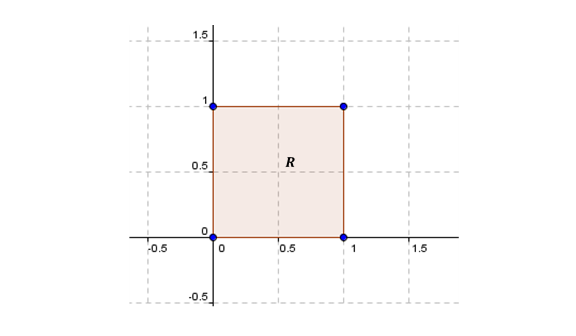
Digamos que llamamos a esta zona el recinto \(R\). ¿En qué se transformaría este recinto bajo el efecto de esa matriz? Para responder esta pregunta podemos ver en que se transforman sus vértices. Sabemos que el vector nulo se va a transformar en el vector nulo. Los demás serán: \[A\left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right) = \left( {\begin{array}{*{20}{c}}3\\1\end{array}} \right)\] \[A\left( {\begin{array}{*{20}{c}}0\\1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}2\\4\end{array}} \right)\] \[A\left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}5\\5\end{array}} \right)\]
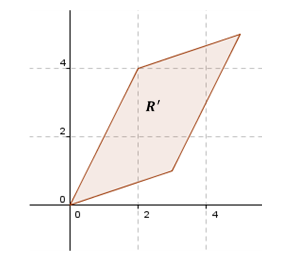
Uno se podría hacer esta pregunta: ¿Habrá vectores que después de la deformación conservan la dirección?
Ese vector que mantuvo su dirección se denomina autovector, y el factor por el cual se dilató es el autovalor correspondiente.
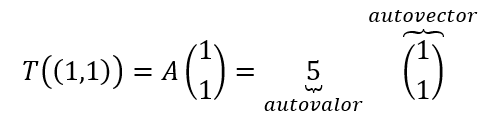
En el ejemplo que vimos recién el transformado de \(\left( {1,1} \right)\) es \(\left( {5,5} \right)\), entonces:
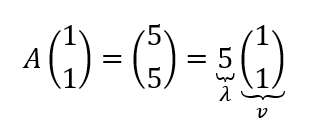
Veamos cómo hallar los autovalores y autovectores: Según la definición, debe cumplirse esta condición: \[Av = \lambda v\;\;{\rm{\;con\;}}v \ne {0_V}\] Restamos a ambos miembros \(\lambda v\): \[Av \; - \; \lambda v = {0_V}\] Premultiplicamos a \(v\) por \(I\), esto lo podemos hacer porque \(Iv = v\): \[Av \; - \; \lambda \,I\,v = {0_V}\]
Entonces:
\[ \underbrace{\left ( A -\lambda I\ \right )}_{\displaystyle{nxn}}\,v = 0_{v} \]Resulta un sistema homogéneo con \(n\) ecuaciones y \(n\) incógnitas, donde \(A - \lambda I\) es la matriz de los coeficientes.
¿Cómo puede ser un sistema homogéneo en cuanto a su compatibilidad?
Respuesta: siempre compatible, porque siempre tiene la solución trivial. ¿Cómo queremos que sea en nuestro problema si estamos buscando vectores que no cambien su dirección?
¿Sistema compatible determinado (SCD) o sistema compatible indeterminado (SCI)?. Si es SCD, tiene únicamente la solución trivial y \(v\) es el vector nulo. Nuestro objetivo es obtener los autovectores (que son distintos del vector nulo), por eso necesitamos que este sistema sea compatible indeterminado.
Entonces: buscamos un sistema compatible indeterminado.
En un sistema cuadrado y homogéneo, el determinante decide: si es distinto de cero, tiene solución única. Entonces queremos que sea igual a cero:
Esta es la ecuación característica de la matriz \(A\).
Y \(p\left( \lambda \right) = {\rm{det}}\left( {A - \lambda I} \right)\) es un polinomio de grado \(n\) dependiente de \(\lambda\, \) que se llama polinomio característico de la matriz \(A\).
Las raíces del polinomio característico son los autovalores de\(A\).
Una vez hallados los autovalores, ¿cómo obtenemos los autovectores?
Volvemos a la expresión original.
Para cada \(\lambda \) resolvemos el sistema:
\[\left( {A - \lambda I} \right)\,v = {0_V}\]Y hallamos los autovectores correspondientes.
Si la matriz es de 2 por 2, el polinomio quedará de grado 2.
Si la matriz es de 3 por 3, el polinomio quedará de grado 3.
Otros nombre que se les suele dar a los autovectores y autovalores son:
Volvamos al ejemplo inicial. \[A - \lambda I = \left( {\begin{array}{*{20}{c}}3&2\\1&4\end{array}} \right) - \lambda \left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{3 - \lambda }&2\\1&{4 - \lambda }\end{array}} \right)\] \[\det \left( {A - \lambda I} \right) = 0\] \[\left( {3 - \lambda } \right)\left( {4 - \lambda } \right) - 2 = 0\] \[{\lambda ^2} - 7\lambda + 10 = 0\] \[{\lambda _1} = 2 \wedge {\lambda _2} = 5\] Para \(\lambda = 2\,\) resolvemos el sistema de ecuaciones: \[\left( {A - 2I} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\]
Consideremos la siguiente matriz de \(3 \times 3\): \[B = \left( {\begin{array}{*{20}{c}}3&2&{ - 1}\\2&3&1\\0&0&5\end{array}} \right)\] Busquemos sus autovalores resolviendo el polinomio característico: \[\left| {\begin{array}{*{20}{c}}{3 -\lambda }&2&{ - 1}\\2&{3 - \lambda }&1\\0&0&{5 - \lambda }\end{array}} \right| = 0\] \[\left( {5 - \lambda } \right)\left( {{{\left( {3 - \lambda } \right)}^2} - 4} \right) = 0\] Luego los autovalores son: \[{\lambda \displaystyle_1} = 5\;\; \vee \;\;\;{\lambda\displaystyle_2} = 5\;\; \vee \;\;{\lambda\displaystyle_3} = 1\] Donde la multiplicidad algebraica de \(5\) es 2. Esto significa que 5 es raíz doble del polinomio característico.
Para cada autovalor debemos resolver el sistema de ecuaciones \[\left( {\begin{array}{*{20}{c}}{3 - \lambda }&2&{ - 1}\\2&{3 - \lambda }&1\\0&0&{5 - \lambda }\end{array}} \right) \left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\] Para obtener cuales son los autoespacios correspondientes a cada autovalor.
Autovectores asociados a \({\rm{\lambda }} = 5\):
Resolvamos el sistema compatible indeterminado: \[\left( {\begin{array}{*{20}{c}}{ - 2}&2&{ - 1}\\2&{ - 2}&1\\0&0&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{ - 2x + 2y - z = 0}\\{2x - 2y + z = 0}\\{0 = 0}\end{array}} \right.\] \[\Rightarrow - 2x + 2y - z = 0\]
El subespacio asociado a este autovalor es: \[{S\large_5} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}0\\{ - 2}\end{array}}\end{array}} \right),\left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}1\\2\end{array}}\end{array}} \right)} \right\}\;\]
Luego dos autovectores son: \[{v_1} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}0\\{ - 2}\end{array}}\end{array}} \right)\;;\;\;\;{v_2} = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}1\\2\end{array}}\end{array}} \right)\]
Autovectores asociados a \({\rm{\lambda }} = 1\):
Resolvamos el sistema compatible indeterminado: \[\left( {\begin{array}{*{20}{c}}2&2&{ - 1}\\2&2&1\\0&0&4\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{2x + 2y - z = 0}\\{2x + 2y + z = 0}\\{4z = 0}\end{array}} \right.\] \[\Rightarrow z = 0 \; \wedge \; y = - x\]
El subespacio asociado a este autovalor es: \[{S\large_1} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ - 1}\\0\end{array}}\end{array}} \right)} \right\}\;\]
Luego un autovector es: \[{v_3} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ - 1}\\0\end{array}}\end{array}} \right)\]
Finalmente hemos obtenido tres autovectores: \[{v_1} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}0\\{ - 2}\end{array}}\end{array}} \right)\;;\;\;\;{v_2} = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}1\\2\end{array}}\end{array}} \right)\;;\;\;{v_3} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ - 1}\\0\end{array}}\end{array}} \right)\]
Donde \({v_1}\) y \({v_2}\) son autovectores asociados al autovalor \(\lambda = 5\) y \({v_3}\) es un autovalor asociado a \(\lambda = 1\).
Consideremos la siguiente matriz de \(2 \times 2\): \[C = \left( {\begin{array}{*{20}{c}}0&{ - 2}\\2&0\end{array}} \right)\]
Busquemos sus autovalores resolviendo el polinomio característico: \[\left| {\begin{array}{*{20}{c}}{ - \lambda }&{ - 2}\\2&{ - \lambda }\end{array}} \right| = 0\] \[ \Rightarrow \;{\lambda ^2} + 4 = 0\] Este polinomio no tiene raíces reales. Con lo cual diremos que \(C\) no tiene autovalores reales. Más adelante estudiaremos los números complejos y podremos hallar las raíces (complejas) del polinomio característico de \(C\).
Demuestre la siguiente propiedad para \(A \in {\mathbb{R}^{n \times n}}\)
\(\lambda = 0\,\) es autovalor de \(A \Leftrightarrow A\) no es inversible
¿Cómo se demuestra esto? Primero veamos un ejemplo para convencernos de que se cumple la propiedad. Consideremos una matriz que no tenga inversa. Por ejemplo escribimos una matriz tal que la fila 2 sea el doble de la fila 1: \[A = \left( {\begin{array}{*{20}{c}}1&2\\2&4\end{array}} \right)\] Escribamos la ecuación característica y hallemos los autovalores: \[{p_A}\left( \lambda \right) = \left( {1 - \lambda } \right)\left( {4 - \lambda } \right) - 4 = 0\]
\[{\lambda ^2} - 5\lambda = 0\; \Rightarrow \lambda = 0 \vee \lambda = 5\] En este caso particular hemos visto que una matriz no inversible tiene autovalor \(\lambda = 0\). Pero quisiéramos demostrar la propiedad. Para demostrar esto hay que recordar que:
\[ \lambda \; \text {es autovalor de}\, A \, \Leftrightarrow \, \det \left( {{\rm{A}} - {\rm{\lambda I}}} \right) = 0\]Pero si \(\lambda = 0\,\) entonces la afirmación queda:
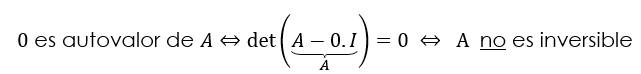
Sea: \(A = \left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)\, \) con autovalores \({\lambda\large_1}\) y \({\lambda \large _2}\) (iguales o distintos).
Demostrar que: \[{\lambda \large _1} + {\lambda\large _2} = Traza\left( A \right)\] \[{\lambda \large _1}.{\lambda \large _2} = \det \left( A \right)\]

Demostración para dos autovalores
Supongamos que tengo dos autovalores distintos: \({\lambda _1} \ne {\lambda _2}\). Como son autovalores, se cumple: \[A\,{v_1} = {\lambda _1}\,{v_1}\] \[A\,{v_2} = {\lambda _2}\,{v_2}\]
Queremos probar que \({v_1}\) y \({v_2}\) son linealmente independientes. Veamos que la única combinación lineal de los vectores que da por resultado el vector nulo es la trivial (todos los coeficientes iguales a cero): \[\;{\alpha _1}\,{v_1} + {\alpha _2}\,{v_2} = {0_V}\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 1 \right)\] Multiplicamos por \(A\) ambos miembros: \[A\left( {{\alpha _1}\,{v_1} + {\alpha _2}\,{v_2}} \right) = {0_V}\]
Distribuimos: \[{\alpha _1}\,A\,{v_1} + {\alpha _2}\,A\,{v_2} = {0_V}\] Como \({v_1}\) y \({v_2}\) son autovectores es posible escribir:
\[{\alpha _1}\,{\lambda _1}\,{v_1} + {\alpha _2}\,{\lambda _2}\,{v_2} = {0_V}\;\;\;\;\;\;\left( 2 \right)\]
Ahora multiplicamos los dos miembros de la ecuación \(\left( 1 \right)\) por \({\lambda _1}\) :
\[{\alpha _1}\,{\lambda _1}\,{v_1} + {\alpha _2}\,{\lambda _1}\,{v_2} = {0_V}\;\;\;\;\;\;\;\left( 3 \right)\] Y restando \(\left( 2 \right) - \left( 3 \right)\) obtenemos:
\[\alpha _{2}\, \underbrace{\left ( \lambda _{2}-\lambda _{1} \right )}_{\large {\neq 0}}\underbrace{v_2}_{\large {\neq 0}}=0_{V}\]
Como \({\lambda _1} \ne {\lambda _2}\;\) por hipótesis entonces su diferencia no puede ser nula. Como \({v_2}\) es un autovector, no puede ser el vector nulo. Entonces: \[{\alpha _2} = 0\] Pero para demostrar que son linealmente independientes, nos falta ver que \({\alpha _1} = 0\).
Sabiendo que \({\alpha _2} = 0\) vamos a \(\left( 1 \right)\):
\[{\alpha _1}\,{v_1} = {0_V} \Rightarrow {\alpha _1} = 0\] Y si \({\alpha _1} = {\alpha _2} = 0\) demostramos que \(\left\{ {{v_1},{v_2}} \right\}\) es linealmente independiente. O sea los autovectores que están en autoespacios diferentes son linealmente independientes.
Sea \(A = \left( {{A\large_1}\;\;\;{A\large_2}\;\;\;{A\large_3}} \right) \in {\mathbb{R}^{3 \times 3}}\;\) con: \[{A\large_1} = \left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}2\\3\end{array}}\end{array}} \right)\;\;\;\;{\rm{y\;\;\;\;\;}}{{\rm{A}}\large_2} = \left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1\\1\end{array}}\\0\end{array}} \right)\]
a) Hallar \({A\large_3}\) para que \(v = \left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}0\\1\end{array}}\\{ - 1}\end{array}} \right)\) sea autovector de \(A\) asociado a \(\lambda = 2\).
b) Hallar los restantes autovalores y autoespacios de \(A\).

Hemos visto que:
\(\lambda \,\) es autovalor de \(A\) \(\; \Leftrightarrow\; \) \(\det \left( {A - \lambda I} \right) = 0\)
Es decir que los autovalores son las raíces del polinomio característico.
La multiplicidad algebraica de un autovalor \(\lambda \) es su multiplicidad como raíz del polinomio característico \(p\left( \lambda \right)\). Denotaremos \({m_\lambda }\) a la multiplicidad algebraica del autovalor \(\lambda \).
Supongamos \(A \in \large{\mathbb{R}^{5 \times 5}}\;\) y \(p\left( \lambda \right) = - \lambda .\left( {\lambda - 1} \right).{\left( {\lambda - 2} \right)^3}\). El polinomio característico tiene grado 5. En la siguiente tabla resumimos los autovalores de \(A\) y sus multiplicidades algebraicas.
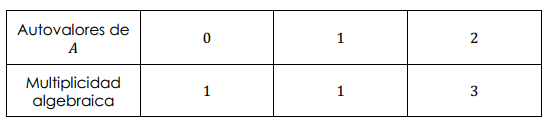
La multiplicidad geométrica de un autovalor \(\lambda \) es la dimensión del autoespacio asociado.
Consideremos la siguiente matriz: \[B = \left( {\begin{array}{*{20}{c}}3&2&{ - 1}\\2&3&1\\0&0&5\end{array}} \right)\] Hemos visto que su polinomio característico es: \[{p_B}\left( \lambda \right) = - {\left( {\lambda - 5} \right)^2}\left( {\lambda - 1} \right)\] Observación. El coeficiente principal de los polinomios característicos asociados a las matrices \(n \times n\) es \({\left( { - 1} \right)\large^n}\). Así que si la matriz es de \(3 \times 3\) el coeficiente principal es \({\left( { - 1} \right)\large^3} = - 1\). Si la matriz es de \(2 \times 2\) el coeficiente principal será \({\left( { - 1} \right)\large^2} = 1\). Consideremos sus autovalores, la multiplicidad algebraica, y la multiplicidad geométrica:

Coinciden \({m_\lambda }\) con \(\dim \left( {{S_\lambda }} \right)\). Uno podría llegar a pensar que esto pasa siempre. Pero… Veamos que no es así. Tomemos la siguiente matriz:
Pueden verificar que el polinomio característico de \(M\) coincide con el de \(B\): \[{p_M}\left( \lambda \right) = - {\left( {\lambda - 5} \right)^2}\left( {\lambda - 1} \right)\] Calculemos el autoespacio asociado al autovalor \(\lambda = 5\) \[\left( {\begin{array}{*{20}{c}}{ - 2}&2&1\\2&{ - 2}&1\\0&0&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\;\] Esta matriz es de rango 2. Entonces ahora da como autoespacio una recta, no un plano. La dimensión del autoespacio será 1. \[\left\{ {\begin{array}{*{20}{c}}{ - 2x + 2y + z = 0}\\{2x - 2y + z = 0}\end{array} \Rightarrow z = 0\; \wedge \; x = y} \right.\] Entonces \[{S\large_5} = gen\left\{ {\left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1\\1\end{array}}\\0\end{array}} \right)} \right\}\] Ahora el autoespacio asociado a \(\lambda = 1\) \[\left( {\begin{array}{*{20}{c}}2&2&1\\2&2&1\\0&0&4\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right) \Rightarrow z = 0 \; \wedge \; x = - y\] \[{S\large_1} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}{ - 1}\\0\end{array}}\end{array}} \right)} \right\}\]

Esto marca la diferencia entre matrices diagonalizables y no diagonalizables.
Nosotros estamos apuntando a diagonalizar una matriz, por lo cual esta diferencia que encontramos entre \(B\) y \(M\) será crucial.
Para cada autovalor \(\lambda \) de una matriz A, se verifica que: \[\dim \left( {{{\bf{S}}_{\bf{\lambda }}}} \right) \le {{\bf{m}}_{\bf{\lambda }}}\] ¿Puede ser cero la dimensión del autoespacio? ¿Qué querría decir que sea 0?
Si la dimensión de un autoespacio fuera cero, significaría que contiene sólo al vector nulo, pero sabemos que el vector nulo no es un autovector. Entonces:
Consecuencia: si \(\lambda \) es un autovalor simple (\({m\large_\lambda } = 1\)) entonces \(\dim \left( {{S\large_\lambda }} \right) = 1\).
a) Dada la matriz \(A = \left( {\begin{array}{*{20}{c}}1&1&2\\2&2&4\\0&0&c\end{array}} \right)\), hallar todos los valores de \(c\) para los cuales \(A\) es diagonalizable.
b) Para \(c\; = \;0\) , hallar si es posible \(P\) inversible y \(D\) diagonal tales que:\(\;{P^{ - 1}}AP = D\) .
Vimos que:
\(A\;\)es diagonalizable si existe \(P\;\)inversible tal que \({P^{ - 1}}AP = D\;\)(diagonal)
Para armar \(P\) inversible, necesitamos tres autovectores LI (que serán las columnas de P).
Teniendo en cuenta que los autovectores asociados a autovalores distintos son L.I., podemos afirmar lo siguiente:
Si todos los autovalores son distintos, la matriz es diagonalizable porque podemos hallar tres autovectores LI.
Ahora bien: ¿qué ocurre si hay autovalores repetidos? En ese caso no podemos anticipar nada, tenemos que analizar cada caso por
separado para comparar la multiplicidad algebraica del autovalor con la dimensión del autoespacio correspondiente.
Hallemos los autovalores de A, que son las raíces del polinomio característico: \[{\rm{p}}\left( {\rm{\lambda }} \right) = \det \left( {\begin{array}{*{20}{c}}{1 - \lambda }&1&2\\2&{2 - \lambda }&4\\0&0&{c - \lambda }\end{array}} \right) = \left( {c - \lambda } \right)\left[ {\left( {1 - \lambda } \right)\left( {2 - \lambda } \right) - 2} \right]\] \[ = \left( {c - \lambda } \right)\left[ { - 3\lambda + {\lambda ^2}} \right] = \left( {c - \lambda } \right)\lambda \left( { - 3 + \lambda } \right)\] Entonces los autovalores son: \[\lambda = c\;\;\; \vee \;\;\;\lambda = 0\;\;\;\; \vee \;\;\;\lambda = 3\] Veamos cómo separar los distintos casos para realizar un análisis completo:
Caso 1: \(\;\;c \ne 0\;\;\;y\;\;\;c \ne 3\)
En este caso los tres autovalores son distintos, y por lo tanto \(A\) es diagonalizable.
Caso 2: \(\;\;c = 3\;\)
En este caso los autovalores son: \(\lambda = 3\;\left( {doble} \right)\;y\;\;\lambda = 0\)
Nos tenemos que centrar en el autovalor doble: ¿qué dimensión tiene el autoespacio? \[\left( {\begin{array}{*{20}{c}}{1 - 3}&1&2\\2&{2 - 3}&4\\0&0&{3 - 3}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\]
Obtenemos entonces \({S\large_3} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\2\\0\end{array}} \right)} \right\}\)
Como el autovalor es doble y el autoespacio tiene dimensión 1, \(A\) no es diagonalizable. ¿Por qué? Porque con un autovector de \({S\large_3}\) y un autovector de \({S\large_0}\) no podemos completar los 3 autovectores L.I. que necesitamos para armar \(P\). ¿Es necesario hallar \({S\large_0}\)? No, porque sabemos que tiene dimensión 1.
Caso 3: \(\;\;c = 0\)
En este caso los autovalores son: \(\lambda = 0\;\left( {doble} \right)\) y \(\lambda = 3\left( {simple} \right)\). Autoespacio asociado a \(\,\lambda = 0\,\): \[\left( {\begin{array}{*{20}{c}}1&1&2\\2&2&4\\0&0&0\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\]\[\Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{x + y + 2z = 0}\\{2x + 2y + 4z = 0}\end{array}} \right. \Rightarrow \;\;x + y + 2z = 0\; \Rightarrow \left( { - y - 2z,\;y,\;z} \right)\]\[{S\large_0} = gen\left\{ {\;\left( {\begin{array}{*{20}{c}}{ - 1}\\1\\0\end{array}} \right),\;\left( {\begin{array}{*{20}{c}}{ - 2}\\0\\1\end{array}} \right)\;} \right\}\]
Como la dimensión del autoespacio coincide con la multiplicidad algebraica del autovalor, \(A\) es diagonalizable. Si tomamos dos autovectores L.I. de \({S\large_0}\) y un tercer autovector de \({S\large_3}\), tendremos los tres autovectores LI necesarios para armar una \(P\) inversible tal que: \(\,{P^{ - 1}}A\;P = D\) , como se pide en el ítem (b).
En conclusión \(A\) es diagonalizable \(\large{\forall c \in} \; \mathbb{R} - \left\{ 3 \right\}\).
Ítem b
Nos falta hallar el autoespacio asociado a \(\lambda = 3\)
\[\left( {\begin{array}{*{20}{c}}{ - 2}&1&2\\2&{ - 1}&4\\0&0&{ - 3}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\] \[ \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{ - 2x + y + 2z = 0}\\{2x - y + 4z = 0}\\{ - 3z = 0}\end{array}} \right.\;\; \Rightarrow \;\;\left\{ {\begin{array}{*{20}{c}}{y = 2x}\\{z = 0}\end{array}} \right.\;\;\; \Rightarrow \;\left( {x,2x,0} \right)\] \[{S\large_{\lambda \, = \, 3}} = \;gen\left\{ {\;\left( {\begin{array}{*{20}{c}}1\\2\\0\end{array}} \right)\;} \right\}\] \[P = \left( {\begin{array}{*{20}{c}}{ - 1}&{ - 2}&1\\1&0&2\\0&1&0\end{array}} \right)\;\;\;,\;\;\;D = \left( {\begin{array}{*{20}{c}}0&0&0\\0&0&0\\0&0&3\end{array}} \right)\]El lector puede verificar que: \({P^{ -1}}AP = D\)
Sean \(A,B \in {\mathbb{R}^{n \times n}}\), decimos que: \(A\) y \(B\) son matrices semejantes \( \Leftrightarrow \) \(\;\exists P \in {\mathbb{R}^{n \times n}}\;\) inversible tal que \(B = {P^{ - 1}}.A.P\) .
Consideremos las siguientes matrices: \[B = \left( {\begin{array}{*{20}{c}}2&1\\0&1\end{array}} \right)\;\;\;\;\;A = \left( {\begin{array}{*{20}{c}}1&3\\0&2\end{array}} \right)\;\;\;\;\;P = \left( {\begin{array}{*{20}{c}}3&0\\1&1\end{array}} \right)\;\;\;\;\;{P^{ - 1}} = \left( {\begin{array}{*{20}{c}}{\dfrac{1}{3}}&0\\{ - \dfrac{1}{3}}&1\end{array}} \right)\] Podemos afirmar que \(B\) es semejante a \(A\) pues: \[B = {P^{ - 1}}.A.P\] \[B = \left( {\begin{array}{*{20}{c}}{\dfrac{1}{3}}&0\\{ - \dfrac{1}{3}}&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&3\\0&2\end{array}} \right)\left( {\begin{array}{*{20}{c}}3&0\\1&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\dfrac{1}{3}}&1\\{ - \dfrac{1}{3}}&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}3&0\\1&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}2&1\\0&1\end{array}} \right)\]
Si \(A\) y \(B\,\) son semejantes, tienen el mismo polinomio característico y por lo tanto, los mismos autovalores.
\[A\;y\;B\;semejantes \Rightarrow {p_A}\left( \lambda \right) = {p_B}\left( \lambda \right) \Rightarrow Los\;mismos\;autovalores\]
\[{p_A}\left( \lambda \right) = \det \left( {A - \lambda I} \right)\] \[{p_B}\left( \lambda \right) = \det \left( {B - \lambda I} \right)\]
Además sabemos que: \[A = {P}BP^{ - 1}\]
Entonces:
\[p_{A}\left ( \lambda \right )=det\left ( A-\lambda I \right )=det\left ( PBP^{-1} -\lambda I\right )=\] \[=det\left ( PBP^{-1}-P\,\lambda\, IP^{-1} \right )=det\left ( P\left ( B-\lambda I \right )P^{-1} \right )=\] \[=det\left ( P \right ) \, det\left ( B-\lambda I \right ) \, det\left ( P^{-1} \right )= det\left ( B-\lambda I \right )det\left ( P \right )det\left ( P^{-1} \right )\] \[=det\left ( B-\lambda I \right )det\left ( PP^{-1} \right )=det\left ( B-\lambda I \right )det\left ( I \right )=\] \[det\left ( B-\lambda I \right ) = p_{B}\left ( \lambda \right )\]Donde hemos reemplazado \(\lambda I\) por \(P\,\lambda\, I{P^{ - 1}}\,\) ya que: \[P\lambda I{P^{ - 1}} =P \lambda {P^{ - 1}} = \lambda P {P^{ - 1}} = \lambda I\] Y hemos utilizado la propiedad distributiva del determinante respecto de la multiplicación de matrices.
Es un caso especial de
Sean \({v_1},{v_2}, \ldots ,{v_n}\;\)autovectores LI de la matriz \(A \in {\mathbb{R}\large^{n \times n}}\). Podemos construir una matriz \(P\) cuyas columnas sean dichos autovectores: \[P = \left( {{v_1}\;\;\;{v_2}\; \ldots \;{v_n}} \right)\] \(P\) es inversible porque sus columnas son LI y por lo tanto tiene rango \(n\) \(\left( {det\left( P \right) \ne 0} \right)\).
Puede demostrarse que: \(\;\;{P^{ - 1}}A\;P = D\;\;\;\) donde \(D\) es una matriz diagonal cuyos elementos son los respectivos autovalores: \[D = \left( {\begin{array}{*{20}{c}}{{\lambda _1}}&0&0&0\\0&{{\lambda _2}}&0&0\\0&0& \ddots &0\\0&0&0&{{\lambda _n}}\end{array}} \right)\]
Consideremos la matriz \(M\): \[M = \left( {\begin{array}{*{20}{c}}3&{ - 1}& 0\\{ - 1}& 3&0\\1&1&2\end{array}} \right)\] Verifique que los autovalores son: \(\lambda = 2\;\left( {doble} \right)\) y \(\lambda = 4\left( {simple} \right)\) y que ambos autoespacios tienen dimensión 1.
No coincide la
Veamos si es posible diagonalizar la siguiente matriz: \[A = \left( {\begin{array}{*{20}{c}}3&1\\2&2\end{array}} \right)\] Verifiquen que los siguientes son sus autovalores: \[\lambda = 4\] \[\lambda = 1\] Si la matriz tiene dos autovalores distintos, sin hacer ninguna cuenta más, ¿podemos asegurar que es diagonalizable?
Sí, porque hay una propiedad que dice que los autovectores asociados a autovalores distintos son linealmente independientes. Los autovectores son: \[{v_1} = \left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right)\;\;\;{v_2} = \left( {\begin{array}{*{20}{c}}1\\{ - 2}\end{array}} \right)\] Armamos la matriz \(P\) poniendo los autovectores como columnas: \[P = \left( {\begin{array}{*{20}{c}}1&1\\1&{ - 2}\end{array}} \right)\] La inversa de \(P\;\) la obtenemos haciendo: \[{P^{ - 1}} = \frac{1}{{\det \left( P \right)}}.adj\left( P \right)\]
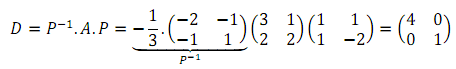
Diagonalizar la siguiente matriz si es posible: \[B = \left( {\begin{array}{*{20}{c}}1&2&4\\2&1&{ - 4}\\0&0&3\end{array}} \right)\] Buscamos los autovalores: \[\det \left( {B -\lambda I} \right) = \left| {\begin{array}{*{20}{c}}{1 - \lambda }&2&4\\2&{1 - \lambda }&{ - 4}\\0&0&{3 - \lambda }\end{array}} \right| = \left( {3 - \lambda } \right)\left( {{{\left( {1 - \lambda \;} \right)}^2} - 4} \right)\] \[\;\lambda = 3\;\left( {doble} \right) \vee \lambda = - 1\] Atención: es un error muy común suponer que la existencia de un autovalor doble implica que la matriz no es diagonalizable.
Para \(\lambda = - 1\) buscamos el autoespacio correspondiente: \[\left( {\begin{array}{*{20}{c}}2&2&4\\2&2&{ - 4}\\0&0&4\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\{\begin{array}{*{20}{c}}y\\z\end{array}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right)\]
Verifiquen que el otro autoespacio es: \[{S\large_3} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\{\begin{array}{*{20}{c}}1\\0\end{array}}\end{array}} \right),\left( {\begin{array}{*{20}{c}}2\\{\begin{array}{*{20}{c}}0\\1\end{array}}\end{array}} \right)} \right\}\] Como pudimos obtener tres autovectores linealmente independientes, la matriz \(P\) existe y la construimos ubicando a los autovectores como columna: \[P = \left( {\begin{array}{*{20}{c}}1 & 2 & 1\\{ - 1}&0&1\\0&1&0\end{array}} \right)\] Ésta es la matriz que permite diagonalizar a la matriz \(B\). \[{P^{ - 1}} = \left( {\begin{array}{*{20}{c}}{\dfrac{1}{2}}&{ - \dfrac{1}{2}}&{ - 1}\\0&0&1\\{\dfrac{1}{2}}&{\dfrac{1}{2}}&-1\end{array}} \right)\] La matriz diagonal correspondiente es: \[{P^{ - 1}} \, A \, P = D = \left( {\begin{array}{*{20}{c}}{ - 1}&0&0\\0&3&0\\0&0&3\end{array}} \right)\]
El orden de los autovalores en \(D\) es el mismo orden que el de los autovectores en las columnas de \(P.\,\) Por ejemplo si construimos la matriz \(P\) así: \[P = \left( {\begin{array}{*{20}{c}}1&2&1\\1&0&{ - 1}\\0&1&0\end{array}} \right)\] Verifique que la matriz \(D\) queda: \[D = \left( {\begin{array}{*{20}{c}}3&0&0\\0&3&0\\0&0&{ - 1}\end{array}} \right)\]
Diagonalizar la siguiente matriz si es posible: \[C = \left( {\begin{array}{*{20}{c}}0&{ - 1}\\1&0\end{array}} \right)\] ¿Qué problema tiene esta matriz? ¿Cuál sería el polinomio característico?
No tiene autovalores reales. Entonces no es diagonalizable en \(\mathbb{R}\). Más adelante veremos que es diagonalizable, pero en el campo de los números complejos.
Sea: \[M = \left( {\begin{array}{*{20}{c}}1&2&3\\2&a&b\\0&0&3\end{array}} \right)\] Determinar los valores de \(a\) y \(b\) de modo que \(\lambda = 3\) sea autovalor doble, y \(M\) sea diagonalizable.

¿Qué puede decirse de las matrices que tienen todos sus autovalores distintos? Recordemos que autovectores asociados a autovalores distintos, son LI.
Por lo tanto:
Si una matriz \(A \in {\mathbb{R}^{n \times n}}\) tiene \(n\) autovalores distintos, entonces tiene \(n\) autovectores LI y en consecuencia es diagonalizable.
Observación importante: Si una matriz es diagonalizable ¿puede afirmarse que todos sus autovalores son distintos?
Veamos el siguiente ejemplo: \[A = \left( {\begin{array}{*{20}{c}}1&0&0\\0&1&0\\0&0&2\end{array}} \right)\] Es una matriz diagonalizable porque es diagonalSea $A \in \mathbb{R}^{nxn}$, se dice que $A$ es diagonalizable $\Leftrightarrow A$ es semejante a una matriz diagonal $\Leftrightarrow \exists P \in \mathbb{R}^{nxn}$ / $P^{-1}AP = D$ diagonal. Si $D$ es diagonal: $I^{-1}.D.I = D$ por lo tanto $D$ es diagonalizable. Probamos que toda matriz diagonal, es diagonalizable.. Sin embargo no tiene todos sus autovalores distintos ya que \(\lambda = 1\) es un autovalor doble.

¿Qué característica tiene una matriz ortogonal? Que la traspuesta de la matriz La traspuesta de una matriz \(A \in \mathbb{R}^{mxn}, \,\) que indicamos como \(A^T\), es la matriz de \(n×m\) que se obtiene a partir de \(A\) cambiando las filas por las columnas. es igual a la inversa: \[P \in {\mathbb{R}^{n \times n}}{\rm{\;es\;ortogonal\;}} \Leftrightarrow {P^{ - 1}} = {P^{\,T}}\] Una matriz \(P \in {\mathbb{R}^{n \times n}}\;\) es ortogonal si y sólo si:
Otra forma de decirlo:
Consideremos los siguientes ejemplos: \[P = \left( {\begin{array}{*{20}{c}}{\dfrac{1}{{\sqrt 2 }}}&{ - \dfrac{1}{{\sqrt 2 }}}\\{\dfrac{1}{{\sqrt 2 }}}&{\dfrac{1}{{\sqrt 2 }}}\end{array}} \right)\;\;\;\qquad \;\;\;Q = \left( {\begin{array}{*{20}{c}}{\dfrac{3}{5}}&{ - \, \dfrac{4}{5}}\\{\dfrac{4}{5}}&{\dfrac{3}{5}}\end{array}} \right)\] Estas matrices son ortogonales. Verifique que efectivamente sus columnas son ortogonales y de módulo 1.
Consideremos la matriz simétrica: \[A = \left( {\begin{array}{*{20}{c}}1&2\\2&4\end{array}} \right)\] Vamos a hacer una diagonalización ortogonal de esta matriz. Los autovalores son: \[\lambda = 0 \vee \lambda = 5\]
El autoespacio asociadoSi \(\lambda\) es un autovalor de \(A\), se denomina autoespacio \(S\large_λ\) al subespacio que contiene todos los autovectores asociados al autovalor \(\lambda\) y además el vector nulo. a \(\lambda = 5\) queda: \[\left( {\begin{array}{*{20}{c}}{ - 4}&2\\2&-1\end{array}} \right) \left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right) \Rightarrow {S\large_5} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\2\end{array}} \right)} \right\}\] Y el autoespacio asociado a \(\lambda = 0\) queda: \[\left( {\begin{array}{*{20}{c}}1&2\\2&4\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right) \Rightarrow {S\large_0} = gen\left\{ {\left( {\begin{array}{*{20}{c}}{ - 2}\\1\end{array}} \right)} \right\}\] Comprobemos que son perpendiculares los autovectores obtenidos: \[\left( {\begin{array}{*{20}{c}}1\\2\end{array}} \right) \left( {\begin{array}{*{20}{c}}{ - 2}\\1\end{array}} \right) = 1.\left( { -2} \right) + 2.1 = 0\] No es casual que los autovectores que hemos obtenido sean perpendiculares:En las matrices simétricas, los autovectores asociados a autovalores distintos son ortogonales.
Ya tenemos dos vectores perpendiculares. \[P = \left( {\begin{array}{*{20}{c}}1&{ - 2}\\2&1\end{array}} \right)\] Con esta matriz \(P\;\) puedo diagonalizar a la matriz \(A\): \[\;{P^{ - 1}}AP = D = \left( {\begin{array}{*{20}{c}}5&0\\0&0\end{array}} \right)\] Esta es una diagonalización de \(A\), similar a otros ejemplos previos. Pero precisamente por ser \(A\) simétrica, los autoespacios son rectas ortogonales. Por lo tanto, podríamos diagonalizar la matriz \(A\) mediante una matriz \(Q\) ortogonal (columnas ortogonales y de módulo 1) ¿Cuál sería la matriz \(Q\,\)?
Falta que los vectores columna sean versores. Para lograr esto hay que dividir cada autovector por su módulo. Tienen módulo igual a \(\sqrt 5\; \): \[Q = \left( {\begin{array}{*{20}{c}}{\dfrac{1}{{\sqrt 5 }}}&{ - \dfrac{2}{{\sqrt 5 }}}\\{\dfrac{2}{{\sqrt 5 }}\;}&{\dfrac{1}{{\sqrt 5 }}}\end{array}} \right)\] Esta matriz es ortogonal: \({Q^T} = {Q^{ - 1}}\). Entonces la diagonalización ortogonal de la matriz \(A\) queda: \[{Q^{ - 1}}AQ = {Q^T}AQ = D = \left( {\begin{array}{*{20}{c}}5&0\\0&0\end{array}} \right)\]
Definición:
Una matriz \(A \in {\mathbb{R}^{n \times n}}\) es diagonalizable ortogonalmente si y sólo si existe \(P\) ortogonal (\({P^{ - 1}} = {P^{\,T}}\)) tal que \({P^{\,T}}AP = D\).
Puede demostrarse que toda matriz simétrica es ortogonalmente diagonalizable. Pero además, las únicas matrices reales que pueden diagonalizarse ortogonalmente son las matrices simétricas.
En resumen:
Sea \(T:V \to V\) una transformación lineal:
\(\lambda \in \mathbb{R}\) es autovalor de \(T \Leftrightarrow \exists \, v \in V\) no nulo, tal que \(T\left( v \right) = \lambda \,v\)
\(v\) es el autovector asociado a \(\lambda \).
Si \(V\) fuera un espacio de polinomios, entonces \(v\) sería un polinomio.
Si \(V\) fuera un espacio de matrices, entonces \(v\) sería una matriz.
Nosotros vamos a trabajar en \(V = {\mathbb{R}^n}\)
Sea \(T:{\mathbb{R}^n} \to {\mathbb{R}^n}\;\) tal que \(A = M{\left( T \right)\large_{EE}}\), entonces:
\(\lambda \) es autovalor de \(T \Leftrightarrow \) \(\lambda \) es autovalor de \(A\)
Por ser \(A\,\) la matriz estándar resulta:
\[T\left( v \right) = A\,v\;\;{\rm{con}}\;\;v = \left( {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\\ \vdots \end{array}}\\{{x_n}}\end{array}} \right)\]
\(\lambda \) es autovalor de \(T\) \( \Leftrightarrow \) \(\exists \, v \in {\mathbb{R}\large{^n}}\) no nulo tal que \(T\left( v \right) = \lambda \, v\) \(\; \Leftrightarrow \) \(\;\exists \, v \in {\mathbb{R}\large^{nx1}}\) no nulo tal que \(A\,v = \lambda \, v\) \(\; \Leftrightarrow \) \(\;\lambda \) es autovalor de \(A\).
Probamos que en una TL en \({\mathbb{R}^n}\), los autovalores y autovectores de la transformación son los mismos que los de su matriz asociada en base canónica.
Sea \(T:V \to V\) una transformación lineal. Decimos que \(T\) es diagonalizable si existe alguna base \(B\;\) tal que la matriz \({M_{BB}}\left( T \right)\) es diagonal.
Dada la transformación lineal:
\[T:{\mathbb{R}^2} \to {\mathbb{R}^2}|\;T\left( {\left( {x,y} \right)} \right) = \left( {x + 2y,\; 3y} \right)\]Hallar los autovectores y autovalores de \(T\), y analizar si es diagonalizable.
1) Buscamos la matriz de \(T\) en la base canónica.
\[A = M{\left( T \right)_{EE}} = \left( {\begin{array}{*{20}{c}}1&2\\0&3\end{array}} \right)\]
\[\lambda = 1 \vee \lambda = 3\]
\[{S\large_1} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right)} \right\}\]
\[{S\large_3} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right)} \right\}\]
3) \(A\) es diagonalizable, con
\[P = \left( {\begin{array}{*{20}{c}}1&1\\0&1\end{array}} \right)\;\;\;y\;\;\;\;D = {P^{ - 1}}\,A\,P = \left( {\begin{array}{*{20}{c}}1&0\\0&3\end{array}} \right)\]
Veamos que representa D:
\(B = \left\{ {\left( {1,0} \right),\left( {1,1} \right)} \right\}\) es una base de \({\mathbb{R}^2}\) formada por autovectores de \(T\),
¿Cómo se busca la matriz asociada a una transformación lineal?
\[M{\left( T \right)_{BB}} = \left( {\left[ {T\left( {{v_1}} \right){]_B}\;\;\;\;} \right[T\left( {{v_2}} \right){]_B}\;} \right)\]
Entonces esas coordenadas son:
\[T\left( {\left( {1,0} \right)} \right) = \left( {1,0} \right) = 1\left( {1,0} \right) + 0\left( {1,1} \right)\;\; \Rightarrow {\left[ {\left( {1,0} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right)\]
\[T\left( {\left( {1,1} \right)} \right) = \left( {3,3} \right) = 0\left( {1,0} \right) + 3\left( {1,1} \right)\;\; \Rightarrow {\left[ {\left( {3,3} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}0\\3\end{array}} \right)\]
Así que la matriz queda:
\[M{\left( T \right)_{BB}} = \left( {\begin{array}{*{20}{c}}1&0\\0&3\end{array}} \right) = D\]
Entonces, si tenemos una base \(B\) formada por autovectores de \(T\), ¡la matriz asociada en esa base es diagonal!
Una TL en \({\mathbb{R}\large^n}\) es diagonalizable si y sólo si existe una base \(B\) de \({\mathbb{R}\large^n}\;\) formada por autovectores de \(T\). En tal caso, \(M{\left( T \right)\large_{BB}} = D\).
Desde la perspectiva matricial, \(T\) es diagonalizable si y sólo si \(A = M{\left( T \right)\large_{EE}}\;\) es diagonalizable.
a) Sea \(T:{\mathbb{R}^n} \to {\mathbb{R}^n}\) una transformación lineal. Probar:
Si \(Nu\left( T \right) \ne \left\{ {{\large 0_{\large{\mathbb{R}^n}}}} \right\}\) entonces \(\lambda = 0\) es un autovalor de \(T\) y el autoespacio correspondiente es\(\;Nu\left( T \right)\)
b) Sea \(T:{\mathbb{R}^3} \to {\mathbb{R}^3}\) una transformación lineal que verifica las siguientes condiciones:
i) \(T\left( v \right) = 2v\;\;\forall v \in S = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}\;\;|\;x - z = 0\;} \right\}\)
ii) \(Nu\left( T \right) = gen\left\{ {\left( {1,0,0} \right)} \right\}\)
Analizar si existe una base \(B\) de \({\mathbb{R}^3}\) tal que la matriz asociada a \(T\) respecto de dicha base sea diagonal. En caso afirmativo indicar \(B\) y \(M{\left( T \right)_{BB}}\).

Como hiciéramos en el capítulo anterior, recurrimos a la IA Gemini 2.0, ahora para descubrir algunas aplicaciones de los autovalores y los autovectores.
Cliquea en el botón superior derecho del interactivo para tener el recurso abierto de forma independiente y navega por las distintas pestañas.
Esta actividad es para conocer una aplicación de los contenidos de este capitulo. Quien quiera profundizar en el tema tratado puede acceder a https://economipedia.com/definiciones/cadena-de-markov.html
Sea \(A \in {\mathbb{R}^{n \times n}}\)
\[{P^{ - 1}}AP = D\]
donde \(D\) es una matriz diagonal.
En la matriz diagonal \(D\) que se obtiene están los autovalores ordenados de acuerdo con el orden de los autovectores en las columnas de \(P\):
\[{P^{ - 1}}AP = D = \left( {\begin{array}{*{20}{c}}{{\lambda _1}}&0&0\\0& \ddots &0\\0&0&{{\lambda _n}}\end{array}} \right)\]
Cómo veremos a continuación esta relación permite calcular fácilmente potencias de matrices diagonalizables.
Considerando que \({P^{ - 1}}AP = D\) y multiplicando a la izquierda por \(P\) y a la derecha por \({P^{ -1}}\), se obtiene:
 \[ \Rightarrow \;\;\;A = PD{P^{ - 1}}\]
\[ \Rightarrow \;\;\;A = PD{P^{ - 1}}\]
Ahora, calculemos \({A^2}\) :
\[{A^2} = \left( {PD{P^{ - 1}}} \right)\left( {PD{P^{ - 1}}} \right) = PD{P^{ - 1}}.PD{P^{ - 1}}\]
El producto de matrices es asociativo, entonces:
\[{A^2} = P\;D\;I\;D\;{P^{ - 1}}\]
\[{A^2} = P{D\,^2}{P^{ - 1}}\]
En general, en términos prácticos, es mucho más sencillo calcular \({D\,^2}\) que \({A^2}\), y más aún en caso de que los exponentes sean mayores.
Las potencias de una matriz diagonal se obtienen calculando las potencias de los elementos que están en la diagonal principal:
\[D = \left( {\begin{array}{*{20}{c}}{{\lambda _1}}& \ldots &0\\ \vdots & \ddots & \vdots \\0& \ldots &{{\lambda _n}}\end{array}} \right)\;\; \Rightarrow \;\;{D~^k} = \left( {\begin{array}{*{20}{c}}{{\lambda _1}^k}& \ldots &0\\ \vdots & \ddots & \vdots \\0& \ldots &{{\lambda _n}^k}\end{array}} \right)\]
En conclusión hemos encontrado que para cualquier matriz \(A\) diagonalizable:
Ejemplo 1
Calcular \({A^{10}}\) , siendo \(A = \left( {\begin{array}{*{20}{c}}1&3\\2&2\end{array}} \right)\)
ResoluciónVamos a intentar diagonalizar \(A\) para no tener que calcular:
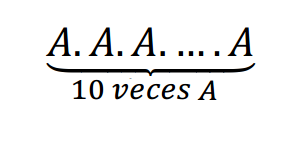
Si \(A\) es diagonalizable será posible hacer:
\[{A^{10}} = P{D^{10}}{P^{ -1}}\]
Veamos si \(A\) es diagonalizable. Se puede verificar que sus autovalores son:
\[{\lambda _1} = 4\;\;\;,\;\;\;{\lambda _2} = - 1\]
Ya es posible afirmar que es diagonalizable, porque autovectores asociados a autovalores distintos son LI.
El lector puede verificar que los autoespacios son los siguientes:
\[{S_{{\lambda _1} \; = \; 4}} = \left\{ {\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right):\;\;y = x} \right\}\]
\[{S_{{\lambda _2} \; = \;- 1}} = \left\{ {\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right):\;\;y = - \; \frac{2}{3}x} \right\}\] Luego podemos armar la matriz \(P\): \[P = \left( {\begin{array}{*{20}{c}}1&3\\1&{ - 2}\end{array}} \right)\] Obtenemos su inversa: \[{P^{ - 1}} = \left( {\begin{array}{*{20}{c}}{\frac{2}{5}}&{\frac{3}{5}}\\{\frac{1}{5}}&{ -\frac{1}{5}}\end{array}} \right)\] Calculamos el producto: \[{P^{ - 1}}AP = \left( {\begin{array}{*{20}{c}}4&0\\0&{ - 1}\end{array}} \right) = D\] Por la propiedad que hemos visto: \[{A^{10}} = P{D^{10}}{P^{ - 1}}\]
\[\Rightarrow {A^{10}} = \left( {\begin{array}{*{10}{c}} 1 & 3 \\ 1 & { -2}\end{array}} \right)\left( {\begin{array}{*{10}{c}}{{4^{10}}} & 0 \\ 0 & {{{\left( { -1} \right)}^{10}}}\end{array}} \right)\left( {\begin{array}{*{10}{c}}{\frac{2}{5}} & {\frac{3}{5}}\\{\frac{1}{5}} & { - \frac{1}{5}}\end{array}} \right) \]
Habíamos visto (en
Si \(A \in {\mathbb{R}^{n~x~n}}\) es simétrica (\(A = {A^t}\)), entonces se verifican las siguientes propiedades:
\(A\;\)simétrica \(\, \Rightarrow \exists P\;\) ortogonal \(|\;{P^{-1}}A\;P = {P~^t}A\;P = D\)
Nota: Recordemos que \(P \in {\mathbb{R}^{n \times n}}\) es ortogonal si y sólo sí \({P~^t} = {P^{ - 1}}\). Las matrices ortogonales se caracterizan porque sus columnas son vectores ortogonales y de norma (módulo) 1.
Ejemplo 2
Calculemos la diagonalización de la matriz:
\(A = \left( {\begin{array}{*{20}{c}}3&4\\4&9\end{array}} \right)\)
El lector puede verificar que sus autovalores y autoespacios son:
\[\lambda = 11\;\;\;,\;\;\;{S_{11}} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\2\end{array}} \right)} \right\}\]
\[\lambda = 1\;\;\;,\;\;\;\;{S_1} = gen\left\{ {\left( {\begin{array}{*{20}{c}}{ - 2}\\1\end{array}} \right)} \right\}\]
Observamos que los autoespacios son ortogonales (propiedad de las simétricas). Podemos construir la matriz \(P\) (cuyas columnas son los autovectores) que permite diagonalizar \(A\) :
\[P = \left( {\begin{array}{*{20}{c}}1&{ - 2}\\2&1\end{array}} \right)\]
\[{P^{ - 1}}AP = D = \left( {\begin{array}{*{20}{c}}{11}&0\\0&1\end{array}} \right)\]
Si bien las columnas de \(P\) son ortogonales, \(P\) no es una matriz ortogonal porque sus columnas no tienen módulo 1. Nos falta normalizar los autovectores, o sea obtener sus versores asociados:
\[ \check{v}_1=\frac{1}{\sqrt{5}}\begin{pmatrix} 1 \\2 \end{pmatrix}, \;\; \check{v}_2=\frac{1}{\sqrt{5}}\begin{pmatrix} -2 \\1 \end{pmatrix} \]
Entonces podemos diagonalizar \(A\) mediante una matriz \(Q\) ortogonal:
\[Q = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 5 }}}&{\frac{{ - 2}}{{\sqrt 5 }}}\\{\frac{2}{{\sqrt 5 }}}&{\frac{1}{{\sqrt 5 }}}\end{array}} \right)\]
Esta matriz sí verifica: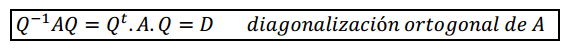
Encontrar una matriz \(A \in {\mathbb{R}^{2 \times 2}}\) simétrica que verifique las siguientes condiciones: \[A\left( {\begin{array}{*{20}{c}}3\\4\end{array}} \right) = \left( {\begin{array}{*{20}{c}}6\\8\end{array}} \right)\;\;\;y\;\;\;det\left( A \right) = - 2\] Sugerencia: Tener en cuenta que \({\lambda _1}\;.{\lambda _2} = det\left( A \right)\)

Dada la ecuación en \({\mathbb{R}^2}\,\): \( \,3{x^2} + 9{y^2} = 6\)
Podemos identificar, por los signos de los coeficientes, que corresponde a una elipse cuya ecuación canónica es:
\[\frac{{{x^2}}}{2} + \frac{{{y^2}}}{{\frac{2}{3}}} = 1\]
Nos interesa descubrir qué curva está representada por la siguiente ecuación:
\[3{x^2} + 8xy + 9{y^2} = 6\;\;\;\;\;\;\;\;\;\left[ 1 \right]\]
Aparece en esta ecuación el término \(8xy\), denominado término rectangular o de producto cruzado.
Usamos GeoGebra para obtener la gráfica de esta cónica:
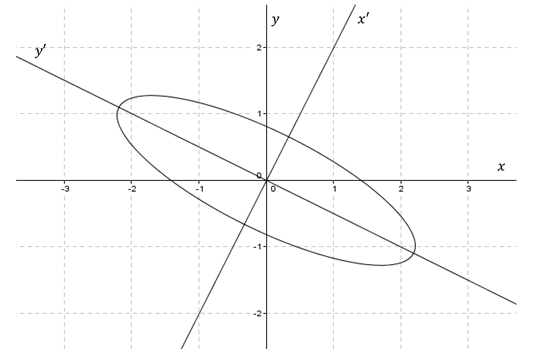
Observamos que se trata de una elipse cuyos ejes no son paralelos a los ejes coordenados. Veremos a continuación cómo hallar las direcciones de esos ejes para obtener la ecuación canónica e identificar analíticamente la cónica.
Retomemos la ecuación [1]:
\[3{x^2} + 8xy + 9{y^2} = 6\] Esta ecuación puede expresarse matricialmente como sigue: \[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}{}&{}\\{}&{}\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\]Los coeficientes de \({x^2}\) y de \({y^2}\) van en la diagonal:
\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}3&{}\\{}&9\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\]
Y el coeficiente del término rectangular se divide por dos para completar una matriz simétrica:
\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}3&4\\4&9\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\;\;\;\;\;\;\;\;\;\;\;\;\left[ 1 \right]\]
Verifiquemos que efectivamente se obtiene lo mismo:
\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}3&4\\4&9\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\]
\[ \Rightarrow \;\left( {3x + 4y\;\;\;\;\;4x + 9y} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\]
\[ \Rightarrow \left( {3x + 4y} \right)x + \left( {4x + 9y} \right)y = 6\]
\( \Rightarrow 3{x^2} + 8xy + 9{y^2} = 6\)
La expresión \(3{x^2} + 8xy + 9{y^2}\) se denomina forma cuadrática y la matriz simétrica que la caracteriza es \(A = \left( {\begin{array}{*{20}{c}}3&4\\4&9\end{array}} \right)\).
Por ser \(A\) una matriz simétrica, es ortogonalmente diagonalizable.
Como habíamos visto en un
La matriz \(Q\), cuyas columnas son autovectores unitarios de A, representa un cambio de base como veremos a continuación.
Se puede leer lo que escribimos sobre cambio de base
Tomemos un par de bases del mismo espacio vectorial \(V\):
\[B = \left\{ {{v_1}, \ldots ,{v_n}}\right\}\; y {\rm{\;}}B~' = \left\{ {{w_1}, \ldots ,{w_n}} \right\}\]Construyamos la matriz asociada a la transformación lineal identidad:
\[M{\left( {Id} \right)_{BB~'}} = \left( {{{\left[ {{v_1}} \right]}_{B~'}},{\rm{\;}} \ldots ,{\rm{\;}}{{\left[ {{v_n}} \right]}_{B~'}}} \right) \in {\mathbb{R}^{n \times n}}\]Esta matriz, llamada matriz de cambio de base de \(B\) a \(B~'\) , permite pasar de coordenadas en \(B\) a coordenadas en \(B~'\):
\[M{\left( {Id} \right)_{BB~'}}.{\left[ v \right]_B} = {\left[ v \right]_{B~'}}\] Resulta:
\[Q = M{\left( {Id} \right)_{BE}}\]
Por lo tanto:
\[Q\;{\left[ v \right]_B} = {\left[ v \right]_E}\]
\[Q\left( {\begin{array}{*{20}{c}}{x~'}\\{y~'}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right)\]
Resulta:
\[Q = M{\left( {Id} \right)_{BE}}\]
Por lo tanto:
\[Q\;{\left[ v \right]_B} = {\left[ v \right]_E}\]
\[Q\left( {\begin{array}{*{20}{c}}{x~'}\\{y~'}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right)\]
Trasponemos ambos miembros de la igualdad:
\[\left( {\;x\;\;\;y} \right) = \left( {x~'\;\;y~'} \right){Q~^t}\]Sustituimos en [1]:
\[\left( {x\;\;\;y} \right)\;A\;\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 6\;\;\;\; \Rightarrow \;\;\left( {{x^{‘\;}}y’} \right){Q^t}AQ\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) = 6\]Como \(Q\) es ortogonal, se verifica:
\[{Q^t}AQ = {Q^{-1}}AQ = D\]Y entonces la ecuación de la cónica en el nuevo sistema de coordenadas es:
\[\left( {x’\;y’} \right)\left( {\begin{array}{*{20}{c}}{11}&0\\0&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) = 6\] \[11{x’^2} + 1{y’^2} = 6\] Observamos que representa una elipse cuya ecuación canónica es: \[\frac{{{{x’}^2}}}{{\frac{6}{{11}}}} + \frac{{{{y’}^2}}}{6} = 1\]¿Cómo se grafica esta elipse? El cambio de base que realizamos define un nuevo sistema de ejes ortogonales. Las columnas de \(Q\) indican dirección y sentido positivo de estos nuevos ejes.
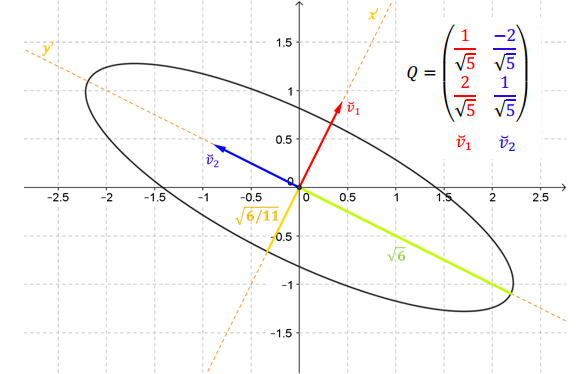
A continuación generalizaremos el método de eliminación de productos cruzados que hemos aplicado en el ejemplo anterior.
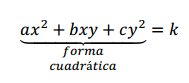 1) Buscamos la expresión matricial de la forma cuadrática:
1) Buscamos la expresión matricial de la forma cuadrática:
La matriz \(A = \left( {\begin{array}{*{20}{c}}a&{\frac{b}{2}}\\{\frac{b}{2}}&c\end{array}} \right)\) es la matriz simétrica que caracteriza a la forma cuadrática.
2) Diagonalizamos ortogonalmente la matriz de la forma cuadrática:
Como la matriz es simétrica, es ortogonalmente diagonalizable. Entonces \(\exists Q\;\)ortogonal tal que \({Q^t}A\;Q = D\). La matriz \(Q\) la obtenemos con los autovectores normalizados.
\[Q=\left ( \check{v_1} \quad \check{v_2}\right)\]Como las columnas de \(Q\) son perpendiculares y unitarias (de norma 1), se verifica que \({Q~^t} = {Q~^{-1}}\).
3) La matriz \(Q\) hallada nos permite proponer un cambio de base o de coordenadas:
\[\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = Q\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\;\; \Rightarrow \;\;\;\left( {x\;\;\;y} \right) = \left( {x’\;\;y’} \right){Q^t}\]
4) Reemplazamos en [1]:
\[\left( {x’\;\;y’} \right)\left( {\begin{array}{*{20}{c}}{{\lambda _1}}&0\\0&{{\lambda _2}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right) = k\]
Con este procedimiento pudimos eliminar el término de producto cruzado, obteniendo la ecuación de la cónica en el nuevo sistema de coordenadas.
\[{x^2} + 4xy + {y^2} = 9\]
El término de producto cruzado \(4xy\) indica que la cónica está rotada respecto de los ejes canónicos.
1) Buscamos la expresión matricial:
\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}1&2\\2&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 9\]
2) Diagonalizamos ortogonalmente la matriz de la forma
cuadrática\(\,A = \left( {\begin{array}{*{20}{c}}1&2\\2&1\end{array}} \right)\;:\)
Dejamos a cargo del lector comprobar que los autovalores son:
\[\lambda = - 1\,,\;\;\;\lambda = 3\]
Y los autoespacios:
\[{S_{ - 1}} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\{ -1}\end{array}} \right)} \right\}\;\;\;,\;\;\;{S_3} = gen\left\{ {\left( {\begin{array}{*{20}{c}}1\\1\end{array}} \right)} \right\}\]
Con los autovectores hallados podemos armar la matriz \(Q\) ortogonal (de columnas ortogonales y de módulo 1):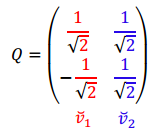
Recordemos que las columnas de \(Q\) indican la dirección y sentido positivo de los nuevos ejes \(\;{x’},\;{y’} \).
3) La matriz \(Q\) hallada nos permite proponer un cambio de base o de coordenadas:

4) Reemplazamos en la expresión matricial:
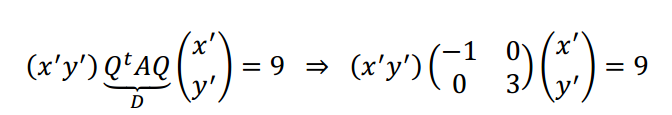
\[ - {x’~^2} + 3{y’~^2} = 9\]
\[ - \frac{{{{x’}~^2}}}{9} + \frac{{{{y’}~^2}}}{3} = 1\]
Ésta es la ecuación canónica de una hipérbola de eje focal \(y’\), cuya gráfica es:
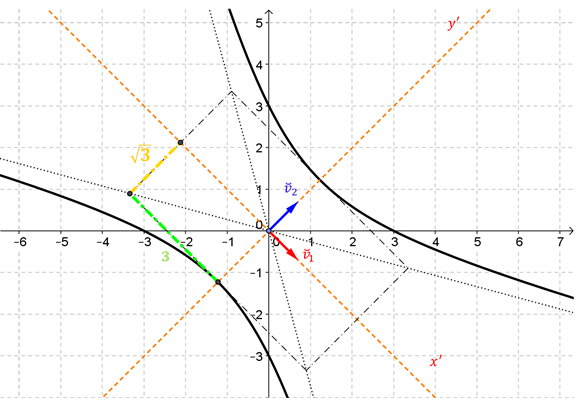
¿Cuáles son las coordenadas de los vértices de la hipérbola respecto de la base canónica?
Las bases de los dos sistemas de coordenadas que estamos utilizando son: \[B = \left\{ {\left( {\begin{array}{*{20}{c}}1\\0\end{array}} \right),\left( {\begin{array}{*{20}{c}}0\\1\end{array}} \right)} \right\}\;\;\;\;\;,\;\;\;\;\;\;\;B~’ = \left\{ {\left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}\\{- \, \frac{1}{{\sqrt 2 }}}\end{array}} \right),\left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}\\{\frac{1}{{\sqrt 2 }}}\end{array}} \right)} \right\}\]De la ecuación canónica se deduce:
Coordenadas de los vértices en \(B~’ = \pm \left( {\begin{array}{*{20}{c}}0\\{\sqrt 3 }\end{array}} \right)\)
Realicemos el cambio de coordenadas:
\[\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = Q\left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\;\;\; \Rightarrow \;\;\;\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\\{ - \, \frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}0\\{ \pm \sqrt 3 }\end{array}} \right) = \pm \left( {\begin{array}{*{20}{c}}{\frac{{\sqrt 3 }}{{\sqrt 2 }}}\\{\frac{{\sqrt 3 }}{{\sqrt 2 }}}\end{array}} \right)\]Éstas son las coordenadas de los vértices de la hipérbola respecto de la base canónica.
Dada la ecuación:
\(\left( {\begin{array}{*{20}{c}}x&y\end{array}} \right)A\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 4\) con \(A = \left( {\begin{array}{*{20}{c}}2&2\\2&5\end{array}} \right)\)
a) Obtener la ecuación canónica e identificar la cónica correspondiente. ¿Cuál es la dirección del eje focal de dicha cónica?
b) Considerando la misma \(A\), analizar qué lugar geométrico representa la ecuación \(\left( {\begin{array}{*{20}{c}}x&y\end{array}} \right)\;A\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = k\) para: \(k > 0\;,\;\;k = 0\;\;,\;\;k < 0.\)

Consideremos la siguiente ecuación:
\[{x^2} + 4xy + {y^2} + 6x - 9y = 9\]
Nos interesa saber qué cónica representa y graficarla.
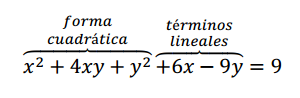
El término de producto cruzado señala que la cónica está rotada respecto de los ejes canónicos.
Además, los términos lineales indican que posiblemente sea necesario realizar una traslación (completando cuadrados) para identificar y graficar la cónica.
1) Buscamos la expresión matricial:
\[\left( {x\;\;y} \right)\left( {\begin{array}{*{20}{c}}1&2\\2&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) + \left( {6\;\; - 9} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 9\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ 1 \right]\]
Les sugerimos comprobar que se obtiene la ecuación dada. Generalizando, la escritura matricial de los términos lineales es la siguiente:
\[dx + ey = \left( {d\;\;\;\;\;\;e} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right)\]2) Diagonalizamos ortogonalmente la matriz de la forma cuadrática
\[A = \left( {\begin{array}{*{20}{c}}1&2\\2&1\end{array}} \right)\]3) La matriz \(Q\) hallada nos permite proponer un cambio de base o de coordenadas:
Estos dos pasos ya se hicieron en el ejemplo anterior, siendo:
\(Q = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\\{-\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\end{array}} \right)\) , \({\rm{\;}}D = \left( {\begin{array}{*{20}{c}}{-1}&0\\0&3\end{array}} \right)\)
\[\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = Q \left( {\begin{array}{*{20}{c}}{x’}\\{y’}\end{array}} \right)\;\;\;\;\;\; \Rightarrow \;\;\;\;\left( {x\;\;\;y} \right) = \left( {x’\;\;y’} \right){Q^t}\]4) Reemplazamos en la expresión matricial [1]:
Observamos que los términos lineales se modifican por el cambio de base realizado.
Hasta aquí, pudimos eliminar el término de producto cruzado definiendo un nuevo sistema de ejes paralelos a los ejes de la cónica.
5) Efectuamos una traslación para obtener la ecuación canónica.
Tal como habíamos visto en la unidad anterior, el método de completar cuadrados nos permite ubicar el centro o el vértice de la cónica y obtener su ecuación canónica.
\[ - {x'~^2} + \dfrac{{15}}{{\sqrt 2 }}x'+ 3{y'~^2} -\dfrac{3}{{\sqrt 2 }}y' = 9\] \[\small -\left[ {{{\left( {x' - \, \frac{{15}}{{2\sqrt 2 }}} \right)}^2} - {{\left( {\frac{{15}}{{2\sqrt 2 }}} \right)}^2}} \right] + 3\left[ {{{\left( {y' - \frac{1}{{2\sqrt 2 }}} \right)}^2} - {{\left( {\frac{1}{{2\sqrt 2 }}} \right)}^2}} \right] = 9\] \[ - \left[ {{{\left( {x’ - \frac{{15}}{{2\sqrt 2 }}} \right)}^2} - \frac{{225}}{8}} \right] + 3\left[ {{{\left( {y’ - \frac{1}{{2\sqrt 2 }}} \right)}^2} - \frac{1}{8}} \right] = 9\] \[ - {\left( {x’ - \frac{{15}}{{2\sqrt 2 }}} \right)^2} + \frac{{225}}{8} + 3{\left( {y’ -\frac{1}{{2\sqrt 2 }}} \right)^2} - \frac{3}{8} = 9\] \[ - {\left( {x’ - \frac{{15}}{{2\sqrt 2 }}} \right)^2} + 3{\left( {y’ - \dfrac{1}{{2\sqrt 2 }}} \right)^2} = - \frac{{75}}{4}\] \[\frac{{{{\left( {x’ - \dfrac{{15}}{{2\sqrt 2 }}} \right)}^2}}}{{\dfrac{{75}}{4}}} - \dfrac{{{{\left( {y’ - \dfrac{1}{{2\sqrt 2 }}} \right)}^2}}}{{\dfrac{{25}}{4}}} = 1\]Obtuvimos la ecuación ordinaria de una hipérbola que tiene las siguientes características:
1) Está rotada respecto de los ejes canónicos. Las direcciones y sentidos positivos de los nuevos ejes \(x’\;y’\;\) están dadas por las columnas de \(Q\,\), como habíamos visto.
2) De acuerdo con los signos en la ecuación, el eje focal es paralelo al eje \(x’\).
3) Las coordenadas del centro de la hipérbola en el sistema \(x’\;y’\) son:
\[\alpha = \frac{{15}}{{2\sqrt 2 }}\;\;\;;\;\;\;\beta = \frac{1}{{2\sqrt 2 }}\]Para obtener la ecuación canónica, planteamos las ecuaciones de traslación:
\[\left\{ {\begin{array}{*{20}{c}}{x'' = x' - \dfrac{{15}}{{2\sqrt 2 }}}\\{y''= y' - \dfrac{1}{{2\sqrt 2 }}}\end{array}} \right.\] \[ \Rightarrow \;\;\;\frac{{{{x''}~^2}}}{{\dfrac{{75}}{4}}} - \frac{{{{y''}~^2}}}{{\dfrac{{25}}{4}}} = 1\]\[semieje\;real = \frac{{5\sqrt 3 }}{2} \cong 4,33\;,\;\;\;\;\;semieje\;imaginario = \frac{5}{2} = 2,5\]
Con esta información podemos realizar un gráfico aproximado de la hipérbola. Primero indicaremos los tres sistemas de ejes:
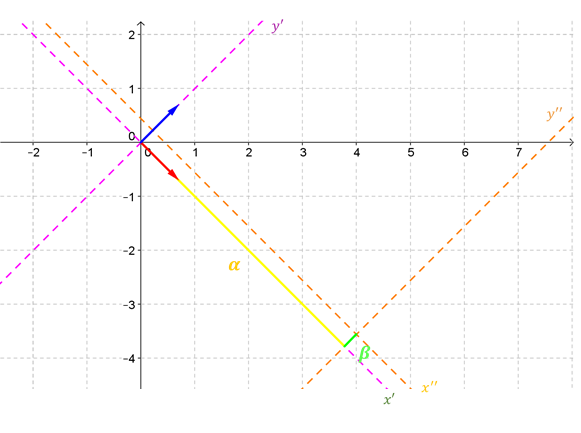
Ahora ya podemos realizar la gráfica de la hipérbola:
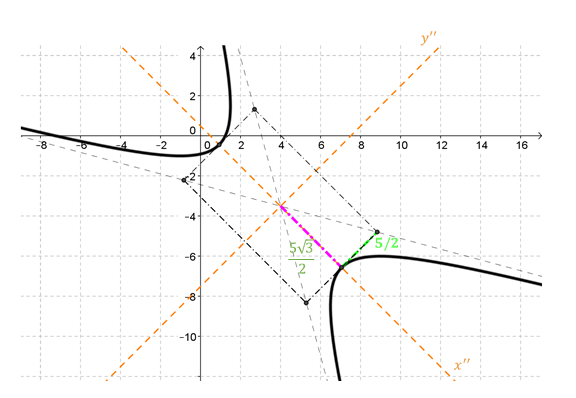
¿Cómo podríamos hallar las coordenadas del centro de la hipérbola respecto de la base canónica?

Consideremos la ecuación:
\[{x^2} - 2xy + {y^2} + \sqrt 2 x - 2\sqrt 2 y = 0\]Nos interesa hallar la ecuación canónica y graficar la cónica correspondiente.
2) Diagonalizamos ortogonalmente y planteamos las ecuaciones de rotación:
3) La matriz \(Q\) hallada nos permite proponer un cambio de base o de coordenadas:
4) Reemplazamos en [1]:
Cómo aparece \({y’^2}\) y no aparece \({x’^2}\) suponemos que será una parábola.
Trataremos de expresarlo como\({\left( {y’ - \beta } \right)^2} = 4c\left( {x’ - \alpha } \right)\):
\[2{y’^2} - 3y’ = x’\] \[2\left[ {{{y’}^2} - \frac{3}{2}y’} \right] = x’\] \[2\left[ {{{\left( {y’ - \frac{3}{4}} \right)}^2} - {{\left( {\frac{3}{4}} \right)}^2}} \right] = x’\] \[2{\left( {y’ - \frac{3}{4}} \right)^2} = x’ + \frac{9}{8}\] \[{\left( {y’ - \frac{3}{4}} \right)^2} = \frac{1}{2}\left( {x’ + \frac{9}{8}} \right)\] \[\alpha = - \frac{9}{8}\;\;\;;\;\;\;\beta = \frac{3}{4}\]Para obtener la ecuación canónica, planteamos las ecuaciones de traslación:
\[\left\{ {\begin{array}{*{20}{c}}{x'' = x' + \dfrac{{9}}{8}}\\{y''= y' - \dfrac{3}{4}}\end{array}} \right.\]Ahora realizamos un gráfico de la parábola indicando los tres sistemas de ejes:
Cómo \(4c = \dfrac{1}{2} > 0\), la parábola se abre hacia el semieje positivo de \({x''}\)
Le proponemos al lector que busque las coordenadas del vértice en la base canónica.
Sea \(A = \left( {\begin{array}{*{20}{c}}2&2\\2&5\end{array}} \right)\), obtener la ecuación canónica y graficar la cónica dada por la ecuación:
\[\left( {\begin{array}{*{20}{c}}x&y\end{array}} \right)\;A\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) + \left( {\begin{array}{*{20}{c}}0&{6\sqrt 5 }\end{array}} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) = 1\]
Notar que la matriz \(A\) es la misma que la dada en el

Sea la ecuación en \({\mathbb{R}^2}\):
\(\left( {\begin{array}{*{20}{c}}x&y\end{array}} \right)\;A\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) + \left( {d\;\;\;\;e} \right)\left( {\begin{array}{*{20}{c}}x\\y\end{array}} \right) + f = 0\;\;\) con \(A \in {\mathbb{R}^{2 \times 2}}\;\) simétrica
De acuerdo con los diferentes ejemplos desarrollados, podemos concluir que los autovalores de la matriz \(A\) permiten identificar el lugar geométrico correspondiente:

En el siguiente gráfico se ven las direcciones de los ejes y la medida del semieje mayor y semieje menor de una elipse rotada:
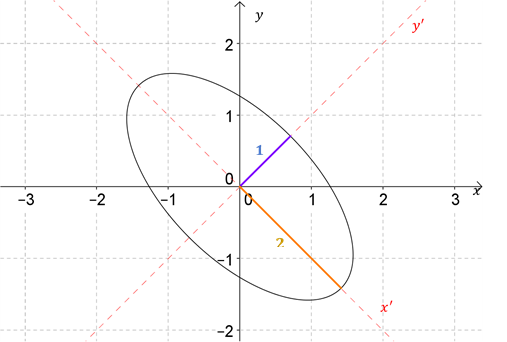
Tomando la información proporcionada en el gráfico, se pide hallar la ecuación de la elipse en términos de \(x\) e \(y\).
Sugerencia: pensar que se trata de resolver el problema inverso al habitual.
Al diagonalizar una matriz simétrica de \({\mathbb{R}^{2 \times 2}}\) se obtienen dos autovectores ortogonales. ¿Qué efecto tiene el orden de los autovectores en la matriz \(Q\) sobre el nuevo sistema de ejes?
| Rotación pura |
|---|
| Queremos eliminar el término rectangular: \[ x^2 + 4xy + y^2 = 1\] \[ \begin{pmatrix} x & y \\ \end{pmatrix}\begin{pmatrix} 1 & 2 \\ 2 & 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix}=1\] Hallamos autovalores y autovectores: \[\lambda =-1\ \Rightarrow S_{-1}=gen\begin{Bmatrix}\begin{pmatrix} 1 \\ -1 \end{pmatrix} \end{Bmatrix}\]\[\lambda =3\ \Rightarrow S_{3}=gen\begin{Bmatrix}\begin{pmatrix} 1 \\ 1 \end{pmatrix} \end{Bmatrix}\]Usamos un orden de los autovectores para construir $Q.\;$Acá está la diferencia: |
Veamos las diferencias entre los desarrollos indicados en cada columna:
| Rotación y simetría |
|---|
| Queremos eliminar el término rectangular: \[ x^2 + 4xy + y^2 = 1\] \[ \begin{pmatrix} x & y \\ \end{pmatrix}\begin{pmatrix} 1 & 2 \\ 2 & 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix}=1\] Hallamos autovalores y autovectores: \[\lambda =3\ \Rightarrow S_{3}=gen\begin{Bmatrix}\begin{pmatrix} 1 \\ 1 \end{pmatrix} \end{Bmatrix}\]\[\lambda =-1\ \Rightarrow S_{-1}=gen\begin{Bmatrix}\begin{pmatrix} 1 \\ -1 \end{pmatrix} \end{Bmatrix}\]Usamos el otro orden de los autovectores para construir $Q.\;$Acá está la diferencia: |
| Rotación pura |
|---|
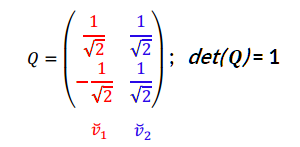 Haciendo el cambio de variables de la ecuación queda: \[ -x'\;^2 + 3y'\;^2 = 1\]
La gráfica correspondiente es: Haciendo el cambio de variables de la ecuación queda: \[ -x'\;^2 + 3y'\;^2 = 1\]
La gráfica correspondiente es:
|
| Rotación y simetría |
|---|
 Haciendo el cambio de variables de la ecuación queda: \[ 3x'\;^2 - y'\;^2 = 1\]
La gráfica correspondiente es: Haciendo el cambio de variables de la ecuación queda: \[ 3x'\;^2 - y'\;^2 = 1\]
La gráfica correspondiente es: |
A los fines de eliminar el término rectangular para reconocer la cónica, cualquiera de las dos formas es válida. Pero es usual trabajar con una matriz \(Q\) tal que \(\det \left( Q \right) = 1\), que caracteriza a una rotación pura.