Al resolver la ecuación obtenemos: $$\left(\begin{array}{cc}x& y\end{array}\right)\left(\begin{array}{cc}2& 2\\ 2& 5\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{cc}0& 6\sqrt{5}\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=1$$ $$2x^2+4xy+5y^2+6\sqrt{5}y=1.$$ Esta es una cónica en forma general. Para identificarla y llevarla a su forma canónica, debemos "diagonalizar" la matriz $A$ (es decir, encontrar un sistema de coordenadas rotado en el que la ecuación no tenga términos cruzados $xy$).

Paso 1: Encontrar los autovalores y autovectores de $A$

Los autovalores de $A$ fueron encontrados en el ejercicio para el lector anterior. Los mismos son: $${\lambda }_1=6\text{y}{\lambda }_2=1.$$ Paso 2: Encontrar los autovectores

Para ${\lambda }_1=6$, resolvemos: $$\left(\begin{array}{cc}2-6& 2\\ 2& 5-6\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=0,$$ $$\left(\begin{array}{cc}-4& 2\\ 2& -1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=0.$$ Resolviendo, obtenemos $y=2x.$ El autovector asociado es: $$v_1=\left(\begin{array}{c}1\\ 2\end{array}\right).$$ Para ${\lambda }_2=1$, resolvemos: $$\left(\begin{array}{cc}2-1& 2\\ 2& 5-1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=0,$$ $$\left(\begin{array}{cc}1& 2\\ 2& 4\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=0.$$ Resolviendo, obtenemos $x=-2y$. El autovector asociado es: $$v_2=\left(\begin{array}{c}-2\\ 1\end{array}\right).$$ Paso 3: Cambio de base y ecuación canónica

La matriz de cambio de base $Q$ tiene como columnas los autovectores normalizados: $$Q=\left(\begin{array}{cc}\frac{1}{\sqrt{5}}& \frac{-2}{\sqrt{5}}\\ \frac{2}{\sqrt{5}}& \frac{1}{\sqrt{5}}\end{array}\right)$$ La matriz $A$ en la base nueva es diagonal: $$Q^{T}AQ=\left(\begin{array}{cc}6& 0\\ 0& 1\end{array}\right).$$ En la nueva base, la ecuación se convierte en: $$6x^{\prime }{}^2+y^{\prime }{}^2+\left(\begin{array}{cc}0& 6\sqrt{5}\end{array}\right)\left(\begin{array}{cc}\frac{1}{\sqrt{5}}& \frac{-2}{\sqrt{5}}\\ \frac{2}{\sqrt{5}}& \frac{1}{\sqrt{5}}\end{array}\right)\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=1.$$ $$6x^{\prime }{}^2+y^{\prime }{}^2+12x^{\prime }+6y^{\prime }=1$$ Completando cuadrados: $$6(x^{\prime }+1{)}^2-6+(y^{\prime }+3{)}^2-9=1.$$ Simplificamos: $$6(x^{\prime }+1{)}^2+(y^{\prime }+3{)}^2-15=1.$$ $$6(x^{\prime }+1{)}^2+(y^{\prime }+3{)}^2=16.$$ Dividimos toda la ecuación por 16 para obtener: $$\frac{(x^{\prime }+1{)}^2}{\frac{8}{3}}+\frac{(y^{\prime }+3{)}^2}{16}=1.$$ Esta es la ecuación de una elipse cuyo semieje mayor es paralelo al eje $y^{\prime }$, y el semieje menor está a lo largo del eje $x^{\prime }$.
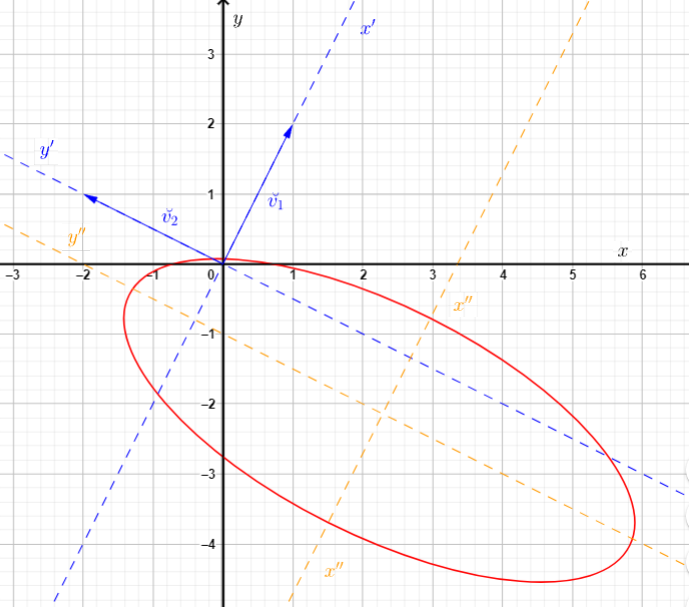
Para obtener la ecuación canónica, planteamos las ecuaciones de traslación: $$\{\begin{array}{c}{x}^{″}=x^{\prime }+1\\ y^{″}=y^{\prime }+3\end{array}$$ $$\Rightarrow \frac{x^{″}{}^2}{\frac{8}{3}}+\frac{y^{″}{}^2}{16}=1$$ Ahora realizamos un gráfico de la parábola indicando los tres sistemas de ejes: