Álgebra Lineal
Interactiva

Ejercicios y problemas

Augusto Spela

Álgebra Lineal Interactiva

Ejercicios y problemas

Universidad Tecnológica Nacional - FRBA

Fondo Editorial RED Descartes

Córdoba (España)
2024

Título de la obra:
Álgebra Lineal Interactiva. Ejercicios y problemas.

Autor:
Augusto Spela
Universidad tecnológica Nacional - FRBA
Buenos Aires (Argentina)

Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Imagen de la portada obtenida de la IA Lexica
Fuentes: Lato y UbuntuMono

Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org

Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm

ISBN: 978-84-18834-86-8

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.

Tabla de contenido

Prefacio5

1. Vectores, rectas y planos7

1.1 Introducción a vectores en

{\mathbb{R}^3}

11

1.2 Producto escalar en

{\mathbb{R}^3}

26

1.3 Producto vectorial y mixto36

1.4 Ecuaciones del plano52

1.5 Ángulos y distancias63

1.6 Haz de planos72

1.7 Recta en

{\mathbb{R}^3}

77

1.8 Recta y plano: intersecciones y ángulos85

1.9 Distancias y proyecciones105

1.10 Ejercicios surtidos de fin de capítulo129

2. Matrices, determinantes y SEL135

2.1 Matrices139

2.2 Operaciones con matrices141

2.3 Determinantes149

2.4 Matrices y sistemas de ecuaciones lineales157

3. Espacios vectoriales163

3.1 Espacios y subespacios vectoriales167

3.2 Conjunto generador. L.I. L.D. Bases180

3.3 Operaciones con subespacios206

iii

4. Tres espacios de una matriz221

4.1 Espacios fila y columna de A. Rango224

4.2 Espacio nulo de A229

4.3 Relación entre las soluciones de

AX = B

y

AX = 0.\;

Variables libres234

Bibliografía recomendada249

iv

Prefacio

Este libro interactivo no busca ser un libro de cabecera, apenas pretende ser un complemento, enfocado en el "hacer", de los buenos textos que existen en la actualidad sobre Álgebra Lineal. Una lista sugerida de los mismos se ofrece en la bibliografía recomendada

Debo hacer un especial agradecimiento a la UDB Matemática de la Universidad Tecnológica Nacional FRBA, que me permitió utilizar parte del excelente material disponible en su sitio web de Álgebra y Geometría Analítica ¹

Algunas de las escenas interactivas fueron tomadas y/o adaptadas de escenas realizadas en DescartesJS por la autoras Elena Álvarez Sáiz y María José García Cebrian [1][2], otras escenas son de autoría de la profesora Melissa Méndez Servin, disponibles en la web [3]. También se han adaptado recursos y applets disponibles en Geogebra.

Profundamente agradecido a los académicos Juan Guillermo Rivera Berrío, Ramiro Antonio Lopera Sánchez, Joel Espinosa Longi y demás desarrolladores del Proyecto iCartesiLibri², por su invaluable ayuda y aporte de conocimientos, brindados siempre de manera generosa.

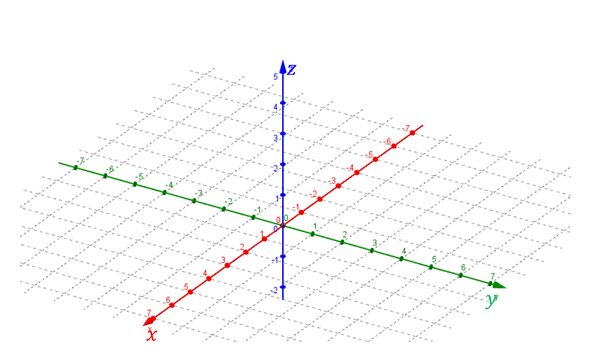
Este libro puede leerse descargándolo en un dispositivo digital, pero para visualizar algunas imágenes o videos es necesario estar conectado a Internet.

https://aga.frba.utn.edu.arhttps://proyectodescartes.org/iCartesiLibri/

5

Capítulo I

Vectores, rectas y planos

1.1 Introducción a vectores en

{\mathbb{R}^3}

11

1.1.1 Vectores en

{\mathbb{R}^3}

13

1.1.2 Operaciones y nociones básicas de vectores en

{\mathbb{R}^3}

13

1.1.3 Propiedades de la suma de vectores y del producto por un escalar15

1.1.4 Módulo o norma de un vector en

{\mathbb{R}^3}

16

1.1.5 Propiedades del módulo o norma de un vector17

1.1.6 Vector determinado por dos puntos18

1.1.7 Distancia entre dos puntos19

1.1.8 Expresión canónica de un vector21

1.1.9 Ángulos directores y cosenos directores de un vector22

1.1.10 Versor asociado a un vector25

1.2 Producto escalar en

{\mathbb{R}^3}

26

1.2.1 Propiedades del producto escalar26

1.2.2 Ángulo entre vectores29

1.2.3 Condición de perpendicularidad30

1.2.4 Proyección de un vector en la dirección de otro31

1.3 Producto vectorial y mixto36

1.3.1 Producto vectorial36

1.3.2 Propiedades del producto vectorial38

1.3.3 Fórmula para calcular el producto vectorial38

1.3.4 Interpretación geométrica del módulo del producto vectorial41

1.3.5 Producto mixto46

1.3.6 Interpretación geométrica del producto mixto48

1.3.7 Coplanaridad50

1.4 Ecuaciones del plano52

1.4.1 Deducción de la ecuación general del plano52

1.4.2 Ecuación segmentaria del plano53

1.4.3 Ecuación vectorial paramétrica del plano56

1.4.4 De la ecuación general a la ecuación vectorial paramétrica59

1.5 Ángulos y distancias63

1.5.1 Ángulo entre dos planos63

1.5.2 Planos perpendiculares y planos paralelos65

1.5.3 Distancia de un punto a un plano67

1.5.4 Distancia entre planos paralelos71

1.6 Haz de planos72

1.7 Recta en

{\mathbb{R}^3}

77

1.7.1 Ecuaciones de la recta en

{\mathbb{R}^3}

77

1.7.2 Ecuación vectorial de la recta78

1.7.3 Ecuaciones paramétricas de la recta80

1.7.4 Ecuaciones simétricas de la recta81

1.7.5 Recta definida como intersección de dos planos83

1.8 Recta y plano: intersecciones y ángulos85

1.8.1 Intersección entre recta y plano85

1.8.2 Paralelismo entre recta y plano89

1.8.3 Perpendicularidad entre recta y plano92

1.8.4 Ángulo entre recta y plano95

1.8.5 Intersección de rectas en

{\mathbb{R}^3}

98

1.8.6 Plano que contiene a dos rectas100

1.8.7 Ángulo entre dos rectas103

1.9 Distancias y proyecciones105

1.9.1 Proyecciones ortogonales105

1.9.2 Planos proyectantes de una recta112

1.9.3 Distancias117

1.9.4 Condición de coplanaridad123

1.10 Ejercicios surtidos de fin de capítulo129

1.1 Introducción a vectores en ${\mathbb{R}^3}$

Puntos en ${\mathbb{R}^3}$

Para ubicar un punto en ${\mathbb{R}^3}$ usaremos como sistema de referencia una terna de ejes perpendiculares entre sí:

eje $\color{red}{x}$ (eje de abscisas, en rojo)
eje $\color{green}{y}$ (eje de ordenadas, en verde)
eje $\color{blue}{z}$ (eje de cotas, en azul)

los cuales se cortan en el punto O (origen de coordenadas).

11

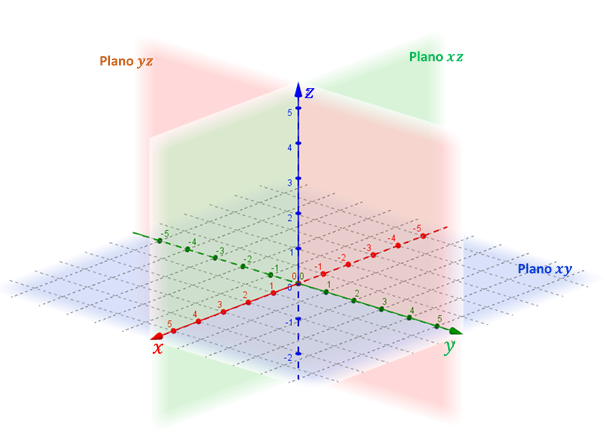
En el siguiente esquema se ven los tres planos que quedan determinados:

el plano $\color{blue}{xy}$ (en azul)
el plano $\color{green}{xz}$ ( en verde)
el plano $\color{red}{yz}$ (en rojo)

Estos planos se conocen como planos coordenados. El nombre del plano $xy$ viene de que este plano contiene al eje $x$ y al eje $y$ . En forma análoga se derivan los nombres de los otros dos planos.

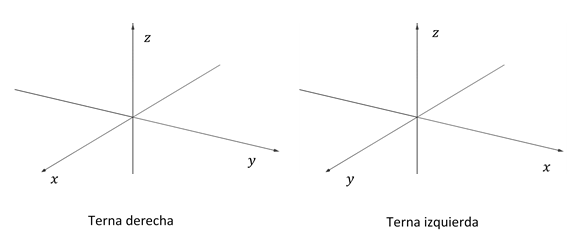
Se puede demostrar que hay dos formas diferentes de armar un sistema de referencia con tres ejes perpendiculares. Una de esas formas se conoce con el nombre de terna derecha (que es la que usaremos en esta materia y la que hemos presentado recién) y la otra como terna izquierda:

12

1.1.1 Vectores en ${\mathbb{R}^3}$

Queda establecido un sistema de coordenadas donde todo punto de ${\mathbb{R}^3}$ se define mediante una terna ordenada de números reales: $P\left( {x,y,z} \right)$ , y tiene asociado un vector posición: $\vec p\; = \;\overrightarrow {OP} \; = \left( {x,\;y,\;z} \right)$

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

1.1.2 Operaciones y nociones básicas de vectores en ${\mathbb{R}^3}$

Sean $\vec v = \left( {{v_x},{v_y},{v_z}} \right)$ y $\vec w = \left( {{w_x},{w_y},{w_z}} \right)$ vectores de ${\mathbb{R}^3}$ .

A continuación definimos algunas operaciones y nociones básicas:

Igualdad: $\vec v\; = \;\vec w\;\;\; \Leftrightarrow \;\;\;{v_x} = {w_x}\;,\;\;\;{v_y} = {w_y}\;,\;\;\;{v_z} = \;{w_z}$
Suma: $\vec v + \vec w = \left( {{v_x} + {w_x},\;\;{v_y} + {w_y},\;\;{v_z} + {w_z}} \right)$

13

Vector nulo:

\; \vec 0\; = \;\left( {0,0,0} \right)

Opuesto de

\vec v

:

- \vec v = \left( { - {v_x}, - {v_y}, - {v_z}} \right)

Resta:

\vec v - \vec w = \vec v + \left( { - \vec w} \right) = \left( {{v_x} - {w_x},{v_y} - {w_y},{v_z} - {w_z}} \right)

El producto de un escalar por un vector se define:

$\vec v = \left( {{v_x},{v_y},{v_z}} \right)\;\;,\;\;k \in \mathbb{R}\;\;\;,k.\vec v = \left( {k.{v_x},k.{v_y},k.{v_z}} \right)\;$

$k.\vec v$ es un vector tal que:

Tiene igual dirección que el vector $\vec v$
Sentido: Si $k > 0$ entonces $\vec v$ y $k.\vec v$ tienen el mismo sentido, si $k < 0\;$ entonces $\vec v$ y $k.\vec v$ tienen sentido opuesto. Si $\;k = 0$ , entonces $\;0.\vec v = \vec 0$ .
$k.\vec v = \left| k \right|\vec v$ . El módulo del vector $k.\vec v$ es $\left| k \right|$ veces el módulo del vector $\vec v$ .

¿Cómo es la longitud del vector $k.\vec v$ respecto de la de $\vec v\;$ ?

Notación

\lVert \vec v\rVert:\;

módulo o norma de un vector

\left| k \right|:\;

módulo o valor absoluto de un número real

14

La definición de producto de un escalar por un vector permite enunciar una condición para que dos vectores (no nulos) sean paralelos:

$\vec v\parallel \vec w\;\; \Leftrightarrow \;\;\;\vec v\; = \;k.\vec w\;\;\;con\;k \in \mathbb{R}$

Ejemplos resueltos

1.1.3 Propiedades de la suma de vectores y del producto por un escalar

Sean $\vec u,\vec v,\vec w \in {\mathbb{R}^3}\;\;y\;\;\alpha ,\;\beta \in \mathbb{R}$ .

Vimos que: $\vec u + \vec v \in {\mathbb{R}^3}$ y $\alpha\, \vec u \in {\mathbb{R}^3}$ . Estas operaciones verifican las siguientes propiedades:

$\vec u + \vec v = \vec v + \vec u\;\;\;\;$
$\left( {\vec u + \vec v} \right) + \vec w = \vec u + \left( {\vec v + \vec w} \right)\;\;\;\;$
$\vec u + \vec 0 = \vec 0 + \vec u = \vec u\;\;\;\;\;$
$\vec u + \left( { - \vec u} \right) = \left( { - \vec u} \right) + \vec u = \vec 0$
$\alpha \left( {\vec u + \vec v} \right) = \alpha \vec u + \alpha \vec v$
$\left( {\alpha + \beta } \right)\vec u = \alpha \vec u + \beta \vec u$
$\alpha \left( {\beta \vec u} \right) = \left( {\alpha \beta } \right)\vec u$
$1\vec u = \vec u$

15

1.1.4 Módulo o norma de un vector en ${\mathbb{R}^3}$

Nos interesa hallar una fórmula para calcular el módulo o norma de un vector. En ${\mathbb{R}^3}$ el módulo es la longitud del vector. Para deducirla usaremos los triángulos rectángulos que quedan determinados tal como se muestra en el siguiente interactivo:

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

En general escribiremos: ${\lVert \vec v\rVert^2} = v_x^2 + v_y^2 + v_z^2$

Aplicando raíz cuadrada a ambos miembros:

\lVert \vec v\rVert = \sqrt {v_x^2 + v_y^2 + v_z^2}

16

1.1.5 Propiedades del módulo o norma de un vector

$\ \lVert \vec v\rVert \ge 0\;\;\; \wedge \;\;\;\lVert \vec v\rVert = 0 \; \Leftrightarrow \;\vec v = \vec 0$
$\;\lVert k.\vec v \rVert = \left| k \right|\;\lVert \vec v\rVert,\;\;k \in \mathbb{R}\;$
Desigualdad triangular: $\lVert \vec v + \vec w\rVert \le \lVert \vec v \rVert + \lVert \vec w \rVert$

¿Qué condiciones tienen que cumplir los vectores $\vec v$ y $\vec w$ para que se verifique la igualdad: $\lVert \vec v + \vec w \rVert = \lVert \vec v \rVert + \lVert \vec w\rVert \;$ ?

Ejemplo

Sean $\vec v = \left( { - 1,1,2} \right)$ y $\vec w = \left( {3,0, - 4} \right)\;$ calcular:

a) $\lVert \vec v\rVert$

b) $\lVert - 2\vec v\rVert$

c) $\lVert \vec w\rVert$

d) $\lVert \vec v + \vec w\rVert$

Resolución

$\lVert \vec v\rVert = \sqrt {{{\left( { - 1} \right)}^2} + {1^2} + {2^2}} = \sqrt 6$

$\lVert - 2\vec v\rVert\ = \sqrt {{{\left( { - 2} \right)}^2} + {2^2} + {4^2}} = \sqrt {24} = 2\sqrt 6$

$\lVert \vec w\rVert\ = \sqrt {{3^2} + {0^2} + {{\left( { - 4} \right)}^2}} = 5$

17

$\lVert \vec v + \vec w\rVert = \lVert \left( {2,1, - 2} \right)\rVert = \sqrt {{2^2} + {1^2} + {{\left( { - 2} \right)}^2}} = 3$

Observemos que $\lVert \vec v + \vec w\rVert \ne \lVert \vec v\rVert + \lVert \vec w\rVert$

1.1.6 Vector determinado por dos puntos

Dados los puntos $A\left( {{X_A},{Y_A},{Z_A}} \right)$ y $B\left( {{X_B},{Y_B},{Z_B}} \right)$ , el vector $\overrightarrow {AB}$ , con origen en $A$ y extremo en $B$ , puede obtenerse cómo sigue:

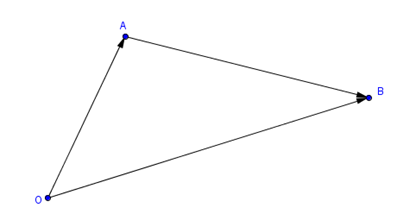
$\overrightarrow {OA} + \overrightarrow {AB} = \overrightarrow {OB}$

$\Rightarrow \overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {{X_B},{Y_B},{Z_{,B}}} \right) -; \left( {{X_A},{Y_A},{Z_A}} \right)$

$\Rightarrow \overrightarrow {AB} = \left( {{X_B} - {X_A},{Y_B} - {Y_A},{Z_B} - {Z_A}} \right)$

En este punto, te proponemos que nuevamente trabajes con el interactivo de la página 16.

18

1.1.7 Distancia entre dos puntos

Problema

¿Cómo podríamos calcular la distancia entre $R\left( {1,1,4} \right)$ y $S\left( {3,0,2} \right)$ ?

Para hallar esta distancia armamos el vector $\overrightarrow {RS}$ (o el $\overrightarrow {SR})$ y calculamos su módulo:

$\overrightarrow {RS} = \left( {2, - 1, - 2} \right)$

$\lVert \overrightarrow {RS}\rVert = \sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt {4 + 1 + 4} = \sqrt 9 = 3$

$\Rightarrow d\left( {R,S} \right) = 3$

En general

Dados dos puntos $A\left( {{x_A},{y_A},{z_A}} \right)$ y $B\left( {{x_B},{y_B},{z_B}} \right)$ la distancia entre los mismos se calcula:

d\left( {A,B} \right) = \lVert \overrightarrow {AB}\rVert = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}}

Problema

Encontrar, si es posible, todos los puntos del eje $z$ cuya distancia al punto $A\left( {3,2,1} \right)$ es $5$ .

19

Es recomendable hacer una figura de análisis del problema:

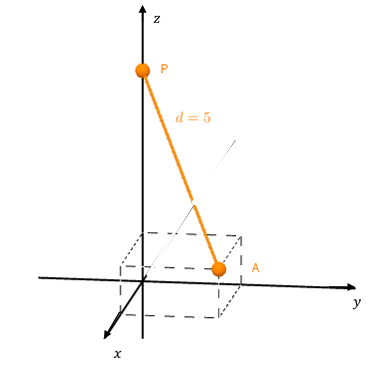
Un punto del eje $z$ tiene la forma $P (0,0,z)$ . Construyamos el vector desde un punto genérico cualquiera del eje $z$ hasta $A$ .

$\overrightarrow {PA} = \left( {3,\;2,\;1 - z} \right)$

Se pide que el módulo (o norma) de $\overrightarrow {PA}$ sea 5, entonces:

\overrightarrow {PA} = \sqrt {{3^2} + {2^2} + {{\left( {1 - z} \right)}^2}} = \sqrt {13 + 1 - 2z + {z^2}} =

= \sqrt {14 - 2z + {z^2}} = 5

$25 = 14 - 2z + {z^2}\;\; \Rightarrow {z^2} - 2z - 11 = 0\;$

$z = \frac{{2 + \sqrt {4 - 4.1.\left( { - 11} \right)} }}{2}\;\;\;\; \vee \;\;\;\;z = \frac{{2 - \sqrt {4 - 4.1.\left( { - 11} \right)} }}{2}\;\;\;$

$z = \frac{{2 + \sqrt {48} }}{2}\;\;\;\; \vee \;\;\;\;z = \frac{{2 - \sqrt {48} }}{2}\;\;\;$

$z = 1 + \sqrt {12} \cong 4,46\;\;\;\; \vee \;\;\;\;z = 1 - \sqrt {12} \cong - 2,46\;\;$

20

Hemos llegado a que $z$ puede tomar dos valores distintos. Entonces existen dos puntos del eje $z$ cuya distancia al punto $A\left( {3,2,1} \right)$ es 5. Son:

${P_1}\left( {0,\;0,\;1 + \sqrt {12} } \right)\;\;\; \wedge \;\;\;{P_2}\left( {0,\;0,\;1 - \sqrt {12} } \right)$

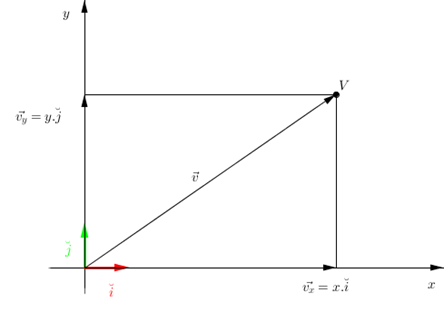
1.1.8 Expresión canónica de un vector

Recordemos que todo vector de ${\mathbb{R}^2}$ puede expresarse como combinación lineal de los versores canónicos $\check i = \left( {1,0} \right)$ y $\check j = \left( {0,1} \right)$ .

\vec v = \left( {x,y} \right)

\vec v = x\left( {1,0} \right) + y\left( {0,1} \right)

\vec v = x.\check i + y.\check j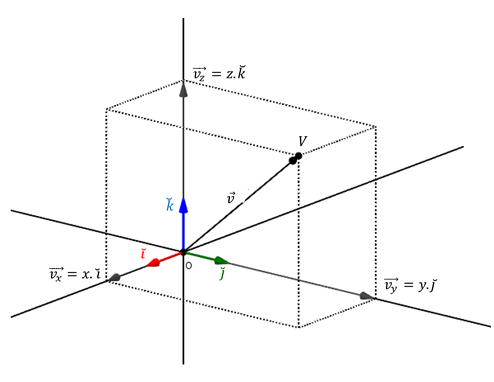

En forma análoga, todo vector de ${\mathbb{R}^3}$ puede expresarse como combinación lineal de los versores canónicos:

$\check i = \left( {1,0,0} \right)$

$\check j = \left( {0,1,0} \right)$

$\check k = \left( {0,0,1} \right)$

21

$\vec v = \left( {x,y,z} \right) = x\left( {1,0,0} \right) + y\left( {0,1,0} \right) + z\left( {0,0,1} \right)$

\large \vec v = x.\check {i} + y.\check {j} + z.\check {k}\:

(expresión canónica de

\vec v \,

)

1.1.9 Ángulos directores y cosenos directores de un vector

Se denominan ángulos directores de un vector a los ángulos determinados por el vector y cada uno de los semiejes positivos, como se muestra en la siguiente figura:

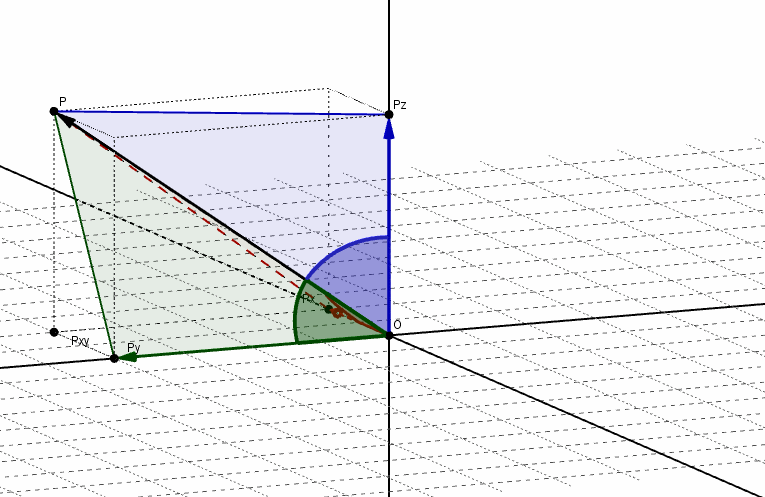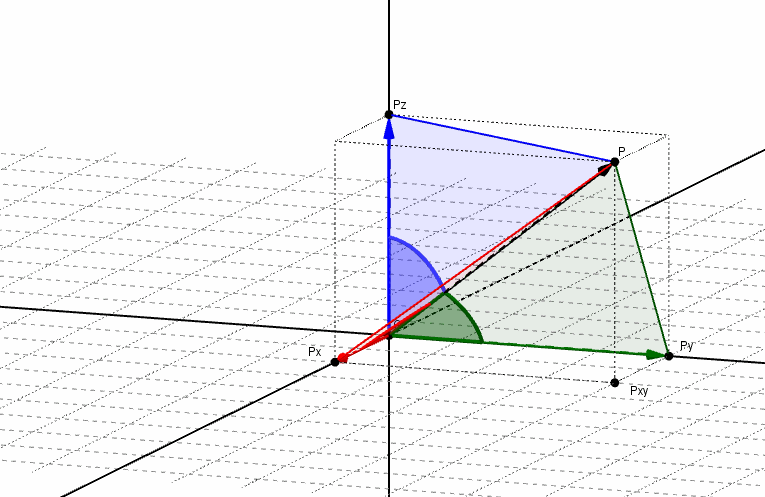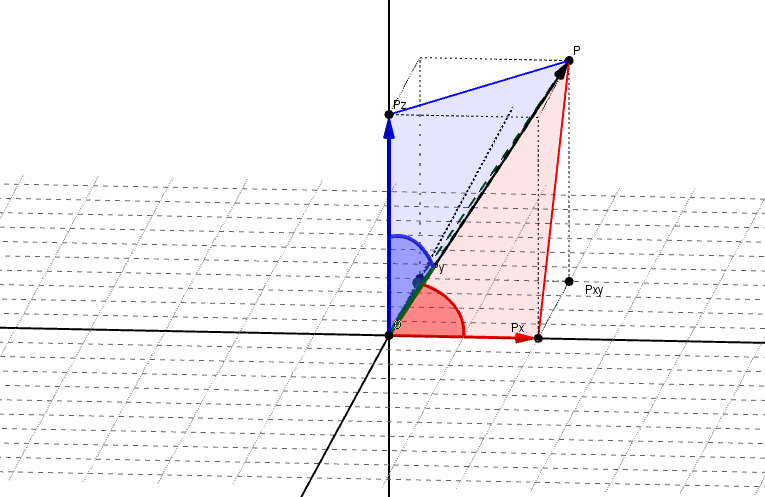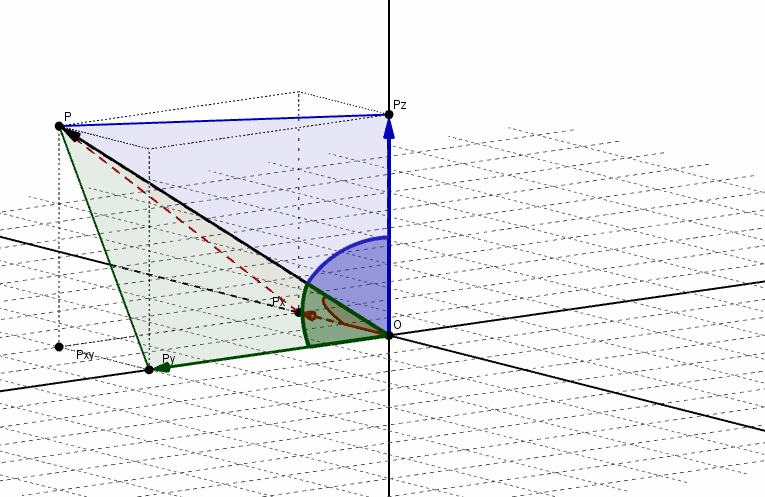
Los cosenos de dichos ángulos se llaman cosenos directores del vector. Aplicando relaciones trigonométricas, podemos obtener los cosenos directores:

$\cos \left( \alpha \right) = \frac{{{v_x}}}{{\lVert \vec v\rVert}}\;\;,\;\;\;cos\left( \beta \right) = \frac{{{v_y}}}{{\lVert \vec v\rVert}}\;\;,\;\;\cos \left( \gamma \right) = \frac{{{v_z}}}{{\lVert \vec v\rVert}}$

22

Por lo tanto, los ángulos directores son:

$\alpha = arcos\left( {\frac{{{v_x}}}{{\lVert \vec v\rVert}}} \right),\;\;\beta = arcos\left( {\frac{{{v_y}}}{{\lVert \vec v\rVert}}} \right),\;\;\gamma = arcos\left( {\frac{{{v_z}}}{{\lVert \vec v\rVert}}} \right)$

Donde $\alpha ,\beta ,\gamma$ están comprendidos entre $0$ y $\pi$ .

Propiedad

${\cos ^2}\left( \alpha \right) + {\cos ^2}\left( \beta \right) + {\cos ^2}\left( \gamma \right) = 1$

Ejemplo

Hallar los ángulos directores de $\vec v = \left( {2,0, -2} \right)$

Resolución

Hallemos el módulo del vector:

$\lVert \vec v\rVert = \sqrt {{2^2} + {0^2} + {{\left( { - 2} \right)}^2}} = \sqrt 8 = 2\sqrt 2$

Ahora calculamos los ángulos con el arco coseno de los cocientes:

$\alpha = \arccos \left( {\frac{2}{{2\sqrt 2 }}} \right) = 45^\circ$

$\beta = \arccos \left( {\frac{0}{{2\sqrt 2 }}} \right) = 90^\circ$

23

$\gamma = \arccos \left( {\frac{{ - 2}}{{2\sqrt 2 }}} \right) = 135^\circ$

Veamos una gráfica del vector y sus ángulos directores:

24

1.1.10 Versor asociado a un vector

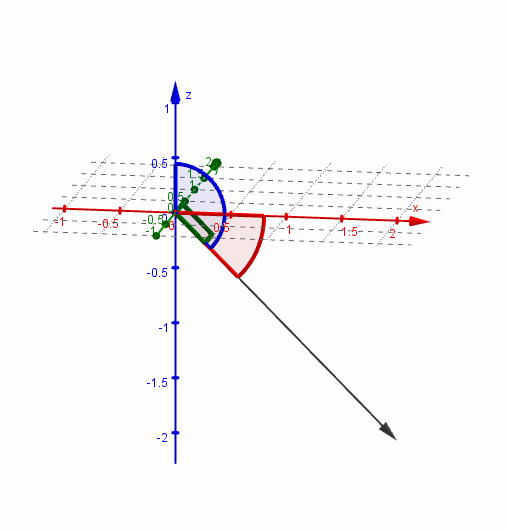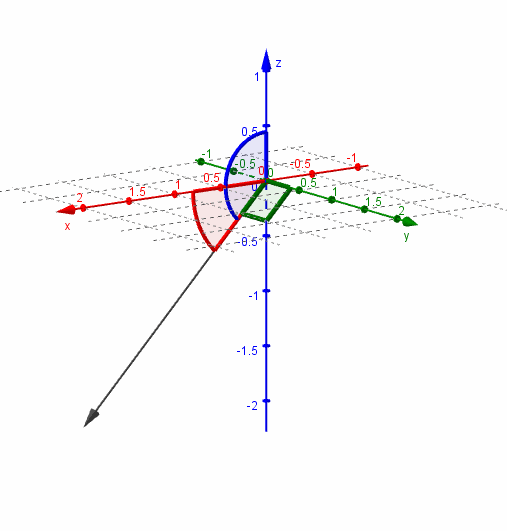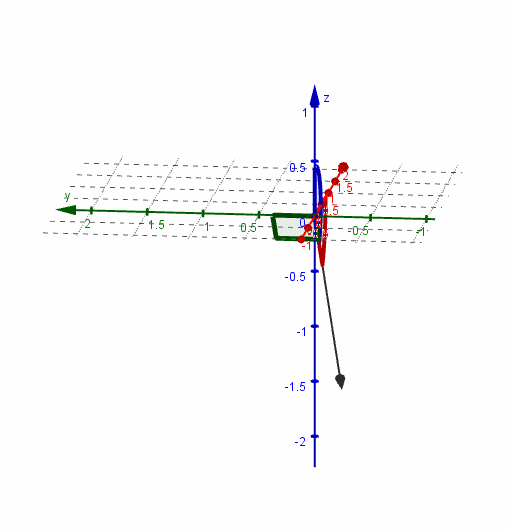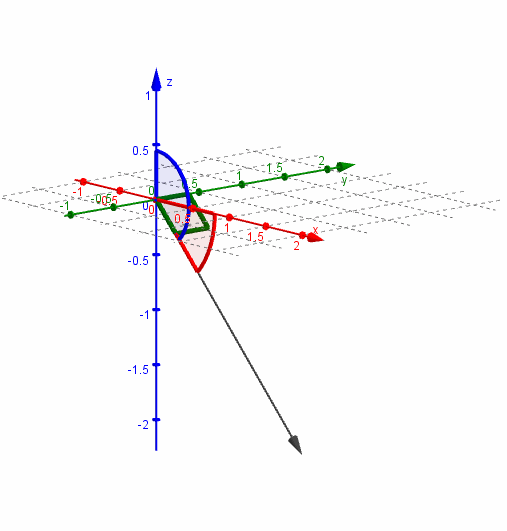
Dado un vector no nulo $\vec v$ , se denomina versor asociado al vector unitario (de módulo 1) que tiene igual dirección y sentido que $\vec v$ .

Dado $\vec v$ distinto de $\vec 0$ , su versor asociado se obtiene dividiendo a este por su norma:

\breve {v} = \frac {\vec v} {\lVert \vec v \rVert}

Tomando en cuenta los cosenos directores,

$\vec v = \left( {\lVert \vec v\rVert\cos \alpha,\;\;\lVert \vec v\rVert\cos \beta,\;\;\lVert \vec v\rVert\cos \gamma} \right)$

Entonces

\frac {\vec v} {\lVert \vec v \rVert} = \breve {v} = (\cos \alpha,\;\; \cos \beta,\;\; \cos \gamma)

Es decir, las componentes del versor $\breve v$ son los cosenos directores de $\vec v$ .

25

1.2 Producto escalar en ${\mathbb{R}^3}$

Sean $\vec u\;,\;\vec v \in {\mathbb{R}^3}$ , y $\theta$ el ángulo entre $\vec u$ y $\vec v$ , entonces el producto escalar entre $\vec u$ y $\vec v$ se define como sigue:

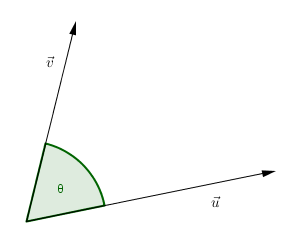
\large \vec u.\vec v = \begin{cases} {\lVert \vec u\rVert\;\lVert \vec v\rVert\cos \left( \theta \right)\;\;si\;\;\vec u \ne \vec 0 \wedge \;\vec v \ne \vec 0}\\ {0\;\;\;\;si\;\;\vec u = \vec 0\;\; \vee \;\vec v = \vec 0} \end{cases}\;\;\;\;\;\;\;\;\;\left[ 2 \right]

1.2.1 Propiedades del producto escalar

1) $\vec u.\vec v\; = \;\vec v.\vec u$

2) $\vec u.\left( {\vec v\; + \;\vec w} \right)\; = \;\vec u.\vec v\; + \;\vec u.\vec w$

3) $k\left( {\vec u.\vec v} \right) = \;\left( {k\vec u.\vec v} \right) = \;\vec u.\left( {k\vec v} \right),\;k \in \mathbb{R}$

26

4) $\:\: \vec v.\vec v = \left( {{v_x},{v_y},{v_z}} \right).\;\left( {{v_x},{v_y},{v_z}} \right) = v_x^2 + v_y^2 + v_z^2 = {\lVert \vec v\rVert^2}$

${\lVert \vec v\rVert^2} > 0\;\forall \vec v \ne \vec 0$

De (4) se deduce que: $\lVert \vec v\rVert = \sqrt {\vec v.\vec v}$

Ejemplo

Hallar $\vec u.\vec v$ para $\vec u = \left( {0,0,1} \right),\;\vec v = \left( {0,3, - 3} \right)$

Resolución

Hagamos una gráfica para visualizar el ángulo entre los dos vectores:

27

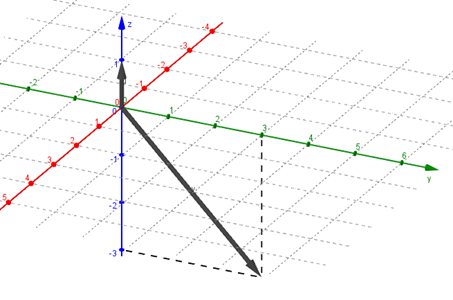
Calculemos los módulos de $\vec u$ . y $\vec v$ :

$\lVert \vec u\rVert = 1$

$\lVert \vec v\rVert = \sqrt {{3^2} + {{\left( { - 3} \right)}^2}} = \sqrt {18} = 3\sqrt 2 \;\;$

A partir del gráfico podemos determinar que el ángulo entre los vectores es $\;\theta = 135^\circ$ , o en radianes: $\;\theta = \frac{3}{4}\pi$ .

Calculemos el producto escalar:

$\vec u.\vec v = 1.\sqrt {18} .\cos \left( {135^\circ } \right) = 3\sqrt 2 .\left( { - \frac{{\sqrt 2 }}{2}} \right) = - 3$

Pero no siempre es tan sencillo. Consideremos los vectores:

$\vec u = \left( { - 3,5,8} \right)\;,\;\;\;\;\;\;\vec v\; = \left( {1,1,1} \right)$

Si quisiéramos calcular el producto escalar entre $\vec u$ y $\vec v$ , deberíamos conocer el ángulo comprendido entre dichos vectores.

Usando el teorema del coseno se puede deducir otra fórmula para calcular el producto escalar en función de las componentes de los vectores.

Sean $\vec u = \left( {{u_x},{u_y},{u_z}} \right),\;\;\vec v = \left( {{v_x},{v_y},{v_z}} \right) \in {\mathbb{R}^3},\;$ entonces:

\boxed{\vec u.\vec v = {u_x}{v_x} + {u_y}{v_y} + {u_z}{v_z}\;}\;\;\;\;\;\;\;\left[ 3 \right]

28

Para los vectores dados, resulta:

$\vec u\;.\vec v\; = \;\left( { -3} \right).1\; + \;5\;.1\; + \;8.1\; = \;10$

1.2.2 Ángulo entre vectores

Dados $\vec u,\vec v$ vectores no nulos de ${\mathbb{R}^3}$ , queremos hallar el ángulo entre ellos.

Si $\theta$ es el ángulo entre $\vec u\;\;y\;\;\vec v$ , de las definiciones [2] y [3] de producto escalar resulta:

$\cos \left( \theta \right) = \left( {\frac{{\vec u.\vec v}}{{\lVert \vec u\rVert \lVert \vec v\rVert}}} \right)$

{\rm{\theta }} = {\rm{\;arccos}}\left( {\frac{{{u_x}{v_x} + {u_y}{v_y} + {u_z}{v_z}}}{{\lVert \vec u\rVert \lVert \vec v\rVert}}} \right),\;\;\;0 \le \theta \le \pi

Por ejemplo, si $\vec u = \left( {1,1,3} \right)$

$\vec v = \left( { - 1,0,4} \right)\;$

$\theta = \arccos \left( {\frac{{1.\left( { - 1} \right) + 1.0 + 3.4}}{{\sqrt {{1^2} + {1^2} + {3^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {0^2} + {4^2}} \;\;}}} \right)$

$\theta = \arccos \left( {\frac{{11}}{{\sqrt {11} .\sqrt {17} \;\;}}} \right) \cong 36,44^\circ$

29

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

1.2.3 Condición de perpendicularidad

Sean $\vec u,\;\vec v$ no nulos,

$\vec u.\vec v = 0 \Leftrightarrow \;\cos \left( \theta \right) = 0 \Leftrightarrow \theta = \frac{\pi }{2}\;$

Esto permite enunciar una condición de perpendicularidad:

\large \boxed{\vec u \; \bot \; \vec v \: \Leftrightarrow \: \vec u.\vec v = 0}

Ejercicio para el lector

Dados $\vec u = \left( {1,2,3} \right)\;\;\;$ y $\;\;\vec v = \left( {0,2,5} \right)\;\;$ encontrar todos los vectores perpendiculares a $\vec u$ y a $\vec v$ de módulo 3.

30

1.2.4 Proyección de un vector en la dirección de otro

El producto escalar es útil en problemas en los que se tiene interés en descomponer un vector como suma de vectores perpendiculares.

Dados dos vectores no nulos $\vec u$ y $\vec v$ , nos proponemos descomponer $\vec u$ como suma de un vector paralelo a $\vec v\;\;$ y otro perpendicular a $\vec v.\;$ O sea:

$\vec u = \vec u_1 + \vec u_2,\: \vec u_1 \parallel \vec v\;$ y $\;\vec u_2 \; \bot \; \vec v$

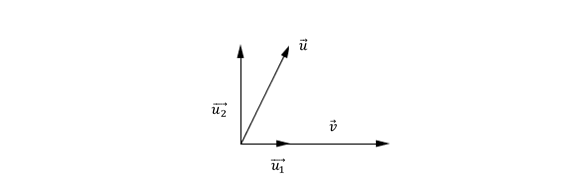
\vec u_1 \parallel \vec v\; \Leftrightarrow \;\;\vec u_1 = k\vec v,\;k \in \mathbb{R}\;\;\; \Rightarrow \;\;\vec u = k\vec v + \vec u_2

Podemos aplicar a ambos miembros producto escalar por $\vec v$ . Teniendo en cuenta que $\vec u_2\; .\; \vec v = 0$ por ser perpendiculares, resulta:

31

\vec u \cdotp \vec v =(k\, \vec v + \vec u_2)\, \cdotp \vec v \; \Rightarrow \;\vec u \,\cdotp \vec v = k \, \underbrace {\vec v \,\cdotp \vec v}_{{\lVert \vec v \rVert}^2} + \underbrace {\vec u_2 \,\cdotp \vec v}_{0} \; \Rightarrow

\Rightarrow \;\vec u \,\cdotp \vec v = k \, \underbrace {{\lVert \vec v \rVert}^2}_{\neq \; 0} \; \Rightarrow k =\frac {\vec u \cdotp \vec v} {{\lVert \vec v \rVert}^2}

Entonces:

$\vec u_1 = \left( {\frac{{\vec u \, \cdotp \vec v}}{{{\lVert \vec v\rVert^2}}}} \right)\vec v$

Este vector es la proyección de $\;\vec u\;$ en la dirección de $\;\vec v$ :

\;{\overrightarrow {proy} _{\vec v}}\left( {\vec u} \right) = \left( {\frac{{\vec u \, \cdotp \vec v}}{{{\lVert \vec v\rVert^2}}}} \right)\vec v

El vector ${\vec u_2}\;$ puede obtenerse por diferencia:

$\vec u = \vec u_1 + \vec u_2 \;\; \Rightarrow \;\vec u_2 = \vec u - \vec u_1$

Recordemos que $\vec u_2$ debe ser perpendicular a $\;\vec v$ .

Para resolver algunos problemas geométricos, es útil calcular el módulo del vector de proyección:

$\lVert {\overrightarrow {proy} _{\vec v}}\left( {\vec u} \right)\rVert = \left| {\frac{{\vec u \, \cdotp \vec v}}{{{\lVert \vec v \rVert^2}}}} \right|\ \lVert \vec v \rVert = \frac{{\left| {\vec u \, \cdotp \vec v} \right|}}{{{\lVert \vec v \rVert^2}}}\;\lVert \vec v \rVert\; = \;\frac{{\left| {\vec u \, \cdotp \vec v} \right|}}{{\lVert \vec v \rVert}}$

32

Ejemplo

Descomponer $\vec u = \left( {1,2,1} \right)$ como suma de un vector paralelo a $\,\vec v = \left( {0,1, - 1} \right)$ más otro perpendicular a $\vec v$ .

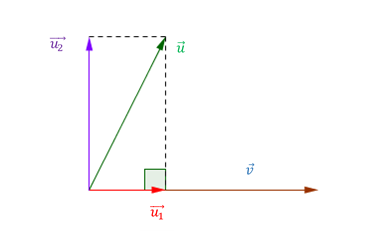
Primero buscamos $\vec u_1$ :

\vec u_1 = \overrightarrow {proy} _{\vec v} ( \vec u ) = \Bigg( \frac{\vec u.\vec v}{{\lVert \vec v \rVert^2}} \Bigg) \vec v =

\vec u_1 = \Bigg( \frac{(1,2,1).(0,1,-1)}{0^2+1^2+(-1)^2} \Bigg) (0,1,-1)

$= \frac{{0 + 2 - 1}}{2}\;\left( {0,1, - 1} \right) = \left( {0,\;\frac{1}{{\;2}}, - \frac{1}{2}} \right)$

$\vec u_2 = \vec u - \vec u_1 = \left( {1,2,1} \right) - \left( {0,\;\frac{1}{{\;2}}, - \frac{1}{2}} \right) = \left( {1,\;\frac{3}{2},\; \frac{3}{2}} \right)$

33

Comprobación: $\;\;\vec u_2 \, \, \bot \, \vec v$

$\left( {1,\;\frac{3}{2},\;\frac{3}{2}} \right).\left( {0,1, -1} \right) = 0$

La siguiente escena de Geogebra nos permite visualizar la proyección de un vector sobre otro en $\mathbb{R}^3$ :

Objeto interactivo de construcción propia

34

A continuación dejamos un ejercicio para que pongas a prueba tus conocimientos sobre producto escalar

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

35

1.3 Producto vectorial y mixto

1.3.1 Producto vectorial

Definición

Para resolver numerosos problemas de Geometría, Física e Ingeniería, interesa construir un vector en ${\mathbb{R}^3}$ que sea perpendicular a dos vectores dados.

O sea: dados $\vec u,\vec v \in {\mathbb{R}^3}$ , nos proponemos hallar un vector $\vec w$ tal que $\vec w \bot \vec u\;$ y $\;\overrightarrow {\;w} \bot \vec v$ .

El producto vectorial es una operación entre vectores que facilita la obtención de $\vec w$ .

Definición: El producto vectorial de $\vec u\;y\;\vec v$ , que indicaremos $\vec u \times \vec v$ es un vector

\vec u \times \vec v = \vec w

Que tiene:

Dirección perpendicular a $\vec u$ y a $\vec v$ : $\;\;\vec w \bot \vec u\;\; \wedge \;\;\vec w \bot \vec v$
Sentido: regla de la mano derecha: si con la mano derecha se recorre el menor ángulo posible entre $\vec u$ y $\vec v$ , el pulgar indica el sentido de $\vec w$ .

36

Módulo:

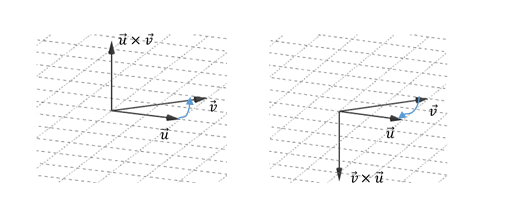
$\lVert \vec w\rVert = \lVert \vec u\rVert\;\lVert \vec v\rVert\;sen\left( \theta \right)$

siendo $\theta \;$ el ángulo comprendido entre $\vec u\;\;y\;\;\vec v$

Se puede ver que no es una operación conmutativa porque si cambiamos el orden de los vectores, se conservan la dirección y el módulo del producto vectorial pero se invierte su sentido:

\vec u \times \vec v = - \left( {\vec v \times \vec u} \right)

Ejemplo

$\vec a = \left( {0,1, - 1} \right)$

$\vec b = \left( {0,0,3} \right)$

Hallar el vector $\vec a \times \vec b$ .

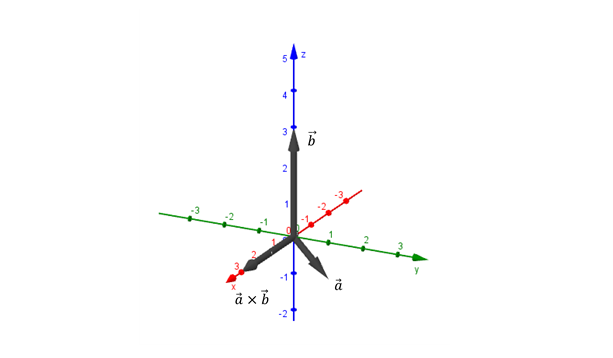
Dirección: eje $x$

Sentido: semieje positivo de $x$

Módulo: $\sqrt 2 .3.sen\left( {135^\circ } \right) = \sqrt 2 .3.\frac{{\sqrt 2 }}{2} = 3\;\;$

Entonces:

$\vec a \times \vec b = \left( {3,0,0} \right)$

37

1.3.2 Propiedades del producto vectorial

$\vec u \times \vec v = - \left( {\vec v \times \vec u} \right)$
$\left( {u + v} \right) \times w = \vec u \times \vec w + \vec v \times \vec w$
$\left( {k\vec u} \right) \times \vec v = k\left( {\vec u \times \vec v} \right) = \vec u\; \times \;\left( {k\vec v} \right)$
$\vec v \times \vec v = \vec 0\;,\;\;pues\;\;\;\lVert \vec v \times \vec v\rVert = \lVert \vec v\rVert\;\lVert \vec v\rVert\;sen\left( 0 \right) = 0$
$\vec u\parallel \vec v\; \Rightarrow \;\vec u \times \vec v = \vec 0\;,\;\;\;pues\;\;\;sen\left( {0^\circ } \right) = sen\left( {180^\circ } \right) = 0$
$\vec 0 \times \vec v\; = \;\vec v \times \vec 0\; = \;\vec 0$

Si $\vec u$ y $\overrightarrow {\;v}$ son vectores no nulos, podemos enunciar una condición necesaria y suficiente de paralelismo:

$\vec u\parallel \vec v\;\; \Leftrightarrow \;\vec u \times \vec v = \vec 0\;\; \Leftrightarrow \;\vec u = k\vec v\;\;\;con\;\;k\; \in {\mathbb{R}}$

1.3.3 Fórmula para calcular el producto vectorial

Dados $\vec u = \left( {{u_x},{u_y},{u_z}} \right)$ y $\vec v = \left( {{v_x},{v_y},{v_z}} \right)$ podemos hallar una fórmula para el producto vectorial expresando los vectores en forma canónica.

Aplicando propiedades del producto vectorial y considerando los productos entre los versores canónicos, se obtiene la siguiente fórmula:

\vec u \times \vec v = ( {{u_{y\;}}{v_z} - {u_{z\;}}{v_y},\; - ( {{u_{x\;}}{v_z} - {u_{z\;}}{v_x}}),\;\;{u_{x\;}}{v_y} - {u_{y\;}}{v_x}})\;

[1]

38

Esta fórmula puede expresarse en forma más sencilla utilizando determinantes, tema que presentaremos brevemente y luego desarrollaremos en la próxima unidad.

Una matriz es un ordenamiento rectangular de números, como caso particular nos interesan las matrices cuadradas (igual número de filas y de columnas).

A =\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \textsf {matriz de 2x2 (2 filas y 2 columnas)}

A =\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \textsf {matriz de 3x3 (3 filas y 3 columnas)}

A cada matriz cuadrada puede asignársele un número real que llamaremos su determinante y designaremos como $det\left( A \right)$ o $\left| A \right|$ . Para matrices de $2 \times 2$ y de $3 \times 3$ el determinante se calcula como sigue:

$A = (\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}) \Rightarrow | A | = a_{11} . a_{22} - a_{12} . a_{21}$

A =\begin{pmatrix} \color{blue} {a_{11}} & \color{fuchsia} {a_{12}} & \color{red} {a_{13}} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \: \Longrightarrow

\Longrightarrow \: \begin{vmatrix} A \end{vmatrix} = \color{blue} {a_{11}} \color{black} \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix} - \color{fuchsia} {a_{12}} \color{black} \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix} + \color{red} {a_{13}} \color{black} \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix}

39

Podemos expresar la fórmula $[1]$ utilizando determinantes como sigue:

\vec u \times \vec v = \begin{vmatrix} \breve{i} & \breve{j} & \breve{k} \\ u_x & u_y & u_z \\ v_x & v_y & v_z \end{vmatrix} =

\vec u \times \vec v = \begin{vmatrix} u_y & u_z \\ v_y & v_z \end{vmatrix}\breve{i} - \begin{vmatrix} u_x & u_z \\ v_x & v_z \end{vmatrix}\breve{j} + \begin{vmatrix} u_x & u_y \\ v_x & v_y \end{vmatrix}\breve{k}

Con la notación habitual de ternas, resulta:

\vec u \times \vec v = \Bigg( \begin{vmatrix} u_y & u_z \\ v_y & v_z \end{vmatrix},\;\; - \begin{vmatrix} u_x & u_z \\ v_x & v_z \end{vmatrix},\;\; \begin{vmatrix} u_x & u_y \\ v_x & v_y \end{vmatrix} \Bigg)

Veamos cómo utilizar esta regla práctica para calcular un producto vectorial:

$\vec u = \left( {1,2,3} \right)$

$\vec v = \left( {0,2,5} \right)$

\vec u \times \vec v = \begin{vmatrix} \breve{i} & \breve{j} & \breve{k} \\ 1 & 2 & 3 \\ 0 & 2 & 5 \end{vmatrix} = \Bigg( \begin{vmatrix} 2 & 3 \\ 2 & 5 \end{vmatrix}, - \begin{vmatrix} 1 & 3 \\ 0 & 5 \end{vmatrix},\; \begin{vmatrix} 1 & 2 \\ 0 & 2 \end{vmatrix} \Bigg)=(4,-5,2)

Comprobemos que el vector obtenido es ortogonal a

\vec u

y a

\vec v

:

$\left( {4, - 5,2} \right).\left( {1,2,3} \right) = 0$

$\left( {4, - 5,2} \right).\left( {0,2,5} \right) = 0$

40

Te invitamos a que escribas los vectores del ejercicio anterior en el siguiente applet:

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

1.3.4 Interpretación geométrica del módulo del producto vectorial

Consideremos los siguientes vectores y calculemos el módulo del producto vectorial.

$\vec u = \left( {1,2,3} \right),\;\;\;\vec v = \left( {0,2,5} \right)$

$\vec u \times \vec v = \left( {4, - 5,2} \right)$

$\lVert \vec u \times \vec v \rVert = \sqrt {45} = 3.\sqrt 5$

¿Qué representa este número $3\sqrt 5$ ?

41

Dibujemos cualquier par de vectores $\vec u$ y $\vec v$ y hagamos el paralelogramo determinado entre ellos:

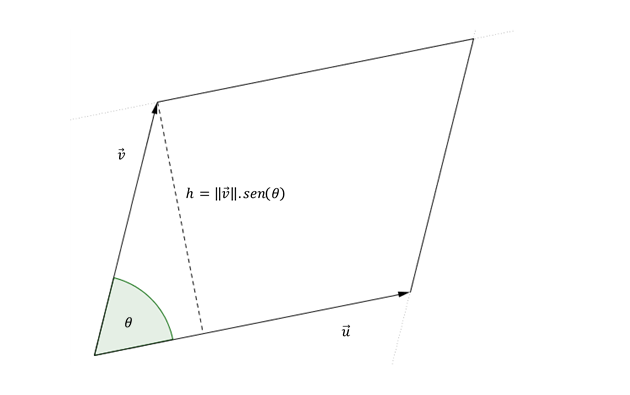
$Área\;del\;paralelogramo = \lVert \vec u \rVert.h$

$sen\left( \theta \right) = \frac{h}{{\lVert \vec v \rVert}}\; \Rightarrow h = \lVert \vec v \rVert sen\left( \theta \right)$

Área\;del\;paralelogramo = \lVert \vec u \rVert\;\lVert \vec v \rVert\;sen\left( \theta \right) = \lVert \vec u \times \vec v\ \rVert

Conclusión: Dados dos vectores no paralelos, el módulo de su producto vectorial representa el área del paralelogramo determinado por dichos vectores.

42

Ejemplo

Dados $A\left( {1,3,1} \right)$ , $B\left( {2, - 3,5} \right)$ y $C\left( {0,2,1} \right)$ calcular el área del ${\rm{\Delta }}ABC$ .

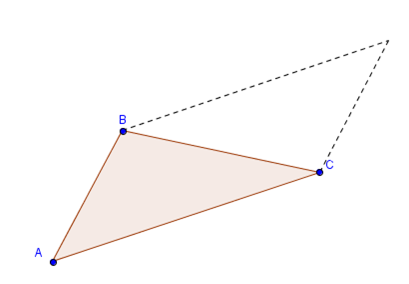
Podemos pensar al área del triángulo como la mitad del área del paralelogramo:

$Área\;del\;triá ngulo = \frac{1}{2}. \lVert \overrightarrow {AB} \times \overrightarrow {AC} \rVert$

$\overrightarrow {AB} = \left( {1, - 6,4} \right)$

$\overrightarrow {AC} = \left( { - 1, - 1,0} \right)$

$\overrightarrow {AB} \times \overrightarrow {AC} = \left( {4, - 4, - 7} \right)$

43

$\lVert \overrightarrow {AB} \times \overrightarrow {AC} \rVert = \sqrt {16 + 16 + 49} = \sqrt {81} = 9$

$Área\;del\;triá ngulo = \frac{1}{2}.9 = 4,5$

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

44

Proponemos la siguiente ejercitación a manera de repaso del tema visto.

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

45

1.3.5 Producto mixto

Definición

Dados tres vectores $\vec u,\vec v,\vec w \in {\mathbb{R}^3}$ , se denomina producto mixto al número real que se obtiene multiplicando $\vec u.\left( {\vec v \times \vec w} \right)$ .

Para obtener el producto mixto, se calcula primero el producto vectorial y luego el escalar.

Dejamos como ejercicio para el lector, demostrar que:

$\vec u.\left( {\vec v \times \vec w} \right) = \left( {\vec u \times \vec v} \right).\vec w$

Veamos un ejemplo:

$\vec u = \left( {1,2,3} \right)$

$\vec v = \left( {0,2,5} \right)$

$\vec w = \left( {0,0,2} \right)\;$

\vec v \times \vec w = \begin{vmatrix} \breve{i} & \breve{j} & \breve{k} \\ 0 & 2 & 5 \\ 0 & 0 & 2 \end{vmatrix} = (4,\,0,\,0)

$\vec u.\left( {\vec v \times \vec w} \right) = (1,\,2\,,3)\, \cdotp (4,\,0,\,0)= 4$

Ahora hagamos al revés:

$\left( {\vec u \times \vec v} \right).\vec w$

46

\vec u \times \vec v = \begin{vmatrix} \breve{i} & \breve{j} & \breve{k} \\ 1 & 2 & 3 \\ 0 & 2 & 5 \end{vmatrix} = (4,\,-5,\,2)

$\left( {\vec u \times \vec v} \right).\vec w = \left( {4, - 5,2} \right).\left( {0,0,2} \right) = 4$

Existe otro procedimiento para calcular el producto mixto a través de un determinante de 3×3.

Dados $\vec u = (u_1,\;u_2,\;u_3),\;\vec v = (v_1,\;v_2,v_3),\;\vec w = (w_1,\;w_2,\;w_3),$ el producto mixto es:

\vec u \, \cdotp (\vec v \times \vec w) = (\vec u \times \vec v) \, \cdotp \vec w = \begin{vmatrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \end{vmatrix} =

\vec u \, \cdotp (\vec v \times \vec w) = u_1 \begin{vmatrix} v_2 & v_3 \\ w_2 & w_3 \end{vmatrix} - u_2 \begin{vmatrix} v_1 & v_3 \\ w_1 & w_3 \end{vmatrix} + u_3 \begin{vmatrix} v_1 & v_2 \\ w_1 & w_2 \end{vmatrix}

Calculemos con este método el producto mixto entre:

$\vec u = (1,2,3), \; \vec v = (0,2,5), \; \vec w = (0,0,2)$

\vec u \, \cdotp (\vec v \times \vec w) = \begin{vmatrix} 1 & 2 & 3 \\ 0 & 2 & 5 \\ 0 & 0 & 2 \end{vmatrix} = 4

¿Qué significado tiene para la Geometría este número que hemos obtenido con el producto mixto?

47

1.3.6 Interpretación geométrica del producto mixto

Consideremos 3 vectores de ${\mathbb{R}^3}$ y construyamos un paralelepípedo (cuerpo cuyas seis caras son paralelogramos):

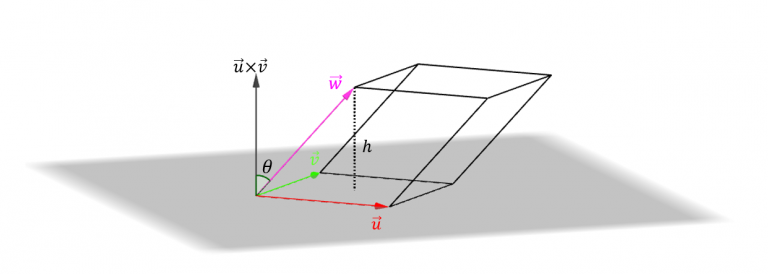
$Volumen\;del\;paralelepípedo = área\;de\;la\;base\;.\;Altura$

$A = \lVert \vec u \times \vec v \rVert$

$h = \left| {\cos \left( \theta \right)} \right|\;\lVert \vec w\rVert$

siendo $\theta$ el ángulo entre $(\vec u \times \vec v) \;\;y\;\;\vec w$ .

Observación: $\cos \left( \theta \right)$ podría ser negativo, por eso tomamos su valor absoluto para el cálculo de la altura.

Entonces:

$V = \lVert \vec u \times \vec v\ \rVert \; \lVert \vec w \rVert \;\left| {\cos \left( \theta \right)} \right|\;\;\;\;\;\;\left[ 1 \right]$

48

Por otra parte:

$\left( {\vec u \times \vec v} \right).\vec w = \lVert \vec u \times \vec v \rVert \; \lVert \vec w \rVert \;\cos \left( {á ng\left( {\vec u \times \vec v\;,\;\vec w} \right)} \right) =$ $= \lVert \vec u \times \vec v \rVert\;\lVert \vec w \rVert \;\cos \left( \theta \right)\;\;\;\;\left[ 2 \right]$

De [1] y [2] resulta:

\boxed { \text {Volumen\;del\;paralelepipedo} = \left| {\;( {\vec u \times \vec v}).\vec w\;} \right|}

Retomando el ejemplo con los vectores $\vec u = \left( {1,2,3} \right),$
$\vec v = \left( {0,2,5} \right),$ $\vec w = \left( {0,0,2} \right)$ ; de acuerdo al valor del producto mixto obtenido, el volumen del paralelepípedo determinado por los tres vectores es igual a 4.

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

49

1.3.7 Coplanaridad

Consideremos los vectores $\vec u = (1,0,3), \vec v = (0,0,2),$
$\vec w = (3,0,4)$ . Te proponemos que verifiques que el producto mixto da cero.

Si el producto mixto es cero, el volumen es 0, o sea que no se forma el paralelepípedo.

Veamos una gráfica de estos tres vectores:

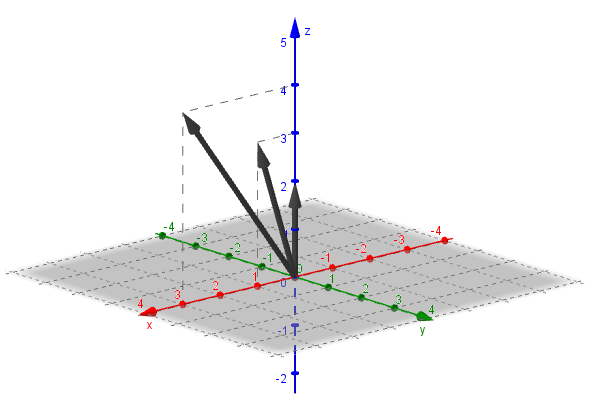
Observamos que los tres vectores están en el plano $y = 0$ , es decir que son coplanares.

50

Tres vectores $\vec u$ , $\vec v$ , $\vec w$ de ${\mathbb{R}^3}$ se denominan coplanares si considerados con un origen común, sus direcciones quedan incluidas en un mismo plano.

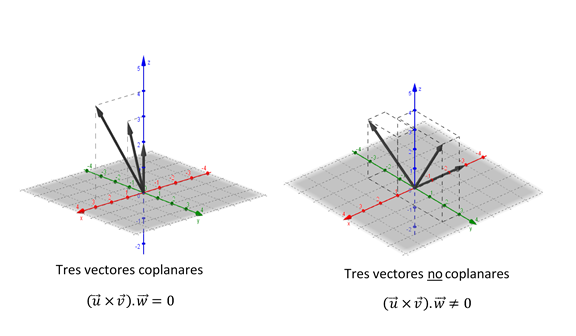
El producto mixto nos permite enunciar una condición de coplanaridad:

$\vec u,\vec v,\vec w\;\;$ son coplanares $\; \Leftrightarrow \;$ $\left( {\vec u \times \vec v} \right).\vec w = 0$

Lo que hemos desarrollado hasta aquí sobre vectores resulta una herramienta potente para el estudio de la geometría de rectas y planos en ${\mathbb{R}^3}$ , como veremos a continuación.

51

1.4 Ecuaciones del plano

1.4.1 Deducción de la ecuación general del plano

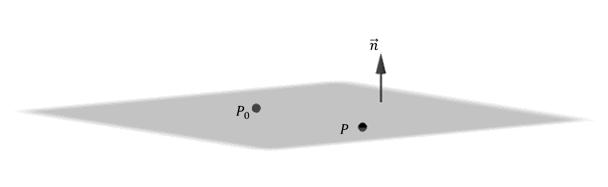
Dada una dirección en ${\mathbb{R}^3}$ , existen infinitos planos perpendiculares a la misma. Si conocemos además un punto del plano, éste queda determinado de forma única.

Nos proponemos hallar la ecuación del plano $\pi$ que pasa por ${P_0}\left( {{x_0},{y_0},{z_0}} \right)$ y es perpendicular al vector $\vec n = \left( {a,b,c} \right).$ El vector $\vec n$ se denomina vector normal del plano.

¿Qué condición debe cumplir un punto $P\left( {x,y,z} \right)$ para estar en el plano $\pi$ ? Si armamos el vector $\overrightarrow {\;{P_0}P} \;$ , éste debe ser paralelo al plano, o sea perpendicular al vector normal del plano:

$P\left( {x,y,z} \right) \in \pi \; \Leftrightarrow \overrightarrow {\;{P_0}P} \; \bot \; \vec n\;\; \Leftrightarrow \;\;\overrightarrow {{P_0}P} .\, \vec n = 0$

$\left( {x - {x_{0\;}},\;y - {y_0},\;z - {z_0}} \right).\left( {a,b,c} \right) = 0$

$a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0$

ax + by + cz + \underbrace {(-ax_0-by_0-cz_0)}_{d} = 0

52

Ecuación general o implícita del plano

\boxed {ax + by + cz + d = 0}

1.4.2 Ecuación segmentaria del plano

Dada la ecuación general de un plano:

$\pi :\;\;ax + by + cz + d = 0$

Si $a,b,c,d\;$ son distintos de cero, es posible obtener otra ecuación del plano como sigue:

$ax + by + cz = - d$

$\frac{a}{{ - d}}\,x + \frac{b}{{ - d}}\,y + \frac{c}{{ - d}}\,z = 1$

53

$\frac{x}{\bigg(- \dfrac{d}{a}\bigg)} + \frac{y}{\bigg(- \dfrac{d}{b}\bigg)} + \frac{z}{\bigg(-\dfrac{d}{c}\bigg)} = 1$

Si llamamos $p = - \dfrac{d}{a},\; q = - \dfrac{d}{b},\; r = - \dfrac{d}{c}$

Resulta:

Ecuación segmentaria del plano

\boxed {\frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1}

Veamos qué indican $\,p,\;$ $q,\;$ y $\,r\,$ :

¿Cuál es la intersección del plano con el eje x?

$y=0,\;z=0 \; \rArr x = p \; \rArr \;$ El plano corta al eje $x$ en $(p,0,0).$

¿Cuál es la intersección con el eje y?

$\left( {0,q,0} \right)$

¿Y con el eje z?

$\left( {0,0,r} \right)$

Podemos observar que p, q y r indican las intersecciones con los ejes.

54

Ejemplo

$2x - 3y + z - 6 = 0$

$2x - 3y + z = 6$

$\frac{{2x}}{6} - \frac{{3y}}{6} + \frac{z}{6} = 1$

$\frac{x}{3} - \frac{y}{2} + \frac{z}{6} = 1$

Esta ecuación parece segmentaria pero no lo es por el signo negativo. La reescribimos así:

$\frac{x}{3} + \frac{y}{{ - 2}} + \frac{z}{6} = 1\;\;\;\;\;\;\;Ecuación\;segmentaria$

La ecuación segmentaria es práctica para graficar un plano porque muestra los tres puntos de corte con los ejes:

55

1.4.3 Ecuación vectorial paramétrica del plano

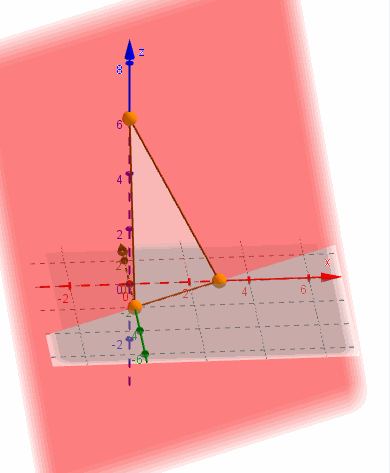
Dados dos vectores $\vec u = \left( {{u_1},{u_2},{u_3}} \right)$ y $\vec {v\;} = \left( {{v_1},\;{v_2},\;{v_3}} \right)$ no paralelos y un punto ${P_0}\;\left( {{x_0},\;{y_0},\;{z_0}} \right)$ , nos proponemos hallar la ecuación del plano $\pi$ que pasa por ${P_0}$ y es paralelo a $\vec u$ y $\vec v$ .

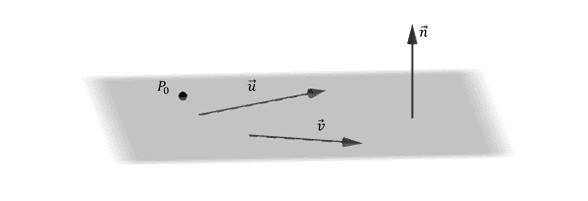
¿Cómo podemos obtener un vector perpendicular al plano conociendo dos vectores paralelos a dicho plano?

$\vec n = \vec u \times \vec v$

Teniendo $\vec n\;$ y el punto ${P_0}$ , podemos hallar la ecuación implícita o general del plano $\pi$ como habíamos visto previamente.

Obtendremos a continuación otro tipo de ecuación del plano, cuya deducción se basa en el concepto de combinación lineal de vectores.

Si $P\left( {x,y,z} \right)$ es un punto cualquiera del plano $\pi$ , los vectores $\overrightarrow {{P_0}P} \;,\;\vec u\;\;y\;\;\;\vec v\;$ son coplanares

56

Entonces
$\exists \alpha ,\beta \in \mathbb{R}\;|\;\;\overrightarrow {{P_0}P} = \alpha \;\vec u + \beta \;\vec v$

Esto significa que el vector $\overrightarrow {{P_0}P}$ puede expresarse como combinación lineal de $\vec u$ y $\vec v$ , como se muestra en la figura:

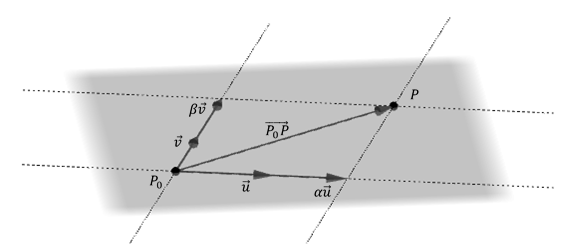
$\left( {x - {x_0}\;,\;y - {y_0},z - {z_0}} \right) = \alpha .\left( {{u_1},{u_2},{u_3}} \right)\; + \beta \;\left( {{v_1},{v_2},{v_3}} \right)$

Por lo tanto:

$\left( {x,y,z} \right) = \left( {{x_0},{y_0},{z_0}} \right) + \alpha \;\left( {{u_1},{u_2},{u_3}} \right) + \beta \;\left( {{v_1},{v_2},{v_3}} \right)$ , $\;\;con\;\alpha ,\beta \in \mathbb{R}$
O en notación vectorial:

Ecuación vectorial paramétrica del plano

\boxed { \left( {x,y,z} \right) = \overrightarrow {O{P_0}} + \alpha .\vec u + \beta .\vec v\; }

57

Ejemplo

Armar la ecuación vectorial paramétrica del plano paralelo a $\vec u = \left( {3, - 1,5} \right)$ y $\vec v = \left( {7,3,2} \right)$ que pasa por el punto ${P_0}\left( {0, - 1,8} \right).$

De acuerdo con lo que hemos visto, tenemos toda la información para escribir la ecuación vectorial paramétrica:

$\left( {x,y,z} \right) = \left( {0, - 1,8} \right) + \alpha \left( {3, - 1,5} \right) + \beta \left( {7,3,2} \right);\;\alpha ,\beta \in \mathbb{R}$

Nota: Para cada $\alpha \;y\;\beta \in \mathbb{R}$ se obtiene un punto del plano. Por ejemplo si $\;\alpha = 1\;\;y\;\;\;\beta = - 1$ se obtiene el punto $\left( {x,y,z} \right) = \left( { - 4,\; - 5,\;11} \right)$ .

Busquemos ahora la ecuación general de este plano.

$\vec n = \vec u \times \vec v = \left( {3, - 1,5} \right) \times \left( {7,3,2} \right) = \left( { - 17,\;29,16} \right)$

Luego: $- 17x + 29y + 16z + d = 0$

Reemplazamos ${P_0}$ para obtener $d$ :

$- 17.0 + 29.\left( { - 1} \right) + 16.8 + d = 0 \Rightarrow \;d = - 99$

Luego: $- 17x + 29y + 16z - 99 = 0$

que es la ecuación general o implícita del plano.

58

1.4.4 De la ecuación general a la ecuación vectorial paramétrica

Dada la ecuación general de un plano, ¿cómo puede obtenerse una ecuación vectorial paramétrica de dicho plano?

Consideremos el siguiente ejemplo:

$\omega :\;\;\;2x - y + 3z + 9 = 0$

Podemos despejar cualquiera de las variables, por ejemplo $y$ :

$y = 2x + 3z + 9$

Entonces: $\omega :\;\;\;\left( {x,y,z} \right) = \left( {x,\;2x + 3z + 9,\;z} \right)$

Reescribimos como suma de tres vectores, de forma tal que uno de ellos tenga los términos con $x$ , otro los términos con $z$ y otro los términos independientes:

$\left( {x,y,z} \right) = \left( {x,2x,0} \right) + \left( {0,3z,z} \right) + \left( {0,9,0} \right)\;$

$\left( {x,y,z} \right) = x\left( {1,2,0} \right) + z\left( {0,3,1} \right) + \left( {0,9,0} \right)\;,\;con\;\;x,z \in \mathbb{R}\;$

Si llamamos $x = \alpha$ , $z = \beta,\;$ resulta:

$\omega:\;\left( {x,y,z} \right) = \left( {0,9,0} \right) + \alpha \left( {1,2,0} \right) + \beta \left( {0,3,1} \right),\;con\;\alpha ,\beta \in \mathbb{R}$

59

Obtuvimos así una ecuación vectorial paramétrica del plano $\omega.$

El lector puede comprobar que:

i) los vectores $\vec u = (1,2,0)\,$ y $\,\vec v = (0,3,1)\;$ son perpendiculares a $\,\vec n = (2,-1,3),\;$ o sea que son paralelos al plano;

ii) $P_0 \: (0,9,0) \in \omega.$

Ecuación vectorial del plano. (Applet de Geogebra de elaboración propia.)

60

Interactivo que permite visualizar la deducción de la página 52:

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

Para practicar:

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

61

Ahora que ya hemos visto distintas ecuaciones de planos, podemos detenernos en el caso particular de los que contienen a los ejes coordenados, estudiemos estos casos:

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

Para practicar:

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

62

1.5 Ángulos y distancias

1.5.1 Ángulo entre dos planos

Sean los planos $\; \pi_1:\;{a_1}x + {b_1}y + {c_1}z + {d_1} = 0\:$ y
$\pi_2:\;{a_2}x + {b_2}y + {c_2}z + {d_2} = 0.$

Dichos planos forman dos ángulos suplementarios, como muestra la figura:

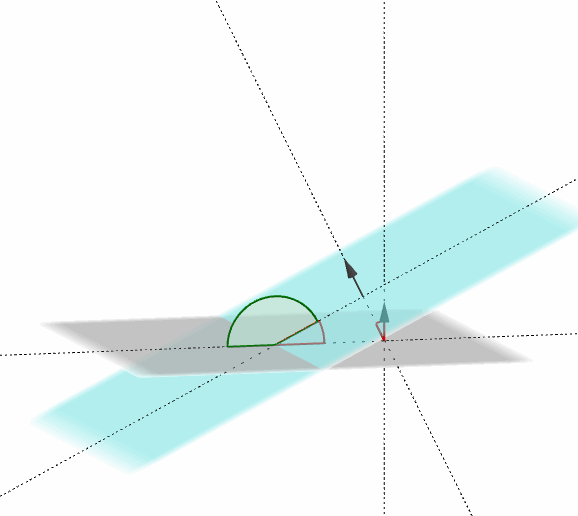
El ángulo entre dos planos es el ángulo entre sus respectivos vectores normales:

63

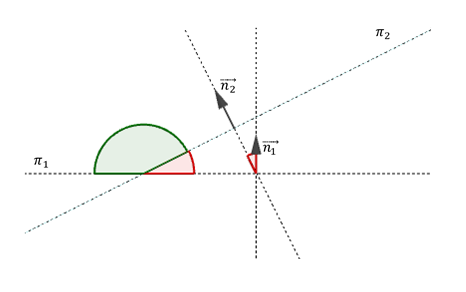
$á ng\left( {{\pi _1},{\pi _2}} \right) = á ng\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)$

Si llamamos $\theta \;$ a dicho ángulo, resulta:

$\cos \left( \theta \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\lVert\overrightarrow {{n_1}}\rVert \lVert\overrightarrow {{n_2}}\lVert }}$

Según el sentido de $\overrightarrow {{n_1}} \;\;y\;\;\overrightarrow {{n_2}}$ , se obtendrá alguno de los dos ángulos suplementarios. Convenimos en tomar el menor de estos ángulos, por lo cual agregamos módulo en la fórmula anterior:

$\cos \left( \theta \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\lVert\overrightarrow {{n_1}}\rVert \lVert\overrightarrow {{n_2}}\rVert }}$

Ángulo entre dos planos

\boxed {\:\: \theta = \arccos \Bigg( {\frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\lVert\overrightarrow {{n_1}} \rVert \lVert\overrightarrow {{n_2}}\rVert }}} \Bigg),\;\;\;0 \le \theta \le \frac{\pi }{2}\:\:}

Ejemplo

Dados los planos: ${\pi _1}:\;\;\;x - y + 2 = 0$ ${\pi _2}:\left( {x,y,z} \right) = \alpha \left( {1,2,3} \right) + \beta \left( {0,1,1} \right)\;$ Calcular $ang\left( {{\pi _1},{\pi _2}} \right)$ .

64

El plano ${\pi _2}$ está dado en forma vectorial paramétrica, para hallar el ángulo pedido necesitamos $\overrightarrow {{n_2}} \;$ :

$\overrightarrow {{n_2}} = \left( {1,2,3} \right) \times \left( {0,1,1} \right) = \left( { - 1, - 1,1} \right)$

$\overrightarrow {{n_1}} = \left( {1, - 1,0} \right)\;$

$\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0$

Esto quiere decir que $\overrightarrow {{n_1}} \; \bot \; \overrightarrow {{n_2}}$ , entonces el ángulo es $\theta = 90^\circ$ .

La definición de ángulo entre planos nos permite enunciar condiciones de perpendicularidad y de paralelismo entre planos.

1.5.2 Planos perpendiculares y planos paralelos

Sean $\;{\pi _1}\;$ y $\;{\pi _2}\;$ planos de vectores normales $\;\overrightarrow {{n_1}}\;$ y $\;\overrightarrow {{n_2}}$
respectivamente:

Planos perpendiculares: $\;\;{\pi _1} \; \bot \; {\pi _2}\;\; \Leftrightarrow \;\;\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0$

Planos paralelos:
${\pi _1} \parallel {\pi _2}\;\; \Leftrightarrow \;\;\overrightarrow {{n_1}} \parallel \overrightarrow {{n_2}} \;\; \Leftrightarrow \;\;\overrightarrow {{n_1}} = k\overrightarrow {{n_2}},\;\;k \in \mathbb{R}$

Consideremos por ejemplo:

{\pi _1}:\;\;2x - 3y + z + 1 = 0\;\;\;\;\;\;\;\;\;\;\overrightarrow {\;{n_1}} = \left( {2, - 3,1} \right)

{\pi _2}:\;\;4x - 6y + 2z + 5 = 0\;\;\;\;\;\;\;\;\;\;\;\overrightarrow {{n_2}} = \left( {4, - 6,2} \right)

{\pi _3}:\;\;4x - 6y + 2z + 2 = 0\;\;\;\;\;\;\;\;\;\;\;\overrightarrow {{n_3}} = \left( {4, - 6,2} \right)

65

Como $\overrightarrow {n_2} = 2\;\overrightarrow {n_1},\;$ podemos afirmar que ${\pi _1}$ y ${\pi _2}$ son paralelos.

Análogamente, como $\overrightarrow {n_3}\; = \;2\;\overrightarrow {n_1},\;$ los planos ${\pi _1}$ y ${\pi _3}$ también son paralelos. Pero además se verifica que ${d_3} = 2\;{d_1}$ , por lo cual ${\pi _1}$ y ${\pi _3}$ son coincidentes, o sea ${\pi _1} = {\pi _3}$ .

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

66

1.5.3 Distancia de un punto a un plano

Dados un plano $\pi :\;\;ax + by + cz + d = 0$ y un punto $A\left( {{x_A},{y_A},{z_A}} \right)$ , nos proponemos calcular la distancia de $A$ a $\pi$ .

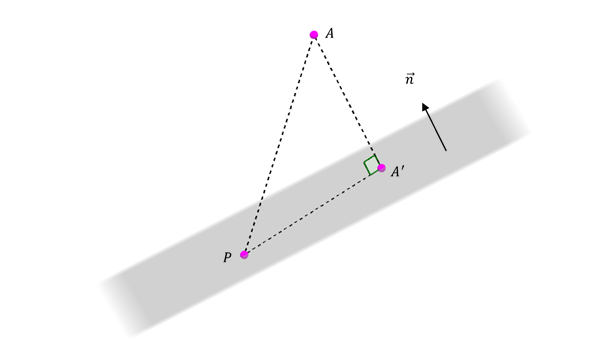
La distancia de $A$ a $\pi$ es la longitud del segmento, siendo la proyección ortogonal (perpendicular) de $A$ sobre $\pi$ .
Consideremos un punto cualquiera $P\left( {x,y,z} \right)$ perteneciente a ${\rm{\pi }}$ .

\overrightarrow {A'A} = {\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right)

Entonces $dist\left( {A,\pi } \right) = \lVert{\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right)\rVert$ siendo $P$ un punto cualquiera del plano.

67

Veamos un ejemplo, dados:

$\pi :\;\;x + 2y + 3z + 1 = 0$

$A\left( {0,2,1} \right)$

Calcular $dist\left( {A,\pi } \right)$

Recordemos que la norma de la proyección de un vector en la dirección de otro se calcula así:

$\lVert{\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right) \rVert = \frac{{\left| {\overrightarrow {PA} .\vec n} \right|}}{{\lVert\vec n\rVert}}$

Tomemos un punto cualquiera del plano, por ejemplo $P\left( { - 1,0,0} \right).\;$ Entonces

$\overrightarrow {PA} = \left( {1,2,1} \right)$

$dist\left( {A,\pi } \right) = \lVert {\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right)\rVert = \frac{{\left| {\overrightarrow {PA} .\vec n} \right|}}{{\lVert\vec n\rVert}} =$ $\frac{{\left| {\overrightarrow {PA} .\vec n} \right|}}{{\lVert\vec n\rVert}} = \frac{{\left| {\left( {1,2,1} \right).\left( {1,2,3} \right)} \right|}}{{\sqrt {{1^2} + {2^2} + {3^2}} }} = \frac{8}{{\sqrt {14} }}$

A continuación deduciremos una fórmula que permite calcular en forma muy sencilla la distancia de un punto a un plano.

68

Sean:
$\pi :\;\;ax + by + cz + d = 0$

$A\left( {{x_A},{y_A},{z_A}} \right)$

Habíamos visto que:

$d\left( {A,\pi } \right) = \lVert{\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right)\rVert\;\;\;\;\;\;siendo\;P\left( {x,y,z} \right) \in \pi$

$\overrightarrow {PA} = \left( {{x_A} - x,{y_A} - y,{z_A} - z} \right)$

$\vec n = \left( {a,b,c} \right)$

Entonces:

\lVert{\overrightarrow {proy} _{\vec n}} ( {\overrightarrow {PA} } )\rVert = \frac{{| {\overrightarrow {PA} .\vec n} |}}{{\lVert\vec n\rVert}} = \frac{{| {a( {{x_A} - x} ) + b( {{y_A} - y}) + c( {{z_A} - z})} |}}{{\lVert\vec n\rVert}}

$\lVert{\overrightarrow {proy} _{\vec n}}\left( {\overrightarrow {PA} } \right) \lVert= \frac{{\left| {a{x_A} + b{y_A} + c{z_A} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$

Concluimos que:

Distancia de punto a plano

\boxed {\;dist\left( {A,\pi } \right) = \frac{{\left| {a\;{x_A} + b\;{y_A} + c\;{z_A} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\;\;}

69

Retomemos el ejemplo que habíamos desarrollado:

$\pi :\;\;x + 2y + 3z + 1 = 0$

$A\left( {0,2,1} \right)$

De acuerdo con la fórmula demostrada, la distancia es:

$dist\left( {A,\pi } \right) = \frac{{\left| {\;0 + 4 + 3 + 1} \right|}}{{\sqrt {{1^2} + {2^2} + {3^2}} }} = \;\frac{8}{{\sqrt {14} }}$

Tal como habíamos calculado antes pero… ¡más fácil!

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

70

1.5.4 Distancia entre planos paralelos

Dados dos planos ${\pi _1}$ y ${\pi _2}\;\;\;$ paralelos, ¿cómo podemos hallar la distancia entre ambos?

Consideremos los siguientes planos paralelos:

{\pi _1}:\;2x -3y + z + 1 = 0,\;\;\;\; {\pi _2}:\;4x - 6y + 2z + 5 = 0

Todos los puntos de ${\pi _1}$ están a la misma distancia de ${\pi _2},\;$ por lo tanto podemos elegir un punto cualquiera de ${\pi _1}$ y calcular su distancia a ${\pi _2}.\,$ Por ejemplo: $\;{P_1}\left( {0,0, - 1} \right)$

Aplicamos la fórmula de distancia de un punto a un plano:

$d\left( {{\pi _1},{\pi _2}} \right) = d\left( {{P_1},{\pi _2}} \right) = \frac{{\left| {4.0 - 6.0 + 2.\left( { - 1} \right) + 5} \right|}}{{\sqrt {{4^2} + {{\left( { - 6} \right)}^2} + {2^2}} }} = \frac{3}{{\sqrt {56} }}$

Observación: Si los planos no son paralelos, la distancia entre ambos es 0.

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

71

1.6 Haz de planos

Sean ${\pi _1}$ y ${\pi _2}$ dos planos no paralelos:

${\pi _1}:\;\;{a_1}\;x + {b_1}\;y + {c_1}\;z + {d_1} = 0$

${\pi _2}:\;\;{a_2}\;x + {b_{2\;}}y + {c_2}\;z + {d_2} = 0$

La intersección de dos planos no paralelos es una recta. Se denomina haz de planos al conjunto de planos que pasan por dicha recta. Uno podría imaginarse al haz de planos como si fueran las hojas de un libro abierto:

72

Haz de planos que pasan por la recta $\;\;r = {\pi _1} \cap {\pi _2}$

Puede demostrarse que la ecuación del haz de planos que pasan por la recta de intersección entre $\;{\pi _1}\;y\;\;{\pi _2}\;$ es la siguiente:

${k_1}\left( {{a_1}x + {b_1}y + {c_1}z + {d_1}} \right) + {k_2}\left( {{a_2}x + {b_2}y + {c_2}z + {d_2}} \right) = 0$ con $\;{k_1},{k_2} \in \mathbb{R}$

Para cada par de valores de ${k_1}$ y ${k_2}$ se obtiene un plano que pasa por la recta $r$ .

Si $\;{k_1} = 0\;$ y $\;{k_2} \ne 0,\;$ se obtiene la ecuación del plano $\;{\pi _2}.$

Si $\;{k_2} = 0\;$ y $\;{k_1} \ne 0,\;$ se obtiene la ecuación del plano $\:{\pi _1}.$

Si suponemos que alguna de las constantes es diferente de cero, por ejemplo ${k_1} \ne 0,\;$ podemos dividir la ecuación del haz por ${k_1}$ :

$\frac{{{k_1}}}{{{k_1}}}\left( {{a_1}x + {b_1}y + {c_1}z + {d_1}} \right) + \frac{{{k_2}}}{{{k_1}}}\left( {{a_2}x + {b_2}y + {c_2}z + {d_2}} \right) = 0$

Y renombrando ${\Large \frac{{{k_2}}}{{{k_1}}}} = k$ queda:

$\left( {{a_1}x + {b_1}y + {c_1}z + {d_1}} \right) + k\left( {{a_2}x + {b_2}y + {c_2}z + {d_2}} \right) = 0$

Esta expresión se llama "ecuación del haz reducido". ¿De dónde proviene el nombre de «reducido»?

73

Falta ${\pi _2}\;$ porque ${\pi _2}\;$ se corresponde con ${k_1} = 0$ . Por lo tanto, en el haz reducido están todos los planos que pasan por $r = {\pi _1} \cap {\pi _2}$ excepto ${\pi _2}.$

Ejemplo

Dados los planos:

${\pi _1}:\;x + 2y + 3z + 1 = 0$

${\pi _2}:\;\;3x - 5y + z + 10 = 0$

Encontrar la ecuación de un plano que pase por la recta de intersección entre ${\pi _1}\;$ y ${\pi _2}\;$ y que:

a) Sea paralelo al eje $x$

b) Sea perpendicular al plano $x + y + z = 0$

Se pide encontrar un plano que pase por la recta de intersección entre ${\pi _1}$ y ${\pi _2},\;$ entonces podemos armar el haz de planos que pasa por dicha recta:

$\alpha \left( {x + 2y + 3z + 1} \right) + \beta \left( {3x - 5y + z + 10} \right) = 0$

a) Para que el plano sea paralelo al eje $x$ su vector normal debe ser $\vec n = \left( {0,\;b,\;c} \right)$ . O sea, el plano debe ser de la forma: $by + cz + d = 0$ .

74

Reescribimos el haz como sigue:

\underbrace{(\alpha + 3\beta)}_{\text{a}}x + \underbrace{(2\alpha - 5\beta)}_{\text{b}}y + \underbrace{(3\alpha + \beta)}_{\text{c}}z + \underbrace{(\alpha + 10\beta)}_{\text{d}} = 0

Para que sea paralelo al eje $x$ , $\;\;\alpha + 3\beta = 0\; \Rightarrow \; \alpha = - 3\beta$

Reemplazando:

$-11\beta y - 8\beta z + 7\beta = 0$

$\beta \left( { - 11y - 8z + 7} \right) = 0$

${\pi _3}:\; - 11y - 8z + 7 = 0$

b) Ahora queremos un plano del haz que sea perpendicular al plano $x + y + z = 0$ . Dos planos son perpendiculares si sus vectores normales son perpendiculares.

Luego:

$\left( {1,1,1} \right)\left( {\alpha + 3\beta, \; 2\alpha - 5\beta, \; 3\alpha + \beta } \right) = 0\;$

$6\alpha - \beta = 0$

$\beta = 6\alpha$

75

Reemplazando:

$19\alpha x - 28\alpha y + 9\alpha z + 61\alpha = 0$

$\alpha \left( {19x - 28y + 9z + 61} \right) = 0$

$19x - 28y + 9z + 61 = 0$

Para practicar:

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

76

1.7 Recta en ${\mathbb{R}^3}$

1.7.1 Ecuaciones de la recta en ${\mathbb{R}^3}$

Sabemos que una recta en ${\mathbb{R}^2}$ puede expresarse por la ecuación:

$y = ax + b$

Pero ¿qué representa esta ecuación en ${\mathbb{R}^3}$ ? En ${\mathbb{R}^3}$ es un plano paralelo al eje $z$ , y en ${\mathbb{R}^2}$ es una recta:

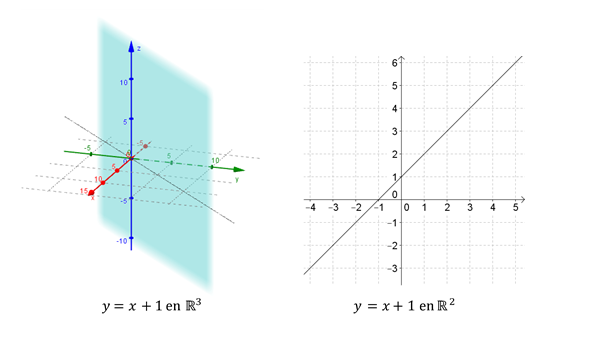
Para definir un plano es suficiente conocer un vector perpendicular al plano y un punto del mismo. ¿Qué datos permiten definir una recta en ${\mathbb{R}^3}$ ?

77

Para definir en forma vectorial una recta en ${\mathbb{R}^3}$ , es suficiente conocer un punto de la recta y un vector director que indique la dirección de la misma, o sea un vector paralelo a la recta.

1.7.2 Ecuación vectorial de la recta

Dados un vector $\vec v = \left( {{v_1},{v_2},{v_3}} \right)$ y un punto ${P_0}\left( {{x_0},{y_0},{z_0}} \right)$ , nos proponemos hallar la ecuación de la recta $r$ que pasa por el punto ${P_0}$ y es paralela al vector $\vec v$ .

Consideremos un punto $P\left( {x,y,z} \right)$ perteneciente a la recta $r$ . El vector $\overrightarrow {{P_0}P} \;$ resultará paralelo al vector director $\vec v$ :

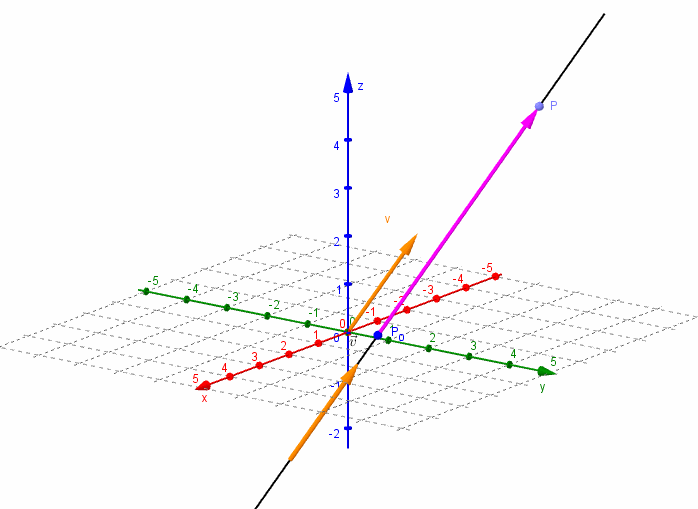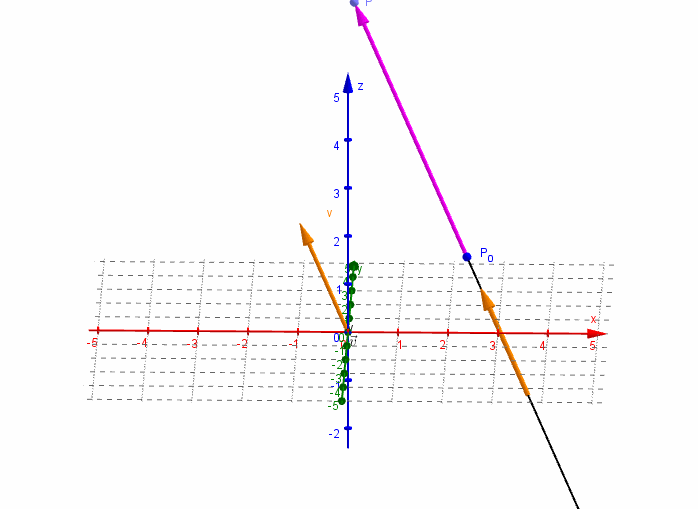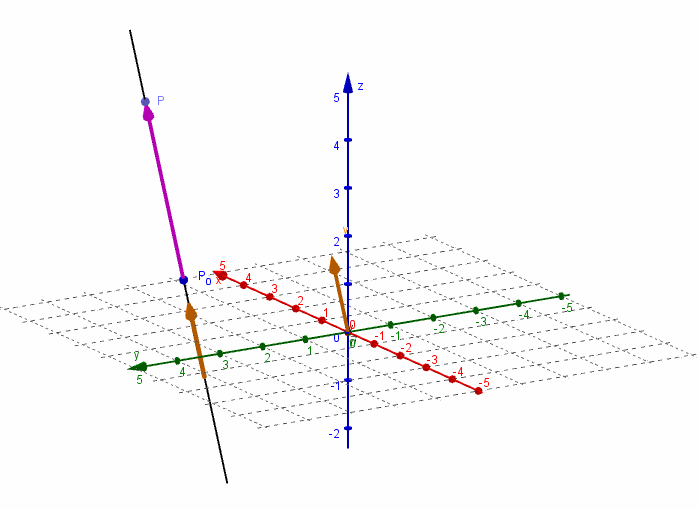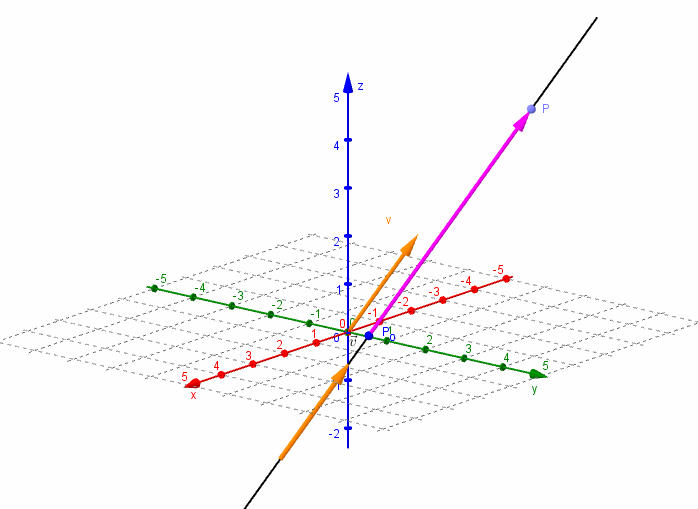
$\overrightarrow {{P_0}P} = \alpha \vec v$

$\left( {x - {x_0},y - {y_0},z - {z_0}} \right) = \alpha \left( {{v_1},{v_2},{v_3}} \right)$

78

Ecuación vectorial de la recta

\boxed {\;( {x,y,z} ) = ( {{x_0},{y_0},{z_0}} ) + \alpha ( {{v_1},{v_2},{v_3}}),\;\;\;\alpha \in \mathbb{R}\;\;}

Ejemplo

Hallar la ecuación vectorial de la recta que pasa por los puntos $M\left( {3,2,1} \right)$ y $S\left( { - 1,1,0} \right)$ .

Tenemos como datos dos puntos de la recta, entonces los vectores $\overrightarrow {MS}$ y $\overrightarrow {SM}$ son paralelos a dicha recta. Elegimos uno de ellos como vector director:

$\vec v = \overrightarrow {MS} = \left( { - 4, - 1, - 1} \right)$

Podemos tomar cualquiera de los dos puntos dados cómo punto de paso, por ejemplo $M.\;$ Entonces la ecuación es:

\left( {x,y,z} \right) = \left( {3,2,1} \right) + \alpha \left( { -4, - 1, - 1} \right),\;\;\;\alpha \in \mathbb{R}

(ecuación vectorial de la recta MS)

Para cada valor de $\alpha \in \mathbb{R},\;$ se obtiene un punto de la recta. Por ejemplo, si $\alpha = - 1$ se obtiene el punto ${P_1}\left( {7,3,2} \right) \in r.$

¿ $\left( {5, - 3,1} \right) \in r\;$ ?

79

Veamos si existe algún valor de $\alpha$ que verifique esta ecuación vectorial:

$\left( {5, - 3,1} \right) = \left( {3,2,1} \right) + \alpha \left( { - 4, - 1, - 1} \right)$

\begin{cases} \begin{align*} 3 - 4 \alpha =& \; 5 \\ 2 - \alpha =& -3 \\ 1- \alpha =& \; 1 \end{align*} \end{cases}

Este sistema es incompatible, así que el punto no pertenece a la recta.

¿Para qué valor de $\alpha$ se obtiene el punto $S$ ?

1.7.3 Ecuaciones paramétricas de la recta

Hemos visto que la ecuación vectorial de una recta es:

$\left( {x,y,z} \right) = \left( {{x_0},{y_0},{z_0}} \right) + \alpha \left( {{v_1},{v_2},{v_3}} \right)$

Por igualdad de vectores:

\begin{cases} \begin{align*} x = x_0 + \alpha \;v_1 \\ y = y_0 + \alpha \;v_2 \\ z = z_0 + \alpha \;v_3 \end{align*} , \:\:\: \alpha \in \mathbb{R} \end{cases}

Éstas son las ecuaciones cartesianas paramétricas de la recta.

80

1.7.4 Ecuaciones simétricas de la recta

Si $\;{v_1},{v_2},{v_3}\;$ son distintos de cero, entonces:

$\alpha = \frac{{x - {x_o}}}{{{v_1}}},\;\;\;\;\alpha = \frac{{y - {y_o}}}{{{v_2}}},\;\;\;\;\alpha = \frac{{z - {z_o}}}{{{v_3}}}$

Igualando, resulta:

Ecuaciones simétricas de la recta

\boxed{ \:\frac{{x - x_o}}{{v_1}} = \frac{{y - y_o}}{{v_2}} = \frac{{z - z_o}}{{v_3}}\;\;}

Ejemplo

Consideremos la ecuación vectorial de la recta $MS$ :

$\left( {x,y,z} \right) = \left( {3,2,1} \right) + \alpha \left( { - 4, - 1, - 1} \right),\;\;\;\alpha \in \mathbb{R}\;$

¿Cómo podemos obtener las ecuaciones paramétricas de la recta? Simplemente por igualdad de vectores escribimos:

\begin{cases} \begin{align*} x &= 3 - 4\alpha \\ y &= 2 - \alpha \\ z &= 1 - \alpha \end{align*}, \:\:\: \alpha \in \mathbb{R} \end{cases}

Ecuaciones paramétricas de la recta MS

81

Para obtener las ecuaciones simétricas, despejamos el parámetro e igualamos:

$\alpha = \frac{{x - 3}}{{ - 4}},\;\;\;\alpha = \frac{{y - 2}}{{ - 1}},\;\;\alpha = \frac{{z - 1}}{{ - 1}}$

$\dfrac{{x - 3}}{4} = y - 2 = z - 1,\;$ ecuaciones simétricas de la recta MS.

Revisión:

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

82

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

1.7.5 Recta definida como intersección de dos planos

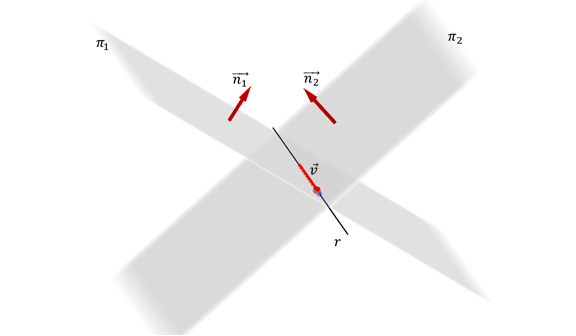
Dos planos no paralelos
${\pi _1}:{a_1}x + {b_1}y + {c_1}z + {d_1} = 0$ ${\pi _2}:{a_2}x + {b_2}y + {c_2}z + {d_2} = 0$ determinan al cortarse una recta en $\mathbb{R^3}$ que queda expresada por el sistema de ecuaciones lineales:

\begin{cases} \begin{align*} {a_1}x + {b_1}y + {c_1}z + {d_1} = 0 \\ {a_2}x + {b_2}y + {c_2}z + {d_2} = 0 \end{align*} \end{cases}

83

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

84

1.8 Recta y plano: intersecciones y ángulos

1.8.1 Intersección entre recta y plano

¿Qué casos pueden presentarse en la intersección entre una recta y un plano?

Caso 1

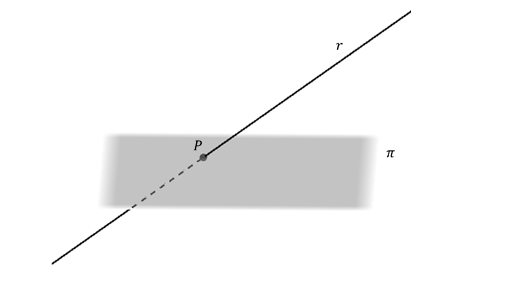
Una recta puede ser concurrente con un plano:

$r \cap \pi = \left\{ P \right\}$

Caso 2

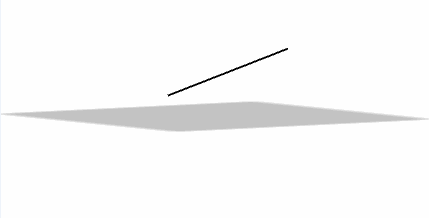
Una recta puede ser paralela a un plano:
$r\parallel \pi$ $r \cap \pi = \emptyset$

Caso 3

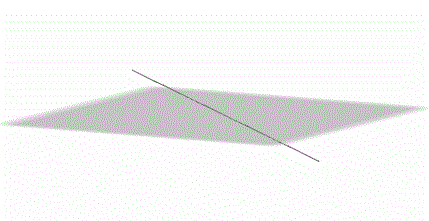
Una recta puede estar incluida en un plano:
$r \subset \pi$ $r \cap \pi = r$

85

Dados:

$\pi :\;\;2x - 3y + z + 1 = 0$

${r_1}:\left( {x,y,z} \right) = \left( {0,1,3} \right) + \alpha \left( {1,0,1} \right)$

¿Cómo se busca la intersección entre la recta y el plano?

Escribimos las ecuaciones paramétricas de la recta y las reemplazamos en la ecuación del plano:

\begin{cases} \begin{align*} x &= \alpha \\ y &= 1 \\ z &= 3 + \alpha \end{align*} \end{cases}

$2\alpha - 3.1 + \left( {3 + \alpha } \right) + 1 = 0\;\; \Rightarrow \;\alpha = - \frac{1}{3}$

Reemplazando el valor del parámetro $\alpha$ en las ecuaciones de la recta, obtenemos el punto de intersección:

${r_1} \cap \pi = \left\{ {\;\left( { - \frac{1}{3},1,\frac{8}{3}} \right)\;} \right\}\;\;$

86

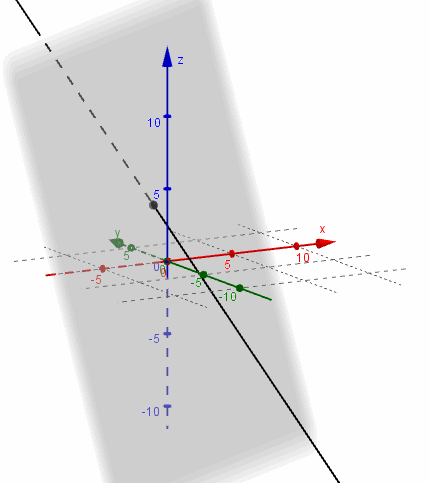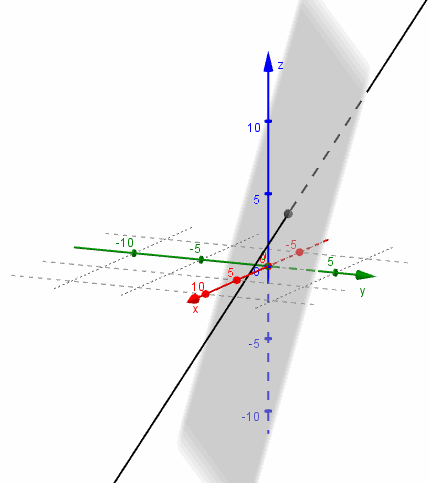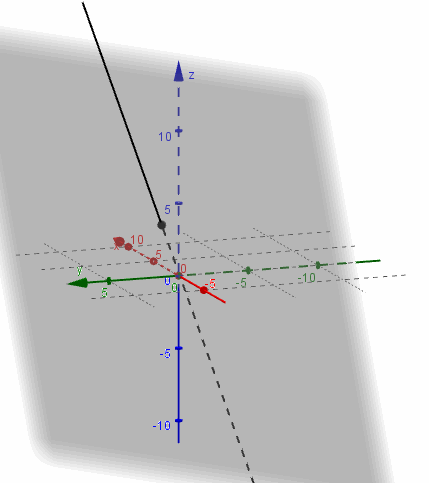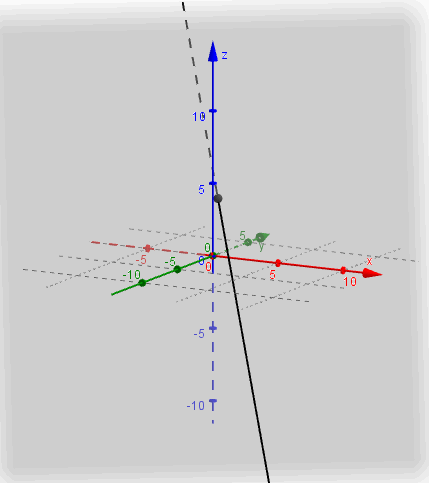
Busquemos ahora la intersección del mismo plano $\pi$ con la recta

${r_2}:\;\left( {x,y,z} \right) = \left( {0,0, - 1} \right) + \lambda \left( {3,2,0} \right)$

Escribimos las ecuaciones paramétricas:

\begin{cases} \begin{align*} x &= 3\lambda \\ y &= 2\lambda \\ z &= -1 \end{align*} \end{cases}

Reemplazamos en la ecuación del plano

$2\left( {3\lambda } \right) - 3\left( {2\lambda } \right) - 1 + 1 = 0\; \Rightarrow \;\;0 = 0\;\;\forall \lambda$

Queda una expresión que es verdadera para todo $\lambda$ . Esto significa que todo punto de la recta verifica la ecuación del plano. En este caso podemos afirmar que la recta está incluida en el plano, por lo tanto: ${r_2} \cap \pi = {r_2}\;.$

87

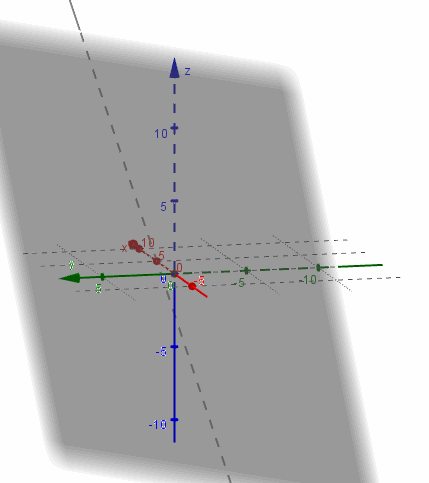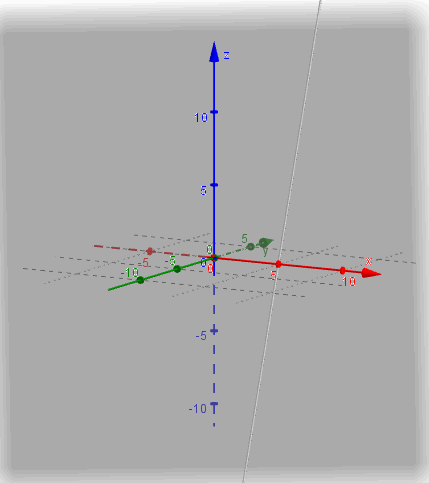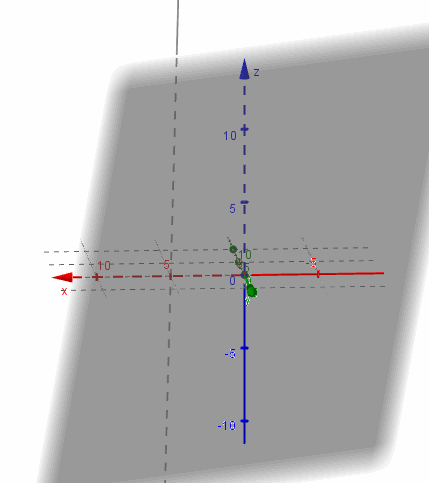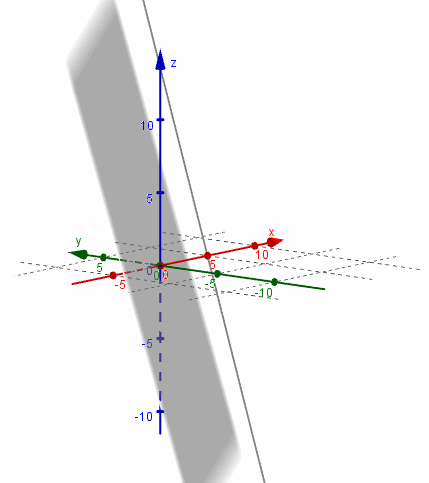
Considerando el mismo plano $\pi$ , hallemos la intersección con la recta

${r_3}:\left( {x,y,z} \right) = \left( {5,0,0} \right) + t\left( {0,1,3} \right)$

Reiterando el procedimiento, resulta:

\begin{cases} \begin{align*} x &= 5 \\ y &= t \\ z &= 3t \end{align*} \end{cases}

$10 - 3t + 3t + 1 = 0\; \Rightarrow \;11 = 0\;\;\;\;$ absurdo

Este absurdo nos indica que la recta y el plano no tienen ningún punto en común, o sea que la recta es paralela al plano y por lo tanto: $r \cap \pi = \emptyset$

88

En resumen:

Para hallar la intersección entre un plano y una recta, se reemplazan las ecuaciones paramétricas de la recta en la ecuación del plano.

Pueden presentarse tres casos:

i) Es posible despejar el valor del parámetro, entonces reemplazando este valor en las ecuaciones de la recta se obtiene el punto de intersección. En este caso:

$r \cap \pi = \left\{ P \right\}$

ii) $0 = 0 \Rightarrow r \subset \pi \Rightarrow r \cap \pi = r$

iii) $0 = k\left( {con\;k \ne 0} \right) \Rightarrow Absurdo$ $\Rightarrow r\parallel \pi \Rightarrow r \cap \pi = \emptyset$

1.8.2 Paralelismo entre recta y plano

¿Existe una manera de anticipar si una recta es paralela a un plano sin buscar la intersección?

Una vez más, los vectores resultarán una herramienta potente para la geometría de rectas y planos.

89

Observemos la siguiente figura:

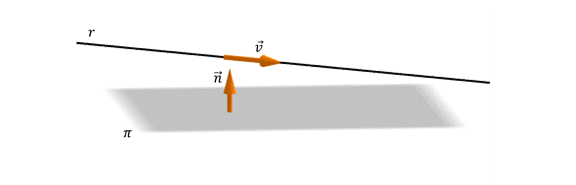
¿Cómo deben ser el vector normal del plano y el vector director de la recta para que $r\parallel \pi$ ?

r\parallel \pi \; \Leftrightarrow \; \vec v \: \bot \; \vec n\; \Leftrightarrow \;\vec v\;.\vec n = 0

¿Qué ocurre si la recta está incluida en el plano?

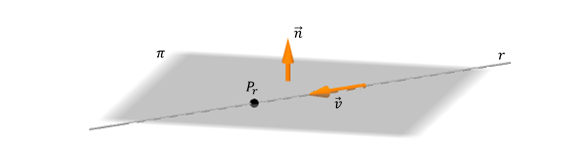
En este caso también se verifica que el vector director de la recta es perpendicular al normal del plano. Pero a diferencia del caso anterior, todos los puntos de la recta están en el plano. Esto nos permite afirmar que:

90

r \subset \pi \; \Leftrightarrow \;\begin{cases} \vec v \; \bot \; \vec n \\ P_r \in \pi \end{cases}

Ejemplo

Dados el plano $\pi:\;x + y - z - 3 = 0$ y la recta
$r:\left( {x,y,z} \right) = \left( {1,0,0} \right) + t\left( {0,2,2} \right)$ , comprobar que la recta es paralela al plano. ¿Está incluida en el plano?

Si la recta es paralela al plano entonces su vector director $\vec v$ debe ser perpendicular al vector normal del plano $\vec n$ . Luego $\vec n.\vec v$ debe ser cero:

$\left( {1,1, - 1} \right)\left( {0,2,2} \right) = 2 - 2 = 0$

Para saber si la recta está incluida en el plano veamos si el punto $\left( {1,0,0} \right)$ satisface la ecuación del plano $\pi$ :

$1\; + 0 - 0 - 3 = 0 \Rightarrow \; - 2 = 0\;\;Absurdo$

Como el punto no satisface la ecuación podemos concluir que $r$ no está incluida en $\pi$ .

Ejercicio para el lector

Sea $\;\pi$ el plano paralelo al eje $y$ que pasa por $\left( {1,1,1} \right)$ y $\left( {1,2,3} \right)$ ,

91

y sea la recta

\begin{cases} \begin{align*} x - y &= 0 \\ x + kz &= 2 \end{align*} \end{cases}

Hallar, si es posible, el valor de $k$ para que la recta $r$ sea paralela a $\pi$ .
Si existe $k$ , analizar si $r \subset \pi$ .

Respuesta: $\;k=0\;$ y la recta no pertenece al plano.

1.8.3 Perpendicularidad entre recta y plano

Así como encontramos una condición vectorial para el paralelismo entre una recta y un plano, nos preguntamos si existirá una condición para la perpendicularidad. Observemos la siguiente figura:

92

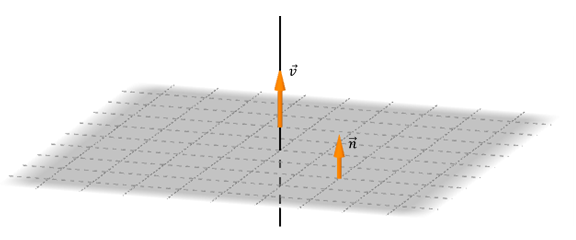
¿Cómo deben ser el vector normal del plano y el vector director de la recta para que $r \; \bot \; \pi$ ?

r \; \bot \; \pi \;\; \Leftrightarrow \;\;\vec v\parallel \;\vec n\; \Leftrightarrow \;\;\vec v = k\vec n\;\;\;

Ejemplo

Dado el plano $\pi:\;x-3y + z + 1 = 0$ , hallar la ecuación de la recta perpendicular a $\pi$ que pasa por $A\left( {1,0,3} \right)$ .

Como la recta es perpendicular al plano $\pi$ entonces su vector director es paralelo al vector normal del plano. Podemos tomar:

$\vec v = \left( {1, - 3,1} \right)$

Ya tenemos el vector director y un punto de paso, luego la ecuación vectorial es:

$r:\left( {x,y,z} \right) = \left( {1,0,3} \right) + \lambda \left( {1, - 3,1} \right),\;\;\;\lambda \in \mathbb{R}$

Ejercicio para el lector

Dado el haz de planos $x + y -z + 2 + k\left( {x - y + z} \right) = 0,$ analizar si existe algún plano del haz que sea perpendicular a la recta $r: \begin{cases} \begin{align*} x - 1 &= 0 \\ y - z &= 0 \end{align*} \end{cases}$

93

Para reforzar y practicar:

Objetos interactivos diseñados por Elena Esperanza Álvarez Sáiz y M. J. García Cebrian

94

1.8.4 Ángulo entre recta y plano

Consideremos el siguiente esquema:

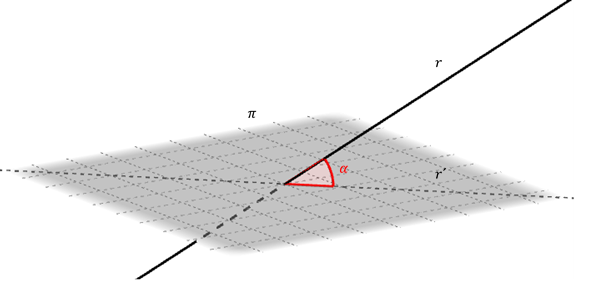
Sea $r$ una recta no paralela ni perpendicular a un plano $\pi$ . Sea la proyección ortogonal de $r$ sobre $\;\pi$ . Se define como ángulo entre $r$ y $\;\pi$ al ángulo agudo que forman $r$ y $r'$ .
¿Cómo podemos hallar dicho ángulo? Veamos la siguiente figura:

95

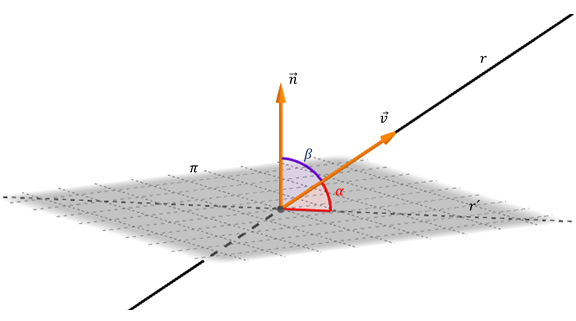
Podemos calcular el ángulo $\beta$ entre $\vec v\;$ y $\;\vec n$ :

$\cos \left( \beta \right) = \frac{{\vec v.\vec n}}{{\lVert\vec v\rVert\;\lVert\vec n\rVert}}$

Como habíamos visto previamente, de acuerdo con las direcciones de $\vec v\;$ y $\vec n$ el ángulo $\beta$ podría ser mayor de 90º. Agregamos módulo para obtener un ángulo agudo:

$\cos \left( \beta \right) = \frac{{\left| {\vec v .\vec n} \right|}}{{\lVert\vec v\rVert\;\lVert\vec n\rVert}}\;$

Como $\alpha$ y $\beta$ son complementarios se cumple la igualdad $sen( \alpha ) = \cos ( \beta),$ entonces:

sen\left( \alpha \right) = \frac{{\left| {\;\vec v.\vec n\;} \right|}}{{\lVert\vec v\rVert\;\lVert\vec n\rVert}}\;\;\;

Por lo tanto:

Ángulo entre recta y plano

\boxed {\;\; \alpha = arcsen \left( \frac{\left| {\vec v .\vec n} \right|}{\lVert\vec v\rVert\;\lVert\vec n\rVert} \right),\;\;0 \le \alpha \le \frac{\pi }{2}\;\;}

96

Casos particulares:

Si ${\rm{\;}}\alpha = 0,\;$ entonces la recta es paralela al plano ( $\vec v.\vec n = 0$ ).
Si $\alpha = \dfrac{\pi}{2},$ entonces la recta es perpendicular al plano ( $\vec v = k\vec n$ )

Ejemplo

Hallar el ángulo entre el plano $\pi:\;x + z - 8 = 0$ y el eje $x$ .

Conocemos el vector normal de $\pi$ y el vector director de la recta. Luego aplicamos directamente la fórmula:

\alpha = {\rm{arcsen}}\left( {\frac{{\left| {\overrightarrow {\;v} .\overrightarrow {n\;} } \right|}}{{\lVert\vec v\rVert\;\lVert\vec n\rVert}}} \right) = {\rm{arcsen}}\left( {\frac{{\left| {\left( {1,0,0} \right).\left( {1,0,1} \right)} \right|}}{{\sqrt 2 }}} \right) =

\alpha = {\rm{arcsen}}\left( {\frac{1}{{\sqrt 2 }}} \right) = \frac{\pi }{4}

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

97

1.8.5 Intersección de rectas en ${\mathbb{R}^3}$

Sabemos que dos rectas en ${\mathbb{R}^2}$ o bien se cortan en un único punto o bien son paralelas.

Pero en ${\mathbb{R}^3}$ , además de estos dos casos, existen rectas que ni se cortan ni son paralelas: son las rectas alabeadas.

Tenemos entonces tres casos en ${\mathbb{R}^3}$ :

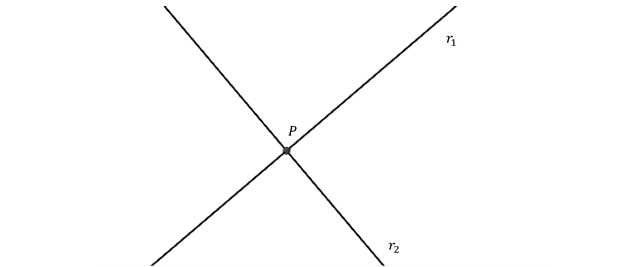
Caso 1: Rectas concurrentes o incidentes

${r_1} \cap {r_2} = \left\{ P \right\}$

Caso 2: Rectas paralelas

{r_1}\parallel {r_2}\; \Leftrightarrow \;{\vec v_1} = k{\vec v_2}

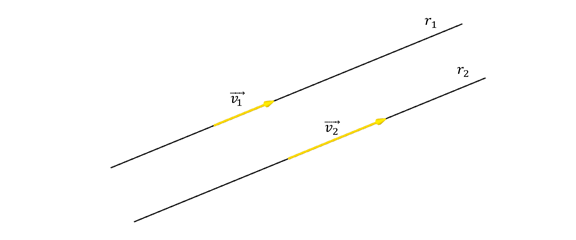
Las rectas paralelas podrían ser coincidentes. Para verificar si dos rectas paralelas son coincidentes basta con ver si un punto de una de ellas pertenece o no a la otra recta.

98

Caso 3: Rectas alabeadas

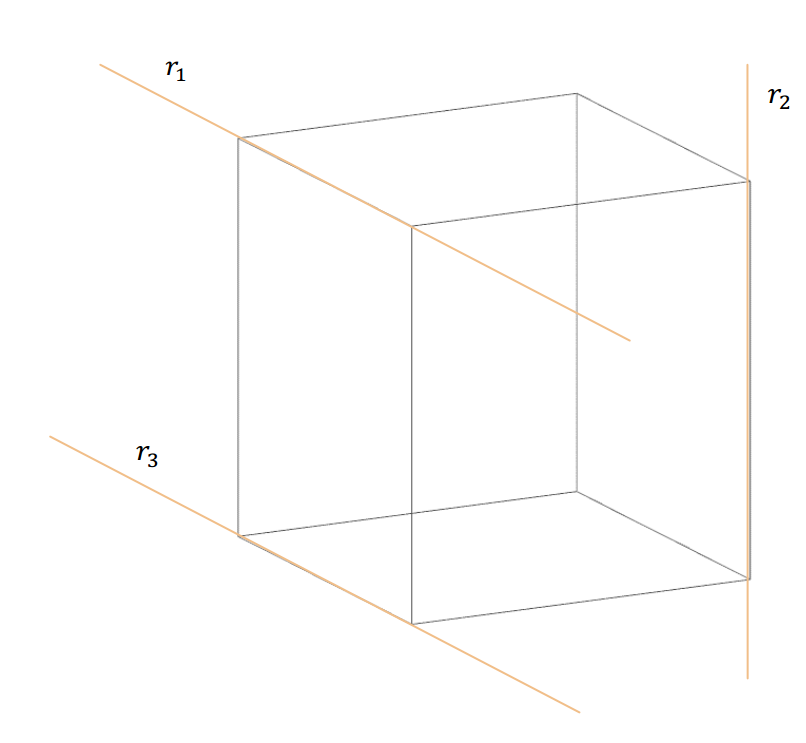
Existe otra posición posible para las rectas en ${\mathbb{R}^3}$ . Consideremos el siguiente esquema en el que las rectas ${r_1}$ , ${r_2}$ y ${r_3}$ contienen a las aristas de un cubo.

Las rectas ${r_1}$ y ${r_3}$ son paralelas. En cambio ${r_1}$ y ${r_2}$ , que no son paralelas ni concurrentes, se denominan alabeadas.

$r_1$ y $r_2$ son alabeadas $\; \Leftrightarrow \; r_1 \nparallel r_2 \land r_1 \cap r_2 = \empty$

99

1.8.6 Plano que contiene a dos rectas

Dos rectas en ${\mathbb{R}^3}$ se denominan coplanares si existe un plano que contiene a ambas rectas.

Habíamos visto que dos rectas en ${\mathbb{R}^3}$ pueden ser concurrentes, paralelas o alabeadas. Veamos en qué casos es posible encontrar un plano que las contenga:

Caso 1: Rectas concurrentes

Veamos el siguiente gráfico que muestra dos rectas concurrentes:

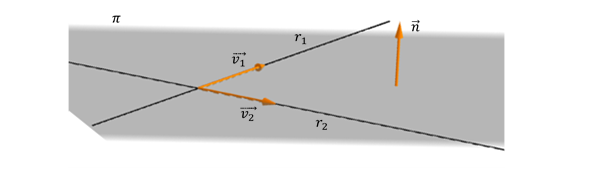
Dadas dos rectas concurrentes ${r_1}$ y ${r_2}$ , ¿cómo podemos encontrar el vector normal del plano?

${\vec v_1} \times {\vec v_2} = \vec n$

Para completar la ecuación del plano, tomamos un punto P de cualquiera de las dos rectas.

100

Ejercicio de aplicación

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

101

Caso 2: Rectas paralelas

Veamos el siguiente gráfico que muestra dos rectas paralelas y el plano que las contiene:

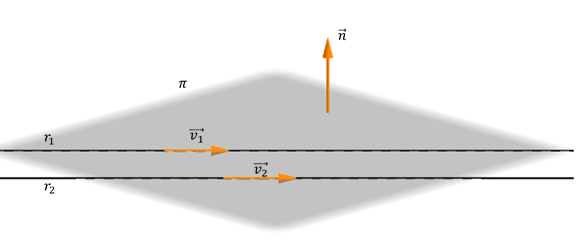
Dadas dos rectas paralelas, existe un plano que las contiene pero no podemos hallar el vector normal como en el caso de las rectas concurrentes. ¿Por qué?

Caso 3: Rectas alabeadas

Dos rectas alabeadas no pueden estar contenidas en un mismo plano.

Ejemplos resueltos

102

1.8.7 Ángulo entre dos rectas

Definición: El ángulo entre dos rectas de ${\mathbb{R}^3}$ es el ángulo entre sus vectores directores.

Sean las rectas ${r_1}$ y ${r_2}$ con vectores directores $\vec v_1$ y $\vec v_2.$ Entonces:

$\cos \left( \alpha \right) = \frac{\vec v_1 .\vec v_2 }{\lVert\vec v_1 \rVert \;\lVert\vec v_2\rVert \ }$

Usamos la misma convención que para ángulo entre planos y para ángulo entre recta y plano, y aplicamos módulo:

$\cos \left( \alpha \right) = \frac{\left| \vec v_1 .\vec v_2 \right|}{\lVert\vec v_1\rVert \;\lVert\vec v_2\rVert }$

Por lo tanto:

Ángulo entre dos rectas

\boxed {\;\;\alpha = arcos\left( {\frac{{\left| {\overrightarrow {{v_1}} .\overrightarrow {{v_2}} } \right|}}{{\lVert\overrightarrow {{v_1}}\rVert \ \;\lVert\overrightarrow {{v_2}}\rVert \ }}} \right),\;\;\;0 \le \alpha \le \frac{\pi }{2}\;\;\;}

Casos particulares:

Si $\,\alpha = 0,\;$ entonces las rectas son paralelas $(\vec v_1 = k\;\vec v_2)$ .

Si $\alpha = \dfrac{\pi}{2},\;$ entonces las rectas son perpendiculares $(\vec v_1 .\vec v_2 = 0)$ .

103

Observación: La definición de ángulo que hemos adoptado no toma en cuenta si las rectas se cortan o no.

Ejemplo

Sean,

\begin{matrix} \begin{align*} &{r_1}:\;\:\left( {x,y,z} \right) = \;\lambda\left( {1,0,0} \right),\;\;\;\lambda \in \mathbb{R} \\ &{r_2}:\;\;\left( {x,y,z} \right) = \left( {0,1,0} \right) + \; t\left( {0,0,1} \right),\;\;t \in \mathbb{R} \end{align*} \end{matrix}

Vimos en un ejemplo anterior que estas rectas son alabeadas. ¿Cuál es el ángulo entre ellas?

Como $\;\;\vec {v_1} .\vec {v_2} = 0,\;$ las rectas son perpendiculares, o sea que

\alpha = \dfrac{\pi}{{2}}

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

104

1.9 Distancias y proyecciones

1.9.1 Proyecciones ortogonales

Proyección de un punto sobre un plano

Dados un plano $\pi$ y un punto $A$ no perteneciente a dicho plano, la proyección ortogonal de $A$ sobre $\pi$ es el punto $A' \in \pi$ tal que $\overrightarrow {AA'}$ es un vector perpendicular a $\pi$ .

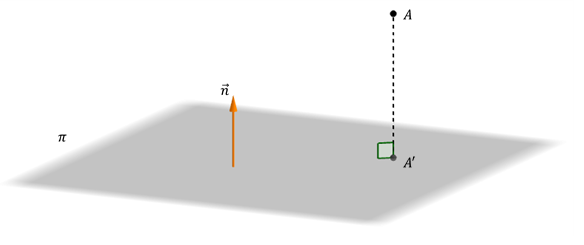
$A' = pro{y_\pi }\left( A \right)\;\;$ si y sólo si $\;\; \begin{cases} A' \in \pi \\ \overrightarrow{AA'} \; \bot \; \pi \end{cases}$

Ejemplo

Dados el plano $\pi: \; 2x - y + 3z + 1 = 0$ y el punto $A \;(4,\;1,\;-3)$ , obtener la proyección ortogonal del punto sobre el plano.

105

Para obtener buscamos la recta perpendicular a $\pi$ que pasa por $A$ . El vector normal del plano es paralelo a esta recta, por lo tanto podemos tomarlo como vector director:

$r:\left( {x,y,z} \right) = \left( {4,1, - 3} \right) + \lambda \left( {2, - 1,3} \right)$

Ahora buscamos la intersección de la recta con el plano, reemplazando las ecuaciones paramétricas de la recta en la ecuación del plano:

\begin{cases} \begin{align*} x &= 4 + 2\lambda \\ y &= 1 - \lambda \\ z &= -3 + \lambda \end{align*} \end{cases}

$2\left( {4 + 2\lambda } \right) - \left( {1 - \lambda } \right) + 3.\left( { - 3 + 3\lambda } \right) + 1 = 0$

$8 + 4\lambda - 1 + \lambda - 9 + 9\lambda + 1 = 0$

$14\lambda - 1 = 0 \Rightarrow \lambda = \frac{1}{{14}}$

Reemplazamos en la ecuación de la recta para obtener las coordenadas del punto $A'\;$ :

$\left( {x,y,z} \right) = \left( {4,1, - 3} \right) + \frac{1}{{14}}\left( {2, - 1,3} \right) =$ $(x,y,z)= \left( {4,1, - 3} \right) + \left( {\frac{1}{7}, - \frac{1}{{14}},\frac{3}{{14}}} \right) = \left( {\frac{{29}}{7},\frac{{13}}{{14}}, - \frac{{39}}{{14}}} \right)\;\;$

106

El lector puede verificar que $A'\;\bigg( {\dfrac{29}{7},\dfrac{13}{14}, - \dfrac{39}{14}}\bigg) \in \pi \;$ y además que $\;\overrightarrow {AA'} \; \bot \; \pi \;.$

Si $A \in \pi \;,$ ¿cuál es la proyección de $A$ sobre $\;\pi$ ?

Proyección de una recta sobre un plano

Dados una recta $r$ y un plano $\pi$ , nos interesa obtener la proyección ortogonal de la recta sobre el plano.

En general, la proyección de una recta sobre un plano es otra recta $r'$ :

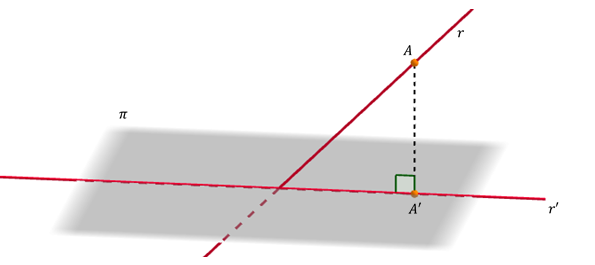
$pro{y_\pi }\left( r \right) = r'$

Para hallar $r'\,$ podemos proyectar dos puntos de la recta sobre el plano. Si llamamos $A$ y $B$ a dichos puntos, resulta

$pro{y_\pi }\left( A \right) = A',\;\;\;\;pro{y_\pi }\left( B \right) = B'\;\;\;\;$

107

La recta $r'$ que buscamos es la recta determinada por $A'$ y $B'$ .

Pero teniendo en cuenta que el punto de intersección entre la recta y el plano pertenece a $r'$ , es suficiente proyectar un solo punto de $r\;$ para que $r'$ quede definida.

También existe un caso especial: si la recta es perpendicular al plano, su proyección es un punto.

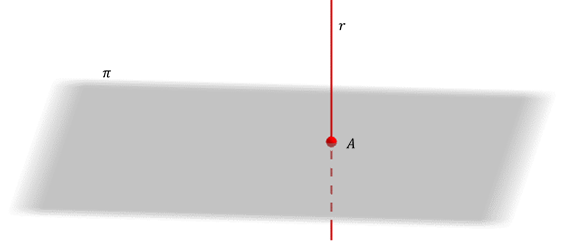
$r \bot \pi \Rightarrow pro{y_\pi }\left( r \right) = A = r \cap \pi$

Ejemplo

Dado $\pi : x + y + z - 3 = 0$
a) Hallar la proyección de la recta $r:\left( {x,y,z} \right) = \lambda \left( {0,2,1} \right)$ sobre $\pi$
b) Dada la recta $\;s:\left( {x,y,z} \right) = \left( {1,0,0} \right) + t.\left( { - 2,b,c} \right)$ , hallar los valores de $b$ y $c$ para que la proyección de $s$ sobre $\pi$ sea un punto. ¿Cuál es dicho punto?

108

Resolución

a) Para hallar la recta $r' = pro{y_\pi }\left( r \right)$ buscamos dos puntos que pertenezcan a $r'$ .

Uno de los puntos puede ser el de intersección:

$2\lambda + \lambda - 3 = 0 \Rightarrow \;\lambda = 1 \Rightarrow \left( {x,y,z} \right) = \left( {0,2,1} \right)$

Tomemos el punto $\left( {0,0,0} \right) \in r$ . Para proyectarlo sobre el plano buscamos la recta perpendicular al plano que pasa por $\left( {0,0,0} \right)$ :

$\left( {x,y,z} \right) = \left( {0,0,0} \right) + \alpha \left( {1,1,1} \right)$

$\left( {x,y,z} \right) = \alpha \left( {1,1,1} \right)$

Reemplazando en la ecuación del plano:

$\alpha + \alpha + \alpha - 3 = 0 \Rightarrow \alpha = 1$

Entonces la proyección del punto $\left( {0,0,0} \right)$ sobre $\pi$ da $\left( {1,1,1} \right)\;$

La recta $r'$ queda definida por los puntos $\left( {0,2,1} \right)$ y $\left( {1,1,1} \right)$ :

$r':\left( {x,y,z} \right) = \left( {0,2,1} \right) + \gamma \left( {1, - 1,0} \right)$

109

b) Para que la proyección de $s$ sobre $\pi$ sea un punto, el vector director de $s$ debe ser paralelo al vector normal del plano. Debe existir un $k \in \mathbb{R}$ tal que:

\left( {1,1,1} \right) = k\left( { - 2,b,c} \right)

De aquí deducimos que deben ser $b = c = - 2$ . La ecuación de la recta queda:
$s:\;\left( {x,y,z} \right) = \left( {1,0,0} \right) + t\left( { - 2, - 2, - 2} \right)$ Para hallar el punto reemplazamos las ecuaciones paramétricas de la recta en la ecuación del plano:

s:\; \begin{cases} \begin{align*} x &= 1 - 2t \\ y &= -2t \\ z &= -2t \end{align*} \:\:\: t \in \mathbb{R}, \;\;\; \pi:\, x+y+z-3=0 \end{cases}

$1 - 2t - 2t - 2t - 3 = 0 \Rightarrow - 2 - 6t = 0 \Rightarrow t = - \frac{1}{3}$

El punto es: $P\left( {\frac{5}{3},\frac{2}{3},\frac{2}{3}} \right)$ Por lo tanto: $pro{y_\pi }\left( s \right) = \;s \cap \pi = \;P\left( {\frac{5}{3},\frac{2}{3},\frac{2}{3}} \right)$

110

En el siguiente interactivo ejercitamos la proyección de una recta sobre un plano.

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

111

1.9.2 Planos proyectantes de una recta

Los planos proyectantes de una recta son aquellos planos que incluyen a la recta y son perpendiculares a los planos coordenados.

Ejemplo 1

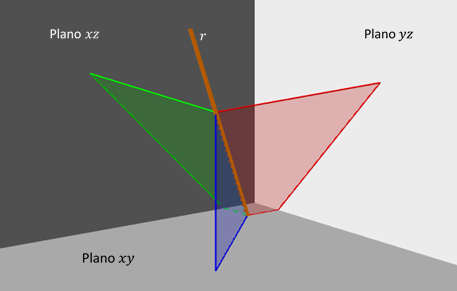
Hallar los planos proyectantes de la siguiente recta:

r: \; \begin{cases} \begin{align*} x - 2y + z + 7 &= 0 \\ -x + y + z - 1 &= 0 \end{align*} \end{cases}

Resolución
Teniendo en cuenta que la recta está definida como intersección de dos planos, una forma práctica de hallar los planos proyectantes es construir el haz de planos que pasan por dicha recta:

112

Construyamos el haz de planos que pasa por $r$ :

$\mathcal{H}:\alpha \left( {x - 2y + z + 7} \right) + \beta \left( { - x + y + z - 1} \right) = 0$

Ahora distribuimos y reordenamos:

\underbrace{(\alpha - \beta)}_{a}x + \underbrace{(-2\alpha + \beta)}_{b}y + \underbrace{(\alpha + \beta)}_{c}z + \underbrace{(7\alpha - \beta)}_{d}

El plano proyectante perpendicular al plano $xy$ (o sea, paralelo al eje $z$ ) es un plano de la forma $ax\; + \;by\; + \;d\; = \;0$ . Por lo tanto:

$\alpha + \beta = 0 \Rightarrow \alpha = - \;\beta$

$\Rightarrow \;\;{\pi _1}:\;\; - 2x + 3y - 8 = 0$

El plano proyectante perpendicular al plano $xz$ (o sea, paralelo al eje y) es un plano de la forma $ax\; + \;cz\; + \;d\; = \;0$ . Por lo tanto:

$- 2\alpha + \beta = 0 \Rightarrow \beta = 2\alpha$

$\Rightarrow \;{\pi _2}:\;\; - x + 3z + 5 = 0$

¿Cuál es el plano proyectante perpendicular al plano $yz$ ?

113

Ejemplo 2

Hallar los planos proyectantes de la recta que pasa por los puntos $A\left( {1,2,3} \right)$ y $B\left( {3,1, - 1} \right)$ .

Resolución

La ecuación vectorial de la recta que contiene a los puntos $A$ y $B$ es $r: (x,y,z) = (1,2,3) +t(2, - 1, - 4)$

Supongamos que llamamos $\pi _1$ al plano proyectante que es perpendicular al plano $xy.\;$ ¿Qué condiciones debe cumplir $\overrightarrow {{n_1}} \,$ ?

Entonces: $\left( {a,b,0} \right).\left( {2, - 1, - 4} \right) = 0 \Rightarrow 2a - b = 0 \Rightarrow b = 2a$

Con $\,a = 1\;\;\;y\;\;b = 2$ , resulta:

Teniendo en cuenta que $r \subset {\pi _1}$ , reemplazamos un punto de la recta (por ejemplo $A$ ) para obtener $d$ .

El plano buscado es: ${\pi _1}:\;x + 2y - 5 = 0$

Dejamos a cargo del lector comprobar que los otros planos proyectantes son:

${\pi _2}:\;2x + z - 5 = 0\,$ y $\;{\pi _3}: - 4y + z + 5 = 0$

114

Ejemplo 3

Retomemos el ejemplo anterior, siendo
$r:\;\left( {x,y,z} \right) = \left( {1,2,3} \right) + \;t\left( {2, - 1, - 4} \right)$

Cuando las componentes del vector director de una recta son distintas de cero, podemos expresarla a través de sus ecuaciones simétricas. En este caso:

$r:\;\;\;\;\;\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 3}}{{ - 4}}$

A partir de las ecuaciones simétricas se deducen tres igualdades, cada una de las cuales se corresponde con la ecuación de un plano proyectante de la recta:

\dfrac{x-1}{2}=\dfrac{y-2}{-1}\; \Rightarrow\;-(x-1)=2(y-2)\;\Rightarrow

$\quad\quad\quad\quad \Rightarrow x + 2y - 5 = 0\;\;\;\;\;\;$ Plano proyectante $\pi_1$

\dfrac{x-1}{2}= \dfrac{z-3}{-4}\; \Rightarrow\;-4(x-1)=2(z-3)\;\Rightarrow

$\quad\quad\quad\quad \Rightarrow 2x + z - 5 = 0\;\;\;\;\;\;$ Plano proyectante $\pi_2$

\dfrac{y-2}{-1} = \dfrac{z-3}{-4}\; \Rightarrow\;-4(y-2)=-(z-3)\;\Rightarrow

$\quad\quad\quad\quad \Rightarrow -4y +z + 5 = 0\;\;\;\;\;\;$ Plano proyectante $\pi_3$

115

El siguiente gráfico muestra la recta y su plano proyectante ${\pi _1}:$

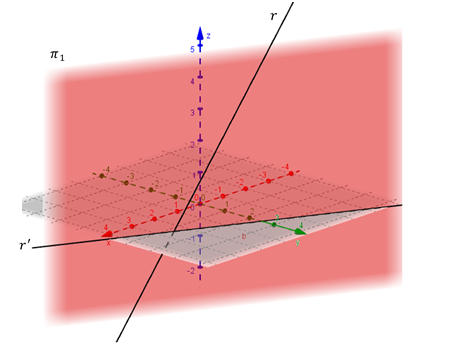
Recta y un plano proyectante

En la figura puede observarse que el plano proyectante ${\pi _1}$ es el plano determinado por la recta $\;r$ y su proyección $r'$ sobre el plano coordenado $xy$ . Lo mismo puede afirmarse de los otros dos planos proyectantes.

116

Actividad (para reflexionar)

Hallar los planos proyectantes de cada una de las siguientes rectas:

$r:\;\;\left( {x,y,z} \right)\; = \;\left( {1,2,3} \right)\; + \;t\left( {1, - 2,0} \right)$

$s:\;\;\;\left( {x,y,z} \right)\; = \;\left( {2,2,1} \right)\; + \;\lambda \left( {0,0,1} \right)$

A partir de los resultados obtenidos, ¿podrías establecer qué condición debe cumplirse para que una recta tenga dos de sus planos proyectantes iguales?

¿Existe algún caso en que no esté definido alguno de los planos proyectantes de una recta?

1.9.3 Distancias

a) Distancia punto-recta en

{\mathbb{R}^3}

Dados un punto $A$ y una recta $r$ de vector director $\vec v$ , queremos hallar la distancia entre $A$ y $r$ (con $A \notin r$ ). Sea $A' \in r$ tal que $\overrightarrow {AA'}$ es perpendicular a la recta.

$d\left( {A,r} \right) = \lVert\overrightarrow {AA'} \rVert$

Consideremos un punto $P \in r$ y el vector $\overrightarrow {PA}$ , y construyamos el paralelogramo determinado por $\vec v$ y $\overrightarrow {PA}$ , tal como lo muestra la figura:

117

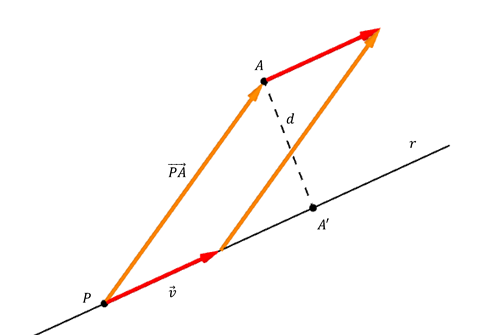
El segmento $AA'$ es la altura del paralelogramo. Si llamamos S al área de dicho paralelogramo, resulta:

$S = b.h = \lVert\vec v\rVert.d\;\;\;\;\;\;\;\;\left[ 1 \right]$

Recordemos que el área del paralelogramo es igual al módulo del producto vectorial:

$S = \lVert\overrightarrow {PA} \times \vec v \rVert\;\;\;\;\;\;\;\left[ 2 \right]$

Igualando $\left[ 1 \right]$ y $\left[ 2 \right]$ podemos despejar $d$ :

$\lVert \vec v\rVert.d = \lVert\overrightarrow {PA} \times \vec v\rVert$

\;\; \Rightarrow \;\;\;d\left( {A,r} \right) = \frac{{\lVert\overrightarrow {PA} \times \vec v\rVert}}{{\lVert\vec v\rVert}}

118

Ejemplo

Calcular la distancia entre la recta

$r:(x,y,z) = (1,0,- 1) + \lambda (- 2,1,1)$ y el punto $A\left( {3, - 1,1} \right)$ .

Resolución

Aplicamos la fórmula:

$\;d\left( {A,r} \right) = \frac{{\lVert\overrightarrow {PA} \times \vec v\rVert}}{{\lVert\vec v\rVert}}$

Tomamos un punto cualquiera de la recta, por ejemplo $P\left( {1,0, - 1} \right)$ y formamos:

$\overrightarrow {PA} = \left( {2, - 1,2} \right)$

$d\left( {A,r} \right) = \frac{{\lVert\left( {2, - 1,2} \right) \times \left( { - 2,1,1} \right)\rVert}}{{\;\lVert\left( { - 2,1,1} \right)\rVert}} = \frac{{\lVert\left( { - 3, - 6,0} \right)\rVert}}{{\sqrt 6 \;}} = \frac{{\sqrt {45} }}{{\sqrt 6 }}$

d(A,r) = \cong 2,74

Objeto interactivo diseñado por Elena E. Álvarez Sáiz y Mª José García Cebrian

119

b) Distancia entre dos rectas paralelas

La fórmula que hemos visto permite calcular la distancia entre dos rectas paralelas. Veamos un ejemplo:

Dadas las rectas ${r_1}:\left( {x,y,z} \right) = \left( {1,0,0} \right) + t\left( {2, - 1,1} \right)\;$ y
$r_2: \: \begin{cases} y + z = 2 \\ x + ky = 0 \end{cases}$

Hallar $k$ tal que ${r_1}\parallel {r_2}$ y calcular $d\left( {{r_1},{r_2}} \right).$

Recordemos la condición para que dos rectas sean paralelas:

${r_1}\parallel {r_2}\; \Leftrightarrow \overrightarrow {{v_1}} = \alpha \;\overrightarrow {{v_2}} \;\;\;\;\;\left[ 1 \right]$

La recta ${r_2}$ está definida como intersección de dos planos. Si hacemos el producto vectorial de los vectores normales tendremos un vector director de la recta:

$\left( {0,1,1} \right) \times \left( {1,k,0} \right) = \left( { - k,1, - 1} \right)$

Por [1]:

(-k, \; 1,\; -1) = \alpha (2,\;-1;1)\; \Rightarrow \; \begin{cases} \begin{align*} -k &= 2\alpha \\ 1 &= - \alpha \\ -1 &= \alpha \end{align*} \end{cases}

$\Rightarrow k = 2$

120

Para calcular la distancia, tomemos dos puntos cualesquiera de las rectas y construyamos el vector $\overrightarrow {{P_1}{P_2}}$ :

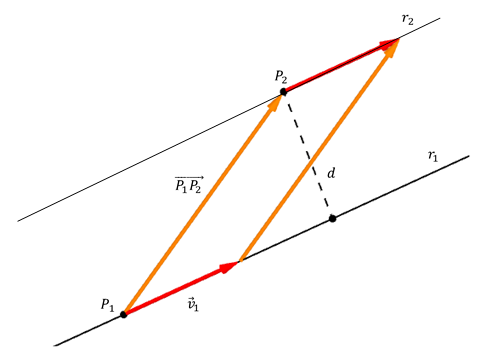
${P_1}\left( {1,0,0} \right) \in {r_1},\;\;\;{P_2}\left( {0,0,2} \right) \in {r_2},\;\;\;\overrightarrow {{P_1}{P_2}} = \left( { - 1,0,2} \right)$

La distancia entre las rectas será la distancia entre ${P_2}$ y ${r_1}$ :

$d\left( {{r_1},{r_2}} \right) = d\left( {{P_2},{r_1}} \right) = \frac{{\overrightarrow {{P_1}{P_2}} \times \overrightarrow {{v_1}} }}{{\overrightarrow {{v_1}} }}$

$\overrightarrow {{P_1}{P_2}} \times {\vec v_1} = \left( { - 1,0,2} \right) \times \left( {2, - 1,1} \right) = \left( {2,5,1} \right)$

\lVert \overrightarrow {{P_1}{P_2}} \times \vec v \rVert = \sqrt {30}

$d\left( {{r_1},{r_2}} \right) = \frac{{\sqrt {30} }}{{\sqrt 6 }} = \sqrt 5$

Como puede observarse, con las mismas herramientas resolvimos un problema diferente.

121

c) Distancia entre rectas alabeadas

Dadas dos rectas ${r_1}$ y ${r_2}$ no paralelas, nos proponemos calcular la distancia entre ambas:

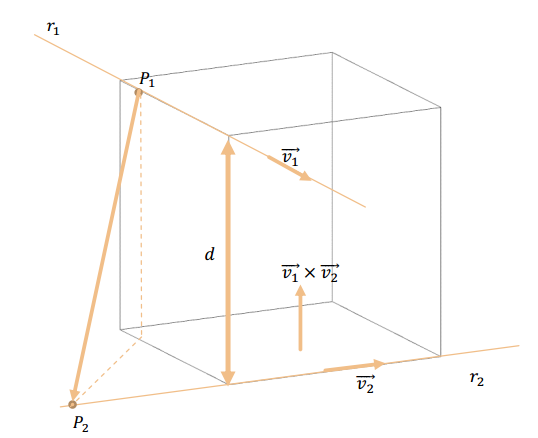
La mínima distancia entre dos rectas alabeadas ${r_1}$ y ${r_2}$ se obtiene al proyectar el vector $\overrightarrow {{P_1}{P_2}}$ sobre la dirección perpendicular a ambas rectas, dada por $\overrightarrow {{v_1}} \times \overrightarrow {{v_2}}$ :

$d\left( {{r_1},{r_2}} \right) = {\lVert\overrightarrow {proy} _{\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} }}\left( {\overrightarrow {{P_1}{P_2}} } \right)\rVert$

Recordemos que:

$\lVert{\overrightarrow {proy} _{\vec v}}\left( {\vec u} \right)\rVert = \frac{{\left| {\vec u.\vec v} \right|}}{{\lVert\vec v\rVert}}$

122

Entonces podemos obtener una fórmula para la distancia entre ${r_1}$ y ${r_2}$ :

Distancia entre rectas alabeadas

\boxed {\;\;\;d\left( {{r_1},{r_2}} \right) = \frac{{\left| {\overrightarrow {{P_1}{P_2}} .\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right)} \right|}}{{\lVert\overrightarrow {{v_1}} \times \overrightarrow {{v_2}}\rVert }}\;\;\;}

¿Qué significa que la distancia dé $0$ ?

1.9.4 Condición de coplanaridad

Habíamos visto que tanto las rectas concurrentes como las paralelas son coplanares (existe un plano que las contiene).

Si las rectas se cortan, la distancia entre ellas es cero y por lo tanto: $\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right)\overrightarrow { \cdot {P_1}{P_2}} = 0$
Si las rectas son paralelas, $\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} = \vec 0$ y por lo tanto también se cumple que $\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right)\overrightarrow { \cdot {P_1}{P_2}} = 0$ .

Entonces estamos en condiciones de enunciar una condición de coplanaridad entre dos rectas:

{r_1}

y

{r_2}

son coplanares

\; \Leftrightarrow \; \left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right).\overrightarrow {{P_1}{P_2}} = 0

123

Ejemplo

Dadas las rectas:

{r_1}:\left( {x,y,z} \right) = \left( {3,2,5} \right) + \lambda \left( {0, - 1,2} \right)

{r_2}:\; \begin{cases} \begin{align*} 2x + y + 3z + 2 = 0 \\ - x + 2y - 4z + 3 = 0 \end{align*} \end{cases}

Calcular $d\left( {{r_1},{r_2}} \right)$

Resolución

Debemos verificar que se trata de rectas alabeadas. Busquemos la dirección de la recta ${r_2}\;$ :

$\overrightarrow {{v_2}} = \left( {2,1,3} \right) \times \left( { - 1,2, - 4} \right) = \left( { - 10,5,5} \right)$

Vemos que las rectas no son paralelas porque sus vectores directores no son paralelos. Luego podemos utilizar la fórmula para distancia entre rectas alabeadas:

$d\left( {{r_1},{r_2}} \right) = \frac{{\left| {\overrightarrow {{P_1}{P_2}} .\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right)} \right|}}{{\lVert\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} \rVert}}$

Para hallar $\;{P_2}\; \in {r_2}\;$ fijamos $z = 0$ , por ejemplo, y averiguamos los valores de $x$ e $y$ resolviendo el sistema de ecuaciones:

124

\begin{cases} \begin{align*} 2x + y + 2 = 0 \\ - x + 2y + 3 = 0 \end{align*} \end{cases} \;\; \Rightarrow \;\;x = - \frac{1}{5},\;\;\;y = - \frac{8}{5}

Obtenemos así ${P_2}\left( { - \dfrac{1}{5}, - \dfrac{8}{5},0} \right) \in {r_2}$

Calculamos:

\overrightarrow {{P_1}{P_2}} = \left( { - \frac{{16}}{5},\; - \frac{{18}}{5}, - 5} \right)

\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} = \left( {0, - 1,2} \right) \times \left( { - 10,5,5} \right) = \left( { - 15,\; - 20, -10} \right)

\lVert\overrightarrow {{v_1}} \times \overrightarrow {{v_2}}\rVert = \sqrt {{{\left( { - 15} \right)}^2} + {{\left( { - 20} \right)}^2} + {{\left( { - 10} \right)}^2}} = \sqrt {725}

\overrightarrow {{P_1}{P_2}} .\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right) = \left( { - \frac{{16}}{5},\; - \frac{{18}}{5}, - 5} \right).\left( { - 15, - 20, - 10} \right)

\overrightarrow {{P_1}{P_2}} .\left( {\overrightarrow {{v_1}} \times \overrightarrow {{v_2}} } \right) = 48 + 72 + 50 = 170

d\left( {{r_1},{r_2}} \right) = \frac{{170}}{{\sqrt {725} }} \cong 6,31

125

Applets para repasar y ejercitar distancia entre rectas:

Objetos interactivos diseñados por E. Álvarez Sáiz y Mª José García Cebrian

126

Ejercicio para el lector 1

Dadas las rectas:

{r_1}:\left( {x,y,z} \right) = \left( {2, 0, -1} \right) + \lambda \left( {3, 1, 2} \right)

{r_2}:\; \begin{cases} x + z - 2 = 0 \\ y = 2 \end{cases}

Hallar la ecuación del plano $\pi$ que contiene a ${r_1}$ y es paralelo a $\;{r_2}$ .

Respuesta: $\: x - 5y + z - 1 = 0$

Nota: en el siguiente applet, uno de los ejemplos corresponde a este ejercicio, pero $r_1$ y $r_2$ están escritas en ecuaciones simétricas. No necesariamente es el primer ejemplo que aparece.

Objeto interactivo diseñado por Elena E. Álvarez Sáiz y Mª José García Cebrian

127

Ejercicio para el lector 2

Dadas las rectas

\begin{matrix} \begin{align*} &{r_1}:\;\:\left( {x,y,z} \right) = \;t\left( {1,1,2} \right) \\ &{r_2}:\;\;\left( {x,y,z} \right) = \left( {1,k,0} \right) + \;\lambda \;\left( {2,1,0} \right) \end{align*} \end{matrix}

Hallar el valor de $k$ para que las rectas sean coplanares y encontrar el plano que las contiene.

Respuesta: $\:\: k = \dfrac{1}{2}, \;\; \pi: 2x - 4y + z = 0$

128

1.10 Ejercicios surtidos de fin de capítulo

Nota: Todos los objetos interactivos utilizados en este apartado fueron diseñados por E. Álvarez Sáiz y Mª José García Cebrian

Punto simétrico respecto de un plano

129

Distancia recta plano

Plano por punto medio de un segmento

130

Ángulo entre rectas

Ángulo entre recta y plano

Distancia de un punto a un eje

131

Aplicación de haz de planos

Determine el plano que contiene a la intersección de los planos

P_1: x + y - z = 1,\;\; P_2: ﻿2x - y + z = 2

y pasa por el punto

P (2,-1,1).

Planteamos una ecuación simplificada del haz de planos

P_1 + k P_2 = 0

x + y - z - 1 + k(2x - y + z - 2) = 0

El punto $P (2,-1,1)\;$ pertenece al haz de planos, por lo que los valores del punto se reemplazan para encontrar el valor de $k$ :
$2 - 1 - 1 - 1 + k (4 + 1 + 1 - 2) = 0$
$-1 + 4k = 0$
$k =\dfrac {1}{4}$

Sustituimos el valor de $k$ en la ecuación de la intersección de los planos:

x + y - z - 1 + \dfrac {1}{4} (2x - y + z - 2) = 0

Simplificando la ecuación del plano obtenida:

\boxed {P: 2x + y - z = 2}

132

Objeto interactivo de construcción propia

Pasaje de ecuación vectorial del plano a ecuación general

Objeto interactivo diseñado por Elena Esperanza Álvarez Sáiz y Mª José García Cebrian

133

Capítulo II

Matrices, determinantes y SEL

2.1 Matrices139

2.1.1 Definición de Matriz139

2.1.2 Matriz columna140

2.1.3 Matriz fila140

2.1.4 Matriz nula140

2.1.5 Igualdad de matrices140

2.2 Operaciones con matrices141

2.2.1 Suma de matrices141

2.2.2 Producto de un escalar por una matriz141

2.2.3 Propiedades de la suma de matrices y del producto por un escalar142

2.2.4 Producto de matrices143

2.2.5 Propiedades del producto144

2.2.6 Matriz traspuesta144

2.2.7 Propiedades de la matriz traspuesta145

2.2.8 Matrices cuadradas: identidad e inversa145

2.2.9 Propiedades de la matriz inversa146

2.2.10 Algunos tipos de matrices146

2.3 Determinantes149

2.3.1 Desarrollo de un determinante por cofactores150

2.3.2 Determinante de una matriz triangular152

2.3.3 Propiedades de los determinantes153

2.3.4 Obtención de la inversa a través de la adjunta155

2.4 Matrices y sistemas de ecuaciones lineales157

2.4.1 Sistemas homogéneos158

2.4.2 Sistemas con parámetros159

2.1 Matrices

2.1.1 Definición de Matriz

Una matriz $A$ de $m \times n$ es un ordenamiento o arreglo rectangular de escalares dispuestos en $m$ filas y $n$ columnas. Para designar a cada uno de los $m.n$ elementos de la matriz se utiliza un doble subíndice que indica el número de fila y número de columna que le corresponde en el arreglo:

$\mathbf{A} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix}$ Así, $\;{a_{34}}$ es el elemento ubicado en la fila tres y la columna cuatro y en general ${a_{ij}}$ es el elemento de la matriz $A$ que está en la fila $i$ y en la columna $j$ .
Las matrices suelen designarse con letras mayúsculas: se anota $A \in {\mathbb{R}^{mxn}}$ para indicar que es una matriz con $m$ filas y $n$ columnas cuyos elementos son números reales. Se indican con paréntesis o con corchetes:

139

Por ejemplo una matriz de dos filas y tres columnas se puede escribir así: $\mathbf{A} = \begin{pmatrix} 3 & 2 & 0 \\ -2 & 4 & 1 \end{pmatrix}, \quad \mathbf{A} \in {\mathbb{R}^{2 \times 3}}$

En este caso, diremos que el tamaño u orden de $A$ es $2 \times 3$ .

2.1.2 Matriz columna

Podemos pensar los vectores como casos particulares de matrices: $\mathbf{C} = \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} \ matriz\;o\;vector\;columna \quad \mathbf{C} \in {\mathbb{R}^{3 \times 1}}$

2.1.3 Matriz fila

O también: $F = \left( {2\;\;\;\;\;0\;\;\;\;\;1} \right)\;\;matriz\;o\;vector\;fila\;\;\;\;F \in {\mathbb{R}^{1 \times 3}}$

2.1.4 Matriz nula

La matriz nula es aquélla cuyos elementos son todos ceros. La simbolizamos con $O$ ó $N$ )

2.1.5 Igualdad de matrices

Dos matrices son iguales si son del mismo orden (tamaño) y sus elementos respectivos son iguales. $A,B \in {\mathbb{R}^{mxn}}\;\;\;\;\;A = B\; \Leftrightarrow \;{a_{ij}} = {b_{ij}}\;\;\forall i,j$

140

2.2 Operaciones con matrices

2.2.1 Suma de matrices

Sean $A,B \in {\mathbb{R}^{m \times n}}$ entonces: $A + B = C \in {\mathbb{R}^{m \times n}}\;\;|\;\;\;{c_{ij}} = {a_{ij}} + {b_{ij}}\;\;\;\forall i,j$

Ejemplo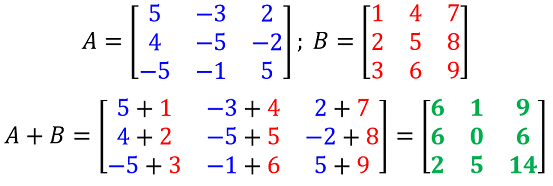

2.2.2 Producto de un escalar por una matriz

Sean $A \in {\mathbb{R}^{m \times n}},\;k \in \mathbb{R}$ , entonces: $kA = B\; \in {\mathbb{R}^{m \times n}}\;\;|\;\;\;{b_{ij}} = k{a_{ij}}\;\;\;\forall i,j$ Por ejemplo,

si $\mathbf{A} = \begin{pmatrix} 0 & -1 & 1 \\ -2 & 3 & 2 \end{pmatrix}$ , entonces $\mathbf{3A} = \begin{pmatrix}0 & -3 & 3\\ -6 & 9 & 6\end{pmatrix}$

Cuando $k = -1$ , obtenemos la matriz opuesta de A: $\mathbf{-A}= \ (-1) \mathbf{A} = \begin{pmatrix} 0 & 1 & -1 \\ 2 & -3 & -2 \end{pmatrix}$

141

Podemos así definir la diferencia (resta) entre dos matrices del mismo tamaño:

A-B = A + \left( {-B} \right)

O sea:

A-B = C \in {\mathbb{R}^{m \times n}}\;\;\;\;|\;\;\;{c_{ij}} = {a_{ij}}-{b_{ij}}

Ejercicio resuelto

2.2.3 Propiedades de la suma de matrices y del producto por un escalar

Sean $A,B,C \in {\mathbb{R}^{mxn}}\;\;y\;\;\alpha ,\;\beta \in \mathbb{R}$ . Vimos que: $A + B \in {\mathbb{R}^{mxn}}$ y $\alpha A \in {\mathbb{R}^{mxn}}$ . Estas operaciones verifican las siguientes propiedades:

$A + B = B + A\;\;\;\;$
$\left( {A + B} \right) + C = A + \left( {B + C} \right)\;\;\;\;$
$A + O = O + A = A\;\;\;\;\;$
$A + \left( { -A} \right) = \left( { -A} \right) + A = O$
$\alpha \left( {A + B} \right) = \alpha A + \alpha B$
$\left( {\alpha + \beta } \right)A = \alpha A + \beta A$
$\alpha \left( {\beta A} \right) = \left( {\alpha \beta } \right)A$
$1A = A$

142

Puede observarse la analogía entre estas propiedades y las que habíamos enunciado en el capítulo anterior para vectores de ${\mathbb{R}^3}$ .

2.2.4 Producto de matrices

Sean $A \in {\mathbb{R}^{m \times n}}$ y $B \in {\mathbb{R}^{n \times p}}$ , o sea que se cumple que la cantidad de columnas de la primera matriz es igual a la cantidad de filas de la segunda: 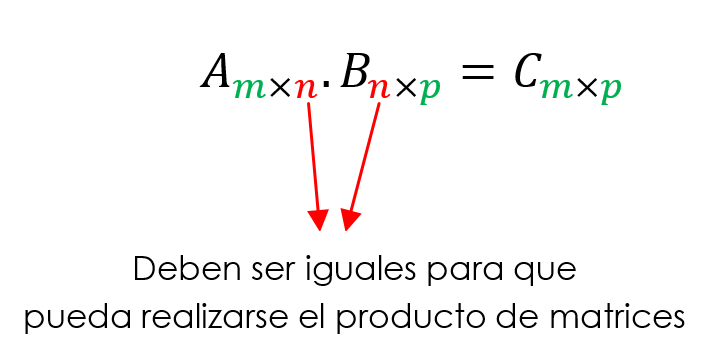Entonces el producto es: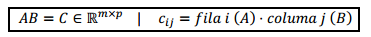

Una forma alternativa de expresar el producto es:

AB = C \in {\mathbb{R}^{m \times p}}\;\;\;|\;\;\;\;\;{c_{ij}} = \mathop \sum \limits_{k = 1}^n {a_{ik}}\;{b_{kj}}

Por ejemplo, al multiplicar una matriz $\mathbf{A}$ de $3\times2$ por una matriz $\mathbf{B}$ de $2\times3$ , tendremos como resultado una matriz de dimensión $(3\times\cancel{2})(\cancel{2}\times3) = 3\times3$ .

143

Objeto interactivo diseñado por Mª José García Cebrian

2.2.5 Propiedades del producto

1) El producto de matrices no es conmutativo. $AB\not=BA$
2) $\left( {AB} \right)C = A\left( {BC} \right)$ asociatividad
3) $\left( {A + B} \right)\;C = AC + BC$ distributividad a derecha
$P\left( {Q + R} \right) = PQ + PR \;$ distributividad a izquierda
4) $\left( {kA} \right)B = k\left( {AB} \right) = A\left( {kB} \right)\;\;,\;\;k \in \mathbb{R}$
5) $OA = O\;\;\;y\;\;\;AO = O,\;$ siendo $O$ la matriz nula

2.2.6 Matriz traspuesta

La traspuesta de una matriz $A \in {\mathbb{R}^{m \times n}}$ , que indicamos como ${A^t}$ , es la matriz de $n \times m$ que se obtiene a partir de $A$ cambiando las filas por las columnas.

Objeto interactivo diseñado por Mª José García Cebrian

144

2.2.7 Propiedades de la matriz traspuesta

1) ${\left( {A + B} \right)^t} = {A^t} + {B^t}$
2) ${\left( {kA} \right)^t} = k{A^t},\;\;k \in \mathbb{R}$
3) ${\left( {{A^t}} \right)^t} = A$
4) ${\left( {AB} \right)^t} = {B^t}{A^t}$

2.2.8 Matrices cuadradas: identidad e inversa

Si $A$ es una matriz con $m = n$ se dice que es una matriz cuadrada. La matriz identidad $\mathbf{I}$ es una matriz cuadrada cuyos elementos de la diagonal principal son iguales a $1$ y todos los demás son $0$ . Por ejemplo la matriz identidad de $3 \times 3$ es

$\mathbf{I} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$ Una matriz cuadrada $A$ es inversible, o regular , si existe otra matriz cuadrada (su inversa), que escribiremos $A^{-1}$ , que cumple: $A^{-1}.A = A.A^{-1} = I.$ Cuando $A$ no tiene inversa se dice que $A$ es singular.

Objeto interactivo diseñado por Mª José García Cebrian

145

2.2.9 Propiedades de la matriz inversa

Sean $A,B \in {\mathbb{R}^{nxn}}$ inversibles. Entonces:

1) $AB$ es inversible y su inversa es: $\left(AB\right)^{-1}=B^{-1}A^{-1}$

Esto significa que la inversa de $AB$ es ${B^{-1}}{A^{-1}}$ , es decir que el producto de matrices inversibles es inversible.
¿Ocurre lo mismo con la suma de matrices inversibles?

2) ${\left( {kA} \right)^{-1}} = \frac{1}{{k\;}}\;{A^{-1}}\;\;\;\left( {k \ne 0} \right)$

3) ${\left( {{A^t}} \right)^{-1}} = {\left( {{A^{-1}}} \right)^t}$

2.2.10 Algunos tipos de matrices

Objeto interactivo diseñado por John Jairo García Mora et al.

146

Ejercicios y problemas

1) En una ciudad hay tres empresas de telefonía celular (A, B y C) que controlan el mercado.

Inicialmente cada empresa tiene una fracción de la clientela que denominaremos ${a_0}$ , ${b_0}$ y ${c_0}$ .

Entonces resulta: ${a_0}\; + \;{b_0}\; + \;{c_0} = 1$ (no hay otras empresas)
La figura resume el porcentaje de clientes que cambian de empresa durante un período de seis meses.

Este modelo matemático se basa en los siguientes supuestos:
– El porcentaje de cambio entre las empresas se mantiene constante con el tiempo.
– Los clientes seguirán siendo consumidores de una de estas tres empresas.
– No se incorporan nuevos clientes al sistema.

Llamemos $X_0=\begin{pmatrix} a_0 \\ b_0\\c_0\end{pmatrix}$ al vector de estado inicial, y $X_1=\begin{pmatrix} a_1\\ b_1\\c_1\end{pmatrix}$ al vector que indica la fracción de la clientela que corresponde a cada empresa al cabo de un semestre.

Veamos cómo puede obtenerse ${X_1}$ a partir de ${X_0}$ .

147

De acuerdo con la figura, podemos deducir que al cabo de un período (semestre) la empresa A conservará 70% de su clientela propia.

¿Qué porcentaje de su clientela conservarán las empresas B y C al cabo de un semestre?

2) Analice si las siguientes proposiciones son verdderas o falsas. Justifique la respuesta.

148

2.3 Determinantes

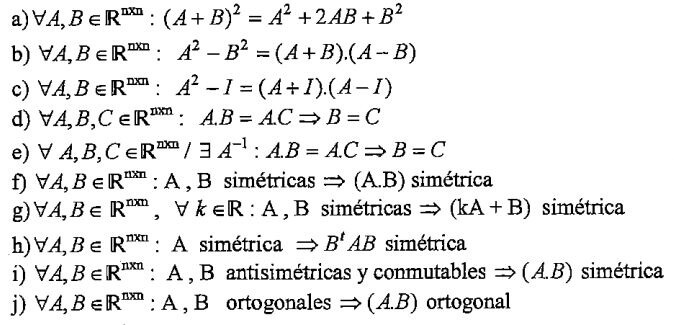
¿Cómo podemos saber si una matriz tiene inversa? El determinante de una matriz proporciona información para responder a esta pregunta.
Cuando vimos producto vectorial y mixto, habíamos definido determinantes de orden 2 y de orden 3. Recordamos aquí las fórmulas presentadas:
A cada matriz cuadrada puede asignársele un número real que llamaremos su determinante y designaremos como $det(A)\space o \begin{vmatrix} A\end{vmatrix}.$

Para matrices $2×2$ y $3×3$ el determinante se calcula como sigue: $A = (\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}) \Rightarrow | A | = | \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} | = a_{11} a_{22} - a_{12} a_{21}$

A =\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{pmatrix} \rArr

\begin{vmatrix} A\end{vmatrix} = a_{11} \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix} - a_{12} \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix} + a_{13} \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix}

Observación: El determinante no está definido para matrices rectangulares.
La regla de Sarrus es una forma práctica de calcular determinantes, sólo aplicable para matrices de $3 \times 3$ .

149

Consideremos el siguiente esquema en el cual agregamos al final de una matriz de $3 \times 3$ las filas 1 y 2. El determinante se calcula sumando los productos indicados por las flechas que que van de izquierda a derecha y restando los productos indicados por las flechas que van de derecha a izquierda:

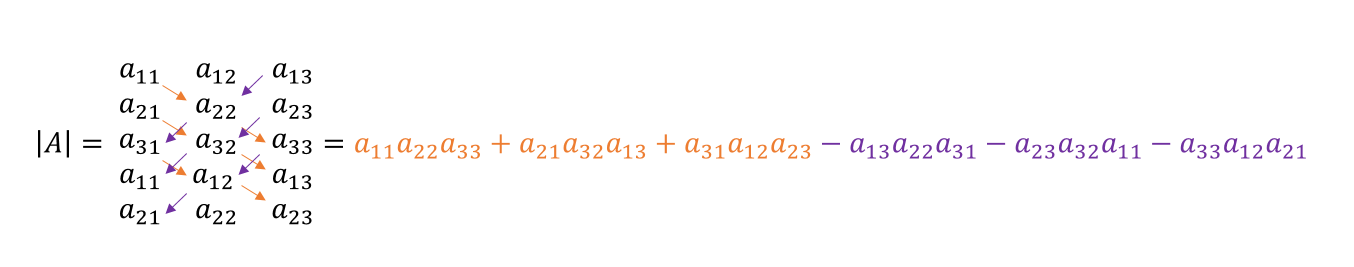
Objeto interactivo diseñado por Mª José García Cebrian

2.3.1 Desarrollo de un determinante por cofactores

Dada $A \in {\mathbb{R}^{nxn}}$ , se denomina menor ${M_{ij}}$ a la submatriz de $\left( {n - 1} \right) \times \;\left( {n - 1} \right)$ que se obtiene a partir de $A$ eliminando la fila $i$ y la columna $j$ .

Se denomina cofactor ${C_{ij}}$ del elemento ${a_{ij}}$ al producto de ${\left( { - 1} \right)^{i + j}}$ por el determinante de la matriz menor ${M_{ij}}\;$ :
${C_{ij}} = {\left( { - 1} \right)^{i + j}}\det \left( {{M_{ij}}} \right)$

150

Por ejemplo para la matriz $A =\begin{pmatrix} 3 & 1 & 4 \\ -1 & 2 & 1 \\ 3 & 2 & 1\end{pmatrix}$ Las matrices menores y los cofactores de la primera fila son:

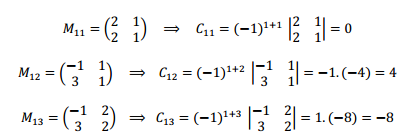
Observación: $(-1)^{(i+j)} = \begin{cases} 1 &\text{si } i + j \; es \; par \\ -1 &\text{si } i + j \; es \; impar\end{cases}$ Con estas definiciones previas, estamos en condiciones de enunciar el desarrollo de un determinante de orden $n$ .
El determinante de una matriz puede calcularse utilizando los cofactores de cualquier fila o cualquier columna.

Desarrollo por fila $i$ :
$\text{det}(A) = a_{i1} C_{i1} + a_{i2} C_{i2} + \dots + a_{in} C_{in} = \sum_{j = 1}^{n} a_{ij} C_{ij} \$ Este cálculo se puede hacer tomando cualquiera de las filas de $A$ , o sea: $\;i = 1,\;2,\; \ldots ,\;n$

151

Desarrollo por columna $j$ :
$\text{det}(A) = a_{1j} C_{1j} + a_{2j} C_{2j} + \dots + a_{nj} C_{nj} = \sum_{i = 1}^{n} a_{ij} C_{ij} \$ Este cálculo se puede hacer tomando cualquier columna de $A$ , o sea: $\;j = 1,\;2,\; \ldots ,\;n$

Objeto interactivo diseñado por Mª José García Cebrian

2.3.2 Determinante de una matriz triangular

Si

A \in {\mathbb{R}^{3 \times 3}}

es triangular:

A =\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33}\end{pmatrix}

152

Podemos calcular el determinante de $A$ por la primera columna:

$\begin{vmatrix} A\end{vmatrix} = a_{11} \begin{vmatrix} a_{22} & a_{23} \\ 0 & a_{33} \end{vmatrix} = a_{11} a_{22} a_{33}$

Hemos llegado a la siguiente conclusión: si $A \in {\mathbb{R}^{3 \times 3}}$ es triangular, su determinante es el producto de los elementos de la diagonal principal.
Esto se puede generalizar para matrices de cualquier orden: si $A \in {\mathbb{R}^{n \times n}}$ es triangular, su determinante es el producto de los elementos de la diagonal principal.

$A \in {\mathbb{R}^{n \times n}} \; triangular \Rightarrow \det \left( A \right) = {a_{11}}.{a_{22}} \ldots {a_{nn}}$ Teniendo en cuenta que la matriz identidad es triangular, se deduce que: $det(I)=1$

2.3.3 Propiedades de los determinantes

En general (es decir, a menos que la matriz sea triangular o tenga alguna otra cualidad especial), el cálculo de determinantes por medio del desarrollo por cofactores no es eficiente por el número de operaciones que implica cuando se trabaja con matrices grandes.

Existen propiedades que facilitan dicho cálculo y que analizaremos aquí en particular para matrices de orden 3, pero se extienden a las columnas y a matrices de cualquier orden.

153

Observación: Si $A \in {\mathbb{R}^{n \times n}}$ , en algunos casos utilizaremos notación:

$A = \left( {{A_1}\;\;{A_2}\;\; \ldots \;\;\;{A_n}} \right)$

donde ${A_j}$ representa la columna $j$ de la matriz $A$ .

Ejercicios y problemas

1) Demostrar que si $k \in \mathbb{N}$ , $\; \text{det}(A^k) = [\text{det}(A)]^k$

2) Demostrar que si $A \in {\mathbb{R}^{n \times n}}\;$ y $\,k \in \mathbb{R}$ entonces $\quad \text{det}(kA) = k^n\,\text{det}(A)$

3) Sea $A \in {\mathbb{R}^{3 \times 3}}\,$ y $\; \text{det}(A) = 2\,$ calcular $\; \text{det}(\frac 32\,A^3)\,$

154

4) Sea $A = \begin{pmatrix} A_{1} & A_{2} & A_{3}\end{pmatrix} \in {\mathbb{R}^{3 \times 3}},\; \text{det}(A)=k\neq 0 \;$ y
$B = \big( \underbrace{A_{2}}_{B_{1}} \quad \underbrace{A_{1}+3A_{3}}_{B_{2}} \quad \underbrace{A_{1}-A_{2}}_{B_{3}}\, \big)$ Mostrar que B es inversible y calcular $\text{det}(-2A^tB^{-1})$

2.3.4 Obtención de la inversa a través de la adjunta

Para calcular la matriz inversa primero necesitamos definir a la matriz adjunta de una matriz cuadrada $A$ .

Llamaremos $Cof(A)$ a la matriz de cofactores de $A$ , es decir, cada elemento $(i,j)$ de $Cof(A)$ es el cofactor (ver §2.3.1)

C_{ij} = (-1)^{i+j}\; \text{det}({M}_{ij}).

Entonces, podemos definir a la matriz adjunta de

A

como a la traspuesta de

Cof(A)

.

Adj(A) =(Cof(A))^{t}

Si $A \in {\mathbb{R}^{n \times n}} \;$ puede demostrarse que:

A.Adj(A)=\text{det}(A).I \quad \land \quad Adj(A).A=\text{det}(A).I

155

Por lo tanto podemos afirmar que si

\text{det}(A)\neq 0,\;

la inversa de

A

es:

A^{-1}=\frac{1}{\text{det}(A)}\, Adj(A)

En particular, calcular la matriz inversa de una matriz de $2\times2$ es muy sencillo.

Consideremos la matriz $A$ de $2\times2$ con $\text{det(A)} \not = 0$ , se tiene

$A^{-1} = \frac{1}{a_{11}a_{22} - a_{12}a_{21}} \begin{bmatrix} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{bmatrix}.$

Ejemplo del cálculo de la inversa de una matriz.

Objeto interactivo diseñado por Melissa Méndez Servin

Se observa cada paso usando los botónes Prev, Sig y Reset (para regresar al primer paso). O bien, ver el desarrollo con otra matriz presionando sobre el botón Otro. Esperar a que automáticamente el applet haga los cálculos.

156

2.4 Matrices y sistemas de ecuaciones lineales

A continuación disponemos de una presentación donde se exponen los contenidos vinculados a sistemas de ecuaciones lineales, su forma matricial, el método de eliminación de Gauss y el teorema de Rouché-Frobenius.

El material original de la presentación es autoría de la profesora María José García Cebrian, (disponible en https://proyectodescartes.org/iCartesiLibri/materiales_didacticos/AlgebraLinealBachillerato-JS/index.html ) y de los profesores Isabel Pustilnik y Federico Gómez, contenido de su página web Matrices y sistemas de ecuaciones lineales

157

2.4.1 Sistemas homogéneos

Un sistema es homogéneo si todos los términos independientes son cero.
Estos sistemas siempre son compatibles ya que r(A) = r(A'), todos tienen al menos la solución x₁ = x₂ = ... = x_n = 0, llamada solución trivial, y lo que interesa es saber si hay más soluciones.

Objeto interactivo diseñado por Mª José García Cebrian

158

2.4.2 Sistemas con parámetros

Son sistemas en los que algunos coeficientes y/o términos independientes se desconocen. Se trata de familias de sistemas de ecuaciones y para cada valor del parámetro o los parámetros se tiene un sistema diferente.
En estos sistemas se analizan los valores de el o los parámetros para distintos valores de los rangos de A y de A'. Se hallan dichos rangos para estos valores del parámetro y se aplica el Teorema de Rouché-Frobenius.

Objeto interactivo diseñado por Mª José García Cebrian

159

Ejercicios y problemas

3) A continuación se presentan más ejercicios para practicar. Todos tienen sus respectivas soluciones.

160

4)

5)

Sean el plano $\pi :\;x + y - 2 = 0 \,$ y la recta $r: \begin{cases} 2y+3kz-2=0 \\ 3x+ky-3z-4=0\end{cases}$

Obtener los valores de k para los cuales:

a) la recta corta al plano en un único punto;
b) la recta no interseca al plano;
c) la recta está incluida en el plano.

Sugerencia: Este ejercicio puede responderse sin hacer cálculos, teniendo en cuenta los resultados del ejemplo anterior.

161

Capítulo III

Espacios vectoriales

3.1 Espacios y subespacios vectoriales167

3.1.1 Definición de espacio vectorial167

3.1.2 Propiedades de los espacios vectoriales171

3.1.3 Subespacios vectoriales172

3.1.4 Subespacios triviales174

3.1.5 Resumen de los subespacios de

{\mathbb{R}^2}

y

{\mathbb{R}^3}

179

3.2 Conjunto generador. L.I. L.D. Bases180

3.2.1 Combinación lineal180

3.2.2 Conjunto generador181

3.2.3 Subespacio generado181

3.2.4 Independencia lineal y dependencia lineal183

3.2.5 Propiedades185

3.2.6 Interpretación geométrica186

3.2.7 Base y dimensión de un espacio vectorial188

3.2.8 Propiedades relacionadas con la dimensión193

3.2.9 Coordenadas de un vector respecto de una base194

3.2.10 Base y dimensión de un subespacio vectorial196

3.2.11 Bases de subespacios definidos por generadores201

3.3 Operaciones con subespacios206

3.3.1 Intersección206

3.3.2 Suma de subespacios209

3.3.3 Suma directa210

3.3.4 Teorema de la dimensión de la suma211

3.3.5 Producto interno214

3.3.6 Complemento ortogonal de un subespacio215

3.3.7 Propiedades del complemento ortogonal216

3.1 Espacios y subespacios vectoriales

Los vectores geométricos y las matrices presentan similitudes. Las propiedades de la suma y del producto por un escalar son idénticas en ambos conjuntos. Podemos generalizar el concepto de vector a partir de estas propiedades en común.

3.1.1 Definición de espacio vectorial

Un espacio vectorial es un conjunto no vacío

V

de objetos (vectores), en el que se definen dos operaciones: la suma y el producto por un escalar; sujetas a diez axiomas que se dan a continuación.

\forall u, v, w \in V \;

y

\,\forall {\alpha}, {\beta} \in \R \,,

los axiomas deben ser válidos. Llamamos

u\, + \,v

a la suma de vectores en

V

, y

\alpha v

al producto de un escalar

\alpha

por un vector

v \in V

.

$u + v\;\; \in \;V$
$u + v = v + u$
$\left( {u + v} \right) + w = u + \left( {v + w} \right)$
Existe un vector nulo ${0_V} \in V$ tal que $v + {0_V} = v$
$\forall v \in V, \;$ existe un opuesto $\left( { -v} \right) \in V$ tal que $v + \left( {- v} \right) = {0_V}$
$\alpha v \in V$
$\alpha \left( {u + v} \right) = \alpha u + \alpha v$
$\left( {\alpha + \beta } \right)v = \alpha v + \beta v$
$\alpha \left( {\beta v} \right) = \left( {\alpha \beta } \right)v$
$1v = v$

167

Observación: En la definición anterior, cuando decimos «escalares» nos estamos refiriendo a números reales. En este caso, se dice que $V$ es un espacio vectorial real.
Pero es posible que los escalares pertenezcan a otro conjunto numérico.

Ejemplo 1

De acuerdo con las propiedades que vimos en el primer capitulo, podemos afirmar que ${\mathbb{R}^3}$ es un espacio vectorial.
Los espacios ${\mathbb{R}^n}$ , con $n \ge 1$ , son los ejemplos principales de espacios vectoriales. La intuición geométrica desarrollada para ${R^3}$ nos ayudará a entender y visualizar muchos conceptos de esta unidad.
Los vectores de ${\mathbb{R}^{\;n}}$ son n-uplas de números reales, o sea:

${\mathbb{R}^n} = \left\{ {\left( {{x_1},\;{x_2},\; \ldots ,\;{x_n}} \right)\;,\;\;\;con\;\;{x_i} \in \mathbb{R}} \right\}$

En ${\mathbb{R}^n}$ , la suma de vectores y el producto por un escalar se definen así:

Sean $\;u = \left( {{u_1},{u_2}, \ldots ,{u_n}} \right)\;\;\;y\;\;\;v = \left( {{v_1},{v_2}, \ldots {v_n}} \right)\; \in {\mathbb{R}^n}\;$

$u + v = \left( {{u_1} + {v_1},\;{u_2} + {v_2},\; \ldots ,\;{u_n} + {v_n}} \right) \in {\mathbb{R}^n}$

$\alpha v = \left( {\alpha {v_1},\;\alpha {v_2},\; \ldots ,\;\alpha {v_n}} \right) \in {\mathbb{R}^n}$

Puede comprobarse que las operaciones definidas verifican los axiomas de espacio vectorial.

168

Ejemplo 2

De acuerdo con las propiedades enunciadas en la segunda unidad, para cada $m$ y $n$ , ${\mathbb{R}^{mxn}}$ es un espacio vectorial.
Tenemos por ejemplo ${\mathbb{R}^{2×3}}$ , espacio vectorial cuyos vectores son las matrices de $2 \times 3$ .

Ejemplo 3

Llamemos ${P_2}$ al conjunto de polinomios de grado menor o igual que 2, incluyendo el polinomio nulo.
Recordemos la suma de polinomios y la multiplicación por un escalar:
Dados $p\left( x \right) = \;{a_o} + {a_1}x + {a_2}{x^2} \in {P_2}$
y $q\left( x \right) = {b_o} + {b_1}x + {b_2}{x^2} \in {P_2}$
Definimos las operaciones:
$({p + q}) (x) =p(x) + q(x) =$ $= ({a_o} + {b_o}) + ({a_1} + {b_1})x + ({a_2} + {b_2}){x^2}\; \in {P_2}$

$\left( {\alpha p} \right)\left( x \right) = \alpha p\left( x \right) = \left( {\alpha {a_o}} \right) + \left( {\alpha {a_1}} \right)x + \left( {\alpha {a_2}} \right){x^2}\; \in {P_2}$

Puede demostrarse que estas operaciones verifican todos los axiomas de espacio vectorial.

En particular, el vector nulo en este espacio es el polinomio nulo, es decir el polinomio cuyos coeficientes son todos iguales a cero.

169

Generalizando, para cualquier $n \ge 0$ , el conjunto ${P_n}$ de todos los polinomios de grado menor o igual que $n$ (incluyendo el polinomio nulo) es un espacio vectorial.

Observación:

¿Por qué no definimos ${P_n}$ como el conjunto de polinomios de grado exactamente igual a $n$ ? Si lo definiéramos así, no sería un espacio vectorial como se muestra en el siguiente ejemplo:

$p\left( x \right) = {x^2}\;$ y $q\left( x \right) = - {x^2} + 1$ son polinomios de grado 2, pero la suma es un polinomio de grado cero. Entonces no se verificaría el primer axioma de espacio vectorial (la suma de vectores de un espacio vectorial $V$ debe estar en $V$ ).

170

3.1.2 Propiedades de los espacios vectoriales

A partir de los axiomas de espacios vectoriales, pueden demostrarse estas propiedades que resultan «naturales»:

Propiedad 1 $0\;u = {0_V}$

Propiedad 2 $\alpha \;{0_V} = {0_V}$

Propiedad 3 $\left( { - \alpha } \right)u = - \left( {\alpha u} \right)$

En particular, para $\; \alpha =-1$ : $\;\;\; \left( { - 1} \right)u = - u$

Propiedad 4 $\alpha \;u = {0_V}\; \Rightarrow \;\;\alpha = 0\; \vee \;\;u = {0_V}$ Veamos cómo puede demostrarse esta última propiedad:
Si $\alpha = 0$ , se cumple la proposición.
Si $\alpha \ne 0$ , podemos multiplicar por $\frac{1}{\alpha }$ :

$\alpha \;u = {0_V}\; \Rightarrow \frac{1}{\alpha }\alpha \;u = \frac{1}{\alpha }\;{0_V} \Rightarrow u = {0_V}\;$

171

3.1.3 Subespacios vectoriales

Definición

Sea $V$ un espacio vectorial y $W$ un subconjunto no vacío de $V$ .

$W$ es un subespacio de $V$ si $W$ es en sí mismo un espacio vectorial con las mismas operaciones (suma de vectores y producto por un escalar) definidas en $V$ .

Ejemplo

$W = \left\{ {\left( {{x_1},{x_2}} \right)\; \in {R^2}:\;{x_2} = 3{x_1}} \right\}$ ¿es un subespacio de ${\mathbb{R}^2}$ ?

Primero analicemos el conjunto $W$ . Son todos vectores de ${\mathbb{R}^2}$ tales que la segunda componente es el triple de la primera:

$\left( {{x_1},3{x_1}} \right) = {x_1}\left( {1,3} \right)$

$W$ es la recta que pasa por el origen y tiene vector director (1,3), o sea la recta de ecuación y = 3x.

Para decidir si $W$ es un subespacio de ${\mathbb{R}^2},$ habría que verificar que se cumplan los axiomas del 1 al 10. El lector puede comprobar que todos se cumplen en este caso.

Pero en general no es necesario verificar los axiomas porque existen condiciones para determinar si un subconjunto $W$ de un espacio vectorial $V$ es un subespacio, son las siguientes:

172

Condiciones necesarias y suficientes para caracterizar subespacios

Sea

W

un subconjunto de un espacio vectorial

V

\left( {W \subseteq V} \right)

.

W

es subespacio de

V

si y sólo si se cumplen las siguientes condiciones:
a.

{0_V}

está en

W

.
b. Si

u

y

v

están en

W

, entonces

u + v

está en

W

.
c. Si

u

está en

W

y

k

es un escalar,

ku

está en

W

.

Observaciones

1. La condición (a) asegura que W no es vacío. La mejor manera de comprobar si W es un subespacio es buscar primero si contiene al vector nulo. Si ${0_V}$ está en W, entonces deben verificarse las propiedades (b) y (c). Si $\;{0_V}$ no está en W, W no puede ser un subespacio y no hace falta verificar las otras propiedades.
2. Las propiedades a, b y c corresponden a los axiomas 4, 1 y 6 de espacios vectoriales.
3. Los axiomas 2, 3, 7, 8, 9 y 10 de espacio vectorial se cumplen para $W$ porque éste es un subconjunto de $V$ . Puede decirse que $W$ «hereda» esas propiedades de $V$ .
4. Faltaría comprobar que cada vector de $W$ tiene su opuesto en $W$ (axioma 5 de espacios vectoriales):
Teniendo en cuenta la condición (c) de subespacios,
si tomamos $k = -1,\;$ resulta:
Para cada $u \in W\;,\left( {-1} \right)u = -u\; \in W$ .
Y por lo tanto cada vector de $W$ tiene su opuesto en $W$ .

173

De las observaciones anteriores se deduce que las condiciones (a), (b) y (c) son suficientes para demostrar que $W$ es un espacio vectorial, y por lo tanto subespacio de $V$ .

3.1.4 Subespacios triviales

Si $V$ es un espacio vectorial, entonces $V$ es un subespacio de sí mismo.
Lo mismo sucede con $\left\{ {{0_V}} \right\}$ ya que $\;{0_V} + {0_V} = {0_V}$
y $k{0_V} = {0_V}\;para\;cualquier\;k\;real$

Se dice que $\left\{ {{0_V}}\right\}$ y $V$ son los subespacios triviales de $V$ .

Ejercitación sobre subespacios

Ejemplo 1

Consideremos el conjunto $W = \left\{ {\left( {x,y} \right) \in {\mathbb{R}^2}\;/\;xy = 0} \right\}$ , ¿Es un subespacio de ${\mathbb{R}^2}$ ?

Se cumple (a) pues $\left( {0,0} \right) \in W$

No se cumple (b) porque la suma de dos vectores de $W$ puede no estar en $W$ , por ejemplo:

$\left( {1,0} \right) + \left( {0,1} \right) = \left( {1,1} \right) \notin W$

Entonces $W$ no es un subespacio de ${\mathbb{R}^2}$ .

174

Ejemplo 2

Consideremos el conjunto $W = \left\{ {\left( {x,y} \right) \in {\mathbb{R}^2}\;/\;x = 0} \right\}$ . Es decir, la recta de ecuación $x = 0.\;$ ¿Es un subespacio de ${\mathbb{R}^2}$ ?

Se cumple (a) pues $\left( {0,0} \right) \in W$

Se cumple (b) pues la suma de dos vectores de $W,\;$ está en $W$ :

$\left( {0,{y_1}} \right) + \left( {0,{y_2}} \right) = \left( {0,{y_1} + {y_2}} \right)$

Se cumple (c) pues el producto de un vector de $W$ por un número real está en $W$ :

$k\left( {0,y} \right) = \left( {0,ky} \right)$

Luego $W$ es subespacio de ${\mathbb{R}^2}$ .

Ejemplo 3

Consideremos el conjunto $W = \left\{ {\left( {x,y} \right) \in {\mathbb{R}^2}/{x^2} -{y^2} = 0} \right\}$ . ¿Es un subespacio de ${\mathbb{R}^2}$ ?

${x^2} - {y^2} = 0 \Leftrightarrow y = x \vee x = -y$

Se cumple (a) pues $\left( {0,0} \right) \in W$

175

No se cumple (b) porque la suma de dos vectores de $W$ puede no estar en $W$ , por ejemplo:

$\left( {1,1} \right) + \left( {1, -1} \right) = \left( {2,0} \right) \notin W$

Entonces $W$ no es un subespacio de ${\mathbb{R}^2}$ .

Ejemplo 4

Consideremos el conjunto $W = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}/x + y + 2z = 0} \right\}$ . Es decir un plano que pasa por el origen. ¿Es un subespacio de ${\mathbb{R}^3}$ ?

De la ecuación del plano se deduce que: $x = - y - 2z$
Por lo tanto los vectores que pertenecen a $W$ responden a la forma $\left( {-y -2z,y,z} \right)$ con $y,z \in \mathbb{R}$ .

Se cumple (a) pues $\left( {0,0,0} \right) \in W$

Se cumple (b) pues la suma de dos vectores del plano, sigue estando en ese plano:

$\left( { -y -2z,\;y,z} \right) + \left( {-y’ -2z’,y’,z’} \right)=$ $= \left( {\; -\left( {y + y’} \right) -2\left( {z + z’} \right)\;,\;y + y’,z + z’\;} \right)$

Se cumple $\left( c \right)$ pues $k\left( { -y -2z,y,z} \right) = \left( { -ky -2kz,ky,kz} \right) \in W$

Entonces $W$ es subespacio de ${\mathbb{R}^3}$ .

176

Ejemplo 5

Consideremos el conjunto $W = \left\{ {p \in {P_2}\;/\;p\left( 0 \right) = 0} \right\}$ .
Es decir, los polinomios de grado menor o igual que dos (incluyendo el polinomio nulo) tales que evaluados en $0$ dan por resultado $0$ . ¿Es un subespacio de ${P_2}$ ?

Se cumple (a) pues el polinomio nulo pertenece a $W$ .

Recordemos la definición de suma de funciones y de producto de un real por una función:

$\left( {f\; + \;g} \right)\;\left( x \right)\; = \;f\left( x \right)\; + \;g\left( x \right)$ , para todo $x$ perteneciente al dominio de $f$ y de $g$

$\left( {kf} \right)\left( x \right) = kf\left(x \right)$ para todo $x$ perteneciente al dominio de $f$ .

Los polinomios son funciones, por lo tanto si consideramos $p\;,\;q \in W$ , resulta:

$\left( {p + q} \right)\left( 0 \right) = p\left( 0 \right) + q\left( 0 \right) = 0 + 0 = 0\; \Rightarrow \;\;p + q \in W$
$\left( {kp} \right)\left( 0 \right) = k.p\left( 0 \right) = k\;0 = 0 \Rightarrow kp \in W\;$

Demostramos que $W$ es un subespacio de ${P_2}$ .

177

Ejemplo 6

Consideremos el conjunto $W = \left\{ {A \in {\mathbb{R}^{n \times n}}/\;A = {A^t}} \right\}$ .
Es decir, el conjunto de matrices simétricas de $n \times n$ .

Se cumple (a) porque la matriz nula pertenece a $W$ .
Se cumple (b) pues si $A,B \in W$ entonces ${(A + B)^t} = {A^t} + {B^t} =$ $= A + B,$ luego ${(A + B)} \in W.$
Se cumple (c) pues si $A \in W$ entonces ${\left( {kA} \right)^t} = k{A^t} = kA$ , luego $\left( {kA} \right) \in W.$
Demostramos que el conjunto de matrices simétricas de $n\times n$ es un subespacio de $\mathbb{R}^{n \times n}$ .

Ejemplo 7

Consideremos el conjunto $W = \left\{ {A \in {\mathbb{R}^{2 \times 2}}/\det \left( A \right) = 0} \right\}$ .
¿Es un subespacio de ${\mathbb{R}^{2 \times 2}}$ ?

Se cumple (a) porque la matriz nula pertenece a $W$ .
En general $\det \left( {A + B} \right) \ne \det \left( A \right) + \det \left( B \right)$ , entonces podría ocurrir que $A,B \in W$ pero que $A + B$ no esté en $W$ . Por ejemplo

A =\begin{pmatrix} 1 & -3 \\ -1 & 3\end{pmatrix},\; B =\begin{pmatrix} 0 & 0 \\ -2 & 5\end{pmatrix},\; A + B =\begin{pmatrix} 1 & -3 \\ -3 & 2\end{pmatrix}

A + B \notin W

entonces no se cumple (b).

$W$ no es un subespacio de ${\mathbb{R}^{2 \times 2}}$ .

178

3.1.5 Resumen de los subespacios de ${\mathbb{R}^2}$ y ${\mathbb{R}^3}$

Después de estos ejemplos podemos resumir cuales son los diferentes tipos de subespacios de ${\mathbb{R}^2\;}$ y ${\;\mathbb{R}^3}$ :

Subespacios de $\mathbf{R^2}$	Subespacios de $\mathbf{R^3}$
{(0; 0)}	{(0; 0; 0)}
Rectas que pasan por el origen.	Rectas que pasan por el origen.
	Planos que pasan por el origen.
${\mathbb{R}^2}$ (como subespacio de sí mismo.)	${\mathbb{R}^3}$ (como subespacio de sí mismo.)

No hay ninguna otra clase de subespacios en ${\mathbb{R}^2\;}$ y ${\;\mathbb{R}^3}$ .

179

3.2 Conjunto generador. L.I. L.D. Bases

3.2.1 Combinación lineal

Definición

Sean $\large{v_1},\;{v_2},\; \ldots ,\;{v_r},\;w$ vectores de un espacio vectorial $V$ . Se dice que el vector $\large w\;$ es una combinación lineal de los vectores $\large{v_1},\;{v_2},\; \ldots \;,\;{v_r}\;$ si se puede expresar como sigue:

\large w = {k_1}{v_1} + {k_2}{v_2} + \; \ldots + {k_r}{v_r}\;

donde $\large{k_1},\;{k_2},\; \ldots ,\;{k_r}$ son escalares.

Observación: Nosotros estamos trabajando con espacios vectoriales reales, o sea que los escalares son números reales.

180

3.2.2 Conjunto generador

Sea $\left\{ {\;{v_1}\;,\;{v_2},\; \ldots \;{v_r}} \right\}$ un conjunto de vectores de un espacio vectorial $V$ .

Si todo vector de $V$ puede expresarse como combinación lineal de ${v_1},\;{v_2},\; \ldots \;,\;{v_r}$ , entonces se dice que $\left\{ {\;{v_1},\;{v_2},\; \ldots \;,\;{v_r}\;} \right\}$ es un conjunto generador de $V$ o también que ${v_1},\;{v_2},\; \ldots \;,\;{v_r}$ generan $V$ .

3.2.3 Subespacio generado

Sean ${v_1},\;{v_2},\; \ldots ,\;{v_r}$ vectores de un espacio vectorial $V$ .
1. El vector nulo puede expresarse como combinación lineal de dichos vectores:

${0_V}\; = \;0\;{v_1}\;\; + \;0\;{v_2}\; + \; \ldots \; + \;0{v_r}$

181

2. Si sumamos dos combinaciones lineales de los vectores dados, obtenemos otra combinación lineal:

( {{a_1}{v_1}\; + \; \ldots \; + \;{a_r}{v_r}} ) + \;( {{b_1}{v_1}\;\; + \; \ldots \; + \;{b_r}{v_r}}) =

$=( {{a_1} + \;{b_1}} ){v_1} + \ldots + ( {\;{a_r} + {b_r}} ){v_r}$

3. Si multiplicamos un escalar k por una combinación lineal de los vectores dados, obtenemos una combinación lineal de dichos vectores:

$k\left( {\;{a_1}\;{v_1}\; + \; \ldots \; + \;{a_r}\;{v_r}} \right)\; = \;\left( {k{a_1}} \right){v_1}\; + \; \ldots \; + \;\left( {k\;{a_r}} \right){v_r}$

Estas tres condiciones permiten afirmar que el conjunto de todas las combinaciones lineales de ${v_1},\;{v_2},\; \ldots ,\;{v_r}$ es un subespacio de $V$ .
Entonces:

Dados los vectores ${v_1},\;{v_2},\; \ldots ,\;{v_r}$ en $V$ , llamamos subespacio generado por ${v_1},\;{v_2},\; \ldots ,\;{v_r}$ al conjunto de todas las combinaciones lineales de estos vectores. Lo denotamos con la expresión $gen\left\{{{v_1},\;{v_2},\; \ldots ,\;{v_r}} \right\}$
$gen\{{v_1},{v_2}, \ldots ,\;{v_r} \} = \{ v \in V: v = \;{\alpha _1}{v_1} + {\alpha _2}{v_2} + \; \ldots + {\alpha _r}{v_r},$ con $\; {\alpha _i} \in R\; \}$ subespacio de $V$ .

182

3.2.4 Independencia lineal y dependencia lineal

En los ejemplos 1 y 2 de Conjunto generador vimos que los conjuntos $\{(1,1),\;(1, - 1)\}\;$ y $\; \{(1,1),\;(1, - 1),\;(2,0)\}$ generan ${\mathbb{R}^2}$ . Si tuviéramos que elegir uno de ellos como generador de ${\mathbb{R}^2}$ , ¿por cuál nos inclinaríamos?
El problema de encontrar los conjuntos generadores más «pequeños» para un e. v., depende de la noción de independencia lineal, que presentamos en esta sección. Si $A = \left\{ {{v_1},{v_2}, \ldots ,{v_r}} \right\}$ es un conjunto de vectores de un espacio vectorial $V$ , entonces:

${\alpha _1}{v_1} + {\alpha _2}\;{v_2} + \ldots + {\alpha _r}\;{v_r} = {0_V}$

tiene al menos la solución trivial:

{\;\alpha _1} = {\alpha _2} = \ldots = {\alpha _r} = 0

Si ésta es la única solución , entonces se dice que

A

es un conjunto linealmente independiente.
Si hay otras soluciones (además de la trivial) entonces A es un conjunto linealmente dependiente.

183

Una forma alternativa de caracterizar la dependencia lineal es la siguiente:
Un conjunto de vectores $\left\{ {\;{v_1},{v_2},\; \ldots ,{v_r}\;} \right\}$ de un espacio vectorial $V$ es linealmente dependiente si y sólo si al menos uno de los vectores puede expresarse como combinación lineal de los demás. {*}

Demostración:

$\Rightarrow$ Si el conjunto $\left\{ {\;{v_1},{v_2},\; \ldots ,{v_r}\;} \right\}$ es linealmente dependiente, la ecuación

${\alpha _1}{v_1} + {\alpha _2}{v_2} + \; \ldots + \;{\alpha _r}{v_r} = {0_V}$ admite otras soluciones además de la trivial. O sea, existe una combinación lineal donde al menos uno de los escalares es distinto de cero, que da el vector nulo.
Supongamos que ${\alpha _1} \ne 0$ . Entonces resulta:

${v_1} = \left( { - \frac{{{\alpha _2}}}{{{\alpha _1}}}} \right){v_2} + \ldots + \left( { - \frac{{{\alpha _r}}}{{{\alpha _1}}}} \right){v_r}$

Por lo tanto, el vector ${v_1}$ es combinación lineal de los demás.

$\Leftarrow$ Sabemos que uno de los vectores puede expresarse como combinación de los demás. Sin perder generalidad, supongamos que:

${\color{red}{v_1}} = {k_2}{v_2} + \ldots + {k_r}{v_r}$

184

Entonces:

$- 1{\color{red}{v_1}} + {k_2}{v_2} + \ldots + {k_r}{v_r} = {0_V}$

Existe una combinación lineal no trivial (al menos uno de los escalares es distinto de cero) que es igual al vector nulo. Por lo tanto, el conjunto $\left\{ {\;{v_1},{v_2},\; \ldots ,{v_r}\;} \right\}$ es linealmente dependiente, como queríamos demostrar.

3.2.5 Propiedades

Propiedad 1

Un conjunto formado por un solo vector, ¿es linealmente independiente (LI) o dependiente (LD)?

Planteamos la combinación lineal: $\alpha \;v = {0_V}$

185

Si $v = {0_V}$ , $\alpha$ puede tomar cualquier valor. Por lo tanto: $\left\{ {{0_V}} \right\}$ es LD.

Si $v \ne {0_V}$ , la única solución es $\alpha = 0$ . Por lo tanto: $\left\{ v \right\}$ es LI.

Propiedad 2

Si un conjunto de vectores contiene al vector nulo, entonces es linealmente dependiente (LD).

Demostración:
Sea $A = \left\{ {{v_1},\;{v_2},\; \ldots ,\;{v_r},\;{0_V}} \right\} \subset V$

Entonces se tiene que:

$0{v_1} + 0{v_2} + \ldots + 0{v_r} + 1\;{0_V} = {0_V}$

Probamos que existe una combinación lineal con escalares no todos nulos, que da el vector nulo. Por lo tanto, $A$ es linealmente dependiente.

3.2.6 Interpretación geométrica

Observación previa: En lo que sigue consideramos los vectores colocados a partir del origen de coordenadas.

De {*} resulta que dos vectores ${v_1}$ y ${v_2}$ son linealmente dependientes (LD) si y sólo si uno de ellos es un múltiplo escalar del otro.

186

Podemos afirmar entonces que dos vectores en ${\mathbb{R}^2}$ o ${\mathbb{R}^3}$ son LD si y sólo si están sobre la misma recta que pasa por el origen (vectores paralelos).

187

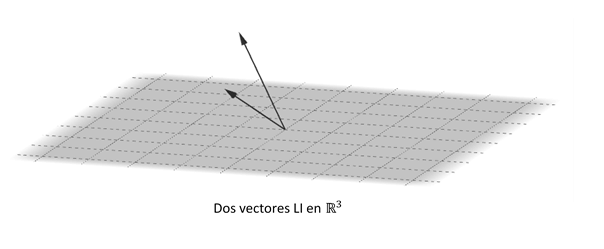
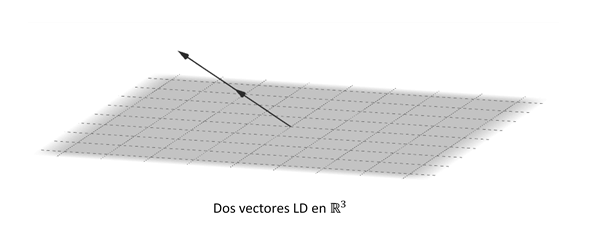
En ${\mathbb{R}^3}$ , tres vectores ${v_1},\;{v_2},\;{v_3}$ son LD si y sólo si están situados en el mismo plano que pasa por el origen (vectores coplanares).

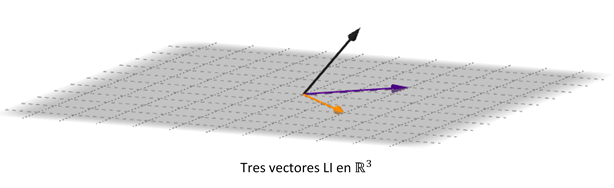
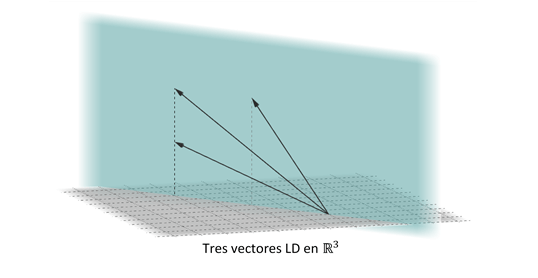
3.2.7 Base y dimensión de un espacio vectorial

Habíamos visto que los conjuntos $B = \left\{ {\left( {1,\;1} \right),\;\left( {1,\; - 1} \right)} \right\}$ y $C = \left\{ {\left( {1,\;1} \right),\;\left( {1,\; - 1} \right),\;\left( {2,\;0} \right)} \right\}$ generan ${\mathbb{R}^2}.$ ¿Cuál es la diferencia entre ellos?

188

$B$ es un conjunto linealmente independiente, en cambio $C$ es linealmente dependiente porque $\left( {2,\;0} \right) = \left( {1,\;1} \right) + \left( {1,\; -1} \right)$ .

Un conjunto de vectores $B\; = \left\{ {{v_1}\;,\;{v_2}\;,\; \ldots ,\;{v_n}} \right\}$ de un espacio vectorial $V$ se denomina base de $V\;$ si y sólo si:

i. $B$ es linealmente independiente;
ii. $B$ genera a $V$ .

Teniendo en cuenta esta definición, $B = \left\{ {\left( {1,\;1} \right),\;\left( {1,\; - 1} \right)} \right\}$ es una base de ${\mathbb{R}^2}$ . Otra base de ${\mathbb{R}^2}$ muy usual es la que contiene a los versores canónicos: $E = \left\{ {\left( {1,\;0} \right)\;,\;\left( {0,\;1} \right)} \right\}$ .

Puede demostrarse que:

Si $B\; = \;\left\{ {{v_1},\;{v_2},\; \ldots ,\;{v_n}} \right\}$ es una base de $V$ , entonces todo conjunto con más de n vectores es linealmente dependiente.

De acuerdo con esta propiedad, podemos deducir una característica común a toda base de un espacio vectorial:

Sean $B = \left\{ {{v_1},{v_2},\; \ldots ,\;{v_n}} \right\}$ y $B' = \left\{ {{w_1},\;{w_2},\; \ldots ,\;{w_q}} \right\}$ dos bases del espacio vectorial $V$ .

Como $B$ es una base, todo conjunto de más de $n$ vectores es LD. Pero $B'$ es LI, entonces:
$q \le n\;\;\;\;\;\left[ 1 \right]$

189

Como $B'$ es una base, todo conjunto de más de $q$ vectores es LD. Pero $B$ es LI, entonces:

$n \le q\;\;\;\;\;\left[ 2 \right]$

De [1] y [2] se deduce que $q = n$ .

En consecuencia:

Si $B = \left\{ {{v_1},{v_2}, \ldots ,\;{v_n}} \right\}$ es una base de $V$ , cualquier otra base de $V$ tiene $n$ vectores. Esto permite definir el concepto de dimensión.

La dimensión de un espacio vectorial $V$ es la cantidad de vectores que componen una base de $V$ .

Si $B = \left\{ {{v_1},{v_2}, \ldots ,\;{v_n}} \right\}$ es una base de $V$ , la dimensión de $V$ es $n$ y lo indicamos como $dim\left( V \right)\; = \;n$ .

Si no existe una base de $V$ formada por un conjunto finito de vectores, se dice que $V$ es un espacio de dimensión infinita. Un ejemplo es el espacio de todos los polinomios (de cualquier grado).

Como el vector nulo es linealmente dependiente, el espacio $\left\{ {{0_V}} \right\}$ no tiene base. A este espacio compuesto únicamente por el vector nulo, se le asigna dimensión cero:

$\dim \left( {\;\left\{ {{0_V}} \right\}\;} \right) = 0$

190

Para determinar la dimensión de un espacio vectorial, es suficiente hallar una base de dicho espacio. Veamos qué dimensión tienen los espacios vectoriales con los cuales trabajaremos:

En ${\mathbb{R}^2}$ conocemos la base canónica:

${E_2} = \left\{ {\left( {1,0} \right),\left( {0,1} \right)} \right\}\; \Rightarrow \dim \left( {{\mathbb{R}^2}} \right) = 2$

En ${\mathbb{R}^3}$ la base canónica es:

${E_3} = \left\{ {\left( {1,0,0} \right),\left( {0,1,0} \right),\left( {0,0,1} \right)} \right\} \Rightarrow \dim \left( {{\mathbb{R}^3}} \right) = 3$

Análogamente en ${\mathbb{R}^4}$ :

${E_4} = \left\{ {\left( {1,0,0,0} \right),\left( {0,1,0,0} \right),\left( {0,0,1,0} \right),\left( {0,0,0,1} \right)} \right\} \Rightarrow$ $\Rightarrow \dim \left( {{\mathbb{R}^4}} \right) = 4$

De acuerdo con el número de vectores que componen cada una de estas bases, podemos afirmar que:

$\dim \left( {{\mathbb{R}^n}} \right) = n$

Para determinar la dimensión de los espacios de matrices, consideremos por ejemplo $V = {\mathbb{R}^{3 \times 2}}$ .
Cualquier matriz de $3 \times 2$ puede expresarse como sigue:

191

\begin{pmatrix} a & b \\ c & d \\ e & f\end{pmatrix} = a\begin{pmatrix} 1 & 0 \\ 0 & 0 \\ 0 & 0\end{pmatrix}+ b\begin{pmatrix} 0 & 1 \\ 0 & 0 \\ 0 & 0\end{pmatrix} + c\begin{pmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 0\end{pmatrix} +

+\; d\begin{pmatrix} 0 & 0 \\ 0 & 1 \\ 0 & 0\end{pmatrix} + e\begin{pmatrix} 0 & 0 \\ 0 & 0 \\ 1 & 0\end{pmatrix} + f\begin{pmatrix} 0 & 0 \\ 0 & 0 \\ 0 & 1\end{pmatrix}

Observemos la similitud con ${\mathbb{R}^6}$ , sólo cambia el formato.

Encontramos seis matrices linealmente independientes que generan $V = {\mathbb{R}^{3 \times 2}}$ . Es decir, encontramos una base (llamada base canónica) de este espacio y por lo tanto:
$\dim \left( {{\mathbb{R}^{3×2}}} \right) = 3×2 = 6$ .

Generalizando, podemos afirmar que:

$\dim \left( {{\mathbb{R}^{mxn}}} \right) = mxn$

Busquemos la dimensión de los espacios de polinomios. Consideremos por ejemplo $V = {P_{2\;}}$ . Cualquier polinomio de ${P_2}$ puede expresarse cómo sigue:

$\;p\left( x \right) = {a_0} + {a_1}x + {a_2}{x^2} = {a_0}\color{red}{1} \color{black} + {a_1} \color{red}{x}\color{black} + {a_2}{\color{red}{x^2}}$

El conjunto $\left\{ {1,x,{x^2}} \right\}$ genera ${P_2}$ y además es linealmente independiente. Hemos obtenido una base (llamada canónica) de ${P_2}$ , y por lo tanto $\dim \left( {{P_2}} \right) = 3$ .

192

Análogamente:

$\left\{ {1,x,{x^2},{x^3}} \right\}\;\;base\;canó nica\;de\;{P_3}$

$\left\{ {1,x,{x^2},{x^3}, \ldots ,\;{x^n}} \right\}\;base\;canó nica\;de\;{P_n}$

Entonces:

$\dim \left( {{P_n}} \right) = n + 1$

3.2.8 Propiedades relacionadas con la dimensión

Si $\dim \left( V \right) = n,\,$ puede afirmarse que:

1) Todo conjunto de $n$ vectores linealmente independientes en $V$ es una base.

193

2) Todo conjunto de $n$ vectores que genere $V$ es una base.

3) Todo conjunto de más de $n$ vectores en el espacio vectorial $V$ es linealmente dependiente.

4) Todo conjunto linealmente independiente en $V$ puede extenderse a una base.

3.2.9 Coordenadas de un vector respecto de una base

Propiedad: Si $B = \left\{ {{v_1},{v_2}, \ldots ,{v_n}} \right\}$ es una base del espacio vectorial $V$ , todo vector de $V\;$ puede expresarse de forma única como combinación lineal de los vectores de $B$ .

194

Esta propiedad permite definir coordenadas de un vector respecto de una base.

Sea $B = \left\{ {{v_1},{v_2}, \ldots ,{v_n}} \right\}$ base de $V$ .

Para cada $u \in V$ , existen únicos escalares ${\alpha _1},{\alpha _2}, \ldots ,{\alpha _n} \in \mathbb{R}$ tales que: $u = {\alpha _1}{v_1} + {\alpha _2}{v_2} + \ldots + {\alpha _n}{v_n}$

Estos escalares se denominan coordenadas del vector $u$ respecto de la base $B$ .

Indicaremos las coordenadas mediante la siguiente notación:

$[u]_{B}= \begin{pmatrix} \alpha_{1} \\ \alpha_{2} \\ \vdots \\ \alpha_{n} \end{pmatrix}$

Ejercicios resueltos

195

3.2.10 Base y dimensión de un subespacio vectorial

Recordemos que un subespacio es un espacio vectorial en sí mismo, por lo tanto podemos hallar una base y su dimensión.

Si S es un subespacio de V, entonces: ${\rm{dim}}\left( S \right) \le {\rm{dim}}\left( V \right)$ .

Veamos cuáles son las dimensiones de los distintos tipos de subespacios de ${\mathbb{R}^3}$ :

$S = \left\{ {\left( {0,0,0} \right)} \right\}$ no tiene base y como habíamos dicho, se le asigna dimensión 0.

$\dim \left( {\left\{ {{0_V}} \right\}} \right)\; = 0$
Rectas que pasan por el origen,
Planos que pasan por el origen y
${\mathbb{R}^3}\,$ (Sabemos que ${\mathbb{R}^3}\,$ tiene dimensión 3.)

Consideremos un plano que pase por el origen, por ejemplo:

$\pi :\;\;x + 3y - 2z = 0$

$x = - 3y + 2z$

$\left( {x,y,z} \right) \in \pi \Leftrightarrow \left( {x,y,z} \right) = \left( {-3y + 2z,y,z} \right) =$ $= \left( { - 3y,y,0} \right) + \left( {2z,0,z} \right) = y\left( { -3,1,0} \right) + z\left( {2,0,1} \right)$

196

Esto quiere decir que cualquier vector en ese plano se puede escribir como combinación lineal de $\left( { - 3,1,0} \right)$ y $\left( {2,0,1} \right)$ . Cómo son LI:

$\left\{ {\left( { - 3,1,0} \right),\left( {2,0,1} \right)} \right\}\;es\;una\;base\;de\;{S_1}$

$\dim \left( {{S_1}} \right) = 2$

Planos que pasan por el origen son subespacios de dimensión 2.

Ahora consideremos el subespacio:

${S_2} = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}|\;\;x + y = 0\;\;\;,\;\;\;\;x - y - z = 0} \right\}$

r: \begin{cases} \pi_{1}: x + y = 0 \\ \pi_{2}: x - y - z = 0 \end{cases}; \;\; r = \pi_{1} \cap \pi_{2}

La intersección de dos planos no paralelos es una recta. ¿Cómo podemos encontrar una base de una recta?

$y = - x\;$

$\; \Rightarrow \;\;x -\left( { - x} \right) - z = 0\; \Rightarrow \;\;z = 2x$

Si llamamos $x = t$ , resulta:

$\left( {x,y,z} \right) = \left( {t, - t,2t} \right) = t\left( {1, - 1,2} \right)$

197

Observamos que todos los vectores de la recta pueden expresarse como combinación lineal del vector director $\left( {1, - 1,2} \right)$ , que además es LI. Por lo tanto, $\left\{ {\left( {1, - 1,2} \right)} \right\}$ es una base de este subespacio.

Rectas que pasan por el origen son subespacios de dimensión 1.

En los ejemplos anteriores observamos cómo disminuye la dimensión de un subespacio a medida que agregamos ecuaciones, tal como se muestra en el siguiente cuadro:

Número mínimo de ecuaciones que definen $S$	Dimensión del subespacio	Objeto geométrico	Ejemplo
0	3	$\mathbf{R^3}$
1	2	Planos por el origen	$\displaystyle z = 0$
2	1	Rectas por el origen	$\begin{cases} y = 0 \\ z = 0 \end{cases}$
3	0	$\Set{(0; 0; 0)}$	$\begin{cases} x = 0 \\ y = 0 \\ z = 0 \end{cases}$

198

Ejercicios y problemas

1) Indicar si $A = \left\{ {\left( {1,1,1} \right),\;\left( {1,3,2} \right)} \right\}$ es una base de
$W = \left\{ {\left( {x,y,z} \right) \in {R^3}:\; x + y - 2z = 0} \right\}$ , justificando la respuesta.
Posible estrategia de resolución: hacer el producto vectorial de los generadores de $A$ y verificar que el resultado es proporcional al vector normal al plano $W$ .

2) Considere el subespacio de $R^4$

${T_1} = \left\{ {\left( {{x_1},{x_2},{x_3},{x_4}} \right) \in {R^4}|\;{x_1} + {x_4} = 0\; \wedge \;{x_2} - {x_4} = 0} \right\}$

Halle base y dimensión.
Teniendo en cuenta las ecuaciones que definen

{T_1}

, ¿podría anticipar su dimensión?

3) Hallar una base y la dimensión del subespacio de matrices simétricas de 2×2:

${T_2} = \left\{ {A \in {R^{2 \times 2}}\;|\;\;A = {A^t}} \right\}$

¿Cómo es una matriz simétrica de 2×2?

$A = \begin{pmatrix} a & b \\ b & d \end{pmatrix}$

199

$\begin{pmatrix} a & b \\ b & d \end{pmatrix} = a\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}+ b\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} + d\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}$

Las tres matrices halladas son L.I. y generan el subespacio de matrices simétricas, por lo tanto hemos encontrado una base de dicho subespacio.

4) Hallar base y dimensión de

$S = \left\{ {p\left( x \right) \in {P_2}|\;{a_0} - 2{a_1} + 3{a_2} = 0} \right\}$

5) Hallar una base y la dimensión del subespacio de matrices antisimétricas de 2×2 y del de 3×3.

200

3.2.11 Bases de subespacios definidos por generadores

Hasta ahora hemos buscado bases de subespacios definidos por ecuaciones. ¿Qué ocurre cuando el subespacio está definido por sus generadores?

Veamos el siguiente ejemplo:

Hallar una base y la dimensión de
S = $gen\left\{ {\left( {1,1,2} \right),\left( {1, -1,0} \right),\;\left( {0,1,1} \right)} \right\} \subset {R^3}$ .

En este caso, por la definición de S sabemos que $\left\{ {\left( {1,1,2} \right),\left( {1, -1,0} \right),\;\left( {0,1,1} \right)} \right\}$ es un conjunto generador de S. Para determinar si es una base, tendremos que analizar la independencia lineal:

- Si son vectores LI, entonces son base del subespacio.

- Si son LD, tendremos que extraer una base eliminando los vectores «que sobren».

En el caso específico de 3 vectores en R³, podemos utilizar el determinante (que es el producto mixto). Como en este caso el determinante da cero, los vectores son coplanares y por lo tanto L.D. Tenemos que extraer una base eliminando alguno de los vectores, por ejemplo:

$\left\{ {\left( {1,1,2} \right),\left( {1, - 1,0} \right)} \right\}$ es una base de S
$\left\{ {\left( {1, - 1,0} \right),\;\left( {0,1,1} \right)} \right\}$ es otra base de S.

201

Podemos afirmar que la dimensión de S es 2.

Una forma práctica de extraer bases es armar una matriz con los vectores dados y llevarla a la forma escalonada:

Una matriz es escalonada (por filas) si satisface las siguientes propiedades:

1. Las filas nulas (todos sus elementos son ceros) se encuentran en la parte inferior.

2. En cada fila no nula, el primer elemento distinto de cero (pivote) está a la derecha del pivote de la fila superior.

Una matriz cualquiera puede llevarse a la forma escalonada aplicando operaciones elementales entre sus filas. Por ejemplo consideremos la matriz que armamos con los generadores de $S$ :

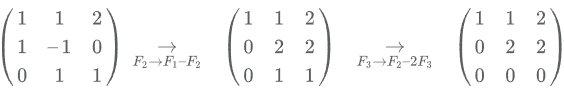
Se denomina rango de una matriz al número de filas LI que tiene la matriz. Veremos en el siguiente capítulo la importancia de este concepto en el estudio de sistemas de ecuaciones lineales.

Puede demostrarse que:

1. Si se realizan operaciones elementales entre las filas de una matriz, el rango se conserva.

2. Las filas no nulas de una matriz escalonada son LI.

202

Por lo tanto, para determinar el rango de una matriz se aplican operaciones elementales para obtener una matriz escalonada y se cuentan las filas no nulas.

En el ejemplo, la matriz escalonada tiene rango 2, por lo tanto la matriz que armamos con los generadores de S tiene rango 2. Esto significa que de los tres generadores de S hay dos linealmente independientes. ¿Cuál es entonces la dimensión de S?
$\dim \left( S \right) = 2\;$

Este método también permite obtener bases: las filas no nulas de la última matriz son otra base de S, ya que fueron obtenidas como combinaciones lineales de los vectores de S:

$\left\{ {\left( {1,1,2} \right),\;\left( {0,2,2} \right)} \right\}\;otra\;base\;de\;S$

Ejemplo

Dado el conjunto:

$A = \left\{ {1 + x;1 -{x^2};2 + 3x + k{x^2}} \right\} \subset {P_2}$

Hallar todos los valores de $k$ para que $A$ genere un subespacio de dimensión 2

Para el $k$ hallado encontrar las ecuaciones del subespacio generado por $A$ .

203

Resolución

Sabemos que $\dim \left( {{P_2}} \right) = 3$ , entonces todo conjunto de 3 vectores LI en ${P_2}$ es base de ${P_2}$ . Como se pide que la dimensión del subespacio sea 2, debemos hallar $k$ de modo que los vectores sean LD.

Los dos primeros vectores de $A$ son LI, entonces se trata de analizar para qué valores de $k$ el tercer vector es combinación lineal de los anteriores:

$2 + 3x + k{x^2} = \alpha \left( {1 + x} \right) + \beta \left( {1 - {x^2}} \right)$

\begin{cases} 2 = \alpha + \beta \\ 3 = \alpha \\ k = -\beta \end{cases} \Rightarrow \alpha = 3,\: \beta = -1,\: k = 1

Para $k = 1$ , el polinomio $2 + 3x + k{x^2}$ es combinación lineal de $1 + x \;$ y $\;1 - {x^2}.\;$ Entonces:

$gen\left\{ {1 + x;1 - {x^2};2 + 3x + {x^2}} \right\} = gen\left\{ {1 + x;1 - {x^2}} \right\}$

$\left\{ {1 + x;1 - {x^2}} \right\}\;es\;base\;de\;{P_2}$

Ahora busquemos la ecuación del subespacio. Tomamos un polinomio genérico, $p\left( x \right) = {a_0} + {a_1}x + {a_2}{x^2}$ y lo escribimos como combinación lineal de los vectores de la base:

${a_0} + {a_1}x + {a_2}{x^2} = \alpha \left( {1 + x} \right) + \beta \left( {1 - {x^2}} \right)$

204

$\begin{cases} \alpha + \beta = {a_0} \\ - \beta = {a_2} \\ \alpha = {a_1} \end{cases} \large \Rightarrow \alpha = {a_1},\: \beta = - {a_2},\: \Rightarrow \;{a_0} = {a_1} - {a_2}$

Entonces esa es la ecuación que define al subespacio:

$S = gen\left( A \right) = \left\{ {p \in {P_2}\;\;|\;\;{a_0} - {a_1} + {a_2} = 0} \right\}$

Como verificación, puede comprobarse que los dos vectores de la base verifican la ecuación obtenida.

Video con ejercicio resuelto

Video 3.1. Ejercicio Álgebra CBC A-62 (video de unamunoenlinea en YouTube, Licencia Atribución de Creative Commons)

205

3.3 Operaciones con subespacios

3.3.1 Intersección

Sean $S$ y $T$ subespacios del mismo espacio vectorial $V$ . Definimos la intersección como sigue:

$S \cap T = \left\{ {v \in V\;:\;v \in S\;\; \wedge \;\;v \in T} \right\}\;$

Propiedad

$S \cap T$ es subespacio de $V$

Ejemplo 1

Sean los subespacios de ${\mathbb{R}^3}$ :

$S = \left\{ {\left( {x,y,z} \right)|\;x - 3z = 0} \right\}$

$T = \left\{ {\left( {x,y,z} \right)|\;x + y - z = 0} \right\}$

Hallar $S \cap T$ .

Resolución

Por definición $S \cap T$ es un conjunto que estará formado por los vectores que pertenezcan a $S$ y a $T$ . Es decir aquellos vectores que satisfagan las ecuaciones de $S$ y las de $T$ :

$S \cap T = \left\{ {\left( {x,y,z} \right)|\;x - 3z = 0\;\; \wedge \;\;\;x + y - z = 0} \right\}$

206

Se trata de una recta definida como intersección de dos planos. Una base de la recta es un vector director.

Geométricamente podemos buscar el vector director como el producto vectorial de los vectores normales a los planos:

$v = n_1 \times n_2 = \begin{vmatrix} i & j & k \\ 1 & 0 & -3 \\ 1 & 1& -1 \end{vmatrix} = \left( {3, - 2,1} \right)$

$S \cap T = \left\{ {\left( {x,y,z} \right) = \lambda \left( {3, - 2,1} \right),\;\lambda \in \mathbb{R}} \right\}$

Entonces $\left\{ {\left( {3, - 2,1} \right)} \right\}$ es una base de $S \cap T$ .

Otra forma de resolverlo es buscar la solución del sistema de ecuaciones:

$\begin{cases} x - 3z = 0 \\ x + y - z = 0 \end{cases} \; \Rightarrow \begin{cases} x = 3z \\ y = z -x = -2z \end{cases} \; \Rightarrow$ $\Rightarrow {(3z, - 2z, z)}, \; \forall z \in \mathbb{R}.$

$\left( {x,y,z} \right) = z\left( {3, - 2,1} \right)$

Y entonces otra vez llegamos a que $\left\{ {\left( {3, - 2,1} \right)} \right\}$ es una base de $S \cap T$ .

207

Ejemplo 2

Sean los subespacios de ${\mathbb{R}^{2 \times 2}}$ :

$S = \left\{ {A \in {\mathbb{R}^{2 \times 2}}\;|\;\;A = {A^t}} \right\}$

T = gen\; \bigg \{\begin{pmatrix} 1 & 0 \\ 2 & -1 \end{pmatrix}, \;\begin{pmatrix} 1 & 0 \\ 1 & 0 \end{pmatrix}\bigg\}

Hallar

S \cap T

.

Video con ejercicio resuelto

Video 3.2. Ejercicio Álgebra CBC A-62 (video de unamunoenlinea en YouTube, Licencia Atribución de Creative Commons)

208

3.3.2 Suma de subespacios

Dados $S\;y\;T\;$ subespacios de $V$ , se define la suma como sigue:

$S + T = \left\{ {v \in V\;|\;\;v = {v_1} + {v_2}\;,\;\;\;con\;\;{v_1} \in S,\;\;{v_2} \in T} \right\}$ suma de subespacios

Propiedad: $S + T$ es un subespacio del espacio vectorial $V$ .

Si conocemos conjuntos generadores de $S$ y de $T$ , podemos hallar generadores de la suma:

$S = gen\left\{ {{v_1},{v_2}, \ldots ,{v_q}} \right\}$ y $T = gen\left\{ {{w_1},{w_2}, \ldots ,{w_r}} \right\}$

\Rightarrow S + T = gen\left\{ {{v_1},{v_2}, \ldots {v_q},{w_1},{w_2}, \ldots ,{w_r}} \right\}

Para hallar la suma es usual buscar las bases de $S$ y $T$ . Como las bases son conjuntos generadores LI, si conocemos una base de cada subespacio podremos obtener un conjunto generador de la suma:

Dadas las bases:

${B_S} = \left\{ {{v_1},{v_2}, \ldots ,{v_q}} \right\}$ y ${B_T} = \left\{ {{w_1},{w_2}, \ldots ,{w_r}} \right\}$

Resulta:

$\left\{ {{v_1}, \ldots ,{v_q},{w_1}, \ldots ,{w_r}} \right\}$ conjunto generador de la suma.

Observación: Se obtiene así un conjunto generador de la suma pero no siempre es linealmente independiente.

209

Si es LI, encontramos una base de la suma.
Si es LD, podemos extraer una base de la suma eliminando los vectores «que sobran».

3.3.3 Suma directa

La suma de dos subespacios es directa si y sólo si la intersección de los subespacios es el vector nulo.

$S + T\;es\;directa\; \Leftrightarrow \;S \cap T = \left\{ {{0_V}} \right\}$

Cuando la suma es directa se escribe:

$S \oplus T$

210

3.3.4 Teorema de la dimensión de la suma

Si ${S_1}$ y ${S_2}$ son subespacios de un espacio vectorial $V$ (de dimensión finita), entonces:

$\dim \left( {{S_1} + {S_2}} \right) = \dim \left( {{S_1}} \right) + \dim \left( {{S_2}} \right) - dim\left( {{S_1} \cap {S_2}} \right)$

En el caso particular de que la suma sea directa, como
${S_1} \cap {S_2} = \left\{ {{0_V}} \right\}$ , resulta:

$\dim \left( {{S_1} \oplus {S_2}} \right) = \dim \left( {{S_1}} \right) + \dim \left( {{S_2}} \right)$

Ejemplo

Dados los subespacios de ${P_2}$ :

${S_1} = \left\{ {p \in {P_2}\;|\;\;p\left( 0 \right) = 0} \right\}$

${S_2} = \left\{ {p \in {P_2}\;|\;\;p\left( 1 \right) = 0} \right\}$

Hallar bases de ambos subespacios y de la intersección.

Resolución

Hallemos una base de ${S_1}$ :

$p\left( 0 \right) = {a_0} + {a_1}0 + {a_2}{0^2} = 0 \Rightarrow {a_0} = 0$

211

Entonces son los polinomios de la forma:

${a_1}x + {a_2}{x^2}$

Luego una base de ${S_1}$ es:

${B_{{S_1}}} = \left\{ {x,{x^2}} \right\} \Rightarrow \dim \left( {{S_1}} \right) = 2$

Hallemos una base de ${S_2}$ :

$p\left( 1 \right) = {a_0} + {a_1}1 + {a_2}{1^2} = 0 \Rightarrow {a_0} + {a_1} + {a_2} = 0$

Entonces son los polinomios de la forma:

$\left( { -{a_1} - {a_2}} \right) + {a_1}x + {a_2}{x^2} = {a_1}\left( { - 1 + x} \right) + {a_2}\left( { - 1 + {x^2}} \right)$

${B_{{S_2}}} = \left\{ { - 1 + x\;\;,\;\;\; - 1 + {x^2}} \right\}\; \Rightarrow \;\dim \left( {{S_2}} \right) = 2$

Para buscar ${S_1} \cap {S_2}$ debemos plantear que se cumplan las ecuaciones de ${S_1}$ y también las de ${S_2}$ :

${a_0} = 0\; \wedge \;\;{a_0} + {a_1} + {a_2} = 0 \Rightarrow \;\;{a_0} = 0\;\; \wedge \;\;{a_1} = - {a_2}$

Los polinomios serán de la forma:

${a_1}x -{a_1}{x^2} = -{a_1}\left( {{x^2} - x} \right)$

Luego:

${B_{{S_1} \cap {S_2}}} = \left\{ {{x^2} - x} \right\}\; \Rightarrow \;\dim \left( {{S_1} \cap {S_2}} \right) = 1$

212

Nótese que como conocemos las dimensiones de ${S_1}$ , ${S_2}$ y ${S_1} \cap {S_2}$ , podemos calcular la dimensión de ${S_1} + {S_2}$ :

$\dim \left( {{S_1} + {S_2}} \right) = 2 + 2 - 1 = 3$

Pero el único subespacio de ${P_2}$ con dimensión 3 es ${P_2}$ . Luego: ${S_1} + {S_2} = {P_2}$ .

Ejercicio para el lector

Dados los subespacios de ${\mathbb{R}^{2 \times 2}}$ :

${W_1}:\left\{ {A \in {\mathbb{R}^{2 \times 2}}\;\;|\;\;A = {A^t}} \right\}$

${W_2}:\left\{ {A \in {\mathbb{R}^{2 \times 2}}\;|\;\;A = - {A^t}} \right\}$

a) Hallar bases de ${W_1}$ y ${W_2}$

b) Obtener ${W_1} \cap {W_2}$ .

c) Sin hallar ${W_1} + {W_2}$ analizar la validez de la siguiente afirmación:

${W_1} \oplus {W_2} = {\mathbb{R}^{2 \times 2}}$

d) Proponer una base de ${\mathbb{R}^{2 \times 2}}\;$ formada por matrices simétricas y antisimétricas.

213

3.3.5 Producto interno

En el primer capítulo vimos producto escalar entre vectores y sus aplicaciones a la Geometría. En esta sección nos proponemos generalizar esta operación a otros espacios vectoriales definiendo la noción general de producto interno a partir de las propiedades del producto escalar.

Definición: Un producto interno en un espacio vectorial real $V$ es una operación que asigna a cada par de vectores $u$ y $v$ de $V$ un número real $u.v$ tal que se verifican las siguientes propiedades $\forall {u,\;v,\;w} \in V$ y $\;\forall \alpha \in \mathbb{R}\;$ :

$u \cdot v = v \cdot u$
$u \cdot \left( {v + w} \right) = \left( {u \cdot v} \right) + \left( {u \cdot w} \right)$
$\alpha u \cdot v = \alpha \left( {u \cdot v} \right)$
$u.u \ge 0\;\;\; \wedge \;\;\;u.u = 0\;\;\;\; \Leftrightarrow \;\;\;\;u = {0_V}$

Es posible definir así distintos productos internos en cualquier espacio vectorial (mientras se verifiquen estas propiedades). En este libro sólo trabajaremos con el producto interno canónico en ${\mathbb{R}^n},\;$ que es la extensión del producto escalar:

$\left( {{x_1},{x_2}, \ldots ,{x_n}} \right).\left( {{y_1},{y_2}, \ldots ,{y_n}} \right) = {x_1}{y_1} + {x_2}{y_2} + \ldots {x_n}{y_n}$

producto interno canónico en $\mathbb{R}^n$

214

Esta definición nos permite extender el concepto de ortogonalidad a ${\mathbb{R}^n}$ :

$u \bot v\;\;\; \Leftrightarrow \;\;u.v = 0\:$ condición de ortogonalidad

Ejemplo

Realicemos el producto interno de los vectores de ${\mathbb{R}^4}$ :

$u = \left( {1,2,3,4} \right)\;\;\;\;\;\;\;\;\;v = \left( {1,0,1, - 1} \right)$

$u.v = 1.1 + 2.0 + 3.1 + 4.\left( { - 1} \right) = 0$

Como $u.v = 0$ entonces $u$ y $v$ son ortogonales. $\;$

3.3.6 Complemento ortogonal de un subespacio

Sea $S$ subespacio de un espacio vectorial $V$ con producto interno.

El complemento ortogonal de $S$ , que denotamos como ${S^ \bot}$ , es el conjunto de vectores de $V$ que son ortogonales a cada uno de los vectores de $S$ :

${S^ \bot } = \left\{ {\;v \in V|\;\;v \cdot w = 0\;\;\;\;\forall w \in S} \right\}$
complemento ortogonal de $S$

Propiedad: ${S^ \bot }$ es un subespacio de $V$ .

215

3.3.7 Propiedades del complemento ortogonal

Sea $V$ un espacio vectorial de dimensión finita, con producto interno, y sea $S$ un subespacio de $V$ . Entonces se verifican las siguientes propiedades:

${\left( {{S^ \bot }} \right)^ \bot } = S$
${V^ \bot } = \left\{ {{0_V}} \right\}\;$ y $\;\left\{ {{0_V}} \right\}^ \bot = V$
$S \cap {S^ \bot } = \left\{ {{0_V}} \right\}$
$S + {S^ \bot } = V$

Esta última propiedad significa que cualquier vector de $V$ puede expresarse como suma de un vector de S más otro de ${S^ \bot }$ .

216

Ilustramos con un ejemplo geométrico de ${\mathbb{R}^3}$ :

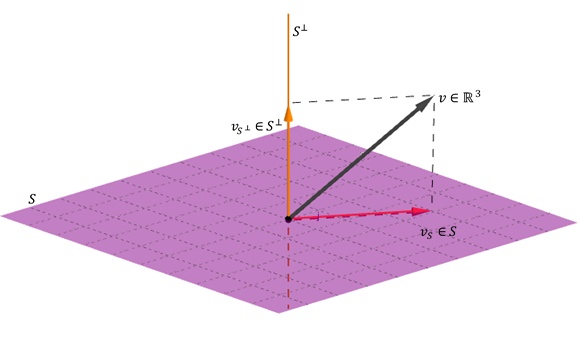
De las propiedades 3 y 4 se deduce:

$S \oplus {S^ \bot } = V$

Y por lo tanto:

$\dim \left( S \right) + \dim \left( {{S^ \bot }} \right) = \dim \left( V \right)$

La unión de una base de $S$ con una base de ${S^ \bot }$ es base de $V.$ Esto se aplica para extender una base de $S\;$ a una base de $V$ , como muestra el siguiente ejemplo.

217

Ejemplo

Sea $S = \left\{ {\left( {{x_1},{x_2},{x_3},{x_4}} \right) \in {\mathbb{R}^4}|\;{x_1} + {x_4} = 0,\;{x_1} - {x_2} + 3{x_4} = 0} \right\}$

Hallar una base de $S$ y extenderla a una base de ${\mathbb{R}^4}$ .

Resolución

Buscamos una base de S, por ejemplo:

${B_S} = \left\{ {\;\left( {1, - 2,0, - 1} \right),\;\left( {0,0,1,0} \right)} \right\}$

Como $dim\left( S \right) = 2,\;$ podemos anticipar que: $\,dim({S^ \bot }) = 4 - 2 = 2$

A partir de la base de $S,\;$ obtenemos las ecuaciones de ${S^ \bot }$ :

S^ \bot: \begin{cases} {x_1} - 2{x_2} - {x_4} = 0 \\ {x_3} = 0 \end{cases}

Y hallamos una base de ${S^ \bot }.\;$ por ejemplo:

{B_{{S^{ \bot \;}}}} = \{\left( {2,1,0,0} \right),\;(\left( {0,1,0, -2} \right)\}

Entonces uniendo las bases de $S$ y ${S^ \bot }$ resulta:

$B = \left\{ {\left( {1, - 2,0, - 1} \right),\left( {0,0,1,0} \right),\left( {2,1,0,0} \right),\left( {0,1,0, - 2} \right)} \right\}$
que es base de ${\mathbb{R}^4}$

218

Videos con ejercicios resueltos

Video 3.3. Ejercicio Álgebra y Geometría Analítica UTN FRBA (video de elaboración propia)

Video 3.4. Ejercicio Álgebra y Geometría Analítica UTN FRBA (video de elaboración propia)

219

Capítulo IV

Tres espacios de una matriz

4.1 Espacios fila y columna de A. Rango224

4.2 Espacio nulo de A229

4.3 Relación entre las soluciones de

AX = B

y

AX = 0.\;

Variables libres234

4.3.1 Espacio solución de un sistema homogéneo234

4.3.2 Relación entre las soluciones de

AX = B

y

AX = 0

236

4.4 Número de variables libres de un sistema241

Muchos problemas de ingeniería, por complicados que sean, se pueden reducir a álgebra lineal:

AX = B \;\; ó \;\; AX = \lambda X \;\; ó \;\; AX \approx B

Si las matrices son cuadradas, el primer problema $AX = B$ tiene una única solución cuando las columnas de $A$ son independientes. El segundo problema $AX = \lambda X,$ cuando tiene solución para $\lambda$ y para $X$ produce vectores independientes (llamados vectores propios). Para resolver el tercer problema, $AX \approx B,$ suele recurrirse a métodos numéricos.
Se puede observar que: $A =\begin{pmatrix} 1 & 1 & 2 \\ 1 & 2 & 3 \\ 1 & 3 & 4\end{pmatrix}$ no tiene columnas independientes. Si sumamos las columnas 1 y 2 obtenemos la columna 3. Un resultado sorprendente e importante del álgebra lineal establece que las filas tampoco son independientes.
Este capitulo analiza La interacción de las columnas y las filas. A continuación se enumeran cuatro de los conceptos más importantes:

El espacio columna (todas las combinaciones de las columnas).
El espacio fila (todas las combinaciones de las filas).
El rango (el número de columnas o filas independientes).
Eliminación (la mejor manera de encontrar el rango de una matriz).

223

4.1 Espacios fila y columna de A. Rango

En esta presentación, resumimos la teoría necesaria para resolver la ejercitación:

Método para hallar el rango de una matriz

Recordemos que:

1. Si se realizan operaciones elementales entre las filas de una matriz, el rango se conserva.

2. Las filas no nulas de una matriz escalonada son LI.

Por lo tanto, para determinar el rango de una matriz se aplican operaciones elementales para obtener una matriz escalonada y se cuentan las filas no nulas.

224

Compatibilidad y rango

Consideremos el siguiente sistema:

\begin{cases} \begin{aligned}{x_1} + {x_2} \:\:\:\:\:\:\:\:\:\:\: + {x_4} = 3 \\ {x_3} - {x_4} = 2 \\ {x_1} + {x_2} - {x_3}+ 2{x_4} = 0 \end{aligned} \end{cases}

Es un sistema de 3 ecuaciones con 4 incógnitas (3 x 4) cuya matriz de coeficientes es la $A$ del ejemplo 4 de los ejemplos precedentes.

El sistema puede expresarse en forma matricial como: $A\,X = B$

225

con $A = \begin{pmatrix} 1 & 1 & 0 & 1\\ 0 & 0 & 1 & -1 \\ 1 & 1 & -1 & 2\end{pmatrix}\:$ y $\:B = \begin{pmatrix} 3 \\ 2 \\ 0\end{pmatrix}$

Este sistema, ¿tendrá solución? ¿Cuántas soluciones tendrá?

Veamos cómo escribir el sistema en función de las columnas de la matriz $A$ :

{x_1} \begin{pmatrix} 1 \\ 0 \\ 1\end{pmatrix} + {x_2}\begin{pmatrix} 1 \\ 0 \\ 1\end{pmatrix} + {x_3}\begin{pmatrix} 0 \\ 1 \\ -1\end{pmatrix} + {x_4}\begin{pmatrix} 1 \\ -1 \\ 2\end{pmatrix} = \begin{pmatrix} 3 \\ 2 \\ 0\end{pmatrix}

Queda una combinación lineal de las columnas de $A$ igualada al vector de los términos independientes:

${x_1}\;{A_1} + {x_2}\;{A_2} + {x_3}\;{A_3} + {x_4}\;{A_4} = B$

¿Cuándo tiene solución el sistema? Cuando podemos encontrar valores para ${x_1},{x_2},{x_3},{x_4}$ que satisfagan la igualdad. Estos valores pueden ser únicos o no.

En otras palabras:

El sistema $AX = B$ es compatible si y sólo si $B$ es combinación lineal de las columnas de $A.$

226

Decir que $B$ es combinación lineal de las columnas de $A$ significa que $B$ está en el subespacio generado por las columnas de $A$ .
O sea:

$El\;sistema\;\;AX = B\;\;es\;compatible\;\;\; \Leftrightarrow \;\;B \in Col\left( A \right)$

Consideremos la matriz ampliada del sistema, que se obtiene agregando la columna de los términos independientes:

$A' = \left( {{A_1}\;\;\;{A_2}\;\;\;{A_3}\;\;\;{A_4}\;\;\;\;B} \right)$

¿Qué valores puede tomar $rg\left( {A'} \right)?$

El rango de $A'$ dependerá de si $B$ es combinación lineal o no de las columnas de $A$ :

$rg\left( {A'} \right) = rg\left( A \right) = 2 \Leftrightarrow B \in Col\left( A \right)$
$rg\left( {A'} \right) = rg\left( A \right) + 1 = 3 \Leftrightarrow B \notin Col\left( A \right)$

Estamos en condiciones de enunciar un teorema central sobre la compatibilidad de sistemas de ecuaciones lineales.

Un sistema de ecuaciones lineales $AX = B$ es compatible si y sólo si el rango de la matriz ampliada es igual al rango de $A$ .

El\;sistema\;\;AX = B\;es\;compatible \Leftrightarrow rg\left( A \right) = rg\left( {A'} \right)

227

Oprimí el botón en la parte inferior derecha del siguiente recurso y podrás trabajar con distintos espacios columna.

Objeto interactivo de construcción propia

228

4.2 Espacio nulo de A.

Dada una matriz $A$ , las soluciones de $AX=0$ constituyen un espacio vectorial, que llamaremos el espacio nulo de $A$ .
Encontremos el Espacio Nulo de la matriz A:

$A = \begin{pmatrix} -1 & 1 & 1 \\ 2 & 3 & 1 \\ 1 & 4 & 2\end{pmatrix}$ Debemos encontrar que matrices $X$ "anulan" a la matriz $A$ . Es decir, el espacio solución del sistema $AX=0.$ La matriz ampliada del sistema es:

$A' = \begin{pmatrix} -1 & 1 & 1 & 0 \\ 2 & 3 & 1 & 0\\ 1 & 4 & 2 & 0 \end{pmatrix}$

Resolviendo el sistema, la solución es

S = \begin{Bmatrix} X = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = z \begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix} \;\; con \; z \in \mathbb{R} \end{Bmatrix}

(Espacio nulo de $A$ )

229

En el siguiente applet podemos observar la interpretación geométrica: todos estos vectores $X$ (en rojo) forman una recta, al ser multiplicados por $A$ se anulan.

Objeto interactivo de construcción propia

Más ejemplos

Puedes oprimír el botón situado en la parte inferior derecha del recurso de la página siguiente. En la actividad, primero elige el rango de la matriz con la que quieras trabajar y podrás encontrar el espacio nulo asociado a la misma. En el applet, a dicho espacio nulo se lo indica como el "núcleo" de $A$ (Terminología que tendrá significado cuano estudiemos transformaciones lineales.)

230

Objeto interactivo de construcción propia

Por último, en el siguiente ejemplo podemos cambiar la matriz con la que trabajamos y graficar los tres espacios asociados (columna, fila y nulo) juntos o por separado.

El applet muestra los espacios de una matriz M de 3x3. El espacio fila se muestra en azul, el espacio columna se muestra en naranja y el espacio nulo se muestra en verde. Puedes editar la matriz para ver cómo cambian estos espacios y puedes alternar la visibilidad de los tres espacios haciendo clic en las casillas de verificación de la derecha. Algunas observaciones notables:

Los espacios fila y columna siempre tienen la misma dimensión, igual al rango de M.
La dimensión de los espacios fila/columna y la dimensión del espacio nulo siempre suman 3, de acuerdo con el Teorema de nulidad-rango.
El espacio de filas siempre es ortogonal al espacio nulo de M.

231

Aquí hay algunas matrices interesantes para probar:

$\begin{pmatrix} 1 & 2 & -1 \\ 2 & 4 & -2 \\ 1& 2 & -1 \end{pmatrix}$ Antes de escribirla en el applet, mirá las columnas de esta matriz: ¿qué observas? ¿Puedes adivinar cómo se verá el espacio columna?
Otra: $\begin{pmatrix} 1 & 2 & -4 \\ 2 & -1 & 7 \\ 1 & 0 & 3 \end{pmatrix}$

¿Cuál es el espacio nulo en este caso? (Pista: recuerda que uno de los subespacios 'triviales' consta solo del vector nulo).

La última:

\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}

¿Cuáles serán los espacio fila y columna en este caso?

Recordá que podés introducir la matriz que desees.

232

Objeto interactivo de construcción propia

233

4.3 Relación entre las soluciones de $AX = B$
y $AX = 0.\;$ Variables libres.

4.3.1 Espacio solución de un sistema homogéneo

Consideremos un sistema homogéneo $AX = 0,\;$ con $A \in {\mathbb{R}^{mxn}}$ .

Sea ${S_h} = \left\{ {X \in {\mathbb{R}^{nx1}}| \; AX = \;0} \right\}$ , el conjunto solución del sistema.

1) $X = 0\;$ pertenece a ${S_h}$ (solución trivial del sistema).

2) Sean ${X_1}$ y ${X_2}$ soluciones del sistema.

$A\left( {{X_1} + {X_2}} \right) = \;A{X_1} + A{X_2} = 0\; \Rightarrow \;{X_1} + {X_2}$ también es solución.

3) Sea $X$ una solución, y $k$ un número real:

$A\left( {kX} \right)\; = k\left( {AX} \right) = k0 = 0$ $kX$ también es solución.

Por lo tanto:

El conjunto solución de un sistema homogéneo

AX\; = \;0

(con

A \in {\mathbb{R}^{mxn}}

) es un subespacio de

{\mathbb{R}^{nx1}}

.

Si el sistema (homogéneo) es compatible determinado, la única solución es la trivial. En ese caso, $\;dim\left( {{S_h}} \right)\; = \;0.$

¿De qué dependerá la dimensión de ${S_h}$ para una matriz $A$ dada?

234

Propiedad

Sea ${S_h}$ el espacio solución del sistema homogéneo $AX = 0$ , con $A \in {\mathbb{R}^{mxn}}.\:$ Puede demostrarse que:

$dim\left( {{S_h}} \right)\; = \;n - rg\left( A \right)$

Nota: Recordamos que el conjunto solución de un sistema homogéneo $AX = 0$ se denomina espacio nulo de la matriz $A$ .

Ejercicio

Dado el sistema homogéneo cuya matriz de coeficientes es

\begin{pmatrix} 1 & 1 & 1 & 0 \\ 1 & 0 & -1 & 1 \\ 0 & 3 & 6 & k \end{pmatrix}

a) Determinar la dimensión del espacio solución y el rango de $A$ de acuerdo con los valores de $k$ .

b) Para $k = 0\;$ hallar una base del espacio solución.

Te pedimos que compruebes en este ejercicio la propiedad mencionada previamente.

235

4.3.2 Relación entre las soluciones de $AX = B$ y $AX = 0$

Consideremos los siguientes sistemas de ecuaciones:

Sistema de ecuaciones:

\begin{cases} \begin{aligned} 2x - y + z = 4 \\ -x +2y - z = 3 \\ \end{aligned} \end{cases}

Sistema homogéneo asociado

\begin{cases} \begin{aligned} 2x - y + z = 0 \\ -x +2y - z = 0 \\ \end{aligned} \end{cases}

Resolvemos primero el sistema de ecuaciones original:

\begin{cases} \begin{aligned} 2x - y + z = 4 \\ -x +2y - z = 3 \\ \end{aligned} \end{cases} \;\; \Rightarrow \;\; \begin{cases} \begin{aligned} -6 +4y -2z - y + z = 4 \\ x = 2y - z - 3 \\ \end{aligned} \end{cases} \;\; \Rightarrow \;\;

\;\; \Rightarrow \;\; \begin{cases} \begin{aligned} z = -10 + 3y \\ x = -y + 7 \\ \end{aligned} \end{cases}

Luego el conjunto solución es:

$\left( {x,y,z} \right) = \left( { - y + 7,\;\;\;y,\; - 10 + 3y} \right) = y\left( { - 1,1,3} \right) + \left( {7,0, - 10} \right)$

$S = \left\{ {\left( {x,y,z} \right) \in {\mathbb{R}^3}|\;\;\left( {x,y,z} \right) = \lambda \left( { - 1,1,3} \right) + \left( {7,0, - 10} \right)} \right\}$

Geométricamente, el conjunto solución es una recta que no pasa por el origen.

236

Resolvamos ahora el sistema homogéneo asociado:

\begin{cases} \begin{aligned} 2x - y + z = 0 \\ -x +2y - z = 0 \\ \end{aligned} \end{cases} \;\; \Rightarrow \;\; \begin{cases} \begin{aligned} 4y -2z - y + z = 0 \\ x = 2y - z \\ \end{aligned} \end{cases} \;\; \Rightarrow \;\;

\;\; \Rightarrow \;\; \begin{cases} \begin{aligned} z = 3y \\ x = - y \\ \end{aligned} \end{cases}

Luego el conjunto solución es:

$\left( {x,y,z} \right) = \left( { - y,\;\;y,\; 3y} \right) = y\left( { - 1,1,3} \right)$

${S_h} = \left\{ {\left( {x,y,z} \right)|\;\left( {x,y,z} \right) = \lambda \left( { - 1,1,3} \right)} \right\}$

Se trata de una recta paralela a la anterior, que pasa por el origen.

Notemos que tal como establecimos previamente, el conjunto solución de un sistema homogéneo es un subespacio.

¿Qué relación existe entre los conjuntos solución del sistema original y de su homogéneo asociado?

En la gráfica de la siguiente página se muestran las soluciones de los sistemas. En naranja la recta solución del sistema no homogéneo, y en violeta la recta solución del sistema homogéneo:

237

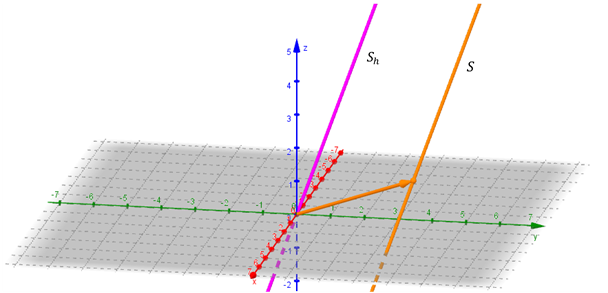
Son dos rectas paralelas: la recta que es solución del sistema homogéneo pasa por el origen y la recta que es solución del sistema no homogéneo no pasa por el origen.

Observamos que:

S = {(x,\;y,\;z) = \lambda \; \underbrace{(-1, \;1, \;3)}_{S_{h}} + \underbrace{(7,\; 0, \; -10)}_{X_{p}}}

$\Rightarrow \;\;S = {S_h} + {X_p}$

A continuación veremos un conjunto de propiedades que permiten generalizar este resultado para un sistema de ecuaciones lineales $AX = B$ con $A \in {\mathbb{R}^{m \times n}},\;\;B \in {\mathbb{R}^{m \times 1}}$ :

238

Propiedad 1

La diferencia de dos soluciones particulares es solución del sistema homogéneo asociado.

Si ${X_1}$ y ${X_2}$ son dos soluciones particulares del sistema $AX = B$ , entonces se cumple que:

A{X_1} = B \;\; \land \;\; A{X_2} = B

Restando miembro a miembro:

A{X_1} - A{X_2} = 0 \; \Rightarrow \; A \;({{X_1} - {X_2}}) = 0

Por lo tanto ${X_1} - {X_2}\;$ es solución de $AX = 0$

Propiedad 2

La suma de una solución particular de $AX = B$ y una solución del homogéneo asociado, es solución de $AX = B.$

Sean:

${X_p}$ una solución particular de $AX = B$
${X_h}$ una solución del sistema homogéneo asociado.

Queremos probar que $\left( {{X_p} + {X_h}} \right)$ es solución de $AX = B$

$A\left( {{X_p} + {X_h}} \right) = A{X_p} + A{X_h} = B + 0 = B$

239

Propiedad 3

En la propiedad anterior habíamos probado que $\left( {{X_p} + {X_h}} \right)$ es solución de $AX = B.\;$ Recíprocamente:

Cualquier solución del sistema $AX = B$ puede expresarse como ${X_p} + {X_h},\;$ siendo ${X_p}\;$ una solución particular del sistema y ${X_h}\;$ una solución del homogéneo asociado.

Sea $X$ una solución del sistema $AX = B,\;$ entonces:

$X = \left( {X - {X_p}} \right) + {X_p}$

Por propiedad 1, $\;\left( {X - {X_p}} \right)$ es solución del homogéneo asociado, por lo tanto:

$X = {X_h} + {X_p}$

A partir de las propiedades 2 y 3 se deduce que:

El conjunto solución de un sistema $AX = B$ puede expresarse como suma de una solución particular y la solución del sistema homogéneo asociado.

S = {X_p} + {S_h} = \begin{Bmatrix} {{X_p} + {X_h}|\;{X_h} \in {S_h}} \end{Bmatrix}

240

4.4 Número de variables libres de un sistema

Recordemos que:

El sistema $AX = B$ es compatible $\Leftrightarrow$ $B \in Col\left( A \right)$ $\Leftrightarrow$ $\Leftrightarrow rg\left( A \right) = rg\left( {A'} \right)$

Supongamos que $B \in Col\left( A \right)$ , es decir que el sistema es compatible. ¿Cuántas soluciones tiene?

Sea $\;rg\left( A \right) = rg\left( {A'} \right) = r$

Si $n$ es el número de incógnitas, puede demostrarse que:

241

Si $r = n$ , el sistema tiene solución única (SCD)
Si $r < n$ , el sistema admite infinitas soluciones (SCI), con $n - r$ variables libres

Observación: El número de variables libres es igual a la dimensión del espacio solución del sistema homogéneo asociado.

Ejemplo

Analizar cada uno de los siguientes sistemas de ecuaciones, e indicar el número de variables libres.

a)

\quad \quad \quad \quad \quad \quad \quad \begin{cases} \begin{aligned} x + y + z = 0 \\ x - y \quad \: \: \: = 1 \\ z = 3 \end{aligned} \end{cases}

b) $\quad \quad \quad \quad \quad \quad \quad \begin{cases} \begin{aligned} x + y + z = 0 \\ x - y \quad \: \: \: = 1 \\ 2x \quad \: + z = 1 \end{aligned} \end{cases}$

c) $\quad \quad \quad \quad \quad \quad \quad \begin{cases} \begin{aligned} {x_1} + {x_2} + {x_3} + {x_4} = 1 \\ \quad {x_2} \quad \quad\; - {x_4} = 0 \\ {x_1} \:\:\:\:\:\:\: + {x_3} + 2{x_4} = 1 \end{aligned} \end{cases}$

242

Resolución

Ítem a

\begin{cases} \begin{aligned} x + y + z = 0 \\ x - y \quad \: \: \: = 1 \\ z = 3 \end{aligned} \end{cases}

Realicemos el análisis a partir del rango de $A$ y de $A'$ :

\begin{pmatrix} 1 & 1 & 1 & 0 \\ 1 & -1 & 0 & 1 \\ 0& 0 & 3 & 3\end{pmatrix} \: F_2 \to F_2 - F_1 \: \begin{pmatrix} 1 & 1 & 1 & 0 \\ 0 & -2 & -1 & 1 \\ 0& 0 & 3 & 3\end{pmatrix}

Como $rg\left( A \right) = rg\left( {A'} \right) = n = 3$ entonces el sistema es SCD. No hay variables libres.

Ítem b

\begin{cases} \begin{aligned} x + y + z = 0 \\ x - y \quad \: \: \: = 1 \\ 2x \quad \: + z = 1 \end{aligned} \end{cases}

Escalonamos $A'$ para hallar $rg(A)$ y $rg(A')$ :

\begin{pmatrix} 1 & 1 & 1 & 0 \\ 1 & -1 & 0 & 1 \\ 2 & 0 & 1 & 1\end{pmatrix} \: \begin{matrix} F_2 \to F_2 - F_1 \\ F_3 \to F_3 - 2F_1\end{matrix} \: \begin{pmatrix} 1 & 1 & 1 & 0 \\ 0 & -2 & -1 & 1 \\ 0 & -2 & -1 & 1 \end{pmatrix}

243

\begin{pmatrix} 1 & 1 & 1 & 0 \\ 0 & -2 & -1 & 1 \\ 0 & -2 & -1 & 1\end{pmatrix} F_3 \to F_3 - F_2 \begin{pmatrix} 1 & 1 & 1 & 0 \\ 0 & -2 & -1 & 1 \\ 0 & 0 & 0 & 0 \end{pmatrix}

Al escalonar $A'$ se elimina una de las filas. Luego:

$rg(A) = rg{A'} = 2 \;$ y $\; n = 3 \; \Rightarrow \;\;$ SCI con una variable libre.

Le proponemos al lector hallar el conjunto solución, comprobar que el sistema es un SCI con una variable libre, e indicar una base de ${S_h}$ .

Ítem c

\begin{cases} \begin{aligned} {x_1} + {x_2} + {x_3} + {x_4} = 1 \\ \quad {x_2} \quad \quad\; - {x_4} = 0 \\ {x_1} \:\:\:\:\:\:\: + {x_3} + 2{x_4} = 1 \end{aligned} \end{cases}

Escalonamos $A'$ para hallar $rg(A)$ y $rg(A')$ :

\begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & -1 & 0 \\ 1 & 0 & 1 & 2 & 1 \end{pmatrix} F_2 \to F_2 - F_1 \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 0 \end{pmatrix}

\begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & -1 & 0 \\ 0 & -1 & 0 & 1 & 0 \end{pmatrix} F_3 \to F_3 + F_2 \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{pmatrix}

Al escalonar $A'$ se elimina una de las filas. Luego:

244

$rg(A) = rg{A'} = 2 \;$ y $\; n = 4 \; \Rightarrow$ SCI con dos variables libres.

Le proponemos al lector hallar el conjunto solución, comprobar que el sistema es un SCI con dos variables libres, e indicar una base de ${S_h}$ .

Resumen

Sea el sistema de ecuaciones $AX = B,\;$ con $A \in {\mathbb{R}^{m \times n}},$
$X \in {\mathbb{R}^{n \times 1}},\;B \in {\mathbb{R}^{m \times 1}},\;$ cuya matriz ampliada es:

$A' = \left( {{A_1}\;\;\;\;{A_2}\;\;\;{A_3}\;\; \ldots \;\;\;{A_n}\;\;\;\;B} \right)$

El siguiente esquema resume el análisis de compatibilidad que realizamos previamente:

245

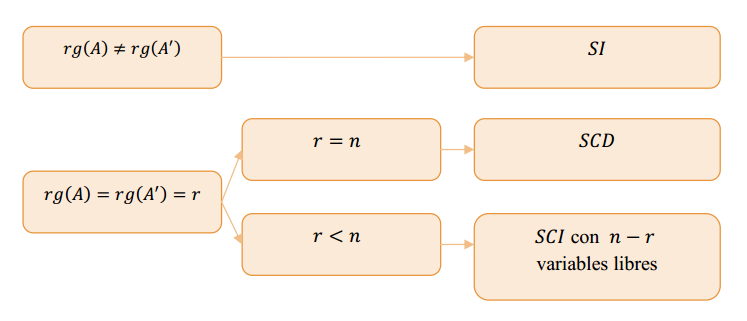
En el caso particular de un sistema homogéneo $AX = 0:$

246

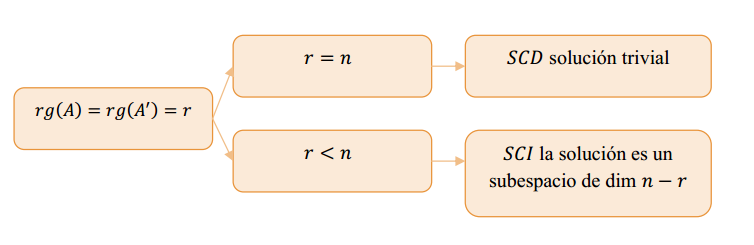
Acerca de los objetos interactivos de esta obra

Todos los objetos interactivos del libro hechos en Geogebra han sido diseñados por el autor.

Los objetos interactivos hechos en Descartesjs utilizados en el capítulo 2 han sido diseñados y creados originalmente por la profesora María José García Cebrian [1] y adaptados a este libro por el autor; con la excepción del interactivo de la página 156, cuya autora es la profesora Melissa Méndez Servin [3] y el objeto interactivo de la página 146 cuyos autores originales son John Jairo García Mora, Sonia Jaquelliny Moreno Jiménez y Margarita Patiño Jaramillo.[4] Este último objeto fue modificado por quien esto escribe para adaptarlo a esta publicación.

Los objetos interactivos hechos en Descartesjs utilizados en el capítulo 1 han sido diseñados y creados originalmente por las profesoras María José García Cebrian y Esperanza Álvarez Sáiz[2] y adaptados a este libro por el autor.

247

Bibliografía recomendada

Lay, D. (2012). Algebra Lineal y sus Aplicaciones.
Ed. Pearson.
Kozak, A., Pastorelli, S. y Vardanega, P. (2007). Nociones de Geometría Analítica y Álgebra Lineal. McGraw-Hill, Buenos Aires.
Merino González, L. y Santos Aláez E. (2010). Álgebra lineal con metodos elementales. Ediciones PARANINFO.
Lipschutz S. (1992). Álgebra lineal. Mc Graw – Hill, Madrid.
Noble B. y Daniel J. W. (1989). Álgebra lineal aplicada.
Ed. Prentice Hall.
Nakos G., Joyner D. (1999). Algebra Lineal con Aplicaciones. Thomson Ed.
Poole D. (2011) Álgebra lineal, Una introducción moderna. Cengage Learning Editores.

249

Álgebra Lineal Interactiva

Tabla de contenido

Prefacio

Vectores, rectas y planos

1.1 Introducción a vectores en R3{\mathbb{R}^3}R3

Puntos en R3{\mathbb{R}^3}R3

1.1.1 Vectores en R3{\mathbb{R}^3}R3

1.1.2 Operaciones y nociones básicas de vectores en R3{\mathbb{R}^3}R3

1.1.3 Propiedades de la suma de vectores y del producto por un escalar

1.1.4 Módulo o norma de un vector en R3{\mathbb{R}^3}R3

1.1.5 Propiedades del módulo o norma de un vector

Resolución

1.1.6 Vector determinado por dos puntos

1.1.7 Distancia entre dos puntos

1.1.8 Expresión canónica de un vector

1.1.9 Ángulos directores y cosenos directores de un vector

1.1.10 Versor asociado a un vector

1.2 Producto escalar en R3{\mathbb{R}^3}R3

1.2.1 Propiedades del producto escalar

Resolución

1.2.2 Ángulo entre vectores

1.2.3 Condición de perpendicularidad

1.2.4 Proyección de un vector en la dirección de otro

1.3 Producto vectorial y mixto

1.3.1 Producto vectorial

1.3.2 Propiedades del producto vectorial

1.3.3 Fórmula para calcular el producto vectorial

1.3.4 Interpretación geométrica del módulo del producto vectorial

1.3.5 Producto mixto

1.3.6 Interpretación geométrica del producto mixto

1.3.7 Coplanaridad

1.4 Ecuaciones del plano

1.4.1 Deducción de la ecuación general del plano

1.4.2 Ecuación segmentaria del plano

1.4.3 Ecuación vectorial paramétrica del plano

1.4.4 De la ecuación general a la ecuación vectorial paramétrica

1.5 Ángulos y distancias

1.5.1 Ángulo entre dos planos

1.5.2 Planos perpendiculares y planos paralelos

1.5.3 Distancia de un punto a un plano

1.5.4 Distancia entre planos paralelos

1.6 Haz de planos

1.7 Recta en R3{\mathbb{R}^3}R3

1.7.1 Ecuaciones de la recta en R3{\mathbb{R}^3}R3

1.7.2 Ecuación vectorial de la recta

1.7.3 Ecuaciones paramétricas de la recta

1.7.4 Ecuaciones simétricas de la recta

1.7.5 Recta definida como intersección de dos planos

1.8 Recta y plano: intersecciones y ángulos

1.8.1 Intersección entre recta y plano

1.8.2 Paralelismo entre recta y plano

1.8.3 Perpendicularidad entre recta y plano

1.8.4 Ángulo entre recta y plano

1.8.5 Intersección de rectas en R3{\mathbb{R}^3}R3

1.8.6 Plano que contiene a dos rectas

1.8.7 Ángulo entre dos rectas

1.9 Distancias y proyecciones

1.9.1 Proyecciones ortogonales

1.9.2 Planos proyectantes de una recta

1.9.3 Distancias

1.9.4 Condición de coplanaridad

1.10 Ejercicios surtidos de fin de capítulo

Matrices, determinantes y SEL

2.1 Matrices

2.1.1 Definición de Matriz

2.1.2 Matriz columna

2.1.3 Matriz fila

2.1.4 Matriz nula

2.1.5 Igualdad de matrices

2.2 Operaciones con matrices

2.2.1 Suma de matrices

2.2.2 Producto de un escalar por una matriz

2.2.3 Propiedades de la suma de matrices y del producto por un escalar

2.2.4 Producto de matrices

2.2.5 Propiedades del producto

2.2.6 Matriz traspuesta

2.2.7 Propiedades de la matriz traspuesta

2.2.8 Matrices cuadradas: identidad e inversa

2.2.9 Propiedades de la matriz inversa

2.2.10 Algunos tipos de matrices

1.1 Introducción a vectores en ${\mathbb{R}^3}$

Puntos en ${\mathbb{R}^3}$

1.1.1 Vectores en ${\mathbb{R}^3}$

1.1.2 Operaciones y nociones básicas de vectores en ${\mathbb{R}^3}$

1.1.4 Módulo o norma de un vector en ${\mathbb{R}^3}$

1.2 Producto escalar en ${\mathbb{R}^3}$

1.7 Recta en ${\mathbb{R}^3}$

1.7.1 Ecuaciones de la recta en ${\mathbb{R}^3}$

1.8.5 Intersección de rectas en ${\mathbb{R}^3}$

3.1.5 Resumen de los subespacios de ${\mathbb{R}^2}$ y ${\mathbb{R}^3}$

4.3 Relación entre las soluciones de $AX = B$
y $AX = 0.\;$ Variables libres.

4.3.2 Relación entre las soluciones de $AX = B$ y $AX = 0$