Este es el nombre del nuevo subproyecto de RED Descartes.
Telesecundaria es una modalidad de los estudios de educación secundaria en el Sistema Educativo de México dirigido a estudiantes adolescentes de 12 a 15 años que viven en comunidades dispersas que carecen de escuela de secundaria.
Se utilizan para ello los avances en tecnologías de la información y comunicación (TIC) como recurso para acercar esta formación a los jóvenes y puedan concluir su educación básica.
En este subproyecto de RED Descartes se han recogido objetos de la Telesecundaria desarrollando los correspondientes materiales con la herramienta Descartes. Las asociaciones de Colombia y España han sido las encargadas de preparar la adaptación a DescartesJS y en consecuencia todos podrán ser consultados en cualquier dispositivo con sistema operativo que admita un navegador compatible con HTML5.
Los materiales, que se irán integrando en el subproyecto corresponde a los tres cursos o grados en que se divide la Secundaria en el Sistema Educativo de México, trata los contenidos de Matemáticas, Física y Química.
En el momento en que se redacta este artículo se pueden consultar ya los 24 recursos del segundo grado de Física (13-14 años). En un corto espacio de tiempo iremos viendo aparecer publicados los restantes hasta un total de 123, con la siguiente distribución:
- 28 de Matemáticas 1º
- 38 de Matemáticas 2º
- 29 de Matemáticas 3º
- 24 de Física 2º
- 4 de Química 3º
Destaca la alta calidad de estos materiales y son perfectamente válidos para ser utilizados complementariamente a los contenidos curriculares de nuestro sistema educativo tanto por alumnos como por profesores.
Enhorabuena y muchas gracias por el esfuerzo y el mérito de quienes han estado vinculados a esta producción.
Asia. Puzles y otras actividades para el estudio de los países
Escrito por Montserrat Gelis BoschEn el vídeo de esta semana se muestra una selección de objetos digitales para el estudio de la geografía pertenecientes al proyecto GEOgráfica, un proyecto promovido por la Red Educativa Digital Descartes de España y Colombia y la Institución Universitaria Pascual Bravo.
A modo de ejemplo, se han seleccionado actividades referentes al continente asiático. En concreto, se ha elegido el libro digital Asia del apartado GEOdiver, que contiene puzles, sopas de letras y demás actividades con aspectos geográficos del continente. Se complementan estas actividades con tres objetos digitales pertenecientes a GEOcolor y GEOcapital, con ejercicios de situación e identificación de países y capitales de Asia.
Estos objetos digitales se insertan en un curso-aula moodle, mediante el recurso etiqueta y utilizando el código para abrir en una ventana emergente.
Un grillo está sobre una superficie, que gira a una velocidad angular constante, y se está desplazando dando saltos siguiendo una línea recta que pasa por el centro de giro. Ha dado un salto inicial y posteriormente cada salto es c veces mayor que el anterior. ¿En qué posición está en cada instante? ¿Cuál es la trayectoria que sigue?
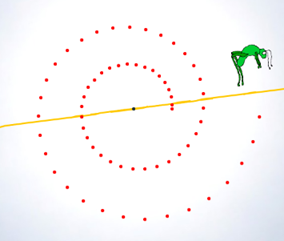
Este planteamiento dinámico conduce a una curva, ampliamente estudiada, la cual es el objeto de este artículo de difusión. En la miscelánea que hemos publicado en nuestro servidor de contenidos puedes ver el camino que sigue nuestro grillo saltarín, pudiendo seleccionar el salto y la velocidad de giro que desees y observando en qué influye tu elección.
Es bien conocido que la circunferencia es una curva equiangular, es decir, que en cualquier punto de la misma, el ángulo que forma el radio con la tangente es siempre constante e igual a un ángulo recto.
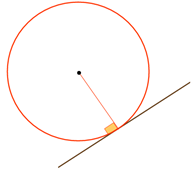
Inicialmente René Descartes (1596-1650) fue quien se planteó la determinación de una curva que también fuera equiangular, pero que el ángulo fuera el que previamente se deseara, es decir, una generalización de lo que acontece en la circunferencia. Jakob Bernoulli (1654-1705) también la analizó y la denominó “Spira mirabilis” o espiral maravillosa, y de acuerdo con sus propiedades, en su epitafio hizo poner “Eadem mutata resurgo”, es decir, “Mutante y permanente vuelvo a resurgir siendo el mismo”. En este recurso podrás comprobar el significado de esta expresión y experimentar que:
¡Ciertamente es maravillosa!
Para ello, planteamos un camino en varias fases, un total de doce, y en cada una de ellas se avanza en el análisis de esta espiral, en sus propiedades. Pulsa sobre la imagen siguiente para acceder al recurso.
En las tres primeras fases se aborda su construcción dinámica —dependiente del tiempo— y se inicia su análisis con la obtención de la relación —digamos estática o atemporal— entre la distancia y el ángulo polar. Ésta, es la ecuación algebraica en coordenadas polares de la espiral y nos permite identificar el significado físico de los parámetros específicos de la misma.
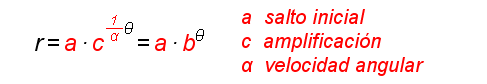
La expresión justifica su denominación como espiral logarítmica, pues se observa que el ángulo polar se puede expresar en función del logaritmo del radio polar. Y en la fase cuarta del recurso se observa y justifica que a es un factor de escala, que para b=1 obtenemos como caso particular la circunferencia y que las espirales de base b y 1/b son simétricas respecto del eje polar.
Una quinta fase permite ver y justificar por qué también se le denomina espiral geométrica ya que los puntos de ella situados sobre una misma semirrecta siguen la relación de una proporción geométrica (aquí se aplica una analogía con la que acontece en la espiral de Arquimedes o espiral aritmética). Y en la sexta se visualiza y demuestra el carácter equiangular que motivó a Descartes.
El hecho de ser equiangular es lo que le confiere a esta espiral su carácter tan especial. Y en base a ello, las últimas fases del recurso se centran en mostrar y demostrar el carácter maravilloso que marcó Bernoulli y que sintetizó en la citada expresión: “Eadem mutata resurgo”. Para una circunferencia es fácil de intuir y ver que su forma es tal que siempre surge o resurge siendo la misma, crece y crece siempre siendo la misma. Y lo maravilloso es que este surgir y resurgir siendo la misma se verifica también en esta “circunferencia generalizada” o espiral logarítmica, es decir, la razón de su crecimiento instantáneo es la unidad. Sintetizando el planteamiento que se realiza en el recurso, pues el detalle lo puedes comprobar interactuando con él, tenemos que:
- Inicialmente el análisis del crecimiento se aproxima mediante rectángulos semejantes circunscritos a la espiral, que siguen un patrón de crecimiento gnomónico en el sentido euclídeo (según lo definido en “Los elementos de Euclides”), que puede interpretarse como el patrón de crecimiento en pasos discretos de π radianes.
- Posteriormente se aborda el crecimiento, pero en el sentido establecido por Aristóteles cuando decía: «Hay ciertas cosas que no sufren alteración salvo en magnitud, cuando crecen...».

Y aquí, esto se aborda planteando el crecimiento con polígonos semejantes construidos sobre radios vectores, correspondientes a puntos de la espiral, que difieren:
-
- En π/2 radianes, lo que conduce a una razón de semejanza b^(π/2):
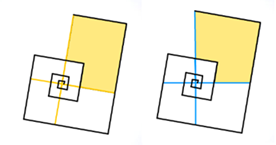
-
- O, en general, con paso 2π/n y razón de semejanza b^(2π/n):
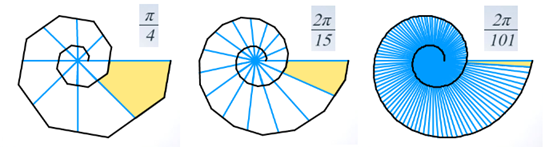
Como ejemplo, sobre la concha del Nautilus pompilius, se muestra un crecimiento gnomónico discreto de paso 2π/16 en una espiral logarítmica cordobesa (b=1.186):

- Finalmente cuando el crecimiento es instantáneo, es decir, si n->infinito y el paso entre radios vectores es por tanto 2π/n->0, la razón de semejanza b^(2π/n) tiende a la unidad: “Eadem mutata resurgo”.
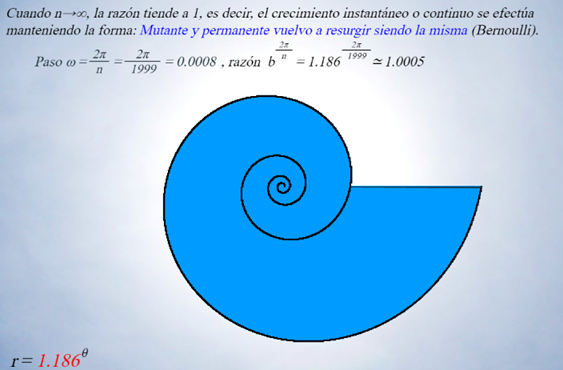
¡Te deseamos un buen aprendizaje siguiendo a nuestro grillo!
Escenas con DescartesJS: Técnicas y trucos (M04)
Escrito por Ángel Cabezudo Bueno Los puzles son un excelente material de motivación y está probado que son facilitadores del aprendizaje.
Los puzles son un excelente material de motivación y está probado que son facilitadores del aprendizaje.
La elaboración de un puzle con DescartesJS es una tarea interesante y ahora nos va a permitir seguir avanzando en la presentación de los distintos recursos que se pueden extraer de esta herramienta de programación.
La propuesta que se hace aquí procede, como ya hemos hecho en las escenas precedentes, de una aportación de técnicas con las que nuestro compañero cartesiano Eduardo Barbero Corral realiza sus propios puzles.
Hago repaso de su esquema de trabajo y aporto conceptos complementarios que pueden ayudar a comprender mejor al lector menos experimentado con DescartesJS.
Hemos clasificado este trabajo como de nivel medio debido a que algunas propuestas que se incluyen requieren tener cierta soltura y conocimiento de la herramienta, pero quien esté trabajando a un nivel básico todavía, bien que podrá superar sin dificultad y con estudio una gran parte del contenido.
Un puzle de arrastre parte de una imagen que está troceada en piezas de igual tamaño, generalmente de forma cuadrada y la actividad consiste en armar o componer la imagen original a partir de dichas piezas.
La programación de un puzle, aunque este sea elemental, p.e de cuatro piezas, va a requerir que se aborden estas cuestiones:
- Trocear una imagen en piezas cuadradas utilizando alguna aplicación como PhotoScape o TileMage-Image Splitter ambas gratuitas.
- Diseñar y realizar un tablero virtual donde hay que situar una cuadrícula – que habrá que dibujar con Descartes y las piezas (imágenes).
- Desplazar las imágenes apoyadas en su correspondiente control gráfico.
- Restringir el movimiento de los controles gráficos para que las piezas no puedan desaparecer de la escena cuando se arrastren.
- Procurar un efecto imán para que la imagen sea atraída y encajada en un cuadro cualquiera cuando aquella se sitúe a una distancia muy próxima del mismo.
- Verificar si hay piezas montadas en el mismo cuadro y comunicarlo mediante un mensaje de texto.
- Verificar si todas las piezas están correctamente encajadas en su cuadro correspondiente y comunicarlo mediante un mensaje de texto.
Dejamos los enlaces a los artículos anteriores por si alguien necesita repasar algún detalle de procedimiento que en este obviamos:
Idea del proyecto
|
Escena_M04: Puzle de arrastre con efecto imán La escena va a ser sencilla. Disponemos a un lado, de una cuadrícula de 2x2 (2 filas y dos columnas) y tendremos al otro lado las cuatro piezas mezcladas, situadas de forma aleatoria cada vez que se inicia la escena. Una vez realizado este trabajo se podrá seguir una pauta similar para programar puzles nxn de mayor dimensión: 3x3, 4x4, 5x5, etc. o más general de forma rectangular nxm. La Figura 1 te lleva al puzle ya elaborado para que puedas practicar y entender mejor los resultados que se pretende conseguir en este proyecto. Figura 1La escena debe permitir interaccionar con las piezas, poderlas arrastrar hacia la cuadrícula y situarlas correctamente en su cuadro. Decimos entonces que el puzle ha quedado armado. En dos momentos se requiere que el usuario reciba información a través de sendos mensajes de texto:
En este proyecto se abordarán los siete puntos de la Introducción. Proponemos la siguiente organización para las carpetas y archivos que se van a utilizar en el proyecto. La siguiente Figura 4, indica una estructura similar utilizada para desarrollar las escenas de los anteriores proyectos
La carpeta lib contiene el intérprete descartes-min.js y se puede generar automáticamente sin más que guardar en la carpeta escena_M04, con la opción Librería portable > sólo para JS, el archivo puzle.html que incluye el código de la escena. La carpeta piezas contiene las 4 piezas que se deberán denominar 1.jpg, 2.jpg, 3.jpg y 4.jpg Para realizar este proyecto debes de conseguir una imagen que sea cuadrada para trocear. Si no lo fuera debes recortarla con un programa de edición de imagen y si fuera el caso redimensionarla. Para este artículo se ha seleccionado una imagen cuadrada de 300x300 px. Cada una de las cuatro piezas del troceado resulta ser una imagen cuadrada de 150x150px. |
Troceado de la imagen
|
Existen diferentes programas que permiten trocear una imagen. Si no dispones de ninguno puedes descargarte PhotoScape que es gratuito e incluye una opción de troceado dentro de una interesante gama de posibilidades de edición. Figura 5 |
 |
Paso 1: Añadir la imagen. Seleccionar 2 columnas y 2 filas. Trocear
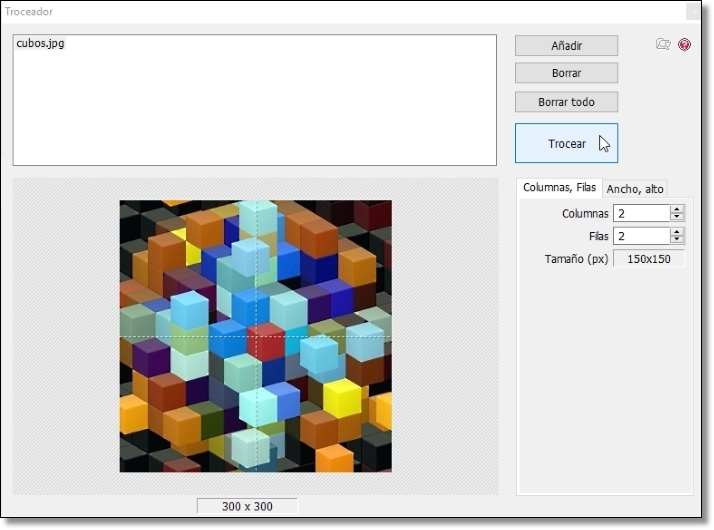
Figura 6
Paso 2: Trocear. Seleccionar carpeta de destino. Trocear.
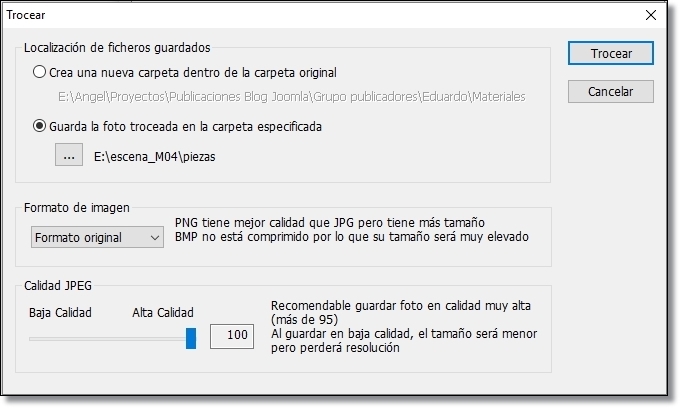
Figura 7
Paso 3: Acceder a la carpeta de destino. Renombrar las imágenes.
PhotoScape nombra cada imagen troceada añadiendo al nombre de la imagen original un número de orden contando de arriba a abajo y de izquierda a derecha es decir sigue un orden por filas y luego por columnas: la pieza 1 es la que corresponde a la casilla (1, 1), la pieza 2 la correspondiente a la casilla (1, 2), la pieza 3 la correspondiente a la casilla (2,1) y la pieza 4 la correspondiente a la casilla (2, 2).
Editor de escenas de Descartes
Abrir el Gestor de escenas y editar la escena, modificando en primer lugar su tamaño a 700x400px.
Escena adecuada para situar una cuadrícula de 300x300px y un espacio separado para situar inicialmente las cuatro imágenes.
Actuaciones en el panel Botones
Desmarcar los cuatro botones.
Actuaciones en el panel Espacio
Ponerlo fijo, para que no se pueda desplazar por arrastre. La escala será de 150 y debe coincidir con la longitud del lado de la pieza para simplificar los cálculos de situación.
Cuida que el tablero esté colocado adecuadamente, debe de estar a la izquierda y verse entero, para ello modificas los valores O.x, O.y según convenga.
 La posición por defecto del origen de coordenadas (O.x, O.y) es el centro de la escena a 350px del borde izquierdo y a 200px del borde superior. La posición por defecto del origen de coordenadas (O.x, O.y) es el centro de la escena a 350px del borde izquierdo y a 200px del borde superior.
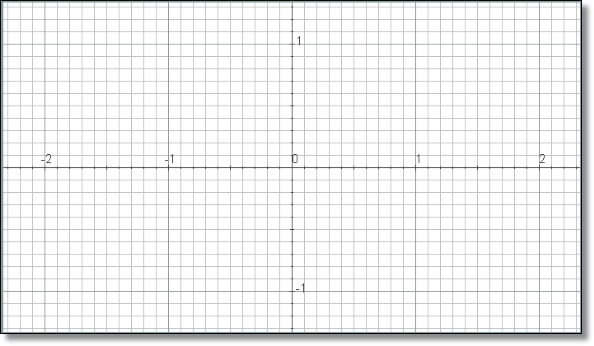
La Figura 8, muestra la red, los ejes y los números en el espacio. Esto nos permite ver mejor cómo organizar los elementos que van a aparecer en la escena. Después hay que quitarlos y poner un color de fondo para la escena al gusto del programador (ver Figura 1)
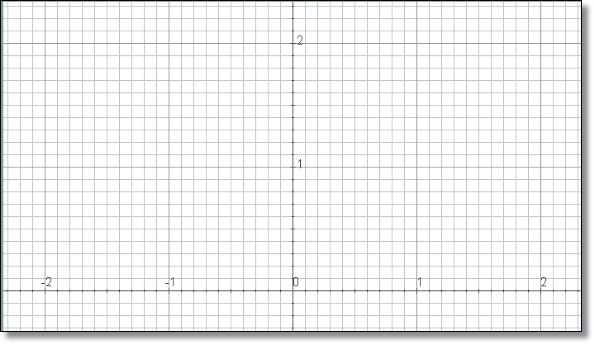
Para dibujar más adelante la cuadrícula 2x2 en el lado izquierdo de la escena, debemos posicionar el origen de coordenadas de tal manera que las coordenadas de los vértices del marco sean valores enteros sencillos. Hemos preferido que estos vértices sean (0,0), (0,2), (-2,2), (-2,0) así que para que la cuadrícula 2x2 quede dentro de la escena hay que situar O.y 150 píxeles más abajo, tal como se aprecia en la Figura 9.
|
Actuaciones en el panel Controles
Las piezas, que son gráficos de imagen, se mueven con controles gráficos que hay que definir previamente.
Agrega el primer control gráfico g1. Ponle un tamaño en número de píxeles que sea la mitad del de la escala, eso significa los pixeles que tiene de radio, para que coincida con el tamaño de una pieza de puzle. Posición (rnd+0.6, rnd*2) para que inicialmente aparezca a la derecha en lugar aleatorio.
Después pon dibujar-si=0 para que sea invisible el disco del control gráfico y no tape la pieza.
Los restantes controles g2, g3 y g4 se definen idénticamente como g1. Para añadir más rápidamente estos controles se pueden copiar g1 tres veces con la herramienta * situada en la ventana de agregar.
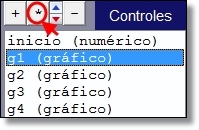 Figura 10
Figura 10
|
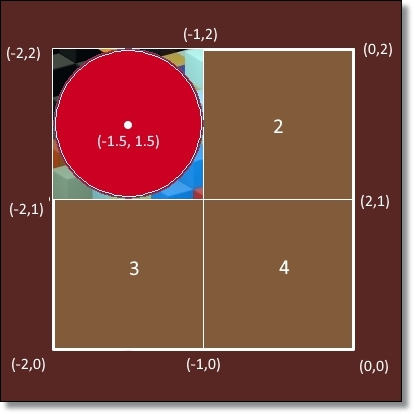
La Figura 11 nos muestra cómo se va a apoyar la pieza del puzle 1.jpg al control gráfico g1. El número de cada celda que aparece en la figura indica el lugar de destino para la correspondiente pieza, ¡no debe de verse en el puzle! La posición de destino correcta de la imagen 1.jpg es (-2, 2) ya que si se da únicamente la expresión de las coordenadas de una imagen, estas se refieren a la posición del vértice superior izquierdo.
Al definir el control g1 con la condición dibujar-si = 0, el control no se verá en la escena y dejará completamente descubierta la imagen que va apoyada. |
Actuaciones en el panel Gráficos
Lo primero es dibujar la cuadrícula 2x2. Esto se consigue, para este caso tan simple, dibujando un polígono de vértices (0,0)(0,2)(-2,2)(-2,0)(0,0) y ancho 6 (ancho en píxeles de la línea) para resolver el borde y dos segmentos perpendiculares para hacer la división en cuatro cuadrados: (-1,0)(-1,2) y (-2,1)(2,1), ancho 1. Poner el mismo color a las líneas (p.e. blanco) y color de relleno al polígono (Ver Figura 10).
Luego se van agregando una a una las imágenes de las piezas.
Para la pieza 1, el archivo es piezas/1.jpg, pones de coordenadas la expresión (g1.x-0.5, g1.y+0.5) para que se pueda mover con el control gráfico y esté centrada. Observar la expresión que ponemos para que la imagen encaje correctamente con el control sobre el que va apoyado, según la Figura 11. Por lo que explicaremos seguidamente escribimos la condición dibujar-si = (c1=0).
 |
dibujar-si es un campo de texto donde puede escribirse una expresión booleana u otra expresión que se interpreta como tal dependiendo del valor que tenga. |
La particularidad de este puzle es el efecto imán. Es decir, que cuando una pieza está muy cerca de ser colocada en una casilla parece como si una fuerza obliga a adaptarse perfectamente en ella. Para conseguir este efecto imán, para cada pieza incluiremos dos entradas de la misma imagen, una se dibuja cuando c1=0 y otra se dibuja cuando c1=1.
Veamos la circunstancia que se da para cada uno de estos valores posibles de la variable auxiliar c1.
Después de leer las actuaciones en el panel Programa para el caso c1=1 hay que añadir una nueva entrada en el panel Gráficos para dibujar la pieza 1.jpg en la posición (ent(g1.x), 1+ent(g1.y)) y dibujar-si = (c1=1).
En resumen, en el panel Gráficos tenemos para cada pieza 1.jpg, 2.jpg, 3.jpg y 4.jpg dos definiciones, una con la condición dibujar-si = (c1=1) y otra con la condición dibujar-si = (c1=0) y en este mismo orden para que las piezas cuando sean arrastradas sobre el tablero lo hagan por encima de las que ya están encajadas.
Es conveniente añadir también un control numérico de botón con la acción de iniciar la escena.
Actuaciones en el panel Programa
En el algoritmo Cálculos y evaluar siempre, en relación con la variable auxiliar c1 asociada a la imagen 1.jpg, escribimos la entrada
c1=(g1.x<0)*(abs(g1.x-ent(g1.x)-0.5)<0.05)*(abs(g1.y-ent(g1.y)-0.5)<0.05)
abs y ent son las funciones valor absoluto y la parte entera respectivamente con la definición matemática habitual.
La parte (g1.x<0) de la expresión es para que el efecto imán solo se produzca cuando la imagen está en el lado izquierdo de la escena, donde está el tablero para situar las piezas.
Observar que c1 tendrá valor 1 cuando la pieza esté colocada a una distancia muy próxima para encajar en una casilla. Esta distancia se ha fijado en menos de 0.05 tanto para la abscisa como para la ordenada de la pieza (0.05 unidades cartesianas de 150 píxeles equivale aproximadamente a 8 píxeles.).
Cuando c1 tome el valor 1, entonces la imagen en las coordenadas (g1.x, g1.y) se sustituye por la misma imagen en las coordenadas (ent(g1.x), 1+ent(g1.y)), es decir en las coordenadas del vértice superior izquierdo de la casilla que tiene tan cerca.
Añadimos después las restantes auxiliares c2, c3 y c4 asociadas a las imágenes respectivas 2.jpg, 3.jpg y 4.jpg.
Para que el proceso sea menos tedioso podemos obtener estas auxiliares copiando cada vez c1 y cambiando las referencias al subíndice 1 por 2, 3 y 4 en su correspondiente caso.
Propuesta final
Son tres las cuestiones que hasta este momento han quedado sin resolver y aunque el puzle, con lo dicho, es funcional conviene no desatenderlas:
- Notificar mediante un mensaje de texto cuando el puzle ha quedado armado. P.e: ¡Enhorabuena!.
Dependiendo del tema tratado en la imagen original, no siempre resulta fácil saber si la imagen ha sido bien recompuesta. - Notificar mediante un mensaje de texto cuando dos piezas se han superpuesto en la misma casilla.
P.e: “Hay piezas montadas! o, mejor, “Hay piezas superpuestas”. - Restringir el movimiento de los controles gráficos para que no puedan desaparecer de la escena cuando se arrastren, pues se corre el riesgo de hacer desaparecer alguna pieza si se arrastra más allá de los bordes del tablero.
El programador de DescartesJS con más recursos podrá resolver estas cuestiones cuando el número de piezas del puzle supere con mucho a cuatro. Pero queremos que también participen de esta actividad cualquier lector con nivel básico y teniendo en cuenta que manejamos pocas piezas, damos las siguientes pautas para ello.
Notificar mediante un mensaje de texto cuando el puzle ha quedado armado
Para verificar que la pieza 1 ha quedado encajada en la casilla 1 basta preguntar si la expresión c1*(ent(g1.x)=-2)*(ent(g1.y)=1) toma el valor 1.
Análogamente haremos para verificar si las restantes piezas 2, 3 y 4 están encajadas en sus respectivas casillas.
La condición para que las cuatro piezas estén encajadas en sus respectivas casillas y el puzle, por tanto, haya quedado armado es que el producto de las cuatro expresiones correspondientes valga 1.
Recomiendo crear un auxiliar, p.e. llamado armado, en el algoritmo CALCULOS del panel Programa y asignarle el valor del producto anterior.
Luego en el panel Gráficos poner la condición dibujar-si = armado, al Texto "¡Enhorabuena!" (ver Figura 3).
Notificar mediante un mensaje de texto cuando dos piezas estén superpuestas en la misma casilla
Supongamos que dos piezas, la 1 y la 2, están superpuestas y encajadas en cierta casilla, no necesariamente la casilla 1 o la casilla 2. Es obvio que se verifica c1*c2=1 pero también ent(g1.x)=ent(g2.x) y ent(g1.y)=ent(g2.y). En consecuencia c1*c2*(ent(g1.x)=ent(g2.x))*(ent(g1.y)=ent(g2.y)) tomará el valor 1.
Análogamente podemos suponer para las parejas de piezas 1 y 3, 1 y 4, 2 y 3, 2 y 4, 3 y 4. ¡En total hay 6 combinaciones posibles!.
Asignemos cada expresión a su correspondiente auxiliar, por ejemplo, s12, s13, s14, s23, s24, s34 y añadámoslos como entradas en el algoritmo CALCULOS.
Añadamos una entrada más, definiendo p.e el auxiliar montadas = s12+s13+s14+s23+s24+s34
Es obvio que montadas tomará el valor 1 cuando alguna pareja de piezas está superpuesta en una determinada casilla. Para notificar al usuario del puzle de esta circunstancia, bastará añadir, en el panel Gráficos, una entrada con el texto “Hay piezas montadas” y dibujar-si=montadas (ver Figura 2).
Restringir el movimiento de los controles gráficos
Es importante limitar el desplazamiento de los controles gráficos y en consecuencia la correspondiente pieza que va apoyada. Con esto evitaremos que por descuido al arrastrar el control más allá de los bordes del tablero la pieza pueda desaparecer y no podamos terminar de montar el puzle.
Sabemos que (g1.x, g1.y) son las coordenadas del control gráfico g1. Estas coordenadas se pueden definir convenientemente como controles numéricos y podemos conseguir esa limitación de movimientos.
En estas condiciones definimos el control gráfico g1 en la posición por defecto (0, 0) y definimos g1.x y g1.y según se indica en las figuras
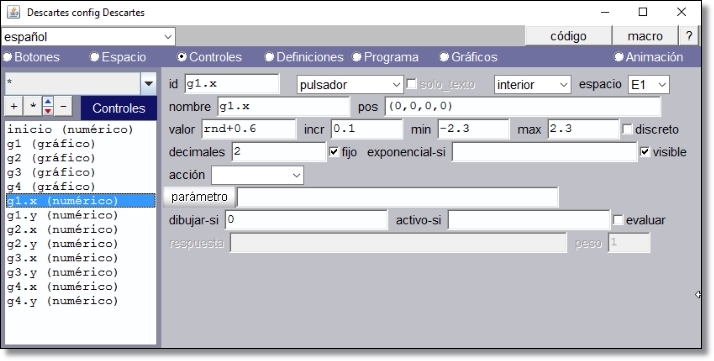
Figura 12
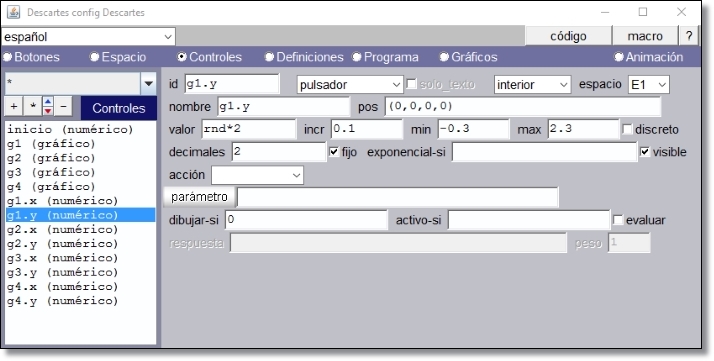
Figura 13
Estos controles quedan ocultos en la escena con la condición dibujar-si=0. El valor se g1.x y g1.y cambia al arrastrar el control gráfico g1 pero el desplazamiento queda restringido al espacio entre los valores mínimo y máximo.
Completamos copiando las mismas definiciones de g1.x y g1.y para g2.x y g2.y, g3.x yg3.y, g4.x yg4.y
Tablero con cuadrícula o sin cuadrícula
El programador del puzle podrá optar por facilitar un tablero con cuadrícula para situar las piezas o prescindir de la misma. El puzle que hemos instrumentado en este artículo podría seguir siendo funcional si prescindimos de los dos segmentos perpendiculares que acompañan al polígono de 4 vértices que delimitan el tablero.
Ahora bien si nos interesa dejar la cuadrícula y pensamos en puzles de mayor dimensión, por ejemplo de 4x5 es más práctico dibujarla utilizando dos familias de segmentos. Solo con el fin de diferenciar aquí las dos familias utilizamos en el ejemplo siguiente un color diferente para dibujar cada una, en el puzle todos los segmentos tendrán el mismo color.

Figura 14
Configuración de la familia de 5 segmentos horizontales:
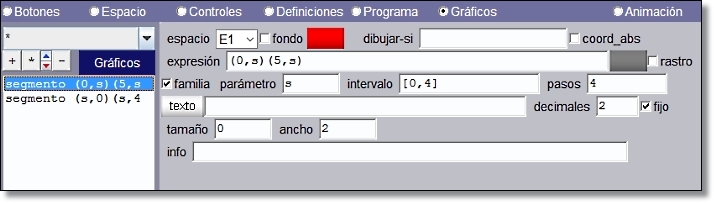
Figura 15
 |
|
Configuración de la familia de 6 segmentos verticales:
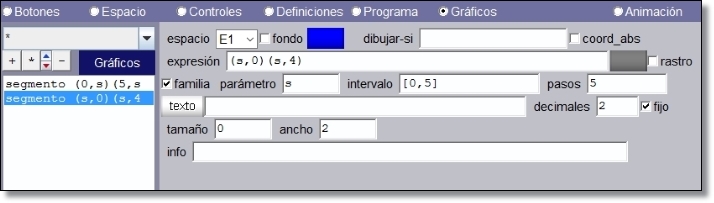
Figura 16
Esperamos haber facilitado con esta nueva edición de Técnicas y Trucos el aprendizaje a los que siguen el nivel básico y estimulado a todos los demás cartesianos para enfocar, con su propia técnica, la solución de los problemas abordados aquí.
Autoría:
Eduardo Barbero Corral (Proyecto y técnicas de programación)
Ángel Cabezudo Bueno (Interpretación, edición de la escena, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Más...
EDAD 4º ESO Opc. A Problemas aritméticos
Escrito por Alfonso Saura EspínEste mes vamos a ver un vídeo de 4ºESO Opción A, correspondiente a proporcionalidad:
En este vídeop hemos tratado los siguientes apartados:
1.Proporcionalidad directa e inversa
Proporcionalidad directa
Proporcionalidad inversa
Repartos proporcionales
Proporcionalidad compuesta
2.Porcentajes
Porcentajes
Aumentos y disminuciones
Porcentajes sucesivos
3.Interés simple y compuesto
Interés simple
Interés compuesto
Tasa anual equivalente (T.A.E.)
Capitalización
Incorporando construcciones Geogebra en escenas Descartes. Ejemplo 1: Ejecutando comandos Geogebra.
Escrito por Elena Álvarez SáizLa posibilidad de comunicar escenas Descartes con páginas html facilita incorporar resultados obtenidos de la ejecución de comandos Geogebra e incluso construcciones completas que pueden ser manipuladas desde la propia escena.
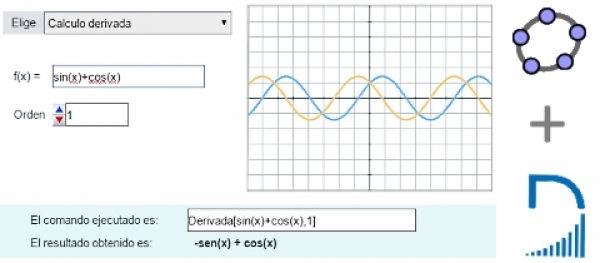
En este artículo se presenta una primera escena de ejemplo que utiliza los resultados de tres comandos Geogebra: Derivada, Integral y Circunferencia. Estos tres comandos tienen en común que su ejecución devuelve un único valor que puede enviarse a la escena Descartes como una cadena de caracteres. En próximos artículos se verá cómo incorporar los resultados de comandos que devuelven una lista de datos o una lista de listas.
Para poder comprender el código con el que se establece la comunicación desde Descartes, se recuerda la sintáxis de los comandos Geogebra que se utilizan en este ejemplo:
- Derivada[función,orden].
Por ejemplo: Derivada[cos(x),2] calcula la segunda derivada de la función cos(x)
- Integral[función,extremo_Inf,extremo_Sup].
Por ejemplo: Integral[cos(x),1,2] calcula la integral definida de la función cos(x) en el intervalo [1,2]
- Circunferencia[Punto1,Punto2,Punto3].
Por ejemplo: Circunferencia[(0,0),(1,1),(2,2)] calcula la ecuación de la circunferencia que pasa por los puntos A=(0,0), B=(1,1) y C=(2,2).
La escena Descartes que se presenta en este artículo incluye cuatro espacios.
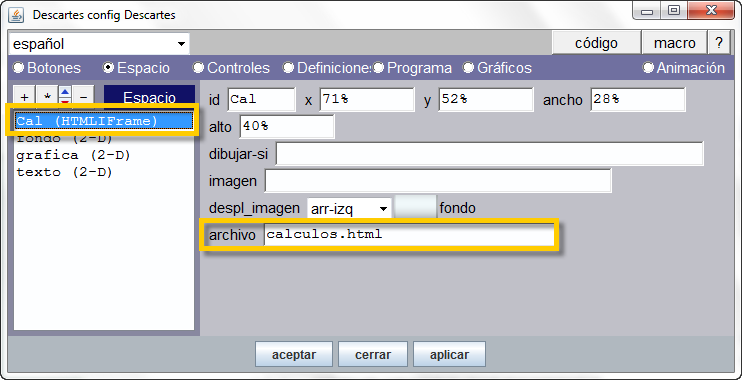
Uno de ellos es un espacio HTMLFrame que tiene como identificador el nombre Cal y será el que permitirá la comunicación con la página calculos.html que está vinculada a este espacio a través del parámetro 'archivo'.
La página calculos.html incluye el código javascript necesario para poder enviar y recibir datos de la construcción Geogebra que está embebida en ella. Esta página no necesita ser modificada y debe incorporarse en el mismo directorio que la página que contenga la escena Descartes (de no ser así se tendrá que modificar la ruta de acceso a ella en el parámetro 'archivo' del espacio HTMLFrame).
El funcionamiento de la escena Descartes que se presenta como ejemplo es sencilla. Elegida una de las tres opciones del menú, se inicia la comunicación con Geogebra. Si la opción elegida del menú es 'Calculo de la Derivada' se ejecuta la función Calculo1(), si se elige la opción 'Circunferencia por tres puntos' la función a ejecutar será Calculo2() y en el caso de que la opción sea 'Cálculo de la integral de un intervalo' la función asociada es Calculo3().
Las tres funciones tienen un código similar, en primer lugar construyen una cadena de caracteres con la sintásis del código Geogebra a ejecutar y después inician la comunicación enviando a la página incluida en el espacio Cal el evento 'evalua' pasándole como parámetro esta cadena de caracteres. Por ejemplo, el código incluido en la función Calculo1() es el siguiente:
n1='Derivada['+f+','+orden+']'
Cal.set('evalua',n1)
A la hora de generar la cadena de caracteres n1 se ha utilizado los valores de f y orden que están vinculados a los dos controles que se muestran en la escena para modificar, respectivametne, la expresión de la función y el orden de la derivada.
La página calculos.html, que está asociada al espacio Cal, recibe entonces el mensaje y ejecuta el código asociado al evento 'evalua' tras lo cual devuelve a la escena Descartes el resultado en una cadena de caracteres que siempre tiene por nombre vCalculado.
Todo este proceso es totalmente transparente al autor de la escena que puede utilizar el valor de la variable vCalculado de la misma forma que cualquier otra variable creada en la propia escena. Así, si por ejemplo se quiere representar la función derivada obtenida tras ejecutar Calculo1(), bastaría con:
- Evaluar la cadena de caracteres que se ha devuelto con el valor de la derivada: f1=_Eval_(vCalculado)
- Definir una función fun1(x)=f1 para poder crear un objeto gráfico de tipo ecuación cuya expresión sea: y=fun1(x)
Se puede practicar con la escena descargándola del siguiente enlace: Ejemplo1_CAS-JS.zip
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)









 CONTACTO
CONTACTO
