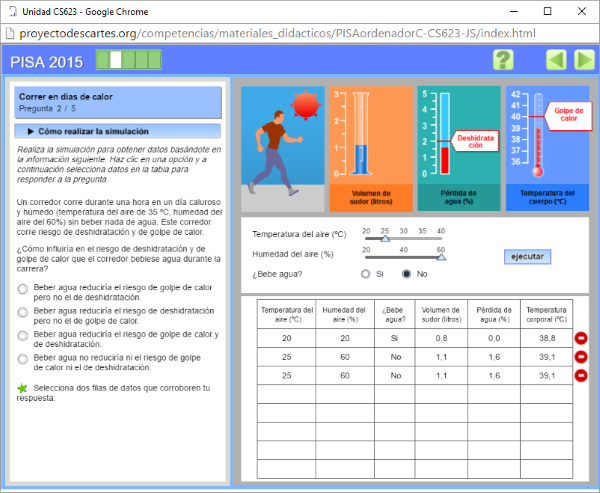
Este mes vamos a ver la siguiende unidad:
Hemos visto los siguientes puntos:
1. Vocabulario estadítico
Población, muestra, individuo y carácter
2. Carácter. Variable estadística
Carácter cualitativo. Atributos
Variables discretas
Variables continuas
3. Ordenación de datos. Tabulación
Para variable discreta
Para variable cualitativa
4. Gráficos para una variable cualitativa
Diagrama de barras
Diagrama de sectores
5. Gráficos para una variable discreta
Diagrama de barras
Polígonos de frecuencias
Diagrama de sectores
6. Medidas de centralización
Media
Mediana
Proporcionalidad. Las Espirales IX. Lugares Geométricos
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales IX
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destaca el subproyecto TELESECUNDARIA.
En palabras del encargado de la presentación del subproyecto en el Blog, Ángel Cabezudo Bueno, "Telesecundaria es una modalidad de los estudios de educación secundaria en el Sistema Educativo de México dirigido a estudiantes adolescentes de 12 a 15 años que viven en comunidades dispersas que carecen de escuela de secundaria.
Se utilizan para ello los avances en tecnologías de la información y comunicación (TIC) como recurso para acercar esta formación a los jóvenes y puedan concluir su educación básica.
En este subproyecto de RED Descartes se han recogido objetos de la Telesecundaria desarrollando los correspondientes materiales con la herramienta Descartes. Las asociaciones de Colombia y España han sido las encargadas de preparar la adaptación a DescartesJS y en consecuencia todos podrán ser consultados en cualquier dispositivo con sistema operativo que admita un navegador compatible con HTML5." los primeros materiales pueden verse y descargarse siguiendo el enlace gráfico siguiente.
Dentro de nuestro ámbito local queremos destacar, entre otros, los siguiente materiales:
- Todos los creados para el subproyecto COMPETENCIAS. Debido a la creciente internacionalización de nuestro sistema educativo, progresiva integración en la comunidad europea, conviene que la manera de evaluar competencias en los ámbitos externos sea conocido con objeto de participar en igualdad de condiciones. Un acercamiento a estos procedimientos lo ofrecen los materiales del proyecto Competencias.
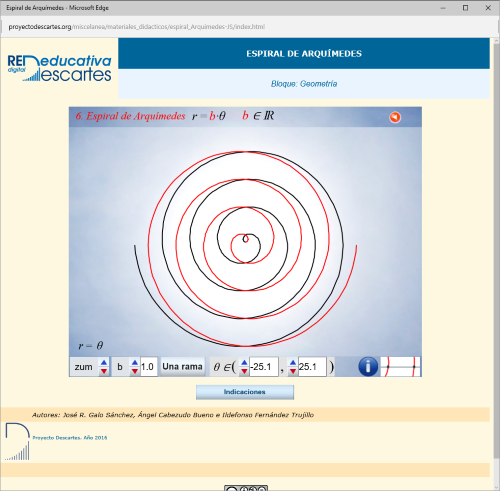
- La Miscelánea sobre la espiral de Arquímedes que sigue la corriente de mostrar los conceptos complicados, composición de movimientos, mediante la visualización del hecho de forma que es posible intervenir en la escena modificando los parámetros que la definen, con lo que la comprensión del concepto se facilita sobremanera, por lo tanto la miscelánea que se presenta es, por derecho propio, un objeto educativo lúdico e interactivo con un potencial formativo sobresaliente; no obstante en esta ocasión queremos enfocar el proceso de creación de la espiral desde el punto de vista de la definición de un lugar geométrico.
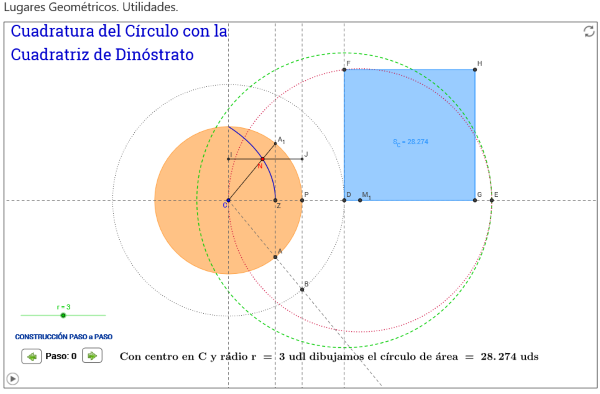
La miscelánea anterior muestra, paso a paso, la creación de un lugar geométrico (l.g.) por un punto que se mueve linealmente en un segmento mientras este gira alrededor de uno de sus extremos. Existen otros muchos lugares geométricos, entre los clásicos y más conocidos destaca la Trisectriz de Hipias que junto con la espiral de Arquímedes se ha usado, además de para otras utilidades, para la trisección de cualquier ángulo. A la Trisectriz de Hipias también se la llama Cuadratriz de Dinóstrato debido a que este geómetra usó el l.g. para la cuadratura del círculo. La Trisectriz (o Cuadratriz) es el l.g. generado por el punto común a dos segmentos uno de los cuales gira alrededor de uno de sus extremos y el otro se desplaza horizontalmente según muestran las siguientes escenas:
- La Trisectriz de Hipias que muestra, mediante una animación, la definición de la curva
- La trisección de un ángulo mediante la Trisectriz de Hipias. También se basa en una animación, en la primera parte se dibuja la curva y a continuación se muestra y explica, de forma dinámica, la trisección de un ángulo. La animación puede detenerse/reanudarse en cualquier instante.
- La cuadratura del círculo mediante la Cuadratriz de Dinóstrato (Primera Parte). Esta escena se basa en un pulsador que muestra, según se pulsa, la explicación del proceso para cuadrar el círculo. También tiene una animación que vuelve a construir la curva. La animación puede activarse/detenerse en cualquier instante.
Conviene analizar las escenas anteriores, reproducirlas y/o mejorarlas y ver la forma de integrarlas en la miscelánea sobre las espirales.
En próximas entradas en el Blog completaremos el estudio de uso de la Cuadratriz y veremos la manera de trisecar un ángulo y cuadrar el círculo con la espiral de Arquímedes.
En esta ocasión, en la sección de vídeo, hemos elegido uno muy particular que muestra la manera de dibujar la Trisectriz de Hipias (Cuadratriz de Dinóstrato) con ¿regla y compás? con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa. Buscando en internet se pone de manifiesto el enorme interés que suscitan, aún hoy en día, los problemas clásicos de la Geometría Griega.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Fermat" tal y como anunciamos en artículos anteriores.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Fermat
- Inclusión del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Y desde este enlace descargar el proyecto con la espiral de Fermat incluida.
También, relacionado con el tema de los lugares geométricos (l.g.) y sus utilidades hemos incluido dos trabajos, realizados con el programa GeoGebra, uno muestra el uso de la espiral de Arquímedes para la trisección de un ángulo y en el otro, enlazado en la imagen que sigue a la trisección, se lleva a cabo la cuadratura de un círculo de forma dinámica.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Bibliografía.- Para la realización de esta entrada y siguientes ha sido de gran ayuda la siguiente información:
- El trabajo sobre las TRISECTRICES de Pedro González Enríquez.
- Cuadratura de un círculo con la Cuadratriz de Dinóstrato
- Cuadratura de un círculo
Ildefonso Fernández Trujillo. Blog ReDescartes 2016
Hoy presentamos dos actividades de iniciación a las ecuaciones pertenecientes a Telesecundaria, un nuevo subproyecto de la Red que contiene una serie de objetos de aprendizaje interactivos con contenidos de matemáticas, física y química para secundaria. Han sido desarrollados en México con la herramienta Descartes para la modalidad educativa de este país que se denomina Telesecundaria.
Accedemos a la página web de este proyecto desde el apartado subproyectos del blog de la Red.
En este caso hemos seleccionados dos unidades para introducir las ecuaciones que pueden ser aplicables en los primeros cursos de secundaria. Se trata de ecuaciones sencillas con las operaciones de suma, resta, multiplicación y división.
En los ejercicios propuestos, el alumnado debe calcular el valor de la incógnita realizando la operación contraria a la propuesta en la ecuación. Se trata de actividades autocorrectivas ya que, una vez escrita la solución en la escena, se muestra el resultado y se puede comprobar si la respuesta es correcta o no.
En el siguiente vídeo también se propone la inserción de estas actividades en un blog didáctico, aunque el procedimiento sería similar en el caso de utilizar una wiki, una página web, un curso moodle o cualquier otro espacio virtual que disponga de la opción de editar en formato html.
Este mes vamos a ver la unidad de Estadística de 4ºESO Opción B:
En este unidad se tratan los siguientes apartados:
1.Estadística descriptiva
Población y muestra.
Variables estadísticas.
Gráficos v. cualitativas.
Gráficos v. c. discretas.
Gráficos v. c. continuas.
2.Medidas de centralización
Media, moda y mediana.
Evolución de la media.
Evolución de la mediana.
Media y mediana comparadas.
Medidas de posición.
3.Medidas de Dispersión
Desviación típica y recorrido.
Calcula las medidas de dispersión.
La media y la desviación típica.
4. Representatividad
Muestreo estratificado.
Muestreo aleatorio. Sesgo.
Más...
Escenas con DescartesJS: Técnicas y trucos (M05)
Escrito por Ángel Cabezudo Bueno
Una cualidad muy importante de la herramienta Descartes es que nos permite elaborar nuevas escenas, modificando otra que ya es funcional, con el objeto de conseguir diferentes resultados: cambiando, añadiendo o eliminando el correspondiente código mediante los paneles de configuración del Editor de Escenas. No se descarta la intervención directa sobre el código HTML en el archivo que contiene la escena, con un editor de texto externo tipo Bloc de notas o Notepad++. Otras veces el cambio de la escena es producido sin alterar el código, simplemente al cambiar los archivos de contenido multimedia que acompañan. Esta es la forma habitual de proceder de los desarrolladores de escenas de Descartes. En este artículo tratamos precisamente como llevar a cabo todo esto.
Contenidos que se abordan
- Basándonos en la escena M04 del puzle 2x2 de arrastre con efecto imán, que desarrollamos en el artículo precedente vamos a elaborar nuevos puzles de tamaño 3x3.
- Después produciremos un determinado número de puzles 3x3 obtenidos a partir del primero utilizado de modelo: todos ellos tienen en común el mismo código de la escena, pero difieren en el conjunto de piezas para montar un puzle particular.
Proyecto para visualizar de forma selectiva una colección de puzles ![]()
- Reuniremos todos los puzles en un mismo proyecto que será gestionado desde otra escena que llamaremos principal. Esta escena principal facilita que podamos seleccionar a voluntad desde un determinado espacio R2 los diferentes puzles que hemos producido para tal fin. Tendremos ocasión de conocer la opción Librería de proyecto del Gestor de Escenas y el espacio HTMLIframe, que es común, donde se visualizan los puzles.
Autoría
- La adaptación de un puzle 2x2 a puzle 3x3 es una propuesta de Eduardo Barbero Corral. Aparte de hacer los cambios propios para redimensionar el puzle y tener en cuenta ahora las 9 piezas en vez de 4, se dan nuevas instrucciones para la detección de piezas montadas (superpuestas) y para controlar las acciones cuando el puzle ha sido armado correctamente.
- La idea de utilizar un espacio HTMLIframe donde presentar las diferentes escenas de los puzles procede de un documento instructivo redactado por nuestro maestro cartesiano Juan Guillermo Rivera Berrío
- La interpretación de estas fuentes, la selección de las imágenes para cada uno de los puzles, la elaboración de las piezas, la edición de las escenas y finalmente la redacción de este artículo es de Ángel Cabezudo Bueno.
Enlaces a los artículos precedentes de esta serie
Dejamos los enlaces a los artículos anteriores por si alguien necesita repasar algún detalle de procedimiento que en este obviamos:
- Escenas con DescartesJS: Técnicas y trucos (B01) – Situar puntos en el plano cartesiano
- Escenas con DescartesJS: Técnicas y trucos (B02) – Identificar nombres en una imagen
- Escenas con DescartesJS: Técnicas y trucos (B03) – Distribución de nombres en un mapa
- Escenas con DescartesJS: Técnicas y trucos (M04) – Puzle de arrastre con efecto imán
Idea del proyecto
|
Escena_M05: Adaptación de escenas. Librería de proyecto. Espacios HTMLIframe Se trata de modificar esta escena, motivo del artículo anterior (la Figura 1 lleva un enlace) Figura 1 Por esta otra (la Figura 2 lleva enlace a la nueva escena) Figura 2 Cuando se superponen dos piezas y también cuando el puzle ha quedado armado debe de indicarse mediante sendos mensajes de texto. También, este segundo caso tendrá que ir acompañado de una señal acústica.
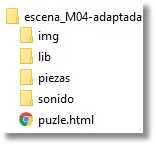
La nueva estructura de carpetas es la que se muestra en la figura 5
Figura 5 La carpeta piezas contiene 9 archivos: 1.jpg, 2.jpg,.. , 9.jpg.
|
|
La figura muestra el caso para el listado del panel Controles que es similar al de los demás.
Figura 6
Figura 7
Figura 8 En esta ventana es posible seleccionar un bloque de elementos, por ejemplo desde g1 a g4 inclusive, copiarlos con ctrl+C, abrir una línea después de g4 y pegarlos con ctrl+V; a continuación se puede modificar uno a uno los elementos de la copia. |
||||||||||
Transformaciones que producen la adaptación del puzle 2x2 al puzle 3x3
Es fundamental repasar las explicaciones que se dieron para elaborar la escena 2x2 del artículo anterior y entender bien el significado de los auxiliares que se utilizaron:
- c1, c2, c3, c4: toman el valor 1 cuando la correspondiente pieza está casi colocada en una casilla, no necesariamente la correcta. Así p.e., c1=(g1.x<0)*(abs(g1.x-ent(g1.x)-0.5)<0.05)*(abs(g1.y-ent(g1.y)-0.5)<0.05)
- s12, s13, s14, s23, s24, s34: toman valor 1 cuando están montadas la pareja de piezas que indican los subíndices. P.e en
s12=c1*c2*(ent(g1.x)=ent(g2.x))*(ent(g1.y)=ent(g2.y)) las piezas 1 y 2 está encajadas en una casilla c1=c2=1 y además sus posiciones coinciden.
- montadas = s12+s13+s14+s23+s24+s34 vale 0 si ninguna pieza está montada. Si al menos un sumando vale 1 hay piezas montadas.
- armado, vale 1 si todas las piezas están encajadas en su corresopondiente casilla. Así p.e. la pieza 1 debe de encajarse en la casilla cuyo vértice superior izquierda es (-2,1) y en consecuencia (ent(g1.x)=-2)*(ent(g1.y)=1) tiene que vale 1. Cada pieza bien encajada se evalúa a través de una expesión similar a la anterior y armado se define como el producto de las cuatro expresiones.
En la adaptación al puzle 3x3 se ha cambiado la lógica y no se utilizan las expresiones s12, s13, ... En su lugar, Eduardo Barbero Corral, propone una definición de los auxiliares p1, p2, p3,.., p9, de tal manera que cada casilla queda identificada por un número diferente y las expresiones para montadas y armado vienen dadas como veremos más adelante en función de estos nuevos auxiliares.
La escena ya adaptada se puede descargar desde aquí y verificar las trasformaciones que se explican a continuación.
| 1. |
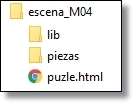
Creación de la carpeta escena_M04-adaptada Simplemente se copia la carpeta escena_M04 que puede descargarse desde aquí y se renombra. |
||
| 2. |
Creación de las subcarpetas img y sonido Se incorporan a las mismas los archivos correspondientes. |
||
| 3. |
Sustitición de las imagenes en la carpeta piezas Las nuevas imagenes se denominan segun el lugar (fila, columna) que ocupan en la cuadrícula, 1.jpg para la casilla (1,1), 2.jpg para la (1,2),... , 9.jpg para la (3,3). Se obtienen troceando una imagen de 450x450 píxeles con alguna herramienta específica. En el artículo anterior explicábamos como se hace con PhotoScape 3.7. Las piezas o trozos obtenidos tienen el tamaño 150x150px. Para la elaboración de este artículo hemos elegido el tema de animales y en particular la adaptación del puzle 2x2 a 3x3 que estamos explicando se basa en la imagen de una ardilla. |
||
| 4. |
Actuaciones en el Gestor de Escenas Configuración: Cambiar las dimensiones a 800x510 Espacio: Escala 150 (no cambia), O.x=80, O.y=225, Imagen de fondo img/fondo.jpg, despl_imagen='expand.' Se expande dado que la imagen tiene menor tamaño que el espacio que debe ocupar. Controles: Eliminar el control de Inicio. La adaptación de esta escena está orientada a poder formar parte de una colección de puzles dentro del mismo proyecto. Cada puzle podrá ser seleccionado y por tanto iniciado de otra forma. Añadir g5,…, g9, g5.x, g5.y,… , g9.x, g9.y y mantener separada cada agrupación de controles. Modificar los valores min y máx de los controles numéricos para acomodarlos al nuevo tamaño del espacio. Desplazar finalmente los controles añadidos a la posición correcta en el listado segun el grupo al que pertenezca (Ver figura 9) 'g1.x' expresión='(0,0,0,0)' valor='rnd+0.6' min='-3.3' max='2.3' antes era min=’ -2.3’ y max=’2.3’
Figura 9 Gráficos Imágenes: Añadir las piezas 5.jpg a 9.jpg (para reducir esfuerzos se puede utilizar las herramientas de gestión del listado similar a Controles, copiando una imagen ya existente y modificando nombres). Cambio de las dimensiones del tablero:
Imagen: dibujar-si='armado', expresión='(1.1, 2, 0.5, 0.5)', archivo='img/feliz.png’
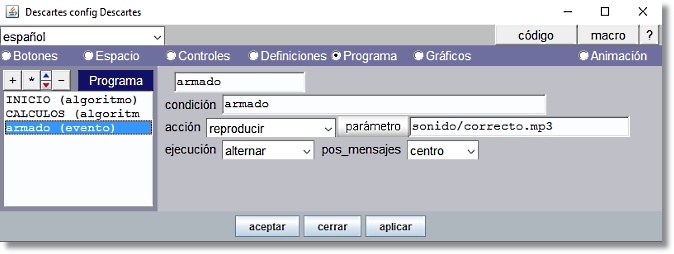
Programa
Figura 11
p1=c1*(ent(g1.x)+10*ent(g1.y)) Si cada pieza ocupa su posición correcta se obtiene un valor diferente para cada expresión: p1=17, p2=18, p3=19, p4=7, p5=8, p6=9, p7=-3, p8=-2, p9=-1 montadas=c1*((p1=p2)+(p1=p3)+(p1=p4)+(p1=p5)+(p1=p6)+(p1=p7)+(p1=p8)+(p1=p9))+c2*((p2=p3)+(p2=p4)+(p2=p5)+(p2=p6)+(p2=p7)+(p2=p8)+(p2=p9))+c3*((p3=p4)+(p3=p5)+(p3=p6)+(p3=p7)+(p3=p8)+(p3=p9))+c4*((p4=p5)+(p4=p6)+(p4=p7)+(p4=p8)+(p4=p9))+c5*((p5=p6)+(p5=p7)+(p5=p8)+(p5=p9))+c6*((p6=p7)+(p6=p8)+(p6=p9))+c7*((p7=p8)+(p7=p9))+c8*(p8=p9) armado=(p1=17)*(p2=18)*(p3=19)*(p4=7)*(p5=8)*(p6=9)*(p7=-3)*(p8=-2)*(p9=-1)
evento='sí', condición='armado', acción='reproducir', parámetro='sonido/correcto.mp3', ejecución='alternar'
|
|
Proyecto para visualizar de forma selectiva una colección de puzles Nuestro objetivo ahora es reunir una colección de puzles similares al adaptado en escena_M04-adaptada y utilizar un espacio HTMLIframe de DescartesJS donde poderlos visualizar de una forma selectiva y controlada. Puede resultar interesante para algún propósito educativo reunir una colección de puzles que trate un mismo tema, por ejemplo “animales”. Una vez elaborado un puzle con la imagen de cierto animal, como la ardilla, es muy sencillo transformarlo en otro puzle con diferente imagen, ya que bastaría tomar una imagen del mismo tamaño 450x450 píxeles y trocearla en 9 cuadrados de 150x150px con la misma numeración 1.jpg, 2.jpg,.. 9.jpg que reemplazarían las correspondientes de la ardilla. Los distintos puzles así obtenidos los guardaríamos en carpetas con nombres diferenciados: puzle1, puzle2, puzle3,… Como cada puzle va a ser consultado desde una misma escena, es conveniente que el mismo interprete descartes-min.js se comparta con lo que se ahorra espacio. Tiene sentido hablar de Librería de proyecto y que otorguemos esta categoría a dicho intérprete. Basta sacarlo de cada carpeta en los diferentes puzles, eliminando la carpeta lib y situando esta al mismo nivel que las carpetas de aquellos. La estructura de carpetas del proyecto sería como la mostrada en la figura 15
Actuaciones sobre los archivos puzle.html Tenemos que cambiar la referencia al lugar que ahora ocupa el intérprete descartes-min.js: Donde dice: <script type='text/javascript' src='lib/descartes-min.js'></script> hay que escribir <script type='text/javascript' src='../lib/descartes-min.js'></script> Ya que la carpera lib está situada ahora fuera de la carpeta que contiene el puzle, un nivel por encima. Esto se puede hacer modificando directamente cada archivo con un editor de texto plano o bien abriéndolo a través del Gestor de Escenas de Descartes, seleccionando la opción Librería de proyecto > solo para JS y guardando, sin más que hacer.
La Figura 18 lleva un enlace al proyecto resultante Figura 18 Interaccionar con la escena y observar los resultados facilita la comprensión del objetivo del proyecto. |
Actuaciones en el Gestor de Escenas
Accedemos al Gestor de Escenas, Descartes.jar. Por defecto obtenemos una escena dimensión 970x550 píxeles con la opción Librería Portable solo para JS. Esta opción es la que nos interesa ahora para la escena que debe contener el archivo index.html según la estructura mostrada en la Figura 15. Abramos el Editor de Escenas para proceder a configurarla.
- Redimensionado de la escena
En primer lugar, abrimos la ventana del código, pulsando el botón código desde cualquiera de los paneles de configuración (por defecto al abrir el Editor de escenas está activo el panel de Espacio).
La dimensión de la escena debe de llevar los valores width=970 y height=610
- Panel Botones
Desmarcar los cuatro botones créditos, config, inicio y limpiar
- Panel Espacio
El espacio por defecto E1 (2-D) lo ocupa todo y lleva por fondo la imagen imagenes/fondo2.jpg que debe expandirse pues el tamaño de esta es menor que el del espacio.
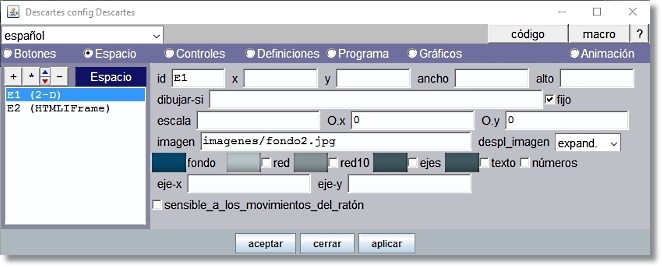
Figura 19
Desmarcar la red, los ejes, el texto y los números.
Se añade el espacio E2 (HTMLIframe) y queda superpuesto a E1.
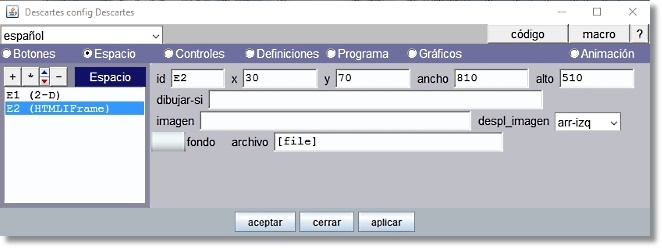
Figura 20
 |
Los espacios HTMLIframe permiten la visualización de todo el contenido incluido en un fichero html. Los parámetros en este tipo de espacio pueden consultarse con más detalle en la documentación técnica sobre Espacios HTMLIframe |
Observar que el ancho 810 píxeles y alto 510 píxeles coincide con la dimensión de la escena de cada puzle que tiene que ser representada en este espacio.
Situamos el comienzo de la representación en x=30 píxeles (distancia al borde izquierdo de E1) y en y=70 píxeles (distancia al borde superior de E1). Es decir hemos dejado un margen lateral de 30 píxeles y un margen en la cabecera donde situar en otro momento el título de la escena “PUZLES DE ANIMALES”
Obsérvese que nos queda a la derecha un margen de representación para E1 de 970 – (810 +30) = 130 píxeles con suficiente holgura para situar los controles de botón rotulados como Puzle1, Puzle2, Puzle3,…
El margen al pie de E1 es 610-(70+510) = 30 píxeles donde se escribirá el nombre del animal cuya imagen representa el puzle seleccionado. (ver Figura 18)
El parámetro archivo lleva la expresión [file], file es una variable que en todo momento contiene la trayectoria al archivo puzle.html que ha sido seleccionado. [file] explicita el contenido actual de la variable file.
La figura 21 muestra la escena tal como se ve en el Editor de escenas hasta este momento de la configuración
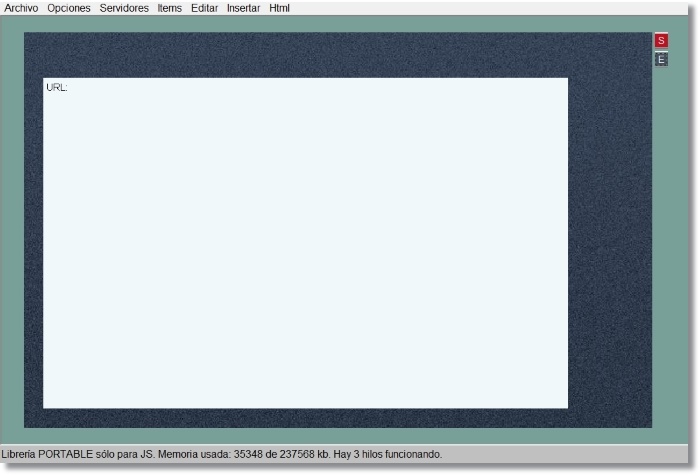
Figura 21
- Panel Controles
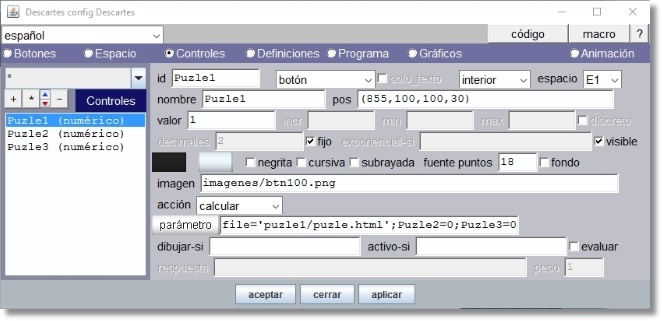
Figura 22
Este panel lleva los controles de botón identificados respectivamente como Puzle1, Puzle2, Puzle3,… tantos como puzles tengamos en la colección, en este caso son tres.
Consultar documentación Imágenes en controles numéricos tipo botón.
El nombre o rótulo que lleva el botón se ha hecho coincidir con el identificador.
La expresión de posición pos=’(855,100,100,30)’ para Puzle1 se ajusta al formato (x,y,w,h) donde x= distancia (píxeles) al borde lateral izquierdo de E1, y= distancia al borde superior de E1, w= ancho del botón, h=alto del botón.
Para Puzle2, y=150 y para Puzle3, y=200. Vamos desplazando 50 píxeles hacia abajo los sucesivos botones.
Valor = 1 es el valor que toma la variable identificada por Puzle1, Puzle2, Puzle3,… cuando se pulsa el botón correspondiente.
El texto del rótulo lleva formato: se escribe con color de relleno y borde y se selecciona un valor (18 puntos) para la fuente.
El archivo imágenes/btn100.png se utiliza en lugar del botón y coincide en tamaño. En la misma carpeta imagenes hay otras dos con el mismo nombre seguido de “_over” y “_down” , en este caso estás imágenes aparecerán en vez de btn100.png cuando el cursor del ratón se encuentra sobre el botón o cuando se pulsa respectivamente.
La acción “calcular” se realiza cuando el botón es pulsado y el parámetro contiene las tres asignaciones separadas por ; que se ejecutan: file='puzle1/puzle.html'; Puzle2=0; Puzle3=0. Las asignaciones para el botón Puzle2 son file='puzle2/puzle.html'; Puzle1=0; Puzle3=0 y para Puzle3, file='puzle3/puzle.html'; Puzle1=0; Puzle2=0.
- Panel Programa
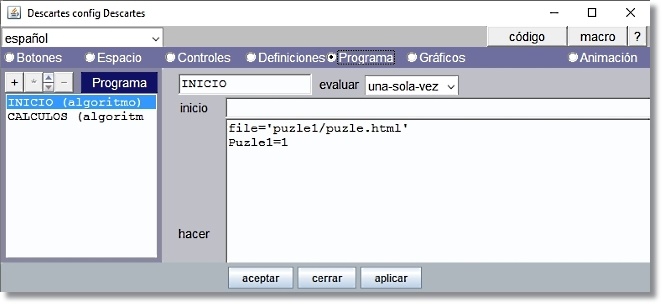
Figura 23
El algoritmo INICIO establece los valores cuando se inicia la escena. Establece que puzle debe de visualizarse al inicio asignando file='puzle1/puzle.html' y Puzle1=1.
El algoritmo CALCULOS (añadido por defecto a Programa) no se utiliza y puede eliminarse.
- Panel Gráficos
Añadimos cuatro elementos gráficos tipo texto. El primero para poner título a la escena “PUZLES DE ANIMALES” en el espacio de cabecera
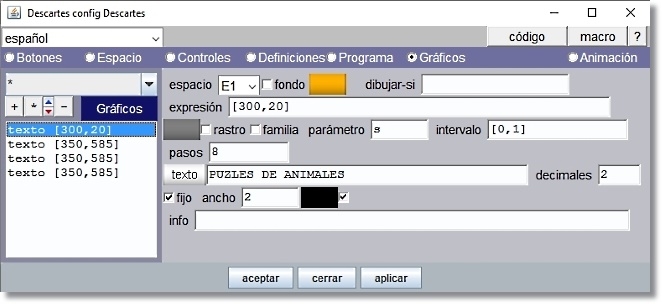
Figura 24
El color de relleno del texto (fondo) es ‘ffa800’ sin trasparencia. Lleva formato Texto simple, tipo de letra SansSerif, negrita, 28 ptos y borde negro.
Los restantes tres textos sirven para informar en el pie de la escena el puzle que se ha seleccionado y el nombre del animal representado en la imagen.
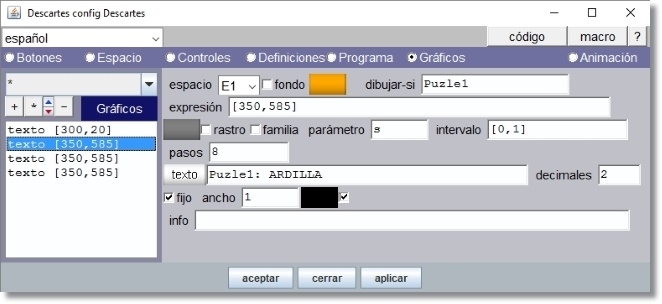
Figura 25
El color de relleno del texto (fondo) es ‘ffa800’ sin trasparencia. Lleva formato Texto simple, tipo de letra SansSerif, negrita, 18 ptos y borde negro.
La diferencia entre estos tres textos está en el identificador que lleva dibujar-si y en el texto que se escribe.
Autoría:
Eduardo Barbero Corral (Programación de la adaptación al puzle 3x3)
Ángel Cabezudo Bueno (Interpretación, elaboración de las escenas, ilustraciones y redacción)
Este material está publicado bajo una licencia:
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional
Proporcionalidad. Las espirales VIII
Escrito por Ildefonso Fernández TrujilloProporcionalidad. Las Espirales VIII
Entre las innovaciones producidas en el ámbito de colaboración de la Red Educativa Digital Descartes destacan las aportadas por la Red Educativa Digital Descartes Colombia (colDescartes) y la Red Educativa Digital Descartes España que, coordinadas por el profesor Juan Guillermo Rivera Berrío, han añadido al subproyecto GEOgráfica una importante cantidad de contenidos, lo que ha hecho necesario dividir el subproyecto inicial en varios subproyectos: GEOcapital, GEOdiver, GEOcolor y GEOevaluación (en estado muy avanzado), estando en fase de desarrollo los de: GEOmontañas y GEOrios, los tres primeros pueden verse y descargarse siguiendo el enlace gráfico siguiente.
El carácter evaluativo - formativo de estas unidades es extraordinario según se manifiesta en la escena anterior y en las que enlazamos a continuación.
También cabe señalar el desarrollo de todo un nuevo subproyecto "PLANTILLAS CON DESCARTES-JS que proporciona herramientas para la creación de contenidos lúdico-didácticos."
Dentro de nuestro ámbito local destacan, entre otras muchas, las siguientes aportaciones:
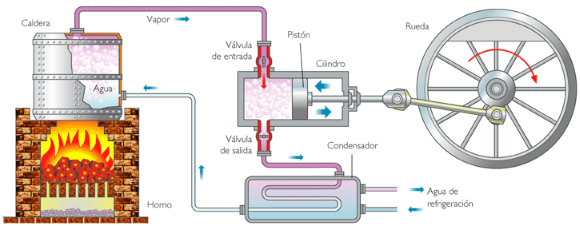
- Dos libros digitales e interactivos en el apartado de Física y Química del subproyecto iCartesiLibri: Teoría de la relatividad y Máquinas térmicas.
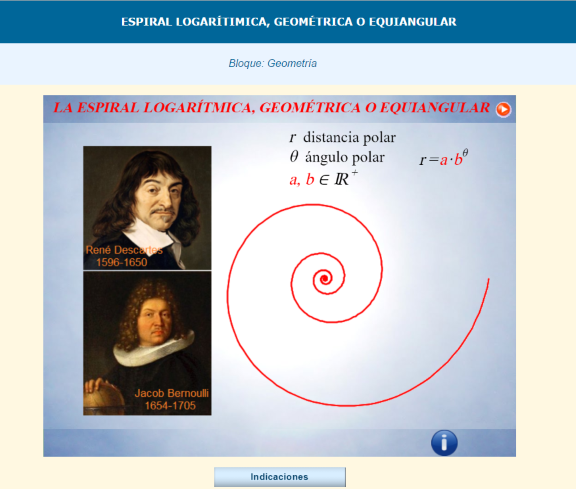
- La sorprendente y hermosa Miscelánea La espiral Logarítmica
- Dentro del subproyecto "Unidades Didácticas" la extensa e instructiva unidad Puzles Descartes que dota a la creación de escenas con el editor DescartesJS de una herramienta versátil y potente para la elaboración de objetos educativos lúdicos e interactivos.
- La Miscelánea sobre la espiral de Arquímedes que sigue la corriente de mostrar los conceptos complicados, composición de movimientos, mediante la visualización del hecho de forma que es posible intervenir en la escena modificando los parámetros que la definen, con lo que la comprensión del concepto se facilita sobremanera, por lo tanto la miscelánea que se presenta es, por derecho propio, un objeto educativo lúdico e interactivo con un potencial formativo sobresaliente.
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra la manera de dibujar la espiral áurea con regla y compás con objeto de apreciar diferentes formas de enfocar el tema que nos ocupa.
Continuando con la creación de la miscelánea "Las Espirales" hemos añadido al menú de tipos de espiral una nueva opción: "la espiral de Fibonacci" tal y como anunciamos en el artículo del mes pasado.
En esta ocasión hemos procedido de la siguiente manera:
- Hemos creado la siguiente escena: Espiral de Fibonacci
- Inclusión del código de la escena anterior en el de la miscelánea en proyecto.
La escena del proyecto puede verse a continuación:
Desde este enlace puede descargarse el proyecto de miscelánea con la espiral de Fibonacci incluida.
También, relacionando, mediante el programa GeoGebra, la espiral con el Fenaquistiscopio, quisiera enlazar el siguiente trabajo de Nicolas Erdrich.
En próximas entradas continuaremos con el paso a paso de la escena incluyendo nuevas espirales entre sus funcionalidades y analizando el subproyecto Misceláneas.
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)









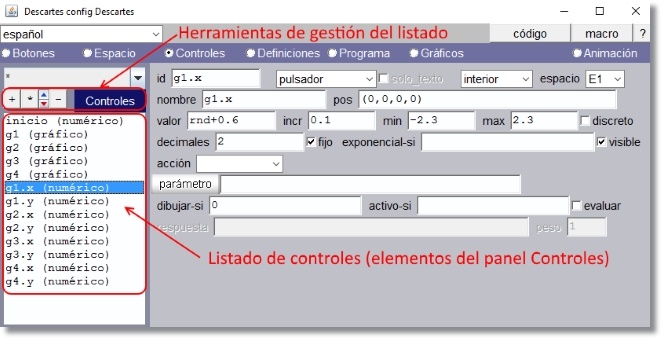




 a ventana con la lista de controles hasta ese momento añadidos con sus definiciones que pueden ser editadas como en un editor de texto (ver Figura 7)
a ventana con la lista de controles hasta ese momento añadidos con sus definiciones que pueden ser editadas como en un editor de texto (ver Figura 7)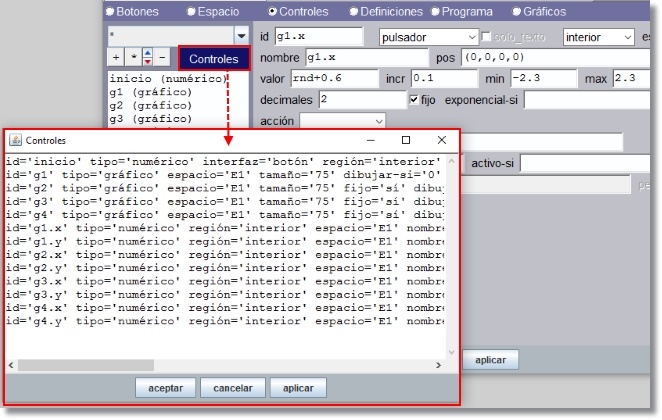
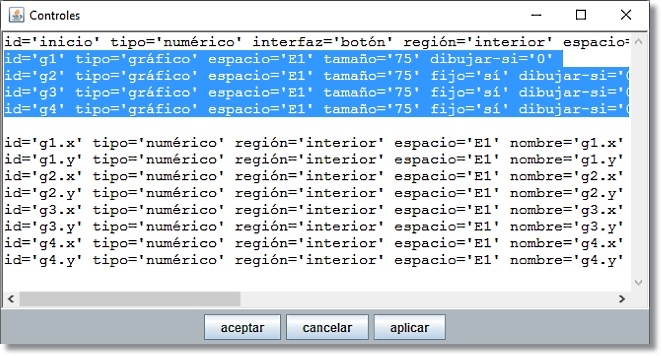
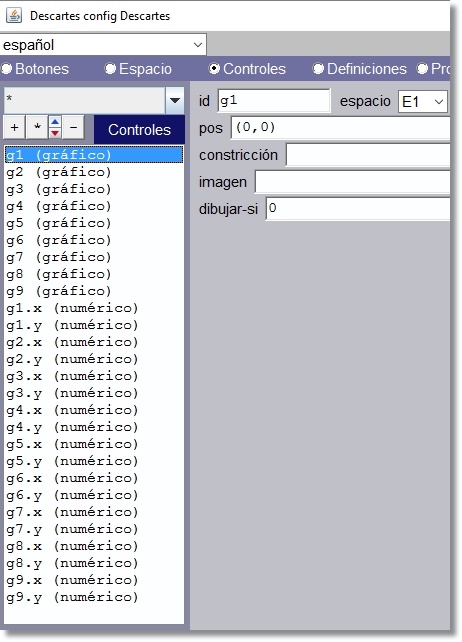

 Figura 10
Figura 10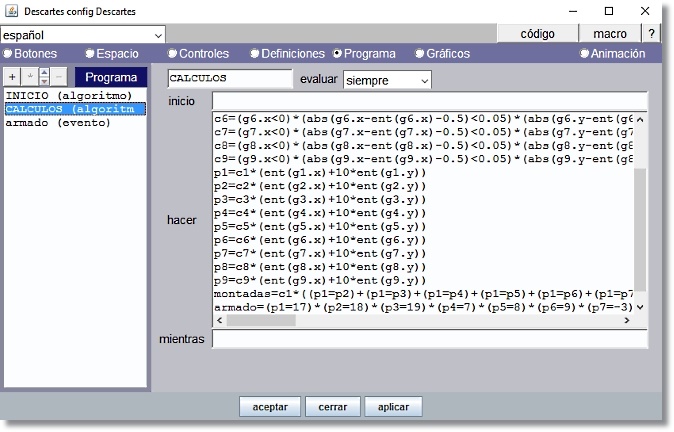
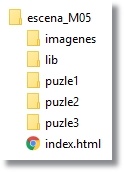
 El archivo index.html lleva la escena que controla la visualización de cada uno de los puzles en un único espacio HTMLIfame que enseguida pasaremos a explicar.
El archivo index.html lleva la escena que controla la visualización de cada uno de los puzles en un único espacio HTMLIfame que enseguida pasaremos a explicar.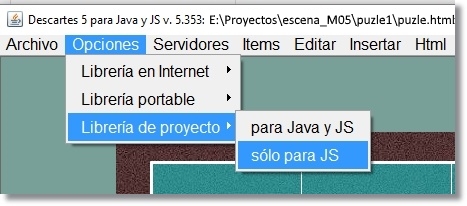






 CONTACTO
CONTACTO
