- La adaptación del juego a las características de los alumnos.
- El número de jugadores y la forma en que intervienen el resto de participantes (público, presentadores, organizadores, guionistas, colaboradores, etc).
- La dinámica (concurso TV, deporte, clásico, nueva creación...) y la compresión de las reglas.
- La cantidad de preguntas necesarias y la clase de respuesta.
- La forma de introducir los contenidos (fichero, oral, directa, específicos o sin preguntas).
- Los recursos necesarios y la adecuación a la puesta en escena.
- La selección del idioma que se va a utilizar
- Las reglas y dinámica del juego deben de poder ser comprendidas y seguidas por los participantes.
- El grado de motivación que el juego genere entre los participantes.
Conocí a Mary Cartwright gracias a mis alumnas. ¿Y tú?
Escrito por José Antonio Salgueiro GonzálezDurante los dos cursos académicos en los que vengo desarrollando el proyecto "La radio ficción en el aula de Matemáticas", con mi alumnado de 3º ESO en el IES Bajo Guadalquivir de Lebrija, no he dejado de sorprenderme por su creatividad, imaginación, capacidades ocultas y habilidades para superar retos y obstáculos tecnológicos. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
Pues bien, en este sencillo y escueto artículo veraniego deseo compartir todo lo que he aprendido de mis alumnas Clara, Ángela y Cristina, que me han presentado aspectos relevantes de la vida y obra de una matemática británica completamente desconocida para mí, dejando constancia pública de cómo los docentes podemos aprender de los discentes.
A lo largo de este proyecto, que no deja de proporcionarme satisfacciones, se han publicado los siguientes artículos:
- La radio ficción en el aula de Matemáticas, que incorpora la entrevista ficticia al ilustre y prolífico matemático Leonhard Euler.
- Entrevistamos a Euclides en 3º ESO, para dar a conocer la vida y obra del autor de los Elementos.
- Alumnas de 3º ESO entrevistan a Mary Somerville.
- Évariste Galois visto e interpretado por alumnos de 3º ESO
También puedes conocer los antecedentes de la iniciativa consultando el artículo titulado "La ficción de Radio Descartes en el programa Boulevard de Radio Euskadi".
Proyecto Canals. Actividades para los más pequeños.
Escrito por Montserrat Gelis BoschEn el vídeo de esta semana, se presenta una pequeña muestra de actividades interactivas de iniciación a diferentes conceptos matemáticos. Se trata de actividades adecuadas para los alumnos de infantil.
Estos objetos interactivos forman parte del Proyecto Canals, una serie de objetos didácticos para infantil y primaria que han sido creados a partir de materiales elaborados por la profesora Maria Antònia Canals.
En concreto, se trata de las siguientes actividades:
El sistema métrico decimal, ¡a la vista!
Escrito por José Antonio Salgueiro GonzálezNuestro alumnado suele manejar con soltura la conversión de unidades del sistema métrico decimal, con una estrategia didáctica tradicional y efectiva como es "la escalera". No obstante, en más de una ocasión, durante la resolución de problemas, nos podemos encontrar con que la solución aportada no sea coherente. Así, durante el curso 2017/2018, nos hallábamos resolviendo problemas aplicados a la estimación y medida de longitudes, capacidades y pesos extraídos del libro interactivo del Proyecto ED@D, cuando se produjo una propuesta de solución completamente desafortunada y distante de la realidad, originándose al momento lo que, en mi opinión, enriquece el proceso de enseñanza y aprendizaje, es decir, el debate en el aula.
Como "es aconsejable utilizar juegos matemáticos y materiales manipulativos para que el alumnado aprenda haciendo, construyendo y «tocando las matemáticas»", pensé que había llegado el momento de diseñar una actividad académica que pudiera contribuir a suavizar y minimizar este tipo de situaciones, observando la importancia de que nuestro alumnado tenga algunas referencias claras de medidas. Así, por ejemplo, es conveniente que use su altura, su peso, las dimensiones de la mesa del aula, la superficie de la clase o de su habitación, la distancia entre las poblaciones cercanas a su ciudad, para que le sirvan a la hora de comparar si el resultado obtenido en la resolución de un problema guarda cierta coherencia con la realidad de la vida cotidiana.
Así que, con esta intención, planifiqué esta humilde y sencilla actividad académica, perfectamente extrapolable a otros entornos. Además, consciente de que el bien más preciado de nuestros alumnos y alumnas es su smartphone, deben hacer uso del mismo para que vayan almacenando recursos de la materia en esos bienes que les acompañan a todos sitios.
| OBJETIVOS |
- Concienciar al alumnado de que el sistema métrico decimal está muy a la vista y que se acostumbren a leer el dorso de los artículos domésticos que abundan en sus casas.
- Analizar la coherencia de la solución obtenida al resolver un problema.
- Establecer conexiones entre el mundo real y el mundo matemático.
- Interpretar la solución matemática del problema en el contexto de la realidad.
- Elaborar documentos digitales propios con imágenes originales citando la autoría de las mismas.
| DESCRIPCIÓN DE LA EXPERIENCIA |
Como otras tareas colaborativas que hemos venido realizando a lo largo del curso, os organizaréis en equipos formados por dos personas, que llevarán el nombre de un concepto matemático.
Durante el plazo establecido para ello, recopilaréis imágenes realizadas con vuestros móviles en las que pueda apreciarse una cantidad de un múltiplo o submúltiplo de una medida de longitud, peso o capacidad de un objeto de la vida cotidiana sin que, en ningún caso, se corresponda con su unidad fundamental, es decir, 1 m, 1 kg o 1 l.
Debéis expresar esa cantidad de la imagen del objeto de la vida cotidiana en todas sus equivalentes, empleando el recurso interactivo denominado "Conversión entre múltiplos y divisores. Unidades de longitud, masa y capacidad", que encontraréis en Twitter, como es habitual, con nuestro hashtag #MATES1BAJO. Haréis una captura de pantalla para, posteriormente, realizar una composición entre la misma y la imagen con el objeto de la vida cotidiana que habéis seleccionado, de tal forma que el efecto conseguido sea similar al que os muestro en la imagen inferior:

Con esta actividad se pretende que tengáis una imagen clara de qué espacio ocupa 237 ml y cómo puede ser de grande un objeto que lo contenga.
Finalmente, cada equipo de trabajo elaborará una presentación o documento de texto con la siguiente estructura y me lo enviará por correo electrónico a la cuenta del Departamento de Matemáticas, cuidando la expresión, ortografía y respetando, como siempre, las partes que componen un mensaje de correo.
- Portada.- Debe contener el título del proyecto, el nombre y composición del equipo, grupo, centro, ciudad, curso escolar y hashtag, insertando el logotipo del IES Bajo Guadalquivir y el del Proyecto Descartes.
- Página 1.- Dedicada a las unidades de longitud, especificando para qué se utilizan, cuál es su unidad fundamental y cómo se produce la conversión, insertando la composición conseguida con las imágenes y citando la autoría y lugar de realización.
- Página 2.- Dedicada a las unidades de peso, especificando para qué se utilizan, cuál es su unidad fundamental y cómo se produce la conversión, insertando la composición conseguida con las imágenes y citando la autoría y lugar de realización.
- Página 3.- Dedicada a las unidades de capacidad, especificando para qué se utilizan, cuál es su unidad fundamental y cómo se produce la conversión, insertando la composición conseguida con las imágenes y citando la autoría y lugar de realización.
| PRODUCTOS FINALES |
Comparto las producciones finales de mis alumnos y alumnas de 1º ESO E del IES Bajo Guadalquivir de Lebrija, a la vez que les transmito públicamente mi felicitación y satisfacción por la calidad y por mostrarme el interés y esfuerzo para superar este nuevo reto, pudiendo apreciar la diversidad de lugares en las que han tomado imágenes con sus móviles y la amplia gama de situaciones y productos ofrecidos en los que el sistema métrico decimal se encuentra ¡a la vista!: alimentos, bebidas, cosméticos, señales de tráfico, productos de ferretería, perfumes, productos farmacéuticos, etc.
Más...
EDAD 1ºESO Polígonos, perímetros y áreas
Escrito por Alfonso Saura EspínEste mes vamos a ver un video sobre polígonos de 1ºESO:
Hemos tratado a grosso modo los siguientes puntos:
1.Líneas poligonales
Definicion y tipos. Polígono.
2.Triángulos
Elementos y clasificación
Construcción de triángulos
Rectas y puntos notables
3.Cuadriláteros
Elementos y clasificación
Paralelogramos
4.Polígonos regulares
Elementos
Ejes de simetría
5.Perímetros y áreas
Definición. Medir áreas
Unidades de superficie
6.Áreas de polígonos
Áreas de cuadriláteros
Áreas de triángulos
Áreas de polígonos regulares
Áreas de polígonos irregulares
Desarrollamos nuestra comunicación audiovisual y nos convertimos en divulgadoras matemáticas
Escrito por José Antonio Salgueiro GonzálezEn Educación Secundaria Obligatoria, sin perjuicio de su tratamiento específico en algunas de las materias de cada etapa, la comprensión lectora, la expresión oral y escrita, la comunicación audiovisual, las Tecnologías de la Información y la Comunicación, el emprendimiento y la educación cívica y constitucional se trabajarán en todas las materias.
Además, la materia de Matemáticas Orientadas a las Enseñanzas Académicas se distribuye a lo largo de tercero y cuarto de Educación Secundaria Obligatoria en cinco bloques que no son independientes entre sí : Procesos, métodos y actitudes en Matemáticas, Números y Álgebra, Geometría, Funciones y, por último, Estadística y Probabilidad.
Entre los contenidos de este bloque se contempla la utilización de medios tecnológicos en el proceso de aprendizaje, entre otros para:
- la elaboración de informes y documentos sobre los procesos llevados a cabo y los resultados y conclusiones obtenidos.
- comunicar y compartir, en entornos apropiados, la información y las ideas matemáticas.
A su vez, en los criterios de evaluación para este bloque aparece emplear las herramientas tecnológicas adecuadas, de forma autónoma, realizando cálculos numéricos, algebraicos o estadísticos, haciendo representaciones gráficas, recreando situaciones matemáticas mediante simulaciones o analizando con sentido crítico situaciones diversas que ayuden a la comprensión de conceptos matemáticos o a la resolución de problemas. CMCT, CD, CAA.
También se dice utilizar las tecnologías de la información y la comunicación de modo habitual en el proceso de aprendizaje, buscando, analizando y seleccionando información relevante en Internet o en otras fuentes, elaborando documentos propios, haciendo exposiciones y argumentaciones de los mismos y compartiendo éstos en entornos apropiados para facilitar la interacción. CCL, CMCT, CD, CAA.
Más específicos aún son los estándares de aprendizaje evaluables, donde se recoge:
12.1. Elabora documentos digitales propios (texto, presentación, imagen, video, sonido,…), como resultado del proceso de búsqueda, análisis y selección de información relevante, con la herramienta tecnológica adecuada, y los comparte para su discusión o difusión.
12.2. Utiliza los recursos creados para apoyar la exposición oral de los contenidos trabajados en el aula.
12.3. Usa adecuadamente los medios tecnológicos para estructurar y mejorar su proceso de aprendizaje recogiendo la información de las actividades, analizando puntos fuertes y débiles de su proceso académico y estableciendo pautas de mejora.
| DESCRIPCIÓN DE LA EXPERIENCIA |
Esta iniciativa, desarrollada desde el Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija, durante el curso escolar 2017/2018 con un grupo de 4º ESO del área de Matemáticas Orientadas a las Enseñanzas Académicas, tienen su origen en el proyecto "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", y se ha coordinado desde el aula virtual de Matemáticas, que tiene acceso para invitados, donde se fueron publicando, paulatinamente, las distintas fases con las correspondientes instrucciones para el alumnado. Así, con la pregunta ¿Qué tienes que hacer?, se decía que el reto a superar consiste en generar contenido audiovisual de Matemáticas. Concretamente, tienes que grabar un vídeo en el que se ejecute y explique la discusión y resolución de sistemas de ecuaciones lineales en sus tres casos: sistema compatible determinado, sistema compatible indeterminado y sistema incompatible.
En el vídeo deberá contemplarse perfectamente, y en este orden:
- Que los tres ejercicios se obtienen de la página del Proyecto Descartes.
- Que la discusión del sistema se realiza con el navegador de Google o con Photomath, como hemos hecho en clase.
- Que, para los casos en que sea un sistema compatible, el equipo lo resuelve por el método más adecuado.
- Que la solución coincide con la proporcionada por la página del Proyecto Descartes.
Para ello, estableceremos distintas etapas o fases.
| PRIMERA FASE |
La clase se organizará en equipos constituidos por dos personas, actuando una de ellas como coordinador o coordinadora del equipo que, además, deberá llevar el nombre de un personaje matemático, hombre o mujer.
Será el coordinador o coordinadora la persona encargada de entregar las tareas en las distintas fases y en los plazos establecidos.
| SEGUNDA FASE |
Comienza la fase de investigación y documentación, así que te propongo algunas sugerencias y te recomiendo espacios y recursos. Por ejemplo:
- Guía rápida para grabar en vídeo. ¡Muy bueno!
Necesitas un guion para tu película, con lo que vas a grabar y a decir, pudiendo alternar planos de lo que se visualiza en el ordenador, tableta o smartphone con planos de la ejecución técnica del ejercicio, es decir, el desarrollo con las fórmulas y operaciones. Puedes realizar los ejercicios en una pizarra, en un cuaderno o folio, con un software que lo permita, grabando en interior o en exterior y, por supuesto, todo lo que se te ocurra. Aquí es donde entra en juego tu creatividad e imaginación.
Recuerda que tú no eres el protagonista de la película, sino la resolución del ejercicio, por lo que no es necesario que aparezcas ni que se te vea.
En cualquier caso, se debe ver y oir cómo se elige el ejercicio desde el libro digital del Proyecto Descartes, comprobando después la solución en el mismo libro y usando, además, una de las dos herramientas tecnológicas que hemos aprendido en clase, es decir, Wiris Calc o Photomath, o incluso ambas.
Recuerda que publicaremos en internet el producto final, así que procura la mejor calidad de imagen y audio posibles.
El lenguaje matemático será primordial para las explicaciones, por eso, me enviaréis, desde el foro "Entrega del guion", el borrador del guion para que yo pueda revisarlo.
No puedes usar ni imágenes ni música con derechos de autor. Para estos casos, te recomiendo:
- Banco de imágenes y sonidos del INTEF.
- Imágenes con licencia Creative Commons, del mismo banco anterior o de Pixabay.
- Jamendo, descarga de música libre y gratis.
En cualquier caso, hay que citar en el vídeo el lugar de procedencia de las imágenes y audios usados.
Deberá aparecer en el vídeo, ya sea al final o al principio, el logotipo del IES Bajo Guadalquivir.
En cualquier caso, hay que dedicar una página de créditos para citar en el vídeo el lugar de procedencia de las imágenes y audios usados.
Si tienes alguna idea y no sabes cómo llevarla a efecto, puedes consultar en el foro del aula virtual denominado "Dudas sobre la segunda fase".
¡Es el momento de la CREATIVIDAD E IMAGINACIÓN!
| TERCERA FASE |
Para entregar el vídeo puedes usar un servicio gratuito para envío de archivos de gran tamaño. Si no conoces ninguno, te recomiendo WeTransfer.
Cuando la página te avise que se ha concluído la transferencia, me envías un mensaje por la plataforma para que me lo descargue. Así quedará constancia de haber entregado el vídeo en su plazo y me llegará un aviso a mi correo para que me descargue vuestra obra.
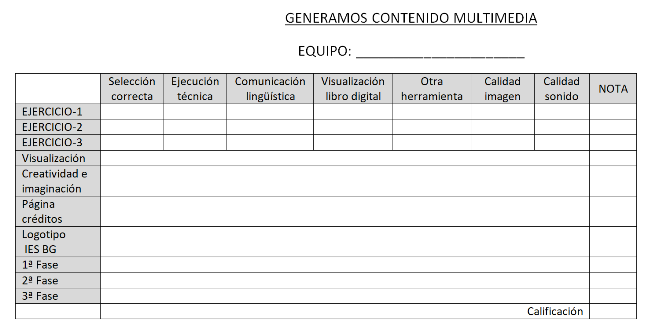
Para evaluar el producto final se tendrán en cuenta las siguientes variables:
La experiencia ha resultado sumamente satisfactoria y quiero felicitar desde el portal de RED Descartes al equipo Sofía Kovalevskaya por la calidad del producto final conseguido. ¡ENHORABUENA!, Ángela y Alba o Alba y Ángela.
Mi agradecimiento también a sus familias por autorizar la difusión de esta obra en entornos apropiados.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
