Uso de dirección URL de ficheros de preguntas para cargarlos en el juego (AJDA)
Escrito por Jesús Manuel Muñoz Calle- Crear el fichero de preguntas, se recomienda usar el generador de ficheros.
- Subir el fichero a Internet. Se puede enviar para ser publicados en la web del Proyecto AJDA o a cualquier otra.
- Copiar la dirección Url del juego (barra de direcciones del navegador).
- Se entra en el juego y en su apartado "Selección de ficheros de preguntas", se pega la dirección Url del juego en el campo "Dirección Url/local". Si el proceso se ha realizado correctamente se mostrarán los datos del fichero cargado.
Energía eléctrica. Proyecto Newton
Escrito por Montserrat Gelis BoschEl subproyecto Problemas del Proyecto Newton contiene una serie de unidades didácticas en las cuales se propone la resolución de diferentes problemas Física y Química para la ESO y el Bachillerato.
Todas las unidades han sido elaboradas siguiendo un mismo diseño, a partir del enunciado de un problema se aborda su resolución cuatro apartados:
Guía del alumno:
En este apartado se plantea el enunciado del problema y distintos puntos de vista sobre aspectos a tener en cuenta e indicaciones para su resolución.
Escenas interactivas:
Se proponen una o varias escenas para que el alumno pueda modificar los datos y comprobar el resultado utilizando las fórmulas correspondientes.
Evaluación:
Consta de uno o varios cuestionarios que hacen referencia al problema propuesto. El alumno puede comprobar si sus respuestas son correctas y repetir las actividades en caso de ser necesario.
Problema resuelto:
Se puede ver e imprimir el problema resuelto en pdf.
A modo de ejemplo, en el siguiente vídeo, se muestra una serie de unidades de dicho proyecto sobre el estudio de las diferentes centrales de producción de energía eléctrica para segundo de bachillerato: eólica, nuclear, térmica e hidroeléctrica.
También se indican los pasos a seguir para insertar estos elementos en un espacio virtual Moodle.
EDAD 4º ESO Académicas - Funciones polinómicas
Escrito por Alfonso Saura EspínHemos visto los siguientes puntos:
1. Funciones polinómicas
Características
2. Funciones de primer grado
Término independiente
Coeficiente de grado uno
Recta que pasa por dos puntos
Aplicaciones
3. Funciones de segundo grado
La parabóla y=ax2
Traslaciones de una parábola
Representar funciones cuadráticas
Aplicaciones
Ada Lovelace, la mujer en la ciencia y el techo de cristal
Escrito por José Antonio Salgueiro GonzálezPrimera píldora otoñal para compartir un nuevo producto final generado por mis alumnas de 3º ESO desde la materia de Matemáticas Orientadas a las Enseñanzas Académicas, dentro del proyecto "La radio ficción en el aula de Matemáticas", iniciado durante el curso escolar 2015/2016 en el Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
En esta ocasión, la cadena "Radio ecuación" entrevista a la mujer que rompió todos los esquemas de la época victoriana, la mujer que no se frenó ante ningún obstáculo, reconocida como la primera programadora de la historia. Por cierto, ¡no te pierdas la respuesta de Ada Lovelace! a la pregunta formulada por la entrevistadora: "actualmente, estamos logrando que se normalice la presencia de ambos sexos en el ámbito científico y que las mujeres vayan consiguiendo cada vez más el protagonismo que se merecen. ¿Qué consejo darías a todas estas mujeres emprendedoras?"
Enlace a la entrevista en nuestro canal de iVoox
Quiero felicitar públicamente a mis alumnas Antonia y Maite, o Maite y Antonia, por la gran calidad del producto conseguido, por el trabajo desempeñado en la fase de documentación, por superar todos los aspectos técnicos para generar el archivo de audio y por sus capacidades para comunicar, interpretar y transmitir emociones.
La fase final del proyecto consiste en realizar un breve análisis de la experiencia que lleve a la reflexión sobre lo aprendido, describiendo todos los detalles, desde la planificación, redacción del guion, grabación del audio , lugar elegido, recursos usados, osbtáculos encontrados y cómo se han afrontado y las conclusiones finales.
Enlace al análisis de la experiencia en nuestro canal de iVoox
Por cierto, aunque no han conseguido encontrar a Ada Lovelace en el portal de RED Descartes, dejo constancia de que, efectivamente, "la hija de la princesa del paralelogramo" forma parte de esta web, por ejemplo:
- Entrevista a Ada Lovelace, interpretada por Montse Gelis Bosch, profesora de matemáticas.
- Puzle dedicado a Ada Lovelace, generado por Ángel Cabezudo.
A lo largo de este proyecto, que no deja de proporcionarme satisfacciones, se han publicado los siguientes artículos:
- La radio ficción en el aula de Matemáticas, que incorpora la entrevista ficticia al ilustre y prolífico matemático Leonhard Euler.
- Entrevistamos a Euclides en 3º ESO, para dar a conocer la vida y obra del autor de los Elementos.
- Alumnas de 3º ESO entrevistan a Mary Somerville.
- Évariste Galois visto e interpretado por alumnos de 3º ESO
- Conocí a Mary Cartwright gracias a mis alumnas. ¿Y tú?
También puedes conocer los antecedentes de la iniciativa consultando el artículo titulado "La ficción de Radio Descartes en el programa Boulevard de Radio Euskadi".
Más...
Misceláneas: Probabilidad. Inferencia II.
Escrito por Ildefonso Fernández TrujilloMisceláneas: Probabilidad. Inferencia. Fundamentos II.
Incertidumbre.
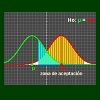
De la pérdida de la incertidumbre en el acto de decidir sobre cualquier asunto son responsables los estudiosos de la Probabilidad y la Estadística. Un estudio, bien fundamentado y realizado, sobre prácticamente cualquier tema, desvelará el desarrollo futuro de un proceso económico, sanitario, social...y si, un puñado de herramientas inmateriales: teoremas, lemas, hipótesis, tesis, etc. cada vez más sofisticadas y eficaces, hacen las veces de bola de cristal de los auténticos videntes actuales, aunque a decir verdad la incertidumbre no desaparece del todo y está en función del dinero a invertir y/o las características propias del tema en estudio pero por lo general suele ser inferior al 5%. O dicho de otra manera el nivel de confianza en los resultados del estudio suele ser superior al 95%.
En la entrada anterior en este blog incrustamos una escena del libro digital: Estadística, Probabilidad e Inferencia, en la que se mostraba el cálculo práctico de los intervalos de confianza en una simulación teórica que permite manipular el tamaño de la muestra, el nivel de confianza exigido y el valor del parámetro en estudio. En esta ocasión, en principio, hemos creído conveniente insistir en la fundamentación elemental teórica de la Inferencia para lo cual proponemos que al introducir (difundir) este tema debemos garantizar el conocimiento de la distribución Normal, sus propiedades y el uso de la tabla para el cálculo de probabilidades de los valores de la variable X cuando esta variable tiene una distribución normal de media µ = 0 y una desviación típica σ = 1. X con distribución N(0,1). Así como el procedimiento de tipificación de variables normales con cualquier media y desviación.
Todo lo anterior queda completamente cubierto en la unidad didáctica dinámica e interactiva INFERENCIA ESTADÍSTICA
Que se complementa con la útil "Calculadora de la Distribución Normal" del profesor Juan Jesús Cañas Escamilla
Ambas utilidades y el resto de las mencionadas constituyen una muy completa documentación para uso personal y como herramientas didácticas para la explicación del tema. Como consecuencia del análisis del material expuesto y de la bondad de los métodos numéricos finitos hemos desarrollado la siguiente utilidad que consiste en una escena que muestra la probabilidad de que una variable que se distribuye según una distribución Normal(0,1) tome un valor menor o igual que otro dado. La escena pretende ser una utilidad simple y eficaz para la introducción al estudio de las distribuciones de probabilidad.
Todo lo expuesto anteriormente además del resto de conocimientos teóricos necesarios para afrontar el estudio de los intervalos de confianza y de los contrastes de resultados se encuentra en los materiales enlazados en esta y en entradas anteriores; no obstante volvemos a mostrar algunos de ellos por su indudable interés:
En esta ocasión, en la sección de vídeo, hemos elegido uno que muestra una clase sobre las distribuciones de probabilidad.
Ildefonso Fernández Trujillo. 2018
Publicación de RED Descartes en el Open Journal "Matemáticas, Educación y Sociedad"
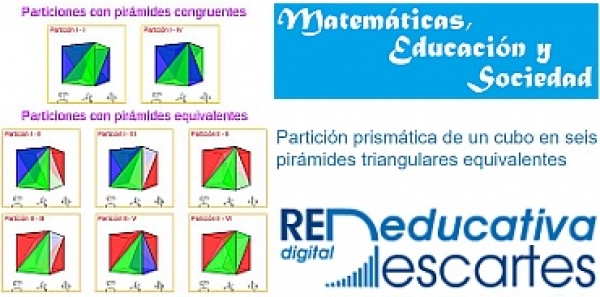
Escrito por Ángel Cabezudo BuenoEn el Vol. I, Núm. 2 del Open Journal "Matemáticas, Educación y Sociedad" (ISSN: 2603-9982) se ha publicado el artículo titulado "Partición prismática de un cubo en seis pirámides triangulares equivalentes". Un detallado trabajo de investigación que, como se refleja en la autoría, ha sido desarrollado dentro de nuestra RED Descartes por nuestro socio José R. Galo Sánchez.
Os invitamos a su lectura, a que realicéis observaciones y comentarios al mismo y a que lo divulguéis a través de vuestras redes sociales y profesionales.
NOTA: En este pdf hay numerosos enlaces externos a recursos interactivos desarrollados con Descartes y que están publicados en nuestro servidor de contenidos. Os aconsejamos que la apertura de cada uno de estos enlaces la realicéis posicionando el ratón sobre el enlace y pulsando Ctrl+clic, de esta manera el recurso enlazado se abre en una nueva pestaña y permite realizar una lectura del pdf sin necesidad de tener que volver a posicionarse en el punto desde el que se produjo el salto.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)











 CONTACTO
CONTACTO
