En el VI Encuentro Utopías Educativas
Escrito por José Antonio Salgueiro GonzálezDurante los días 25 y 26 de mayo de 2018 se celebró, en el Centro de Arte y Tecnología - ETOPIA de Zaragoza, el VI Encuentro Utopías Educativas, organizado por la Asociación Utopías Educativas, y se trata de un evento anual destinado a la presentación e intercambio de “Experiencias de Innovación Educativa” y un espacio de conocimiento, diálogo, contraste de ideas y contagio de ilusiones entre los docentes.

La RED Descartes estuvo representada por Rita Jiménez Igea, profesora de matemáticas en el IES Tomás Mingot de Logroño, quien presentó el taller titulado "Aprendiendo con el Proyecto Descartes", con el objetivo de dar a conocer el portal de Red Educativa Digital Descartes a los profesores, mostrar sus recursos educativos para tablets, smartphones y PC de Matemáticas, Física y Química, Biología, Lengua, Inglés , Tecnología y Geografía para Infantil, Primaria, Secundaria, Bachillerato y Universidad, que pueden usarse libremente, haciendo un recorrido por distintas unidades didácticas digitales y objetos interactivos y proponiendo distintas formas de llevar al aula estos materiales en función de los recursos tecnológicos de cada centro.

Desde RED Descartes felicitamos a la organización, no sólo por la iniciativa y el esfuerzo que ello conlleva, sino por la amplia y completa difusión, ya que en su portal podemos encontrar los vídeos de cada experiencia, imágenes del momento. documentos con los detalles de las mismas, etc.
Finalmente, compartimos en nuestro portal la presentación y el texto íntegro de la comunicación presentada por Rita Jiménez Igea.
Creación de juegos y escenas. Aspectos generales
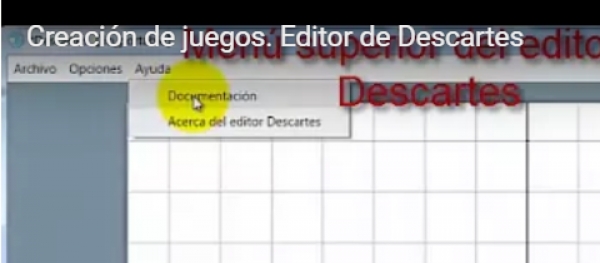
Escrito por Jesús Manuel Muñoz CalleEl editor de escenas se puede descargar para distintos sistemas en el siguiente enlace. Además desde el propio editor se pueden cargar las actualizaciones y mejoras que se van incorporando. Cuando el editor detecta una nueva actualización indica mediante un mensaje la posibilidad de proceder a realizarla.
Évariste Galois visto e interpretado por alumnos de 3º ESO
Escrito por José Antonio Salgueiro GonzálezLa dimensión histórica, social y cultural de las matemáticas debe programarse de manera cuidada y coordinada para ayudar a la comprensión de los conceptos a través de la perspectiva histórica, así como para contrastar las situaciones sociales de otros tiempos y culturas con la realidad actual, conociendo de manera más humana a los personajes y sus aportaciones, visibilizando las circunstancias personales de mujeres matemáticas y las dificultades que han tenido para acceder a la educación y a la ciencia. Resulta idóneo el uso de Internet y de las herramientas educativas existentes, de vídeos y películas sobre la vida y obra de los personajes matemáticos para lo que es de gran ayuda la pizarra digital, o el tradicional trabajo monográfico que ahora puede crear nuestro alumnado de forma colaborativa haciendo uso de los documentos compartidos. También podemos ir más allá, pues resulta sumamente enriquecedor para la formación competencial crear de forma colaborativa una línea del tiempo con la secuenciación cronológica de descubrimientos matemáticos. Además, debemos enseñar a nuestro alumnado a generar contenido matemático inédito y desarrollar la comunicación audiovisual desde las matemáticas con la creación de un audio o vídeo o poniendo voz a los personajes célebres de ambos géneros, organizando una cadena de radio matemática o un canal de televisión que entreviste de forma ficticia a dichos personajes.
El párrafo anterior están literalmente extraídos de la Orden de 14 de julio de 2016, por la que se desarrolla el currículo correspondiente a la Educación Secundaria Obligatoria en la Comunidad Autónoma de Andalucía, se regulan determinados aspectos de la atención a la diversidad y se establece la ordenación de la evaluación del proceso de aprendizaje del alumnado, que es la que conozco como docente en activo, pero estoy convencido de que las orientaciones y estrategias metodológicas aportadas serán de gran similitud con las ofrecidas por otras comunidades autónomas en el ámbito de sus competencias.
| ANTECEDENTES |
RED Descartes posee una gran experiencia, reconocida además, en la radio ficción en Matemáticas, gracias a su programa "El personaje misterioso" conducido por Eva Perdiguero y Ángel Cabezudo, con el objetivo de dar a conocer un poco más de cerca la parte humana de los personajes matemáticos famosos a lo largo de la historia. Pues bien, "La radio ficción en el aula de Matemáticas" es un proyecto del Departamento de Matemáticas del IES Bajo Guadalquivir de Lebrija con los mismos objetivos que los de Radio Descartes, pero entre discentes en vez de entre docentes, que empieza durante el curso escolar 2015/2016, continuando en el curso escolar 2017/2018, con un grupo de alumnos y alumnas de Matemáticas Orientadas a las Enseñanzas Académicas en 3º de ESO, es decir, con 14 y 15 años de edad, que se coordina desde el aula virtual y comprende las fases que se relacionan a continuación.
| ELECCIÓN DEL PERSONAJE MATEMÁTICO Y DIFUSIÓN EN TWITTER |
Cada equipo estará constituido libremente por dos personas que deberán elegir a un personaje matemático para entrevistar en un programa de radio, masculino o femenino garantizando la paridad en el aula, de modo que una persona ejerza de entrevistador y la otra represente al personaje seleccionado. Seguidamente, para información de todos y no repetir personajes, un miembro del equipo publicará un tuit con la composición del mismo, incluyendo el personaje seleccionado con una imagen y el hashtag del curso #MATES3BAJO.
| DOCUMENTACIÓN |
En la segunda fase, cada equipo realizará una búsqueda de información en internet sobre la vida y obra del personaje elegido para entrevistar.
Pueden ser documentos de texto, imágenes con información, presentaciones, infografías, vídeos, audios y cualquier multimedia, en general.
Es fundamental que la información provenga de fuentes fiables, así que se hará una selección de dos o tres recursos y se compartirán en el foro habilitado en el aula virtual las direcciones de cada uno de ellos.
Después, cuando el profesor aprueba los recursos seleccionados, se tendrán que difundir esas direcciones por Twitter con el hashtag del curso #MATES3BAJO.
| ELABORACIÓN DEL GUION |
Cada equipo tiene que elaborar un guion en un documento de texto con la entrevista completa y enviarla al profesor desde la tarea habilitada en el aula virtual, cuidando la expresión, el vocabulario y la escritura.
| INSTRUCCIONES PARA LA GRABACIÓN DE LA ENTREVISTA |
¡Ha llegado el momento! Recuerda que son fundamentales la creatividad e imaginación del equipo, así que, si no tienes experiencia anterior a la hora de protagonizar un programa de radio, te daré algunos consejos:
- Busca un espacio exento de ruidos, internos o externos, y evitarás sorpresas de última hora y pérdida de tiempo.
- Es muy importante ensayar algunas veces y vocalizar perfectamente, haciendo algunas pruebas hasta conseguir el efecto deseado.
- Es muy complicado grabar la entrevista de una sola vez, por ello aconsejamos grabarla por partes, según se estime oportuno.
- Conviene dejar grabando unos segundos de silencio después de cada intervención, lo que facilita la edición y montaje de la entrevista completa.
- Tenéis que hablar con tranquilidad y vocalizando lo mejor posible.
- El protagonista es el entrevistado, es decir, el personaje matemático, no el periodista. No obstante, ambos deben transmitir emociones al público, evitando usar un tono constante.
- Evitar apostillar las respuestas del entrevistado. Conforme el entrevistado va contestando, no debemos decir “ya”, “claro”.
- Como todo programa de radio, deberá contener una presentación, donde se explique el objetivo de la sesión, y una despedida, dando un pequeño resumen de lo tratado y agradeciendo, en nombre de la cadena, la presencia del entrevistado.
La mejor forma de conocer el producto final deseado es oir algunas entrevistas similares.
Encontrarás una docena de entrevistas a personajes matemáticos que te servirán de orientación, sin olvidar que están realizadas por docentes para docentes, mientras que las vuestras son de alumnos para alumnos, y se recomienda que no sobrepasen los cinco minutos de duración.
| EDICIÓN DEL AUDIO |
Una vez grabada la entrevista, te aconsejo hacer una copia de la misma y guardarla en una carpeta llamada copia de seguridad, para evitar posibles problemas, ya que ahora procede editar los distintos archivos para proceder a enriquecer el audio con las uniones correspondientes, incluyendo la presentación, despedida, sintonía del programa de radio, efectos sonoros, etc, para lo que es fundamental la creatividad e imaginación del equipo.
En ningún momento podrás incluir música o sonidos que tengan derechos de autor, es decir, copyright, debiendo usar recursos originales o que tengan licencias que lo permitan, como las Creative Commons. Así que, para ello, te recomiendo que uses el
Descárgate los archivos que sean de tu agrado en formato mp3, preferiblemente.
Abrimos en el aula virtual un foro denominado "Soporte técnico" para que, entre todos, planteemos las dificultades que encontremos y poder compartir soluciones conforme vayamos aprendiendo.
| ENTREGA DEL AUDIO |
Una vez finalizada la edición del audio con los efectos especiales y el equipo considere concluída la entrevista, deberá generar con el software empleado un archivo en formato mp3 para entregarlo desde la tarea habilitada en la plataforma, o bien usar un conversor para pasar su archivo al formato solicitado.
Pues bien, en el marco del proyecto "La radio ficción en el aula de Matemáticas", compartimos en este primer artículo del curso escolar 2017/2018 la entrevista realizada por dos alumnos de 3º ESO al gran matemático francés Évariste Galois.
Felicito a Pablo García y Pablo Gutiérrez por su creatividad, imaginación y transmisión de emociones para interpretar y divulgar la vida y obra de Galois, a quien conocían gracias al canal Derivando de Eduardo Sáenz de Cabezón.
| ANÁLISIS DE LA EXPERIENCIA |
Con la entrevista al personaje matemático has adquirido, quizás sin darte cuenta, una importante experiencia en comunicación verbal, relacionada con las Matemáticas, que antes no poseías. Estoy convencido de que si tuvieras que grabarlo otra vez no saldría el mismo, porque cambiarías alguna cosa en base a esa experiencia o le darías otro enfoque o incluso usarías otras herramientas.
Has sido pionero y pionera en este aspecto, por ello, tu experiencia debe ser aprovechada para los que te sigan. ¿Y cómo se hace ésto? Pues sencillamente como hacen los científicos, divulgando tus experiencias y conclusiones en las revistas especializadas y en los medios de comunicación del s. XXI.
¿Qué tienes que hacer? Pues sencillamente grabar otro audio, con total libertad, es decir, tú decides sin incluyes o no efectos especiales y música, pero no es necesario, sino que lo importante es oir tu experiencia con absoluta sinceridad, hablando y vocalizando lo mejor posible.
¿Qué temas hay que tratar?
Hay que contar todos los detalles, desde la planificación, redacción del guion, grabación del audio , lugar elegido, recursos usados, osbtáculos que habéis encontrado y cómo los habéis resuelto y vuestras conclusiones finales. Por ejemplo, a modo de guión:
- ¿Conocías al personaje matemático anteriormente?
- ¿Qué te ha llamado la atención de su vida? ¿Y de su obra?
- ¿Crees que esta experiencia contribuye al desarrollo de tu creatividad e imaginación?
- ¿Cómo has planificado la tarea?
- ¿Qué heramientas has empleado? ¿Sabías manejarlas?
- ¿Qué lugar has elegido para la grabación y por qué?
- ¿Qué dificultades has encontrado para realizar todas las tareas que esta acción conlleva y cómo las has resuelto?
- ¿Has tenido que solicitar ayuda externa?
- ¿Qué has aprendido con esta experiencia que antes no sabías?
- ¿Aparece tu personaje matemático en el portal de la RED Descartes? ¿Qué has encontrado?
- ¿Cuáles son tus conclusiones y valoraciones al finalizar esta acción innovadora?
- Puedes añadir cualquier otra pregunta que consideres interesante o hacer la crítica 3x1, es decir, tres cosas que te han gustado y una que cambiarías.
Unidades Descartes. Actividades interactivas también para el verano
Escrito por Montserrat Gelis BoschEsta semana proponemos un nuevo enfoque sobre el uso de los materiales del proyecto Descartes.
Como la mayoría de unidades pertenecientes a los diferentes proyectos de la Red Descartes contienen actividades para practicar con autocorrección de los ejercicios, serán útiles para trabajar también en verano ya sea para consolidar contenidos trabajados durante el curso o bien como refuerzo sobre algunos temas que ofrecieron más dificultad y que es necesario recuperar.
El alumno puede realizar las actividades que necesite ya sea individualmente, con algún compañero o con la ayuda de un tutor.
A modo de ejemplo vamos a ver en el siguiente vídeo algunas de las actividades propuestas en la unidad expresiones algebraicas del proyecto ED@D para primero de la ESO.
Más...
EDAD 3ºESO Académicas - Cuerpos geométricos
Escrito por Alfonso Saura EspínEste mes vamos a ver un vídeo de 3º ESO Académicas sobre los cuerpos geométricos:
La unidad trata los siguientes epígrafes:
1.Poliedros regulares
Definiciones
Desarrollos
Planos de simetría
Poliedros duales
2.Otros poliedros
Prismas
Pirámides
Planos de simetría
Poliedros semirregulares
3.Cuerpos de revolución
Cilindros
Conos
Esferas
Planos de simetría
4.La esfera terrestre
Coordenadas geográficas
Husos horarios
5.Mapas
Proyecciones
Vacaciones con Descartes para las familias - 2018
Escrito por José Antonio Salgueiro GonzálezNuestros niños y niñas se encuentran disfrutando del período vacacional de verano, con mucho tiempo para compartir con sus familias y amigos, así como para el descanso y ocio. No obstante, siempre es recomendable encontrar el momento adecuado para sugerirles una interesante lectura y realizar, en nuestra compañía o junto a sus hermanos y hermanas mayores, algunas actividades de las áreas básicas del conocimiento. Ahora bien, para ello, las familias requieren de una orientación y asesoramiento que pueden recibir por diferentes canales de comunicación.
Con este fin, la Red Educativa Digital Descartes, ofrece una amplia selección de recursos digitales interactivos a los que pueden accederse desde cualquier lugar y hora, en el campo o en la playa, con un simple ordenador personal, portátil, tableta o smartphone y conexión a la red de internet, aunque también es posible descargarse el objeto de aprendizaje para usarlo en local, es decir, sin conexión a internet.
Estos recursos están organizados y catalogados por etapa educativa y edad, como se aprecia en la imagen inferior, así , las familias podrán seleccionar, con un simple clic sobre la imagen correspondiente o sobre el texto que la acompaña a su derecha, los adecuados para sus hijos e hijas, encontrando la relación con los nombres de las actividades y una breve descripción de la misma.
No obstante lo anterior, cada familia, como mejor conocedora de las capacidades de los niños y niñas, podrá optar por realizar las actividades de diferente edad.
La LOMCE no contempla los tres ciclos de Primaria, sino seis cursos independientes. lo que no supone obstáculo alguno para que los niños y niñas disfruten con estos recursos de gran calidad, pues accediendo al ciclo en cuestión, según la edad, y seleccionando el recurso deseado puede verse con detalle a qué curso concreto corresponde.
Esperamos que esta aportación, completamente gratuita, de la RED Descartes sea de utilidad para el mayor número posible de familias y animamos a dejar comentarios con sus opiniones.
El mapeado de la imagen se ha realizado desde la nube con la herramienta Image-Maps.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)











 CONTACTO
CONTACTO
