En mi pueblo. Formación en competencias. 4º de Primaria
Escrito por Montserrat Gelis BoschLa formación en competencias y la introducción de las TIC en el aula han transformado la educación en los últimos años.
En los problemas competenciales el alumnado debe resolver problemas relacionados con la vida cotidiana aplicando y relacionando conocimientos de diferentes áreas. Por su parte, el uso de la tecnología ha permitido la creación de materiales que por su interactividad facilitan la docencia, motivando y fomentando el autoaprendizaje del alumnado.
El Proyecto Competencias de la Red Educativa Digital Descartes consta de una serie de unidades didácticas para la formación en competencias. Se trata de materiales elaborados a partir de unidades liberadas PISA y pruebas de evaluación diagnostico realizadas por diferentes Comunidades Autónomas. En este proyecto se proponen actividades para diferentes niveles, desde 3º de primaria hasta 4º de la ESO.
En siguiente vídeo y a modo de ejemplo, se muestra con detalle la unidad "en mi pueblo", para 4º de primaria.
El diseño es común en todas las unidades, a partir de un estímulo se plantean una serie de preguntas relacionadas. En este caso, el estímulo es cierta información sobre un pueblo. A partir de ello, el alumno deberá resolver determinadas cuestiones en las cuales deberá mostrar su conocimiento sobre diferentes aspectos matemáticos: localización en un mapa, cálculo con fracciones, superficies y operaciones combinadas.
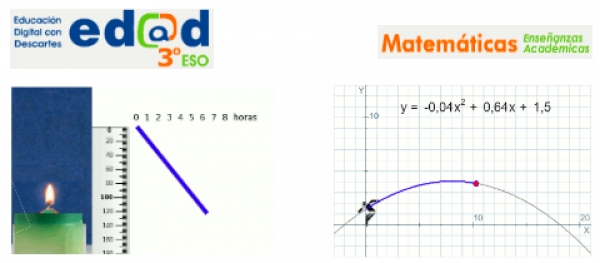
EDAD 3º ESO Académicas - Funciones lineales y cuadráticas
Escrito por Alfonso Saura EspínEste mes vamos a ver la unidad de funciones linales de 3º eso:
En el video hemos seguido el siguiente esquema:
1.Función de proporcionalidad directa
Definición
Representación gráfica
2.Función afín
Definición
Representación gráfica
3.Ecuación de la recta
Forma punto-pendiente
Recta que pasa por dos puntos
Forma general
4.Posición relativa de dos rectas
Análisis en forma explícita
Análisis en forma general
5.Aplicaciones
Problemas simples
Problemas combinados
6.Funciones cuadráticas
La parábola y=ax²
Traslaciones de una parábola
Aplicaciones
Ejemplo de uso de tres juegos del Proyecto AJDA (I)
Escrito por Jesús Manuel Muñoz CalleBatalla naval. Es un juego original del proyecto AJDA en el que dos jugadores o equipos se enfrentan en una "guerra de preguntas" que gana el equipo que hunde el barco del adversario alcanzándole cinco veces.
Descomposición factorial. Primeras nociones.
Escrito por Montserrat Gelis BoschLa unidad, Descomposición de un número en factores, está formada por varias actividades de iniciación a la descomposición factorial de un número.
Este objeto digital forma parte del proyecto Pizarra Interactiva y sus contenidos están orientados a la Educación Primaria, aunque también pueden ser adecuados para alumnos de 1º de la ESO que presenten dificultades en el proceso de aprendizaje.
El diseño de la unidad, como todos los objetos del proyecto PI, consta de cuatro fases: Introducción, Exploración, Ejercicios y Evaluación.
A partir de las propuestas de las escenas interactivas se pretende que el estudiante adquiera sus primeras nociones sobre la descomposición en factores. Todas las escenas se pueden reutilizar con diferentes datos de forma que el alumnado pueda practicar tantas veces como necesite para consolidar su aprendizaje.
Más...
EDAD 2ºESO Áreas de cuerpos geométricos
Escrito por Alfonso Saura EspínEste mes vamos a ver la unidad de áreas de cuerpos geométricos de 2ªESO:
Hemos tratado los siguientes puntos:
1. Área de los prismas
Área de los prismas
2. Área de la pirámide y del tronco de pirámide
Área de la pirámide
Área del tronco de pirámide
3. Área de los cuerpos de revolución
Área del cilindro
Área del cono
Área del tronco de cono
Área de la esfera
4. Resolución de problemas
Resolución de problemas
Libro interactivo para formarse en Descartes JS
Escrito por José R. Galo SánchezEl Fondo editorial de la Institución Universitaria Pascual Bravo de Medellín (Colombia) ha publicado un libro interactivo de formación en la herramienta de autor “Descartes JS”.
Los autores son Juan Guillermo Rivera Berrío --vicerrector de dicha institución--, Joel Espinosa Longi y Alejandro Radillo Díaz --técnicos académicos del Instituto de matemáticas de la Universidad Autónoma de México--.
El libro como se indica en su título “Descartes JS nivel I” tiene como objetivo introducir a sus lectores-actores en el desarrollo con esta herramienta de escenas interactivas para alcanzar un primer nivel de capacitación, estando previsto darle continuidad en próximos libros complementarios. No se presuponen conocimientos previos en Descartes y su contenido está configurado para el aprendizaje autónomo mediante la elaboración de proyectos en los que se acompaña al discente en su elaboración. Mira esta escena:
Como puedes observar, la catalogación como nivel I o introductorio no debe de llevar a la presunción de que los proyectos elaborados sean muy básicos, muy al contrario podrá experimentarse el potencial de Descartes y cómo pueden conseguirse recursos educativos muy interesantes con un coste formativo asumible. Por ejemplo, la actividad del capítulo sexto en la que se desarrolla un vídeo interactivo que embebemos aquí:
O la elaboración de secuencias temporales como ésta:
¡Ánimo! ¡Aprende con este interesante libro interactivo y desarrolla tus recursos educativos con DescartesJS!
(Pulsa sobre la imagen para acceder al libro interactivo)
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
