Descartes en moodle: recurso “URL” (Proyecto PI)
Escrito por Montserrat Gelis BoschIniciamos esta semana una serie de vídeos con indicaciones acerca de la inserción de unidades de la RED Descartes en moodle, utilizando algunos de los recursos y tareas que nos proporciona dicha plataforma de aprendizaje.
En este primer vídeo, se ha seleccionado la unidad “el sustantivo” del subproyecto PI y el recurso "URL" para su inserción en moodle.
Los objetos digitales del proyecto Pizarra Interactiva están orientados a la Educación Primaria y presentan unidades con actividades de Lengua Castellana y Matemáticas. La unidad “el sustantivo” consta de diferentes actividades de definición y clasificación de los sustantivos. El diseño de la unidad, como todos los objetos del proyecto PI, consta de cuatro fases: Introducción, Exploración, Ejercicios y Evaluación. Todas las escenas se pueden reutilizar con diferentes datos de forma que el alumnado pueda practicar tantas veces como sea necesario para consolidar su aprendizaje.
Para su inserción en moodle podemos utilizar diferentes códigos:
- Copiando el enlace de la dirección
- A partir del código para abrir en ventana emergente
- A partir del código para embeber
EDAD 4º ESO Académicas - Funciones racionales, exponenciales y logarítmicas
Escrito por Alfonso Saura EspínEste mes vamos a ver en un vídeo la profundización de las funciones de cuarto de la eso, es decir las funciones racionales, exponenciales y logarítmicas.
Hemos tratado los siguientes puntos en este vídeo:
1.Funciones racionales
Función de proporcionalidad inversa
Las asíntotas
Otras funciones racionales
2.Funciones exponenciales
Características
Crecimiento exponencial
Aplicaciones
3.Funciones logarítmicas
Función inversa de la exponencial
Función logarítmica
Logaritmos
Más de diecisiete millones de páginas servidas en 2018
Escrito por José R. Galo SánchezEn 2018 hemos servido más de diecisiete millones de páginas (casi dieciocho millones) desde nuestro dominio proyectodescartes.org y a través de ellas han sido distribuidos hacia nuestros usuarios más de dos mil quinientos Gigabytes. Estos son sólo dos parámetros que dan una pincelada del alcance logrado por nuestra organización no gubernamental "Red Educativa Digital Descartes" (RED Descartes).
Como ya indicamos en el artículo que publicamos el pasado año nuestra reflexión como asociación, al inicio de este año 2018, no puede limitarse a analizar aspectos meramente cuantitativos, pero estos sí nos pueden servir como base informativa del alcance conseguido y también para ver la evolución acaecida entre el año 2017 y el de 2018. De partida adelantamos que hemos incrementado un 20% las páginas servidas y un 50% en los GB transmitidos.
Tomamos como base la información que podemos obtener a partir de las estadísticas que se generan automáticamente en nuestro servidor proyectodescartes.org con la herramienta Webalizer. En la ayuda de esta herramienta se describen los caracteres estadísticos que se registran: accesos (hits) , archivos (files), páginas (pages), visitas (visits), clientes (sites) y kbytes.
La siguiente tabla refleja el resumen mensual y anual de este año 2018:
En la primera columna de esta tabla se cuenta con un enlace que da acceso a un desglose detallado por días y horas para cada uno de los meses.
En la columna de páginas podemos observar el dato relativo al número de páginas servidas, el cual es el que hemos destacado en el título de este artículo. Son más de diecisiete, casi dieciocho, millones de páginas las que han sido requeridas por nuestros usuarios y que han sido servidas desde nuestro servidor, una media mensual aproximada de un millón quinientas mil páginas, más de cuarenta y ocho mil diarias, dos mil a la hora, casi treinta y cuatro cada minuto, 1 página aproximadamente cada dos segundos.
El siguiente diagrama de barras muestra ese desglose mensual de páginas servidas.
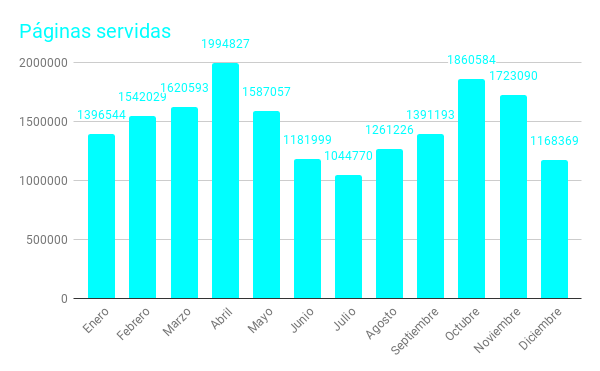
En la columna "kB F" se reflejan el número de kbytes transferidos desde el servidor hacia los usuarios a través de las páginas solicitadas. Aquí no se contabilizan, no se incluyen, los bytes correspondientes a las descargas que se realizan de nuestras publicaciones anuales en DVD (Vol. I, Vol. II y Vol. III) ya que los archivos de estos DVD están alojados en otros servidores. Son más de dos mil quinientos Gigabytes los transferidos este año, lo que equivale a haber replicado el contenido de nuestro servidor en la red unas noventa veces a lo largo de este año, casi dos veces cada semana.
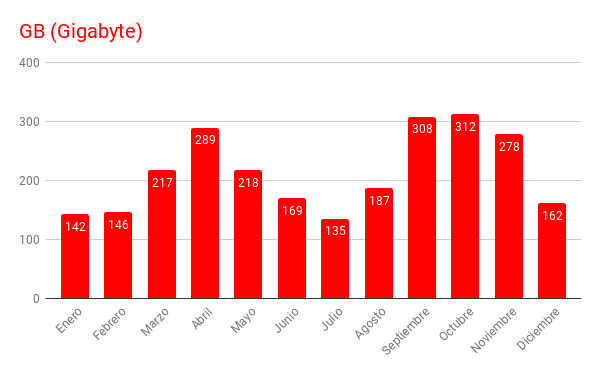
La columna de "clientes" o "sites" refleja la cantidad de direcciones IP diferentes que realizan solicitudes al servidor y es como un indicador aproximado de la cantidad de visitantes recibidos en nuestro servidor. La media mensual alcanzada es de unos ciento cuarenta mil y diariamente serían unos cuatro mil ochocientos.
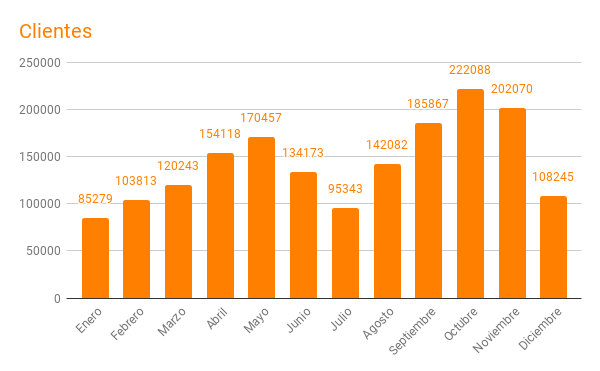
La procedencia de estos visitantes también queda reflejada en el control estadístico del servidor y estos proceden principalmente de toda iberoamérica encabezados, generalmente, por España, Colombia, México, Argentina y Ecuador, pero no siempre en ese orden siendo claramente dependiente del periodo lectivo en cada país. En los meses vacacionales en España es Colombia quien ha estado liderando esta procedencia. Desde aquí felicitamos a nuestros colegas de RED Descartes Colombia por la labor que realizan y que queda reflejado en todos los datos aquí expuestos y en particular en este liderazgo.
Comparación 2017 y 2018
Realizando una comparación entre el año 2017 y 2018 podemos observar el incremento de páginas servidas. Globalmente han sido casi tres millones más de páginas las servidas en 2018, respecto a 2017. Pero en marzo se ve un decremento sustancial, quizás causado porque en 2017 la Semana Santa (periodo vacacional) cayó en Abril en 2017 y sin embargo en 2018 fue en marzo. También hay decrementos en mayo, junio y diciembre, pero obviamente todos compensados por el incremento acaecido en otros meses, en especial el ocurrido en abril de 2018. Porcentualmente ha acontecido un incremento del 20% anual.
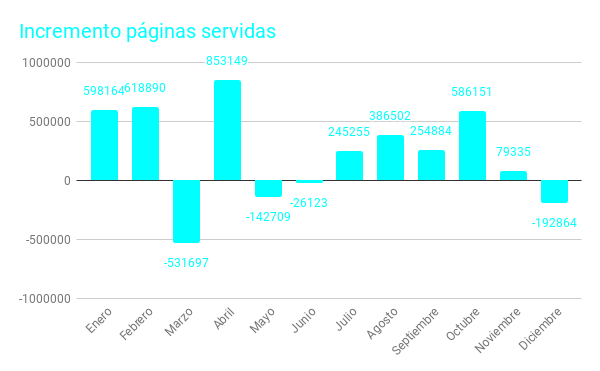
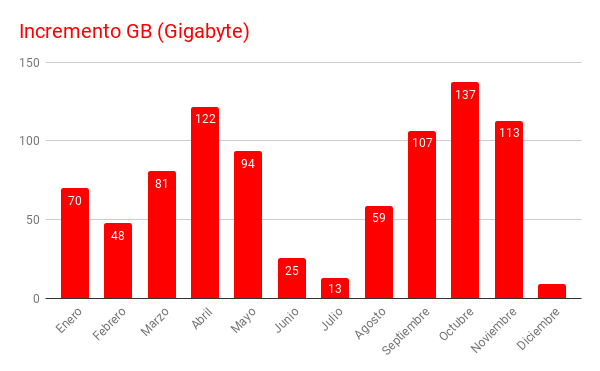
En lo relativo a los GB servidos se ha producido un sustancial incremento en todos los meses, y globalmente en 2017 fueron 1687 GB y en 2018 un total de 2563. Un 50% más. Al ser este porcentaje superior al acontecido con el de páginas podríamos intuir que nuestros usuarios han procedido a realizar un mayor número descargas de nuestros recursos para su uso en local.
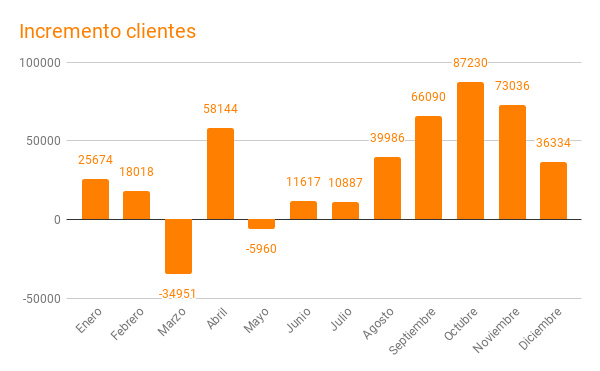
Y en lo que respecta a clientes en 2017 fueron algo más de un millón trescientos mil y en 2018 se paso a un millón ochocientos mil, un 40% adicional.
Nuestro agradecimiento a todos los que, accediendo a nuestro dominio proyectodescartes.org, han ido contribuyendo página a página a incrementar estos y cada uno de los caracteres estadísticos que perfilan el nivel de utilidad de nuestro servicio y, así, estiman y valoran nuestra dedicación altruista en pro de la comunidad educativa de la aldea global.
¡Feliz 2019! y ¡A aprender con Descartes!
Alumnas comunicando y compartiendo ideas matemáticas con Descartes
Escrito por José Antonio Salgueiro GonzálezPrimera píldora invernal para compartir otra experiencia de aula realizada con mi alumnado de 4º de Educación Secundaria Obligatoria del IES Bajo Guadalquivir de Lebrija, en la materia Matemáticas Orientadas a las Enseñanzas Académicas, durante el curso escolar 2017/2018, dando continuidad al proyecto "Desarrollo de la comunicación audiovisual a través de las Matemáticas con Descartes", que puse en marcha hace ya cuatro años con el alumnado de 1º de Bachillerato, unos vanguardistas que inspiraron a sus sucesores. En el artículo enlazado pueden encontrarse los orígenes, objetivos, fundamentación de este proyecto, referencia normativa y los detalles con las distintas fases que deben ir superando los alumnos y alumnas, de forma completamente autónoma, con trabajo colaborativo y sin la intervención del profesor.
Cada año procuro elegir una temática diferente, correspondiendo esta edición a la discusión y resolución de sistemas de ecuaciones lineales, habiendo publicado anteriormente los artículos "Desarrollamos nuestra comunicación audiovisual y nos convertimos en divulgadoras matemáticas" y "¿Son incompatibles el aprendizaje y la diversión en el segundo ciclo de la ESO?".
A pesar del tiempo transcurrido y del número de alumnos y alumnas participantes en la experiencia, no dejan de sorprenderme con su creatividad e imaginación, pues todos los vídeos son completamente diferentes, así como la diversidad en el uso de editores de vídeo y sus estrategias de dirección y realización para desarrollar su comunicación audiovisual a través de las matemáticas, contenidos incorporados en el bloque de “Procesos, métodos y actitudes en Matemáticas”, que debe desarrollarse de modo transversal y simultáneamente al resto de bloques, constituyendo el hilo conductor de la asignatura. Un bloque que se articula sobre procesos básicos e imprescindibles en el quehacer matemático: la resolución de problemas, proyectos de investigación matemática, la matematización y modelización, las actitudes adecuadas para desarrollar el trabajo científico y la utilización de medios tecnológicos, proporcionando, además, una formación competencial.
La organización y planificación de la experiencia se coordina desde el aula virtual Moodle de RED Descartes, que dispone de acceso a invitados.
Quiero felicitar públicamente a Natalia y Celeste, Celeste y Natalia que, constituídas en el equipo María Gaetana Agnesi, en homenaje a esta gran matemática italiana, han conseguido un producto final de calidad con el que nos enseñan a discutir y resolver sistemas 2x2 por los métodos algebraicos conocidos y usando herramientas tecnológicas. Por cierto, en el momento de redactar este artículo, Natalia y Celeste se encuentran ya cursando el primer curso de bachillerato en la modalidad de ciencias sociales.
Mi agradecimiento, como es habitual, a sus familias por autorizar la difusión de este audiovisual en portales educativos y redes sociales.
Más...
Feliz Navidad 2018 con Descartes
Escrito por Juan Guillermo Rivera BerríoDesde RED Descartes Colombia y desde la Institución Universitaria Pascual Bravo os deseamos una Feliz Navidad para todos los cartesianos y pascualinos.
Guardado y continuación de partidas de juegos del Proyecto AJDA
Escrito por Jesús Manuel Muñoz Calle- Pas partidas cuya duración sea grande pueden ser fraccionadas.
- Se puede guardar la partida en diferentes puntos y se podrá continuar desde el punto que se desee.
- Se puede empezar una partida de un juego en una modalidad y continuarse en otra. Por ejemplo, se puede empezar en la modalidad de introducción de preguntas mediante un fichero, continuarla en la modalidad de preguntas orales y terminarla en una sin preguntas.
- Se guardar una partida nada más cargar los nombres y las opciones iniciales y guardarla. De esta forma se puede llevar preparada una partida directamente para empezar a jugar.
- Se puede guardar una partida tras finalizar y servir así para tener registrado el resultado que se haya producido.
- Si se quiere hacer una modificación en los jugadores, opciones del juego, fichero de preguntas, etc., se puede guardar la partida y continuarla con los nuevos datos que deseemos.
- Si se desea cambiar de equipo o navegador, también se puede utilizar este procedimiento.
- Las partidas se podrán guardar cuando el control del menú superior Guardar partida esté activo. Estará activo siempre al comenzar y al terminar una partida y en otras ocasiones según la dinámica del juego.
- Al pulsar el botón Guardar partida se abrirá una ventana de exploración de archivos para indicar el nombre y la ubicación del fichero que contiene los datos y estado de la partida que se guarda.
- En algunos navegadores se producen errores al guardar ficheros. Se debe verificar que se ha guardado correctamente y si no es así se debe repetir el proceso de guardado.
- El nombre por defecto de un fichero para guardar una partida será partida-nombre del juego, pero se puede guardar con el nombre que se desee.
- Una partida guardada en una modalidad de introducción de preguntas de un juego se podrá continuar en cualquier modalidad del propio juego, pero no en otro juego diferente.
- Una partida guardada podrá continuarse cargando el fichero con los datos y estado de una partida guardada a través del control Continuar partida que aparece al principio del juego (en la ventana de introducción de los nombres de los jugadores).
- Al pulsar el botón Continuar partida se abrirá una ventana de exploración de archivos que permitirá buscar y seleccionar el fichero de continuación de una partida anteriormente guardada.
- Si el fichero cargado es correcto dicho botón se pondrá de color azul oscuro con el nombre Partida cargada. Además se podrá ver se han cargado los nombres y las opciones específicas de la partida que se continua.
- En general y salvo que no lo permita la dinámica del juego, una vez cargada una partida guardada, se pueden modificar os nombres y las opciones del juego si se desea.
- Si una vez cargado el fichero de continuación de una partida se carga otro, la partida cargada será la del último fichero válido introducido.
- Si se carga el fichero de continuación de una partida y se quiere anular, se debe utilizar el control de la esquina superior izquierda Reiniciar juego.
- Si se carga un fichero no válido, el botón de Continuar partida se volverá rojo e indicará Fichero no válido. Las cargas de los ficheros no válidos no serán tenidas en cuenta y se considerará cargado el último fichero correcto y si no se ha cargado ninguno correcto el juego comenzará sin considerar continuación alguna de partida.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)








 CONTACTO
CONTACTO
