Vacaciones con Descartes para las familias en 2019
Escrito por José Antonio Salgueiro GonzálezNuestros niños y niñas se encuentran disfrutando del período vacacional de verano, con mucho tiempo para compartir con sus familias y amigos, así como para el descanso y ocio. No obstante, siempre es recomendable encontrar el momento adecuado para sugerirles una interesante lectura y realizar, en nuestra compañía o junto a sus hermanas y hermanos mayores, algunas actividades de las áreas básicas del conocimiento. Ahora bien, para ello, las familias requieren de una orientación y asesoramiento que pueden recibir por diferentes canales de comunicación.
Con este fin, la Red Educativa Digital Descartes ofrece una amplia selección de recursos digitales interactivos a los que pueden accederse desde cualquier lugar y hora, en el campo o en la playa, con un simple ordenador personal, portátil, tableta o smartphone y conexión a la red de internet, aunque también es posible descargarse el objeto de aprendizaje para usarlo en local, es decir, sin conexión a internet.
Estos recursos están organizados y catalogados por etapa educativa y edad, como se aprecia en la imagen inferior, así , las familias podrán seleccionar, con un simple clic sobre la imagen correspondiente o sobre el texto que la acompaña a su derecha, los adecuados para sus hijos e hijas, encontrando la relación con los nombres de las actividades y una breve descripción de la misma.
No obstante lo anterior, cada familia, como mejor conocedora de las capacidades de los niños y niñas, podrá optar por realizar las actividades de diferente edad.
La LOMCE no contempla los tres ciclos de Primaria, sino seis cursos independientes. lo que no supone obstáculo alguno para que los niños y niñas disfruten con estos recursos de gran calidad, pues accediendo al ciclo en cuestión, según la edad, y seleccionando el recurso deseado puede verse con detalle a qué curso concreto corresponde.
Esperamos que esta aportación, completamente gratuita, de la RED Descartes sea de utilidad para el mayor número posible de familias y animamos a dejar comentarios con sus opiniones.
El mapeado de la imagen se ha realizado desde la nube con la herramienta Image-Maps.
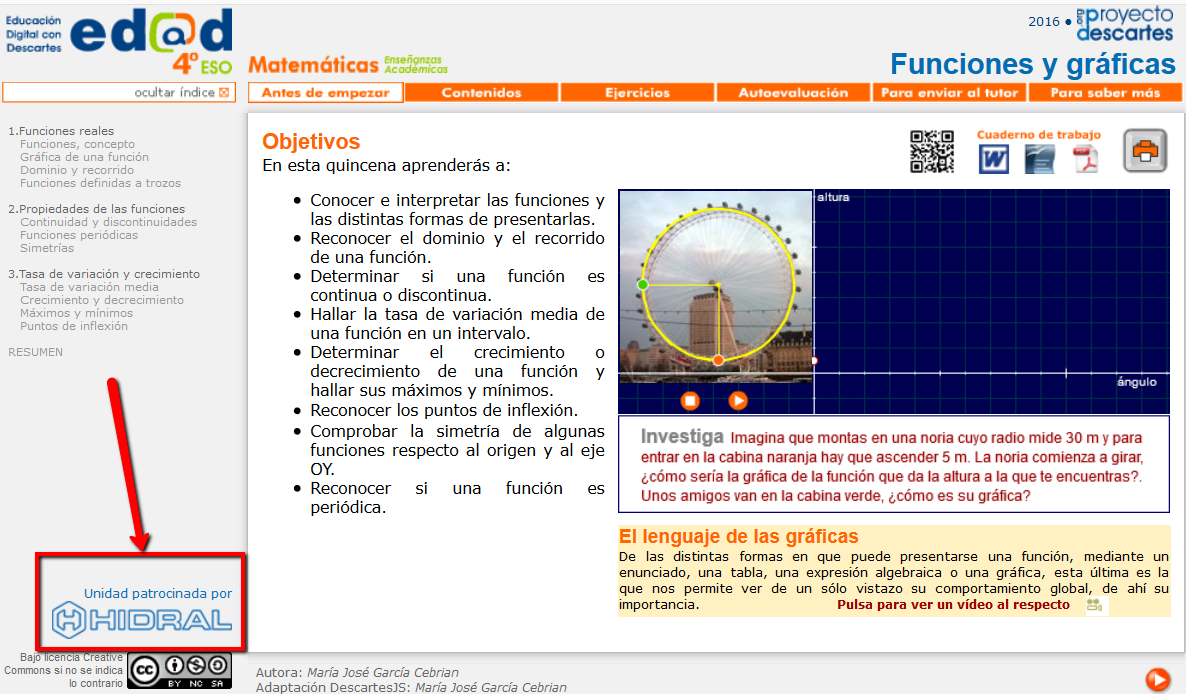
HIDRAL eleva la educación en el siglo XXI
Escrito por José Antonio Salgueiro GonzálezLa empresa HIDRAL, dedicada a la fabricación de elevadores y ascensores para el suministro al profesional, está especializada en el campo de la hidráulica, aunque hoy en día también ofrece soluciones de tracción y VVV F. Con unos objetivos muy claros, que abarcan investigación, desarrollo y un amplio concepto de servicio al cliente que se extiende desde el asesoramiento inicial hasta la atención postventa, Hidral proporciona soluciones innovadoras que superan los modelos estándar y que satisfacen las exigencias concretas de cada cliente, creando diseños personalizados para cada necesidad:
- Elevadores Montacargas: para el transporte de mercancías o elevadores de carga acompañada.
- Montacargas acompañados: ascensores y elevadores destinados al transporte de grandes cargas.
- Ascensores comerciales: con gran adaptabilidad para el sector comercial y servicios.
- Montacoches: ascensores y elevadores para el transporte vertical de vehículos y acompañante.
- Residenciales: elevadores para el transporte vertical de personas con movilidad reducida y residencias.
- Accesibilidad: toda una gama destinada a la eliminación de barreras arquitectónicas.
- Minicargas: elevadores para el transporte de pequeñas cargas.
- Plataformas de tijera: elevación de cargas y personas a alturas relativamente cortas.
- Especiales: proyectos a medida que cubren necesidades totalmente personalizadas
Hidral cuenta con un posicionamiento firme y destacado en el mercado global, pues el 70% del volumen de su producción va destinado a mercados internacionales con presencia en más de 50 paises. Pero, además, Hidral es una empresa comprometida con el mundo de la educación y la difusión del conocimiento, como base de cualquier actividad humana, y por ello ha patrocinado cuarenta recursos educativos interactivos generados con Descartes JS, que son funcionales en cualquier tipo de dispositivo (ordenador, tableta o smartphone). Concretamente, acaba de auspiciar tres libros interactivos de 4º de ESO correspondientes al currículo de Matemáticas Orientadas a las Enseñanzas Académicas, respectivamente en castellano, catalán y gallego.
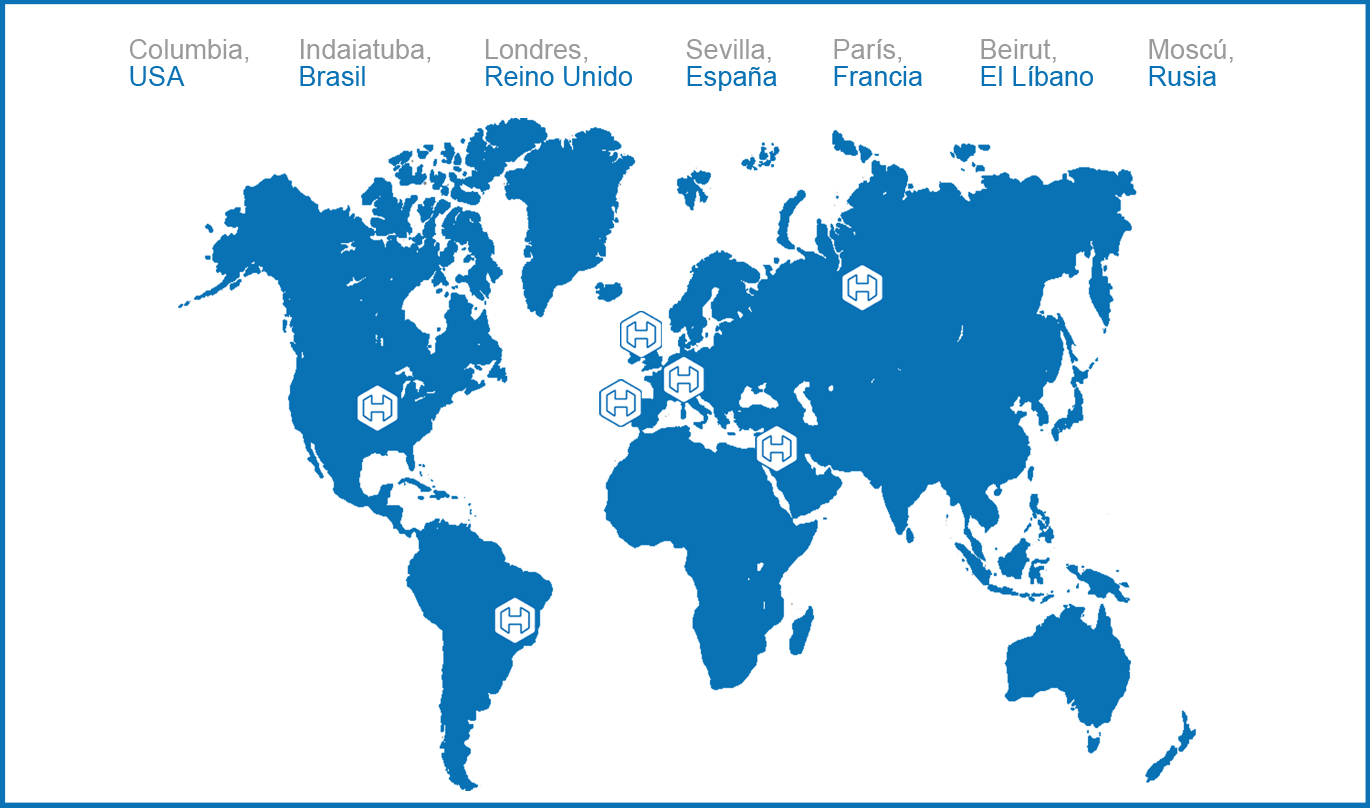
Inmersos en un ambicioso proyecto de internacionalización, Hidral dispone actualmente de más de 20.000 m² repartidos en dos fábricas en Sevilla (España) y otras instalaciones en Brasil, USA, Rusia, Francia, Oriente Medio y Reino Unido.
Proyecto de investigación en AJDA (I)
Escrito por Jesús Manuel Muñoz Calle- Elaboración del Proyecto de Investigación I+D+I titulado "Estudio Integral del Impacto de la Gamificación Digital (GAIMS)".
- Realización de los siguientes Trabajos Fin de Grado (TFG):
- "Integración de herramientas de gamificación en plataformas de Enseñanza Virtual", Pedro García Frutos, 2018.
- "Aplicación web para la creación y modificación de ficheros de juegos para la Aplicación de Juegos Didácticos en el Aula (AJDA)", Carlos Ramos León, 2019.
- "Aplicación Web multiusuario para gamificación educativa en el aula basada en Websocket", Alberto Jiménez Vázquez, 2019.
- En desarrollo hay otros TFG.
- Ampliación y mejora de los espacios Web del Proyecto AJDA y de sus recursos.
- Estudiar y cuantificar el impacto de diferentes técnicas digitales de gamificación, particularizándolas al campo educativo y sentar las bases para futuros estudios en los entornos sanitario, corporativo, comercio y consumo saludable. Dichos estudios se apoyarán en diversas implementaciones tecnológicas para la implantación y obtención de datos. El objetivo final es obtener un protocolo que permita la prescripción adaptativa de técnicas de gamificación adecuadas al nivel, entorno, grupo e incluso individuo sobre el que se aplica. Esto se concretará, entre otros aspectos, en la creación de una herramienta informática que, a través de una búsqueda parametrizada, permitirá seleccionar y ofrecer las recomendaciones sobre técnicas de gamificación que más se ajuste al caso en cuestión.
- Las mejoras técnicas de los recursos del Proyecto AJDA que se concretan en:
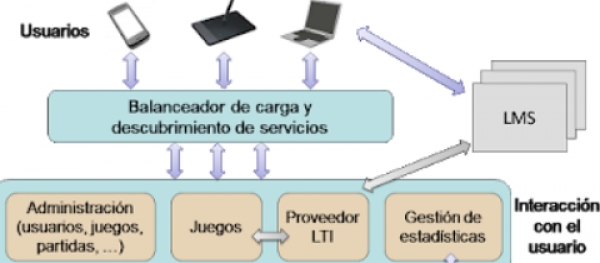
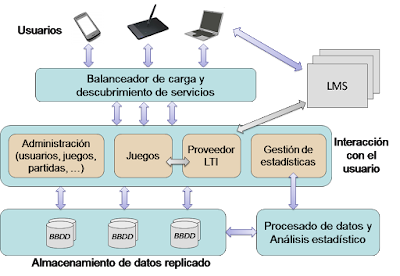
- Interacción con el usuario: alberga toda la lógica de control e interacción con los usuarios, presentando 4 componentes principales, encargados de la administración global de la plataforma, la gestión de los juegos, la gestión de los datos estadísticos y la integración de los juegos en plataformas externas, tales como sistemas LMS mediante el uso de la especificación LTI.
- Almacenamiento replicado de datos: consta de bases de datos, de diversas tecnologías (SQL y no-SQL), que intentan garantizar un almacenamiento y acceso eficiente a los grandes volúmenes de datos, de distinta naturaleza, que deberán procesarse.
- Análisis estadístico y procesado de datos: controlado desde el componente de gestión de datos estadísticos, contienen toda la lógica necesaria para procesar la información obtenida, con técnicas de big data cuando resulte necesario, y extraer los resultados estadísticos útiles para alimentar el modelado propuesto.
- Balanceador de carga: controla el acceso de los usuarios desde los diferentes dispositivos de acceso previstos (ordenadores personales, terminales móviles, tablets, etc.) garantizando la escalabilidad del sistema.
Descartes en Moodle. Actividad “Tarea”
Escrito por Montserrat Gelis BoschVamos a crear en este caso una tarea de moodle. Se trata de una actividad que permite al estudiante entregar material en cualquier tipo de formato para su corrección.
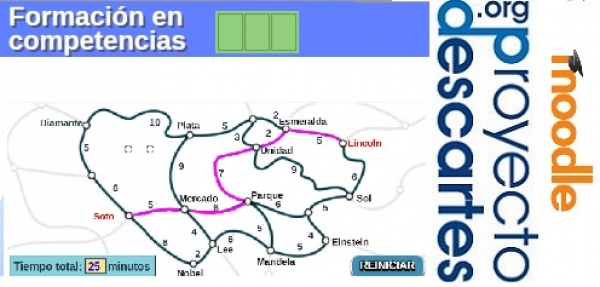
La unidad seleccionada es Tráfico, una unidad perteneciente al grupo PISA 2017 del subproyecto Competencias. Las unidades pertenecientes a este subproyecto se han creado a partir de unidades liberadas PISA y Pruebas de Evaluación Diagnóstico de diferentes Comunidades Autónomas.
En el diseño de las unidades PISA 2017, una vez realizadas las actividades propuestas, se contemplan diferentes opciones, una de ellas es la creación de un documento con las respuestas del alumnado que usaremos en este caso para subir en el lugar correspondiente de la tarea para su corrección.
En el siguiente vídeo se muestra con detalle la creación de una actividad tarea de moodle en la cual se inserta la unidad Tráfico a partir del código para abrir en ventana emergente.
Más...
Nuevo récord mensual de páginas servidas desde proyectodescartes.org
Escrito por José R. Galo Sánchez¡De nuevo hemos alcanzado un nuevo récord mensual en el número de páginas servidas desde nuestro servidor proyectodescartes.org!
No nos gusta ser pesados, ni reiterativos, ni cansar a nuestros usuarios con noticias con contenidos similares o parecer presuntuosos ante una mejora, pero tampoco queremos adolecer de falta de comunicación y de guardarnos noticias que puedan ser origen de satisfacción a todos los que contribuyen a la consecución de estos logros. Así pues, os comunicamos que gracias a todos vosotros en el mes de mayo de 2019 hemos contabilizado más de dos millones cuatrocientas mil páginas servidas.
Hace dos meses os comunicamos que habíamos superado la barrera de dos millones trescientas mil páginas servidas desde nuestro, de todos vosotros, servidor de contenidos. Hoy nos toca anunciar que en el mes de mayo, de este año 2019, hemos llegado a 2413688 páginas, dos millones cuatrocientas trece mil seiscientas ochenta y ocho páginas. Un pasito más en nuestra labor divulgadora y en nuestro objetivo de contribuir a la mejora educativa de una manera altruista, desinteresada en ganancias económicas y muy interesada en ganancias académicas y de igualdad social a través de la educación, de la formación y del conocimiento individual y colectivo, eso que se suele etiquetar como "ascensor social". Y queremos contribuir a que ese elevador pueda estar más cercano y más asequible a más y más personas de nuestro entorno cercano y del lejano gracias a los beneficios que nos pueden aportar las TIC. Un incremento estadístico de accesos no necesariamente tiene correlación directa con el objetivo indicado, pero probabilísticamente es un posible indicador positivo y que, con certeza, contribuye a que incrementemos nuestro interés en continuar trabajando desde nuestra asociación no gubernamental "Red Educativa Digital Descartes" para la comunidad educativa de la aldea global.
¡Muchas gracias a todos! Nos congratulamos mutuamente del nuevo dato estadístico y os animamos a seguir trabajando, estudiando y aprendiendo intensamente para que dentro de pocas semanas podamos volver a felicitarnos con un nuevo récord. No tenemos problema en reiterarnos de nuevo y que podáis pensar y decirnos que somos unos pesados.
Aprovechamos para recordar que hoy hace seis años que constituimos la ong RED Descartes. El 1 de junio de 2013 fue la asamblea constituyente en Alcalá de Henares (Madrid, España). Seis años ampliando y dando continuidad a los veintiún años que ahora también cumple el proyecto Descartes. Sumamos al récord de páginas servidas estas dos celebraciones y nos congratulamos de todos estos años en los que hemos compartido ilusión, trabajo altruista y ganas de contribuir a la Educación. ¡Felicidades a todos! y ¡Continuamos...!
La siguiente tabla refleja lo acontecido estadísticamente en este mes de mayo de 2019
Ejemplo de uso de tres juegos del Proyecto AJDA (II)
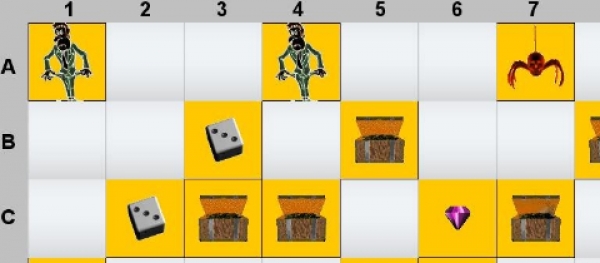
Escrito por Jesús Manuel Muñoz CalleLa última llamada. Es uno de los juegos del concurso de TV "Saber y ganar". En él los concursantes deben emparejar una de las 6 opciones de respuesta con el enunciado que se va planteando. Cuando un jugador falla se acumulan 100 puntos en el bote y cuando acierta se lleva la cantidad acumulada en el mismo.
Tesoro escondido. Es un juego original del proyecto AJDA en el que dos jugadores o equipos deben buscar un diamante en el panel y deberán evitar encontrarse con el fantasma o quedarse sin puntos.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)









 CONTACTO
CONTACTO
