¡Acumulación de acontecimientos, de sentimientos y de agradecimientos!
Escrito por José R. Galo Sánchez¡Séptimo aniversario de RED Descartes! ¡Vigésimo segundo del proyecto Descartes! ¡Nuevo récord de páginas servidas desde nuestro servidor!... centros educativos cerrados, sociedad confinada, enfermedad, sufrimiento, muerte... pandemia. ¡Ciencia, investigación, estudio, aprendizaje, esfuerzo, colectividad, solidaridad!
¡Acumulación de acontecimientos, de sentimientos y de agradecimientos!
Cumplir años en tiempos de pandemia superando récords mes a mes gracias al incremento en el número de nuevos amigos que, estando confinados, necesitan satisfacer su aprendizaje y ejercer su docencia en entornos virtuales, provoca una acumulación de sentimientos contrapuestos. Todo acontece a causa de la concatenación de las extrañas y duras circunstancias en las que vivimos en estos días, pero contribuye a la consecución de nuestros objetivos como asociación. Un paradójico oxímoron que desde RED Descartes tratamos de revestirlo aglutinando la ilusión que nos motiva a trabajar altruistamente con el agradecimiento a quienes nos eligen y, que al hacerlo, dan valor y sentido a nuestro esfuerzo. Agradecimiento que hemos de hacer explícito a nuestros patrocinadores: grupo IC e Hidral que desde el mundo empresarial, con profunda visión social, han apoyado nuestro proyecto educativo y obviamente estos logros también son suyos. Gratitud al Ministerio de Educación español por impulsar y promover el desarrollo del proyecto y la herramienta Descartes durante sus primeros catorce años, al Instituto de Matemáticas de la UNAM por auspiciar el desarrollo de DescartesJS, a la Institución Universitaria Pascual Bravo de Medellín (Colombia) promotora de los libros interactivos y a nuestra red hermana ColDescartes. Y a todos los que en estos veintidós años habéis contribuido a que este proyecto, esta RED, sea una realidad.
¡Felicidades a todos los socios y miembros de RED Descartes!

Los cumpleaños, a cierta edad, suelen acumular sentimientos encontrados pues son hitos significativos en los que se interseca el pasado y el futuro, momentos de reflexión en la transición o continuidad vital. Generan alegría y tristeza, esperanza y añoranza, certeza y duda, perdurabilidad y caducidad. Son momentos en los que lo transcurrido puede, debe, actuar de trampolín para la mejora, más cuando las circunstancias en el entorno no son óptimas y mucho más cuando son más bien desfavorables.
Hoy, 1 de junio de 2020, cumplimos siete añitos como organización no gubernamental sin ánimo de lucro. Hace siete años que decidimos y llevamos a cabo la constitución de la asociación "Red Educativa Digital Descartes". ¡Ya! siete no es mucho, pero es que son veintidós los transcurridos desde que en 1998 surgió el proyecto Descartes, un proyecto de profesorado centrado en la mejora de la educación matemática —en sus orígenes, pero despúes en cualquier materia— usando las TIC y los recursos interactivos desarrollados con la herramienta Descartes. A este proyecto, inicialmente promovido por el Ministerio de Educación español y desarrollado a través de él hasta el año 2012, le tuvimos que dar continuidad, impulso y mejora desde una perspectiva independendiente no gubernamental.
 |
 |
 |
Este aniversario acontece en el preocupante y difícil contexto de una pandemia que se ha adentrado drásticamente en el entorno educativo impidiendo la relación cotidiana directa entre el alumnado y el profesorado dado que los centros escolares de todos los niveles ¡están cerrados! Un cambio drástico en los procedimientos y metodologías que han tenido que encaminarse al uso intensivo y extensivo de las TIC. Pero para poder llegar a una planificación adecuada, que contribuya a intensificar la adquisición de la competencia de "aprender a aprender" y la de autonomía personal, es necesario contar con recursos que potencien y ayuden a ese logro. Y los recursos de nuestra RED, que han sido desarrollados por profesorado que imbuye en ellos su experiencia de aula, pensamos y valoramos que pueden ayudar significativamente a la consecución de ese objetivo, ahora y siempre. Pero el navegante discente y/o docente que llega a nuestro servidor de contenidos es quien tiene en su mano, literalmente, la capacidad de elección. ¡Y eso es lo que ha hecho!
En junio del pasado año coincidió que festejábamos nuestro aniversario con un récord en el número de páginas servidas en un mes (más de dos millones cuatrocientas mil) y estos tiempos de pandemia se han ido incrementando el número de páginas servidas y a la vez se han concatenando nuevos récords. En marzo, con sabor agridulce, superamos los cuatro millones de páginas, en abril ¡ayudamos en los tiempos del COVID-19! con más de cuatro millones seiscientas mil y en este aniversario comunicamos nuestro nuevo récord al haber superado los cinco millones de páginas en el recién acabado mes de mayo.
La siguiente tabla refleja un detalle de lo acontecido estadísticamente en este mes de mayo de 2020 en proyectodescartes.org
Si estos logros estadísticos se han ido sucediendo es porque al otro lado de nuestro/vuestro servidor estáis todos vosotros que nos elegís y que retornáis para dar continuidad a vuestro aprendizaje o docencia. Consecuentemente, también hemos de hacer una acumulación equitativa de agradecimientos y daros millones de gracias por dar sentido a nuestra labor altruista.
En ese cúmulo de agradecimientos hemos de ser especialmente explícitos en nuestro reconocimiento al grupo empresarial IC S. L. (consultar artículo I y artículo II) y a la empresa HIDRAL (consultar artículo), porque desde la perspectiva empresarial han puesto de manifiesto de manera nítida que la formación y la educación es un pilar básico en su modelo de empresa y que en la reinversión social de sus logros y éxitos, ése es un foco básico de interés. Gracias a su patrocinios económicos hemos tenido suficiente holgura monetaria para disponer y mantener, durante los años 2017, 2018 y 2019, la imprescindible infraestructura TIC para el alojamiento de contenidos y difusión de los mismos y, así, poder llegar a todos los amantes del saber y del aprender que nos visitáis. Este agradecimiento se refleja en muchos recursos (pulsad sobre las imágenes para ver un par de ejemplos)
 |
 |
También hemos de agradecer grandemente al Instituto de Matemáticas de la UNAM (Universidad Nacional Autónoma de México) el patrocinio para el mantenimiento y mejora de la herramienta DescartesJS y a José Luis Abreu León que con genialidad y eficiencia ha mimado y mima a Descartes en esta extensa e intensa trayectoria de veintidós años. Y a Joel Espinosa Longi y a Alejandro Radillo Díaz que aportan su buen hacer y saber, y su juventud, dando continuidad vital a la herramienta y con ella al proyecto.
Nuestro agradecimiento a la Institución Universitaria Pascual Bravo de Medellín (Colombia) por su apoyo directo al proyecto Descartes y especialmente por impulsar los libros interactivos y publicarlos bajo su sello editorial, y a nuestra red hermana "Red Educativa Digital Descartes Colombia" que no sólo suma sino que multiplica poniendo de manifiesto la sinergia de la colaboración.
Y en la reflexión acerca de lo vivido hay que remontarse al nacimiento y a los primeros años, aquellos en los que se asientan los pilares de un futuro seguro y firme, y así agradecer a Agustín Quintana Alonso y a Juan Madrigal Muga, que desde el Intef del Ministerio de Educación español, vislumbraron y trazaron las líneas primigenias del proyecto Descartes, atisbando que este proyecto educativo tenía que configurarse como un proyecto de profesorado en pro de la comunidad educativa, que llegara y se desarrollara a pie de aula y que introdujera cambios metodológicos apoyados en la tecnología, pero donde ésta quedara diluida.
Agradecimiento a todos los pioneros cartesianos que, en el interludio de cambio del siglo XX al XXI, acudieron con ilusión a trasladar su inquietud y experiencia profesional en los albores de Descartes y que aportaron los mimbres con los que se empezó a dar forma a un proyecto y a una realidad —perdonad que no detalle aquí vuestros nombres, la lista es amplia y sería muy probable que cometiera una omisión imperdonable, todos estáis reflejados en nuestro servidor de contenidos a través de las aportaciones que habéis ido realizando—. Gratitud a quienes conformaron proyectos de profesorado análogos usando la herramienta Descartes como el proyecto Newton (hoy unificado dentro de la RED Descartes) y a todos los que en estos veintidós años habéis dedicado en algún momento parte de vuestro saber, de vuestro tiempo y de vuestra experiencia aportando lo que habéis podido, sin cuantificar si es poco o mucho porque toda contribución es importante.
Y, finalmente, agradecimiento infinito a todos los socios de RED Descartes por haber constituido esta asociación y seguir con empeño contribuyendo día a día a la consecución de sus objetivos estatutarios.
¡Continuamos...! ¡Con ilusión iniciamos un nueva vuelta al Sol... con Descartes!
Superficies desarrollables con Descartes
Escrito por José R. Galo SánchezEn este artículo se describen y clasifican las superficies regladas desarrollables poniendo de manifiesto que éstas son cilindros, conos y superficies tangenciales. Y, mediante el uso de Descartes, se permite al usuario abordar la construcción virtual de "su" cilindro y cono personalizado, pero también se le da la posibilidad de convertirlo en un objeto tridimensional tangible sin más que proceder a la obtención automática de su desarrollo plano y, mediante su impresión en papel, proceder a su construcción.
Superficies regladas desarrollables
Una superficie es reglada si está constituida por una familia de rectas. Todas estas superficies se pueden parametrizar como:
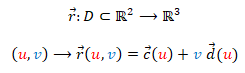 (1)
(1)
donde 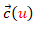 y
y 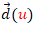 son curvas en el espacio tridimensional. La primera es la curva base o curva directriz y la segunda es el vector director de cada una de las rectas (generatriz). Efectivamente, fijado un valor del parámetro u puede observarse que la expresión obtenida es la ecuacion de una recta y, variando u, geométricamente lo que se puede interpretar es que se va recorriendo cada punto de la curva base
son curvas en el espacio tridimensional. La primera es la curva base o curva directriz y la segunda es el vector director de cada una de las rectas (generatriz). Efectivamente, fijado un valor del parámetro u puede observarse que la expresión obtenida es la ecuacion de una recta y, variando u, geométricamente lo que se puede interpretar es que se va recorriendo cada punto de la curva base 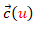 y por él pasa una recta cuya dirección viene dada por
y por él pasa una recta cuya dirección viene dada por 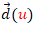 .
.
También puede expresarse de manera equivalente como:
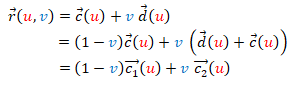 (2)
(2)
que algebraicamente representa, para cada valor de u, a una recta (o un segmento si consideramos 0 ≤ v ≤ 1), pero en este caso lo que se pone de manifiesto es que esa recta se apoya en un punto de la curva 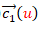 y en otro de la
y en otro de la 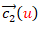 .
.
El ejemplo más simple de superficie reglada es un plano, pero entre otras, también lo son los cilindros, los conos, la banda de Moebius, el hiperboloide, etc.
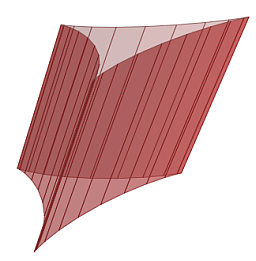 |
 |
| Cilindro generalizado | Cono generalizado |
 |
 |
| Banda de Möbius | Hiperboloide |
Una herramienta matemática que permite caracterizar la curvatura de cualquier superficie regular es la denominada curvatura de Gauss, y se verifica que dicha curvatura es invariante por isometrías. Todas las superficies regladas cumplen que su curvatura de Gauss es menor o igual que cero y, en particular, que la curvatura de Gauss de un plano es identicamente nula. En base a lo anterior, todas las superficies regladas que tienen curvatura cero son isométricas con el plano y son denominadas como superficies desarrollables ya que, consecuentemente, pueden construirse a partir de su desarrollo plano.
En la parametrización (1) la condición de curvatura nula equivale a que el denominado parámetro de distribución sea nulo, y éste viene dado por:
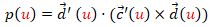 (3)
(3)
o en el caso de la parametrización (2) como:
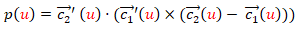 (4)
(4)
De (4) se observa que para que la superficie reglada sea desarrollable tiene que ocurrir que para todo u el vector tangente a la curva 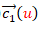 , el vector tangente a
, el vector tangente a 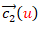 y el vector director de la recta que une a ambas curvas sean coplanarios al ser el producto mixto de los tres cero, o dicho de otra forma que el plano tangente es constante lo largo de cada recta generatriz.
y el vector director de la recta que une a ambas curvas sean coplanarios al ser el producto mixto de los tres cero, o dicho de otra forma que el plano tangente es constante lo largo de cada recta generatriz.
Pero un análisis más detenido de cuándo es identicamente nulo el parámetro de distribución nos puede permitir clasificar a las superficies desarrollables. Así en la expresión (3):
- Si
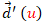 es identicamente nulo, entonces
es identicamente nulo, entonces 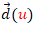 es un vector constante, es decir que todas las rectas tienen la misma dirección y la superficie es un cilindro generalizado de ecuación
es un vector constante, es decir que todas las rectas tienen la misma dirección y la superficie es un cilindro generalizado de ecuación 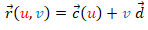 .
. - Si
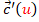 es idénticamente nulo, entonces
es idénticamente nulo, entonces 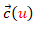 es el vector de posición de un punto V y la superficie desarrollable es un cono generalizado de vértice V, cuya ecuación sería
es el vector de posición de un punto V y la superficie desarrollable es un cono generalizado de vértice V, cuya ecuación sería 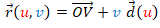 . También puede expresarse en función de una curva base como
. También puede expresarse en función de una curva base como 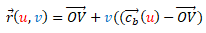 .
. - En cualquier otro caso se demuestra que es una superficie tangencial, que mediante un cambio de parámetro se puede expresar como
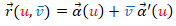 .
.
- Si
Superficies desarrollables con Descartes
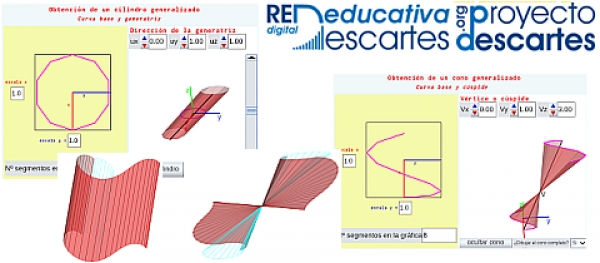
En el proyecto "El metro: patrón inexacto para medir exactamente", que en el año 2004 contó con una ayuda de la Junta de Andalucía (España) para la elaboración de materiales y recursos educativos digitales, desarrollamos con Descartes en su versión Java algunos objetos educativos interactivos sobre conos y cilindros generalizados incluyendo la posibilidad de obtener su desarrollo plano. En este año 2020 hemos procedido a adaptarlos a DescartesJS y a mejorar sus posibilidades, en particular en lo relativo a forma de obtener ese desarrollo plano, a incluir la posibilidad de su impresión y consecuentemente a la posibilidad de su reproducción tangible tridimensional. Estos recursos actualizados están publicados en el subproyecto "misceláneas" de la RED Descartes y los enlazamos a continuación aquí en dos triadas de imágenes que respectivamente se corresponden con cilindros y conos generalizados.
En la primera triada correspondiente a los cilindros tenemos:
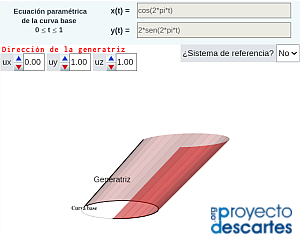
- "Cilindro generalizado" donde se muestra la construcción de un cilindro tomando como curva base una elipse y en la que podemos cambiar la dirección de la recta generatriz. La escena permite reproducir la generación del cilindro mediante desplazamiento de la generatriz sobre la curva base; simular y obtener el desarrollo plano; imprimir dicho desarrollo y el de las bases del cilindro. Adicionalmente, dado el contexto en el que se desarrolló originalmente esta escena —el metro—, se puede obtener un sistema de referencia basado en meridianos y paralelos.
- "Ejemplos de cilindros generalizados" donde se puede elegir diferentes curvas base (circunferencia, elipse, parábola, rama de hipérbola, segmento, cardiode, deltoide, bifolium, astroide, bicircular) y reproducir las acciones indicadas en la escena anterior.
- "Construyo mis cilindros" que como indica el título permite al usuario definir la curva base en coordenadas paramétricas y la dirección de la generatriz que desee y con ellas construir su cilindro generalizado. De nuevo puede realizar de manera virtual interactiva las acciones ya indicadas, pero también procediendo a la impresión del desarrollo pasar a disponer de la versión tangible de "su" cilindro. Para cada curva base cambiando el número de segmentos que se desean considerar en la representación se obtienen diferentes cilindros, para simular el caso continuo basta seleccionar un número de segmentos suficientemente elevado.
 |
 |
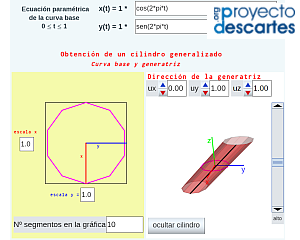 |
| Cilindro generalizado | Ejemplos de cilindros generalizados | Construyo mis cilindros |
De manera análoga en la triada correspondiente a los conos generalizados tenemos:
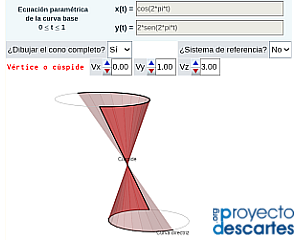
- "Cono generalizado" en el que se muestra la construcción de un cono tomando como curva base una elipse y en la que podemos cambiar su vértice. La escena interactiva permite reproducir la generación del cono mediante desplazamiento de la generatriz sobre la curva base; visualizar el cono completo; simular y obtener el desarrollo plano; imprimir dicho desarrollo y el de la base del cono. Adicionalmente, dado el contexto en el que se desarrolló originalmente esta escena —el metro—, se puede obtener un sistema de referencia basado en meridianos y paralelos.
- "Ejemplos de conos generalizados" donde se puede elegir diferentes curvas base (las mismas que en el caso de los cilindros) y reproducir las acciones indicadas en la escena anterior.
- "Construyo mis conos" que permite al usuario definir la curva base y el vértice y construir su cono generalizado tanto virtual como tangible..
 |
 |
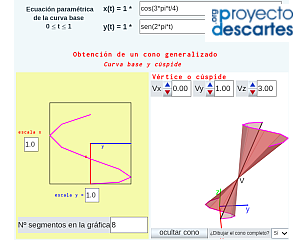 |
| Cono generalizado | Ejemplos de conos generalizados | Construyo mis conos |
En estos objetos interactivos se ha considerado que la curva base es una curva plana, así pues, he de ponerme la tarea de incorporar la tridimensionalidad de la curva base y presentarlo en un próximo artículo en este blog. Y, adicionalmente, este trabajo debería incoporar el caso de superficies tangenciales que implictamente, a priori, entraña cierta dificultad si se deja libertad de definición al usuario, pero sobre ello ya hablaremos.
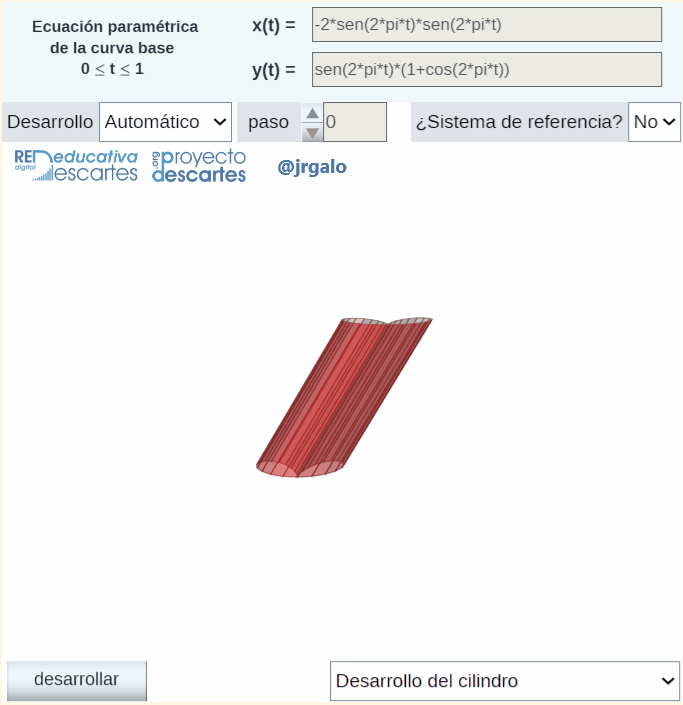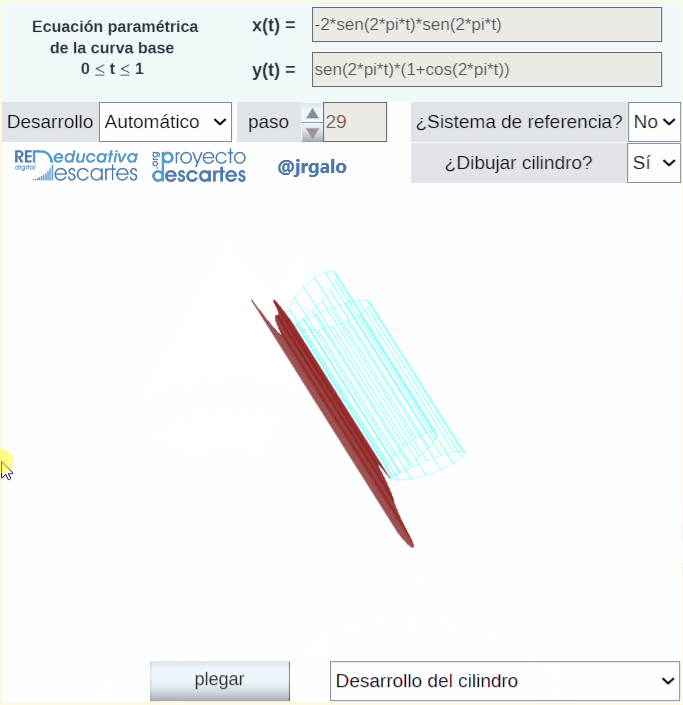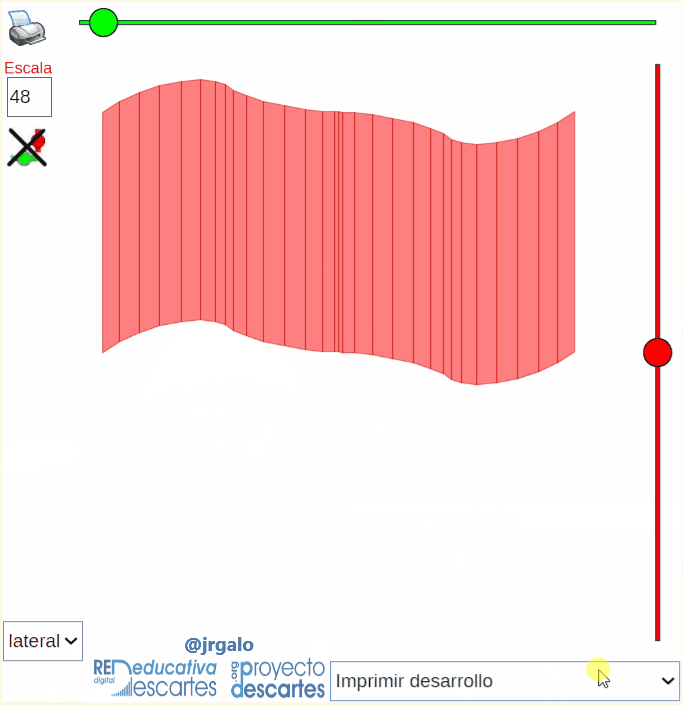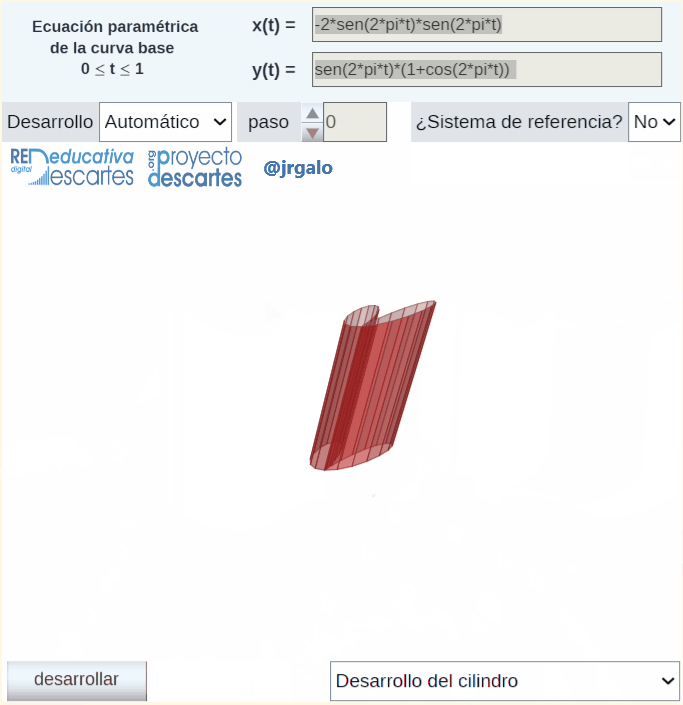
Finalizo reseñando que para la obtención automática y animada del desarrollo plano del cilindro y el cono se aplica la rotación de Rodrigues descrita en un artículo anterior de este blog. Lo que se hace es plantearlo como el desarrollo plano de un prisma o una pirámide que se ajuste suficientemente al cilindro o cono dado. En la animación siguiente se refleja el desarrollo plano de un cilindro generalizado en el que su base es la curva denominada bifolium.
Pulsa sobre la imagen para ampliarla
Bibliografía
Lucas, E. (2017). Superficies regladas [Trabajo fin de grado]. Universidad de Murcia.
Rosado, E (2010). Superficies regladas [Apuntes docentes]. Universidad Politécnica Madrid.
- Propuestas de realización de nuevos juegos.
- Mecánicas o metodologías en el uso de juegos.
- Mejora en los materiales de formación: cursos, tutoriales, guías...
- Recursos y portales del Proyecto.
- Difusión del Proyecto.
- Sobre cualquier otra cuestión relacionada.
El cese de la actividad lectiva debido a las medidas excepcionales por la evolución del COVID-19 durante este tercer trimestre, nos ha obligado a replantear algunos aspectos relacionados con la docencia en las diferentes etapas educativas.
La etapa final de bachillerato merece especial atención ante la inminente realización de la Evaluación de Bachillerato para el acceso a la Universidad, que se llevará a cabo, previsiblemente, antes del verano. Muchos de los proyectos de la RED contienen materiales interactivos para 2º de bachillerato, que permiten al alumnado seguir el curso desde su casa y con la ayuda del profesorado, prepararse para las pruebas de selectividad.
En el siguiente vídeo presentamos la unidad Matrices, Determinantes y Sistemas de Ecuaciones del proyecto iCartesiLibri de la RED para el estudio del álgebra matricial y sus aplicaciones en la resolución de sistemas de ecuaciones. Su diseño, en forma de libro dinámico interactivo, proporciona una forma ágil y sencilla de navegación entre las diferentes páginas.
El contenido se ha elaborado siguiendo las pautas que marca el currículo de Matemáticas II de 2º de bachillerato y contiene, además de la parte teórica, muchos ejemplos y ejercicios para practicar.
Al final de la unidad se presenta una escena con los problemas de Álgebra propuestos en la Evaluación de Bachillerato para el acceso a la Universidad del año 2018, en cada distrito universitario de España.
Más...
RED Descartes, ¡ayudando en tiempos de COVID-19!
Escrito por José R. Galo SánchezEn RED Descartes finalizamos el mes de marzo con sabor agridulce, pues en el tristísimo contexto de una pandemia global logramos ¡un nuevo récord en nuestro servidor proyectodescartes.org! El mes de abril transcurrió en confinamiento y a la amarga suma de tantos y tantos fallecidos se hace muy difícil anexar ninguna otra contabilización. Sólo constatando que hay unicidad entre vida y muerte y que en el transcurso o ciclo de un estado a otro la formación es imprescindible, nos atrevemos a cuantificar, en cierta forma, nuestra altruista contribución a la comunidad educativa de la aldea global en estos tiempos de COVID-19. En el mes de abril de 2020 hemos alcanzamos un nuevo récord y han sido más de cuatro millones seiscientas mil páginas las que hemos servido y en cada una de ellas hemos añadido siempre ¡mucha ilusión, ánimo y esperanza!
En el mes de abril de 2020, el número de páginas servidas desde nuestro servidor proyectodescartes.org ha experimentado un incremento de más de quinientas mil páginas con respecto al mes de marzo, un 14% más que el récord alcanzado ese mes y casi un 200% respecto al anterior récord que conseguimos hace un año, en mayo de 2019. En total: 4 666 818 páginas.
El cierre de los centros educativos, motivado por la pandemia del COVID-19, ha provocado perspectivas educativas diferentes, han surgido nuevas necesidades y muchas de ellas han podido ser satisfechas a través de nuestro proyecto educativo. Eso es lo que hemos podido constatar en nuestro servidor que ha estado bastante ocupado dando servicio a las peticiones realizadas y que, afortunadamente, se ha portado de manera eficiente en casi todo el tiempo transcurrido. En algún momento el elevado número de conexiones ralentizó la respuesta y casi llegó al bloqueo, pero una reconfiguración del sistema ha devuelto la agilidad necesaria.
En la siguiente tabla se puede consultar en detalle parte de lo que acontecido observando las estadísticas de los registros automáticos en nuestro dominio proyectodescartes.org. Quien se adentre un poco en esa tabla puede observar que el día 10 y el 11 hay reflejadas unas cantidades muy bajas en relación al resto, la razón es que esos dos días tuvimos problemas con los archivos de "log" y no contabilizaron adecuadamente lo acontecido esos dos días, por tanto, el récord podría haber sido mayor al que reflejamos aquí. Pero no es nuestra preocupación, ni objetivo esencial, el superar récords, establecer marcas, nuestro fin es únicamente educativo y el seguimiento de estas estadísticas es meramente para tener una orientación del servicio que damos y de la utilidad de nuestro trabajo, con el matiz de que somos conscientes que la cantidad aporta sólo una visión parcial. Visión que hay que complementar cualitativamente con otras informaciones conseguidas por otros medios y que no son objeto de análisis aquí.
La siguiente tabla refleja un detalle algo más extenso de lo acontecido estadísticamente en este mes de abril de 2020 en proyectodescartes.org
Nuestro agradecimiento a todos los que os acercáis a este servidor, a los que hacéis una valoración positiva de nuestra labor y a los que regresáis para que podamos aprender todos juntos.
¡Continuamos...!
Congruencias en el triángulo de Pascal
Escrito por José R. Galo SánchezEn el artículo "El rectángulo de Newton como «simétrico» del triángulo de Pascal" llegamos a la conclusión de que si conocemos las congruencias con cero de los coeficientes en el Triángulo de Pascal, según la orientación dada por Pascal a su triángulo, entonces, por simetría, tenemos las correspondientes al rectángulo de Newton. Eso es lo que se refleja en la siguiente imagen.
Imagen de las congruencias con cero módulo dos de los coeficientes binomiales en el rectángulo de Newton.
Simetría respecto a esas congruencias en el Triángulo de Pascal
En este artículo vamos a centrarnos en analizar cuándo un coeficiente binomial es divisible por un determinado número primo, un problema sobre el que podemos encontrar bastantes resultados con fundamento aritmético y algebraico. Aquí, nos centraremos en aquellos resultados que nos permitan determinar y visualizar gráficamente esas congruencias, es decir, poder obtener el gráfico de la imagen anterior, u otros análogos, sin necesidad de calcular el coeficiente binomial y determinar su congruencia u obtener ésta mediante una recurrencia.
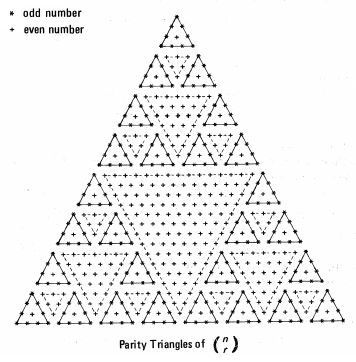
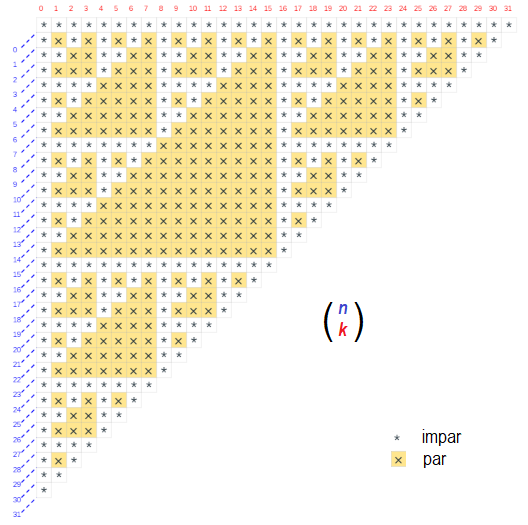
La primera representación gráfica de estas congruencias puede situarse en un brevísimo artículo de Kung (1976). Esa gráfica se muestra en la siguiente imagen, la situada a la izquierda, y en la de la derecha se refleja la gráfica análoga, pero mostrándola según la orientación original de Pascal y coloreando en naranja los números combinatorios pares (en ella cada número se determina observando el correspondiente índice superior en color azul y en rojo el inferior):
 |
 |
|
Triángulos de paridad en el Triángulo de Pascal. Kung, S. H. L. (1976). |
Triángulos de paridad en el Triángulo de Pascal en su orientación original |
Kung adicionalmente afirma, sin incluir la demostración, que para i entero no negativo:
- Si n = 2i y 1 ≤ k ≤ n-1, entonces
 es par.
es par. - Si n = 2i-1 y 0 ≤ k ≤ n, entonces
 es impar.
es impar.
Y ello se observa en las imagenes anteriores ya que para n = 0, 3, 7, 15, 31, todos los símbolos en esas filas o diagonales, respectivamente, son asteriscos (números impares). Y para n = 2, 4, 8, 16, 32, son todos cruces (números pares), salvo el primero y el último.
Ese es un breve artículo, pero que marca unas pautas que son extrapolables a la obtención de patrones en las congruencias con cero módulo otros números primos. De hecho, ese resultado es un caso particular de los dos que fueron enunciados en 1947 por N. J. Fine en su artículo "Binomial coefficients modulo prime", si bien el primero de ellos (según Joris et al. en un artículo de 1985) ya lo formuló Ram en 1909 (B. RAM, Common factors of n!/m!(n-m)!, (m= 1, 2 ,..., n- l), J. Indian Marh. Club (Madras) 1 (1909), 39-43):
- La condición necesaria y suficiente para que todos los coeficientes binomiales
 con 0 < k < n, sea divisible por un primo p es que n sea una potencia de p.
con 0 < k < n, sea divisible por un primo p es que n sea una potencia de p. - La condición necesaria y suficiente para que ningún coeficiente binomial de índice superior n, con n = n0 + n1 p + n2 p2 + ⋅⋅⋅ + nm pm, siendo 0 ≤ nr < p y nr > 0, sea divisible por p es que nr = p - 1 para r < m.
Veamos cómo se reflejan estos resultados de una manera gráfica en las dos imágenes siguientes:
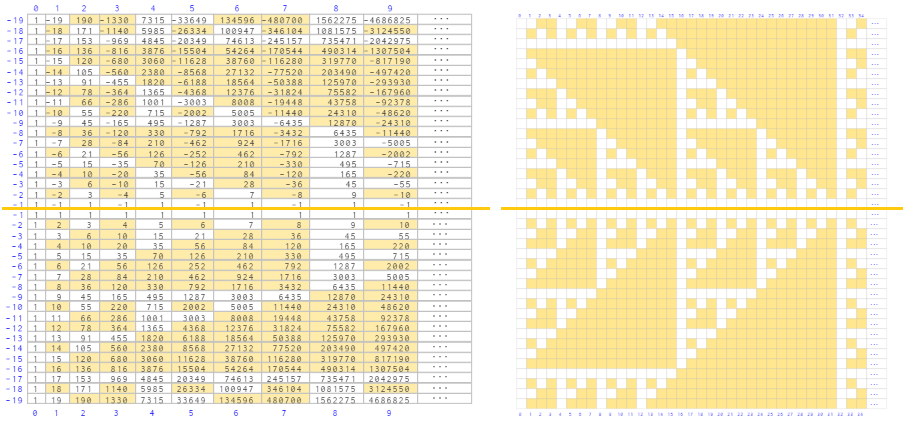
- En la imagen izquierda, se refleja gráficamente el primer resultado cuando p = 3, mostrándose todas las líneas en las que todos los números combinatorios son divisibles por 3, salvo el primero y el último. Esas líneas se corresponden con
 con 0 < k < n y n = 30, 31, 32, 33,... Gráficamente vienen a ser las "hipotenusas" de los triángulos rectángulos que particionan al triángulo de Pascal y que lo muestran a diferentes escala y posteriormente utilizaremos esta analogía y terminología coloquial para ubicar y describir otros resultados.
con 0 < k < n y n = 30, 31, 32, 33,... Gráficamente vienen a ser las "hipotenusas" de los triángulos rectángulos que particionan al triángulo de Pascal y que lo muestran a diferentes escala y posteriormente utilizaremos esta analogía y terminología coloquial para ubicar y describir otros resultados. - En la de la derecha se reflejan aquellas líneas en las que ningún número combinatorio es divisible por 3. En la parte superior de esa imagen se reflejan las separaciones entre esas filas (por falta de espacio tipográfico no se refleja el caso 30) y a la derecha se muestra la descomposición p-ádica del índice n correspondiente a los números combinatorios de cada una de esas líneas (expanda la imagen pulsando sobre ella para verlo). Por ejemplo, para 53 = 2 30 + 2 31 + 2 32 + 1 33 y eso nos muestra el camino de "saltos" de amplitud potencias de tres que se han de dar para, partiendo de 0, llegar a 53 (dos de amplitud 30, dos de 31, dos de 32 y uno de 33). Es decir, logramos mostrar visualmente, geométricamente, lo que queda escondido en un abstracto resultado algebraico, el cual puede ser chocante a cualquiera que accede a él por primera vez. Emulando a nuestro alumnado a la pregunta: ¿a quién se le ocurre que la descomposición p-adica da respuesta a este problema? le mostramos que el resultado algebraico, posiblemente, fue consecuencia de su visualización y la "pureza" matemática procedió a esconderlo.
En la miscelánea del final de este artículo podemos reproducir las situaciones descritas para cualquier primo hasta el 31 y en este enlace se tiene un muestrario rápido de las mismas.
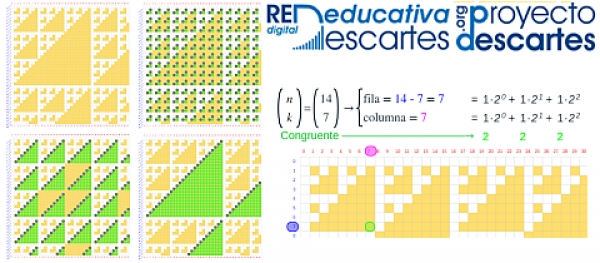
Y justamente, en base a la observación de esos patrones geométricos, podemos visualizar y deducir la propiedad que nos permite detectar todas las hipotenusas de todos los triángulos rectángulos isósceles que muestran esas congruencias. Podemos ver cómo hay triángulos de diferente tamaño, siendo pa-1 el tamaño de las hipotenusas respectivas, y cada uno de ellos tienen una distribución periódica en horizontal y vertical con un periodo pa. Por ejemplo, en la siguiente imagen se reflejan en color naranja los números combinatorios congruentes con cero módulo 5 y se observan tres tipos de triángulos según su tamaño: los de hipotenusa 4 = 51-1, los de 24 = 52-1 y parcialmente (en la esquina inferior derecha) el de 124 = 53-1. La hipotenusa del primero se ha reflejado en color verde y el triángulo se repite periódicamente en horizontal y vertical con un periodo 5, según se ve en dicha imagen. La del segundo está reflejada en color violeta y se repite también periódicamente con periodo 52, y así sería de manera análoga y sucesiva.
 Periodicidad en las hipotenusas de los triángulos congruentes
Periodicidad en las hipotenusas de los triángulos congruentes
Lo anterior, ahora le invito a que mire con ojos algebraicos, queda englobado en el resultado que enuncio a continuación:
p es divisor de todos los números combinatorios 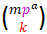 con m, a, k ∈ ℕ, 0 < k < mpa y k no divisible por pa (1)
con m, a, k ∈ ℕ, 0 < k < mpa y k no divisible por pa (1)
Este resultado personal puede relacionarse o considerarse como una reinterpretación —que se centra, enfoca y destaca el aspecto de periodicidad— del aportado por Ram (1909) —del que puede verse la demostración realizada por Albree (1972)— que afirma:
Para cualquier entero positivo n , pr = mcd {  con 0 < k < n, y mcd (k, p)=1 } donde p es primo, r es un entero positivo y pr divide a n.
con 0 < k < n, y mcd (k, p)=1 } donde p es primo, r es un entero positivo y pr divide a n.
Y ¿por qué les remarco que es de gran interés determinar esas hipotenusas? La respuesta también puede visualizarse en la imagen anterior y lo detallamos a continuación ya que conocida una hipotenusa de números congruentes con 0 módulo p,  con r < k < s, por la propiedad de los números combinatorios que relaciona los de índice superior n+1 con los de índice n,
con r < k < s, por la propiedad de los números combinatorios que relaciona los de índice superior n+1 con los de índice n,
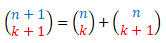
se deduce que los números combinatorios que componen el triángulo rectángulo T(n; r, s)
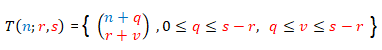 (2)
(2)
—ver imagen siguiente— son también congruentes con 0 módulo p. La justificación es simple, dado que la suma de dos números divisibles por p es un número divisible por p.
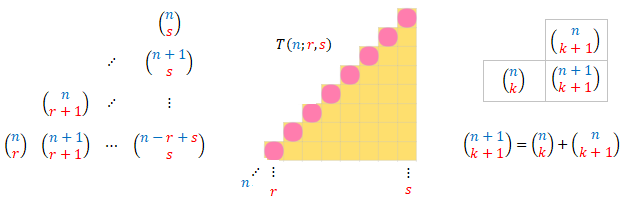 Transmisión de la congruencia en las hipotenusas a los triángulos rectángulos
Transmisión de la congruencia en las hipotenusas a los triángulos rectángulos
Joris et al. (1985) abordan un estudio más profundo al que necesitamos aquí de las propiedades de estos triángulos y a él dirigimos a quienes estén interesados en incrementar su conocimiento en este tema.
Combinando (1) y (2), concluyo que los números combinatorios congruentes con 0 módulo p siguen un patrón de triángulos "rectángulos" T(pa; 1, pa-1) cuyas hipotenusas están constituidas por los números combinatorios 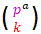 con a, k ∈ ℕ, 0 < k < pa.
con a, k ∈ ℕ, 0 < k < pa.
 Patrón de triángulos T(pa; 1, pa-1) con p=3 y a = 1,2, y 3
Patrón de triángulos T(pa; 1, pa-1) con p=3 y a = 1,2, y 3
distribuyéndose de forma periódica según el esquema:
T(m pa; 1+k pa, (1+k)pa-1) con 0 ≤ k < m y a, m ∈ ℕ
Eso es lo que se observa en el siguiente mosaico de imágenes donde se refleja:
-
- imagen superior izquierda: números combinatorios congruente con 0 módulo 3 en color naranja.
- imagen superior derecha: triángulos congruentes con T(31; 1, 31-1) en color verde claro y las hipotenusas en verde oscuro, y desplazamiento periódico en horizontal y vertical con periodo 3.
- imagen inferior derecha: triángulos congruentes con T(32; 1, 32-1) en color verde claro y las hipotenusas en verde oscuro, y desplazamiento periódico en horizontal y vertical con periodo 32.
- imagen inferior derecha: triángulos congruentes con T(33; 1, 33-1) en color verde claro y las hipotenusas en verde oscuro, y desplazamiento periódico en horizontal y vertical con periodo 33.
 Esquema de periodicidad de los triángulos T(pa; 1, pa-1) con p=3 y a = 1, 2, y 3
Esquema de periodicidad de los triángulos T(pa; 1, pa-1) con p=3 y a = 1, 2, y 3
Así pues la reproducción de todas las congruencias con 0 es una mera reiteración gráfica, periodicidad, de esos triángulos básicos citados.
Pero dado un número combinatorio  ¿podemos saber si es o no congruente con 0 módulo p sin necesidad de calcularlo, de una manera sencilla, rápida y sin aplicar recursividad, o lo que es equivalente, sin basarse en diagonales, es decir, en números combinatorios con índice superior menor que n? ¡Veamos que sí! y para ello nos vamos a basar en la posición relativa (fila y columna) que ocupa cada número combinatorio en el triángulo de Pascal original. Observemos que el número
¿podemos saber si es o no congruente con 0 módulo p sin necesidad de calcularlo, de una manera sencilla, rápida y sin aplicar recursividad, o lo que es equivalente, sin basarse en diagonales, es decir, en números combinatorios con índice superior menor que n? ¡Veamos que sí! y para ello nos vamos a basar en la posición relativa (fila y columna) que ocupa cada número combinatorio en el triángulo de Pascal original. Observemos que el número  ocupa la fila n-k y la columna k, que todos los números combinatorios de índice n cumplen que la suma de la fila y la columna que ocupan es n, y que los números combinatorios del triángulo rectángulo T(n; r, s) cumplen que la suma de la fila y la columna de todos ellos es mayor o igual que n. Con este dato y en base a la periodicidad podemos afirmar lo siguiente:
ocupa la fila n-k y la columna k, que todos los números combinatorios de índice n cumplen que la suma de la fila y la columna que ocupan es n, y que los números combinatorios del triángulo rectángulo T(n; r, s) cumplen que la suma de la fila y la columna de todos ellos es mayor o igual que n. Con este dato y en base a la periodicidad podemos afirmar lo siguiente:
Dado el número combinatorio  , consideremos la descomposición p-ádica de n-k y de k
, consideremos la descomposición p-ádica de n-k y de k
n-k = a0 + a1 p + a2 p2+ ⋅ + am pm
k = b0 + b1 p + b2 p2+ ⋅ + bm pm
con m = max (ent(logp(n-k)), ent(logp(k)) ), 0 ≤ aj, bj < p, se verifica que:
 es divisible por p si y solo si aj + bj ≥ p al menos para algún j, 0 ≤ j ≤ m.
es divisible por p si y solo si aj + bj ≥ p al menos para algún j, 0 ≤ j ≤ m.
Además, para los valores de j en los que aj + bj ≥ p, entonces  está en un triángulo T(pj+1; 1, pj+1-1) de números congruentes con 0 módulo p.
está en un triángulo T(pj+1; 1, pj+1-1) de números congruentes con 0 módulo p.
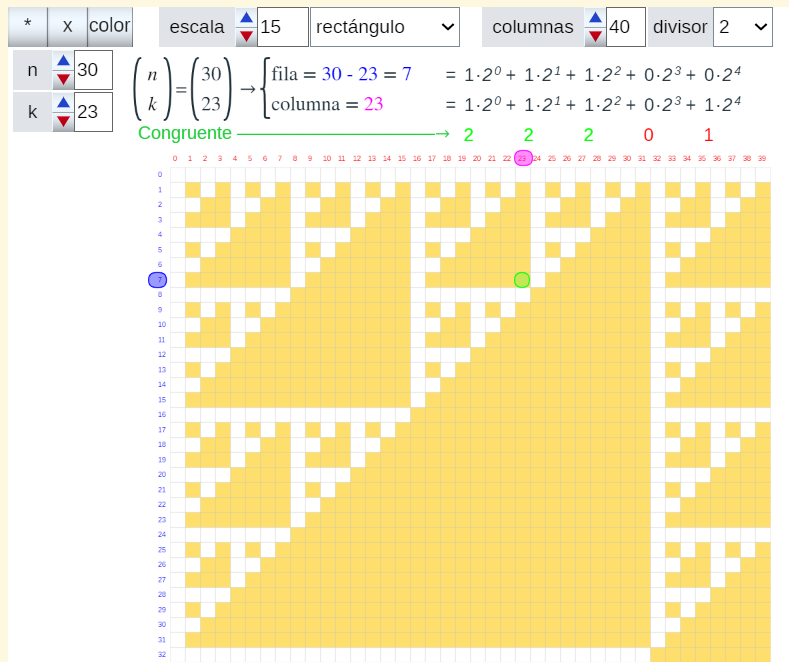
En la siguiente escena se puede reproducir visualmente todos los resultados indicados anteriormente y profundizar en el conocimiento de las interioridades del Triángulo de Pascal.
Pulsa sobre la imagen para abrir la escena
En la imagen anterior se observa como el número combinatorio 30 sobre 23 es congruente con cero módulo 2 y forma parte de un triángulo rectángulo básico de hipotenusa 1 , otro de hipotenusa 3 y otro de hipotenusa 7 (para éste último es evidente, para los dos anteriores haga traslaciones de los triángulos básicos, según el periodo antes indicado, y verá que ese número combinatorio está incluido en ellos). Todo se obtiene sin más que observar la relación de los coeficientes en la descomposición 2-ádica de la fila y columna que ocupa, ya que en este caso, para las tres primeras potencias de 2 la suma de los coeficientes es mayor o igual que el valor del módulo (en este caso 2).
Llegados a esta meta, estando aún confinados por la pandemia del COVID-19, cabe preguntarse si este artículo, y los dos anteriores publicados en este blog sobre este tema, tendrá o no continuidad... el tiempo lo dirá o quizás la necesidad de cambiar de temática para relajar la mente en otros ámbitos lo interrumpa. Tenga o no alguna nueva adenda, gracias a todos los que habéis dedicado parte de vuestro tiempo en leer lo descrito y los nuevos resultados hallados y expuestos en esta trilogía.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)














 CONTACTO
CONTACTO
