En tu Planificación didácTICa ¡cuenta con el Proyecto Descartes!
Escrito por José R. Galo SánchezComienza un nuevo curso académico intensamente cargado, rebosante, desbordante de sensaciones, de inquietudes, de incertidumbres, de dudas, de desconfianzas, pero también de ilusiones y de esperanzas. Nada anormal, ¡todos los inicios de curso son así!, ¿verdad? Y como en todo amanecer, el sol surge con ambiguas luces matutinas que no permiten entrever con claridad ni lo que nos rodea, ni lo que se aproxima, y consecuentemente ello coadyuva a la generación de cavernarias sombras platónicas, pero la experiencia y lo que es más certero: el conocimiento y la ciencia, nos muestra y nos da certeza de lo que acontecerá: el sol periódicamente alumbrará nuestro existir.  E incluso, aunque haya nubes que, aglutinándose en densos conglomerados de oscuras gotas, logren mitigar su fulgor y consigan filtrar su luminosidad, en el horizonte el alba marcará con firmeza un nuevo día que difuminará las nocturnas tinieblas y que nos dará claridad, fuerza y vigor.
E incluso, aunque haya nubes que, aglutinándose en densos conglomerados de oscuras gotas, logren mitigar su fulgor y consigan filtrar su luminosidad, en el horizonte el alba marcará con firmeza un nuevo día que difuminará las nocturnas tinieblas y que nos dará claridad, fuerza y vigor.
Sí, soy consciente, que posiblemente estés pensando dejar de leer este artículo, pues puede que no estés para interpretaciones o imágenes poéticas cuando lo que observas sobre ti son extensos nubarrones y oyes y sientes las vibraciones de los truenos que anuncian una muy próxima tormenta, pero te comento que tú y yo estamos en el mismo lugar, en análoga aula docente, es decir, bajo el mismo cielo y recibiremos el mismo aguacero. Sé, sin duda, que la lluvia calará nuestros cuerpos, pero como aprendiz de científico seguiré aferrándome a la Ciencia, y obviaré todos los mensajes con los que nuestros administradores-gobernantes y pseudo-científicos oficiales quieren mostrarnos una fantasiosa #VueltaSegura, porque me niego a que nos hagan dudar de qué es la verdad científica, por mucho que reiteradamente transmitan una nueva verdad que pendula a su conveniencia y a la que quieren vendernos cual elixir de buhonero. Y por ello, pienso que, he de empecinarme aún más y hacer hincapié en formar a mi alumnado como personas críticas capaces de colaborar y liderar acciones conducentes a escenarios éticos y solidarios, de verdadera Justicia Social, ¡qué sepan distinguir nítidamente las sombras de la luz! y eviten que aparezcan ilusionistas que con un único interés finalista propio sean capaces de producir esas engañosas penumbras.
Así pues, para conseguir ese objetivo y en este contexto y circunstancias, y obviando aquí lo relativo al cumplimiento de las condiciones sanitarias y laborales legalmente establecidas y que revindicaré en todo momento en los foros adecuados, he de centrarme en analizar la necesidad docente de estar preparado para los diferentes escenarios posibles y, para ello, contar con una "Planificación didácTICa" acorde a las necesidades de cada situación. Y, aunque es gramaticalmente incorrecto, he destacado en la palabra didáctica lo de "TIC" porque hablan de presencialidad, pero con la boca pequeña le añaden con voz queda el prefijo "semi" y parece ser que abordan compras e inversiones en hard ware y plataformas "educativas" con las que aparentar que ellos son los que cubren todo lo que el profesorado tuvo que gestionar motu proprio cuando en el mes de marzo quedamos desamparados. Pero no es aquello lo que me motiva, pues esto de las TIC es lo usual, básico e intrínseco en el proyecto Descartes, y es en lo que llevamos trabajando desde hace 22 años, ¡sí, veintidós años! Ahora parece que esto es nuevo, pero realmente no sería nada más que un redescubrimiento, una vuelta a la invención de la rueda, pues desde el proyecto Descartes se han desarrollado y hemos llevado a buen término programas educativos que han sido olvidados o que han sido tan hábilmente enterrados que parecen que son meros acontecimientos oníricos, por ejemplo: ¿qué se programó sobre centros TIC en Andalucía (el 2x1 o dos alumnos por ordenador)? o ¿qué era eso del Programa Escuela 2.0 y el 1x1? En el año 2005 se inició la "Experimentación con Descartes en el Aula" promovido por el INTEF, organismo del Ministerio de Educación, y hasta el 2010 se abordaron experiencias formativas en el proyecto EDA (Experimentación didácTICa en el aula) que dieron lugar a redes sociales de profesorado (ahora eso de red social suena habitual, pero todo tuvo su principio) como el proyecto HEDA y educ@conTIC. Y cuando desde los organismos oficiales decidieron dejar de apoyar proyectos de profesorado como el proyecto Descartes no dudamos y constituimos la ong "Red Educativa Digital Descartes" para preservar toda esa experiencia adquirida, canalizarla adecuadamente y potenciar el uso de las TIC en el proceso de enseñanza-aprendizaje.
ware y plataformas "educativas" con las que aparentar que ellos son los que cubren todo lo que el profesorado tuvo que gestionar motu proprio cuando en el mes de marzo quedamos desamparados. Pero no es aquello lo que me motiva, pues esto de las TIC es lo usual, básico e intrínseco en el proyecto Descartes, y es en lo que llevamos trabajando desde hace 22 años, ¡sí, veintidós años! Ahora parece que esto es nuevo, pero realmente no sería nada más que un redescubrimiento, una vuelta a la invención de la rueda, pues desde el proyecto Descartes se han desarrollado y hemos llevado a buen término programas educativos que han sido olvidados o que han sido tan hábilmente enterrados que parecen que son meros acontecimientos oníricos, por ejemplo: ¿qué se programó sobre centros TIC en Andalucía (el 2x1 o dos alumnos por ordenador)? o ¿qué era eso del Programa Escuela 2.0 y el 1x1? En el año 2005 se inició la "Experimentación con Descartes en el Aula" promovido por el INTEF, organismo del Ministerio de Educación, y hasta el 2010 se abordaron experiencias formativas en el proyecto EDA (Experimentación didácTICa en el aula) que dieron lugar a redes sociales de profesorado (ahora eso de red social suena habitual, pero todo tuvo su principio) como el proyecto HEDA y educ@conTIC. Y cuando desde los organismos oficiales decidieron dejar de apoyar proyectos de profesorado como el proyecto Descartes no dudamos y constituimos la ong "Red Educativa Digital Descartes" para preservar toda esa experiencia adquirida, canalizarla adecuadamente y potenciar el uso de las TIC en el proceso de enseñanza-aprendizaje.

Gracias a ello durante el confinamiento pudimos ayudar a numerosos colegas y alumnos en su labor docente y discente. Así, con sabor agridulce, superamos los cuatro millones de páginas en marzo, en abril ¡ayudamos en los tiempos del COVID-19! con más de cuatro millones seiscientas mil y en junio, coincidiendo con nuestro aniversario, comunicamos nuestro nuevo récord al haber superado los cinco millones de páginas servidas en el mes de mayo.
Por tanto estimo que desde el proyecto Descartes hemos contribuido a la educación con TIC tanto presencial como a distancia, también lo haremos en este nuevo invento de la semipresencialidad, y consecuentemente considero que los recursos educativos que ponemos a tu disposición con licencia Creative Commons pueden servirte en tu planificación docente. Son recursos que fomentan la autonomía del aprendizaje gracias a la interactividad, con ejercicios tipo que usan semillas aleatorias y cuentan con corrección automática. Nuestro objetivo es ayudar, ahora y siempre, a todo discente y docente en la planificación de su proceso de enseñanza y aprendizaje y aquí, en nuestro servidor de contenidos, con seguridad encontrarás ayuda y colaboración. Y, por ello, como indicaba en el título: En tu planificación didácTICa ¡cuenta con proyecto Descartes!
En posteriores artículos que iremos publicando sucesivamente en este blog, con ánimo de aportar una ayuda descriptiva adicional, os iremos detallando por niveles educativos los diferentes subproyectos que hemos ido desarrollando durante estos veintidós años. ¡Queda atento!
Evaluación, durante el estado de alarma, de la práctica docente a distancia con un modelo sin videoconferencia
Escrito por José Antonio Salgueiro GonzálezAnte el estado de alarma decretado durante la segunda quincena de marzo como consecuencia de la pandemia de COVID-19, en el ámbito docente nos vimos en la necesidad imperiosa y urgente de buscar alternativas para garantizar, con la mayor calidad posible, la continuidad del proceso de enseñanza y aprendizaje con nuestro alumnado. Cada docente, en base a su experiencia, formación, competencia digital y conocimiento de su alumnado, arbitró el proceso metodológio y empleó las herramientas tecnológicas que consideró más adecuadas para intentar superar el reto al que se enfrentaba por vez primera en su vida profesional y que tenía una duración prevista de quince días.
En primer lugar, dejaremos constancia de que este artículo no se fundamenta en ningún trabajo de investigación educativa ni en una experimentación didáctica previamente planificada y diseñada con unos objetivos concretos, sino que pretende difundir entre el claustro virtual una experiencia surgida de la improvisación y compartir los recursos generados con la práctica docente a distancia y sin videoconferencia en la materia de Matemáticas-II del Bachillerato de Ciencias con el alumnado del IES Bajo Guadalquivir de Lebrija, por si fuera de utilidad para otros compañeros y compañeras.
En segundo lugar, decidimos utilizar Moodle como entorno virtual de aprendizaje porque, tanto el alumnado como el profesor, ya tenían experiencia previa de años anteriores. Más confianza aún para el profesor por haber tutorizado cursos de formación a distancia durante bastantes ediciones, pero la dificultad se encontraba en que había que dotar de contenido el aula virtual y, simultáneamente, atender al alumnado, tarea que asumimos teniendo en cuenta que se trataba de una quincena. Sin embargo, transcurrido el tiempo y viendo cómo se desarrollaban los acontecimientos, el profesor se dirigió a su alumnado desde el aula virtual con las siguientes palabras:
"El viernes 13 de marzo fue la última vez que compartimos una clase a la antigua usanza, en el aula 2.11 donde hemos convivido durante seis meses y que tanto echamos de menos. ¡Quién nos lo iba a decir! ¿Cuántos años has estado en el instituto dejando de asistir a clases la semana antes de Navidad, dos o tres días antes de Semana Santa y una semana antes de las vacaciones de verano? ¿Cuánto no darías ahora mismo por ir al instituto? Como todo es relativo, nunca valoramos lo que tenemos y, sobre todo, si es gratis.
Hacíamos en ese momento el examen de integrales y te comenté que, después de 30 años dedicado a la enseñanza, nunca había vivido una situación similar, recordando que una vez se suspendieron las clases en la provincia de Sevilla por riesgo a desbordarse el río Guadalquivir, pero un solo día, comparativa que me llevó a la conclusión evidente de que estábamos ante un gran peligro.
Cuando cerré la puerta de mi última clase aquel día, mirando al aula vacía, pensé: ojalá regrese, no falte nadie de mi familia, ni de mis alumnos y los suyos, ni mis compañeros de trabajo, ni mis amigos ni mis vecinos.
Una vez en casa, y recibidas las instrucciones de continuar el proceso de enseñanza-aprendizaje en la distancia, estuve valorando distintas opciones y alternativas para hacer frente a este reto, al que nunca me había enfrentado, e intentar cumplir de la mejor manera posible el gran compromiso que tengo contigo.
Cuando se estudia o trabaja a distancia, las personas no se conocen, pero tienen que desempeñar sus funciones, como te puede ocurrir en un futuro en tu profesión. Afortunadamente, no es el caso, pues hemos compartido seis meses en este curso y otros en años anteriores. Ahora bien, cuando las personas no conviven físicamente en el aula, no hay posibilidad de transmitir emociones o sentimientos como sucede en la comunicación verbal, por lo que no pueden intuir si están tristes, alegres, cansadas ni conocer, en general, su estado de ánimo, tan importante para las relaciones humanas.
Por esta última razón, me he motivado para, al menos, enviar algunos audios cortos con los que deseo explicar el por qué de este proceso metodológico".
Compartimos aquí los audios tal y como fueron grabados de forma espontánea para el alumnado el 13 de abril, sin edición ni revisión alguna, antes de abrir la encuesta para que evaluaran la práctica docente a distancia y determinar acciones de mejora.
| POR QUÉ NO ELEGÍ LA VIDEOCONFERENCIA |
| Enlace al audio en iVoox |
| ACCESO A LOS RECURSOS DEL AULA VIRTUAL |
|
El curso que compartimos en el aula de formación de RED Descartes contiene únicamente los contenidos de Matemáticas-II tratados durante el estado de alarma, concretamente una parte de Álgebra Lineal y el bloque completo dedicado a la Geometría Analítica en el espacio, de manera que, día a día, se iba publicando la clase correspondiente a esa fecha en el foro de novedades, aunque en el curso que ofrecemos con acceso a invitados podrás apreciar las fechas en las que hemos realizado la migración manual. Puedes acceder desde el enlace anterior o sobre la imagen inferior siguiendo las indicaciones. Por razones obvias, en esta copia del curso no se encuentran los foros en los que participaron los alumnos y alumnas, llevando sus enlaces al curso original. |
| POR QUÉ UTILIZAR FOROS PARA ENTREGAR TAREAS |
| Aunque Moodle dispone de un módulo que facilita enormemente la entrega de tareas por parte del alumnado y su calificación o valoración por parte del docente, con retroalimentación incluida, todo quedaría en beneficio de una alumna o alumno concreto. Aunque el alumnado conocía esa dinámica desde el año anterior, cuando compartimos el primer curso del bachillerato, se optó por usar foros y así se explicó en su momento. |
| Enlace al audio en iVoox |
| ENCUESTA ANÓNIMA PARA EVALUAR LA PRÁCTICA DOCENTE A DISTANCIA |
| A partir del día 20 de abril se pone a disposición del alumnado una encuesta anónima, gracias a esta funcionalidad de Moodle, con objeto de evaluar la práctica docente a distancia y poder implantar las mejoras necesarias hasta el final de curso, tratando cinco temáticas, a saber, sobre el enfoque y tratamiento de los contenidos en cada clase, sobre el enfoque y tratamiento de las tareas en cada clase, sobre el entorno virtual de aprendizaje, sobre el proceso metodológico y la atención prestada y sobre la evaluación a distancia, cuyos resultados se comparten en el siguiente informe: |
| METODOLOGÍA DURANTE LA PRIMERA QUINCENA DE JUNIO |
|
Una vez impartido el temario exigido para la Prueba de Evaluación y Acceso a la Universidad que, con motivo de la pandemia, se aplazó al mes de julio y se amplió el calendario escolar hasta el día 16 de junio, como es habitual en estos casos nos dedicamos a repasar modelos de pruebas de otras ediciones para afianzar los conocimientos, orientar, asesorar, practicar y transmitir confianza al alumnado. Sin embargo, era el momento de abrir debates, aclarar dudas finales, contagiar entusiasmo y ánimo y acompañar al alumnado, por lo que se decidió cambiar el proceso metodológico incorporando la videoconferencia con Meet desde la cuenta de G Suite del IES Bajo Guadalquivir, con una tableta digitalizadora para las expresiones y simbología matemáticas y el software de MimioStudio, todo gracias a las recomendaciones de mis compañeras del Departamento de Matemáticas. Para quien desconozca el software mencionado, decir que permite una gran calidad a la hora de preparar una presentación previa a la clase y se visualiza con nitidez al compartir la pantalla en la videoconferencia, permitiendo guardar el contenido en formato PDF para su difusión posterior desde el aula virtual, especialmente para el alumnado que no pudo asistir a clase. |
| PEQUEÑA VALORACIÓN |
|
A modo de epílogo, y cambiando el tiempo verbal, la experiencia ha sido muy satisfactoria y ha requerido una gran inversión para dotar de contenido el entorno virtual de aprendizaje día a día, razón por la cual, y ante lo que se avecina, he decidido abrir el aula y compartirlo con el claustro virtual, por si alguien considera de utilidad alguna de las clases y puede hacer uso de la misma, resultando cómoda, además, la adaptación a sus necesidades desde otro espacio análogo o enlazando a la clase concreta, si lo considera válido para su alumnado. También ha sido titánico el esfuerzo de mis alumnos y alumnas, asistiendo a todas las clases diariamente, aprendiendo solos en sus domicilios, sin la explicación verbal, el debate y las consultas, entregando todas las tareas demandadas en tiempo y forma y respondiendo a las revisiones y retroalimentación en los foros habilitados al efecto. Y como el éxito no llega por suerte, sino que es fruto del sacrificio y el esfuerzo de días, meses y años de trabajo, todos consiguieron superar la Prueba de Evaluación y Acceso a la Universidad. Me siento muy orgulloso de cada alumno y cada alumna de este grupo, por quienes siento admiración y un gran aprecio, pues hemos compartido casi tres cursos consecutivos, siendo una pena que tuviéramos que despedirnos por una videoconferencia después de tantos años. Os deseo todo lo mejor en vuestra vida universitaria y estoy convencido de que conseguiréis superar los nuevos retos a los que os váis a enfrentar. Como homenaje, divulgo la fotografía que me envió una alumna desde su perfil de Twitter el viernes 13 de marzo, último día que compartimos en el instituto, cuando celebrábamos el Día Internacional de las Matemáticas. |
El metro: patrón inexacto para medir exactamente
Escrito por José R. Galo Sánchez"El metro: patrón inexacto para medir exactamente" es el título de un proyecto que desarrollamos en el año 2006 y cuya temática giraba en torno al patrón de longitud en el sistema métrico decimal: "el metro". Comprendía 50 objetos de aprendizaje, 117 escenas interactivas y 50 test también interactivos, todo desarrollado con la versión 3 de la herramienta Descartes que, recordemos, tenía como soporte la máquina virtual de Java. La adaptación al estándar HTML5 condujo en el 2013 a iniciar el desarrollo en javascript de DescartesJS y a la conversión y adaptación de las escenas de Descartes en Java a la nueva versión. El proyecto "El metro" quedó pendiente de esa adaptación y ahora, a través de este artículo, procedemos a presentarla.
 |
 |
Sí, hemos tardado en abordar esta adaptación, pero es evidente que no hay tiempo para todo y además cualquiera puede reconocer que una adaptación siempre es menos satisfactoria que un nuevo desarrollo y que a veces es más eficaz hacer que rehacer. También obliga a tomar decisiones sobre mantener lo que se hizo, con los estándares y limitaciones existentes en su momento, o remodelar totalmente, o quedarse entre Pinto y Valdemoro. La decisión final adoptada ha sido mixta:
- Por un lado se ha dado libertad a cada uno de esos objetos readaptándolos como misceláneas independientes, es decir, siguiendo el formato de presentación que se utiliza en ese subproyecto de RED Descartes y así, de esta manera, han pasado a estar disponibles sin necesidad de acceder a través del núcleo agregador que representa el proyecto.
- Pero también, por otro lado, para recordar y comprender cómo fue ese proyecto se ha mantenido el acceso original a través del índice y las páginas web auxiliares que aglutinaban a esos recursos y que detallaban su conceptuación y desarrollo, obviamente actualizando aquellos aspectos modificados.
En el proyecto misceláneas y en el servidor de contenidos ya están disponibles lo objetos adaptados, que todavía no son todos, y con este artículo se busca la divulgación de la web adaptada del proyecto. Al pulsar sobre la siguiente imagen tendremos acceso a la portada e índice del mismo.
 Pulsa sobre la imagen para acceder al proyecto
Pulsa sobre la imagen para acceder al proyecto
En la portada se muestra una suscinta galería de personajes
 |
 |
Y pulsando sobre las imágenes de cada uno de ellos, en dicha galería, accedemos a su respectiva biografía:
Jorge Juan y Antonio de Ulloa, junto a los franceses Bouguer, Godín y La Condamine, como medidores de la longitud del grado de meridiano en el ecuador y que junto a la medición del grado en Laponia, realizada por Maupertuis, permitió verificar que la Tierra estaba achatada por los polos. Un trabajo previo e independiente del sustentador de la definición del metro, pero con base técnica común: la triangulación geodesica.- Méchain y Delambre que abordaron la medición del meridiano desde Dunkerque (latitud 51 N) a Barcelona (latitud 41 N). Se seleccionaron esas ciudades por estar ubicadas en un arco que podía ser medido al ser accesible mediante desplazamiento sobre el terreno y por ser un arco ubicado en la parte intermedia del cuadrante. De esa medición se pasaría a la extrapolación de la medida del cuadrante de meridiano y a la definición del metro.
- Agustín de Pedrayes como representante español en el establecimiento del sistema métrico decimal.
- Méchain y Aragó que en una segunda expedición extendieron la medición del meridiano desde Barcelona a Formentera (latitud 38 N).
Os invitamos a navegar por las páginas enlazadas en el índice del proyecto y desde ellas profundizar en el planteamiento del proyecto, leer cuáles eran los objetivos y qué contenidos fueron los desarrollados. El proyecto era más amplio y ambicioso en alcance de lo que finalmente se realizó, pero hubo que poner cota a nuestros deseos, más cuando era un proyecto sometido a unos plazos y compromisos administrativos al haber sido seleccionado y subvencionado en convocatoria pública por la Consejería de Educación de la Junta de Andalucía en el año 2005.
De todas las opciones disponibles en el índice destacamos aquí, dentro de la descripción del proyecto: la motivación y los objetivos.
Y, obviamente, el repositorio o índice de contenidos donde hay que señalar que los iconos identificadores de los objetos que se observan en tonos de grises son objetos pendientes de adaptar y los coloreados ya han sido adaptados.
Es bien conocida la variabilidad continua y la amplia caducidad de la información que circula por la red y el peligro de pérdida de información en el que continuamente nos vemos involucrados por la simple variación en una página web o por su eliminación o bien por reiterados cambios de formatos y dispositivos que rápidamente van quedando obsoletos. Afortunadamente, hay grandes proyectos como Internet Archive que persiguen contrarrestarlo y hacer que lo efímero sea durarero. Aquí, en una línea paralela muy modesta hemos tratado de dar un poquito más de perdurabibilidad a nuestro proyecto de "El metro" dentro de la RED Descartes.
Más...
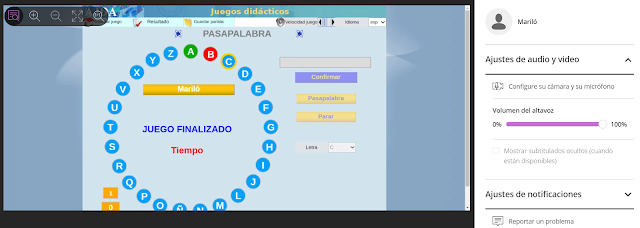
Juegos didácticos a través de vídeo-conferencia
Escrito por Jesús Manuel Muñoz Calle- Permite la utilización de las herramientas propias de la aplicación con la que se realiza la vídeo-conferencia, como por ejemplo el uso de temporizadores, cuestionarios, herramientas de participación, etc.
- Se puede sistematizar mejor la forma de participación y de turnos de palabra.
- Permite la introducción de nuevas dinámicas de juego, permitiendo respuestas simultáneas, realización de grupos separados, competiciones paralelas, etc.
- Se produce otra forma de interacción y de desarrollo de competencias que también es bastante interesante.
- Se puede desarrollar sin limitación de tiempo, espacio, PDI, etc, es decir, sin necesidad de ajustarse a las limitaciones de la enseñanza presencial.
- Los participantes afectados por la brecha digital tienen mayor dificultad al acceso y uso de estos recursos.
- Se pierde la interacción personal directa, que en algunos juegos es muy interesante.
Estamos en tiempo de vacaciones y esta semana proponemos la creación de un blog con actividades de aprendizaje atractivas y divertidas para nuestros alumnos.
Hemos seleccionado dos unidades del Proyecto Canals para 5º de primaria que se basan en el conocido juego de memoria.
El Proyecto Canals, de la Red Educativa Digital Descartes, contiene una serie de objetos de aprendizaje interactivos que han sido creados a partir de los materiales elaborados por la profesora Maria Antònia Canals.
Para el acceso del alumnado de estas actividades, hemos creado un blog muy sencillo en el cual insertar estas actividades. En el siguiente vídeo se muestra con detalle los pasos a seguir.
Siguiendo este ejemplo se pueden añadir cuantas actividades se deseen y, para los más habituados a trabajar con estas herramientas, se pueden crear diferentes páginas que permitirán organizar las distintas actividades, ya sea por temas o por niveles.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)








 CONTACTO
CONTACTO
