Estrategia
Estrategia
Hacer cualquier cosa que se esté haciendo de la mejor manera posible es inherente a la acción, parte de ella y muchas veces la manera de hacer eclipsa al hecho.
Conseguir hacer algo, o conseguir algo, que a priori no es evidente ni inmediato por propia iniciativa y esfuerzo produce satisfacción intelectual y muchas veces placer, particularmente cuando en el desarrollo del proceso intervienen el mundo de las formas, el mundo de las ideas, las metafísicas de ambos mundos, y las realidades paralelas con sus respectivas metafísicas.
Crear es seguir el método adecuado. Por eso la estrategia es arte.
Arte de planear y dirigir las operaciones bélicas o militares.
Arte de dirigir las operaciones militares.
Técnica y conjunto de actividades destinadas a conseguir un objetivo.
Arte, traza para dirigir un asunto.
En un proceso regulable, conjunto de las reglas que aseguran una decisión óptima en cada momento.
Camuflaje - estratega - estratégico - táctica - maniobra - habilidad - pericia
Construir - Dibujar - Pintar - Esculpir - Resolver
Tocar - Hablar - Componer - Escribir
Pensar.
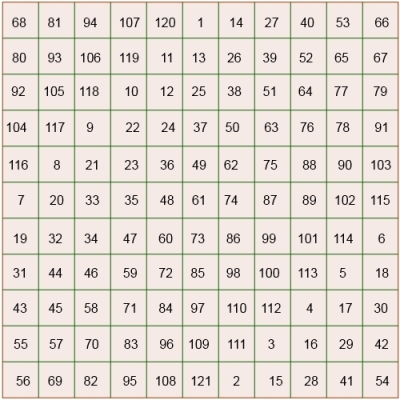
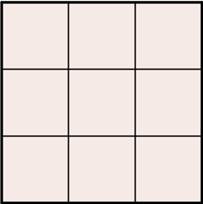 En la situación concreta que nos ocupa, en la que tenemos un cuadrado con nueve celdas iguales, las cuales debemos rellenar con los números del 1 al 9, sin repetirlos y de manera que la suma de los números de cada fila, cada columna, la diagonal principal y la diagonal secundaria sea la misma, la intuición nos indica que los números de mayor peso: 7, 8 y 9 no pueden estar en la misma fila, columna o diagonal por razones obvias. También se llega rápidamente, por los mismos motivos anteriores, a que dos de ellos no pueden estar alineados.
En la situación concreta que nos ocupa, en la que tenemos un cuadrado con nueve celdas iguales, las cuales debemos rellenar con los números del 1 al 9, sin repetirlos y de manera que la suma de los números de cada fila, cada columna, la diagonal principal y la diagonal secundaria sea la misma, la intuición nos indica que los números de mayor peso: 7, 8 y 9 no pueden estar en la misma fila, columna o diagonal por razones obvias. También se llega rápidamente, por los mismos motivos anteriores, a que dos de ellos no pueden estar alineados.
Entonces esas tres cifras deben ocupar las posiciones siguientes.
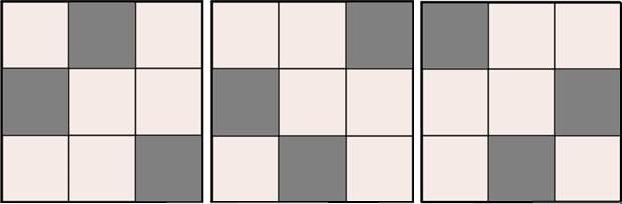
Por señalar algunas de ellas.
Con un número mínimo de pruebas observamos que el 9 no puede ir en los vértices de las diagonales ni tampoco el siete pues de inmediato se produce sobresuma o necesidad de duplicidad, así que la disposición de las tres cifras mayores está perfectamente delimitada.
Ahora podríamos seguir nuestra conjetura con la cifra que va en el centro, que a poco que ensayemos resulta que únicamente puede ser el... y claro, encontrar la posición de las demás cifras es trivial.
Siguiendo esta estrategia preguntarse cuanto debe sumar cada línea es redundante pues los propios ensayos van delimitando lo que es; o no, posible para cumplir el objetivo.
Si se quiere proponer esta situación en clase y a la par desarrollar otras competencias del currículo puede usarse la intuitiva miscelánea de Salvador Calvo-Fernández Pérez "cuadrado mágico" para efectuar los ensayos hasta dar con la solución usando el siguiente enlace, o bien puede descargarse la miscelánea desde este enlace, donde también puede usarse directamente.
Para comprobar la bondad de la estrategia encontrada podemos intentar extenderla a cuadrados de 4x4, 5x5 ect. en este vídeo. Puede observarse como se crea una estrategia para cuadrados de 4x4 y a partir de dicha observación podemos extender la solución a cuadrados más complejos.
En el enlace vinculado a la siguiente imagen nos lleva a una hoja de Excel donde puede observarse el método para obtener cuadrados mágicos de hasta 11x11 pudiendose ampliar facilmente la dimensión del cuadrado y, si se desea, analizar la estrategia de construcción de los mismos.
Las misceláneas
Como hemos comprobado en este artículo para casi cualquier situación que planteemos en clase existe una miscelánea que puede ayudarnos en el desarrollo de la práctica. En el siguiente video se muestra como acceder a las misceláneas del Proyecto Descartes, como usarlas en línea o como descargarlas para su uso en local.
Desde aquí os animamos a participar en el proyecto aportando misceláneas o sugiriendo utilidades que no existan y considereis que sería conveniente disponer de ellas.
Este mes vamos a retomar el bloque de álgebra con una unidad de 2ºESO. Es una unidad muy corta porque deja las ecuaciones para la unidad siguiente:
En el video hemos tratado los siguientes contenidos:
1.Expresiones algebraicas
¿Qué son?
¿Cómo las obtenemos?
Valor numérico
2.Monomios
¿Qué son?
Sumar y restar
Multiplicar
3.Polinomios
¿Qué son?
Sumar y restar
Multiplicar por un monomio
DESCUBRIMOS al Personaje Misterioso (IX)
Escrito por Ángel Cabezudo BuenoLa semana pasada en Radio Descartes, en el espacio “¿Quién es el personaje misterioso?” entrevistamos a una genial matemática nacida en Londres en 1815. Fue una adelantada a su tiempo en más de 100 años al ser capaz de describir con acierto las posibilidades de la máquina analítica que diseñara en aquel tiempo Charles Babbage y para la cual desarrolló un sistema simbólico de representación de instrucciones y concibió un “plan” o secuencia de instrucciones, basadas en tarjetas perforadas, para calcular la serie de números de Bernoulli utilizando los conceptos de bucle y subrutina.
Si a Charles Babbage se le considera el padre del hardware de un ordenador que podría funcionar de forma muy similar a como lo hacen los actuales, nuestra matemática, colaboradora en el proyecto de Babbage, se convirtió en la primera programadora de la historia y por tanto considerada madre de la programación de ordenadores.
Muestra genial matemática, cuya identidad se puede desvelar al montar el puzle realizado con DescartesJS que se acompaña a este artículo, en 1843 pudo asegurar que la máquina analítica no sólo podría servir para hacer cálculos matemáticos sino otras operaciones con informaciones de cualquier naturaleza como música o imágenes.
La imagen del puzle tipo jigsaw (piezas irregulares), es una composición donde aparece la elegante figura de nuestro personaje femenino y de fondo diferentes alusiones a la máquina analítica y a su “plan” de instrucciones.
Las 16 piezas barajadas, obtenidas al cortar la imagen, se sitúan amontonadas a la derecha de la escena. Para descubrir a nuestro personaje misterioso hay que montar estas piezas sobre una cuadrícula 4x4 a la izquierda de la escena arrastrándolas con clic mantenido y soltarlas sobre el cuadro donde quedan encajadas. Si la pieza se sitúa correctamente ya no es posible arrancarla de su cuadro. Si se montan dos piezas sobre un mismo cuadro, éste, quedará resaltado con color rojo advirtiendo de esta situación.
Inicialmente, a modo de ayuda, se puede ver detrás de la cuadrícula la composición en escala de grises. Un control de tipo botón permite ocultarla y así se sugiere para que el montaje del puzle suponga un mayor reto.
Cuando el puzle se completa aparece el nombre del personaje, una caricatura y se puede visionar un vídeo: se trata de un cuento audio descrito extraído del libro "La Liga de las Mujeres Extraordinarias" y que por su formato y contenido puede resultar interesante y muy motivador para los alumnos de Primaria y Educación Secundaria Obligatoria aunque a mí que ya peino canas también me ha gustado mucho.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana cuyo tamaño se adapta automáticamente al dispositivo de visualización y se acomoda manualmente al gusto personal pues emplea un Diseño Web Adaptativo (RWD).
El autor de este artículo, la edición de las imágenes y la programación del puzle es de Ángel Cabezudo Bueno y tiene licencia CC BY-NC-SA 4.0
El puzle de arrastre básico, tipo jigsaw, tiene su origen en una documentación aportada por Juan Guillermo Rivera Berrío.
Gracias por la atención que ha recibido la entrevista de este noveno personaje matemático y quedáis invitados para la siguiente.
Audios y Vídeos Interactivos con Descartes
Continuación de la práctica (2)
Los contenidos de la Documentación técnica de la herramienta de autoría DescartesJS son dinámicos debido a la permanente labor de mantenimiento y actualización del código fuente de la librería descartes-min.js por parte de los responsables de la Red Digital Descartes de México, España y Colombia. Hay épocas en las que este dinamismo es vertiginoso tal y como ocurre actualmente. Por eso comenzamos esta nueva entrada del Blog recomendando la visita a dicha documentación mediante el enlace del título y también de este otro que llevan, respectivamente, a la información sobre el uso de vídeos interactivos, tanto en local como en línea y a la información sobre cómo comunicar las escenas con el HTML y viceversa.
Continuando con la práctica, recordamos que ya hemos definido en los espacios: E1, E2 y E3, los gráficos (textos) necesarios para dirigir y complementar el flujo de la actividad. Ahora, siguiendo el paso 7 crearemos los dos controles, tipo botón, para manipular el vídeo ya que los propios del mismo están enmascarados.
Abrimos la opción de menú Controles y procedemos como muestra el vídeo siguiente.
Recordamos que la expresión '\n' que aparece en el vídeo puede interpretarse como un salto de línea y permite introducir una nueva instrucción.
El paso 8 consite en definir, en la opción de menú Programa, dos eventos para controlar la reproducción del vídeo mediante el manejo de la animación tal y como se explica detalladamente en la documentación.
Después de seguir las instrucciones, la opción de menú Programa debe tener el aspecto que muestra el gráfico siguiente.
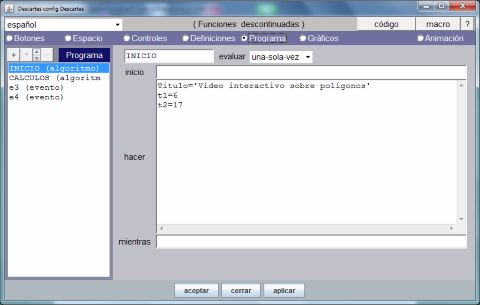
A continuación, siguiendo las indicaciones del paso 9, volvemos a seleccionar la opción de menú Controles para definir en los espacios E1 y E3 los botones, cuadros de texto y controles de tipo menú que son el soporte de la interactividad de la escena tal y como se muestra en el documento videos_interactivos.pdf enlazado al principio del artículo.
El gráfico siguiente muestra cómo debe quedar la opción de menú Controles después de completar el paso anterior.
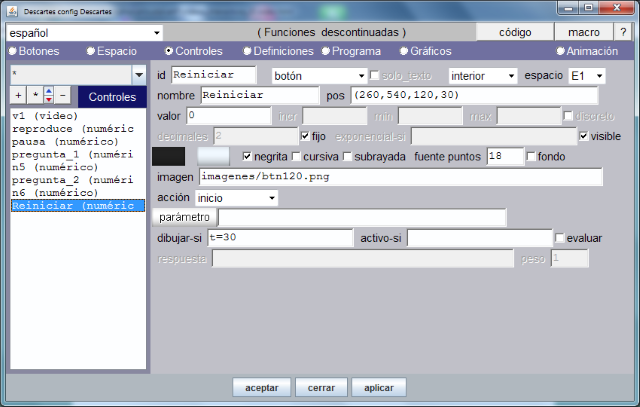
En próximas entradas se completará la práctica y continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
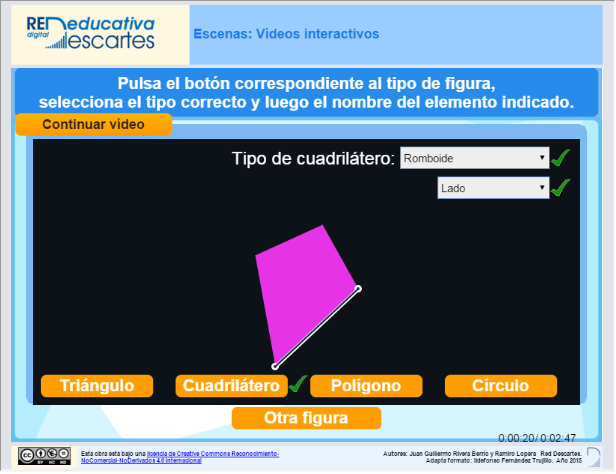
El siguiente gráfico es un enlace a un ejemplo de la implementación de vídeos interactivos dentro de una escena DescartesJS. Este ejemplo, realizado por Juan Guillermo Rivera Berrío y que es una propuesta para evaluación de la viabilidad del proyecto y su potencial formativo y que aún está en fase de prueba, ha sido posible gracias a la colaboración de la Red Descartes de Colombia (Juan Gmo. Rivera y Ramiro Lopera) y de España (José R. Galo).
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Audios y Vídeos Interactivos con Descartes
Continuación de la práctica (1)
En el artículo anterior creamos los espacios: E2 y E3, semitransparente el primero y transparente el segundo, para mostrar mensajes y enmascarar los controles del vídeo, estas especificaciones están ampliamente detalladas en la documentación enlazada en el título del artículo.
En el espacio E2 se mostrarán dos tipos de mensajes: los de información al comenzar la actividad (t=0), y las preguntas con el cuadro de texto, menú desplegable o botón, para introducir, elegir o pulsar la respuesta correcta, y el mensaje de acierto o fallo, una vez se ha respondido y a continuación, pulsado sobre el botón verificar que aparece, en los tiempos de reproducción t1 y t2 (t=t1) y (t=t2).
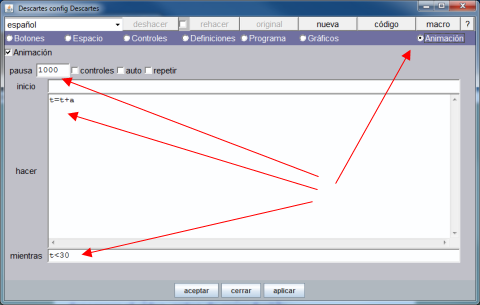
Pasamos a desarrollar el paso 4. Siguiendo las instrucciones de la documentación activamos la opción de menú Animación y tecleamos los valores indicados. Recordamos que el "id" del control de vídeo es "v1" esto signifíca que para su manejo debemos usar las instrucciones: v1.play() para reproducirlo, y v1.pause() para que se detenga. La animación hace que el valor de t se actualice cada segundo (1000 milisegundos) y únicamente se incrementará si el vídeo se está reproduciendo (a = 1).
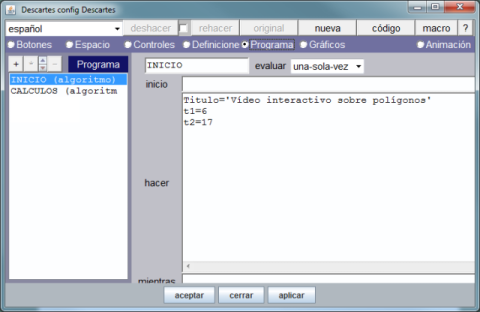
El paso 5 consite en activar la opción de menú Programa y dentro del algoritmo INICIO, que se ejecuta una única vez al iniciar la actividad, definimos tres constantes: Titulo (texto para el encabezado de la escena), t1 (valor en segundos para detener el vídeo por primera vez y efectuar la primera pregunta) y t2 (idem para la segunda pregunta). En el siguiente gráfico observamos lo expuesto.
A continuación, siguiendo las indicaciones del paso 6, seleccionamos la opción de menú Gráficos para definir en qué espacio va a ir cada texto, imagen, gráfico etc. cuál va a ser su situación dentro de la escena, y si es texto, qué formato (tamaño, color, tipo de letra, estilo, etc.) va a tener y, en general, cuando el objeto va a estar visible y cuando oculto.
El siguiente vídeo muestra, paso a paso, como insertar texto en la escena. En primer lugar se inserta, en el espacio E1, dentro de una fórmula, la expresión que contiene el valor de la variable Titulo que hemos creado. Luego en E2 y E3 se van creando los textos necesarios para dirigir y documentar la acción de la actividad.
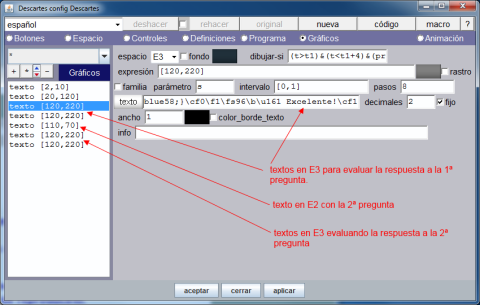
A continuación se crean en E3 los textos "¡EXCELENTE!" de tamaño 48 y color verde que será visible si: (t>t1)&(t<t1+4)&(pregunta_1='4') y "¡No es cierto! Tiene cuatro lados" de igual tamaño y color rojo que será visible si: (t>t1)&(t<t1+4)&(pregunta_1!='4')
En E2, en la posición (110,70) se introduce la segunda pregunta, que será visible si: t=t2, y en E3 se definen los textos a mostrar según sea la respuesta de forma análoga a como lo hemos hecho para la primera pregunta.
El aspecto que debe tener el submenú Gráficos y la escena en este momento del desarrollo es el que muestran estas imágenes.
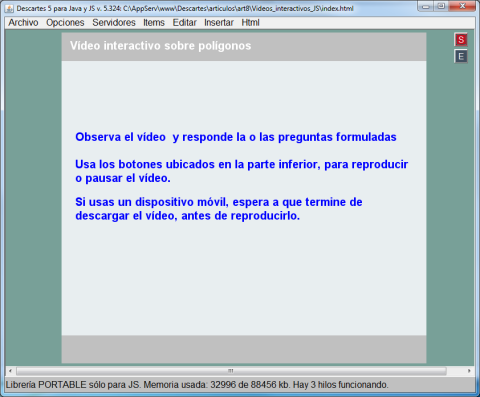
En próximas entradas se completará la práctica y continuaremos analizando el subproyecto Misceláneas, y las nuevas posibilidades que el código ofrece.
El logo del subproyecto GEOgráfica hace de enlace a una recreación de la actividad de colorear las provincias de las distintas Comunidades Españolas realizada por Juan Guillermo Rivera Berrío y que en este primer ensayo se centra en la Comunidad Andaluza. Tras un vídeo, alojado en YouTube y que se reproduce dentro de una escena Descartes, donde se hace una presentación cartográfica de la Comunidad, se ejecuta la utilidad de colorear que solicita un clic en una de las provincias, según sea la respuesta, el programa advierte del error o reproduce un vídeo relativo a lo más significativo de dicha provincia. Aunque aún está en fase de pruebas, damos a conocer este subproyecto de GEOgráfica por su gran potencial educativo y cultural ya que pueden incluirse tantos vídeos como se precisen sin que esto influya en el peso de la unidad. Esto ha sido posible gracias a la colaboración de la Red Descartes de Colombia (Juan Gmo. Rivera y Ramiro Lopera) y de España (José R. Galo).
Animamos a los lectores a colaborar en el proyecto elaborando contenidos o aportando ideas y sugerencias.
Ildefonso Fernández Trujillo
Hoy nos vamos en centrar en contar algunas de las cosas que aprendemos cuando somos tutores de un curso.
En principio tu rol es el de corrector pero eso no impide que no pares de aprender, todos los que nos dedicamos a la educación lo sabemos.
En la segunda edición del curso Aplicaciones de juegos didácticos en el aula, dentro de los ofertados por la CEJA, he encontrado bastantes participantes que han realizado muy buenos trabajos. Como no puedo extenderme demasiado os voy a mostrar cuatro ejemplos. Os ponemos los enlaces a los juegos con sus trabajos precargados, solo tenéis que empezar a jugar.
El primero es un fichero para Cruzar la línea realizado por Raquel Crespo Gutiérrez. Tiene varias cosas que lo hacen destacable. Se ha realizado para alumnos de la EOI en la modalidad a distancia. Solo disponen de unas pocas horas presenciales en las que se resuleven dudas y Raquel ha aprovechado para ponerlos a jugar. Esto ya me parece suficiente para mostrarlo. Otra cosa llamativa es el uso de las contracciones. En los juegos no podemos utilizar el símbolo ' pero es el que debemos escribir en las contracciones. Hemos tenido que cambiarlo por nuestra tilde ´ asumiendo que es un error pero no había otra forma de utilizarlas. Si advertimos a los alumnos no habrá problema. por cierto, no olvidéis poner la interface en inglés, solo hay que cambiar "esp" por "eng" en la casilla del idioma.
El segundo es de Manuel Fernández Labrada que ha creado un fichero muy completo para El primero de la clase. El tema es la música, una materia que no había imaginado que pudiese sacarle tanto partido a los juegos. Para comenzar a jugar debemos elegir la introducción direccta del nombre de los jugadores. Al poder introducir hasta 30 podemos usar un fichero que nos facilite el trabajo. Veréis que el trabajo de Manuel permite realizar un evaluación completa de lo que han aprendido. Es una muy buena muestra de las grandes posibilidades de los juegos.

El tercero es el más sorprendente para mí. Nuria Estébanez Campos ha creado una batería de preguntas para Danza contemporánea. En este caso el juego elegido es Parejas ocultas en el que debemos unir el nombre de la figura con su explicación. Realmente todas las materias tienen su opción de aprovechar estos recursos pero nunca hubiese pensado en la aplicación para danza. El resultado fue muy bueno, imaginad a los alumnos/as cuando Nuria les pidiese que cogiesen los ordenadores, su sorpresa y lo que disfrutarían. Aquí aparece un pequeño problema con la extensión de la explicación ya que el juego no permite todos los caracteres que queramos. Debemos adaptarnos o buscar entre la multitud de juegos disponibles otro que se adpate a lo que necesitemos en cada momento.
Termino con un ejemplo de programación del uso de los juegos en el aula en el caso de La calculadora. Ya estamos empezando a aplicar la nueva ley de educación y Francisca Gallardo Salas nos enseña cómo hacerlo. Las competencias clave, comentando en cada una qué esperamos conseguir, unos criterios de evaluación muy claros y unas observaciones perfectas son lo mínimo que debes revisar en este documento que no tiene desperdicio alguno.
Como hemos dicho al principio, no paramos de aprender.
Terminamos con los enlaces que os permitirán acceder a los juegos en la web o descargarlos:
Esperamos que os sean de utilidad y os animen a utilizar los juegos en el aula
Código iframe. Embeber un objeto digital en nuestro blog.
Escrito por Montserrat Gelis BoschEn el siguiente vídeo mostramos el procedimiento a seguir para embeber en un blog una escena de la unidad Funciones y gráficas para 4º de la ESO del proyecto ED@D.
Para insertar escenas de la Red Educativa Digital Descartes en un blog o cualquier otro espacio web, deberemos activar la edición en html y pegar el código correspondiente.
En la página de materiales del blog encontramos para cada unidad dos códigos, el código para embeber como iframe y el código para abrir en una ventana emergente. El código iframe permite que el estudiante pueda empezar a realizar las actividades desde la misma página del blog mientras que si utilizamos el código para abrir en ventana emergente, deberemos pulsar sobre la imagen para que se cargue la actividad en una nueva ventana.
En este ejemplo nos interesa que el estudiante pueda realizar las actividades directamente desde el mismo blog, así que utilizaremos el código iframe.
De la unidad Funciones y gráficas queremos embeber la primera actividad:
1.- Desde el apartado materiales del blog, seleccionamos ED@D y buscamos Funciones y gráficas.
2.- En la página de esta unidad, encontramos los dos códigos. Copiamos el código iframe:
<iframe style="width: 1120px; height: 690px;" src="https://proyectodescartes.org/EDAD/materiales_didacticos/EDAD_4eso_B_funciones1-JS/index.htm"></iframe>
3.- La dirección que aparece en el código es la de la página inicial de la unidad, en nuestro caso deberemos modificar la dirección web para que se abra en la primera actividad: https://proyectodescartes.org/EDAD/materiales_didacticos/EDAD_4eso_B_funciones1-JS/q8_contenidos_1a.htm
Pero veamos con detenimiento cuáles son los pasos que deberemos seguir:
Descartes en nuestra Aula Moodle. Geometría del plano. Parte II
Escrito por Montserrat Gelis Bosch¿Quieres ver cómo organizar materiales interactivos en tu Aula Moodle?
Hoy presentamos la segunda parte del tema "Descartes en nuestra Aula Moolde. Geometría del plano".
En el primer vídeo se analizaron y seleccionaron algunos objetos digitales pertenecientes a los distintos proyectos de la Red Educativa Digital Descartes, para trabajar la geometría del plano en 1º de la ESO.
Una vez seleccionados los materiales, en este segundo vídeo podemos ver cómo organizar los contenidos en un curso en nuestra Aula Moodle.
Utilizamos distintos recursos: enlaces URL para las unidades EDAD y tablas, en cuyas celdas pegamos el código para abrir en ventana emergente, con enlaces a los objetos pertenecientes a los proyectos ASIPISA, Canals, Competencias, Miscelánea y PI:
Proyecto Canals I. Objetos de aprendizaje para Educación Infantil
Escrito por Xosé Eixo BrancoEn este y en sucesivos vídeos presentaremos el Proyecto Canals.
Este subproyecto del proyecto Descartes, recoge 375 objetos de aprendizaje interactivo basados en los materiales que diseñó y elaboró la profesora Mª Antonia Canals durante su extensa vida docente.
Desde el Ministerio de Educación, Cultura y Deporte de España se abordó la producción de recursos TIC que buscaban contribuir a la difusión y conocimiento de dichos materiales, introduciendo una perspectiva enmarcada en el uso educativo de las Tecnologías de la Información y de la Comunicación.
En el año 2013 la asociación no gubernamental Red Educativa Digital Descartes (http://ProyectoDescartes.org) ha convertido estos materiales a DescartesJS pudiéndose, desde este momento, trabajar con ellos en dispositivos tipo tabletas y smartphones, además de los ordenadores personales.
En este primer vídeo nos centraremos en los materiales correspondientes a Educación Infantil.
Esta semana vamos a ver cómo insertar en nuestro blog un objeto digital de la Red Educativa Digital Descartes.
Hemos seleccionado una actividad de cálculo con fracciones para 1º de la ESO, que pertenece a la unidad Fracciones del Proyecto ED@D. Esta actividad es autocorrectiva y permite al estudiante practicar y consolidar el cálculo con operaciones combinadas de fracciones. Se proponen diferentes tipos de ejercicios que el estudiante deberá realizar correctamente ya que en caso contrario no podrá pasar a la siguiente operación.
Para insertar dicho objeto digital en una página de nuestro blog, activaremos la edición en HTML y pegaremos el código para abrir en una ventana emergente.
En el apartado materiales del blog de la Red podemos encontrar el código para insertar de la mayoría de actividades. En caso de no disponer del código deberemos actualizarlo escribiendo la dirección web de nuestro recurso y comprobar las dimensiones de la escena. También necesitaremos una imagen desde la cual abrir el recurso. Podemos seleccionar una imagen de la misma unidad (copiando la ruta del enlace) o cualquier otra imagen ya sea desde nuestro ordenador, subiéndola directamente al blog, o desde algún álbum virtual (por ejemplo Picasa).
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri Matemáticas)







 CONTACTO
CONTACTO
