Por Ángel Cabezudo Bueno, 2-febrero-2015

Bienvenidos a Radio Descartes y a la serie de entrevistas al personaje misterioso donde pretendemos mostrar la parte humana de los matemáticos célebres aparte de dar a conocer su contribución a la ciencia.

Hoy entrevistaremos a un genio indiscutible, un personaje de psicología compleja y un científico controvertido en su época. De pensamiento universal y abierto a múltiples áreas del conocimiento pudo aprovecharse de las aportaciones de los científicos que le precedieron y a cambio supo interpretar con más acierto y profundidad los cambios que se producen en la naturaleza. La herramienta de cálculo de la que entonces disponía le resultó insuficiente para expresar sus nuevas formulaciones y tuvo que crear, a su medida, otra más potente.

En ningún momento nos dirigiremos a él por su nombre, pues se trata de que los escuchantes lo descubran con los datos que nos irá aportando a lo largo de la entrevista.

Autores del guion: Ángel Cabezudo Bueno y Xosé Eixo Blanco (ambos de Red Descartes)

Conductor de la entrevista y realizador del podcast: Ángel Cabezudo Bueno

Interpreta al personaje matemático: Xosé Eixo Blanco, profesor de matemáticas en el IES Antón Losada Diéguez de A Estrada (Pontevedra-España). Participa regularmente en ponencias y comunicaciones a congresos  difundiendo la utilización de los recursos del Proyecto Descartes en el aula y reciente colaborador en este blog con artículos donde nos explica a través de sus vídeos las unidades del Proyecto Un_100.

El trabajo lleva licencia CC BY-NC-SA 4.0.

Como os prometimos volvemos sobre el tema de las unidades didácticas de secundaria y bachillerato que se están adaptando a Descartes JS.

Dentro de las publicadas sobre Física y Química tenemos bastantes novedades.

La adaptación de las unidades de Newton al formato JS, válido para todo tipo de dispositivos móviles, está siendo coordinada por Enric Ripoll Mira que realiza un gran trabajo dada la complejidad que presenta en muchos casos este cambio. Gracias Enric por tu trabajo y tu paciencia con los colaboradores que se retrasan.

Desde la última vez que hablamos del tema en el blog, allá por junio, hemos avanzado bastante. Se ha pasado de siete a dieciseis unidades.

Para Física y Química de 3º de ESO disponemos de:

Factores de conversión

El átomo

Para Física y Química de 1º Bachillerato:

Movimiento (I)

Movimiento (II)

Composición de movimientos

Las reacciones químicas

Para Física de 2º bachillerato:

Movimiento Armónico Simple

Campo gravitatorio

Mecánica cuántica

Campo magnético

Teoría de la Relatividad

Movimiento ondulatorio

Para Química de 2º bachillerato:

Ácidos y bases

El equilibrio químico

Termoquímica

Reacciones de transferencia de electrones

Como podéis ver seguimos avanzando y ya tenéis a vuestra disposición una cantidad importante de materiales.

Esperamos que os sean de utilidad

Esta entrada participa en la edición 5.X: Sofia Kovalévskaya del Carnaval de Matemáticas, cuyo blog anfitrión es ::ZTFNews.

El Carnaval de Matemáticas es una iniciativa que tiene por objeto acercar las Matemáticas al público, en general, e intentar mostrar que son más accesibles de lo que aparentan. Para ello, durante una semana al mes, se publican artículos de divulgación matemática en la blogosfera de habla hispana, consiguiendo una mayor densidad de producciones sobre "La reina de las ciencias", como la denominó Carl Friedrich Gauss.

Desde RED Descartes hemos decidido contribuir a esta edición con nuestro pequeño homenaje a la protagonista de este Carnaval, así que os dejamos una entrevista en Radio Descartes, publicada como VI Personaje Misterioso, y un puzle realizado con DescartesJS para tablet, smartphone y cualquier ordenador, que se publicó en su momento como Descubrimos al VI Personaje Misterioso.

¿Se te ocurre mejor forma de conocer a la protagonista de este Carnaval que dialogar con ella?

Esperamos que sea de vuestro agrado.

Podemos estar muy orgullosos de las actividades que realiza la Red Descartes, además de trabajar matemáticas, física o química estamos empezando con otras materias. En esta ocasión vamos a revisar los materiales de idiomas.

A partir de las preguntas de las pruebas propuestas en el primer Estudio Europeo de Competencia Lingüística (EECL), realizado en 2011,se han creado recursos interactivos. Se trata de ocho pruebas en inglés y otras tantas en francés, de las que cuatro son de comprensión lectora y otras cuatro de comprensión oral. Estas escenas interactivas ha sido desarrollados por María José García Cebrian a petición del INEE.

• Enlace a las páginas del proyecto
• Enlace a los materiales
• Los materiales en educaLAB

Como podemos leer en la introducción de la web del proyecto en la que ha sido publicadas:

En su desarrollo se ha sido fiel al marco teórico, al planteamiento y a los procedimientos que se establecieron, introduciéndose interactividad y autocorrección. Estos recursos son funcionales en ordenadores, tabletas y smartphones independientemente del sistema operativo que porten, y constituyen un excelente instrumento didáctico para el aprendizaje de idiomas, en cualquiera de los cursos de la Educación Secundaria obligatoria, aunque inicialmente fueran diseñados para su aplicación en 4º curso.

Con la traslación y presentación de estos materiales como recursos TIC se busca aprovechar estas tecnologías para conseguir una amplia difusión del trabajo realizado y, adicionalmente, contribuir a que el alumnado y el profesorado dispongan no solo de una fuente informativa, sino que esta sea también formativa

Así pues, disponemos de actividades interactivas para autoevaluar el aprendizaje en inglés y francés.

Aunque la utlización de los materiales es muy sencillo os dejamos un vídeo:

Bien, ¿a qué esperas?, demuestra lo que sabes

Versión actual

Podemos estar muy orgullosos de las actividades que realiza la Red Descartes, además de trabajar matemáticas, física o química estamos empezando con otras materias. En esta ocasión vamos a revisar los materiales de idiomas.

A partir de las preguntas de las pruebas propuestas en el primer Estudio Europeo de Competencia Lingüística (EECL), realizado en 2011,se han creado recursos interactivos. Se trata de ocho pruebas en inglés y otras tantas en francés, de las que cuatro son de comprensión lectora y otras cuatro de comprensión oral. Estas escenas interactivas ha sido desarrollados por  María José García Cebrian  a petición del INEE.

Enlace a las páginas del proyecto

Enlace a los materiales

Los materiales en educaLAB

 Como podemos leer en la introducción de la web del proyecto en la que ha sido publicadas:

En su desarrollo se ha sido fiel al marco teórico, al planteamiento y a los procedimientos que se establecieron, introduciéndose interactividad y autocorrección. Estos recursos son funcionales en ordenadores, tabletas y smartphones independientemente del sistema operativo que porten, y constituyen un excelente instrumento didáctico para el aprendizaje de idiomas, en cualquiera de los cursos de la Educación Secundaria obligatoria, aunque inicialmente fueran diseñados para su aplicación en 4º curso.

Con la traslación y presentación de estos materiales como recursos TIC se busca aprovechar estas tecnologías para conseguir una amplia difusión del trabajo realizado y, adicionalmente, contribuir a que el alumnado y el profesorado dispongan no solo de una fuente informativa, sino que esta sea también formativa

Así pues, disponemos de actividades interactivas para autoevaluar el aprendizaje en inglés y francés.

Aunque la utlización de los materiales es muy sencillo os dejamos un vídeo:

Bien, ¿a qué esperas?, demuestra lo que sabes

Bienvenidos a Radio Descartes y a la serie de entrevistas al personaje misterioso donde pretendemos mostrar la parte humana de los matemáticos célebres aparte de dar a conocer su contribución a la ciencia.

Hoy entrevistamos a una imaginativa y genial mujer nacida en Londres en 1815: en la actualidad es considerada madre de la programación de ordenadores y por tanto una adelantada en más de 100 años a su tiempo pues entonces la electricidad, verdadera energía que ha permitido el desarrollo de la informática, estaba aún siendo ensayada y estudiada científicamente y su uso no formaba parte de los planes de la tecnología de la época.

No desvelaremos su nombre hasta una semana más tarde en este mismo blog a través de la imagen de un puzle, como hemos venido haciendo con los personajes precedentes. Los escuchantes del podcast que se acompaña sois los que tenéis que descubrirla a través de datos que iremos aportando a lo largo de la entrevista.

Autor del guion, conductor de la entrevista y realizador del podcast: Ángel Cabezudo Bueno

Interpreta al personaje matemático femenino: Montse Gelis Bosch (profesora de matemáticas en el INS Montsacopa de Olot en Girona y colaboradora semanal en este blog donde a través de sus artículos y sus videos nos explica cómo se pueden utilizar con los alumnos los distintos materiales de Descartes integrándolos en cursos Moodle)

Los efectos especiales pertenecen al Banco de sonidos del INTEF-MECD-ESPAÑA, tienen licencia CC BY-NC-SA 3.0 y han sido adaptados para esta ocasión.

El trabajo lleva licencia CC BY-NC-SA 4.0.

En esta entrevista descubrimos la relación entre cine y matemáticas. ¿Hay muchas películas donde aparezcan las matemáticas? ¿Cómo se utilizan las matemáticas en las películas? ¿Qué tipos de películas tienen matemáticas? ¿Hay muchos personajes matemáticos? ¿Cómo podemos utilizar estas películas en nuestras aulas? Las respuestas a todas estas preguntas las encontrarás en nuestra entrevista.

José Mª Sorando es profesor de Matemáticas en la Educación Pública desde hace 35 años. Premio Santillana 2010 de experiencias docentes. Ha desarrollado actividades dentro y fuera del aula, ha escrito artículos, y ha impartido conferencias, todo ello entorno a la didáctica y a la divulgación. Siempre, intentando mostrar unas matemáticas útiles, amables y atractivas, para así vencer la resistencia que muchos tienen ante ellas.

Nuestro entrevistado tiene una mágnifica web donde encontraremos más de 200 películas clasificadas en relación con las matemáticas. Su dirección: http://catedu.es/matematicas_mundo/CINE/cine.htm

Y la entrevista paso a paso:

1. Presentación. 1:12
2. ¿Hay muchas matemáticas en el cine? 2:22
3. Tengo entendido que tienes una magnifica página web donde consultar todo tipo de películas relacionadas con las matemáticas, ¿Puedes decirnos su dirección (URL)? Una vez dentro de la web ¿cómo buscamos el material de matemáticas que tienen las películas? 5:36
4. ¿Qué película o porción de película que contenga matemáticas te gusta más? ¿Por qué? 6:42
5. ¿Pueden utilizarse las películas que tienes recopiladas en tu web en el aula de cualquier profesor? ¿Cómo? 8:05
6. Además de las películas en tu web tienes publicados varios artículos sobre el cine y las matemáticas en varios medios. Todo ello lo pones a disposición de cualquier cibernauta que navegue por tu red. ¿No crees que cualquiera puede apropiarse de tu trabajo? 9:32
7. ¿Qué me dices de las series de TV? ¿Hay alguna en la que aparezcan de forma asidua las matemáticas? 11:25
8. ¿Nos recomiendas una película para ver el próximo fin de semana? Por supuesto, en la que podamos disfrutar también de las matemáticas. 12:34

En esta ocasión, para adentrarnos en la estructura interna de una miscelánea, haremos una síntesis de la documentación técnica y de usuario de Descartes v5, analizando simultáneamente el editor de escenas y el código que genera.

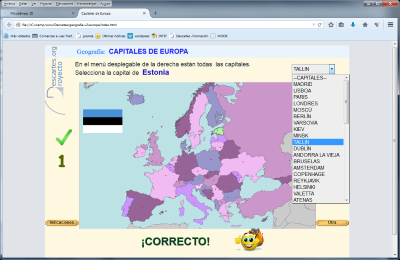
Si navegamos por la página Capitales de Europa y observamos el código fuente de la misma vemos que las primeras líneas de este es lo que muestra la imagen siguiente.

Los parámetros de la etiqueta <ajs> de apertura de la escena y los valores de la configuración base se establecen seleccionando la opción de menú: "Botones" en el Editor de Escenas y marcando/desmarcando o eligiendo las características que queremos para nuestra utilidad según se muestra a continuación.

En el vídeo del artículo anterior mostramos como crear los espacios de dos dimensiones: R2 y HTMLIFrame que van a contener a los diversos protagonistas de la escena. En el gráfico inicial se observa el código generado con aquellas acciones. Conviene señalar que se han creado seis espacios, que el principal es el primero, con id = E1, y que en el código todos los espacios comienzan con: <param name=E...

Ahora pasamos a la opción de menú: Controles, aquí definimos los botones, campos de texto, pulsadores etc... que vayamos a necesitar. En nuestro caso particular hemos definido controles para los botones: Otra, Indicaciones,Finalizar y Continuar. También hemos definido dos controles que su única función es contener un gráfico y hemos introducido un cambio respecto al código publicado anteriormente, hemos definido un control tipo menú según muestra esta imagen,

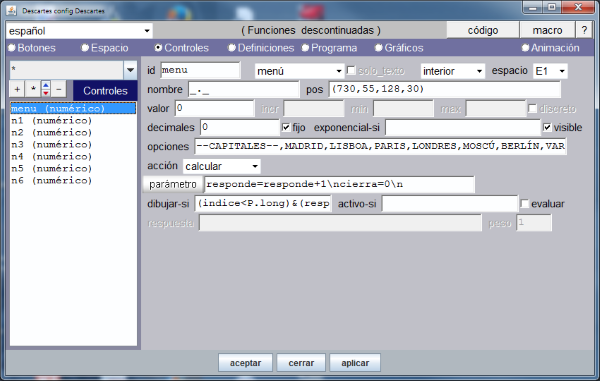
La introducción del control tipo menú ha sido debida a que vamos a elaborar una nueva versión de la utilidad basada en la selección del nombre de la capital en un menú desplegable que muestra todas las capitales administrativas del continente; en lugar de en el evento click sobre un punto en un gráfico como sucedía en la primera versión. Así conocemos si la persona que usa la utilidad ha memorizado el nombre de la capital del país y puede identificar en un mapa mudo el lugar donde está esa capital. Los resultados obtenidos con este cambio son los que pueden observarse siguiendo el siguiente enlace

El código producido por la opción Controles de esta nueva versión es:

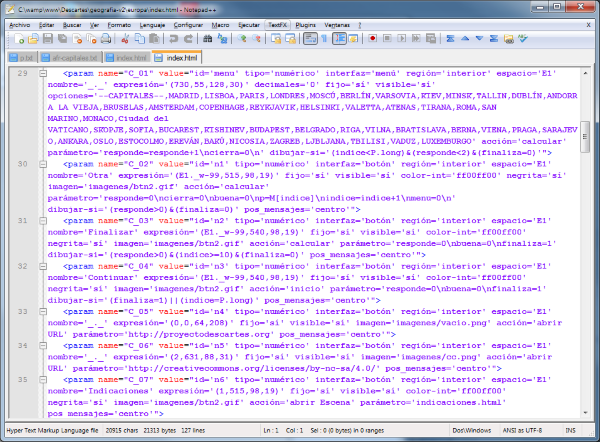
Que debe analizarse y comparar con el código de la versión anterior para apreciar las diferencias. También es conveniente observar el funcionamiento de esta versión de la utilidad para posteriormente poder comprender el significado de cada línea de código contrastandolo con el de la primera versión.

Llegados a este punto se muestra la necesidad de tener una idea clara de como deseamos que reaccione la utilidad que estamos creando a las acciones procedentes de la interactividad, esto se traduce en que debemos tener perfectamente definido cuando queremos que un control se muestre o se oculte, como y cuando debe reaccionar el control ante un evento etc, etc es decir debemos tener un buen guión para la utilidad.
En la práctica lo anterior se traduce, entre otras acciones, en que debemos tener definidas las variables necesarias para controlar las situaciones que puedan producirse. Por ejemplo en el gráfico donde se muestra el control menú puede observarse que el campo de texto parámetro tiene el contenido: responde=responde+1\ncierra=0\n el significado de esto es que cuando hagamos una selección entre las opciones del menú, el valor de la variable responde se incrementa en uno y la variable cierra toma el valor 0. Más adelante veremos como y donde se definen las variables pero todo el que tenga interés en la creación de utilidades debe acudir a la documentación que se enlaza al comienzo del artículo donde hay explicaciones más explícitas y documentadas sobre el tema.

En siguientes artículos se continuará con la explicación del código generado por las opciones: Definiciones, Programa y Gráficos del menú principal del Editor de Escenas para la elaboración de la utilidad.

Creamos un Libro Digital de Moodle con Objetos interactivos Descartes.

Hoy presentamos una serie de objetos interactivos de la Red Educativa Digital Descartes para el estudio de las Funciones en 4º de la ESO.

En concreto trabajaremos con una selección de ejercicios que forman parte de la unidad Funciones y gráficas perteneciente al Proyecto ED@D.

Para su aplicación en el aula vamos a utilizar el recurso Libro Digital de Moodle en cuyos capítulos se insertarán de forma embebida los diferentes objetos.

También incluiremos en el Libro Digital dos unidades de Formación Competencial: Tarifas postales y Velocidad de un coche de carreras.

En el siguiente vídeo se muestran las actividades seleccionadas y los pasos a seguir para embeberlas en el Libro Digital.

En algunas ocasiones nos resulta mucho más cómodo disponer de algo en nuestro blog que tener que buscarlo, y si tienes que hacerlo con toda una clase más aun.

Disponemos de dos opciones para poner un juego en nuestro blog, enlazarlo o incrustarlo. Los juegos están creados con un tamaño demasiado grande para el espacio que te ofrece el blog y al insertarlo solo se verá una parte. La mejor solución es enlazar el juego para que se abra en otra ventana. Utilizaremos como ejemplo el juego "Dos puentes". Entrando en él, vamos a la versión que nos interese, por ejemplo la de ficheros, y copiamos la dirección web.

Para ello seleccionamos las palabras que formarán el enlace y pinchamos en enlace en el editor. Pegamos la dirección del juego y seleccionamos la opción de abrir en otra ventana:

Enlace al juego

Otra opción es la de poner un imagen y que pinchando sobre ella se abra el juego. Solo tendremos que pinchar en la imagen y, una vez seleccionada, hacer clic en enlace y pegar la dirección. Habrá que indicarlo en el texto de la entrada. Pincha sobre la imagen para acceder al juego.

Vamos a ahora con la otra opción, ya hemos comentado que no es del todo satisfactoria pero permite ver el juego y además nos sirve para hacerlo en Moodle editando una página. Para insertar un juego en una entrada solo tenemos que poner el siguiente código

<iframe src="/descartescms/dirección_del_juego.html" style="height: 500px; width: 650px;"></iframe&gt

Cambiando la parte del enlace en la que pone dirección del juego por la del juego que nos interese. En nuestro ejemplo: http://newton.proyectodescartes.org/juegosdidacticos/images/juegos/unzip-juegos/jug-dos_puentes/dos_puentes-fich.html, quedaría así:

<iframe src="http://newton.proyectodescartes.org/juegosdidacticos/images/juegos/unzip-juegos/jug-dos_puentes/dos_puentes-fich.html" style="height: 500px; width: 650px;"></iframe&gt

Este código tenemos que pegarlo en la entrada pero utilizando la vista HTML. Pinchamos arriba a la izquierda, junto a Redactar ejn el botón HTML y pegamos el código. Lo mejor es hacerlo al final para no modificar nada de lo ya escrito. Haciendo clic en el botón Redactar todo volverá a verse como antes. Puedes modificar el tamaño, en el ejemplo es de 500 píxeles de alto y 650 de ancho, con modificar los números podrás ajustarlo a tus necesidades. Aquí tenéis un vídeo con todo el proceso:

Con el frío de diciembre nos viene bien un buen libro que poder leer, calentitos en casa. Hoy presentamos cuatro libros para diferentes edades. Para los más pequeños, diversas historias cuyos personajes son los propios números u objetos matemáticos que explican y hacen más entretenido el aprendizaje de sus propiedades. Para la siguiente etapa, también cobran vida los números y las rectas y curvas. Todos ellos incluidos en obras de teatro muy divertidas. Con el tercer libro descubriremos la historia de las matemáticas en sus personajes, a través de un cómic. Y por último para los mayores, nos adentraremos en el mundo del descubridor del último teorema de Fermat.

En el siguiente vídeo descubrirás todos los detalles de estos libros.